Компьютерная графика
Лекция 1.
Введение.
При обработке информации, связанной с изображением на мониторе, принято выделять три основных направления: распознавание образов, обработку изображений и машинную графику.
Основная задача распознавания образов состоит в преобразовании уже имеющегося изображения на формально понятный язык символов. Распознавание образов или система технического зрения (COMPUTER VISION) – совокупность методов, позволяющих получить описание изображения, поданного на вход, либо отнести заданное изображение к некоторому классу (так поступают, например, при сортировке почты). Одной из задач COMPUTER VISION является так называемая склетизация объектов, при которой восстанавливается некая основа объекта, его «скелет».
Обработка изображений (IMAGE PROCESSING) рассматривает задачи в которых и входные и выходные данные являются изображениями. Например, передача изображения с устранением шумов и сжатием данных, переход от одного вида изображения к другому (от цветного к черно белому) и т.д.
Компьютерная (машинная) графика (COMPUTER GRAPHICS) воспроизводит изображение в случае, когда исходной является информация неизобразительной природы. Например, визуализация экспериментальных данных в виде графиков, гистограмм или диаграмм, вывод информации на экран компьютерных играх, синтез сцен на тренажерах.
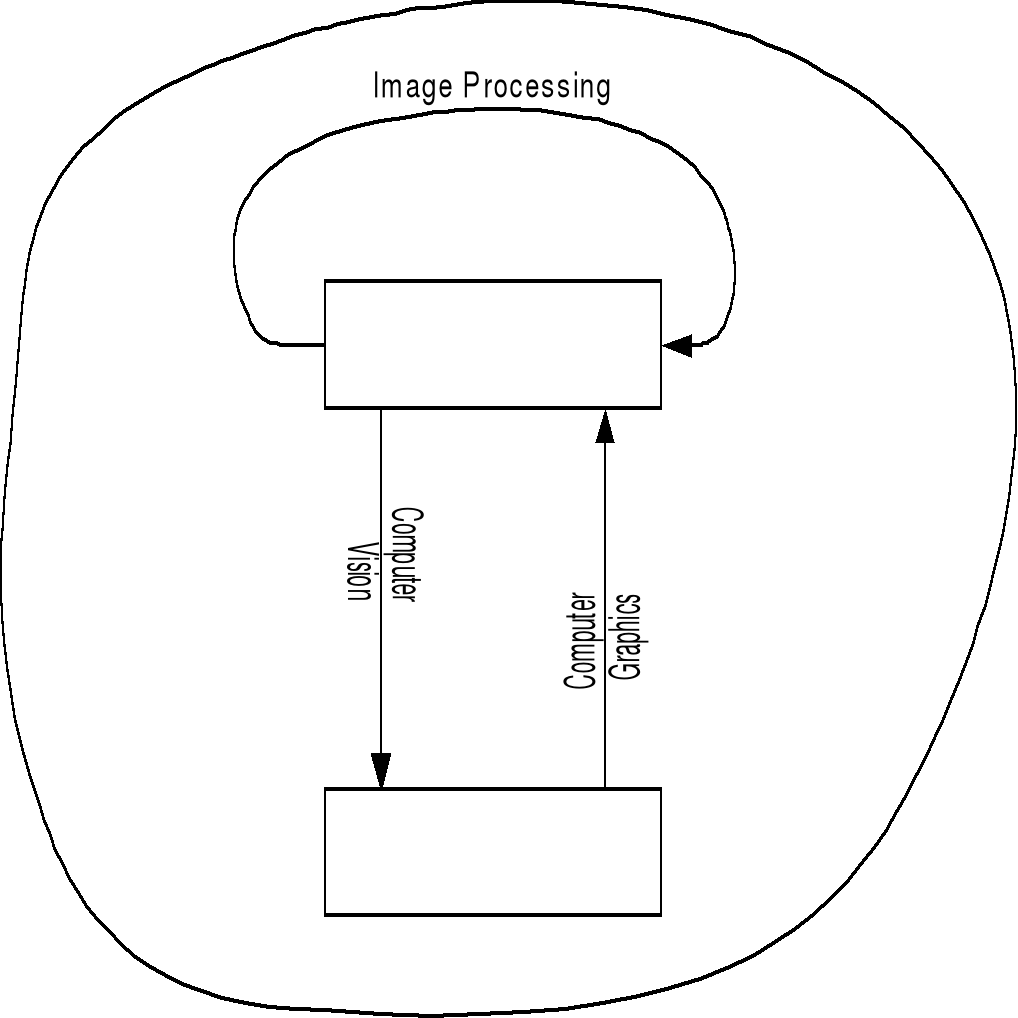
Рис. 1.1
Компьютерная графика – это наука, предметом изучения которой является создание, хранение и обработка моделей и их изображений с помощью ЭВМ. В том случае, если пользователь может управлять характеристиками объектов, говорят об интерактивной
компьютерной графике
Геометрические преобразования
Координаты и преобразования
Описание, конструирование, манипулирование и представление геометрических объектов являются центральными работами в графических системах. Их поддержка в требуемом объеме за счет соответствующих математических методов, алгоритмов и программ оказывают существенное влияние на возможности и эффективность графической системы. В данном разделе будут рассмотрены математические методы для описания геометрических преобразований координат в двух и трехмерном случае, будут обсуждены некоторые вопросы эффективности, рассмотрены геометрические преобразования растровых картин.
Далее большими буквами X, Y, Z будут обозначаться обычные декартовые координаты, а маленькие буквы x, y, z будут использоваться для обозначения т.н. однородных координат.
Двумерные геометрические преобразования
Параллельный перенос
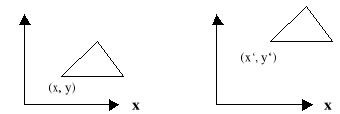
Параллельный перенос в плоском случае имеет вид:
x` = x + Dx
y` = y + Dy
[x’, y’] = [x, y] + [Dx, Dy]
P’ P T
или в векторной форме:
где P` = [x` y`] - вектор-строка преобразованных координат,
где x, y - исходные координаты точки,
Tx, Ty - величина сдвига по осям,
x`, y` - преобразованные координаты.
P = [x y] -- вектор-строка исходных координат,
P` = [x` y`] -- вектор-строка преобразованных координат,
T = [Tx Ty] -- вектор-строка сдвига.
Масштабирование
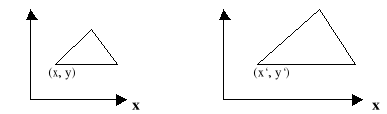
Преобразование масштабирования относительно начала координат имеет вид:
x` = x ·Sx
y` = y ·Sy или
Sx 0
[x`, y`] = [x, y] ·
0 Sy
P` P
S
или в матричной форме:
где Sx, Sy -- коэффициенты масштабирования по осям, а
S - матрица масштабирования
Поворот
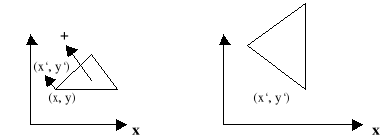
Преобразование поворота относительно начала координат имеет вид:
x`= x·cos() – y·sin()
y`= x·sin() + y·cos()
или
cos() sin()
[x`, y`] = [x, y] ·
–sin() cos()
P` P
R
Где R – матрица поворота
– положительный угол поворота
или в матричной форме:
Столбцы и строки матрицы поворота представляют собой взаимно ортогональные единичные векторы. В самом деле квадраты длин векторов-строк равны единице:
|
(-sinf) ·(-sinf)+cosf·cosf = 1,
|
а скалярное произведение векторов-строк есть
|
cosf·(-sinf) + sinf·cosf = 0.
|
Так как скалярное произведение векторов A ·B = |A| ·|B| ·cosy, где |A| - длина вектора A, |B| - длина вектора B, а y - наименьший положительный угол между ними, то из равенства скалярного произведения двух векторов-строк длины 1 следует, что угол между ними равен 90°.
Аналогичное можно показать и для векторов-столбцов. Кроме того вектора-столбцы представляют собой такие единичные векторы, которые после выполнения преобразования, заданного этой матрицей, совпадут с осями. В самом деле, произведение первого столбца на матрицу есть
|
|
|
|
cosf
|
-sinf
|
|
|
·
|
|
|
cosf
|
sinf
|
|
|
=
|
|
|
1 0
|
|
|
|
,
|
|
|
|
|
|
|
|
|
|
|
|
|
-sinf
|
cosf
|
|
|
|
|
|
|
|
|
|
|
т.е. это единичный вектор вдоль оси X.
Аналогично, произведение второго столбца на матрицу даст вектор [ 0 1 ]. Это позволяет сформировать матрицу, если известны результаты преобразования.
Преобразование в однородную систему координат
Как видно двумерные преобразования имеют различный вид. Сдвиг реализуется сложением, а масштабирование и поворот - умножением. Это различие затрудняет формирование суммарного преобразования и устраняется использованием двумерных однородных координат точки, имеющих вид:
Здесь W - произвольный множитель не равный 0.
Двумерные декартовые координаты точки получаются из однородных делением на множитель W:
|
x = X / W, y = Y / W, W 0
|
|
Однородные координаты можно представить как промасштабированные с коэффициентом W значения двумерных координат, расположенные в плоскости с Z = W.
В силу произвольности значения W в однородных координатах не существует единственного представления точки, заданной в декартовых координатах.
Преобразования параллельного переноса, масштабирования и поворота в однородных координатах относительно центра координат все имеют одинаковую форму произведения вектора исходных координат на матрицу преобразования.
Будем брать W=1.
Параллельный перенос:
1 0 0
[X`, Y`, 1]=[X, Y, 1] 0 1 0
Dx Dy 1
Перемножив, получим: [X + Dx, Y + Dy, 1].
Масштабирование:
P` = P·S; где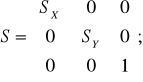
Поворот:
Рё = Р·R; где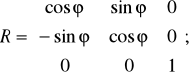
Поворот вокруг фиксированной точки