Растровые представления изображений

Лекция 2

Растровые представления изображений.

Цифровое изображение – набор точек (пикселей) изображения; каждая точка изображения характеризуется координатами x и y и яркостью V(x,y), это дискретные величины, обычно целые. В случае цветного изображения, каждый пиксель характеризуется координатами x и y, и тремя яркостями: яркостью красного, яркостью синего и яркостью зеленого (VR , VB , VG). Комбинируя данные три цвета можно получить большое количество различных оттенков.

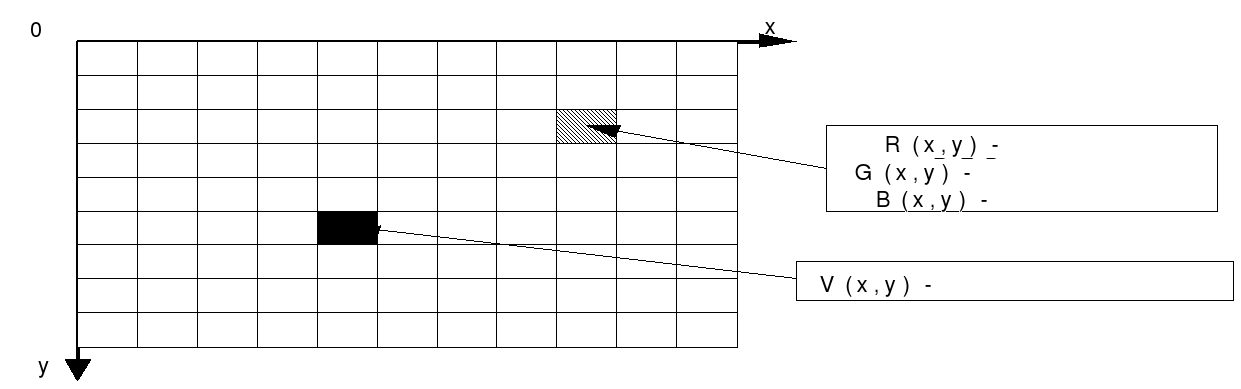
Рис. 2.1.1

Под градацию яркости обычно отводится 1 байт, причем 0 – черный цвет, а 255 – белый (максимальная интенсивность). В случае цветного изображения отводится по байту на градации яркостей всех трех цветов. Возможно кодирование градаций яркости другим количеством битов (4 или 12), но человеческий глаз способен различать только 8 бит градаций на каждый цвет, хотя специальная аппаратура может потребовать и более точную передачу цветов.

Цветовое пространство, образуемое интенсивностями красного, зеленого и синего, представляют в виде цветового куба.

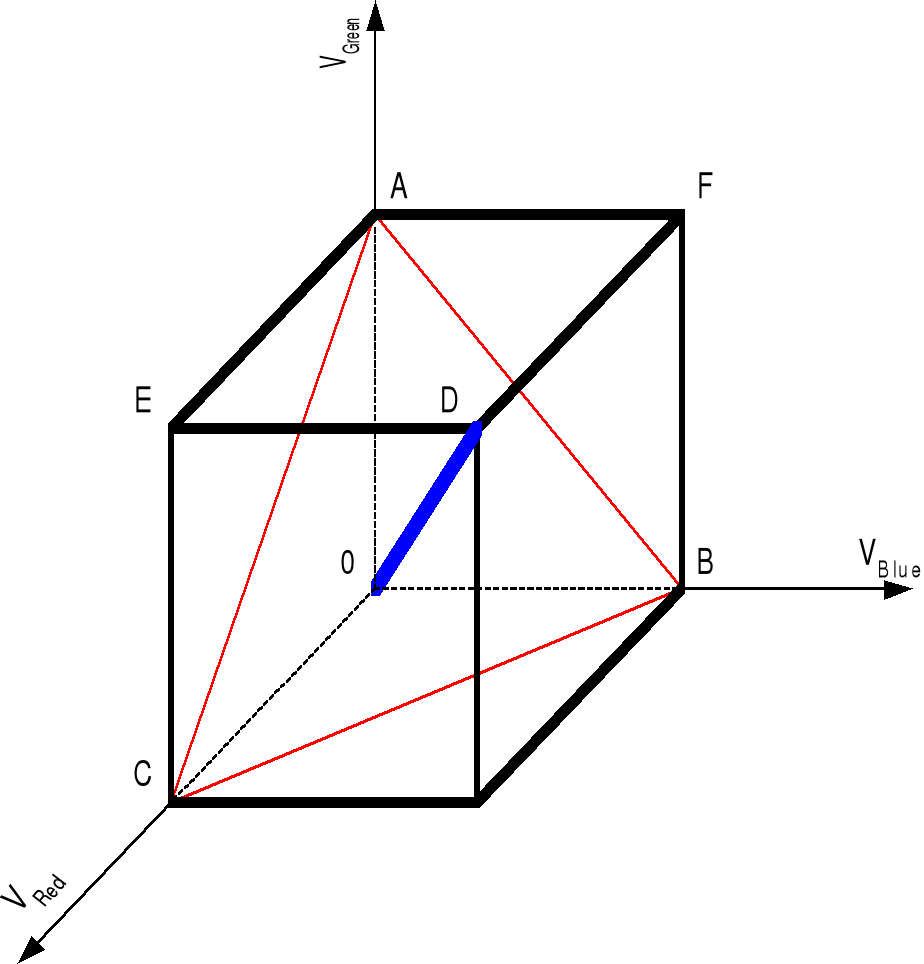
Рис. 2.1.2 «Цветовой Куб»

Вершины куба A, B, C являются максимальными интенсивностями зеленого, синего и красного соответственно, а треугольник которые они образуют называется треугольником Паскаля периметр этого треугольника соответствует максимально насыщенным цветам. На отрезке OD находятся оттенки серого, причем тока O соответствует черному, а точка D белому цвету.

Растр – это порядок расположения точек (растровых элементов). На рис. 2.1.1 изображен растр элементами которого являются квадраты, такой растр называется квадратным, именно такие растры наиболее часто используются. Хотя возможно использование в качестве растрового элемента фигуры другой формы, соответствующего следующим требованиям:

1. Все фигуры должны быть одинаковые;

2. Должны полностью покрывать плоскость без наезжания и дырок.

Так в качестве растрового элемента возможно использование равностороннего треугольника рис. 2.1.3, правильного шестиугольника (гексаэдра) рис. 2.1.4. Можно строить растры, используя неправильные многоугольники, но практический смысл в подобных растрах отсутствует.

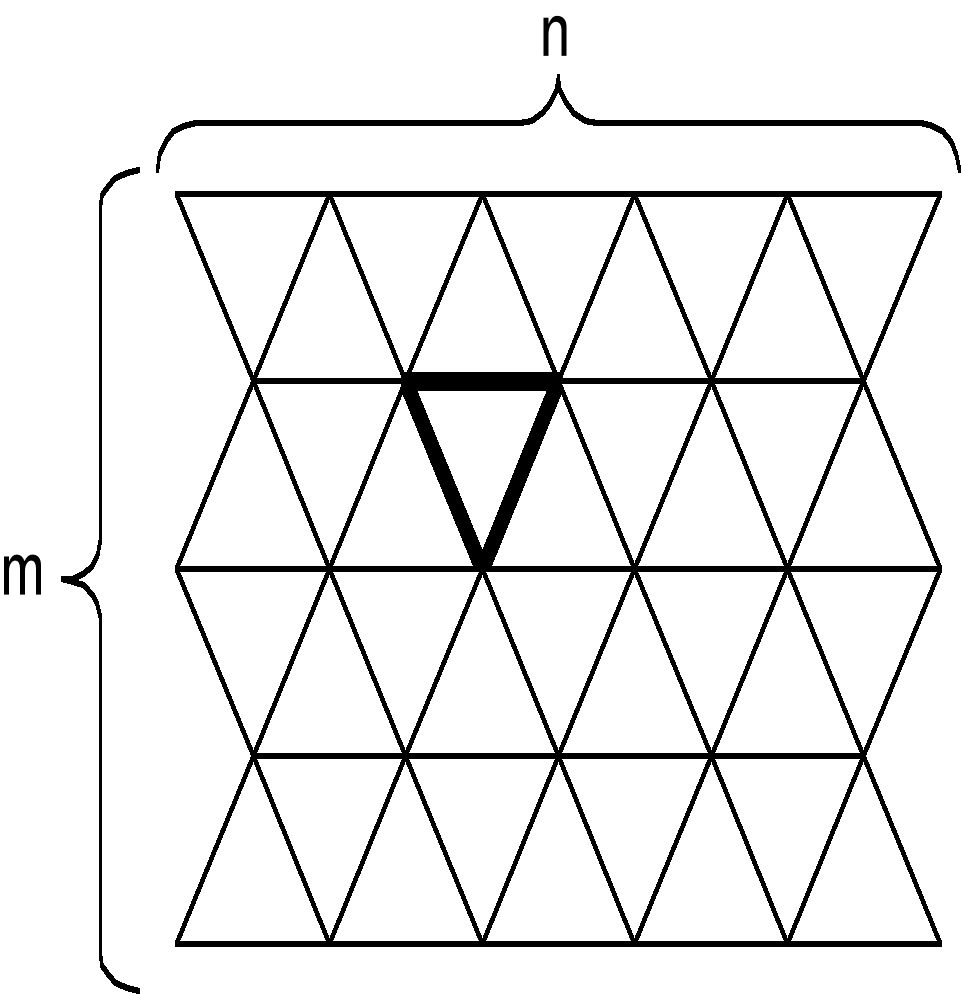
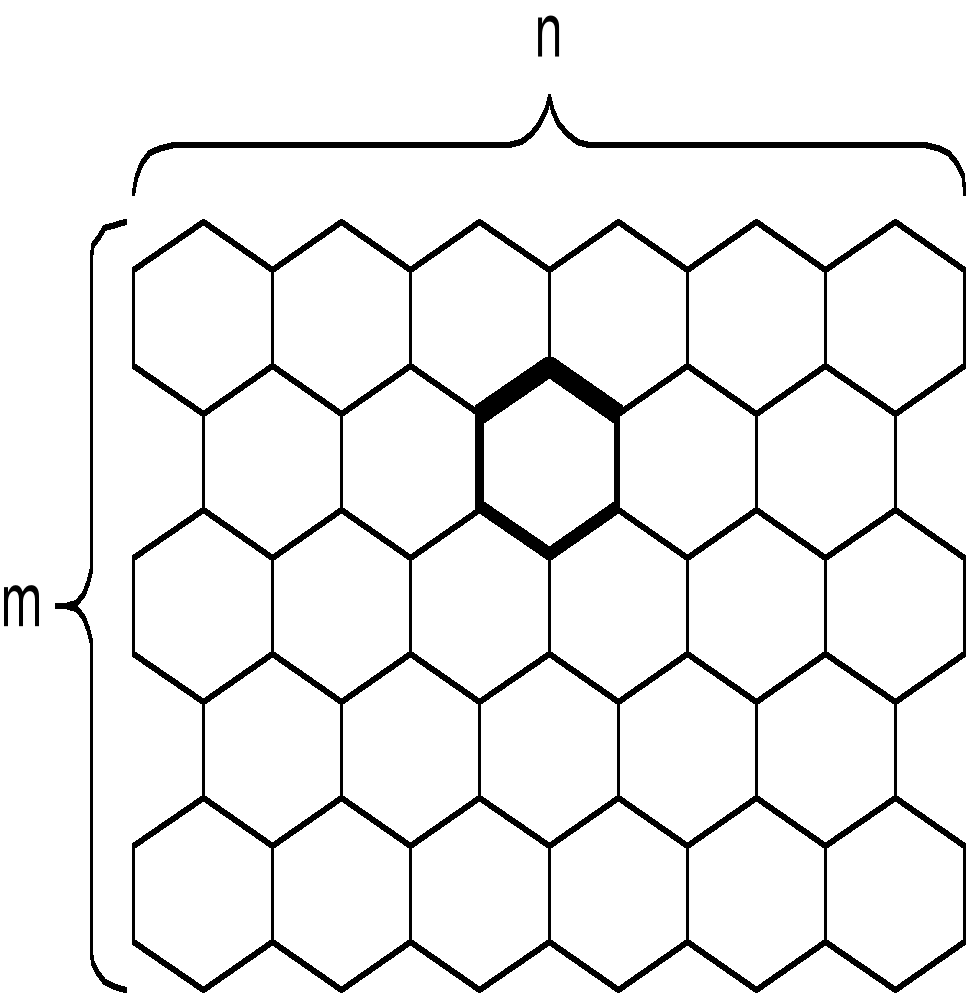
Рис. 2.1.3 «Треугольный растр» Рис. 2.1.4 «Гексагональный растр»

Рассмотрим способы построения линий в прямоугольном и гексагональном растре.

В квадратном растре построение линии осуществляется двумя способами:

1) Результат – восьмисвязная линия. Соседние пиксели линии могут находится в одном из восьми возможных (см. рис. 2.1.5а) положениях. Недостаток – слишком тонкая линия при угле 45°.

2) Результат – четырехсвязная линия. Соседние пиксели линии могут находится в одном из четырех возможных (см. рис. 2.1.5б) положениях. Недостаток – избыточно толстая линия при угле 45°.

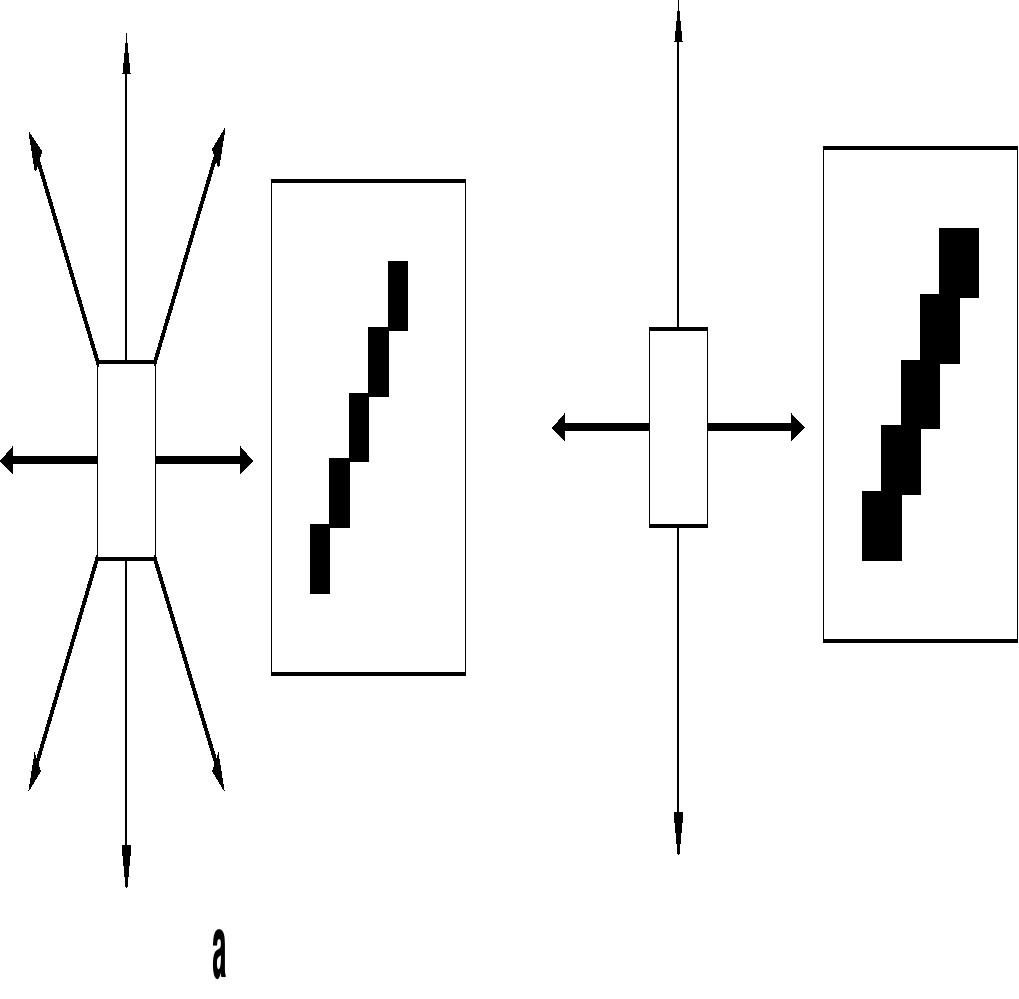
Рис. 2.1.5 «Построение линии в прямоугольном растре»

В гексагональном растре линии шестисвязные (см. рис. 2.1.6) такие линии более стабильны по ширине, т.е. дисперсия ширины линии меньше, чем в квадратном растре.

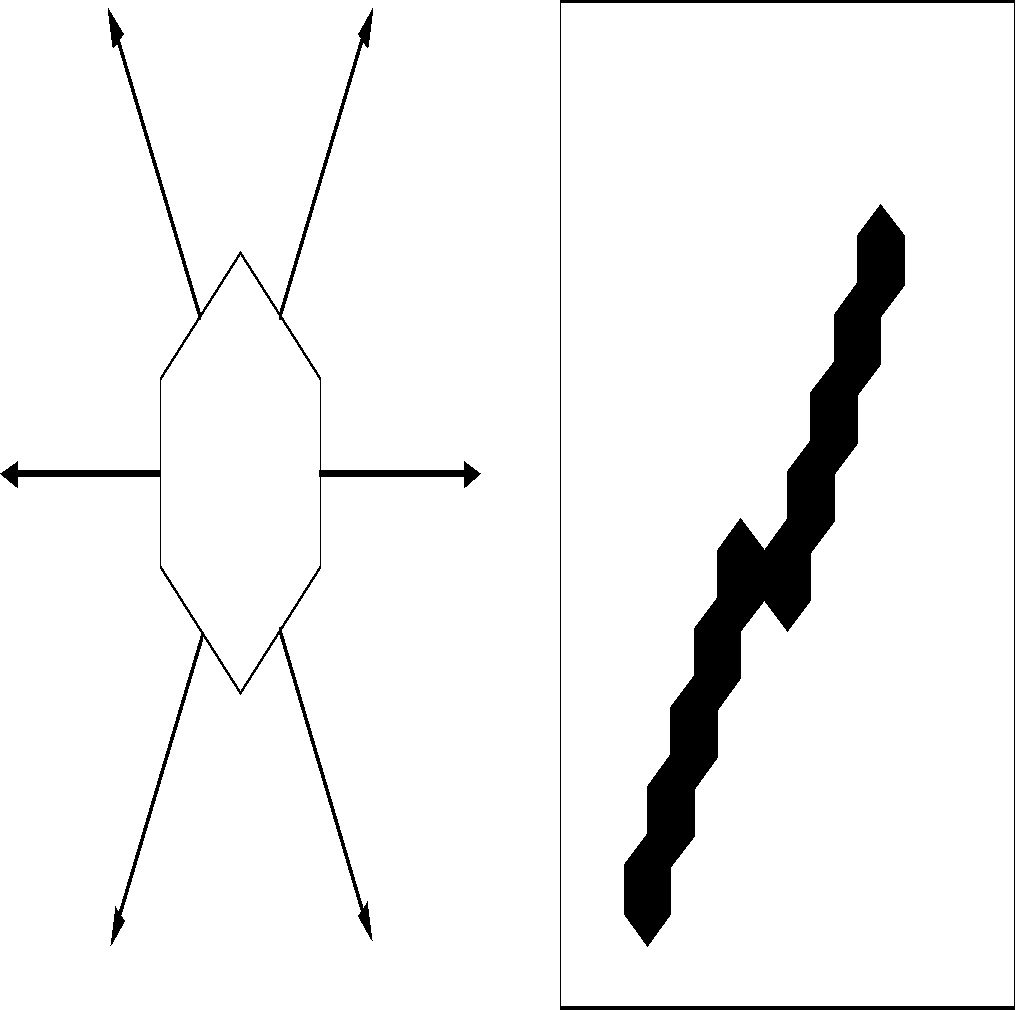
Рис. 2.1.6 «Построение линии в гексагональном растре»

Каким образом можно оценить, какой растр лучше?

Одним из способов оценки является передача по каналу связи кодированного, с учетом используемого растра, изображения с последующим восстановлением и визуальным анализом достигнутого качества. Экспериментально и математически доказано, что гексагональный растр лучше, т.к. обеспечивает наименьшее отклонение от оригинала. Но разница не велика.

Моделирование гексагонального растра.

Возможно построение гексагонального растра на основе квадратного. Для этого гексаугольник представляют в виде прямоулогьника (см. рис. 2.1.7).

Определим, какие пропорции должно иметь гексагональное изображение?

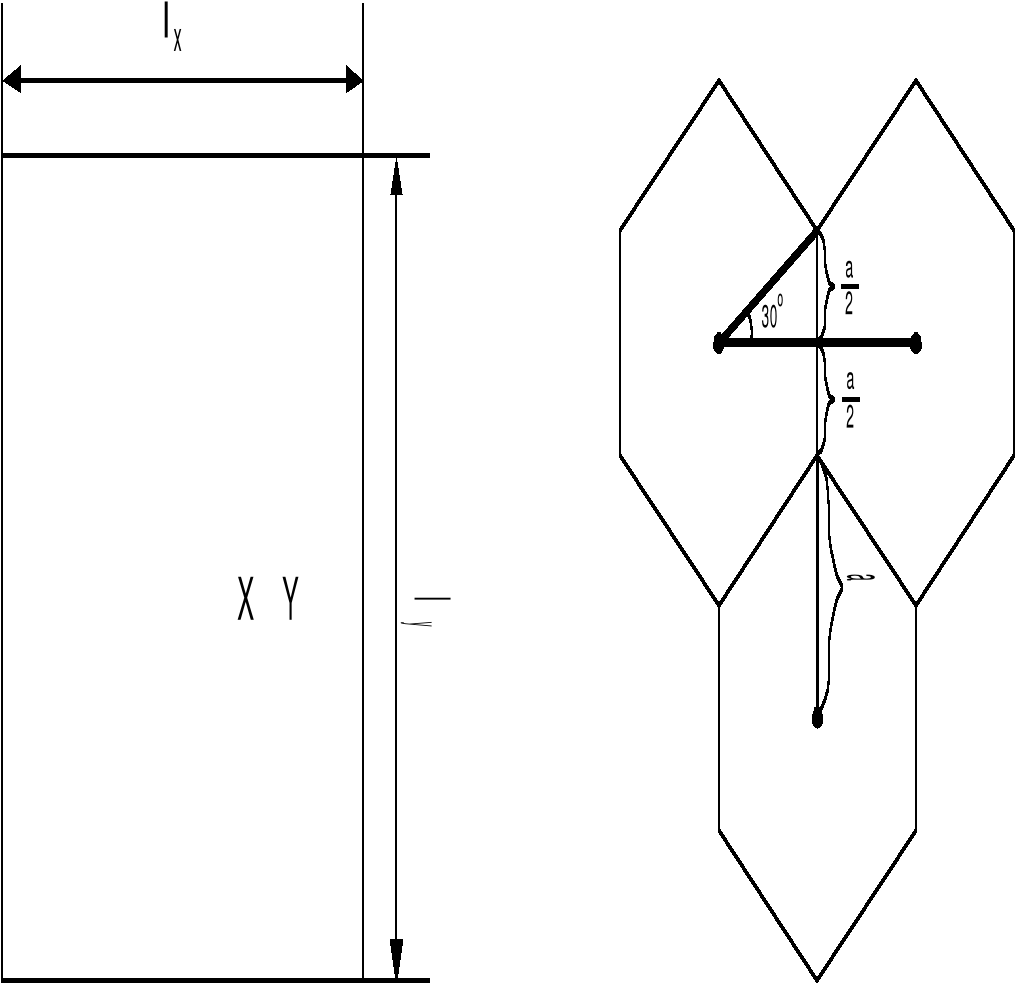
Рис. 2.1.8

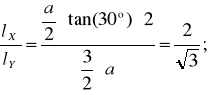
Можно получить модель гексагонального растра из прямоугольного, задержав на 1 пиксель каждую нечетную строчку изображения, и растянув изображение на экране таким образом, чтобы 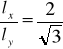. Это чисто аппаратный метод.

Рис. 2.1.7 «Построение гексагонального растра на квадратном»

Тот факт, что гексагональный растр не используется, объясняется следующими причинами:

1. некоторое усложнение алгоритмов;

2. преимущество гексагонального растра не очень велико;

3. историческая ориентация на прямоугольный растр.

Для программного построения гексагонального растра в квадратном можно использовать модель представленную на рис. 2.1.8.

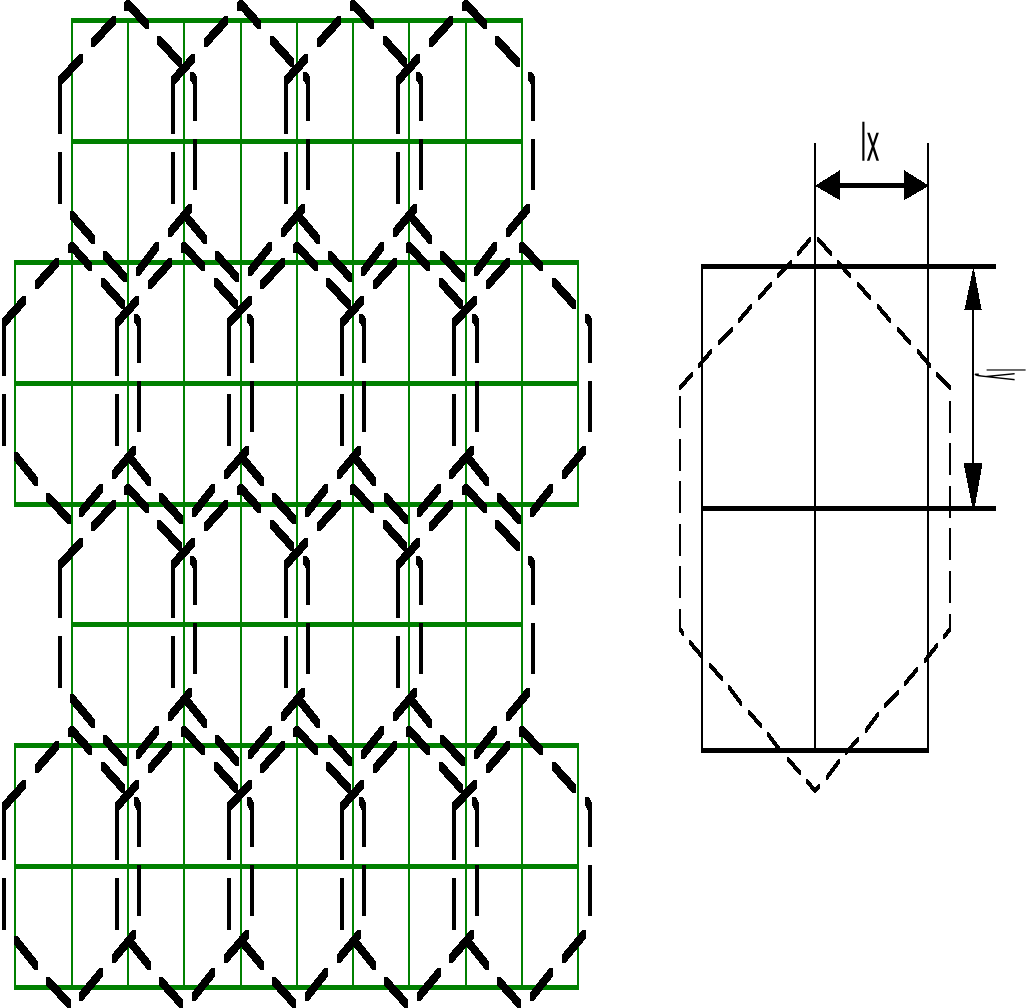
Рис. 2.1.8 «Построение гексагонального растра в квадратном»

Построение линии в квадратном растре.

Поскольку экран растрового дисплея с электронно-лучевой трубкой (ЭЛТ) можно рассматривать как матрицу дискретных элементов (пикселей), каждый из которых может быть подсвечен, нельзя непосредственно провести отрезок из одной точки в другую. Процесс определения пикселей, наилучшим образом аппроксимирующих заданный отрезок, называется разложением в растр. В сочетании с процессом построчной визуализации изображения он известен как преобразование растровой развертки. Для горизонтальных, вертикальных и наклоненных под углом 45° отрезков выбор растровых элементов очевиден. При любой другой ориентации выбрать нужные пиксели труднее, что показано на рис. 2.2.1.

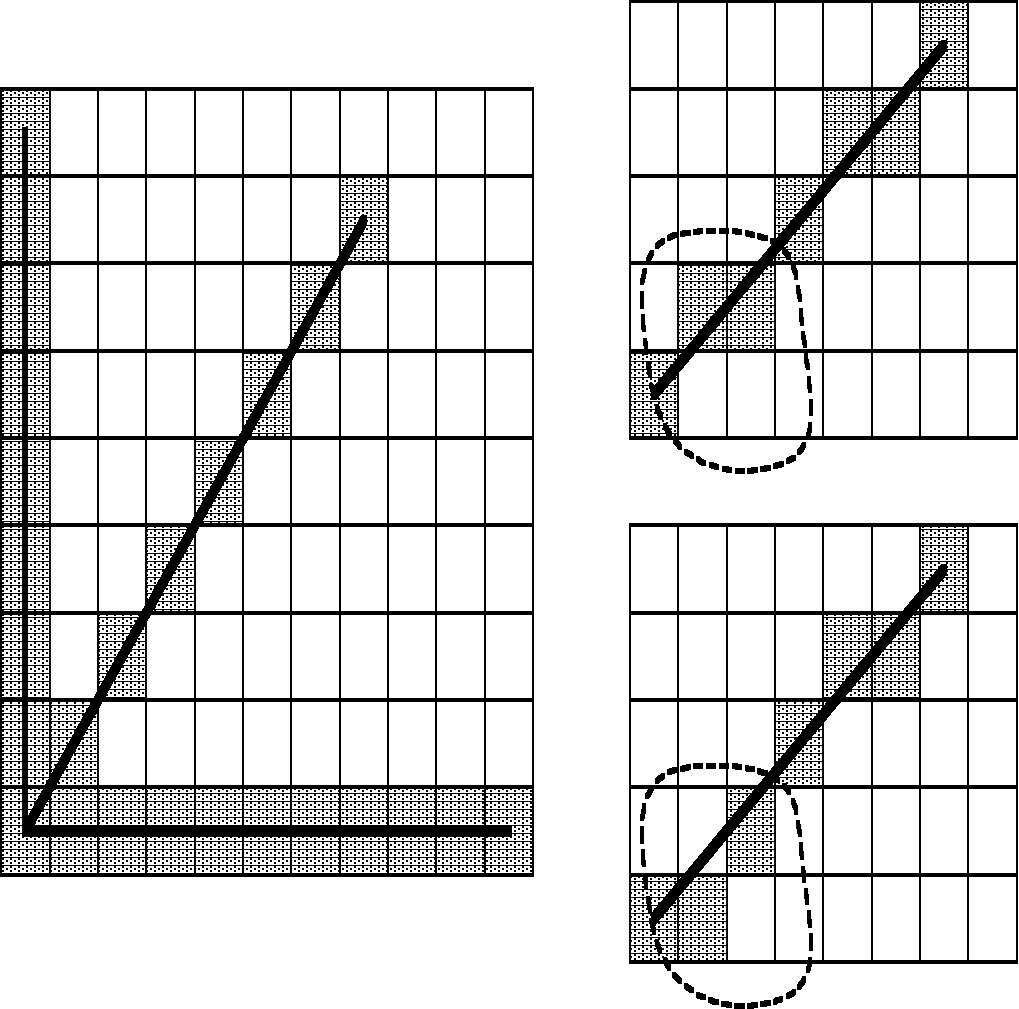
Рис. 2.2.1 «Разложение в растр отрезков»

Общие требования к изображению отрезка.

· концы отрезка должны находиться в заданных точках;

· отрезки должны выглядеть прямыми,

· яркость вдоль отрезка должна быть постоянной и не зависеть от длины и наклона.

Ни одно из этих условий не может быть точно выполнено на растровом дисплее в силу того, что изображение строится из пикселов конечных размеров, а именно:

· концы отрезка в общем случае располагаются на пикселах, лишь наиболее близких к требуемым позициям и только в частных случаях координаты концов отрезка точно совпадают с координатами пикселов;

· отрезок аппроксимируется набором пикселов и лишь в частных случаях вертикальных, горизонтальных и отрезков под 45° они будут выглядеть прямыми, причем гладкими прямыми, без ступенек только для вертикальных и горизонтальных отрезков (рис. 2.2.1);

· яркость для различных отрезков и даже вдоль отрезка в общем случае различна, так как, например, расстояние между центрами пикселов для вертикального отрезка и отрезка под 45° различно (см. рис. 2.2.1).

Объективное улучшение аппроксимации достигается увеличением разрешения дисплея, но в силу существенных технологических проблем разрешение для растровых систем приемлемой скорости разрешение составляет порядка 12801024.

Субъективное улучшение аппроксимации основано на психофизиологических особенностях зрения и, в частности, может достигаться просто уменьшением размеров экрана. Другие способы субъективного улучшения качества аппроксимации основаны на различных программных ухищрениях по "размыванию" резких границ изображения.

Параметрический алгоритм рисования линии.

Необходимо провести линию из точки (x1, y1) в точку (x2, y2) с линейной интерполяцией по яркости. рис. 2.3.1

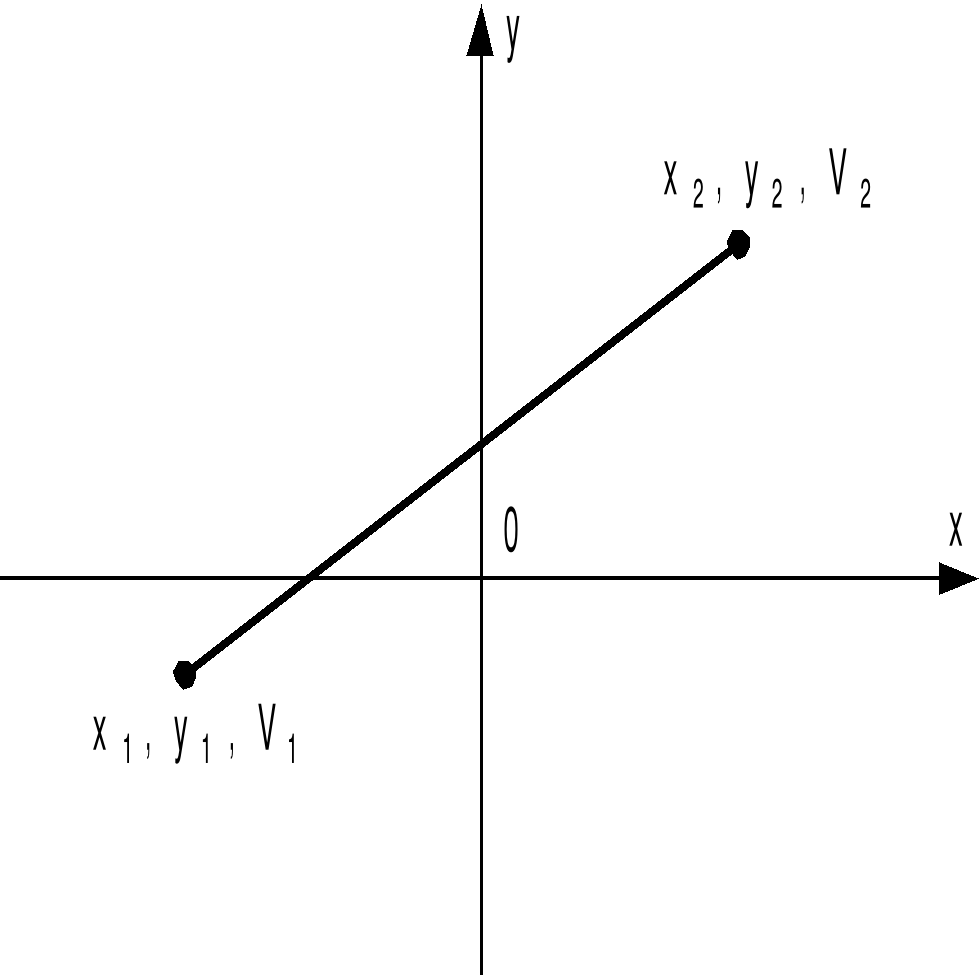
Рис. 2.3.1

Любую точку на этой линии можно представить в виде

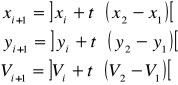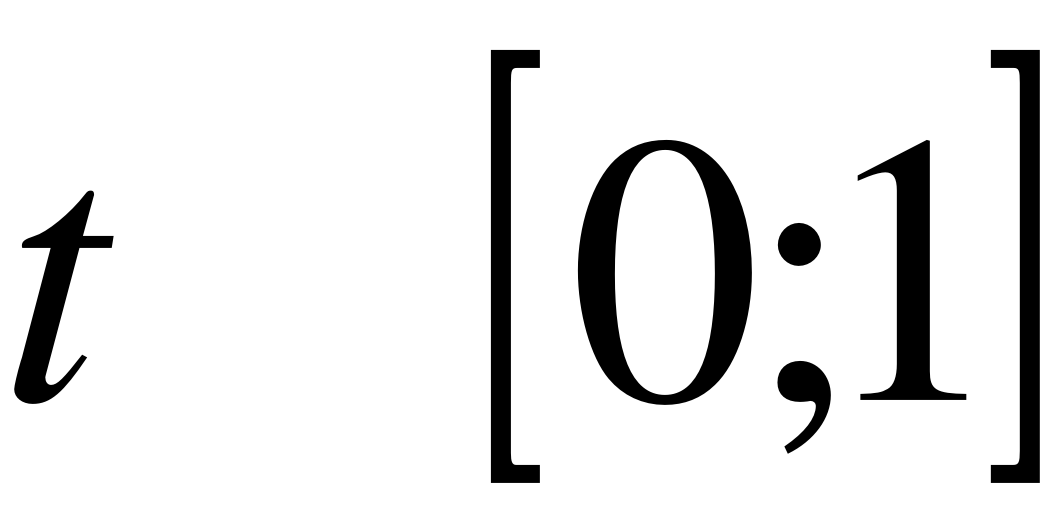; где , ][ – знак округления до целого.

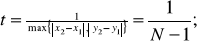N – длина линии в пикселях.

Можно проводить вычисления через приращение координат.

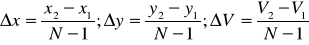
Значения приращений считаются в начале функции и не входят в цикл построения линии на экране, за счет чего повышается быстродействие.

Недостатки алгоритма:

· Необходимость работать с вещественными числами.

· В алгоритме есть операция деления, что значительно усложняет аппаратную организацию и увеличивает время работы алгоритма..

Достоинства алгоритма:

· Простота программной реализации.

· Простота реализации линейной интерполяции по яркости.

Алгоритм Брезенхема рисования линии.

В 1965 году Брезенхеймом был предложен простой целочисленный алгоритм для растрового построения отрезка. В алгоритме используется управляющая переменная di, которая на каждом шаге пропорциональна разности между s и t (см. рис.2.4.1). На рис.2.4.1 приведен i-ый шаг, когда пиксел Pi-1 уже найден как ближайший к реальному изображаемому отрезку, и теперь требуется определить, какой из пикселов должен быть установлен следующим: Ti или Si.

Если s<t, то Si ближе к отрезку и необходимо выбрать его; в противном случае ближе будет Ti. Другими словами, если s-t<0, то выбирается Si; в противном случае выбирается Ti.

рис. 2.4.1.

Изображаемый отрезок проводится из точки (x1, y1) в точку (x2, y2). Пусть первая точка находится ближе к началу координат, тогда перенесем обе точки, T(x1, y1) так, чтобы начальная точка отрезка оказалась в начале координат, тогда конечная окажется в (D x, D y), где D x= x2- x1 , D y= x2- x1. Уравнение прямой теперь имеет вид y=x D y/Dx. Из рисунка следует, что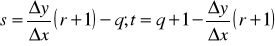

поэтому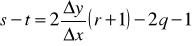

помножим на D x: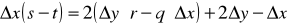

так как D x>0, величину D x(s-t) можно использовать в качестве критерия для выбора пиксела. Обозначим эту величину di :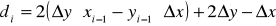

так как r = xi-1, q = yi-1, получаем: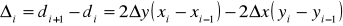

Известно, что xI - xi-1=1.

Если di >= 0, то выбираем Ti, тогда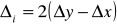

Если di <0, то выбираем Si, тогда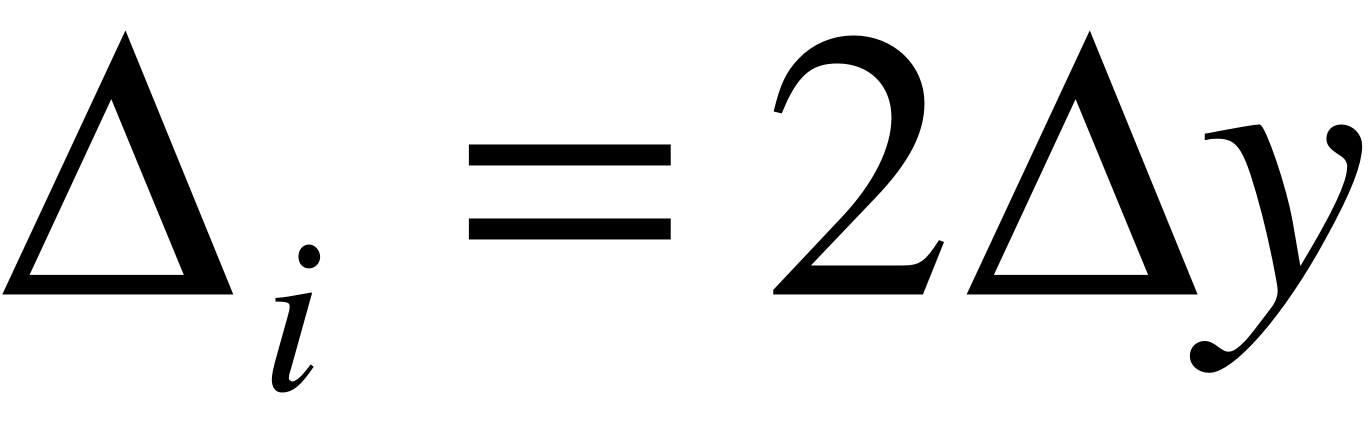

Таким образом, мы получили итеративную формулу для вычисления критерия di.
Начальное значение d1=2D y-D x.

Можно построить блок схему алгоритма:

рис. 2.4.2

Линейная интерполяция по яркости при построении отрезка по алгоритму Брезенхема получается параметрическим способом, т.е. 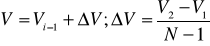, где N – длина отрезка в пикселях.

Алгоритмы построения окружности.

Рассмотрим окружность с центром в начале координат, для которой x2+y2=R2, или в параметрической форме:

1. x=R cos(a);

2. y=R sin(a).

То есть легко написать программу рисования окружности:

void Circle (int x, int y, int R, int color)
{

int a;
int x1;
int x2;
int y1;
int y2;
x2=x+R;
y2=y;
for ( int a=1; a<=360; a++)
{

x1=x2; y1=y2;
x2=round(R*cos(a))+x;
y2=round(R*sin(a))+x;
Line (x1, y1, x2, y2, color);

}

рис. 2.5.1.

Если воспользоваться симметрией окружности, то можно построить более эффективный алгоритм. Если точка (x, y) лежит на окружности, то легко вычислить семь точек, принадлежащих окружности, симметричных этой. То есть, имея функцию вычисления значения y по x=0..R/SQRT(2) для построения дуги от 00 до 450. Построим процедуру, которая будет по одной координате ставить восемь точек, симметричных центру окружности.

void Circle_Pixel(int x0, int y0, int x, int y, int color);
{

putpixel(x0 + x, y0 + y, color);
putpixel(x0 + y, y0 + x, color);
putpixel(x0 + y, y0 - x, color);
putpixel(x0 + x, y0 - y, color);
putpixel(x0 - x, y0 - y, color);
putpixel(x0 - y, y0 - x, color);
putpixel(x0 - y, y0 + x, color);
putpixel(x0 - x, y0 + y, color);

}

Таким образом можно написать программу рисование окружности по точкам:

void Circle (int x0, int y0, int R, int color)
{

for ( int x=0; x<=R/sqrt(2); x++)
{

int y = (int)(sqrt(sqr(R)-sqr(x)));
Circle_Pixel (x0, y0, x, y, color);

}

Алгоритм Брезенхема генерации окружности

Брезенхем разработал алгоритм более эффективный, чем каждый рассмотренный выше. Здесь используется тот же принцип, что и для рисования линии.

рис. 2.6.1

Будем рассматривать сегмент окружности, соответствующий x=x0.. x0+R/sqrt(2). На каждом шаге выбираем точку, ближайшую к реальной окружности. В качестве ошибки возьмем величину D(Pi)=(x2i+ y2i) – R2.

Рассмотрим рис. 2.6.1 , на котором показаны различные возможные способы прохождения истинной окружности через сетку пискселов. Пусть пиксел Pi-1 уже найден как ближайший к реальной изображенной окружности, и теперь требуется определить, какой из пикселов должен быть установлен следующим: Ti или Si. Для этого определим точку, которой соответствует минимальная ошибка:

D(Si)=((q+1)2+ p2 ) – R2, D(Ti)=((q+1)2+ (p+1)2 ) – R2.

Если |D(Si)| < |D(Ti)|, то выбираем Si, иначе - Ti. Введем величину di = |D(Si)| - |D(Ti)|, тогда Si выбирается при di < 0, иначе выбирается Ti. Если рассматривать только часть окружности, дугу от 00 до 450, то D(Si) > 0 так как точкаSi лежит за пределами окружности, а D(Ti) < 0, так как Ti находится внутри окружности, поэтому
di = D(Si) + D(Ti).

Алгебраические вычисления, аналогичные тем, которые проводились для линии, приводят к результату:

d1=3-2R.

Если выбираем Si (когда di < 0 ),

Di=4xi-1+6;

если выбираем Ti (когда di >=0 ),

D i=4(xi-1 * yi-1) +10.

Блок-схема этого алгоритма (рис. 2.6.2).

рис. 2.6.2

Алгоритм хорош тем что отсутствуют операции с плавающей точкой, а также операции деления и извлечения корня.

Отсечение по полю вывода

На рис.2.7.1. показана плоская сцена и отсекающее окно регулярной формы. Окно задается левым (Л), правым (П), верхним (В) и нижним (Н) двумерными ребрами. Регулярным отсекающим окном является прямоугольник, стороны которого параллельны осям координат объектного пространства или осям координат экрана. Целью алгоритма отсечения является определение тех точек, отрезков или их частей, которые лежат внутри отсекающего окна. Эти точки, отрезки или их части остаются для визуализации. А все остальное отбрасывается.

Поскольку в обычных сценах или картинках необходимо отсекать большое число отрезков или точек, то эффективность алгоритмов отсечения представляет особый интерес. Во многих случаях подавляющее большинство точек или отрезков лежит целиком внутри или вне отсекающего окна. Поэтому важно уметь быстро отбирать отрезки, подобные аb, или точки, подобные р, и отбрасывать отрезки, подобные ij, или точки, подобные q на рис.2.7.1.

Точки, лежащие внутри отсекающего окна, удовлетворяют условию:

xл <= х <= xп и ун <= у <= ув.

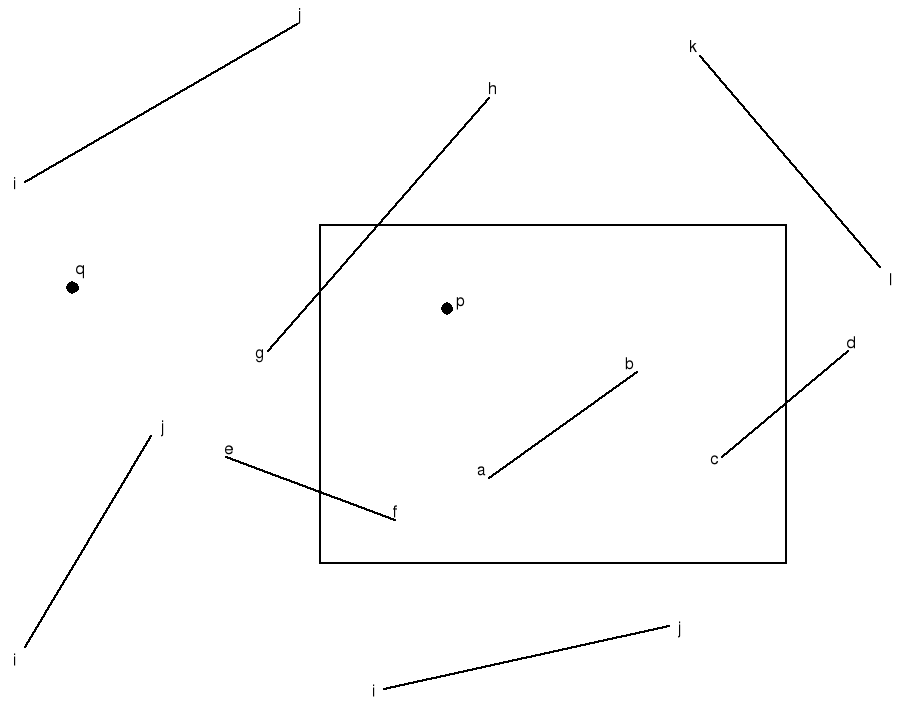
рис. 2.7.1.

Знак равенства здесь показывает, что точки, лежащие на границе окна, считаются находящимися внутри него.

Отрезок лежит внутри окна и, следовательно, является видимым, если обе его концевые точки лежат внутри окна, например отрезок ab на рис. 2.7.1. Однако если оба конца отрезка лежат вне окна, то этот отрезок не обязательно лежит целиком вне окна, например отрезок gh на рис. 2.7.1. Если же оба конца отрезка лежат справа, слева, выше или ниже окна, то этот отрезок целиком лежит вне окна, а значит, невидим. Проверка последнего условия устранит все отрезки, помеченные ij на рис. 2.7.1. Но она не устранит ни отрезка gh, который видим частично, ни отрезка kl, который целиком невидим.

Пусть а и b - концы отрезка, тогда можно предложить алгоритм, определяющий все полностью видимые и большинство невидимых отрезков.

Алгоритм Коэна-Сазерленда

Для решения задачи определения принадлежности отрезка полю вывода используется следующий метод. Пространство разбивается на 9 областей, каждая из областей кодируется бинарным 4-х битным кодом рис. 2.7.2.

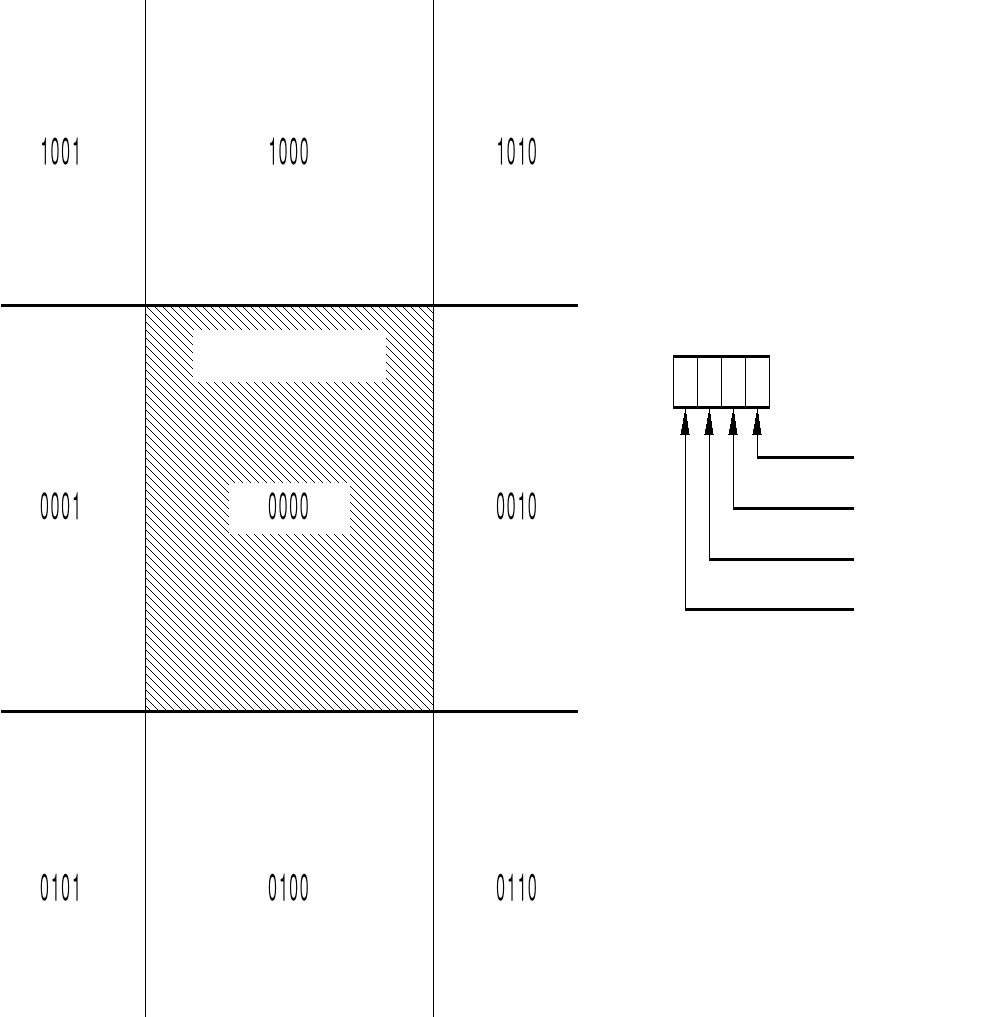
«Кодирование пространства» рис. 2.7.2.

Для каждого отрезка рассчитываются коды концов (К1, К2) затем производится экспресс анализ:

· Если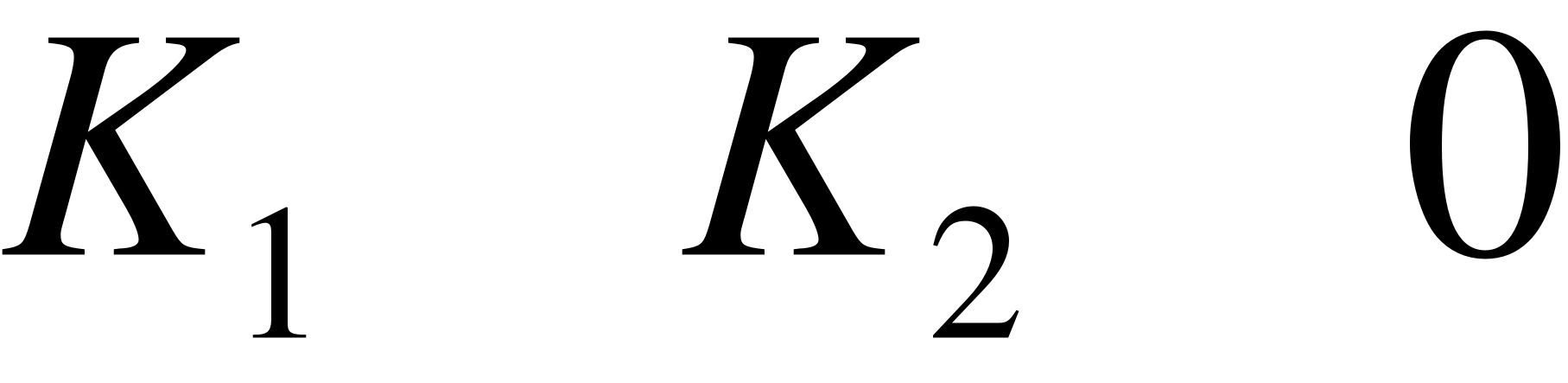, тогда отрезок лежит вне поля вывода – отрезок отбрасывается

· Если , тогда отрезок полностью лежит внутри поля вывода – отсечение не нужно, отрезок полностью прорисовывается

· Если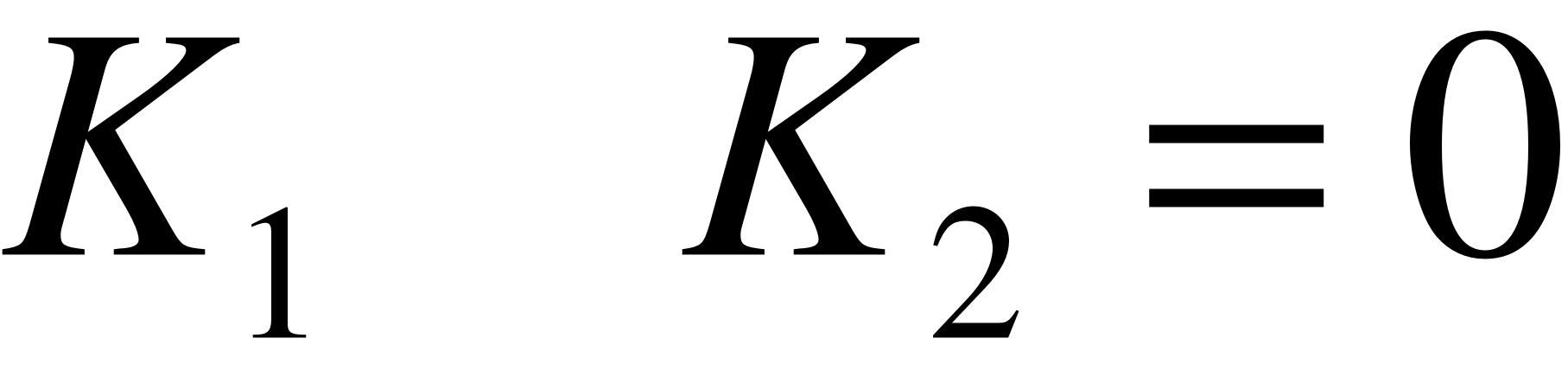, отрезок может частично лежать внутри поля вывода – необходимо отсечение по полю вывода.

Алгоритм отсечения по прямоугольной области