3D-ВИЗУАЛИЗАЦИЯ

Министерство образования и науки РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТИМЕНИ Н.Г.ЧЕРНЫШЕВСКОГО»

Кафедра материаловедения, технологии и управления качеством

3D-ВИЗУАЛИЗАЦИЯ

ПРАКТИЧЕСКАЯ РАБОТА

студента 4 курса 441 группы направления «Инноватика»

факультета нано - и биомедицинских технологий

Зыкова Кирилла Александровича

Преподаватель

профессор, д.т.н.

Симаков В.В.

должность, уч. степень, уч. звание

подпись, дата

инициалы, фамилия

Саратов 2015

СОДЕРЖАНИЕ

ВВЕДЕНИЕ……………………………………………………………...………...3

1Теоретическая часть.…………………………………………………………….4

2 Практическая часть……………………………………………….…………….7

ЗАКЛЮЧЕНИЕ…………………………………………………………..……...11

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ…………………………....12

ВВЕДЕНИЕ

LabVIEW - это среда графического программирования, которую используют технические специалисты, инженеры, преподаватели и ученые по всему миру для быстрого создания комплексных приложений в задачах измерения, тестирования, управления, автоматизации научного эксперимента и образования. В основе LabVIEW лежит концепция графического программирования - последовательное соединение функциональных блоков на блок-диаграмме[1].

Целью данной работы является провести визуализацию углового распределения волновой функции электрона для водородоподобной модели атомов.

Задачи:

1) Построить 3D график 4d-орбитали (l=2, m=0).

2) Составить отчет по проделанной работе.

1 Теоретическая часть

Волновая функция для водородоподобной модели атома

Простейшая химическая система - атом водорода, который состоит из отрицательно заряженного электрона и ядра, несущего положительный заряд.

Все электронные свойства атома описываются уравнением Шредингера(1) – уравнением квантовой механики, которое позволяет вычислить все возможные значения энергий, которыми электрон может обладать в атоме, а также зависящую от координат электрона волновую функцию , с помощью которой можно вычислить различные характеристики электрона [2].
. (1)

Перейдем от декартовых координат к сферическим координатам .

Связь между координатами точки, в которую направлен радиус-вектор в разных системах, описывается следующим образом:

	,	;

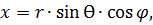
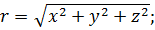
Переход к сферической системе координат позволяет представить волновую функцию в виде произведения :

, радиальной и угловой частей.

Такое представление волновой функции позволяет разбить уравнение Шредингера для атома водорода на три уравнения в сферических координатах. Решая эти уравнения по отдельности, можно получить волновую функцию и рассчитать возможные значения энергии атома водорода.

Изменение угла может рассматриваться, как вращение электрона в плоскости, которое описывается уравнением бегущей волны . Согласно условию однозначности волновой функции, один полный оборот приводит систему в исходное положение, в итоге:

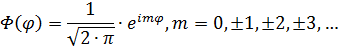
В атоме угловой механический момент электрона жестко связан с вектором магнитного момента, энергия которого во внешнем магнитном поле зависит от . Поэтомуназывается магнитным квантовым числом. Это число определяет возможные проекции вектора углового момента электрона на ось , то есть ориентацию механического углового момента электрона в пространстве. В силу целочисленности , эти проекции дискретны.

Зависимость от угла имеет вид:

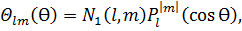
где, - множитель, зависящий от ; , .

Функции называются нормированными присоединенными полиномами Лежандра.

Решение для угловой части уравнения Шредингера для атома водорода имеет следующий вид[3]:

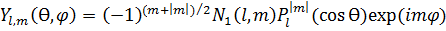
Комплексные функции называются сферическими гармониками .

Для конкретного имеется поверхностей, проходящих через положение ядра, где функция обращается в нуль, они называются узловыми поверхностями или просто узлами. Вероятность найти электрон в узле равна нулю. Таким образом, для каждого имеются сферических гармоник, отличающихся положением в пространстве узловых поверхностей, квантовое число определяет ориентацию узловых поверхностей.

Наличие узловых поверхностей у волновой функции атомов связано с волновыми свойствами электронов. В любой волне имеются точки, в которых смещение колеблющейся величины равно нулю, а в случае, когда

колебания происходят в трех измерениях, совокупность этих точек образует узловую поверхность.

2 Практическая часть

Построить график функции 4d-орбиталь (l=2,m=0).

Итак, преступим к решению нашей задачи:

1) Зададим диапазон аргумента и ординаты (Xmin; Xmax;Ymin;Ymax).

2) Затем определимся с количеством разбиений нашего аргумента (N).

3) Выведем формулу. Пусть x будет , а y ,тогда для (l=2, m=0) получается формула следующего вида[4]:

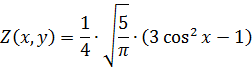
(2)

4) Приступаем к реализации этой формулы в среде LabView.

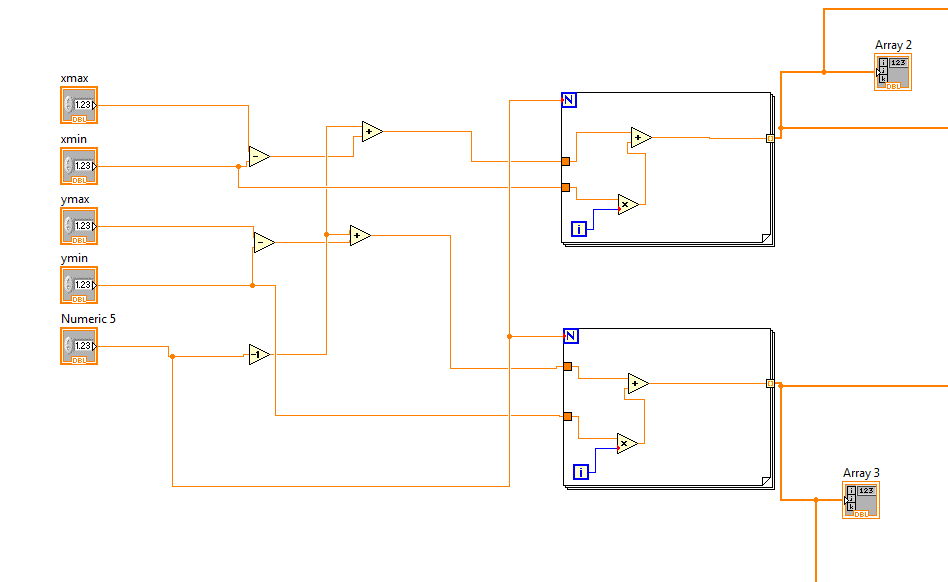
Рисунок 1 - Циклы Forloop для перебора x и y

5) Для перебора всех x и y используем цикл Forloop, который позволяет перебрать все значения Xi и Yi от 0 до N. Получившиеся значения сохраняем в массивах Array 2 и Array 3.

Теперь, когда у нас есть значения Xi иYi, приступаем к нахождениюZi.

6) Создадим цикл Forloop и внутрь которого вложим еще один цикл Forloop и реализуем формулу (1) для нахождения Zi.

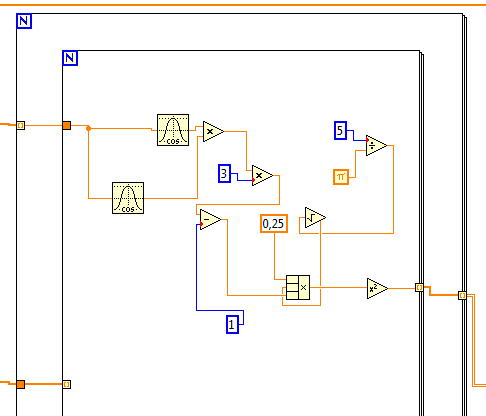
Рисунок 2 – Формула для нахождения Zi на блок диаграмме

7) Включаем индексацию, для того чтобы все x перебрались относительно y, а yотносительно x.

8) На выходе создаем массив Arrayи записываем в него все получившие значения Zi.

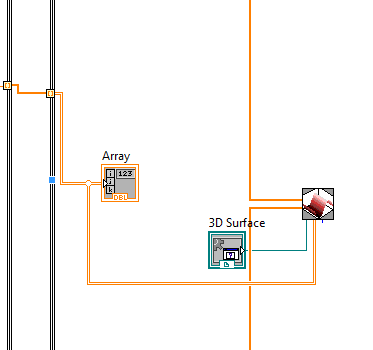
Рисунок 3 – Массив Arrayи 3DSurface

9) Подключаем массивы Zi ,Yi ,Xi к 3DSurface и получим график.

Заменим систему координат на сферическую:

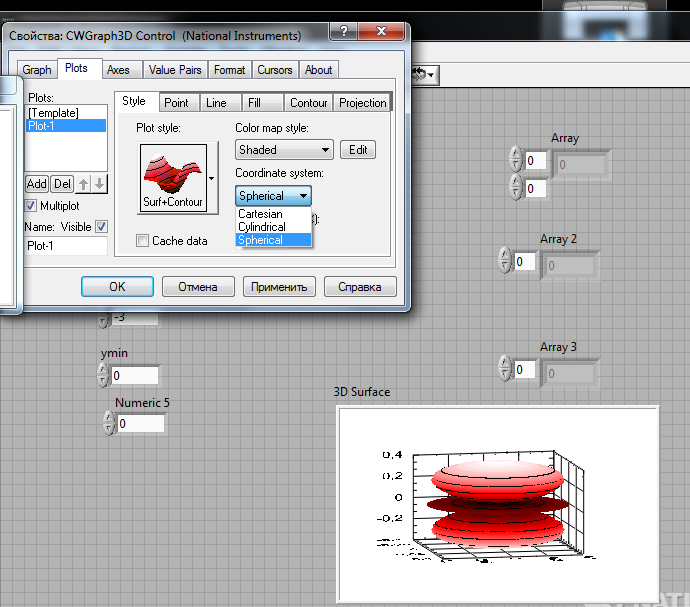
Рисунок 4 – Замена системы координат

Так выглядит решение на блок-диаграмме:

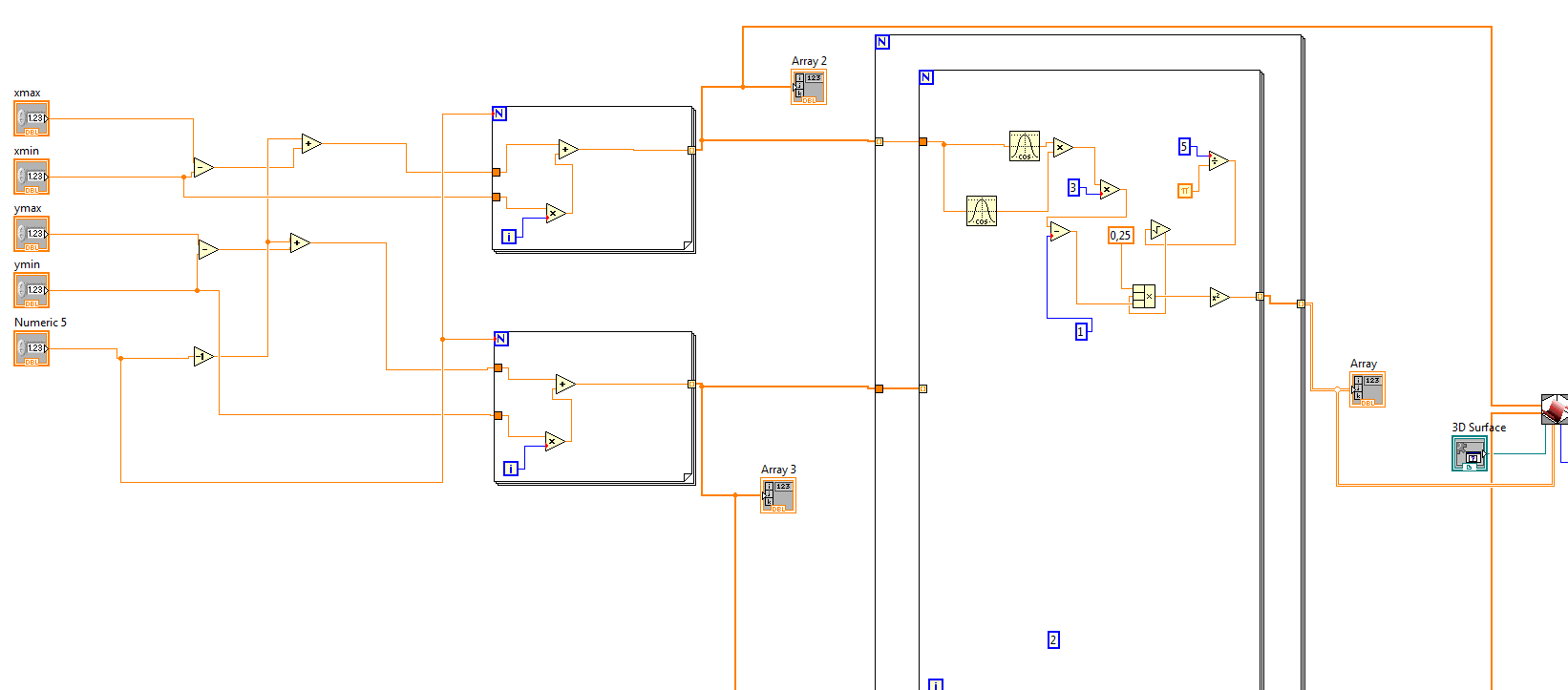
Рисунок 5 – Формула на блок диаграмме

ЗАКЛЮЧЕНИЕ

В ходе осуществления данной работы были решены поставленные задачи, и построен график 3D4d-орбитали (l=2, m=0).Были получены навыки построения трехмерных графиков и замены системы координат.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

LabVIEW[Электронный ресурс]: [сайт]. URL: http://www.labview.ru/labview/what_is_labview/ (дата обращения 9.10.2015)
LabVIEW[Электронный ресурс]: [сайт]. URL: http://cxem.net/software/labview.php (дата обращения 9.10.2015)
LabVIEW[Электронный ресурс]: [сайт]. URL: https://en.wikipedia.org/wiki/Schr%C3%B6dinger_equation (дата обращения 9.10.2015)

3D-ВИЗУАЛИЗАЦИЯ