ОБЩИЕ СВЕДЕНИЯ О ПОСТРОЕНИИ ГОСУДАРСТВЕННОЙ ГЕОДЕЗИЧЕСКОЙ СЕТИ, СЕТЕЙ СГУЩЕНИЯ И СЪЕМОЧНЫХ СЕТЕЙ
ЛЕКЦИЯ 6. «ОБЩИЕ СВЕДЕНИЯ О ПОСТРОЕНИИ ГОСУДАРСТВЕННОЙ ГЕОДЕЗИЧЕСКОЙ СЕТИ, СЕТЕЙ СГУЩЕНИЯ И СЪЕМОЧНЫХ СЕТЕЙ»
1. Общие сведения о геодезической сети.
2. Государственная геодезическая сеть СССР.
3. Государственная геодезическая сеть Республики Беларусь.
. Закрепление пунктов геодезической сети.
5. Сети сгущения и съёмочные сети.
Рекомендуемая литература: [1], гл. X, §§134–; [2], гл. VIII, §§40–; [3], гл.5, §§5.1–.4; [4], гл. 10, §§10.1–.4; [6], гл.5, §§5.1–5.3; [7], гл. 5, §§6.4.1–.4.9; [8]; [9], гл.9, §§56–; [10], гл.XII, §§42–44; [21], гл.IV, §§83–; [22], §1.5; [23], гл. 16, §§16.1–.8; [38], гл. II, §§II.1–II.3.
- Общие сведения о геодезической сети.
Геодезическая сеть представляет собой совокупность закрепленных на местности точек, для которых в единой системе определены координаты и высоты.
Основной принцип построения геодезической сети - от общего к частному. Он заключается в том, что вначале c высокой точностью определяется взаимное положение сравнительно небольшого числа пунктов, расположенных на большой территории. Затем, используя эти пункты, переходят к построению более густой сети меньшей точности.
Такой метод позволяет быстро распространить единую координатную систему на большие расстояния, производить съёмку местности одновременно в разных местах, обеспечивает надёжный контроль работ и равномерное распределение ошибок по всей территории.
Геодезические сети могут быть плановыми, высотными или одновременно теми и другими.
Плановая сеть устанавливает взаимное положение точек на плоскости или на поверхности земного сфероида. Создается она методами триангуляции, полигонометрии, трилатерации и GPS.
Высотная геодезическая сеть устанавливает положение точек относительно уровня моря. Высотная геодезическая сеть создана для распространения по всей территории страны единой системы высот. За начало высот принят средний уровень Балтийского моря, отмеченный горизонтальной чертой на металлической пластине, укрепленной в устое моста через обводной канал в Кронштадте.
Высотная сеть создается методами геометрического, тригонометрического и барометрического нивелирования.
Геодезические сети подразделяются на 3 вида:
. Государственная геодезическая сеть.
. Геодезические сети сгущения.
. Съемочные сети.
2. Государственная геодезическая сеть СССР.
Государственной геодезической сетью (ГГС) называют сеть закрепленных точек земной поверхности, обеспечивающей распространение координат на территорию государства и являющейся исходной для создания других геодезических сетей.
ГГС является главной геодезической основой топографических съемок всех масштабов.
Геодезическая основа Республики Беларусь реализована в виде части государственной геодезической сети (ГГС), ранее созданной на территории бывшего СССР.
Государственная (опорная) геодезическая сеть СССР подразделялась на:
а) сети триангуляции, полигонометрии и трилатерации 1, 2, 3 и 4 классов;
б) нивелирные сети I, II, III, IV классов.
При методе триангуляции в треугольниках измеряют все углы и минимум две стороны на разных концах сети (вторая сторона для контроля). Остальные стороны вычисляют, используя теорему синусов. Для вычисления координат всех точек надо знать координаты хотя бы одной точки и дирекционный угол одной линии. Метод триангуляции (от лат. triangulum –треугольник) был предложен голландским ученым Снеллиусом около 1610 г.
Метод полигонометрии заключается в построении сети ходов, в которых измеряются все углы и стороны. Полигонометрические ходы отличаются от теодолитных более высокой точностью измерений.
Метод трилатерации (от лат. trilaterus –трехсторонний) отличается от триангуляции тем, что в треугольниках измеряются не углы, а стороны. Для измерения сторон обычно используют электронные дальномеры. Углы вычисляются по измеренным сторонам, например, по теореме косинусов.
Триангуляция 1 класса строилась в виде системы замкнутых полигонов периметром 800–км. Полигоны образовывали триангуляционными рядами, которые стремились разместить в направлении меридианов и параллелей. Длина звена около 200 км.
В местах пересечения звеньев измеряли базисные стороны, или строили базисные сети для определения длины выходной стороны. На обоих концах базисных сторон определяли астрономические широты, долготы и азимуты.
В закрытых, залесенных районах звенья триангуляции могли заменяться звеньями полигонометрии I кл.
Триангуляция 2 кл. строилась в виде сплошных сетей треугольников, заполняющих полигоны триангуляции I кл.
Триангуляция 3 и 4 классов является дальнейшим сгущением государственной геодезической сети для целей крупномасштабного картографирования и обоснования строительства. Схема построения сети показана на рис. 2.1.
Государственная полигонометрия 1 кл. строится в виде ходов, заменяющих ряд триангуляции 1 кл.
Полигонометрические сети 2 кл. строятся по особо разработанной программе.
При построении сетей 3 и 4 кл. прокладывают системы полигонометрических ходов или одиночные ходы, опирающиеся на пункты высшего класса.
Достоинство полигонометрии –простота геометрического построения сетей и большая гибкость, экономия в затратах труда. Недостатки – слабый контроль угловых и линейных измерений, менее равномерная плотность сети по сравнению с триангуляцией.
Основные характеристики плановой государственной сети: S –длина сторон, m –средняя квадратическая ошибка измерения угла, 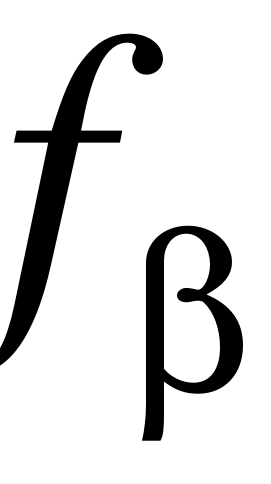 –допустимая угловая невязка и mS:S –относительная средняя квадратическая ошибка измерения сторон приведена в табл.2.2
–допустимая угловая невязка и mS:S –относительная средняя квадратическая ошибка измерения сторон приведена в табл.2.2
Таблица 2.2. Основные характеристики плановой государственной сети
|
Класс |
Триангуляция |
Полигонометрия |
Трилатерация |
|
S, км |
m," |
|
mS:S |
m," |
mS:S |
mS:S |
|
|
1 |
,7 |
:400000 |
,4 |
:300000 |
|||
|
2 |
-20 |
,0 |
1: 300000 |
1,0 |
1:250000 |
||
|
3 |
-8 |
,5 |
б |
:200000 |
,5 |
:200000 |
:100000 |
|
4 |
-5 |
,0 |
:200000 |
,0 |
:150000 |
I: 40000 |
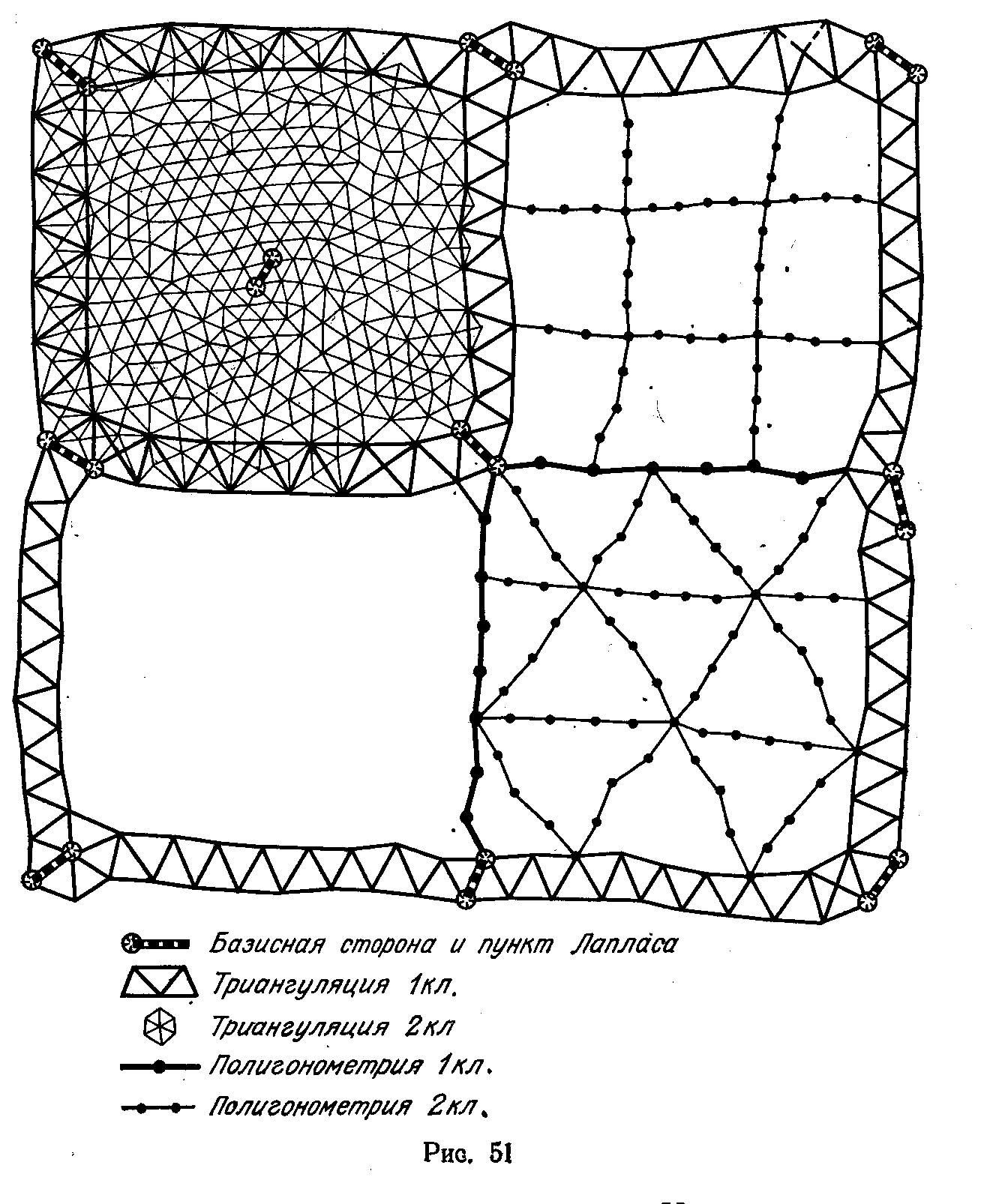
Рис. 2.1. Схема построения Государственной плановой геодезической основы.
Для каждого пункта сети определяется его высота методом геометрического или тригонометрического нивелирования.
Государственная нивелирная сеть является главной высотной основой для решения научных и инженерно-технических задач. Создается методом геометрического нивелирования.
Сети I и II кл. обеспечивают единую систему высот на территории всей страны, а также используются для научных целей. Сети III и IV кл. служат для обеспечения топографических съёмок и решения инженерных задач. Нивелирные ходы I и II кл. через каждые 50–км закрепляются фундаментальными реперами. Ходы всех классов через 5–км закрепляются реперами и марками.
Предельные невязки в превышениях нивелирных ходов определяются по формулам
I кл.  ,
,
II кл. ,
,
III кл.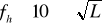 ,
,
IV кл.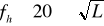 .
.
Здесь невязки выражены в миллиметрах, а длина хода L в километрах. Плотность пунктов государственной сети зависит от масштаба съёмки и характеризуется данными табл. 2.3.
Таблица 2.3. Густота пунктов государственной сети
|
Масштаб съемки |
Один пункт на площадь, км2 |
Один репер на площадь, км2 |
|
1:25000 |
–60 |
|
|
1:10000 |
(1, 2, 3 классов) |
|
|
1:5000 |
–30 |
–15 |
|
1:2000 |
–15 |
–7 |
Рассмотренная ГГС строилась по единой программе на территорию всего Советского Союза в течение многих десятилетий. Она включала около 164 тыс. пунктов 1 и 2 классов. На территории Беларуси таких пунктов было около 2,5 тыс.
Плановые сети в течение многих лет не обновлялись. По своему состоянию и точности они уже не отвечают современным требованиям. Поэтому в России и Республике Беларусь разработаны программы модернизации ГГС на основе спутниковых методов определения координат. Основные положения построения современной ГГС РБ изложены ниже.
3. Государственная геодезическая сеть Республики Беларусь.
ГГС Республики Беларусь предназначена для:
- распространения единых установленных систем координат на территории Республики Беларусь;
- геодезического обеспечения картографирования территории Республики Беларусь;
- геодезического обеспечения изучения земельных ресурсов и землепользования, создания кадастров, строительства, разведки и освоения природных ресурсов Республики Беларусь;
- изучения поверхности и гравитационного поля Земли и их изменений во времени;
- изучения геодинамических явлений и др.
ГГС является носителем геодезической системы координат и высот Республики Беларусь. Началом единого отсчета плановых координат служит центр круглого зала Пулковской обсерватории в Санкт-Петербурге. При производстве геодезических и картографических работ в Республикке Беларусь применяется единая система геодезических координат 1942 года и Балтийская система высот 1977 года. Для вычисления геодезических координат принимаются размеры референц-эллипсоида Ф.Н.Красовского со следующими параметрами: большая полуось –6378245,000 метра, малая полуось –6356863,019 метра и сжатие –:298,3 [16].
Создание, развитие и поддержание в рабочем состоянии ГГС обеспечивает Государственный комитет по имуществу Республики Беларусь.
ГГС состоит из взаимосвязанных геодезических сетей различных классов точности, создаваемых по принципу от общего к частному.
ГГС включает:
- фундаментальную астрономо-геодезическую сеть (ФАГС);
- высокоточную геодезическую сеть (ВГС);
- спутниковую геодезическую сеть 1-го класса (СГС-1);
- геодезические сети сгущения (ГСС).
Плотность пунктов ГГС должна составлять не менее одного пункта на 30 кв. км земной поверхности.
В основу создания ГГС РБ положен принцип сохранения единства геодезических сетей Беларуси и России (рис. 2.2).
В 2000 г. создан пункт фундаментальной астрономо-геодезической сети «Минск». Пункт имеет 1 основной и 4 рабочих цента. На одном из рабочих центров установлена совмещенная GPS/ГЛОНАСС постоянно действующая базовая станция Legasi E GGD. Пункт связан геодезическими измерениями с аналогичными по точности определения координат геодезическими пунктами на территории Российской Федерации и других сопредельных государств. ФАГС уравнена в системе координат WGS-84, ошибка взаимного положения пунктов составляет не более 0,5 см по каждой из плановых координат и 1–см по геодезической высоте. Средние квадратические погрешности взаимного положения ФАГС по каждой из плановых координат не превышают величин 1,5 см и по геодезической высоте 2–см.
Пункт ФАГС также связан относительными методами космической геодезии не менее чем с четырьмя пунктами астрономо-геодезической сети (АГС) со средней квадратической погрешностью менее ±3 см.
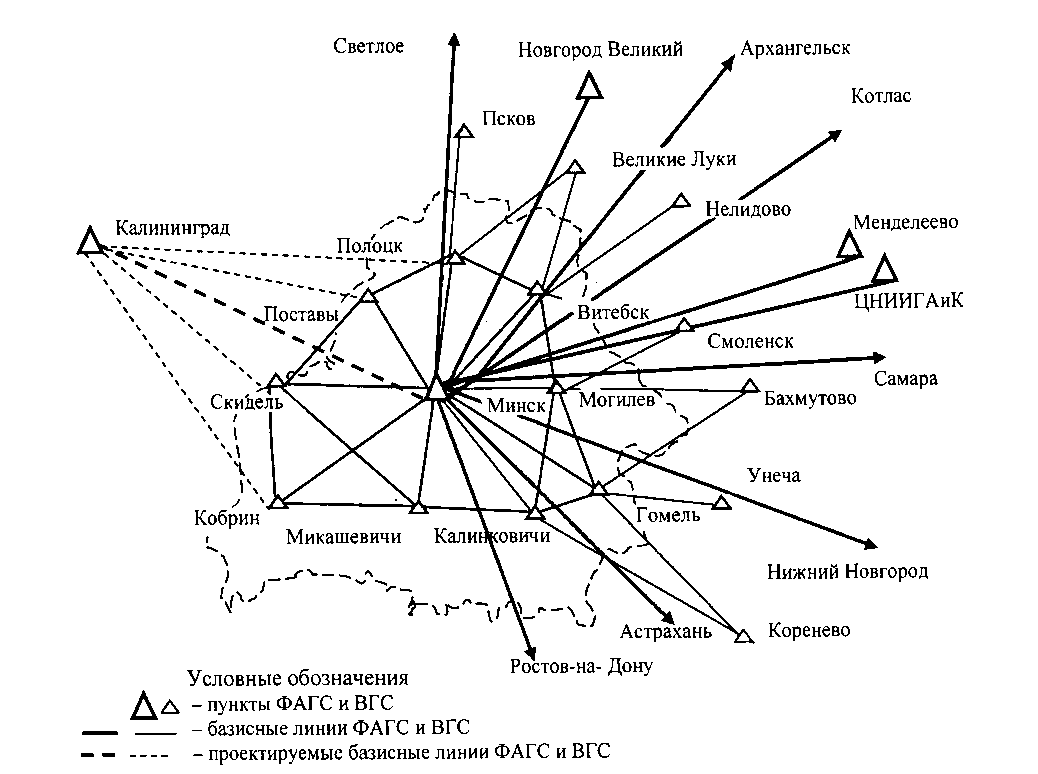
Рис. 2.2. Схема связи государственной геодезической сети Беларуси и России.
На пункте ФАГС определены нормальные высоты нивелированием не ниже II класса точности.
Пространственное положение пункта ФАГС уточняется с периодичностью 1 раз в 5 лет
Также в Республике Беларусь создана высокоточной геодезической сети (ВГС). Она включает пункты Поставы, Полоцк, Витебск, Могилев, Гомель, Калинковичи, Микашевичи, Кобрин и Скидель (рис. 2.4). ВГС это пространственное геодезическое построение, опирающееся на пункты ФАГС. Пространственные прямоугольные координаты пунктов ВГС определены методами космической геодезии.
Спутниковая геодезическая сеть 1 класса (СГС-1) представляет собой пространственное геодезическое построение, опирающееся на пункты ФАГС и ВГС. Расстояние между пунктами CГС-1 должно составлять 15–км, а на территориях городов, больших промышленных объектов ––км. Пространственные прямоугольные координаты пунктов СГС-1 также определяются методами космической геодезии.
Часть пунктов СГС-1 совмещается с пунктами АГС или привязана к ним. Расстояние между пунктами АГС, совмещаемыми с пунктами СГС-1 или привязываемыми к ним, не должно превышать 70 км. Привязка должна осуществляться относительными методами космической геодезии со средними квадратическими погрешностями, не превышающими ±2 см по каждой из плановых компонент.
Основные характеристики геодезических сетей создаваемых спутниковыми методами приведены в табл. 2.4.
Таблица. 2.4. Характеристики геодезических сетей создаваемых спутниковыми методами.
|
Параметр |
ФАГС |
ВГС |
СГС-1 |
|
Расстояние между пунктами, км |
800-1000 |
-300 |
-25 (8-12 в городах) |
|
Средняя квадратическая погрешность взаимного положения пункта или относительно сети высшего класса, не более, мм: плановая по каждой из осей по высоте |
mх=my= ±3 мм+510-8D mz = ± 5 мм+710-8D |
mx=my= ±3 мм+110-7D mz = ± 5 мм+210–D |
где D –расстояние между центрами пунктов.
Геодезическая сеть сгущения (ГСС) включает геодезические сети 1–классов, построенные в соответствии с требованиями Основных положений о государственной геодезической сети СССР 1954–гг., и новые сети сгущения, построенные в соответствии с требованиями стандарта.
Новые пункты ГСС определяются относительными методами космической геодезии, а также традиционными геодезическими методами: триангуляции, полигонометрии, трилатерации и с применением астрономических измерений. Cредняя квадратическая погрешность определения положения пунктов ГСС относительно ближайших пунктов ФАГС, ВГС, СГС-1 не должна превышать ±10 см. Cредняя квадратическая погрешность определения взаимного положения пунктов ГСС не должна превышать ±5 см.
Длины сторон ГСС должны находиться в пределах 2–км. Нормальные высоты пунктов ГСС должны определяться со средней квадратической погрешностью, не превышающей ±5 см.
4. Закрепление пунктов геодезической сети.
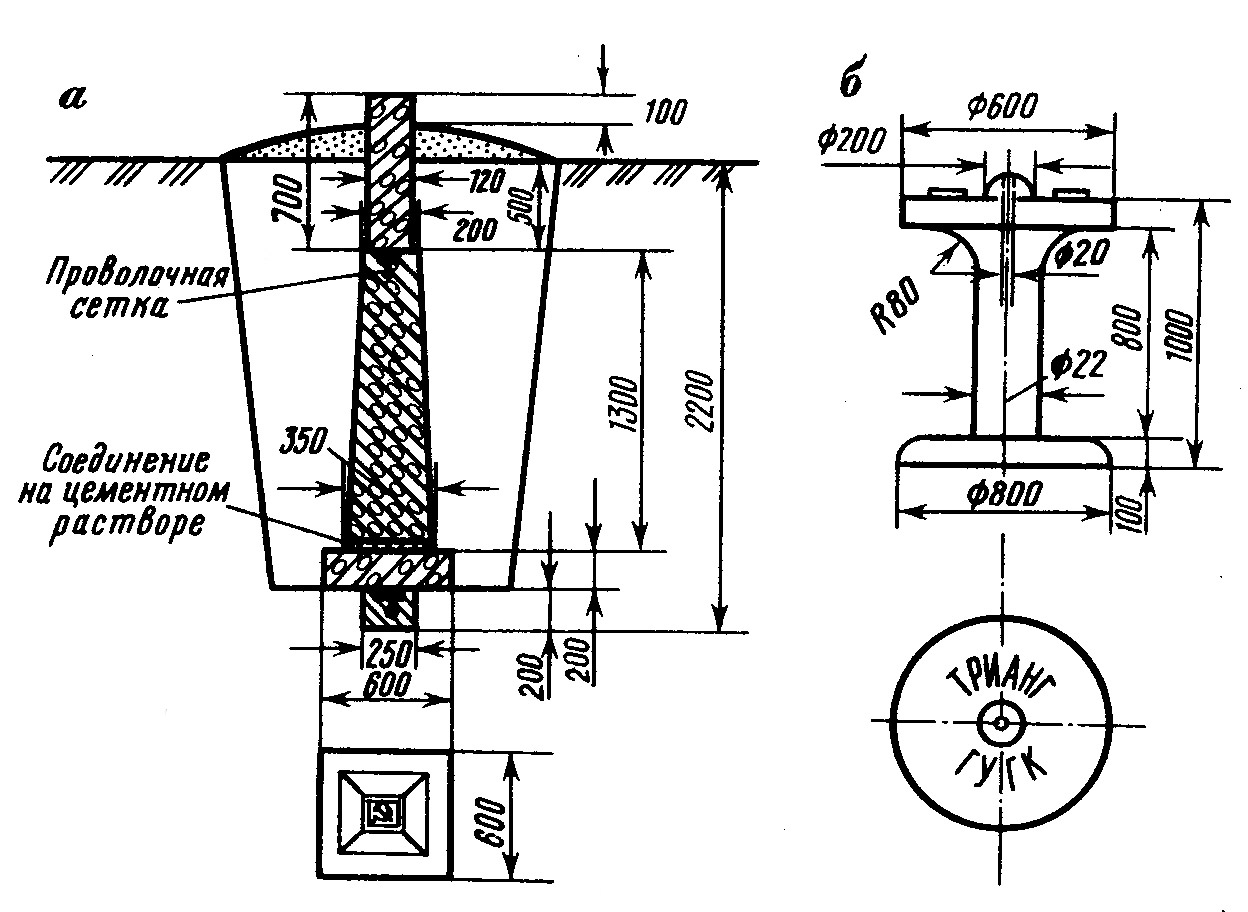
В целях долговременной сохранности сетей их пункты закрепляют на местности особо надёжными сооружениями –центрами.
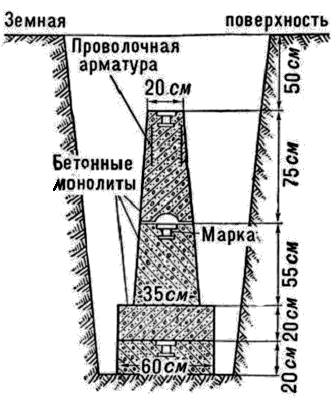
В зависимости от природно-климатических условий применяют различные типы центров. В районах неглубокого промерзания грунта (1,5 м) применяют центр из трех бетонных монолитов (рис. 2.2). Верхняя марка закладки монолитов находится на глубине 50 см от поверхности. Нижний монолит закладывается на 50 см ниже промерзания грунта. Над центром устанавливается опознавательный бетонный столб.
Для удобства привязки на всех пунктах государственной геодезической сети устанавливается по два ориентирных пункта на расстоянии от него 500–м. На ориентирном пункте закладывается в землю бетонный монолит с маркой, а сверху устанавливается деревянные или бетонный опознавательный столб.
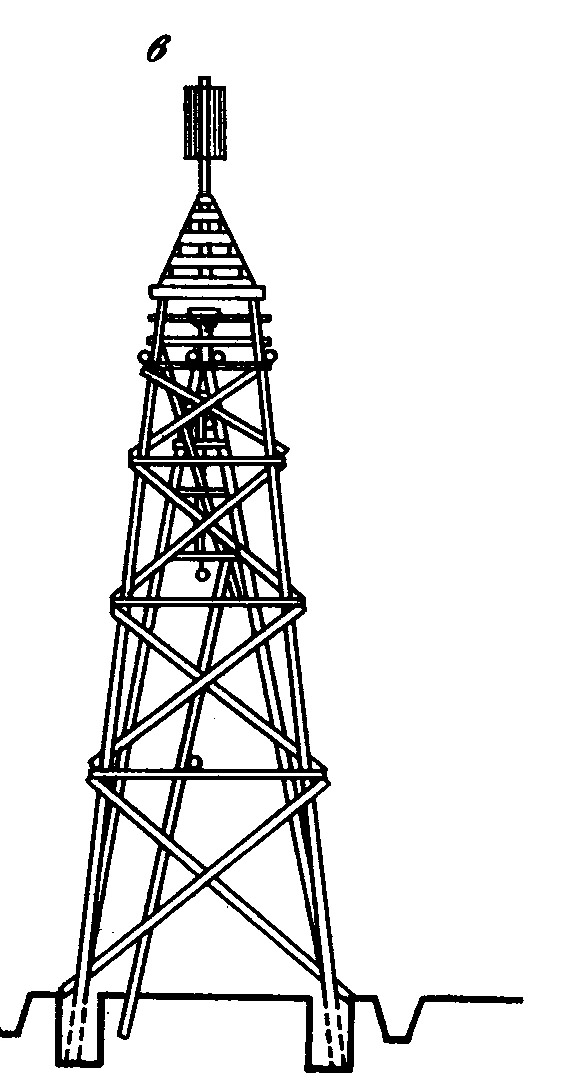
Над центрами пунктов сооружают наружные знаки (рис. 2.3), которые служат визирными целями при измерении углов и линий (туры, пирамиды, простые сигналы, сложные сигналы).
В соответствии со ст. 18 закона Республики Беларусь «О геодезической и картографической деятельности» [12] пункты государственных геодезических сетей (астрономо-геодезические, геодезические, нивелирные и гравиметрические), наземные знаки и центры этих пунктов относятся к республиканской собственности и находятся под охраной государства. Снос наружных знаков или перезакладка центров геодезических пунктов производятся только с разрешения республиканского органа государственного управления по геодезии и картографии.
e0
|
|
Рис. 2.3. Закрепление на местности пунктов государственной геодезической основы
а –центр для закрепления пунктов триангуляции; б –чугунная марка.
|
Рис. 2.4. Геодезический сигнал. |
Юридические и физические лица при выполнении геодезических и картографических работ обязаны обеспечивать сохранность геодезических пунктов. Согласно п. 2 положения [14] земельные участки, на которых расположены геодезические пункты, и полоса земли шириной 1 метр вдоль границ геодезических пунктов, являются охранными зонами этих пунктов. Границами геодезических пунктов являются внешние края опознавательных канав, ограды, а при их отсутствии –основания наружных знаков. В охранных зонах геодезических пунктов запрещается- производить работы, которые могут повредить геодезические пункты а также складировать корма, строительные материалы и др. |
Для выполнения работ на пунктах СГС-1 закрепляют ориентирные пункты (пункты-спутники). Основной пункт и пункты-спутники должны быть объединены в локальную геодезическую сеть. Пункты-спутники должны располагаться на расстоянии от 500 до 1000 м от основного центра пункта СГС-1. На застроенной и закрытой местности расстояние от основного центра пункта СГС-1 до пунктов-спутников не должно превышать 250 м. Средняя квадратическая погрешность определения расстояния между пунктом-спутником и основным центром пункта СГС-1 не должна превышать ±0,05 м при расстоянии от 500 до 1000 м и ±0,01м при расстоянии до 250 м. Пункты-спутники допускается совмещать с реперами государственной нивелирной сети.
5. Сети сгущения и съёмочные сети.
Геодезические сети сгущения создаются на основе государственной сети для обоснования топографических съёмок масштабов 1:5000–:5002. При этом в основном применяются те же методы, как и в государственных сетях. Они подразделяются на аналитические сети триангуляции 1 и 2 разрядов, полигонометрические сети 1 и 2 разрядов и сети технического нивелирования. Характеристики плановых сетей приведены в табл. 2.5.
Таблица 2.5. Основные характеристики сетей сгущения
|
Разряд |
Триангуляция |
Полигонометрия |
|
S, км |
m |
|
mS:S |
S, км |
m |
|
|
|
|
1 |
" |
" |
:50000 |
" |
"n |
:10000 |
||
|
2 |
" |
" |
:20000 |
" |
"n |
:5000 |
Триангуляция 1 и 2 разряда обычно строится в виде типовых фигур (рис. 2.5)
|
|
|
|
|
|
|
Рис. 2.5. Типовые фигуры триангуляции.
а) – вставка в угол;
б) – геодезический четырехугольник;
в) – центральная система;
г) – цепь треугольников между исходными сторонами;
д) – цепь треугольников между исходными пунктами.
Могут строиться сети, включающие несколько типовых фигур.
Минимальный угол в сплошной сети 1 и 2 разрядов –°, в цепочке треугольников –°. Число треугольников между исходными пунктами не более 10. Минимальная длина выходной стороны 1 км.
Плановые сети сгущения можно создавать также методом трилатерации, полярно-лучевым методом и др.
Высотные сети сгущения создаются техническим нивелированием. Длины визирного луча допускается до 150 м. Предельная невязка в сумме превышений определяется по формуле
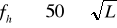 или
или 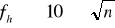 ,
,
где L –длина хода в км,
n –число станций в ходе.
Cъемочные сети являются непосредственной основой съёмок всех масштабов и других геодезических работ. Они могут строиться на основе государственных сетей, сетей сгущения или в условной системе координат.
Точность съёмочных сетей, способы закрепления пунктов и другие требования устанавливаются соответствующими инструкциями.
Средняя ошибка в плановом положении точек съёмочной сети относительно ближайших пунктов государственной геодезической сети не должна превышать 0,1 мм в масштабе плана, а предельная –0,2 мм.
Средние ошибки высот точек съёмочного обоснования относительно ближайших пунктов государственной геодезической сети в равнинных районах не должны превышать 1/10 высоты сечения рельефа.
При создании плановых съёмочных сетей применяется метод триангуляции, трилатерации, теодолитные хода, полярно-лучевой метод, различные засечки и др.
Высоты точек съёмочного обоснования определяются геометрическим или тригонометрическим нивелированием.
Допустимые невязки в превышениях определяются по формулам:
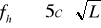 –при техническом нивелировании;
–при техническом нивелировании;
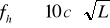 –при нивелировании горизонтальным лучом теодолитом или кипрегелем;
–при нивелировании горизонтальным лучом теодолитом или кипрегелем;
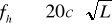 –при тригонометрическом нивелировании.
–при тригонометрическом нивелировании.
Лекция 9–. «ОПРЕДЕЛЕНИЕ ДОПОЛНИТЕЛЬНЫХ ПУНКТОВ»
1. Снесение координат с вершин знака на землю.
2. Прямая засечка.
. Обратная засечка.
. Линейная засечка.
Рекомендуемая литература: [1], гл. XV, §§159–; [11], гл. XV, §§123–; [21], §129; [24], гл. 16, §§16.2–.3; [27], гл. 11, §§105–; [30], гл. VIII, §§51–2; [31], гл. VII, задание VII.5.
1. Снесение координат с вершин знака на землю.
Дополнительные пункты определяются наряду со съемочной сетью в основном для сгущения существующей геодезической сети пунктами съемочного обоснования. Они строятся прямыми, обратными, комбинированными угловыми, а при наличии электронных дальномеров –линейными засечками и лучевым методом.
В некоторых случаях дополнительный пункт определяется передачей (снесением) координат с вершины знака на землю.
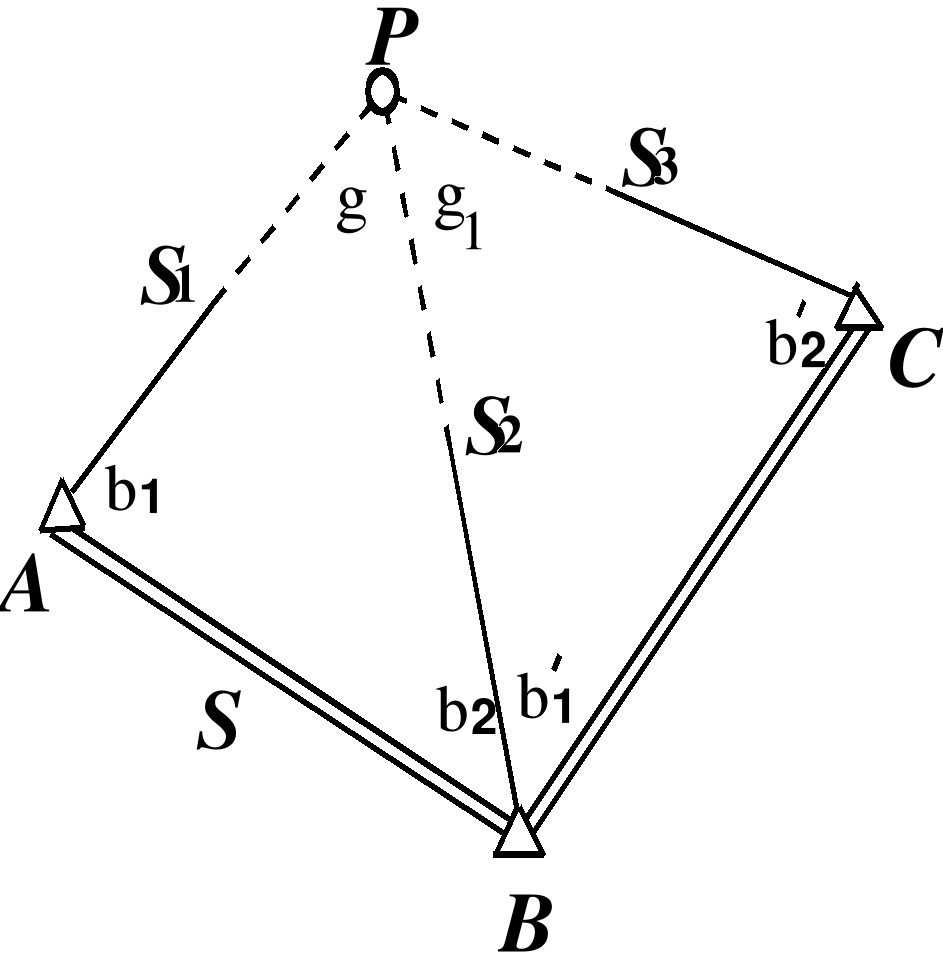
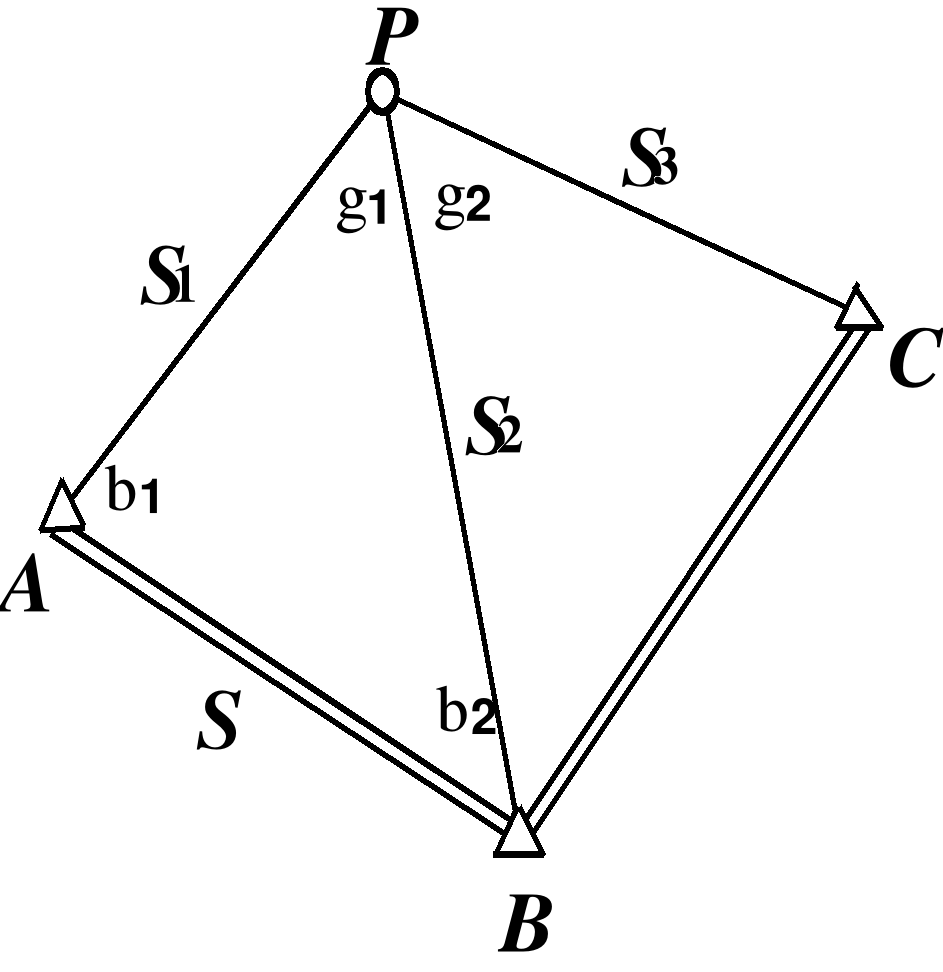
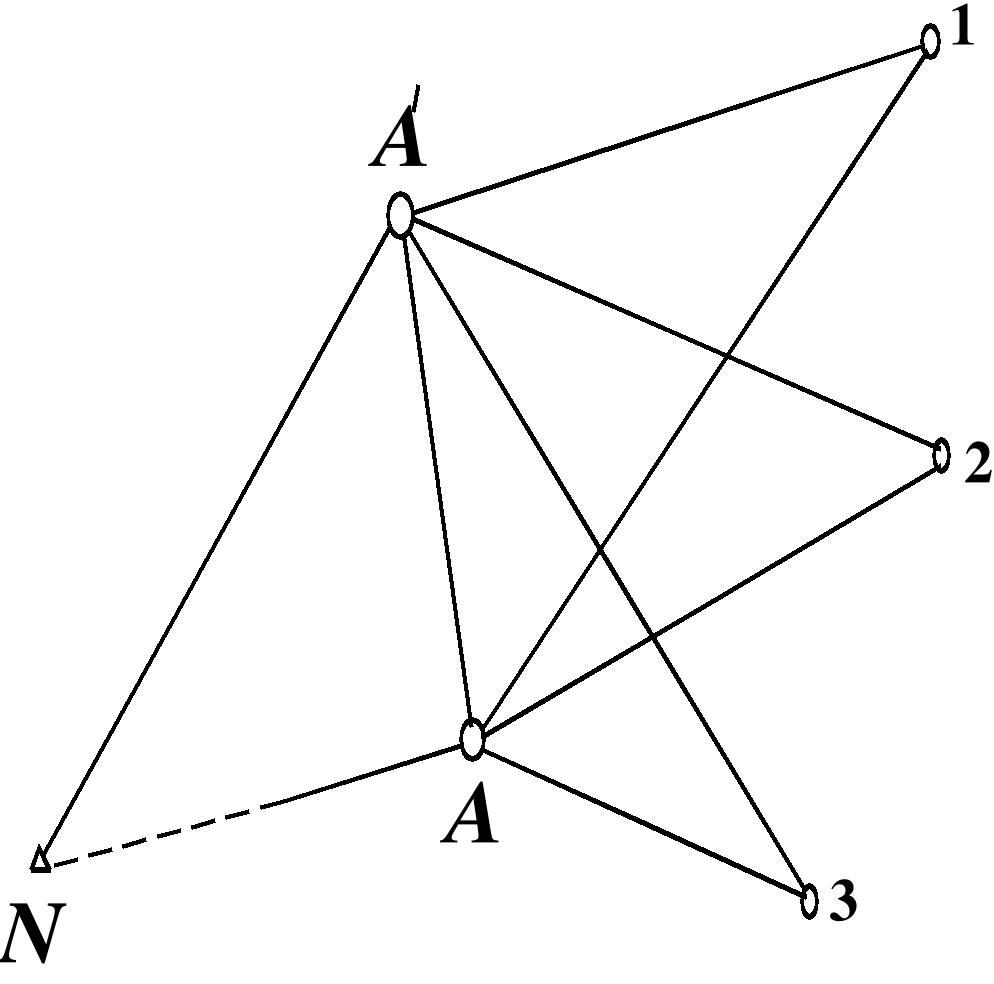
При привязке полигонометрического (теодолитного) хода к пункту триангуляции, на котором нельзя установить прибор, выбирают на земле вблизи этого пункта А (на расстоянии 50–м от него) точку Р в таком месте, чтобы, кроме пункта А были видны два удаленных пункта исходной сети В и С (один из них необходим для контроля) и удобно было измерить два базиса для определения неприступного расстояния АР (рис. 2.13).
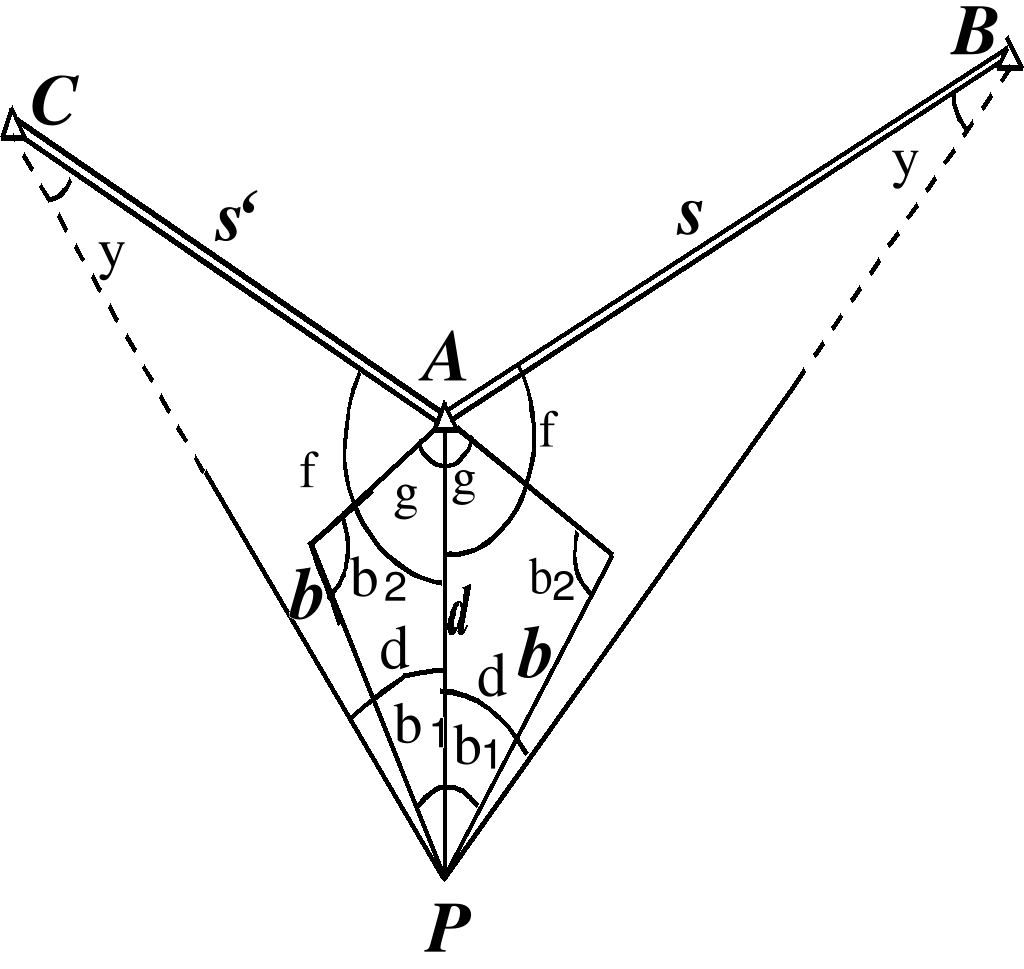
Рис. 2.13.
Для решения задачи измеряют базисы b и b' и шесть углов 1, 2, '1, '2, и ' причем второй базис и углы при нем используют для контроля определения расстояния АР и повышения точности получения окончательного его значения, а угол ' –для контроля правильности произведенных измерений, выписки исходных данных и повышения точности определения окончательных значений координат точки Р (если их получают по результатам решений двух вариантов задачи).
Рассмотрим решение задачи по этапам.
1. Вычисление дирекционных углов (АВ), (АС) и расстояний АВ=s, AC=s'.
Имея координаты пунктов А и В, вычисляют дирекционный угол (АВ)
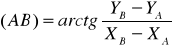 (1)
(1)
и расстояние АВ = s
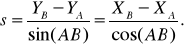 (2)
(2)
Если полученные значения s различаются на две единицы последнего знака, то за окончательное принимают среднее арифметическое.
Точно так же определяют дирекционный угол (АС) и расстояние АС. Иногда дирекционные углы (АВ), (АС) и расстояния АВ, АС не приходится вычислять, так как они бывают известны из материалов исходной геодезической сети.
2. Вычисление расстояния АР=d.
Недоступное расстояние АР = d определяют дважды:
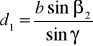 и
и 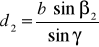 , (3)
, (3)
где = 1800 –(1 + 2), ' = 1800 –('1 + '2).
Разность |d1 –d2| не должна превышать 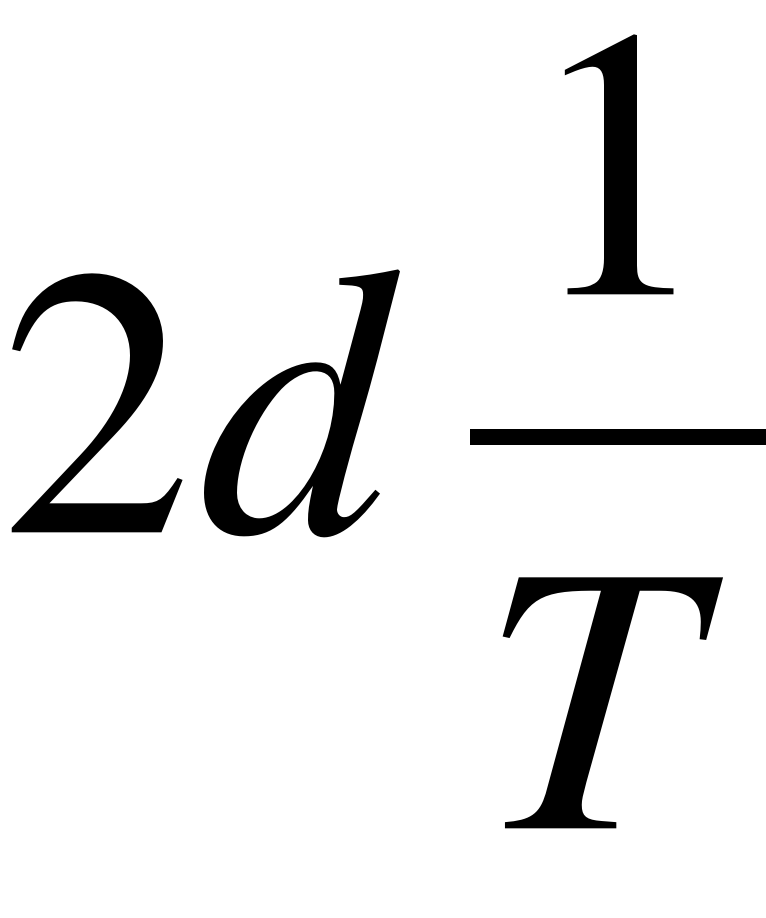 , где
, где  –предельная относительная погрешность измерения базисов b и b'.
–предельная относительная погрешность измерения базисов b и b'.
За окончательное значение расстояния АР принимают среднее арифметическое значение
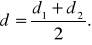 (4)
(4)
3. Вычисление дирекционного угла (AP).
Решая треугольники ABP и ACP, находят
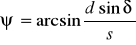 и
и 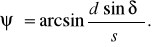 (5)
(5)
Затем вычисляют вспомогательные углы и '
= 1800 –( + ), ' = 1800 –(' + '). (6)
По этим углам определяют два значения дирекционного угла (AP)
(AP)1 = (АВ) + , (AP)2 = (АС) –'. (7)
Расхождение между значениями (АР)1 и (АР)2 должно удовлетворять неравенству
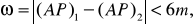 (8)
(8)
где m –средняя квадратическая погрешность измерения угла.
4. Вычисление координат точек P
По расстоянию AP = d и дирекционному углу (АР) находят, приращения координат
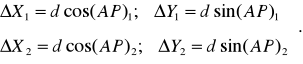 (9)
(9)
Затем вычисляют координаты точки Р
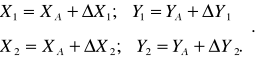 (10)
(10)
Полученные из двух решений значения координат не должны различаться больше, чем на величину 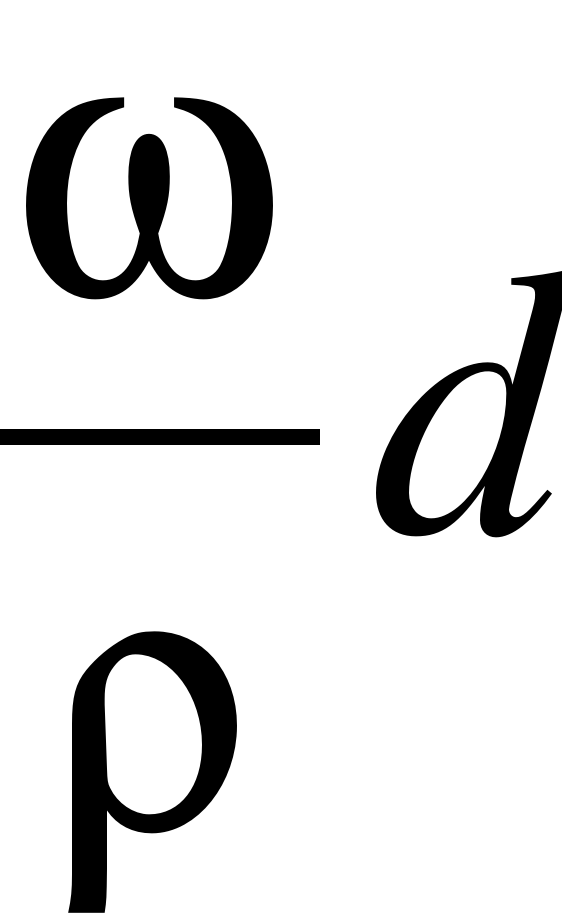 .
.
За окончательные значения координат принимают средние арифметические значения
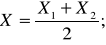
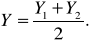 (11)
(11)
5. Оценка точности положения точки Р. Средней квадратической ошибкой положения точки называется средняя величина смещения относительно ее точного положения и определяемая в общем случае соотношением
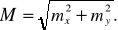 (12)
(12)
В данном случае средняя квадратическая ошибка положения точки Р может быть получена приближенно по формуле
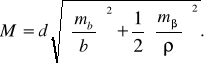 (13)
(13)
2. Прямая засечка.
Для решения прямой засечки, заключающейся в определении координат третьего пункта по координатам двух исходных пунктов и измеренным при них углам, предложено много различных формул. Рассмотрим некоторые их них.
а) Формулы Юнга
|
Рис. 2.14. |
Даны координаты точек А, B, C (рис. 2.14). Измерены углы 1, 2, 1/, 2/. Требуется определить координаты точки P (x, y). С выводом формул Юнга следует ознакомиться по учебнику [1, §161]. Если встать между исходными пунктами и смотреть на определяемый пункт P, то пункт А будет левым, а В –правым. |
Условимся обозначать соответствующими индексами координаты исходных пунктов и измеренные углы. Тогда формулам Юнга можно придать следующий вид:
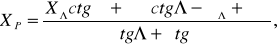 (14)
(14)
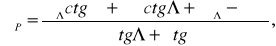 (15)
(15)
где и П –значения углов при левом и правом пунктах (=1, П = 2).
В целях контроля находят угол =1800–1 –2, а затем по координатам пункта В (левый) и координатам пункта Р (правый) по формулам (14) и (15) вычисляют координаты пункта А, которые должны совпадать с заданными.
Для полного контроля полевых измерений и выписки исходных данных нужно решить, задачу, используя координаты точек В и C.
Расхождение между абсциссами и ординатами при первом и втором решении должны удовлетворять условию
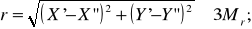 (16)
(16)
где Мr –среднее квадратическое расхождение в положении пункта Р из двух решений.
В свою очередь,
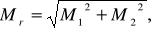 (17)
(17)
где М1 и М2 –средние квадратические ошибки положения пункта Р из первого и второго решения.
Средняя квадратические ошибки М положения пункта Р, определяемого прямой засечкой, вычисляется по формуле
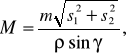 (18)
(18)
где m –средняя квадратическая ошибка измерения углов;
s1 и s2 –расстояние от исходных пунктов до определяемого (можно вычислить по координатам точек);
–угол засечки.
Под величиной М понимается выражение
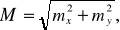 (19)
(19)
где mx и my –средние квадратические ошибки по осям координат.
Если расхождение r окажется допустимым, то за окончательное значение координат пункта Р берут среднее арифметическое, которое будет иметь ошибку
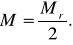 (20)
(20)
б) Формулы Гаусса.
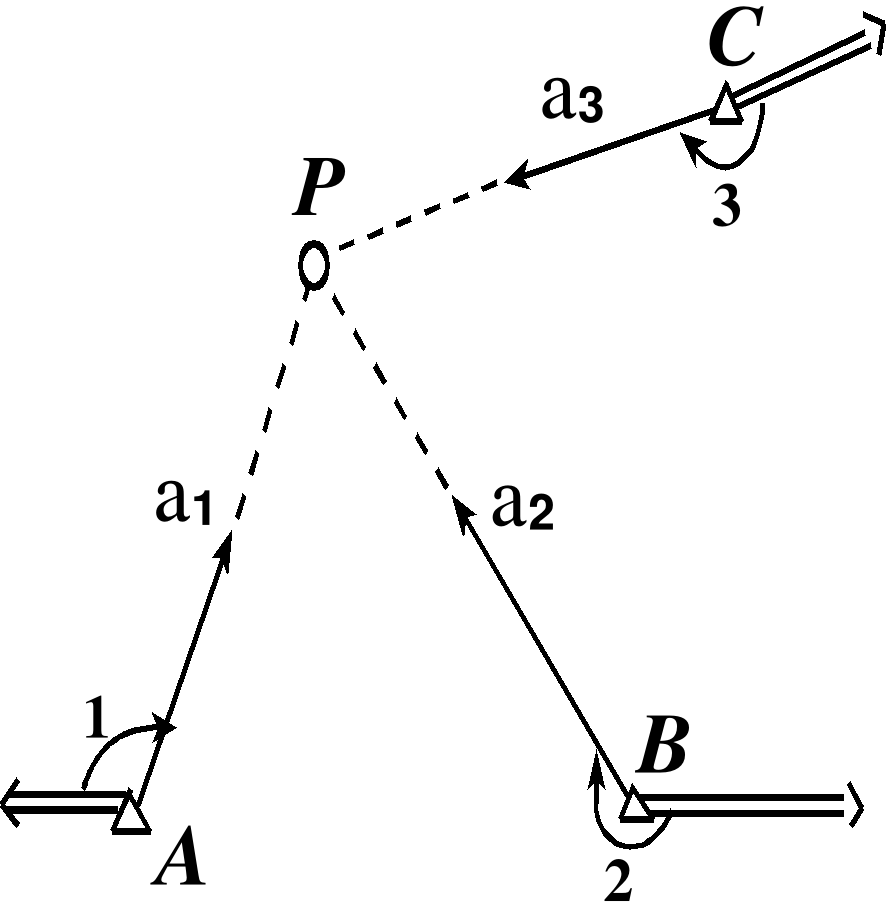
При определении точки прямой засечкой может не быть видимости между смежными точками А, В и С. В таком случае целесообразно пользоваться формулами Гаусса, в которые входят дирекционные углы направлений с данных пунктов на определяемый (рис. 2.15).
|
Рис. 2.15. |
Известны координаты точек А, B, C. Измерены углы 1, 2, 3. Требуется определить координаты точки P (X, Y). По измеренным углам и дирекционным углам направлений на другие исходные пункты, находим дирекционные углы направлений на определяемую точку 1, 2 и 3. |
Запишем соответствие
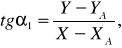
откуда
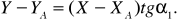 (21)
(21)
Аналогично получим
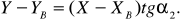 (22)
(22)
Найдем разность
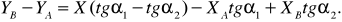
Отсюда
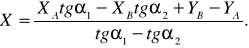 (23)
(23)
Вместо (21) и (22) можно записать
 (24)
(24)
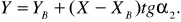 (25)
(25)
Нахождение ординат по двум формулам (24) и (25) позволяет проконтролировать вычисления. Таким образом, формулы (23), (24) и (25) –формулы Гаусса для определения координат.
Для контроля правильности полевых измерений вычисляют координаты точки Р вторично, используя другую пару исходных пунктов В и С и соответствующие дирекционные углы.
3. Обратная засечка (задача Потенота)
Сущность обратной засечки заключается в определении положения четвертого пункта (точки стояния) по трем исходным. Эта задача встречается при создании съёмочных сетей, привязке аэрофотоснимков, выносе проектов в натуру и других случаях.
Для ее решения предложено много аналитических и графических способов. При аналитическом способе задаются координаты трех исходных пунктов и измеренные углы или направления на определяемом пункте.
На основе трех исходных пунктов задача решается без контроля правильности измерения углов и выборки исходных данных. Поэтому на практике используют четыре исходных пункта.
Точность определения положения пункта обратной засечкой зависит от ошибок измерения углов, ошибок исходных данных и взаимного расположения пунктов. Если определяемый пункт находится вблизи окружности, проходящей через исходные пункты, то задача решается грубо. В связи с этим обратную засечку рекомендуется делать с предвычислением точности.
В учебнике [1, §162] приводится решение обратной засечки с использованием формул Кнейссля, однако она требует графических построений или дополнительных расчетов.
Приведем вывод формул, которые позволяют решить задачу с оценкой точности без графических построений.
|
Рис. 2.16. |
Даны координаты пунктов А, B, C. Измерены углы 1, 2 (рис. 2.16). Требуется определить координаты точки P (X, Y). В начале решением обратных геодезических задач определим дирекционные углы и длины исходных линий: |
 , (26)
, (26)
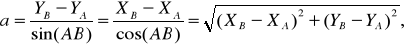 (27)
(27)
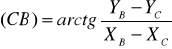 , (28)
, (28)
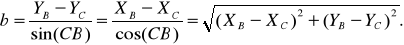 (29)
(29)
Далее задача сводится к определению углов и . Определим полусумму углов и , которую обозначим как А
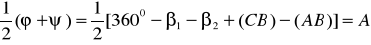 . (30)
. (30)
Определим полуразность этих углов, которую обозначим через В
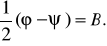 (31)
(31)
Определим диаметры описанных окружностей около треугольников ABP и BCP:
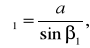
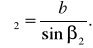 (32)
(32)
Выразим сторону ВР через Д1, Д2 и углы и .
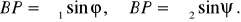 (33)
(33)
Откуда
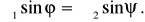
Разделив две части этого равенства на Д1sin , получим
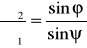 .
.
Образуем пропорцию и введем обозначение N:
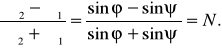 (34)
(34)
С учетом (32)
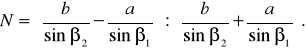 (35)
(35)
С учетом тригонометрических формул
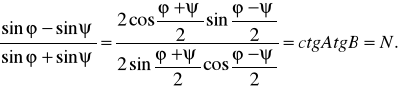
Отсюда
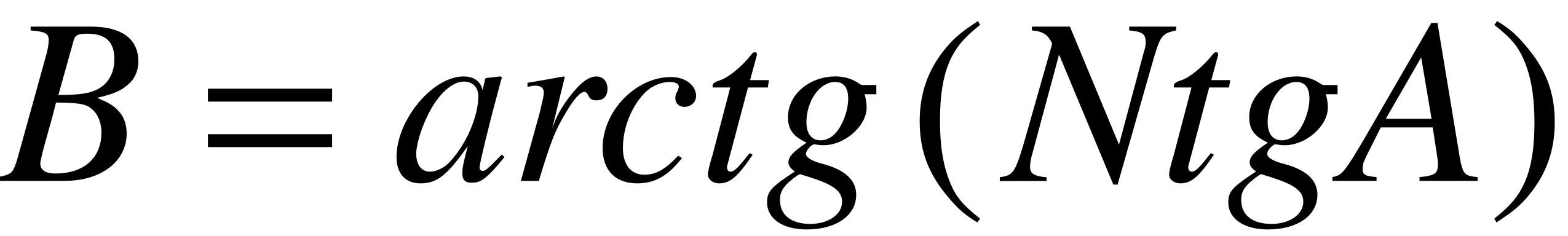 . (36)
. (36)
Вычислив значения А и В, определим углы и
= А+ В, (37)
= А –В. (38)
Далее определим длину линии АР
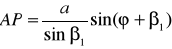 (39)
(39)
и координаты точки Р:
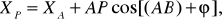 (40)
(40)
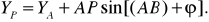 (41)
(41)
Таким образом, задача решается по формулам 26–.
Для контроля координат точки Р можно вычислить второй раз, используя формулы
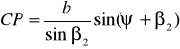 ,
,
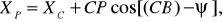
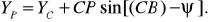
Среднюю квадратическую ошибку в положении пункта Р, определенного обратной засечкой, можно вычислить по формуле
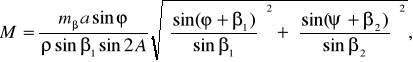 (42)
(42)
где m –средняя квадратическая ошибка измерения углов 1 и 2.
Рассмотренная обратная засечка по трем исходным пунктам называется однократной. В таком виде она, как правило, не допускается, т.к. не контролируется правильность измерения углов и выписка исходных данных.
Для полного контроля наблюдается не 3, а минимум 4 пункта (рис. 2.17).
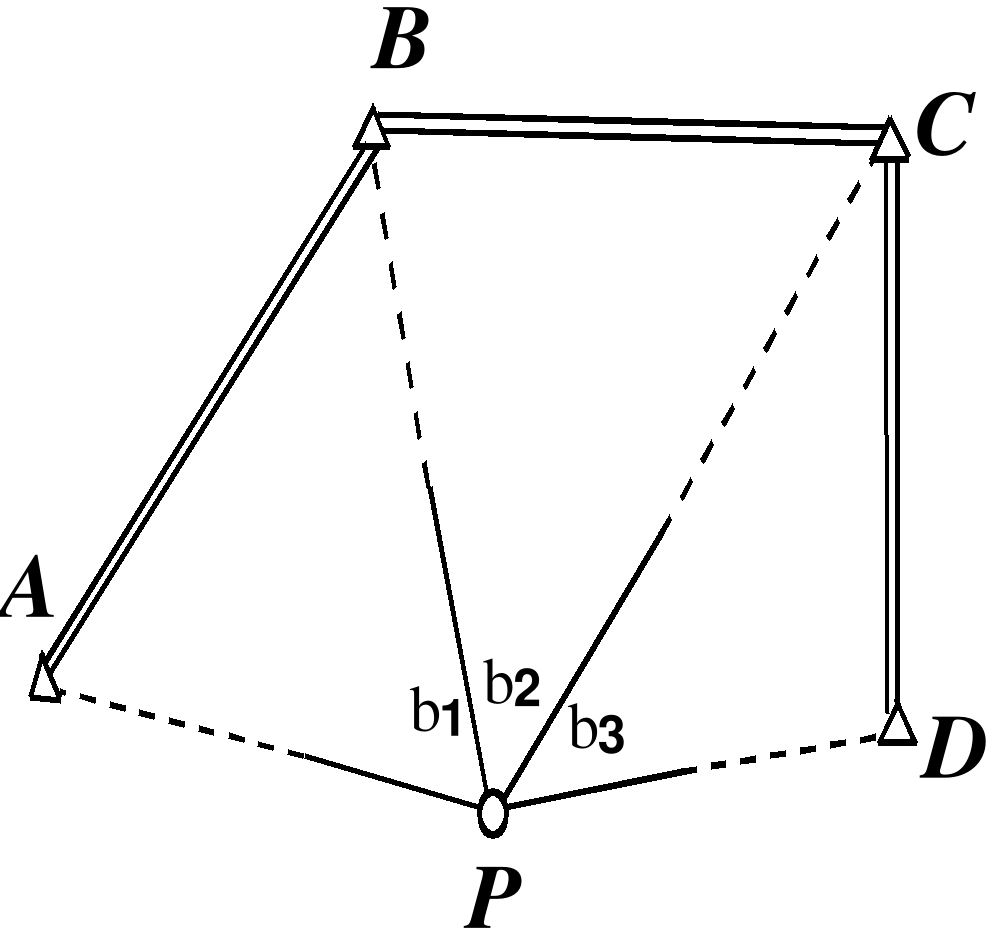
Рис. 2.17.
Задача решается дважды при различном сочетании исходных пунктов. Например, первый раз используются пункты А, В, С и второй раз пункты В, С, D. Для каждого варианта решения определяется средняя квадратическая ошибка положения пункта М по формуле (42). Ожидаемое среднее квадратическое значение Mr расхождения в положении пункта Р при двух решениях составит
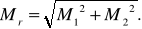
Отсюда допустимое расхождение в значениях вычисленных координат можно установить по формуле
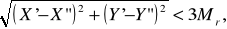
где X/ , Y/ –координаты точки из первого решения;
X// , Y// –координаты точки из второго решения.
За окончательное значение координат пункта Р берут среднее арифметическое, которое будет иметь ошибку
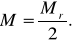
4. Линейная засечка.
Задача линейной засечки заключается в определении координат третьего пункта по координатам исходных пунктов и измеренным расстояниям от определяемого пункта до исходных (однократная засечка). Для контроля определения используются координаты третьего исходного пункта и расстояния до него от определяемого.
|
Рис. 2.18. |
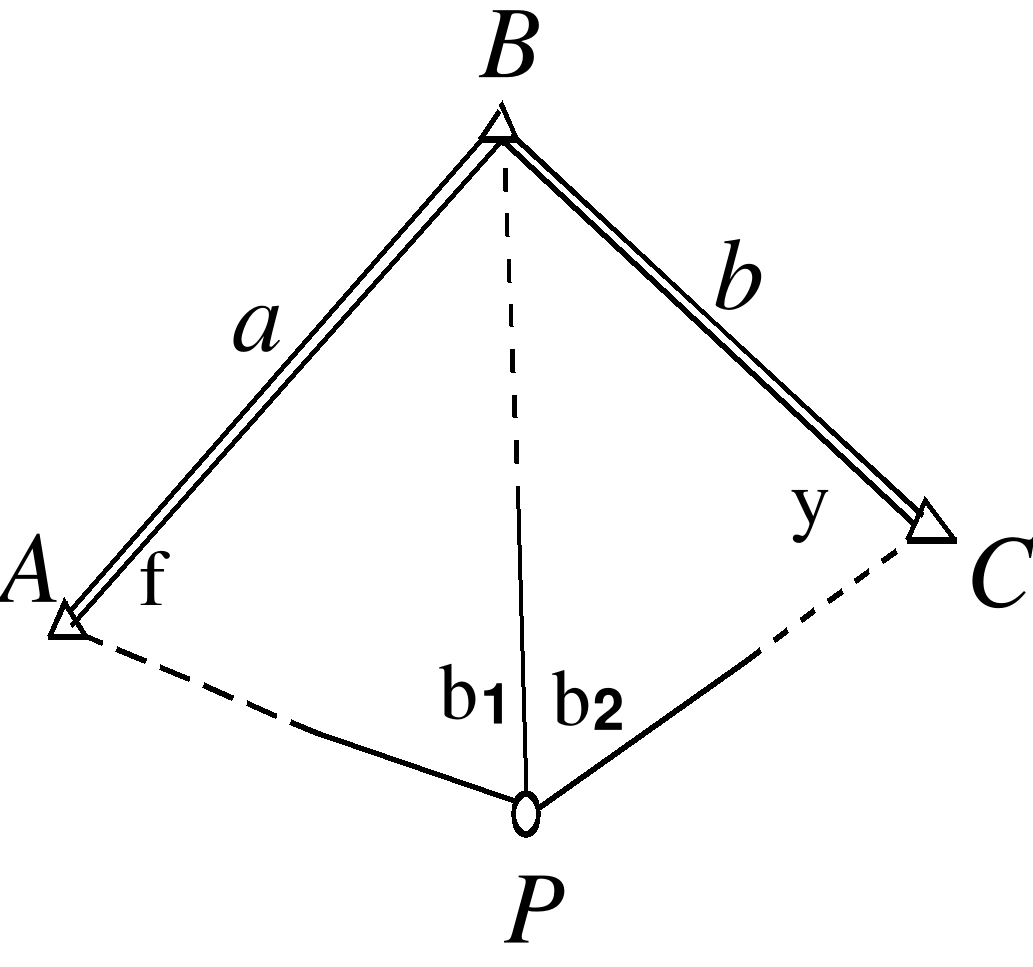
Даны координаты пунктов А, B, C. Измерены линии S1, S2, S3. Требуется определить координаты точки P (X, Y). Рассмотрим однократную засечку с использованием пунктов А и В (рис. 2.18). . Решением обратной геодезической задачи определим дирекционный угол и длину линии АВ: |
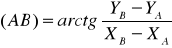 ,
,
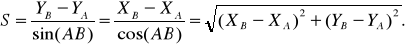
2. Определим угол 1, используя теорему косинусов:
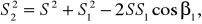 (43)
(43)
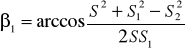 . (44)
. (44)
3. Определим дирекционный угол линии АР
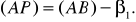 (45)
(45)
4. Определим координаты точки Р:
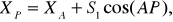 (46)
(46)
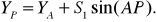 (47)
(47)
Для контроля решения задачи вычисляется длина линии ВР и сравнивается с измеренной
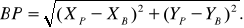 (48)
(48)
Расхождение не должно превышать 3 единиц последнего знака в измеренном значении линии S2.
Для полного контроля определения вычисляется сторона СР и сравнивается с измеренной S3
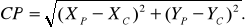 (48)
(48)
Допускается
|СР–S3| <6ms, (49)
где ms –средняя квадратическая ошибка измерения расстояний S3.
Однако в целях повышения точности окончательных значений искомых координат задачу лучше решать дважды. При втором решении используют исходные пункты В, С и расстояния S2, S3.
Допустимое расхождение в координатах определяют по формуле
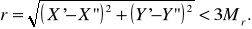
В свою очередь
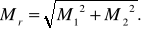
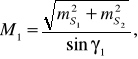
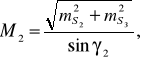 (50)
(50)
где М1 и М2 –средняя квадратическая ошибка положения пункта Р, определенного линейной засечкой в первом и втором вариантах;
–угол засечки.
Величину угла засечки (для первого решения) можно найти из выражения
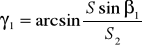 .
.
За окончательное значение координат пункта Р берут среднее арифметическое, которое будет иметь ошибку
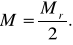
ЛЕКЦИЯ 11-12. «МЕТОДЫ СОЗДАНИЯ СЪЕМОЧНЫХ СЕТЕЙ»
- Теодолитные ходы.
- Микротриангуляция.
- Четырехугольники без диагоналей проф. Зубрицкого И.В.
- Полярно-лучевой метод.
- Боковые засечки профессора Дурнева
- Уравнивание полигонов коррелатным способом проф. В.В. Попова
- Уравнивание полигонов способом красных чисел проф. В.В. Попова
Рекомендуемая литература: [1], гл. XV, §§164; [21], гл. VI, §106; [27], гл. 11, §105, §112; [29], §§5.1–.4; [37], гл. 8, §46.
- Теодолитные ходы.
При создании съемочных сетей, в частности, для целей землеустройства, широко применяются теодолитные ходы. Этот метод весьма эффективен в условиях закрытой и полузакрытой местности.
|
Рис. 2.19. |
Если необходимо выполнить съемку какого-то землепользования, то основной теодолитный ход прокладывается по его границе. Внутри прокладываются диагональные ходы. Кроме того, прокладываются ходы для привязки к пунктам государственных геодезических сетей |
В результате, как правило, создается система замкнутых и разомкнутых теодолитных ходов, например, как на рис. 2.19. Углы в теодолитных ходах измеряются теодолитами не менее 30-секундной точности. Предельные угловые невязки определяются по формуле
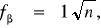 (1)
(1)
где n –число углов в ходе (полигоне).
Стороны теодолитных ходов измеряются светодальномерами, оптическими дальномерами, 20-ти метровыми лентами, рулетками и другими приборами. Теодолитные ходы в зависимости от условий местности прокладываются с предельными относительными погрешностями 1:3000, 1:2000, 1:1000.
Допустимые длины ходов размеры сторон и их число в ходе зависят от масштаба съемки и указываются в инструкциях.
- Микротриангуляция.
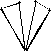
В условиях открытой и всхолмленной местности съемочные сети взамен теодолитных ходов могут развиваться методами триангуляции, которую в данном случае часто называют «микротриангуляцией». Она строится в виде несложных сетей треугольников (рис. 2.20, а), цепочек треугольников (б), вставок отдельных пунктов, определяемых прямыми (в), обратными (г) и комбинированными засечками (д).
e2)
e1)
e3)
e4)
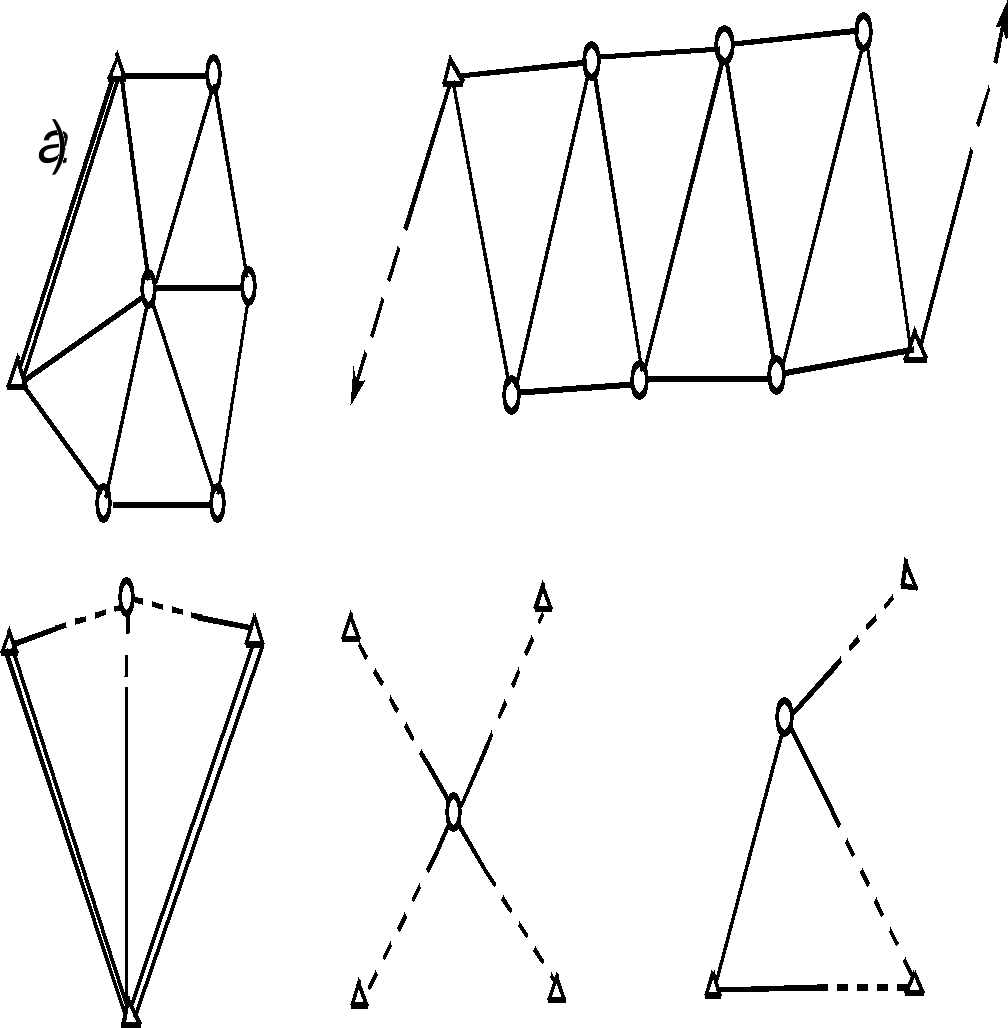
Рис. 2.20.
Применяются такие типовые фигуры: вставка в угол, центральная система, геодезический четырехугольник, цепь треугольников между исходными сторонами.
В качестве исходных сторон используется стороны триангуляции или полигонометрии 1 и 2 разрядов, а также специально измеренные базисные стороны с относительной ошибкой не более 1:5000.
Углы треугольников должны быть не менее 200, а стороны не короче 150 м.
Измерение углов производится теодолитами не менее 30-секундной точности двумя круговыми приемами. Невязки в треугольниках не должны превышать 1,5/.
Определение точек прямой засечкой производится не менее чем с трех пунктов, при этом углы засечки должны находиться в пределах от 30 до 1500.
Определение точек обратной засечкой производится не менее чем по четырем исходным пунктам.
3. Четырехугольники без диагоналей проф. Зубрицкого И.В.
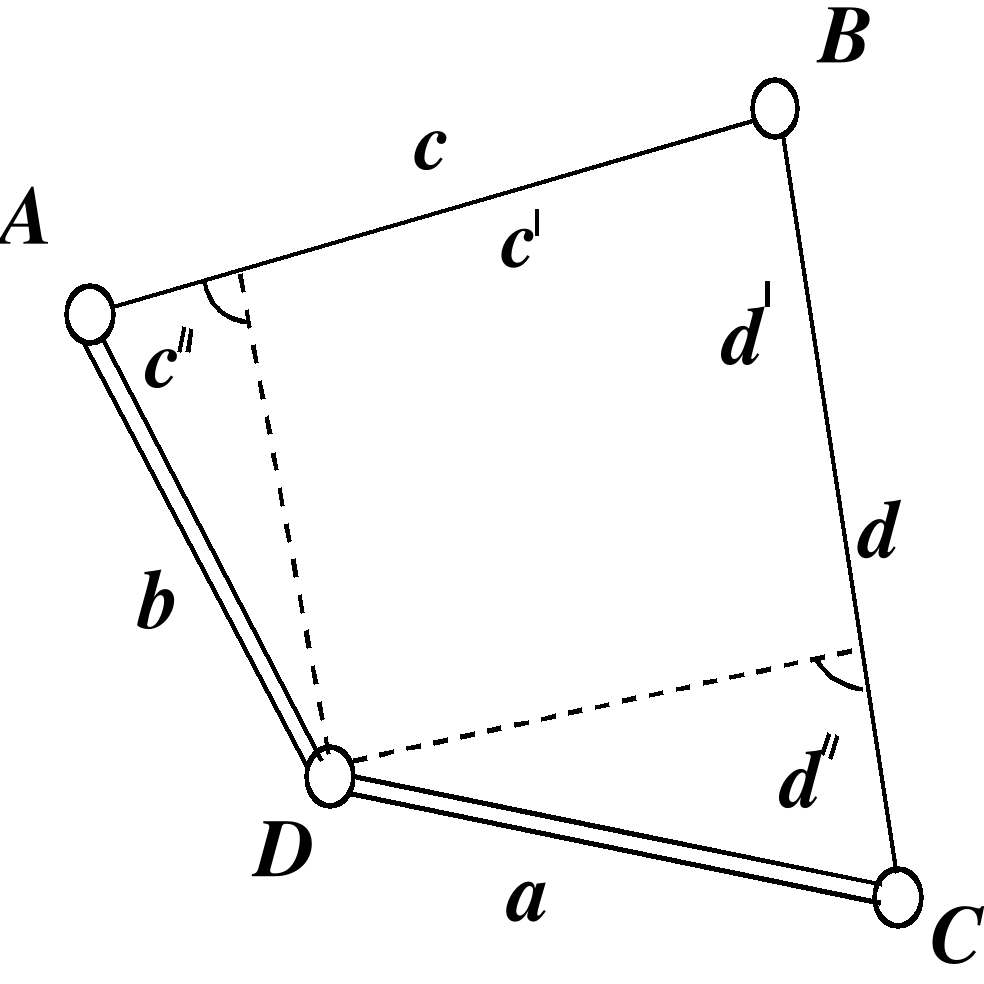
В условиях полузакрытой местности, в населенных пунктах с квартальной застройкой и в ряде других случаев обоснование можно создавать по методу четырехугольников без диагоналей, предложенному проф. И.В.Зубрицким, многие годы проработавшего в Белорусской сельскохозяйственной академии.
На местности создается система примыкающих друг к другу четырехугольников. В них измеряются все углы и некоторые стороны. Остальные стороны вычисляются. В исходном четырехугольнике обязательно должны быть известны две смежные стороны.
|
Рис. 2.21. |
Рассмотрим четырехугольник ABCD, в котором известны стороны a, b и углы А, B, C, D. Необходимо определить стороны c и d. Проведем из точки D линии, параллельные сторонами AB и BC (рис. 2.21). Непосредственно из чертежа получим: |
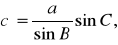
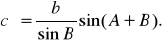
Отсюда
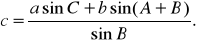 (2)
(2)
Аналогично найдем
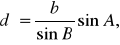
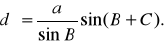
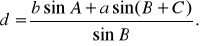 (3)
(3)
Решение четырехугольников можно проконтролировать путем вычисления сторон a и b, считая исходными стороны c и d по формулам
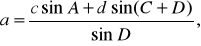 (4)
(4)
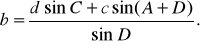 (5)
(5)
Съемочное обоснование можно создавать в виде цепей или сетей четырехугольников. При этом число необходимых исходных сторон, без которых нельзя вычислить все стороны, с увеличением числа фигур в процентном соотношении уменьшается. В качестве необходимых выбирают стороны благоприятные для измерений, чтобы можно было решить все четырехугольники.
4. Полярно-лучевой метод.
При наличии электронных дальномеров и тахеометров съемочное обоснование можно создавать полярно-лучевым методом. Схемы сетей могут быть разнообразными. Например, между исходными пунктами А и F прокладывается основной ход ABCDEF (рис. 2.22).
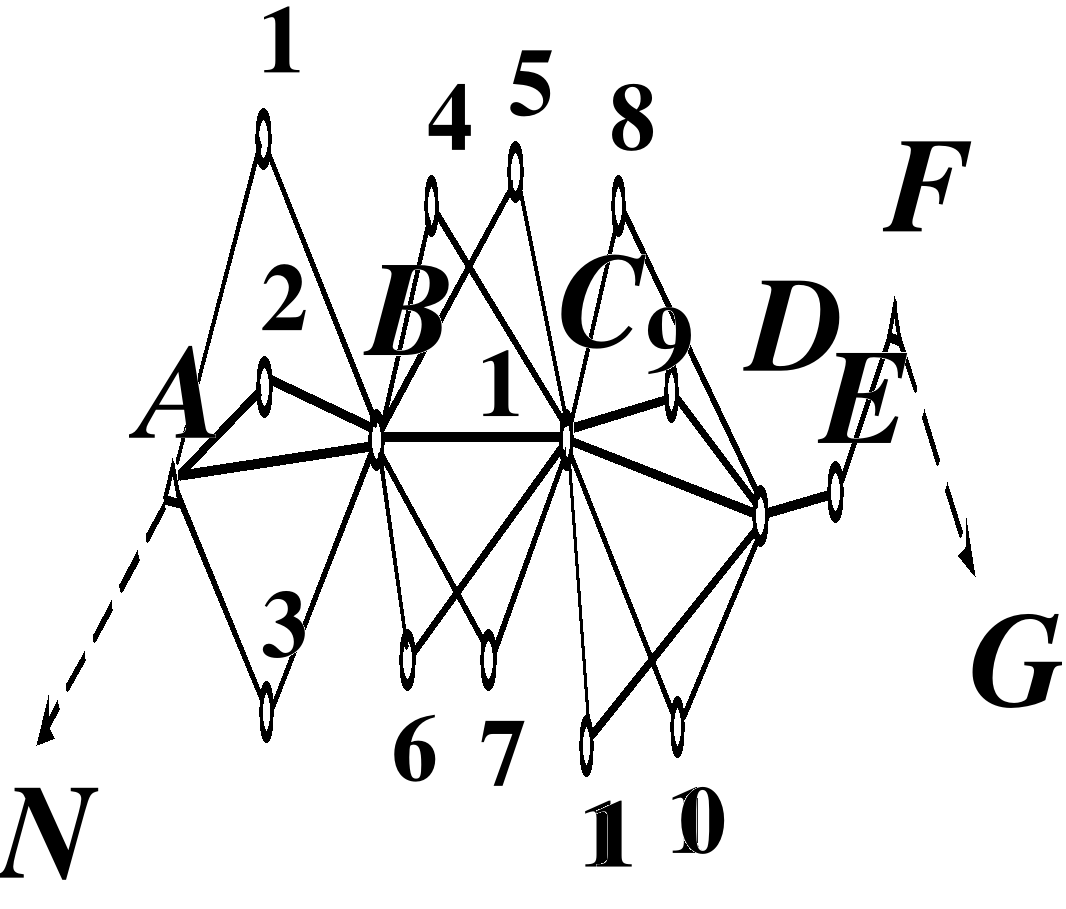
Рис. 2.22.
Относительно точек этого хода определяются точки 1…11 полярным способом.
Координаты точек 1, 2, …, 11 в целях контроля необходимо получать дважды. Поэтому их определяют полярным способом с двух станций. например, точки 1, 2, 3 определены с пунктов А и В. Если по условиям местности этого сделать нельзя, то используют дополнительную станцию, расположенную вблизи основной (рис. 2.23).
|
Рис. 2.23. |
Порядок наблюдений следующий. Устанавливают прибор на пункте А и измеряют направления на точки N, А/, 1, 2 и 3. Здесь АN – направление на другой исходный пункт, А/ – дополнительная точка, расположенная на расстоянии 5–10 м от точки А. |
Затем измеряют расстояния АА/ – рулеткой, а до точек 1, 2 и 3 электронным дальномером.
Зная дирекционный угол линии AN, по измеренным направлениям вычисляют дирекционные углы линий AA/, A1, A2, A3, а затем и координаты этих точек.
Для контроля устанавливают прибор в точке А/ и также измеряют направления и расстояния. Потом по координатам точек А/ и N вычисляют дирекционный угол линии А/N, находят дирекционные углы других линий и вычисляют повторно координаты точек А, 1, 2, 3. При допустимом расхождении за окончательное значение координат берется среднее.
Полярно-лучевой метод применим для любых условий местности, позволяет очень быстро выполнить полевые и вычислительные работы. При этом методе удобно координировать местные предметы. При наличии соответствующих приборов он будет эффективнее всех других методов.
Метод боковых засечек профессора Дурнева
В открытой местности когда выполнение линейных измерений в теодолитном ходе затруднено, целесообразно использовать метод боковых засечек.
Рассмотрим теодолитный ход (рис). В начале теодолитного хода измеряется одна сторона S1. В качестве такой стороны может выступать и сторона между исходными пунктами, в этом случае ее длину вычисляют по координатам. На местности выбирают твердые точки (1, 2, 3, 4, 5, 6), каждая из которых видна не менее чем с трех станций. В качестве таких твердых точек выступают столбы, колокольни, водонапорные башни, громоотводы и т.д. На каждой станции (А,В… G) измеряют не только углы в ходу, но и на выбранные точки – боковые пункты. В конце хода для контроля также измеряют одну сторону S2.
При обработке результатов измерений сначала вычисляют длины сторон. Рассмотрим треугольник АВ1. В этом треугольнике имеется 2 угла измеренные на станциях А и Б а также одна сторона с известной длины. По теореме синусов можно определить длину стороны В1. При этом синус угла на пункте 1 будет равен синусу суммы углов А и В. Решая по теореме синусов треугольник ВС1, можно определить ВС.
Рис 2.24. Схема теодолитного хода с боковыми пунктами
Полученное значение длины стороны является бесконтрольным. Для контроля необходимо решить треугольники АВ4, ВС4. В результате будет получено второе значение длины стороны ВС. Разность между первым и вторым значением длины стороны не должна превысить установленного допуска 1:2000 SBC. Если расхождение в допуске, то для дальнейших расчетов принимают среднее. Далее решая оставшиеся треугольники находят остальные стороны. Из решения треугольников будет получена длина стороны FG. Если ее значение отличается от S2 не более чем на 1:2000 S2 , то можно приступать к обработке теодолитного хода.
Обработка теодолитного хода выполняется по общепринятой методике. Допустимая относительная невязка хода не должна превысить 1:2000. После вычисления координат точек хода, решая прямые засечки, определяют координаты боковых пунктов. Их также включают в каталог координат пунктов съемочного обоснования, а в последующем используют при съемке.
Также возможно построение из замкнутого теодолитного хода используя один боковой пункт (рис ). В этом случае необходимо тщательно измерить расстояние S1, так в данной сети отсутствует контроль линейных измерений.
Рис 2.25. Схема замкнутого теодолитного хода с одним боковым пунктом
2 – в настоящее время сети сгущения включены в ГГС.
ОБЩИЕ СВЕДЕНИЯ О ПОСТРОЕНИИ ГОСУДАРСТВЕННОЙ ГЕОДЕЗИЧЕСКОЙ СЕТИ, СЕТЕЙ СГУЩЕНИЯ И СЪЕМОЧНЫХ СЕТЕЙ
 ,"
,"

 а)
а) б)
б)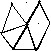 в)
в)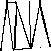 г)
г)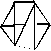 д)
д)