Кривые второго порядка

План-конспект лекции

Учитель: Тырышкина Ксения Викторовна.

Дисциплина: геометрия (элективный курс).

Тема лекции: Кривые второго порядка.

Тип лекции: лекция, основанная на имитации деятельности учреждений и организаций.

Цель лекции: способствование повышению уровня компетентности учащихся в сфере применения и способах построения кривых второго порядка.

Задачи лекции:

- образовательная: обеспечить условия для овладения учащимися компетенциями в сфере построения кривых второго порядка и области их применения;

- воспитательная: способствовать воспитанию интереса к изучению математики через рассмотрение исторического материала и межпредметных связей;

- развивающая: создать условия для развития мышления и коммуникативной компетентности учащихся; способствовать активизации самостоятельной работы и организации рефлексии собственной деятельности.

Оборудование к уроку, средства обучения: слайд – презентация PowerPoint с рисунками к заданиям; компьютер; проектор, экипировка для судьи в виде черной мантии и шляпы, «Большой энциклопедический словарь», ободки на голову для подсудимых и обвиняемых.

План занятия

№	Этап занятия	Время (мин.)	Средства обучения
1	Мотивационно-ориентировочная часть	4	-
2	Операционно-познавательная часть	80	презентация
3	Рефлексивно-оценочная часть	6	презентация

Ход занятия

1. Мотивационно-ориентировочная часть

Я: Здравствуйте, сегодня у нас необычное занятие, на котором мы познакомимся с историей возникновения кривых и областью их применения.

Все просто: наш мир не прямой из кривых.

Давно?

Так с рожденья Галактики было.

А кто же его искривляет?

Светило.

Все солнца, все звезды,

Как будто магниты,

Тянут планеты,

Кривят орбиты,

Они заставляют планеты кружиться,

А чья в том вина?

Тяготенья вина.

Время – пространство.

Оно искривляет

И геометрию мира меняет.

А если все звезды учесть, то на практике

Мы круг совершили б,

Летя сквозь Галактики.

2. Операционно-познавательная часть

Я: Встать! Суд идет!

Сегодня в этом зале слушается дело по обвинению кривых в бесполезности и вредительстве. К суду привлекаются: парабола, эллипс, гипербола. Обвинение представляют: треугольник, трапеция, квадрат.

Прошу всех сесть!

Первым слушается дело по обвинению параболы в бесполезности и даже вредности ее существования. Подсудимая, прошу встать!

Я: Ваше имя?

Парабола: Парабола.

Я: Год рождения?

Парабола: 350 год до н. э.

Я: Ваши родители?

Парабола: Конус и плоскость.

Я: Национальность?

Парабола: Гречанка

Я: Признаёте ли вы себя виновной?

Парабола: Нет!

Я: В таком случае слово представляется обвинителю. Господин Треугольник, прошу встать. Клянитесь говорить правду и ничего, кроме правды.

Треугольник: Клянусь говорить правду, только правду и ничего, кроме правды. Господа! Парабола является, пожалуй, одной из самых известных кривых в математике и, наверное, никакая другая кривая не имеет в своём характере столько ужасных черт, как она.

На вопрос: «Что такое парабола?» - большинство отвечает, что это график функции Но это неверно! Параболой называется график функции без всяких. Итак, обвинение первое: завоевав наше доверие, сделав головокружительную карьеру, парабола даже не сочла нужным представиться нам, так и ходит из тетради в тетрадь, из книги в книгу важный полный многочлен второй степени, а не скромная, изящная Но эта черта характера параболы не худшая. Оказывается, парабола – чётная функция. Замаскировавшись под своим квадратом, она всегда так и ждёт момента, чтобы сбить с толку несведущего человека. Действительно, пусть имеется значение функции для требуется узнать, какой аргумент у функции. Многие ответят, что х=1. Да но «плюс» или «минус» ? Это никому не известно: ведь и в квадрате есть . Поэтому мы и пишем

Но это ещё что! Самым ужасным является то, что парабола любит совать свой нос туда, куда её не просят. Например, параболе очень нравится формула . А это ни больше, ни меньше, как траектория полёта бомбы, сброшенной с самолёта. А парабола описывает полёт снаряда. Вот, оказывается, какой опасный преступник эта парабола! Миллионы жертв на её совести! Итак, в результате тщательного расследования вина подсудимой полностью доказана. Следствие считает необходимым рекомендовать суду высшую меру наказания и считать коэффициент «а» при равным 0. Тогда парабола превратится в прямую. У меня всё, господа!

Я: Слово для защиты предоставляется подсудимой. Парабола, что вы можете сказать в своё оправдание?

Парабола: Высокий суд! Только что меня здесь обвинили в бесполезности и вредности. Горько и обидно мне слушать эти слова. Оглянитесь вокруг – вы всюду увидите меня.

Я: Спасибо, парабола, присаживайтесь! Давайте подумаем, где мы можем в жизни встретить параболу? Может она все-таки не является бесполезной для нас?

Учащиеся: Абажур и лампочка имеют форму параболы, струя жидкости описывает параболу. Если свет конической лампочки направить на плоскость, освещённая часть плоскости будет ограничена параболой. Траектория, по которой двигается скакалка во время прыжков на ней, имеет вид параболы.

Я: Верно сказано! Нас повсюду окружает парабола. А какая она красивая, изящная. Давайте попробуем нарисовать ее такой, какая она встречается нам в жизни: стройной, четко устремившейся вверх.

Будем строить по определенному алгоритму. А вот по какому алгоритму, вы должны догадаться сами. Внимательно смотрите на доску и следите за построением параболы, а в тетрадях вам необходимо будет записать только алгоритм, по которому были выполнены построения.

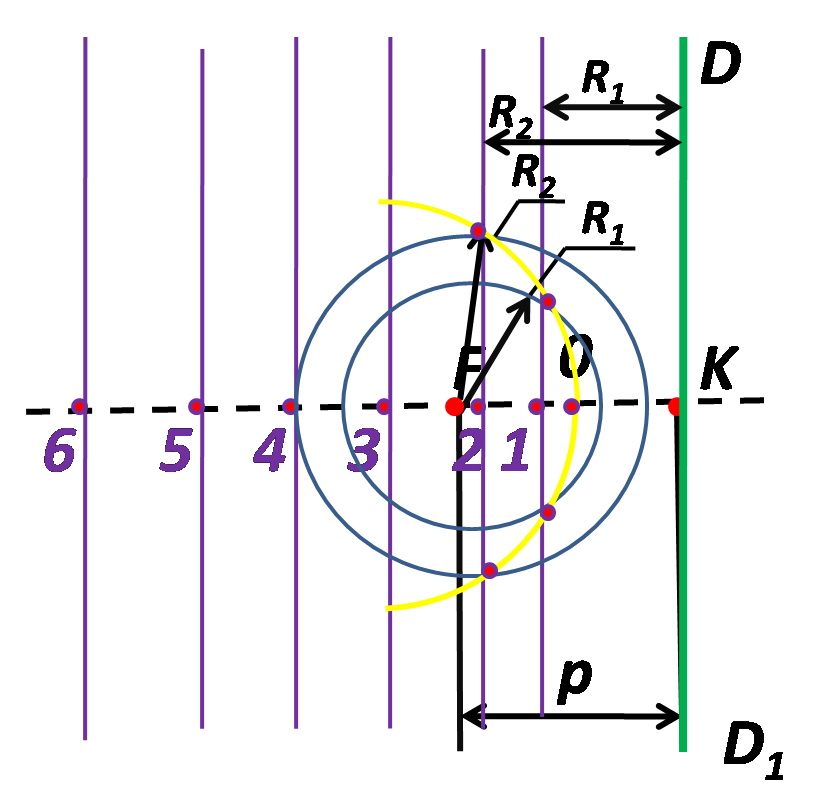
Учащиеся по очереди называют каждый элемент в построении.

Построение параболы при заданной величине параметра p выполняется в следующей последовательности:

1) Проводят ось симметрии параболы и откладывают на ней отрезок KF=p;

2) Через точку K перпендикулярно оси симметрии проводят директрису DD1;

3) Отрезок KF делят пополам получают вершину 0 параболы;

4) От вершины отмеряют ряд произвольных точек 1, 2, 3, 5, 6 с постепенно увеличивающемся расстоянием между ними;

5) Через эти точки проводят вспомогательные прямые перпендикулярные оси параболы;

6) На вспомогательных прямых делают засечки радиусом равным расстоянию от прямой до директрисы;

7) Полученные точки соединяют плавной кривой.

Я: Парабола, вы хотите еще что-нибудь сказать в свою защиту?

Парабола: У меня есть такие замечательные свойства, без знаний которых плохо приходилось человеку. Вы видели, какие ровные лучи пускает в ночное небо прожектор? Это достигается с помощью параболических отражателей. Если источник света поместить в фокус параболического зеркала, лучи, отразившись, пойдут параллельным пучком и, наоборот, параллельные пучки света, отразившись от зеркала, соберутся в одной точке – фокусе параболы. Это свойство применяется в рефлекторных антеннах, радиотелескопах, солнечных установках, радиолокаторах.

Мчится поезд, поворот и … взрыв, крушение, сотни жертв. А сами попытайтесь повернуть на велосипеде не по параболе. Видно, без меня не обойтись. Но я могу не только помогать людям, я могу их веселить. Во многих парках есть аттракцион «Парабола чудес», здесь снова я.

Мне кажется, я привела достаточно доказательств моей полезности и необходимости. Я считаю обвинение, предъявленное мне, необоснованным и прошу Высокий суд пересмотреть моё дело.

Треугольник: Господин судья, прошу слова.

Я: Суд разрешает.

Треугольник: Вы сказали много красивых слов в свою защиту. А что вы скажете о своей причастности к упомянутым мною формулам?

Парабола: Да! Это ужасно! Но надо уметь правильно использовать меня. Космические корабли, станции, доставившие лунный грунт на Землю, - ведь только я могла это сделать!

Я: У вас есть ещё вопросы, господин Треугольник?

Тогда переходим к слушанию дела по обвинению Эллипса в бесполезности его существования. Слово для обвинения предоставляется госпоже Трапеции.

Трапеция: Господа, осмелюсь вас заверить, что я решительный противник всех кривых, в том числе и эллипсов.

Господин судья! Углы, которые я имею честь представлять, в тесном содружестве с прямыми линиями идут прямой дорогой жизни, никогда не скрывают своих недостатков, везде действуют прямо, открыто.

А что представляют собой они? Одно слово – кривые. Эти подозрительные элементы не прочь покривить душой. Вот, скажем для примера эллипс. Он нам не нужен ввиду его бесполезности. Во-первых, его очень трудно чертить. Чертишь, чертишь, ничего не получается, да ещё и оценку плохую получишь. Эллипс очень похож на окружность, только деформированную, и ничем от этой выскочки окружности не отличается. Да ещё хуже её: что ни эллипс - то фокус. Заметьте, господа: никакого роста, прогресса, замкнутая, ограниченная фигура. Я думаю, мои коллеги со мной согласны. Мою правоту подтверждают и слова поэта: Я с детства не любил овал, Трапецию я с детства рисовал.

Я: Спасибо, Трапеция, присаживайтесь! Ребята, неужели вы согласитесь с Трапецией, что эллипс это бесполезная фигура? (дождусь ответа от детей). Я, например, не услышала ни одного аргумента, чтобы так считать. А то, что Трапеция не умеет строить эллипс – это лишь доказывает отсутствие ее внимательности на занятиях по геометрии. Давайте же покажем, что, если правильно построить эллипс, он будет красивым и стройным.

Вызываю кого-нибудь к доске строить эллипс. Остальные у себя в тетради.

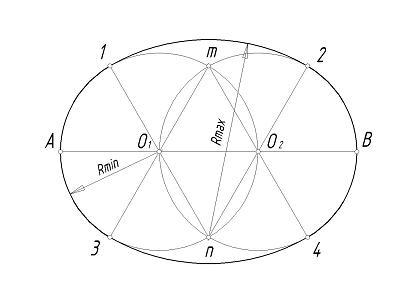
Я: Вот он, какой красивый и стройный эллипс у нас получился.

Я: Слово для защиты предоставляется подсудимому. Эллипс, что вы можете сказать в своё оправдание?

Эллипс: Господин судья! Уважаемая публика. Сегодня здесь, в зале суда, обвинив меня в бесполезности, мне нанесли тяжёлое оскорбление. Я не согласен с обвинениями и докажу, что они несправедливы. Мои родители – конус и плоскость - были вполне порядочными фигурами. Они были знакомы с греческим учёным Менком ещё в 350 году до н.э. Дальше меня воспитывали Эйлер, Паскаль, Декарт. А теперь самое главное: что было бы, если бы меня не было? Плохо было бы, очень плохо, смею вас заверить! Невозможно было бы жить.

Я: Присаживайтесь Эллипс! А что имел ввиду Эллипс, когда говорил, что без него невозможно жить? Давайте подумаем об этом! Представьте машину. Как можно связать машину с эллипсом?

Учащиеся: Маховики и другие элементы в машине имеют в сечении эллипс.

Я: Верно! Если бы не было эллипса, мы бы с вами ходили сейчас пешком. Давайте еще вспомним астрономию. По каким орбитам двигаются наши планеты?

Учащиеся: По эллиптическим орбитам.

Я: Это действительно так. Если бы планеты двигались по другим орбитам, то неизвестно где бы мы с вами сейчас были. Может быть, жили уже на Марсе. А так эллиптические орбиты наиболее выгодные.

Вот как наш эллипс связан и с конструкторскими науками, и с астрономией. Но это еще не все. Оказывается наш знаменитый эллипс оставил свой вклад и в литературу. Эллипс или эллипсис означает опущение, пропуск элемента речи, обычно - такого, который может быть легко восстановлен в данном контексте.

Я: Переходим к слушанию дела по обвинению Гиперболы в бесполезности её существования. Слово для обвинения предоставляется господину Квадрату.

Квадрат: Высокий суд! Госпожа трапеция совершенно верно охарактеризовала Эллипс. Совершенно с нею согласен. То же самое хочу сказать о Гиперболе. Смею вас заверить, что в ней тоже ничего хорошего нет. Ниоткуда пришла и туда же, в никуда, ушла. Распалась на две части - и не поймёшь: то она тут, то она там. Никакой самостоятельности. Всю жизнь стремится к прямым, жить без них не может. Куда прямые, туда и она. Всю жизнь бежит рядом с ними, но всё – таки в стороне держится, нет, чтобы схлестнуться характерами. Гипербола – кривая двуличная, и решения она принимает тоже раздвоенные, ни к селу, ни к городу. Мы, фигуры почётные и уважаемые, смириться с её существованием в математике не можем. Вот я, к примеру, или мой коллега Треугольник - у нас всё определённо, строго, чётко. Ученики нас не бояться, мы их тоже. Рисуют нас красиво, мы на них не в обиде. А вас, уважаемая, даже и нарисовать – то с ходу нельзя. Ещё «кривее», чем на самом деле получается. Да ещё и обижаетесь. Уж если вас ученики не любят, то плохи ваши дела. Призываю Высокий суд изгнать её, эту самую гиперболу, из математики. Пусть она бежит за своей спутницей – прямой, и назад не возвращается. Коллеги со мной согласны, надеюсь? У меня всё, господа!

Я: Слово для защиты предоставляется подсудимой. Что вы можете сказать в своё оправдание?

Гипербола: (350 год до н. э., родители – конус и плоскость, гречанка). Как вы сами, господин Квадрат, сказали, я – кривая, и ничего общего с прямыми не имею. Где вы видите у меня прямые? Молчите? Вам нечего сказать. Но я действительно распалась, да, только на пару кривых. А где вы были, когда я, бедная, несчастная, распалась? Вы не помогли мне, вы только обвинять умеете. Но все, же нашлись люди, которые не только поддержали в трудную минуту, но и нашли способ использовать меня.

Я: Да, трагична судьба гиперболы. Но радует то, что она смогла все преодолеть и даже больше. Все мы с вами ежедневно смотрим телевизор, но никто из нас не задумывался, что радиобашня на Шабаловке в Москве имеет форму гиперболоида. Она была создана по проекту и под руководством В.Г.Шухова – великого русского инженера.

А, знаете ли, почему некоторые кометы, один раз пролетев мимо Солнца, уже никогда не возвращаются?

Учащиеся: Потому что они сгорают.

Я: Но это не главное, главное то, что многие из них движутся по гиперболе, а ее ветки, как вы знаете, бесконечны.

Каждый из нас очень часто говорит такую фразу: «Я тебя уже сто лет не видел». А знаете ли как в литературе называется данная стилистическая фигура?

Учащиеся: преувеличение

Я: Верно, это преувеличение, или по-другому гипербола.

А как вы думаете, это понятие пришло в литературу из математики или наоборот?

Учащиеся: Так как мы математики, то мы ответим, что гипербола пришла в литературу из математики.

Я: Интересный конечно у вас подход. Но, если порассуждать, то гипербола в математике появилась в 350 г. до н.э., а стилистическая фигура гипербола стала использоваться в ХIII веке для обозначения стилистического и риторического приема чрезмерного преувеличения каких-либо свойств изображаемого предмета. Причем, термин «гипербола» был введён в научный обиход древнегреческим математиком Аполлонием Пергским. Поэтому вы оказались правы, и данное понятие пришло в литературу из математики.

Я: Зато, что касается построения гиперболы, то здесь дело обстоит немного сложнее, чем с параболой и эллипсом, поэтому построение будем производить следующим образом: одну ветвь я строю, с подробным объяснением, а вторую, вы строите самостоятельно, после чего обменяйтесь тетрадями с соседом и поставьте друг другу оценки за выполнение данного задания. А я потом соберу тетради и проверю, как вы друг друга оценили.

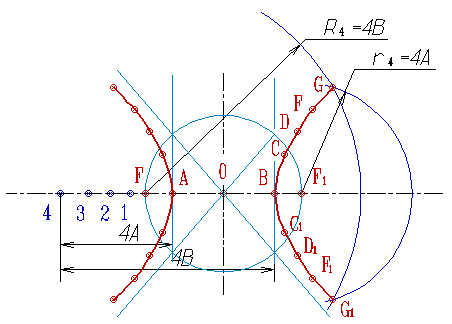
Я: Мы с вами рассмотрели некоторые способы построения параболы, гиперболы и эллипса, познакомились с историей их возникновения и областью применения, но это лишь самый минимум, который включен в раздел «Кривые второго порядка».

Дома, предлагаю вам решить деятельностно - ценностную задачу «Замечательные кривые второго порядка и область их применения». Для нахождения ее решения можно воспользоваться следующей литературой: И.И. Привалов «Аналитическая геометрия», А.Ж.Жафяров «Аналитическая геометрия», Л.С. Атанасян «Аналитическая геометрия».

3. Рефлексивно-оценочная часть

Я: И так, перед вынесением приговора нашим обвиняемым, давайте вспомним все то, что мы сегодня про них говорили.

1. Какие основные кривые нами были рассмотрены?

2. Где в жизни применяется каждая из них?

3. В каких науках используются кривые второго порядка, которые сегодня были рассмотрены?

Я: Именем Высшего Совета науки Высокий суд постановляет:

Параболу и Гиперболу считать полностью оправданными ввиду их необходимости в жизни вообще и в математике в частности. Суд считает, что обвинение, выдвинутое против этих кривых, необоснованно. Суд предупреждает Треугольник и Квадрат, что за дачу ложных показаний они будут привлечены к уголовной ответственности.
Рассмотрев показания госпожи Трапеции, суд постановил: в связи с тем, что Эллипс находит широкое применение в науке и технике, считать его оправданным.

Кривые второго порядка