РЕШЕНИЯ СКАЛЯРНЫХ УРАВНЕНИЙ МЕТОДОМ ХОРД

СОДЕРЖАНИЕ

ВВЕДЕНИЕ......................................................................................................................3

ГЛАВА 1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РЕШЕНИЯ СКАЛЯРНЫХ УРАВНЕНИЙ МЕТОДОМ ХОРД……………………………..…….4

1.1. Численное решение скалярных уравнений........................................................... 4

1.2. Метод хорд................................................................................................................7

ГЛАВА 2. ПРАКТИЧЕСКАЯ ЧАСТЬ. РЕШЕНИЕ ЗАДАЧ…..………..................10

2.1.Пример 1. Решение скалярного уравнения методом хорд...............................…10
2.2.Пример 2. Решение скалярного уравнения методом хорд ……………………..11

ЗАКЛЮЧЕНИЕ..............................................................................................................13

СПИСОК ЛИТЕРАТУРЫ.............................................................................................14

ВВЕДЕНИЕ

На практике в большинстве случаев найти точное решение возникшей математической задачи не удается. Многие задачи требуют численных методов для своего решения. Особенность же этой области знания в том, что «наилучшего» численного метода обычно не существует, так как в одних условиях лучшим будет один метод, в то время как для других условий успешнее работает другой метод. Понять и обосновать, какой же метод выбрать как лучший, можно лишь проводя вычислительные эксперименты с различными методами и для различных задач и условий.

Актуальность темы обоснована тем, что благодаря методу хорд, можно решить скалярные уравнения, которые не решаемы с помощью алгебраических преобразований.

Целью курсовой работы является изучение теоретических основ метода хорд для решения скалярных уравнений.

Задачи курсовой работы:

1. Изучить метод хорд для решения скалярных уравнений.

2. Систематизировать материал о методе хорд для решения скалярных уравнений.

3. Рассмотреть решение скалярных уравнений методом хорд на конкретных примерах.

Курсовая работа состоит из двух глав, введения и заключения. Первая глава - теоретическая и содержит общие сведения о методе хорд. Вторая - это практическая часть. Здесь описывается метод хорд, разобранный на конкретных примерах. В заключении представлен вывод о проделанной работе.

ГЛАВА 1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РЕШЕНИЯ СКАЛЯРНЫХ УРАВНЕНИЙ МЕТОДОМ ХОРД

  1. Численное решение скалярных уравнений

Скалярными (нелинейными) уравнениями называются уравнения вида f(x) =0 (1.1)

где функция f(x) = 0 нелинейная:

  • нелинейная алгебраическая функция вида ;
  • трансцендентная функция (тригонометрическая, обратная тригонометрическая, логарифмическая, показательная или гиперболическая функция);
  • функция, полученная комбинированием этих функций [3].

Численное решение скалярных (нелинейных) уравнений вида f(x) = 0 заключается в нахождении значений x, удовлетворяющих (с заданной точностью) данному уравнению и состоит из следующих основных этапов:

1. Отделение (изоляция, локализация) корней уравнения, то есть нахождение интервалов из области определения функции f(x), в каждом из которых содержится только один корень уравнения (1.1).

2. Уточнение с помощью некоторого вычислительного алгоритма конкретного выделенного корня с заданной точностью [5].

Целью первого этапа является нахождение отрезков из области определения функции f(x), внутри которых содержится только один корень решаемого уравнения. Иногда ограничиваются рассмотрением лишь какой-нибудь части области определения, вызывающей по тем или иным соображениям интерес. Для реализации данного этапа используются графические или аналитические способы.

При аналитическом способе отделения корней полезны следующие теоремы [12]:

Теорема 1.1. Если непрерывная функция y = f(x) принимает на концах отрезка [a, b] значения разных знаков, т.е. f(a)-f(b)<0, то на этом отрезке содержится, по крайней мере, один корень уравнения (1) (рис. 1).

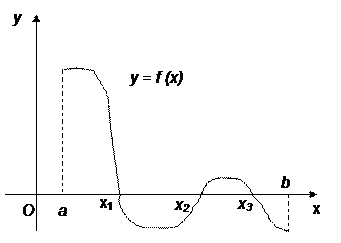
Рис. 1. Существование корня на отрезке.

Теорема 1.2. Если непрерывная на отрезке [a, b] функция  y = f(x) принимает на концах отрезка  значения разных знаков, а производная   сохраняет знак внутри отрезка [a, b] , то внутри отрезка существует единственный корень уравнения f(x) = 0 (рис. 2).

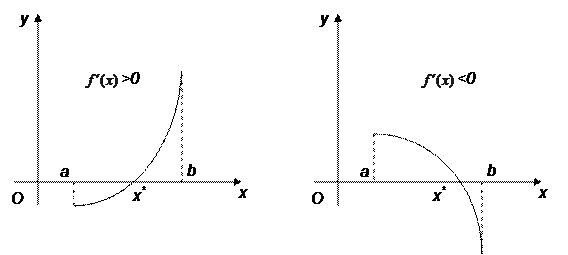
Рис. 2. Существование единственного корня на отрезке.

Достаточным признаком монотонности функции f(x) на отрезке [a, b] является сохранение знака производной функции.

Графический способ отделения корней целесообразно использовать в том случае, когда имеется возможность построения графика функции y = f(x). Наличие графика исходной функции дает непосредственное представление о количестве и расположении нулей функции, что позволяет определить промежутки, внутри которых содержится только один корень. Если построение графика функции y = f(x) вызывает затруднение, часто оказывается удобным преобразовать уравнение (1.1) к эквивалентному виду и построить графики функций и . Абсциссы точек пересечения этих графиков будут соответствовать значениям корней решаемого уравнения (рис. 3).

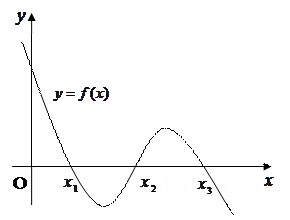
Рис. 3. Графическое отделение корней

Так или иначе, при завершении первого этапа, должны быть определены промежутки, на каждом из которых содержится только один корень уравнения.

Для уточнения корня с требуемой точностью обычно применяется какой-либо итерационный метод, заключающийся в построении числовой последовательности (k=0,1,2,…), сходящейся к искомому корню уравнения (1.1).


  1. Метод хорд

Метод, основанный на нахождении  по двум приближениям  и  с помощью линейной интерполяции, называемый методом хорд.

Идея метода состоит в том, что по двум точкам  и  построить прямую   (то есть хорду, соединяющую две точки графика y = f(x)) и взять в качестве следующего приближения  абсциссу точки пересечения этой прямой с осью . Иными словами, приближенно заменить на этом шаге функцию f(x) ее линейной интерполяцией, найденной по двум значениям x:  и . (Линейной интерполяцией функции f(x) назовем такую линейную функцию , значения которой совпадают со значениями f(x) в двух фиксированных точках, в данном случае - в точках  и ) [10].

В зависимости от того, лежат ли точки  и  по разные стороны от корня  или же по одну и ту же сторону, получаем рисунок 4: 

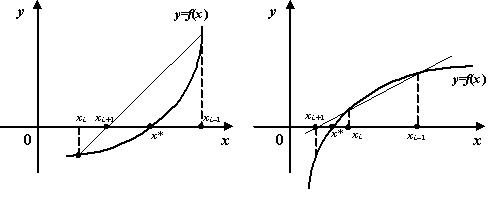
Рис. 4.Построение последовательного приближения по методу хорд: два случая

Очередное последовательное приближение будет зависеть от двух предыдущих: . Найдём выражение для функции .

Интерполяционную линейную функцию  будем искать как функцию с угловым коэффициентом, равным разностному отношению

,

построенному для отрезка между  и , график которой проходит через точку :

,

Решая уравнение , находим

,

то есть

. (1.2)

Заметим, что величина  может рассматриваться как разностное приближение для производной f’(x) в точке . Тем самым полученная формула (1.2) - это разностный аналог итерационной формулы метода Ньютона.

Вычисление по формуле (1.2) гораздо предпочтительнее вычисления по другой полученной нами формуле

,

хотя эти две формулы математически тождественны, поскольку при использовании формулы (1.2) в случае вычислений с округлениями (например, на компьютере) достигается меньшая потеря значащих цифр.

Имеются две разновидности применения формулы (1.2).

Первая разновидность: вычисления ведутся непосредственно по формуле (1.2) при i = 1, 2, 3… , начиная с двух приближений   и , взятых, по возможности, поближе к корню . При этом не предполагается, что  лежит между   и  (и что значения функции f в точках   и  имеют разные знаки). При этом не гарантируется, что корень попадёт на отрезок между  и  на каком-либо следующем шаге (хотя это и не исключено). В таком случае затруднительно дать оценку погрешности, с которой  приближает истинное значение корня , и поэтому довольствуются таким эмпирическим правилом: вычисления прекращают, когда будет выполнено неравенство  , где  - желаемая точность нахождения корня. При этом полагают приближенное значение корня равным .


Глава 2. ПРАКТИЧЕСКАЯ ЧАСТЬ. РЕШЕНИЕ ЗАДАЧ

2.1. Пример 1. Решение скалярного уравнения методом хорд

Дано уравнение х3-0,2x2+0,5x+1,5=0. Уточнить корень с погрешностью <0,001.

Решение:

Запишем f(х)=х3-0,2x2+0,5x+1,5.

Проведя процедуру отделения корней, получим, что корень находится в промежутке [-1; 0], т. е. а=-1; b=0.

f(-1)=-1-0,2-0,5+1,5=-0,2<0;

f(0)=1,5>0.

Находим вторую производную f"(х)=6х–0,4.

f"(-1)=-6-0,4=-6,4<0;

f"(0)=0,4=-0,4<0.

На конце а отрезка [а, b] выполняется условие f(-1) f"(-1)>0, поэтому для вычислений применяем формулу:

 ,                                          

где x0=b; f(a)=f(-1)=-1–0,2–0,5+1,5=-0,2.

Все вычисления сведены в таблице 1.

Таблица 1 

Результаты расчетов по методу хорд

i

xi

f(xi)

xi-a

0

0

1,5

1

1

-0,882

0,2173

0,118

2

-0,943

0,0121

0,057

3

-0,946

0,0014

0,054

4

-0,946

 

 

  Ответ: х=-0,946.

2.2. Пример 2. Решение скалярного уравнения методом хорд

Нахождение корня на отрезке [-2;-1] . Так как 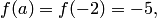 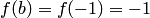, a 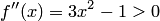   на отрезке [-2;-1] , то  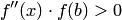и, следовательно, имеем второй случай.

Положим 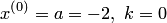. Тогда по формуле

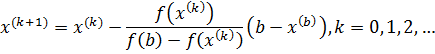
получаем

Так как , то положим 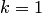 и продолжим процесс:

.

Так как 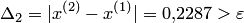, то положим  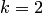и продолжим процесс:

.

Поскольку 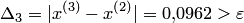, положим 

.

Так как 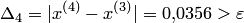, положим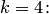 

.

Поскольку , положим 

.

Так как 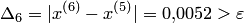, положим 

.

Поскольку , положим 

.

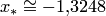Так как , то корень уравнения . Из анализа поведения  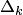следует, что сходимость метода хорд линейная, однако более быстрая, чем сходимость метода половинного деления.


ЗАКЛЮЧЕНИЕ

В данной курсовой работе был рассмотрен метод хорд. В ходе изучения темs «Метод хорд решения скалярных уравнений» выявили, что более быструю сходимость может обеспечить метод хорд. Но он оказывается тем более эффективным, чем более гладкой является функция f(x) на рассматриваемом интервале.

Метод хорд очень хорошо работает в условиях малого интервала (близости обеих границ интервала к корню), но неспособен сам создать себе эти условия (приблизить обе границы к корню).

Применяя метод хорд несколько раз, и результат применения каждый раз будет таким же хорошим (будет существенно поднимать точность), но последующие применения метода хорд, скорее всего, вообще не изменят гарантируемой точности.

Поставленные цели и задачи были выполнены. Был изучен метод хорд, научились применять его при решении скалярных уравнений.

СПИСОК ЛИТЕРАТУРЫ

  1. Бахвалов Н. С. Численные методы / Н. С. Бахвалов, Н. П. Жидков, Г. Н. Кобельков. М.: БИНОМ. Лаб. знаний, 2003. - 632 с.
  2. Бахвалов Н. С. Численные методы в задачах и упражнениях / Н. С. Бахвалов, А. В. Лапин, Е. В. Чижонков. М.: Высш. шк., 2000. - 192 с.
  3. Вержбицкий, В. М. Численные методы. Линейная алгебра и нелинейные уравнения. М.: Высш.шк., 2000. - 268 с.
  4. Вержбицкий В. М. Численные методы. Математический анализ и обыкновенные дифференциальные уравнения. М.: Высш.шк., 2001. - 383 с.
  5. Волков Е. А. Численные методы. СПб.: Лань, 2004. - 248 с.
  6. Калиткин Н. Н. Численные методы. М.: Наука, 2008. - 512 с.
  7. Киреев В. И., Пантелеев А. В. Численные методы в примерах и задачах М: Высшая школа, 2002. - 208 с.
  8. Моулер С. Нэш. М.: Мир, 2009. - 575 с.
  9. Пирумов У. Г. Численные методы М.: Дрофа, 2003. -221 с.
  10. Самарский А. А. Введение в численные методы. М.: Наука, 2007. - 286 с.
  11. Самарский А. А. Численные методы / А. А. Самарский, А. В. Гулин. М.: Наука, 2009. - 256 с.
  12. Турчак Л. И., Плотников П. В. Основы численных методов М: Физ.мат лит., 2002. - 300 с.
  13. Формалев В. Ф., Ревизников Д. Л. Численные методы М: Физ.мат.лит., 2004. - 298 с.

PAGE \* MERGEFORMAT2

РЕШЕНИЯ СКАЛЯРНЫХ УРАВНЕНИЙ МЕТОДОМ ХОРД