Решение задачи о распределении заказов по транспортным средствам в MS Excel
Лабораторная работа №1.
«Решение задачи о распределении заказов
по транспортным средствам в MS Excel»
Задание на лабораторную работу
Создать и оптимизировать в Microsoft Excel табличную модель задачи о распределении заказов по транспортным средствам.
|
Номер варианта |
Подвижной состав |
Максимальное количество заказов |
Номера заказов по табл. 1 |
|
8 |
ГАЗ-3307 – 2 ед.; ГАЗ-52 – 2 ед.; ГАЗ-3302 «Газель» – 2 ед. |
12 |
96 – 110 |
Порядок выполнения работы:
- Ознакомиться с теоретическим введением и примером выполнения задания в Microsoft Excel.
- Получить индивидуальное задание у преподавателя.
- Открыть новую рабочую книгу MS Excel.
- Создать табличную модель данной задачи. В рабочий лист также должны быть занесены расчетные формулы, связывающие переменные модели.
- Оптимизировать модель, т.е. получить оптимальный вариант распределения заказов по автомобилям, используя средство Поиск решения.
- Проанализировать полученное решение и сделать выводы.
Теоретическое введение
Предположим, что имеется n различных работ, каждую из которых может выполнить любой из n привлеченных исполнителей. Стоимость выполнения i-й работы j-м исполнителем известна и равна (в денежных единицах). Необходимо распределить исполнителей по работам (назначить одного исполнителя на каждую работу) так, чтобы минимизировать суммарные затраты, связанные с выполнением всего комплекса работ.
В исследовании операций задача, сформулированная выше известна как задача о назначениях. Введем в рассмотрение двоичные (булевы) переменные , которые будут соответствовать назначению кандидатов на выполнение работ. В этом случае резонно предположить, что , если i-й кандидат назначается на выполнение j-й работы, и , если i-й кандидат не назначается на выполнение j-й работы. Стоимость выполнения всего комплекса работ равна .
Таким образом, задача о назначениях имеет вид:
(1)
Задача о назначениях является частным случаем классической транспортной задачи, в которой надо положить , , . В математической постановке задачи о назначениях (1), первая группа ограничений гарантирует выполнение каждой работы лишь одним исполнителем, вторая группа ограничение гарантирует, что каждый из исполнителей будет выполнять лишь одну работу. При этом условие , означает выполнение требования булевости (двоичности) переменных . Это связано с тем, что мощности всех источников и стоков равны единице, откуда следует, что в допустимом решении значениями переменных могут быть только 0 и 1. При этом в любом допустимом решении лишь n переменных могут принимать значения 1. Таким образом, любое допустимое базисное решение задачи о назначениях будет вырожденным, т.е. представлено вырожденной квадратной матрицей, определитель которой равен нулю.
На практике встречаются задачи о назначениях, в постановках которых параметр , понимается как эффективность выполнения i-й работы j-м исполнителем. В этих случаях нужно так распределить работы между исполнителями, чтобы суммарная эффективность их выполнения был бы максимальной, т.е. , где максимум ищется при указанных выше ограничениях.
В управлении цепями поставок существует ряд задач, математическая постановка которых может быть сведена к задаче о назначениях, например, задача о распределении заказов по транспортным средствам, возникающая при организации доставки мелкопартионных грузов.
Рассмотрим постановку задачи о распределении заказов по транспортным средствам при мелкопартионных перевозках и методику ее решения. Такая задача, по нашему мнению, является более актуальной, поскольку первым этапом формирования развозочных маршрутов является именно раскладка заказов по транспортным средствам. Данную задачу можно решить как частный случай задачи о назначениях. Ниже рассматривается алгоритм решения данной задачи и пример его практического использования.
Рассмотрим локальную задачу обеспечения поставок мелкопартионных грузов. Особенностью данной задачи является то, что клиенты компактно расположены внутри одного территориального района и обеспечиваются с одного склада. Такое упрощение имеет практическое обоснование. Действительно, при договоре аренды автомобиля часто обговаривается район его использования и от этого зависит арендная плата. Итак, предположим, что нам необходимо обеспечить множество клиентов грузами в количестве .
Для перевозки грузов мы можем задействовать множество автомобилей . Каждый j-й автомобиль характеризуется грузоподъемностью и затратами на использование , которую мы будем называть арендной платой. Мы предполагаем, что в арендную плату включены все затраты, которые не зависят от пробега, времени использования и т.д. Чтобы учесть пробег автомобиля, маршрут должен состоять не только из списка клиентов, но также из последовательности их объезда по строгому маршруту следования. Но для данной задачи этот подход не представляется целесообразным по следующим причинам.
- Задача маршрутизации транспортных средств (Vehicle Routing Problem VPR), представляет из себя одну из сложнейших задач целочисленного программирования и не существует эффективных методов решения таких задач большой размерности, которые возникают на практике.
- Для формализации данной задачи потребуется нахождение оптимальных маршрутов между всеми парами узлов транспортной сети. С математической точки зрения это не сложная задача, но ее наполнение фактическими данными является задачей нетривиальной даже с использованием современных геоинформационных систем.
- В связи с постоянными изменениями ситуации на дорогах, оптимальные маршруты следования изменяются. Оперативно отслеживать эти изменения не представляется возможным в силу причин перечисленных выше.
- Опыт практического решения данной задачи показывает, что в тех случаях, когда клиенты расположены компактно, эффект от решения оптимальной маршрутизации незначителен. Причем решение на момент использования может стать неоптимальным или даже недопустимым.
Далее, предполагаем, что все клиенты требуют, чтобы их заказы были доставлены не позднее некоторого времени, причем время перемещения между клиентами и время их обслуживания (погрузка, разгрузка, оформление документов) одинаково. Это ограничение можно выразить простейшим способом – заданием максимального числа клиентов в каждом рейсе, скажем, величиной L.
Рассмотрим математическую формулировку этой задачи.
Введем переменные , принимающие значение . Очевидно, что принимает значение 1, если i-й клиент включен в рейс j-го автомобиля, и значение 0, если i-й клиент не включен в рейс j-го автомобиля.
Введем дополнительные переменные , представляющие собой затраты на транспортировку на j-м маршруте, , принимающие значения:
и рассмотрим задачу
(2)
при ограничениях
(3)
Целевая функция (2) равна реальным транспортным расходам. Первая группа ограничений в системе (3) нам гарантирует, что все клиенты будут обслужены. Вторая группа ограничений в (3) одновременно гарантируют обслуживание только арендованными автомобилями и удовлетворение условий грузоподъемности. Третья группа ограничений в (3) ограничения на количество обслуживаемых одним автомобилем клиентов, которые косвенно учитывают ограничения по времени доставки, и, наконец, последние две группы ограничений – это условия двоичности переменных и . Данная задача относится к классу обобщенных задач о назначениях (Generalized Assignment Problem – GAP).
Исходные данные
Решить задачу о распределении заказов по транспортным средствам, используя в качестве исходных данных данные о клиентах компании и о заказах, представленные в табл. 1.
Таблица 1
Данные о клиентах компании и о заказах
|
№ п/п |
Регион развозки |
Код клиента |
Адрес клиента |
Вес заказа, кг |
|
1 |
Московский р-н РЦ «Центр» |
40414 |
СПб, Московский пр., д.36/38 |
62,50 |
|
2 |
42815 |
СПб, Московский пр.д.186 |
181,60 |
|
|
3 |
42818 |
СПб, ул. Решетникова д.12 |
66,40 |
|
|
4 |
42819 |
СПб, Благодатная д.42 |
88,00 |
|
|
5 |
42828 |
СПб, ул.Коли Томчака д.28 |
196,10 |
|
|
6 |
42830 |
СПб, ул.Свеаборгская д.15 |
70,40 |
|
|
7 |
42841 |
СПб, Московский пр.д.128 |
178,40 |
|
|
8 |
42845 |
СПб, ул.Заозерная д. 8 |
68,00 |
|
|
9 |
42968 |
СПб, ул.Благодатная, 34 |
639,60 |
|
|
10 |
43006 |
СПб, пр.Московский, д.109 |
483,00 |
|
|
11 |
43009 |
СПб, ул. Киевская, 5, конт. № 38 |
155,70 |
|
|
12 |
43175 |
СПб, ул.Иркутская, д.4 а, склад 25 |
288,00 |
|
|
13 |
43351 |
СПб, ул.Цветочная д.16 |
194,40 |
|
|
14 |
43448 |
СПб, ул.Парковая, д.6 |
81,66 |
|
|
15 |
43455 |
СПб, пр.Космонавтов, д.45 |
618,60 |
|
|
16 |
Московский р-н РЦ «Сервис» |
1638 |
СПб, ул.Варшавская д.112 |
70,40 |
|
17 |
3062 |
СПб, пр. Космонавтов д.42 |
163,40 |
|
|
18 |
4271 |
СПб, Московское шоссе д.36 |
41,76 |
|
|
19 |
4276 |
СПб, ул. Костюшко д. 2 (больница № 26) |
65,90 |
|
|
20 |
4277 |
СПб, Пулковское шоссе 3 |
533,35 |
|
|
Продолжение табл. 1 |
||||
|
№ п/п |
Регион развозки |
Код клиента |
Адрес клиента |
Вес заказа, кг |
|
21 |
Московский р-н РЦ «Сервис» |
4335 |
СПб, Авиагородок, ул.Штурманская д.36 |
88,20 |
|
22 |
4568 |
СПб, Московское ш.14 к.1 |
252,96 |
|
|
23 |
4615 |
СПб, ул.Варшавская д.56 |
76,00 |
|
|
24 |
4677 |
СПб, пр.Витебский д.23/1 |
61,00 |
|
|
25 |
4683 |
СПб, ул.Бассейная д.12 |
145,33 |
|
|
26 |
4686 |
СПб, пр.Московский д.155 |
77,10 |
|
|
27 |
4896 |
СПб, пр.Космонавтов д.29 к.7 |
578,10 |
|
|
28 |
5030 |
СПб, Авиагородок, ул. Пилотов д.28 |
74,00 |
|
|
29 |
5041 |
СПб, ул. Гастелло д.16 |
91,10 |
|
|
30 |
5069 |
СПб, Пулковское ш.д.91 |
86,88 |
|
|
31 |
5340 |
СПб, ул.Авиационная д.15 |
518,20 |
|
|
32 |
5360 |
СПб, Московское ш.д.6 |
323,00 |
|
|
33 |
5555 |
СПб, Пулковское ш.д.107 |
201,55 |
|
|
34 |
5685 |
СПб, ул.Фрунзе д.6 |
69,76 |
|
|
35 |
5798 |
СПб, пр.Космонавтов д.17 |
76,70 |
|
|
36 |
5985 |
СПб, ул.Краснопутиловская 66 |
342,20 |
|
|
37 |
6166 |
СПб, Пулковское ш. 13/4 |
94,60 |
|
|
38 |
6455 |
СПб, ул. Орджоникидзе д. 61 |
582,30 |
|
|
39 |
6501 |
СПб, Витебский пр. д.41 |
351,20 |
|
|
40 |
6518 |
СПб, ул. Фрунзе д.7 |
80,96 |
|
|
41 |
6540 |
СПб, Авиагородок ул.Взлетная д.7 |
351,60 |
|
|
42 |
6794 |
СПб, пр. Московский д.207 |
74,34 |
|
|
43 |
8290 |
СПб, ул.Варшавская д. 48 |
38,20 |
|
|
44 |
8366 |
СПб, Краснопутиловская д. 121 |
47,80 |
|
|
45 |
8375 |
СПб, Московский пр.д. 171 |
328,90 |
|
|
46 |
8989 |
СПб, ул. Пулковская, 11 |
66,40 |
|
|
47 |
9190 |
СПб, ул.Звездная д.16 |
733,60 |
|
|
48 |
9208 |
СПб, ул. Ленсовета д.34 |
72,00 |
|
|
49 |
9556 |
СПб, ул. Кузнецовская д.11 |
412,30 |
|
|
50 |
9603 |
СПб, пр. Космонавтов д.48 к.2 |
72,69 |
|
|
51 |
9719 |
СПб, ул.Благодатная д.35 |
285,20 |
|
|
52 |
9742 |
СПб, ул. Фрунзе д.16 |
145,38 |
|
|
53 |
991 |
СПб, пр.Московский д.205а |
200,40 |
|
|
54 |
Фрунзенский р-н РЦ «Центр» |
41114 |
СПб, ул.Фучика д.8 |
800,55 |
|
55 |
42846 |
СПб, Лиговский пр., 222 |
108,00 |
|
|
56 |
42857 |
СПб, ул. Бухарестская д.90 |
782,80 |
|
|
57 |
42858 |
СПб, ул.Пражская д.26к.1 |
1337,00 |
|
|
58 |
42860 |
СПб, Будапештская д.33 |
690,80 |
|
|
59 |
42861 |
СПб, ул.Бухарестская д.31/1 |
496,90 |
|
|
60 |
42864 |
СПб, пр.Славы д.30/1 |
465,70 |
|
|
61 |
42865 |
СПб, ул.Пражская д.35 |
654,10 |
|
|
62 |
42867 |
СПб, ул.Будапештская ,д.3 |
108,11 |
|
|
63 |
42868 |
СПб, ул. Софийская д.39 |
156,75 |
|
|
Продолжение табл. 1 |
||||
|
№ п/п |
Регион развозки |
Код клиента |
Адрес клиента |
Вес заказа, кг |
|
64 |
Фрунзенский р-н РЦ «Центр» |
42870 |
СПб, ул.Софийская д.44 |
227,70 |
|
65 |
42873 |
СПб, ул.Софийская д.47 (универмаг "Василек") |
367,96 |
|
|
66 |
42875 |
СПб, ул.Софийская д.33 |
123,60 |
|
|
67 |
42917 |
СПб, ул.Софийская д.22 |
95,76 |
|
|
68 |
42878 |
СПб, ул.Тамбовская д.4 |
89,00 |
|
|
69 |
42881 |
СПб, ул. Курская ,д.11/72 |
203,10 |
|
|
70 |
42887 |
СПб, ул.Пражская д.11 б |
112,70 |
|
|
71 |
42891 |
СПб, ул.Бухарестская д.74 (Т.Ц.) |
169,70 |
|
|
72 |
42903 |
СПб, ул.Турку д.12 |
99,60 |
|
|
73 |
42914 |
СПб, Лиговский пр. д.198 |
112,20 |
|
|
74 |
42916 |
СПб, ул.Белградская , д.6/1 |
196,30 |
|
|
75 |
42919 |
СПб, Лиговский пр. д.177-179 |
77,36 |
|
|
76 |
42924 |
СПб, Будапештская д.19 к.1 лит.Б |
76,20 |
|
|
77 |
42930 |
СПб, ул.Тамбовская д.43 |
73,76 |
|
|
78 |
42931 |
СПб, ул.Бухарестская д.23 |
91,00 |
|
|
79 |
43256 |
СПб, Лиговский пр., д.210 |
73,50 |
|
|
80 |
43281 |
СПб, ул. Будапештская д.44 |
128,80 |
|
|
81 |
43362 |
СПб, наб.Обводного канала, д.38 |
47,54 |
|
|
82 |
43394 |
СПб, ул.Бухарестская, д.69 |
1797,80 |
|
|
83 |
43465 |
СПб, ул.Курская, д.24 |
96,00 |
|
|
84 |
43477 |
СПб, ул.Стрельбищенская, д.16 |
79,60 |
|
|
85 |
43495 |
СПб, ул.Будапештская, д.19 |
150,85 |
|
|
86 |
43537 |
СПб, ул.Пражская, д.29 |
41,56 |
|
|
87 |
43543 |
СПб, пр.Славы, д.15 |
110,70 |
|
|
88 |
43552 |
СПб, ул. Будапештская, д.11 |
83,40 |
|
|
89 |
43554 |
СПб, ул.Будапештская, д.19 |
358,30 |
|
|
90 |
43577 |
СПб, ул.Софийская, д.29 |
142,10 |
|
|
91 |
Фрунзенский р-н РЦ «Сервис» |
1559 |
СПб, пр.Славы д.43\49 |
129,80 |
|
92 |
4382 |
СПб, ул. Пловдивская д. 1/10 |
311,88 |
|
|
93 |
4392 |
СПб, ул. Купчинская д.32/1 |
544,22 |
|
|
94 |
4498 |
СПб, ул.Будапештская д.97 павильон "Ладога" |
198,30 |
|
|
95 |
4543 |
СПб, ул.Белградская д.40 |
251,20 |
|
|
96 |
4814 |
СПб, ул.Будапештская д.94 |
717,26 |
|
|
97 |
4971 |
СПб, ул.Димитрова д.22 к.2 |
529,60 |
|
|
98 |
42894 |
СПб, пр.Славы д.58а |
55,00 |
|
|
99 |
5641 |
СПб, ул.Будапештская д.49 |
906,10 |
|
|
100 |
6243 |
СПб, ул.Будапештская д.68 |
125,45 |
|
|
101 |
6587 |
СПб, ул. Димитрова д. 12/1 |
99,96 |
|
|
102 |
6743 |
СПб, ул. М.Балканская д. 60/1-А |
85,00 |
|
|
103 |
8077 |
СПб, ул. Пловдивская д.9 |
358,30 |
|
|
104 |
8104 |
СПб, ул.Купчинская д.1/5 |
818,60 |
|
|
105 |
8268 |
СПб, ул.Димитрова д. 16/1 |
136,00 |
|
|
106 |
Фрунзенский р-н РЦ «Сервис» |
8326 |
СПб, ул.Димитрова д.20/1 |
123,30 |
|
107 |
8354 |
СПб, ст. метро «Купчино» |
63,76 |
|
|
108 |
8618 |
СПб, ул. Ярослава Гашека, 7 |
139,56 |
|
|
109 |
8929 |
СПб, ул. Бухарестская, 144 |
1404,30 |
|
|
110 |
9580 |
СПб, Загребский б-р д.21 |
285,70 |
|
|
Итого: |
29357,20 |
Пример выполнения задания
Допустим, нам необходимо сформировать развозочные маршруты для обслуживания пятнадцати клиентов, представленных в табл. 1 с номерами заказов 96-110. Все клиенты территориально расположены в Московском районе Санкт-Петербурга их обслуживание производится из РЦ «Сервис». Вес партии товара каждого из них колеблется в диапазоне от 55 до 1404,3 кг, а общий вес всех товаров составляет 5847,89 кг. В нашем распоряжении имеется шесть автомобилей:
- ГАЗ-3307 грузоподъемностью 4500 кг – 2 ед.;
- ГАЗ-52 грузоподъемностью 2500 кг – 2 ед.;
- ГАЗ-3302 «Газель» грузоподъемностью 1500 кг – 2 ед.
Стоимость аренды автомобиля ГАЗ-3307 составляет 3600 руб., автомобиля ГАЗ-52 – 3200 руб., а автомобиля ГАЗ-3302 «Газель» – 2800 руб. Таким образом, имеется избыток провозных возможностей, следовательно, необходимо определить подвижной состав, использование которого минимизирует транспортные издержки, и оптимально загрузить его, т.е. распределить заказы по транспортным средствам.
Решение
Для решения задачи откроем новую рабочую книгу Excel и выполним следующие подготовительные действия:
- Внесем необходимые надписи в ячейки рабочего листа, как это изображено на рис. 1 и рис. 2.
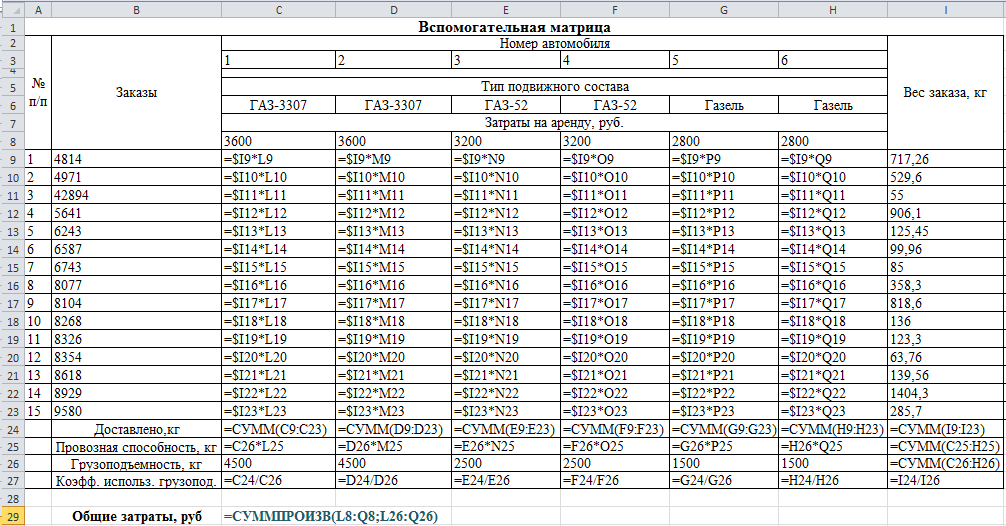
Рис. 1. Исходные данные и табличная модель (начало)
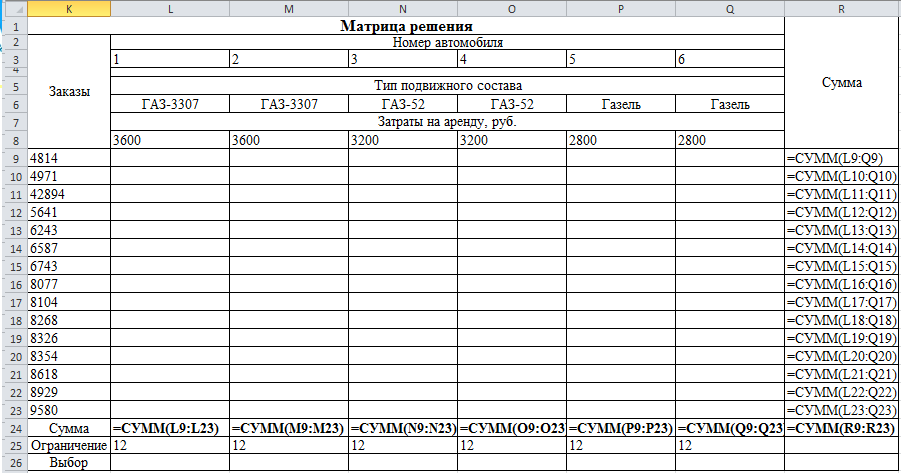
Рис. 2. Исходные данные и табличная модель (продолжение)
- В ячейках L24:Q24 суммируются значения переменной по столбцам.
- В ячейку C29 введем формулу: =СУММПРОИЗВ (L8:Q8;L26:Q26), которая представляет собой целевую функцию (2) рассматриваемой задачи.
Остальные данные и вычисления, произведенные на рабочем листе, носят вспомогательный характер.
Для дальнейшего решения задачи следует вызвать мастер поиска решения, для чего необходимо выполнить операцию главного меню: СервисПоиск решения.
После появления диалогового окна Поиск решения следует выполнить следующие действия:
- В поле с именем Установить целевую ячейку: ввести абсолютный адрес ячейки $C$29.
- Для группы Равной: выбрать вариант поиска решения - минимальному значению.
- В поле с именем Изменяя ячейки: ввести абсолютный адрес диапазона ячеек $L$9:$Q$23;$L$26:$Q$26.
- В поле с именем Ограничения: ввести ограничения, как показано на рис. 3
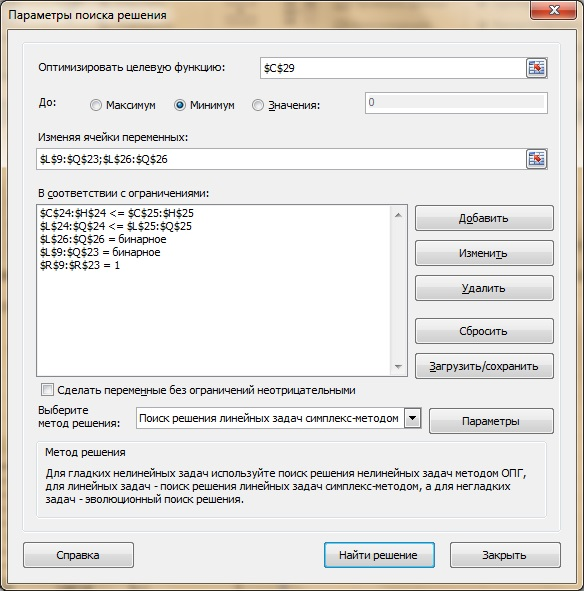
Рис. 3. Окно Поиск решения с введенными ограничениями
- В окне дополнительных параметров поиска решения выбрать отметки Линейная модель и Неотрицательные значения.
После задания ограничений и целевой функции можно приступить к поиску численного решения, для чего следует нажать кнопку Выполнить. Результат выполнения расчетов программой MS Excel представлен на рис. 4 и 5.
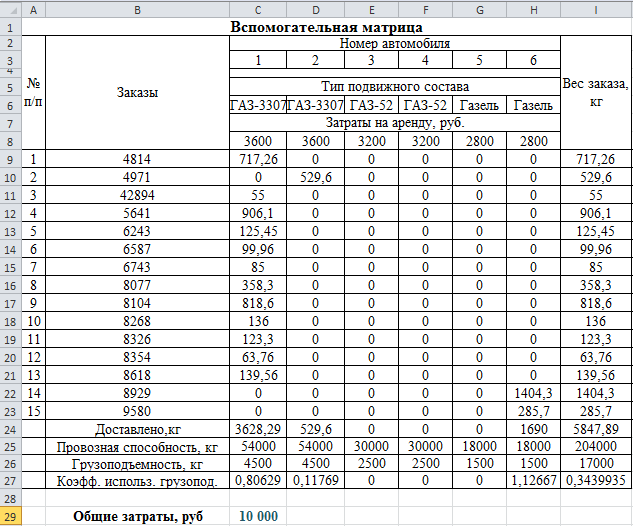
Рис. 4. Результат решения задачи (начало)
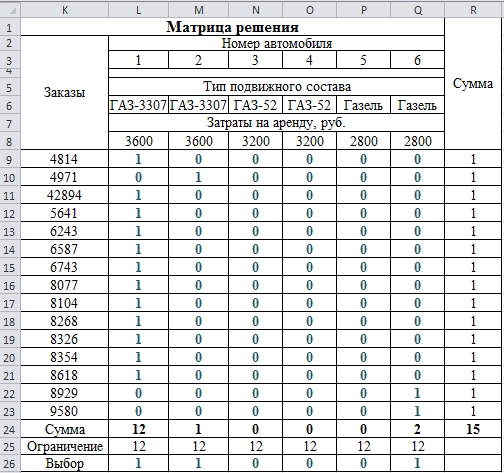
Рис. 5. Результат решение задачи (окончание)
Вывод. В представленном решении используются три единицы подвижного состава: ГАЗ-3307 грузоподъемностью 4500 кг – 2 ед.; ГАЗ-3302 «Газель» грузоподъемностью 1500 кг – 1 ед. Автомобилем ГАЗ-3307 обслуживается 12 и 1 заказ, общий вес которых составляет 3628,29 кг и 529,6 кг соответственно. Автомобилем ГАЗ-3302 «Газель» обслуживается 2 заказа, общий вес которых составляет 1690 кг. Коэффициент использования грузоподъемности при выполнении рейса автомобилем ГАЗ-3307 составляет 0,8 и 0,11 соответственно для каждого из двух автомобилей, а при выполнении рейса автомобилем ГАЗ-3302 «Газель» – 1,13. Общие затраты на перевозку при этом минимальны и составляют 10 000 руб.
Решение задачи о распределении заказов по транспортным средствам в MS Excel