Решение задачи хищник- жертва. Решение задачи на составление рациона питания
СОДЕРЖАНИЕ
ВВЕДЕНИЕ…………………………………………………........................................2
ГЛАВА1.Теорeтическая часть. Компьютерное моделирование………………………………………………………………...…3
1.1.Понятие моделирования……………………………………………………………5
1.2 Гносеологическая специфика модели и ее определение………………….……...9
1.3. Моделирование в биологии………………………………………………...…….13
1.4. О формах моделирования биологических понятий………………………….....19
ГЛАВА2. Практическая часть. Решение задач…………….…..……....20
2.1. Решение задачи хищник- жертва……...…………………………………..……..20
2.2.Решение задачи на составление рациона питания …….………………….….....21
ЗАКЛЮЧЕНИЕ………………………………………………………………………..27
ЛИТЕРАТУРА…………………………………………………………………………29
ВВЕДЕНИЕ
В течении большого периода времени биология была описательной наукой, и мало приспособленной для прогнозирования наблюдаемых явлений. Но уже с появлением компьютерной техники многое поменялось. Вначале, наиболее востребованными в биологии были методы математической статистики, они позволяли корректно обрабатывать данные экспериментов и оценивать определенную значимость, благодаря которым делаются определенные выводы. Но, уже со временем, благодаря химии и физики в биологии стали использоваться сложные математические модели, позволяющие не только обрабатывать данные реальных экспериментов, но и способные предсказывать протекание биологических процессов в ходе виртуальных экспериментов.
Итак, что же означает понятие модели? Модель - образ или прообраз какого-либо объекта или системы объектов, используемый, при определенных условиях в качестве их заместителя. Модели в биологии используются для моделирования биологических структур, функций и процессов на разных уровнях организации живого: молекулярном, субклеточном, клеточном, органно-системном, организменном и популяционно-биоценотическом. Возможно также моделирование разных биологических феноменов, а также условий жизнедеятельности отдельных особей, популяций и экосистем.
Значение моделей компьютерного моделирования почти во всех областях биологии быстро растёт. Помимо анализа расчётных данных, в который входит обработка изображений, анализ нуклеотидных последовательностей, кодирующих гены и отдельные белки и компьютерное обучение, в современной биологии также применяется компьютерное моделирование. В «виртуальных экспериментах» на компьютере возможно контролировать все переменные и факторы воздействия, что позволяет проанализировать биологические системы, разрабатывать физические модели для компонентов этих систем, которые нельзя осуществить в реальных экспериментах.
Актуальность курсовой работы. В современной биологии накоплены беспрецедентно огромные объемы экспериментальных данных, хранение, обработка и осмысление которых невозможно без моделирования биологических систем и процессов. Методы и инструменты математического моделирования и компьютерных наук играют решающую роль в развитии современных областей молекулярной и клеточной биологии, структурной биологии, физико-химической биологии.
Цель курсовой работы: изучить и исследовать основы и методы компьютерного моделирования различных биологических процессов и научить применять полученные знания и навыки при решении задач.
Задачи курсовой работы: систематизировать материал по теме «Компьютерное моделирование в области биологии»; Изучить основные понятия о компьютерном моделировании; рассмотреть этапы компьютерного моделирования на примере решения конкретных задач.
Структура курсовой работы. Курсовая работа состоит введения, двух глав, заключения и списка литературы.
ГЛАВА 1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ. КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ
1.1 Компьютерное моделирование
Моделирование - познавательный прием, одна из форм отражения. Моделирование характеризует один из важных путей познания. Возможность моделирования, т.е. переноса результатов, полученных в ходе построения и исследования моделей, на оригинал, основана на том, что модель в определенном смысле отображает, какие-либо его черты. При этом такое отображение основано на понятиях изоморфизма и гомоморфизма между изучаемым объектом и некоторым другим объектом-оригиналом и часто осуществляется путем предварительного исследования (теоретического или экспериментального) того и другого. Поэтому для успешного моделирования необходимо наличие уже сложившихся теорий исследуемых явлений, или хотя бы обоснованных гипотез, указывающих предельно допустимые при построении моделей упрощения. Результативность моделирования значительно возрастает, если при построении модели и переносе результатов с модели на оригинал, можно воспользоваться некоторой теорией, уточняющей связанную с используемой процедурой моделирования, идею подобия.
Для явлений одной и той же физической природы такая теория, созданная на понятии размерности физических величин, хорошо разработана. Но для моделирования сложных систем и процессов, например, биологических, используется теория больших систем, модели сложных динамических систем живой природы.
Моделирование всегда используется вместе с другими общенаучными и специальными методами. Можно разделить «материальное» и «идеальное» моделирование. Первое можно рассматривать как экспериментальное, второе - как теоретическое. Такое разделение условно как в силу взаимосвязи обоюдного влияния этих методов, так и наличия гибридных форм, например, «мысленный эксперимент». «Материальное» моделирование делится на физическое и предметно-математическое. «Идеальное» моделирование может совершаться на уровне самых общих, может быть не до конца осознанных, «модельных представлений». Моделирование на ЭВМ, получившее значительное распространение в последние годы, еще называют «кибернетическим», оно является предметно-математическим по форме и идеальным по содержанию.
Моделирование тесно связано с экспериментом. Изучение какого-либо явления на его кибернетической модели можно рассматривать как особый вид эксперимента: «модельный эксперимент», различающийся от обычного («прямого» эксперимента) тем, что в процесс познания «промежуточное звено» - модель, являющаяся и средством и объектом экспериментального исследования, заменяющим изучаемый объект. Модельный эксперимент позволяет изучать такие объекты, прямой эксперимент над которыми затруднен, экономически не выгоден или вообще невозможен в силу тех или иных причин.
Моделирование предполагает использование абстрагирования и идеализации. Отображая существенные свойства оригинала и отвлекаясь от несущественного, модель выступает как специфическая форма реализации абстракции. Выделяются три уровня абстракции: уровень потенциальной осуществимости, уровень «реальной» осуществимости и уровень практической целесообразности. На всех уровнях, однако, необходимо учесть, что моделирование оригинала не может дать полного знания о нем. Эта черта особенно существенна, когда предметом моделирования выступают сложные системы, поведение которых зависит от большого числа взаимосвязанных факторов разной природы. Такие системы отображаются в различных моделях. Поэтому появляется проблема сравнения (оценки адекватности) разных моделей одного и того же явления, что требует формулировки критериев сравнения. Примером такого рода моделей может служит моделирование различных форм деятельности мозга. Создаваемые модели интеллекта и психических функций - например, в виде эвристических программ на ЭВМ - показывают, что моделирование мышления как информационного процесса возможно в различных аспектах: формально-логическом, индуктивном, нейрологическом, эвристическом и др.
1.2 Гносеологическая специфика модели и ее определение
На сегодняшний момент нет устоявшейся общепринятой точки зрения на место моделирования среди методов познания. Множество мнений исследователей, занимающихся данным вопросом, тем не менее, помещаются в некоторую область, ограниченную двумя полярными мнениями. Одно из них рассматривает моделирование как некий вторичный метод, подчиненный более общим (менее радикальный вариант той же по сути позиции— моделирование рассматривается исключительно как разновидность такого эмпирического метода познания как эксперимент). Другое же, наоборот, называет моделирование «главным и основополагающим методом познания», в подтверждение доводится тезис, что «всякое вновь изучаемое явление или процесс бесконечно сложно и многообразно и потому до конца принципиально не познаваемо и не изучаемо».
Главной причиной возникновения столь разнообразных позиций автору видится отсутствие общепринятого и устоявшегося в науке определения моделирования. Ниже предпринята попытка анализа некоторых определений термина «моделирование» и непосредственно связанного с ним термина «модель». Это вполне оправдано, так как подавляющее большинство источников находят моделирование как «исследование процессов, явлений и систем объектов через построение и изучение их моделей». То есть наибольшую сложность показывает проблема определения модели.
Сперва выделим определение, которое предлагает Оксфордский Толковый Словарь [10]. В нем приведено семь определений понятия «модель», из которых наибольший интерес представляют два: «Модель — трехмерное представление субъекта, вещи или структуры; обычно в уменьшенном масштабе» и «Модель — упрощенное описание некоей системы для дальнейших расчетов». Другими словами, авторам не удается выделить настоящие существенные признаки модели и они предлагают различные определения для различных видов моделей (более подробное обсуждение классификации моделей приведено ниже, здесь же отметим, что первое оксфордское «определение» описывает достаточно узкий класс предметных моделей, а второе лежит где-то в плоскости абстрактно-знаковых моделей). Основная ошибка данных определений — их узость, объем понятия «модель» неизмеримо больше, чем предлагаемый авторами словаря.
Похожая проблема (только в менее значительных масштабах) возникает и при анализе определения «модели» в Советском Энциклопедическом Словаре (СЭС). Модель авторами рассматривается двояко. В узком смысле — это «устройство, воспроизводящее, имитирующее строение и действие какого-либо другого (моделируемого) устройства в научных, производственных или практических целях» [11]. Опять-таки слово «устройство», встречающееся в определении автоматически приводит к сужению понятия «модель» как минимум до понятия «материальная модель». Тем не менее, это определение представляет собой гораздо большую ценность, чем первое определение оксфордского словаря, так как включает внутри себя чрезвычайно важную (как будет показано далее) формулировку, раскрывающую сущность моделирования — «строение и действие».
Второе определение СЭС («Модель — любой образ какого-либо объекта, процесса, явления, употребляемый в качестве его заместителя или представителя), наоборот, является слишком широким. Сложно предположить, что снимок ядерного взрыва может служить моделью самого взрыва. В данном случае, авторы в стремлении к краткому, но емкому определению принесли в жертву сущность понятия «модель». Данное определение отображает скорее внешние признаки, которыми обладает модель, но не её внутреннее содержание. Однако, рациональное зерно есть и в этом определении — за словом «образ» определяется более важное (с философской точки зрения) понятие — «отражение».
Ещё одно определение «модели» приведено в учебнике [9]: «Модель является представлением объекта в некоторой форме, отличной от формы его реального существования». Фактически, оно почти совпадает с «широким» определением СЭС, но и здесь авторы заменяют слово «отражение» синонимичным оборотом. Кроме того, использование термина «объект» может быть оправдано в рамках школьного (но не вузовского) учебника, но неприемлемо для полного определения. Современная наука занимается изучением не столько отдельных самостоятельных элементов, сколько их взаимодействий. Потому более оправдано употребление в определении термина «система», который вбирает в себя как отдельные элементы, так и их отношения и связи.
В целом же, последние два определения можно признать вполне удовлетворительными и пользоваться ими.
Дальнейший путь развития и улучшения определений связан с целями метода моделирования. Большинство исследователей выделяют три [2]:
· Понимание устройства конкретной системы, её структуры, свойств, законов развития и взаимодействия с окружающим миром
· Управление системой, определение оптимальных способов управления при заданных целях и критериях
· Прогнозирование прямых и косвенных последствий реализации заданных способов и форм воздействия на систему
Все три цели подразумевают в той или иной степени наличия механизма обратной связи, то есть необходима возможность не только переноса элементов, свойств и отношений моделируемой системы на моделирующую, но и наоборот.
В таком случае, определение моделирования может быть сформулировано так [14]:
«Моделирование-это прямое практическое или теоретическое исследование объекта, при котором непосредственно изучается не сам интересующий нас объект, а некоторая вспомогательная искусственная или естественная система:
1) находящаяся в некотором объективном соответствии с познаваемым объектом;
2) способная замещать его в определенных отношениях;
3) дающая при её исследовании, в конечном счете, информацию о самом моделируемом объекте» (три перечисленных признака по сути являются определяющими признаками модели).
Данное определение, принадлежащее И.Б.Новику и А.А.Ляпунову Единственное замечание (скорее методологического плана) заключаетс в том, что автор рассматривает отражение «объект–система», вместо «система–система». Данный недочет вполне простителен, так как определение дано более 50 лет назад, когда уровень науки отличался от современного и теория систем находилась в стадии становления.
Для сравнения:
Опpеделение И.Т. Фpолова:
«Моделирование означает материальное или мысленное имитирование реально существующей системы путем специального констpуиpования аналогов (моделей), в котоpых воспpоизводятся пpинципы оpганизации и функциониpования этой системы». [12] Здесь в основе мысль, что модель —сpедство познания, главный ее пpизнак — отобpажение. В то же время механизм обратной связи (третий признак у Ляпунова) четко в определении не прослеживается.
В западной философии эталонным является определение, которое дает В.А. Штофф в своей книге «Моделиpование и философия»: «Под моделью понимается такая мысленно пpедставляемая или матеpиально peализуемая система, котоpая отобpажая или воспpоизводя объект исследования, способна замещать его так, что ее изучение дает нам новую инфоpмацию об этом объекте».[14] .Оно практически полностью совпадает с определением Новика-Ляпунова, но имеет один недостаток — в определении не содержится указаний на относительный характер модели.
1.3. Моделирование в биологии
Модели в биологии применяются для моделирования биологических структур, функций и процессов на различных уровнях организации живого: молекулярном, субклеточном, клеточном, органно-системном, организменном и популяционно-биоценотическом. Возможно также моделирование разных биологических феноменов, а также условий жизнедеятельности отдельных особей, популяций и экосистем.
В биологии применяются в основном три вида моделей: биологические, физико-химические и математические (логико-математические). Биологические модели отображают на лабораторных животных определённые состояния или заболевания, встречающиеся у человека или животных. Это позволяет изучать в эксперименте механизмы возникновения данного состояния или заболевания, его течение и исход, воздействовать на его протекание. Примеры таких моделей — искусственно вызванные генетические нарушения, инфекционные процессы, интоксикации, воспроизведение гипертонического и гипоксического состоянии, злокачественных новообразований, гиперфункции или гипофункции некоторых органов, а также неврозов и эмоциональных состояний. Для создания биологической модели применяют разные способы воздействия на генетический аппарат, заражение микробами, введение токсинов, удаление отдельных органов или введение продуктов их жизнедеятельности (например, гормонов), различные воздействия на центральную и периферическую нервную систему, исключение из пищи тех или иных веществ, помещение в искусственно создаваемую среду обитания и многие другие способы. Биологические модели широко применяются в генетике, физиологии, фармакологии.
Физико-химические модели воспроизводят физическими или химическими средствами биологические структуры, функции или процессы и, как правило, являются далёким подобием моделируемого биологического явления. Начиная с 60-х гг. 19 в. были сделаны попытки создания физико-химической модели структуры и некоторых функций клеток. Так, немецкий учёный М. Траубе (1867) имитировал рост живой клетки, выращивая кристаллы CuSО4 в водном растворе К4[Fе(СN)6]: французский физик С. Ледюк (1907), погружая в насыщенный раствор К3РО4 сплавленный СаСl2, получил — благодаря действию сил поверхностного натяжения и осмоса — структуры, внешне напоминающие водоросли и грибы. Смешивая оливковое масло с разными растворимыми в воде веществами и помещая эту смесь в каплю воды, О. Бючли (1892) получал микроскопические пены, имевшие внешнее сходство с протоплазмой; такая модель воспроизводила даже амебовидное движение. С 60-х гг. 19 в. предлагались также разные физические модели проведения возбуждения по нерву. В модели, созданной итальянским учёным К. Маттеуччи и немецким — Л. Германом, нерв был представлен в виде проволоки, окруженной оболочкой из проводника второго рода. При соединении оболочки и проволоки с гальванометром наблюдалась разность потенциалов, изменявшаяся при нанесении на участок "нерва" электрического "раздражения". Такая модель воспроизводила отдельные биоэлектрические явления при возбуждении нерва. Французский учёный Р. Лилли на модели распространяющейся по нерву волны возбуждения воспроизвёл ряд явлений, наблюдаемых в нервных волокнах (рефрактерный период, "всё или ничего" закон, двустороннее проведение). Модель представляла собой стальную проволоку, которую помещали сначала в крепкую, а затем в слабую азотную кислоту. Проволока покрывалась окислом, который восстанавливался при ряде воздействий; возникший в одном участке процесс восстановления распространялся вдоль проволоки. Подобные модели, показавшие возможность воспроизведения некоторых свойств и проявлений живого посредством физико-химических явлений, основаны на внешнем качественном сходстве и представляют лишь исторический интерес.
Позднее более сложные модели, основанные на гораздо более глубоком количественном подобии, строились на принципах электротехники и электроники. Так, на основе данных электрофизиологических исследований были созданы электронные схемы, моделирующие биоэлектрические потенциалы в нервной клетке, её отростке и в синапсе. Построены также механические машины с электронным управлением, моделирующие сложные акты поведения (образование условного рефлекса, процессы центрального торможения и пр.).
Значительно большие успехи были достигнуты в моделировании физико-химических условий существования живых организмов или их органов и клеток. Так, подобраны растворы неорганических и органических веществ (растворы Рингера, Локка, Тироде и др.), имитирующие внутреннюю среду организма и поддерживающие существование изолированных органов или культивируемых вне организма клеток.
Модели биологических мембран (плёнка из природных фосфолипидов разделяет раствор электролита) дозволяют исследовать физико-химические основы процессов транспорта ионов и влияние на него различных факторов. С помощью химических реакций, протекающих в растворах в автоколебательном режиме, моделируют колебательные процессы, характерные для многих биологических феноменов, — дифференцировки, морфогенеза, явлений в сложных нейронных сетях и т. д.
Математические модель (математическое и логико-математическое описания структуры, связей и закономерностей функционирования живых систем) строятся на основе данных эксперимента или умозрительно, формализованно описывают гипотезу, теорию или открытую закономерность того или иного биологического феномена и требуют дальнейшей опытной проверки. Различные варианты подобных экспериментов выявляют границы применения математической модели и дают материал для её дальнейшей корректировки. Математическая модель в отдельных случаях позволяет предсказать некоторые явления, ранее не известные исследователю. Так, модель сердечной деятельности, предложенная голландскими учёными ван дер Полом и ван дер Марком, основанная на теории релаксационных колебаний, указала на возможность особого нарушения сердечного ритма, впоследствии обнаруженного у человека. Из математической модели физиологических явлений следует назвать также модель возбуждения нервного волокна, разработанную английскими учёными А. Ходжкином и А. Хаксли. На основе теории нервных сетей американских учёных У. Мак-Каллока и У. Питса строятся логико-математические модели взаимодействия нейронов. Системы дифференциальных и интегральных уравнений положены в основу моделирования биоценозов (В. Вольтерра, А. Н. Колмогоров). Марковская математическая модель процесса эволюции построена О. С. Кулагиной и А. А. Ляпуновым. И. М. Гельфандом и М. Л. Цетлиным на основе теории игр и теории конечных автоматов разработаны модельные представления об организации сложных форм поведения. В частности, показано, что управление многочисленными мышцами тела создается на основе выработки в нервной системе некоторых функциональных блоков — синергий, а не путём независимого управления каждой мышцей. Создание и использование математических и логико-математических М., их совершенствование содействует дальнейшему развитию математической и теоретической биологии.
Метод моделирования в биологии является средством, позволяющим устанавливать все более глубокие и сложные взаимосвязи между биологической теорией и опытом. В последнее столетие экспериментальный метод в биологии начал наталкиваться на определенные границы, и выяснилось, что целый ряд исследований невозможен без моделирования. Если остановиться на отдельных примерах ограничений области применения эксперимента, то они будут в основном следующими:
- эксперименты могут проводиться лишь на ныне существующих объектах;
- вмешательство в биологические системы иногда имеет такой характер, что невозможно определить причины появившихся изменений (вследствие вмешательства или по другим причинам);
- некоторые теоретически возможные эксперименты неосуществимы вследствие низкого уровня развития экспериментальной техники;
- большую группу экспериментов, связанных с экспериментированием на человеке, следует отклонить по морально - этическим соображениям.
Но моделирование находит широкое применение в области биологии не только из-за того, что может заменить эксперимент. Оно имеет большое самостоятельное значение, которое выражается, по мнению ряда авторов, в целом ряде преимуществ:
1. С помощью метода моделирования на одном комплексе данных можно разработать целый ряд различных моделей, по-разному интерпретировать исследуемое явление, и выбрать наиболее плодотворную из них для теоретического истолкования;
2. В процессе построения модели можно выработать различные дополнения к исследуемой гипотезе и обрести ее упрощение;
3. В случае сложных математических моделей можно применять ЭВМ;
4. открывается возможность проведения модельных экспериментов (синтез аминокислот по Миллеру).
Все это ясно показывает, что моделирование выполняет в биологии самостоятельные функции и становится все более необходимой ступенью в процессе создания теории. Однако моделирование свое эвристическое значение только тогда, когда учитываются границы применения всякой модели.
1.4. О формах моделирования биологических понятий
Построение моделей как одна из сторон диалектической пары противоположностей анализ-синтез имеет много аспектов, из которых некоторый выдвигается на первый план.
Особенно существенным при построении моделей является аспект отражения, понимаемого в смысле теории познания.
Каждая модель хранит знания в надлежащей форме; при этом запоминание знаний, как правило, связано с уменьшением избыточности. Поэтому каждая модель имеет языковую функцию. Содержание знаний является семантической стороной; способы, с помощью которых знания вводятся в модель, кодируются в ней, являются синтаксической стороной. Последний языковой компонент содержит большое значение при активизации модели при каждом приведении ее в действие.
Но в то же время модель в своей функции как структура для хранения знаний является связующим звеном между теоретическим и эмпирическим познанием. Фразу «нет ничего проще хорошей теории» следует воспринимать дословно. Формализованная теория позволяет изобразить большое число частных фактов с помощью наибольшего числа основных результатов. Следовательно, главное назначение теории – в уменьшении избыточности, обусловленной изобилием частных фактов, и связанных с этим более глубоким познанием закономерных связей.
В основе каждой модели лежит более или менее развитая теория отображаемого объекта; эта теория укладывается в синтаксически установленные рамки, в концепцию системы, положенную в основу конкретного построения модели.
Системная концепция фиксирует общие рамки модели, иначе говоря, определяет структуру памяти модели. Конкретная форма модели, в которой она может действовать в качестве замены только одного конкретного объекта, получается благодаря тому, что экспериментальные, то есть эмпирические, данные приводятся в соответствии с этими рамками, то есть для параметров модели, ее степеней свободы шаг за шагом устанавливаются все более достоверные значения. В этом смысле каждая разработанная модель выражает компромисс между теорией и практикой, между теоретическими познаниями и эмпирическими данными.
Основным стержнем системы развивающего обучения является деятельностный подход. Поэтому содержание обучения задано в виде способов детских действий, а значит, результатом такого обучения будет ряд способностей, которыми овладеют дети в ходе обучения. Но какие именно человеческие способности кроются в способах работы с биологическими объектами? Какие из этих способностей уместно делать предметом школьного курса обучения биологии? Что такого особенного есть в биологии, чего не может дать детям изучение химии, физики и истории? Таким образом, я, как будущий учитель биологии, должна найти то уникальное, чтобы показать, что мой предмет может дать формирующемуся сознанию ученика.
Для биологии ключевым словом является слово «развитие». Философы биологии все чаще обращают внимание на то, что биология со времени Ч.Дарвина все более формируется как наука о возникновении и развитии органического мира. Преимущественное внимание именно к аспекту развития до сих пор отличает биологию от физики и химии, как бы ни усиливалась ее зависимость от этих наук.
Усвоение понятия развития предполагает овладение особым способом рассмотрения живого – потенциальным действием с ним. Овладение понятием развития помогает становлению у человека способности к осторожной и внимательной оценке событий, умению видеть эти события в связи с другими, а не изолированно; способности предвидеть разные возможные варианты развертывания событий, последствия вмешательства в динамику сложных системных объектов; способности реконструировать ход уже свершившегося процесса. Это и есть, с моей точки зрения, те базовые компетентности, которые возможно формировать у школьников на биологическом материале при соответствующем построении содержания, форм и методов учебной работы. Очень важно отметить то, что, хотя эти способности могут и должны быть выращены у каждого человека именно в ходе изучения биологии (на биологическом материале), они могут быть применены в самых разных сферах повседневной социальной жизни людей. Поэтому такой базовый курс школьной биологии будет нужен всем без исключения подросткам.
При изучении любого раздела биологии, важно не только продемонстрировать учащимся, но и предоставить им возможность самим убедиться в том, что каждый специальный термин несет в себе информацию о природе явления, структуре объекта, принципе работы объекта, его свойствах, взаимной связи структуры вещества с его свойствами, строения объекта с его функционированием [8].
Учащиеся часто не соотносят между собой теоретические знания об объекте исследования и его строением, попросту говоря, не могут по описанию составить «портрет» объекта, и наоборот. Путают понятия: вещество - тело, структура вещества - форма тела, структурные единицы - части целого. Применение в обучении информационных устройств: компьютера, телевизора, магнитофона, мобильного телефона, принтера, интерактивной доски позволяет по-новому решать учебные задачи. Однако электронные модели не всегда дают полное представление об объекте. Вследствие чего мы предлагаем проводить занятия по моделированию биологических объектов с использованием пластилина.
Моделирование – это метод создания и исследования моделей. Изучение модели позволяет получить новое знание, новую целостную информацию об объекте.
Существенными признаками модели являются: наглядность, абстракция, элемент научной фантазии и воображения, использование аналогии как логического метода построения, элемент гипотетичности. Иными словами, модель представляет собой гипотезу, выраженную в наглядной форме.
В ходе занятия учащимся предлагают выполнить модели из курса биологии (вирусы, бактерии, клетка – в общей биологии, так же такой метод можно применять и в ботанике, зоологии, анатомии). Важным свойством модели является наличие в ней творческой фантазии. Процесс создания модели достаточно трудоемкий, учащиеся как бы постигают через несколько этапов.
Первый – тщательное изучение опыта, связанного с интересующим исследователя явлением, анализ и обобщение этого опыта и создание гипотезы, лежащей в основе будущей модели.
Второй – составление программы исследования, организация практической деятельности в соответствии с разработанной программой, внесение в неё коррективов, подсказанных практикой, уточнение первоначальной гипотезы исследования, взятой в основу модели.
Третий – создание окончательного варианта модели. Если на втором этапе исследователь как бы предлагает различные варианты конструируемого явления, то на третьем этапе он на основе этих вариантов создает окончательный образец того или проекта, который собирается воплотить.
Другими словами учащиеся «пропускают» через себя информацию, анализируют ее и воплощают модель. Проводя такие занятия, преподаватель довольно легко может определить, насколько ученик понимает предмет. При использовании пластилина в занятиях по моделированию биологических объектов не возникает проблем восприятия: самого задания, стереотипа мышления, видение объекта только в одной плоскости, смешение цветов и форм.
Главными задачами такого метода обучения являются:
- получение фактических знаний;
- изучение наиболее сложных для познания вопросов по биологии;
- формирование навыка поиска правильного решения задания с применением анализа и синтеза;
- изучение и применение метода моделирования на практике;
- ознакомление с разрабатываемыми в последнее десятилетие в России и за рубежом биологическими проблемами при проведении работ в компьютерном классе.
Самым главным в этой работе оказалось детское открытие, что любое действие может привести к изменению формы и структуры объекта; и то, что всякое словесное объяснение нужно доказать изготовлением модели, желательно действующей. После «пластилиновых» работ лучше воспринимается электронные модели, теоретический материал. В свою очередь, мультимедийная информация предоставляет новые возможности использования различных «неожиданных» материалов для объемного моделирования объектов исследования в классе и дома.
На большинстве уроков происходит совместная работа учеников и учителя по открытию общих принципов функционирования, устройства и развития живых существ и других биологических систем. Эти общие принципы воплощаются в разнообразных моделях. Эти модели впоследствии становятся основой детской самостоятельности, средством понимания учебных и авторских текстов и исследования нового.
По нашему мнению, подобный тип обучения вырабатывает у детей умение учиться, учить себя. Наиболее важные, ключевые, содержательные шаги в развитии важных биологических понятий, с моей точки зрения, необходимо строить как собственные детские исследования и открытия. Понятие развития выстраивается как итог всей учебной работы учащихся по ходу разворачивания предметной логики. Оно опирается на многообразную работу с модельными формами, обслуживающими формирование ключевых понятий биологии: понятий органа, организма, индивидуального развития, эволюции, популяции, экосистемы. Эти базовые понятия становятся «очками» нового видения ребенком мира живых существ и возможных собственных действий в этом мире.
ГЛАВА 2.ПРАКТИЧЕСКАЯ ЧАСТЬ. РЕШЕНИЕ ЗАДАЧ.
Задача 1. Модели хищник-жертва. Рассмотрим простую модель хищник-жертва, представляющую акул и рыб. Обозначим F(t) численность рыб в момент времени t, а S(t) – численность акул в этот же момент времени. Пусть рост популяции рыб ничто не ограничивает. Тогда скорость увеличения численности рыб пропорциональна общей численности рыб – b1F(t), где b1 – коэффициент рождаемости рыб. Скорость вымирания акул в отсутствие рыб пропорциональна количеству акул – d2S(t), где d2 – коэффициент смертности акул. Предположим, что количество уничтожаемой каждой акулой рыбы пропорционально полному числу рыб d1S(t), где d1 – коэффициент смертности рыб. Последнее допущение было бы верным, если бы район охоты каждой акулы был неизменным, районы охоты разных акул не пересекались и каждая акула находила бы в своем районе постоянную часть рыбного косяка. Тогда количество рыб, съеденных каждой акулой равно d1S(t)F(t). Прирост численности акул также пропорционален этой величине, но с меньшим коэффициентом – b1F(t)S(t). Если предположить, что функции F(t) и S(t) непрерывны, то можно записать
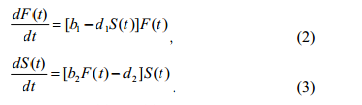
Уравнения (1) и (2) известны как уравнения Лотки- Вольтерра. Эта система уравнений имеет устойчивое решение F=b1/d1 ; S=b2/d2, т.е. численность хищников и жертв должна в конце концов становится постоянной. Однако это равновесие является нейтральным, т.е. если вывести систему из равновесия, в ней возникнут колебания, незатухающие во времени. При малом возмущении решение уравнения будет описывать эллипс (рис. 9) с периодом колебания
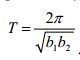
T = В состоянии ли вы объяснить почему динамика поведения решений уравнений (1) и (2) обладает цикличностью? В приведенной модели хищник-жертва предполагалось, что число хищников меняется непрерывным образом. Теперь рассмотрим другую модель хищник-жертва, которую проще сформулировать с помощью следующего вычислительного алгоритма. Данная модель является двумерным клеточным автоматом, называемым Ва-Тор.
1. 1. Исходя из требуемой концентрации рыб и акул они помещаются случайным образом в узлы прямоугольной сетки. Всем рыбам и акулам присваивается случайный возраст.
2. 2. На временном шаге tn рассматривается по очереди каждая рыба. Определяется число ближайших соседних узлов, которые не заняты в момент времени tn-1, и рыба передвигается в один из свободных узлов случайным образом. Если все четыре соседних узла заняты, рыба не перемещается.
3. 3. Если рыба выживает за время, кратное числу шагов fbreed, у рыбы появляется один потомок. Новая рыба помещается в старую позицию рыбы- родителя.
4. 4. На временном шаге tn рассматривается по очереди каждая акула. Если все ближайшие к акуле соседние узлы в момент времени tn-1 не заняты, акула перемещается в один из свободных узлов случайным образом. Если хоть в одном соседнем узле находится рыба, то акула перемещается случайным образом в один из этих занятых узлов и поедает рыбу.
5. 5. Если за nstarve шагов акула ничего не съедает, она погибает. Если акула выживает в течение времени, кратного sbreed шагов, то она обзаводится одним детенышем. Новая акула помещается в предыдущую позицию своего родителя.
Для описания каждой рыбы при компьютерном моделировании используется три переменных: координаты x, y и возраст sday. Логично и очень удобно было бы каким-то образом сгруппировать эти три переменные. Для этого в языке С есть специальное средство – структуры.
struct fishtype {
int x,y;
int fday;
};
Этим определением мы ввели новый тип переменных, теперь можно описать переменные этого типа:
fishtype fish;
Группировка данных в структуры полезна тем, что когда нам нужно думать о рыбе как о целом, мы оперируем всей структурой. В то же время есть возможность работать и с полями структуры по отдельности, обращаясь к ним следующим образом: fish.x, fish.y, fish.fday.
Аналогичные определения можно сделать и для моделирования акулы, сгруппировав в структуру координаты акулы x и y, возраст акулы sday, и количество дней, прошедших после последней съеденной рыбы eat.
struct sharktype {
int x,y;
int fday;
int eat;
};
В данной ситуации, когда количество рыб и акул заранее неизвестно и может изменяться в очень широких пределах, удобнее распределять память компьютера динамически (по мере надобности в процессе выполнения программы). Поэтому вместо переменной типа sharktype удобнее описать переменную-указатель на этот тип:
sharktype *shark;
В этом случае обращение к полям структуры уже будет не через точку, а через стрелку: shark-> sday, shark->eat и т. д. Указатель занимает гораздо меньше памяти, чем сама структура, поэтому можно объявить большие массивы указателей с запасом. Необходимо только написать процедуры создания и удаления акул и рыб, не забывая аккуратно выделять и освобождать память для структур.
Листинг 5. Фрагмент программы моделирования клеточного автомата Ва-Тор fishtype *fish[32000]; // объявляем большой массив указателей на рыб. sharkty*shark pe [32000]; // и большой массив указателей на акул.
void MakeFish(int i,int x,int y) // процедура «рождения» новой рыбы
{
fish[i]=(FISH *)malloc(sizeof(FISH)); // выделяем память для размещения структуры
fish[i]->x=x; // помещаем рыбу в точку с заданными координатами
fish[i]->y=y;
fish[i]->fday=0; // ее возраст равен нулю
}
void MakeShark(int i,int x,int y) // процедура «рождения» акулы
{
shark[i]=(SHARK *)malloc(sizeof(SHARK)); // выделяем память для размещения
структуры
shark[i]->x=x; // помещаем акулу в точку с заданными
координатами
shark[i]->y=y;
shark[i]->sday=0; // возраст равен нулю
shark[i]->eat=0; // акула не ела 0 дней
}
void KillFish(int i) // «смерть» рыбы
{
free(fish[i]); // освобождаем память
fish[i]=NULL; // обнуляем значение указателя
}
void KillShark(int i) // «смерть» акулы
{
free(shark[i]); // освобождаем память
shark[i]=NULL; // обнуляем значение указателя
Задача 2.Составление рациона питания
Необходимо составить самый дешевый рацион питания цыплят, содержащий необходимое количество определенных питательных веществ тиамина Т и ниацина Н. Пищевая ценность рациона (в калориях) должна быть не менее заданной. Смесь для цыплят изготавливается из двух продуктов - К и С. Известно содержание тиамина и ниацина в этих продуктах, а также питательная ценность К и С (в калориях). Сколько К и С надо взять для одной порции куриного корма, чтобы цыплята получили необходимую им дозу веществ Н и Т и калорий (или больше), а стоимость порции была минимальна? Исходные данные для расчетов приведены в рисунке 1.
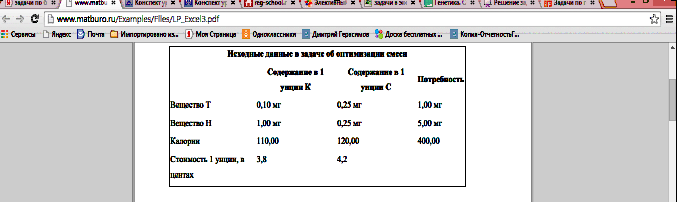
Рис. 1. Исходные данные к задаче
РЕШЕНИЕ.
Решим задачу средствами программы MS Excel. Внесем данные в исходный рисунок 2.
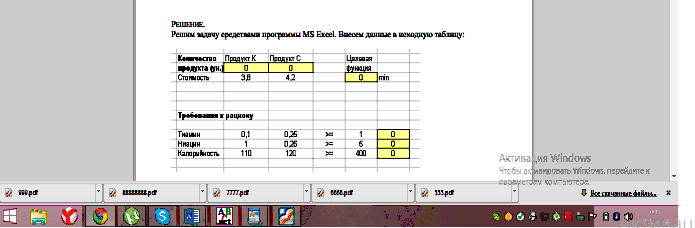
Рис.2. Решение задачи средствами программы MS Excel
Формулы. Рисунок 3.
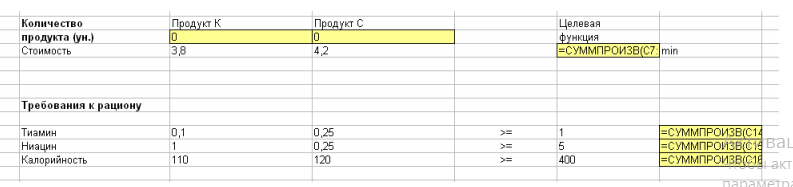
Рис. 3. Таблица формул
Вызываем надстройку «Поиск решения» и заполняем параметры. Вносим целевую функцию и ограничения. (Рисунок 4).
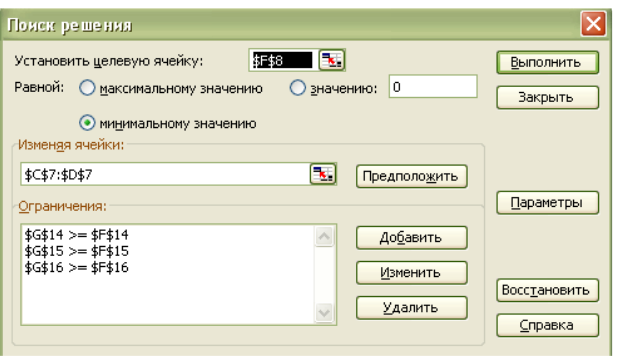
Рис.4. Таблица целевых функций и ограничений
Указываем линейность задачи и неотрицательность переменных (рисунок 5).
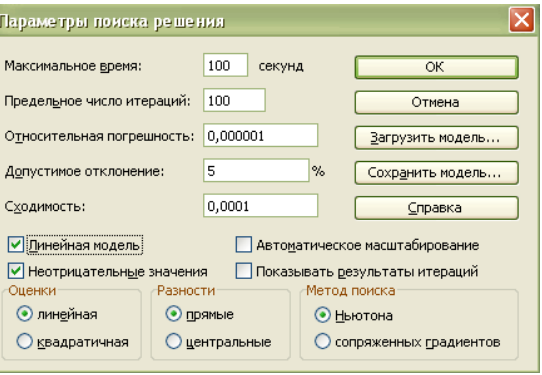
Рис.5.Таблица линейности задачи и неотрицательности переменных.
Запускаем решение (рисунок 6).
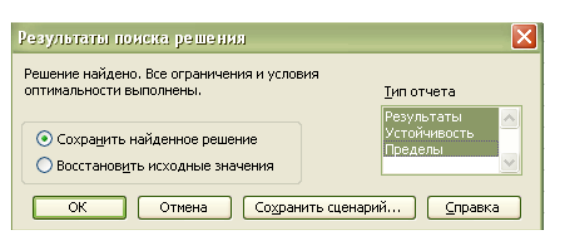
Рис.6.Таблица результатов поиска решения
Получаем решение (рисунок 7).
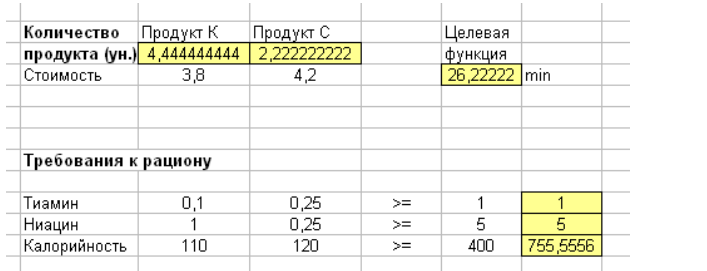
Рис.7. Таблица нахождения самого дешевого рациона.
То есть при данных ограничениях самый дешевый рацион стоит 26,22 цента и содержит 4,44 унции продукта К и 2,22 унции продукта С. Если предположить, что вес продуктов должен быть целым (целочисленные переменные) (рисунок 8).
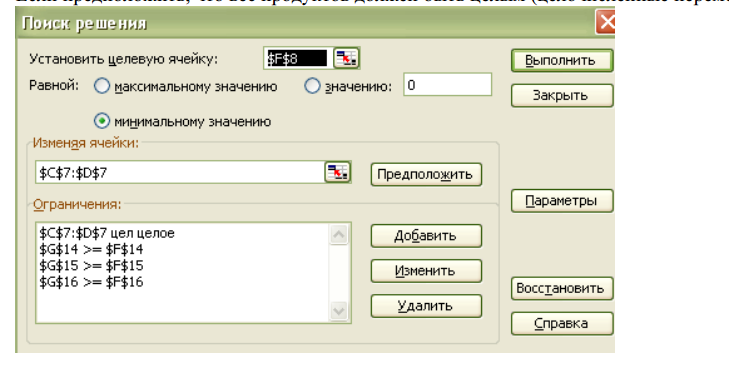
Рис 8. Таблица целочисленных переменных
То получим другое решение (рисунок 9).
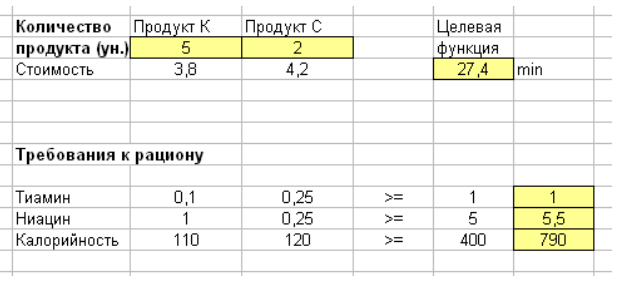
Рис.9.Таблица нахождения решения
Следует взять 5 унций продукта К, 2 унции продукта С, рацион выйдет немного дороже, стоимость составит 27,4 цента.
ЗАКЛЮЧЕНИЕ
Для формирования информационных компетенций во время изучения школьного курса биологии учитель должен развивать способность обучающегося самостоятельно искать, извлекать, систематизировать, анализировать и отбирать необходимую для решения учебных задач информацию, организовывать, передавать ее [7].
Содержание предмета биологии позволяет ребенку в содружестве с учителем познавать мир живой природы, себя, закономерности развития органического мира. Проблемы природы – это проблемы и человека. Поэтому обучение на уроках биологии должно проходить под девизом: «Живя в мире, будь его полноценной частью!».
Перед учеными и учителями стоит постоянный вопрос: как развивать мышление учащихся в процессе обучения?
В действующие программы по предметам, в том числе по биологии, включен раздел «Требования к знаниям и умениям учащихся». Однако практика показывает, что учителя далеко не в полной мере реализуют эти требования, уделяя основное внимание формированию у учащихся знаний, а не умений. И происходит это не потому, что не хотим, а потому, что не знаем или не догадываемся, что важнее: знать или уметь?
Связь между знаниями и умениями можно охарактеризовать так: «Умения – это знания в действии». Без знаний нет умений, но сами знания не могут быть усвоены и сохранены без умений.
Часто к конечному результату ученик подводится посредством выполнения требований учителя: думай, спрашивай, слушай, повторяй. А как думать? Как смотреть? От ученика скрыты действия и порядок их выполнения. Поэтому необходимо раскрыть приемы, то есть надо показать, из каких действий прием состоит (состав) и в какой последовательности надо учебные действия (структура приема).
Воспитание ученика-исследователя – это процесс, который открывает широкие возможности для развития активной и творческой личности, способной вести самостоятельный поиск, делать собственные открытия, решать возникающие проблемы, принимать решения и нести за них ответственность. Только в поиске, в ходе самостоятельных исследований развивается мышление ребенка, знания и умения добываются в результате его собственного познавательного труда. Одним из таких самостоятельных исследований является моделирование.
Моделирование – это наглядно-практический метод обучения. Наглядность является необходимым и закономерным средством образовательного процесса на всех этапах изучения биологии в средней школе, так же как и практический метод. Специальные психолого-педагогические исследования показали, что эффективность обучения зависит от степени привлечения всех органов чувств человека. Чем разнообразнее чувственное восприятие учебного материала, тем прочнее он усваивается. Вследствие этого мы считаем, что совокупность наглядного и практического методов обучения, в виде метода моделирования является самодостаточным и должна занять достойное место среди современных методов обучения.
СПИСОК ЛИТЕРАТУРЫ
1. Аверьянов А.Н. Системное познание мира: методологические проблемы. М., 2001.- 204, 261–263 с.
2. Алтухов В.Л., Шапошников В.Ф. О перестройке мышления: философско-методологические аспекты. М., 2008 – 34 с.
3. Батоpоев К.Б. Кибеpнетика и метод аналогий. М., Высшая школа, 2004. - 23 с.
4. Биология 9-11. Экспресс методика быстрого усвоения школьного курса и подготовки к экзаменам. Новая школа. 2005. - 23 с.
5. Богомолов А.С. Античная философия. М., МГУ, 2005. - 134 с.
6. Будущее искусственного интеллекта. М., Наука,2001. - 280–302 с.
7. Ермаков В.П.Якунин Г.А.; «Основы тифлопедагогики», М., «Владос», 2000. -69-76 с.
8. Конюшенко В.С. Павлюченко С.Е., Чубаро С.Ф.; «Методика обучения биологии». Минск, «Книжный Дом», 2004. - 45 с.
9. Могилев А.В., Пак Н.И., Хеннер Е.К. Информатика, М., Академия, 2009. - 674–677 с.
10. Ребер.А. Оксфордский Толковый словарь, 2002. - 356 с.
11. Советский энциклопедический словарь (под ред. А.М. Прохорова) -М., Советская Энциклопедия, 2000. - 828 с.
12. Фpолов И.Т. Гносеологические проблемы моделирования. М., Наука, 2001. - 20 с.
13. Фролов И.Т. "Жизнь и познание. О диалектике в современной биологии" М.: Мысль, 2001. - 34 с.
14. Штофф В.А. Моделирование и философия. М., Наука, 2006. - 256 с.
PAGE \* MERGEFORMAT2
Решение задачи хищник- жертва. Решение задачи на составление рациона питания