Однородные системы линейных оду с постоянными коэффициентами на плоскости

Оглавление

Введение 3

1. Однородные системы линейных оду                     
   с постоянными коэффициентами на плоскости 4
2. Пример 7

Заключение 10

Литература 11

Введение

В настоящей работе исследуется вопрос о поведении фазовых кривых однородной системы линейных дифференциальных уравнений первого порядка с постоянными коэффициентами на плоскости. Задачи такого рода часто возникают при математическом моделировании объектов и процессов самой разной природы. Известно, что фазовые кривые такой системы заполняют собой всю плоскость, причем точка с координатами является одной из фазовых кривых (это положение равновесия системы).

Цель курсовой работы рассмотреть систему линейных дифференциальных уравнений с постоянными коэффициентами на плоскости.

Задача курсовой состоит в том, чтобы выяснить, как ведут себя остальные фазовые кривые. Как показывает теория, они могут вести себя примерно 15-ю разными способами, и для каждой конкретной системы не составляет большого труда узнать, с каким типом мы столкнулись.

Настоящая работа состоит из Введения, двух глав, Заключения и списка литературы, включающего 4 пункта. В первой главе мы кратко излагаем теорию линейных однородных систем дифференциальных уравнений первого порядка с постоянными коэффициентами на плоскости. Глава 2 посвящена разбору одного примера такой системы: для него мы строим фазовый портрет. В Заключении подводятся итоги проделанной работы. В список литературы включены книги учебного характера, на основании которых была написана глава 1.

1. Однородные системы линейных оду
   с постоянными коэффициентами на плоскости

Рассмотрим систему дифференциальных уравнений

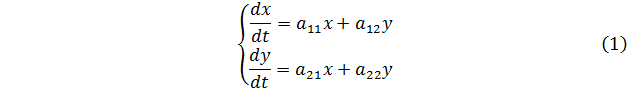
Здесь и — неизвестные функции вещественной переменной ; , , и — известные вещественные коэффициенты. Введем в рассмотрение неизвестную вектор-функцию:

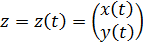
и матрицу

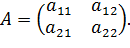
Тогда систему можно переписать в виде

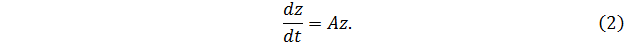
Сформулируем некоторые определения, касающиеся системы или .

Во-первых, это система уравнений первого порядка: в уравнениях участвуют только первые производные неизвестных функций, а производных второго порядка и выше в системе нет. Заметим также, что уравнения разрешены относительно производной.

Во-вторых, это линейная система: неизвестные функции входят в нее линейно, то есть кроме умножения на постоянные коэффициенты и сложения, никаких действий над неизвестными функциями не совершается. Если обратиться к векторной форме записи (2), то можно сказать, что в правой части стоит линейный оператор, примененный к неизвестной вектор-функции .

В-третьих, система является однородной (неоднородная система записывалась бы не в виде , а в виде , где — известная вектор-функция).

В-четвертых, рассматриваемая система — это система с постоянными коэффициентами: коэффициенты не зависят от .

Кривая на плоскости , где является решением системы , называется фазовой кривой. Совокупность фазовых кривых образует фазовый портрет системы. Из однородности рассматриваемой системы следует, что у нее имеется решение, тождественно равное нулю: . Эта фазовая кривая состоит всего из одной точки (расположенной в начале координат), которая называется точкой покоя системы.

Теория показывает (см. [1–4]), что ключевым моментом в отыскании общего решения системы или и построении фазового портрета является нахождение собственных значений матрицы , то есть таких чисел , для которых уравнение имеет ненулевое решение. Эти ненулевые решения называются собственными векторами матрицы .

Собственные значения матрицы суть корни характеристического уравнения

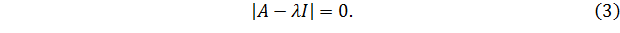
Повнимательнее посмотрим на левую часть уравнения :

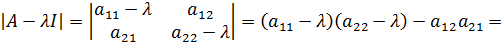
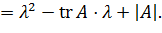
Здесь — след матрицы (сумма ее диагональных элементов), — определитель матрицы .

Многочлен в зависимости от того, какие у него коэффициенты, может иметь два различных или совпадающих вещественных корня или два комплексно сопряженных корня. Эти корни и определяют тип фазового портрета.

Если оба корня вещественны и имеют один знак, то фазовый портрет называется узлом (устойчивый узел, если корни отрицательны — в этом случае все решения стремятся к точке покоя, и неустойчивый узел, если корни положительны — решения стремятся убежать от точки покоя: см. рис. 1.1).

Рис. 1.1: Устойчивый и неустойчивый узлы.

Если оба корня вещественны и имеют разные знаки (один положителен, а другой отрицателен), то фазовый портрет называется седлом (см. рис. 1.2). Седло неустойчиво: решения проходят мимо точки покоя по гиперболе и убегают в бесконечность.

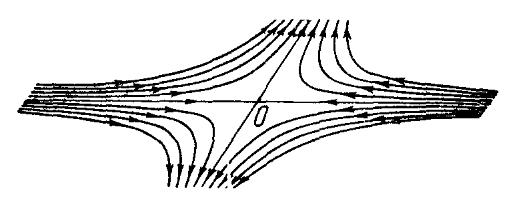
Рис. 1.2: Седло.

Если корни комплексно сопряжены: , то при точка покоя называется фокусом: устойчивым при и неустойчивым при (см. рис. 1.3).

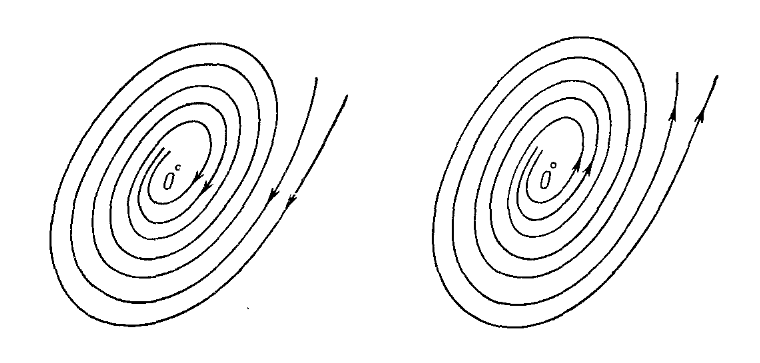
Рис. 1.3: Устойчивый и неустойчивый фокусы.

Если вещественная часть комплексно сопряженных корней нулевая: , то точка покоя называется центром (см. рис. 1.4): фазовые кривые не убегают от точки покоя, но и не стремятся к ней. В этом случае говорят, что точка покоя устойчива, но не асимптотически устойчива (в случае устойчивых узла и фокуса устойчивость асимптотическая).

Рис. 1.4: Центр.

Если корень кратный и ненулевой: , то фазовый портрет зависит от знака корня. Если кратный корень отрицателен, то точка покоя называется устойчивым узлом, как и в случае различных отрицательных корней. В зависимости от собственных векторов (линейно независимых собственных векторов может быть два или один) фазовый портрет может выглядеть несколько по-разному — см. рис. 1.5. Для случая, изображенного на правой части рисунка (это случай двух собственных векторов, то есть двумерного собственного пространства) узел называется дикритическим.

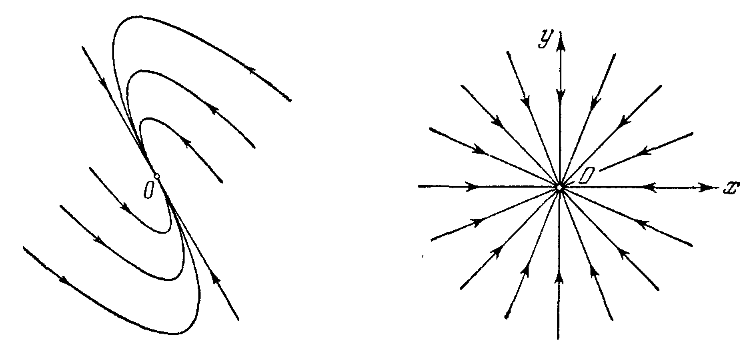
Рис. 1.5: Устойчивый узел в случае кратных корней.

Если кратный корень положителен, то мы имеем неустойчивый узел: он выглядит так же, как на рис. 1.5, с той лишь разницей, что стрелки на фазовых кривых будут направлены в противоположную сторону.

Остается рассмотреть случай, когда один из корней нулевой, или оба корня совпадают и равны нулю. В этом случае у системы есть точки покоя, отличные от начала координат (они образуют прямую, натянутую на собственный вектор, отвечающий нулевому собственному значению, или даже всю плоскость, если матрица системы нулевая). Фазовые кривые, отличные от точек покоя, представляют собой лучи, причем движение по этим лучам происходит либо в сторону прямой покоя, если второе собственное значение отрицательно (устойчивый случай — см. рис. 1.6), либо от этой прямой в бесконечность, если второе собственное значение положительно.

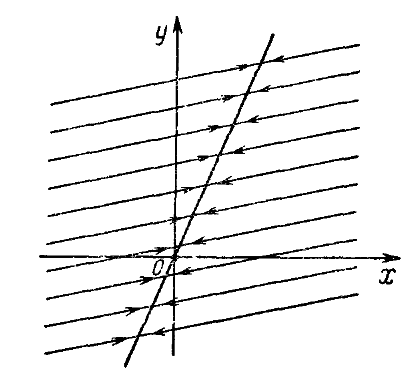
Рис. 1.6: Случай нулевого и отрицательного корней.

Иллюстрации позаимствованы нами из книги [4].

2. Пример

Рассмотрим систему

Матрица этой системы имеет вид

Характеристическое уравнение:

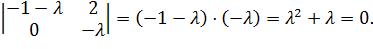
Собственные значения: , .

Найдем собственный вектор для :

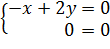
Собственные векторы определяются соотношением : качестве собственного вектора можно взять .

Найдем собственный вектор для :

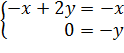
Собственные векторы определяются соотношением : качестве собственного вектора можно взять .

Общее решение системы имеет вид:

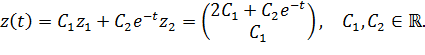
Мы имеем случай нулевого и отрицательного собственных значений, то есть точка покоя, во-первых, не единственна, а есть целая прямая покоя (натянутая на собственный вектор : если в формуле общего решения положить , то как раз мы получим общий вид точки покоя), а во-вторых, нулевая точка покоя устойчива, но не асимптотически устойчива.

Фазовый портрет системы изображен на рисунке 2.1.

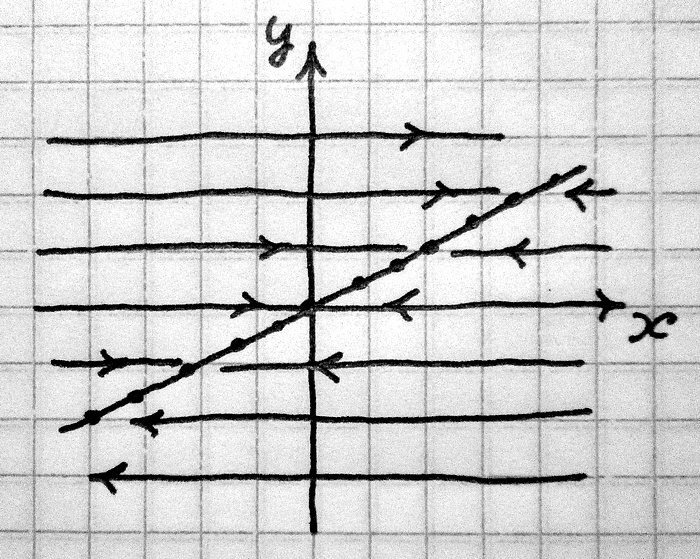
Рис. 2.1: Фазовый портрет системы .

Заключение

В настоящей работе была выполнена поставленная задача: построен фазовый портрет для линейной системы дифференциальных уравнений первого порядка с постоянными коэффициентами на плоскости.

Список использованной литературы

1.  Карташев А. П., Рождественский Б. Л. Обыкновенные дифференциальные уравнения и основы вариационного исчисления. М., 1980.

2.  Пушкарь Е. А. Дифференциальные уравнения: Учебное пособие. М., 2007.

3. Письменный Д.Т. Конспект лекций по высшей математике.Полный курс.-2-е изд. Айрис-пресс, 2004.-608с.

4.  Романко В. К. Курс дифференциальных уравнений и вариационного исчисления. М., 2001.

5.  Эльсгольц В. К. Дифференциальные уравнения и вариационное исчисление. М., 1969.

Однородные системы линейных оду с постоянными коэффициентами на плоскости