Решение системы дифференциальных уравнений, исследование фазовых кривых
Оглавление
Введение 3
1. Необходимые теоретические сведения 4
2.Решение системы дифференциальных уравнений,
исследование фазовых кривых 7
Заключение 10
Список использованной литературы 11
Введение
Очень многие природные процессы удается научно исследовать, моделируя их с помощью дифференциальных уравнений или систем дифференциальных уравнений. Поэтому теория дифференциальных уравнений — это важная прикладная математическая наука.
Среди всевозможных дифференциальных уравнений самыми простыми и доступными для изучения являются линейные уравнения, а самые простые среди линейных уравнений — уравнения с постоянными коэффициентами. Несмотря на их простоту, линейные дифференциальные уравнения с постоянными коэффициентами имеют достаточно богатую теорию (особенно в случае систем) и являются важным прикладным инструментом.
Цель курсовой работы рассмотреть систему линейных дифференциальных уравнений с постоянными коэффициентами на плоскости.
Задача курсовой работы исследовать фазовые кривые одной конкретной системы. Она решается во втором разделе основной части работы, в первом разделе излагаются необходимые определения и результаты из теории.
При написании этой работы использовалась учебная литература. Список использованной литературы приведен в конце работы.
1. Необходимые теоретические сведения
Однородная система линейных дифференциальных уравнений с постоянными коэффициентами в общем случае имеет вид
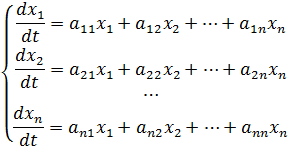
Здесь — неизвестные функции, () — известные коэффициенты (вещественные числа). Если обозначить вектор неизвестных функций через , а матрица коэффициентов через , то систему можно переписать в векторно-матричном виде
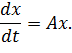
Если в этой записи понимать как обычную функцию, а не вектор, а — как число, то, как известно, общее решение такого уравнения имеет вид:
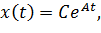
где — произвольная константа. Оказывается, что подобным образом можно записывать и общее решение системы дифференциальных уравнений, только если является матрицей, то надо определить, что такое .
Рассмотрим случай . Тогда однородная система приобретает вид
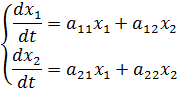
Чтобы найти ее общее решение, надо найти собственные числа матрицы . Для этого решается характеристическое уравнение:
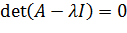
относительно параметра . Подробно расписывая левую часть характеристического уравнения, мы видим, что она представляет собой многочлен второй степени относительно :
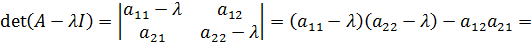
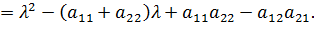
В зависимости от значений коэффициентов этот многочлен может иметь два различных вещественных корня, один двукратный вещественный корень (в том случае, если выражение является полным квадратом), или же, наконец, два комплексно сопряженных корня. Поведение решений системы (каждому решению геометрически соответствует кривая на плоскости, которая называется фазовой кривой) зависит именно от корней характеристического уравнения, причем не только от того, вещественные они или комплексные, различные или совпадающие, но и от знака каждого вещественного корня, а в случае комплексных корней — от знака вещественной и мнимой части. Здесь возможно много разных вариантов, и соответственно выделяется много типов поведения фазовых кривых.
Однородная система всегда имеет стационарное (то есть постоянное) нулевое решение: . Про него еще говорят, что оно определяет точку равновесия системы. Особое внимание уделяется тому, является ли нулевое решение устойчивым, то есть удаляются ли от него или, наоборот, стремятся к нему остальные решения системы, когда аргумент стремится к бесконечности. Ответ на этот вопрос полностью определяется знаками вещественных частей собственных чисел матрицы : если хотя бы одно из собственных чисел положительно или имеет положительную вещественную часть, то нулевое стационарное решение неустойчиво, то есть существуют решения, которые при убегают от точки равновесия в бесконечность. Если оба собственных числа имеют отрицательные вещественные части, то нулевое решение асимптотически устойчиво: все остальные решения стремятся к нулю при . Если же оба собственных числа имеют нулевые вещественные части, или одно равно нулю, а другое отрицательно, то нулевое решение устойчиво, но не асимптотически: в этом случае никакие решения не убегают от точки равновесия в бесконечность, но и не все стремятся к нулю: есть такие решения, которые остаются от нуля на конечном расстоянии. Случай, когда одно или оба характеристических числа нулевые, интересен тем, что в этом случае, кроме нулевого положения равновесия, система имеет и другие стационарные точки. Чтобы их найти, надо найти собственный вектор нулевого собственного значения, то есть решить векторно-матричное уравнение
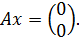
2. Решение системы дифференциальных уравнений, исследование фазовых кривых
В этом разделе работы мы исследуем фазовые кривые системы уравнений:
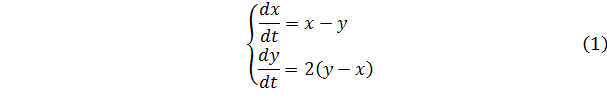
Эта система является линейной, автономной и однородной системой уравнений первого порядка. Поскольку система однородна, у нее есть нулевое решение: , . Перепишем систему в виде:
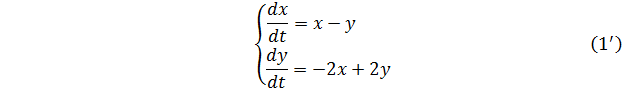
Выпишем матрицу коэффициентов системы, обозначим ее :
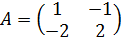
Составим характеристическое уравнение и решим его:
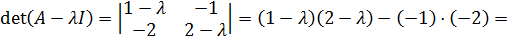
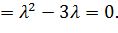
Корнями этого уравнения являются числа и . Это собственные числа матрицы . Необходимо найти соответствующие этим числам собственные векторы. Заметим, что, поскольку имеется нулевое собственное значение, система является сложной: у нее есть положения равновесия, отличные от точки .
Рассмотрим матрично-векторное уравнение (то есть ), где — это вектор с координатами и . Перепишем это уравнение в координатах, то есть запишем его как систему уравнений относительно и :
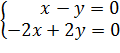
Второе уравнение можно поделить на (эта операция не меняет множества решений), и тогда мы получим систему, в которой два одинаковых уравнения:
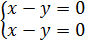
Понятно, что общее решение этой системы определяется равенством , так что в качестве собственного вектора годится любой ненулевой вектор, у которого первая координата совпадает со второй. Например, можно взять вектор .
Теперь рассмотрим уравнение , то есть . Как и раньше, . В координатах это уравнение будет выглядеть так:
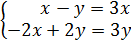
Перенесем в левые части уравнений слагаемые, стоящие в правых частях:
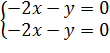
Эта система содержит два одинаковых уравнения, и одно из них можно отбросить. В данном случае в качестве собственного вектора можно взять .
Общее решение системы уравнений имеет вид:
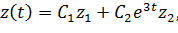
где — произвольные вещественные константы.
В координатах решение запишется так:
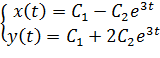
Поскольку один из корней характеристического уравнения положителен, стационарное решение неустойчиво: если, например, положить , , то мы получим решение , которое с ростом будет удаляться от положения равновесия (то есть от начала координат) в бесконечность.
Фазовые кривые схематично показаны на рисунке:
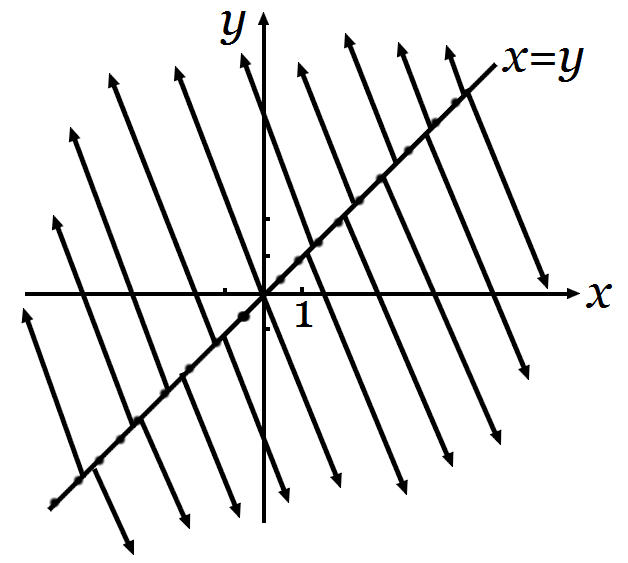
Каждая точка прямой является стационарной фазовой кривой, то есть положением равновесия системы. Остальные фазовые кривые представляют собой лучи, уходящие от прямой в бесконечность. Все эти лучи параллельны вектору .
Заключение
Рассмотрев и изложив необходимый теоретический материал, мы решили задачу о поведении фазовых кривых линейной автономной системы на плоскости.
Список использованной литературы
1. Пушкарь Е. А. Дифференциальные уравнения. — М.: МГИУ, 2007. —254 с.
2. Романко В. К. Курс дифференциальных уравнений и вариационного исчисления. — 2 изд. — М.: Лаборатория базовых знаний, 2001. — 344 с.
3. Эльсгольц В. К. Дифференциальные уравнения и вариационное исчисление. — М.: Наука, 1969. — 424 с.
4. Письменный Д.Т. Конспект лекций по высшей математике.Полный курс.-2-е изд. Айрис-пресс, 2004.-608с.
5. Карташев А. П., Рождественский Б. Л. Обыкновенные дифференциальные уравнения и основы вариационного исчисления. М., 1980
Решение системы дифференциальных уравнений, исследование фазовых кривых