Работа и расчет элементов металлических конструкций

Лекция 7.

Работа и расчет элементов металлических конструкций

Расчет центрально растянутых элементов

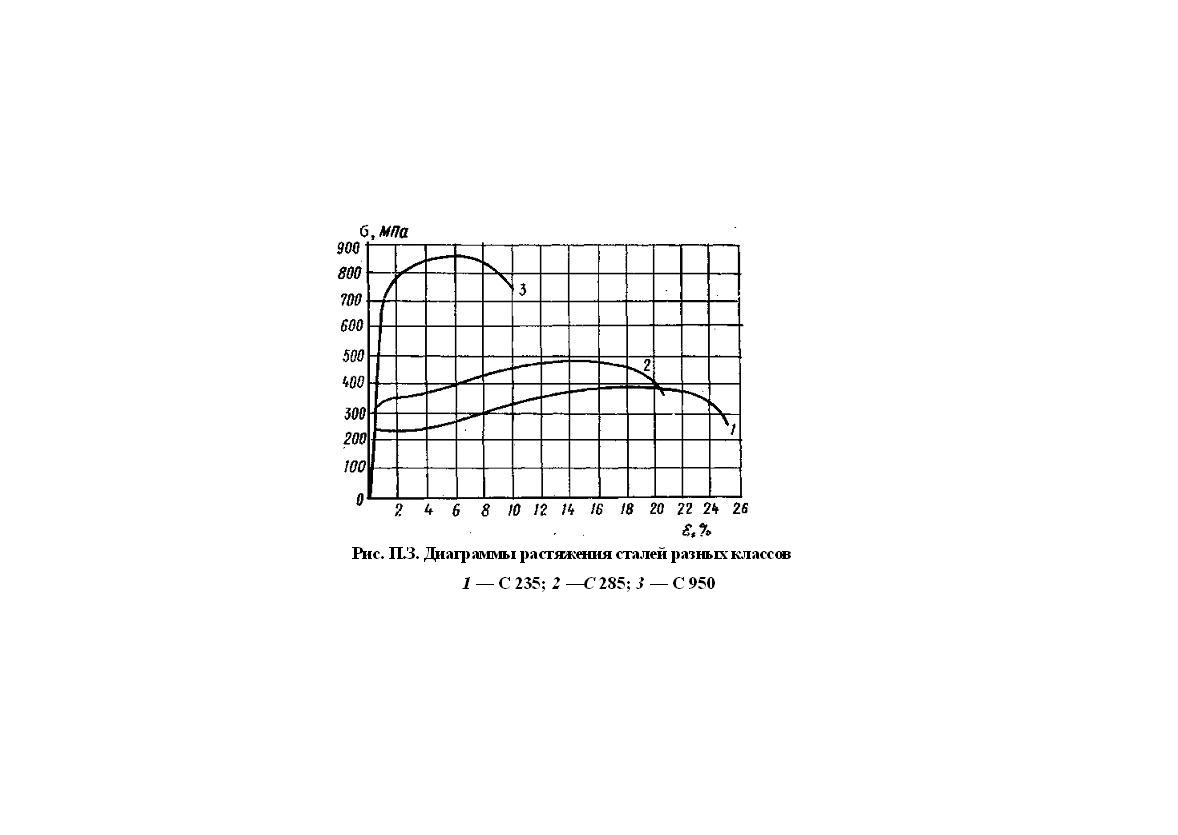
Поведение под нагрузкой центрально растянутого элемента полностью соответствует работе материала при простом растяжении (рис. Р1. ) Предельное состояние первой группы центрально растянутых элементов

проверяются расчетом на прочность по формуле

(Р.1).

В случае, если рассчитываемый элемент выполнен из стали с отношением

Ru /gu Ry (Р.2).

эксплуатация которого возможна и после достижения металлом предела текучести расчет на прочность следует выполнять по формуле

(Р.3)

Расчет изгибаемых стержней

Для изгибаемых элементов в большинстве случаев их работы расчетом проверяются следующие предельные состояния: первой группы — вязкое или усталостное разрушение, потеря устойчивости, а также текучесть материала; второй группы — достижение предельных перемещений.

Расчет изгибаемых элементов в пределах упругости. Предельное состояние в этом случае определяется достижением максимальными нормальными или касательными напряжениями значений предела текучести. Прочность изгибаемых элементов, работающих в пределах упругих деформаций, при изгибе в одной из главных плоскостей проверяется по формулам:

s = (И.1) и

t = (И.2)

где М и Q — изгибающий момент и поперечная сила, определенные по расчетным нагрузкам; Wm,min — момент сопротивления ослабленного сечения, определенный по упругой стадии работы элемента; S — статический момент (брутто) сдвигающейся части сечения относительно нейтральной оси; Rу — расчетное сопротивление изгибу, определенное по пределу текучести; Rs — расчетное сопротивление срезу; gc — коэффициент условий работы.

Прочность элементов при изгибе их в двух главных плоскостях (косой изгиб) проверяется по формуле:

(И.3)

где х и у — координаты рассматриваемой точки селения относительно главных осей.

Работа изгибаемых элементов с учетом развития пластических деформаций.

После исчерпания упругой работы (рис. 3.12, а) в сплошных изгибаемых элементах, выполненных из пластичных сталей, пластические деформации начинают распространяться в глубь сечения (рис. 3.12,6) и в предельном состоянии они пронизывают все сечение (рис. 3.12,в), образуя так называемый «ш а р н и р пластичности».

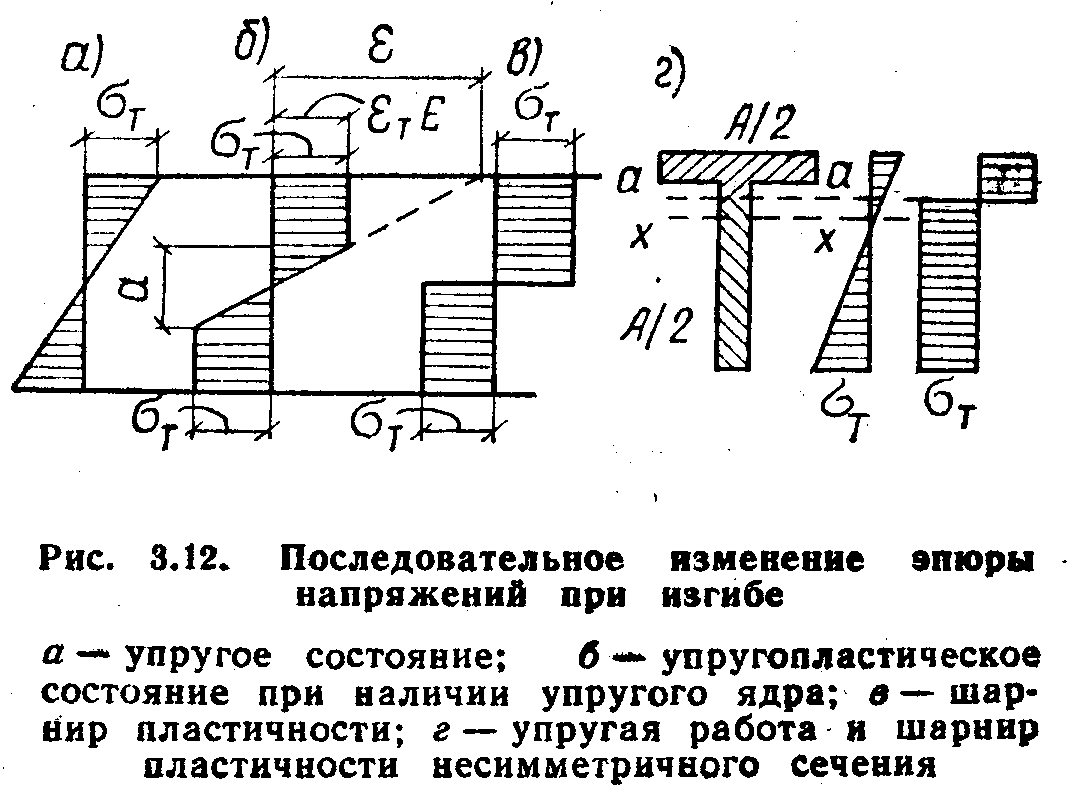
При образовании шарнира пластичности все фибры сечения находятся в стадии текучести и, следовательно, их длина может изменяться при постоянном напряжении, вследствие чего изгибаемый элемент может поворачиваться вокруг нейтральной оси, как вокруг оси шарнира. Работа шарнира пластичности возможна только в направлении действия предельного момента; при действии изгибающего момента в обратном направлении напряжения уменьшаются, материал снова становится упругим и шарнир пластичности замыкается. В отличие от обычного шарнира в пластическом шарнире момент не равен нулю.

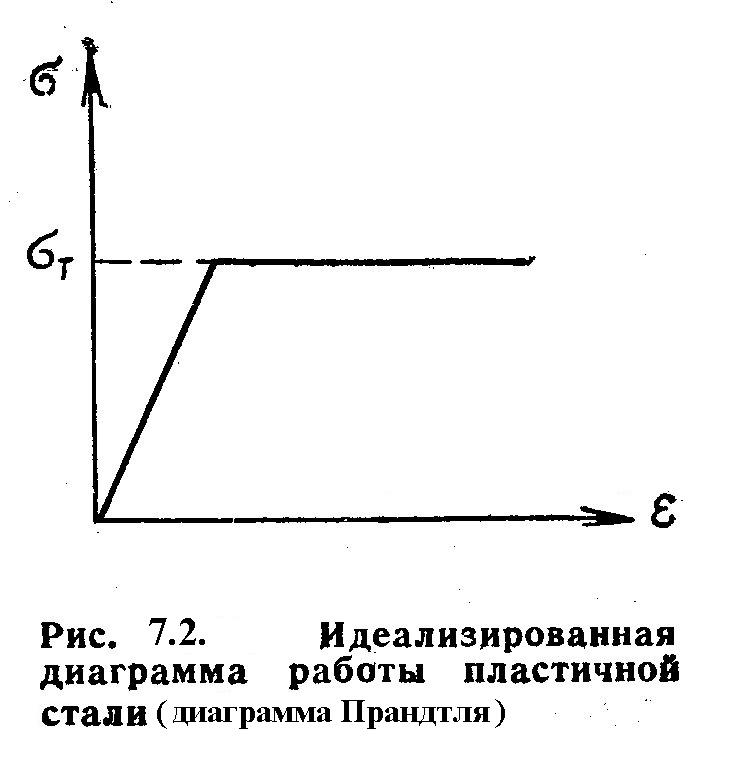
Предполагая сталь идеально упругопластическим материалом, описываемым диаграммой Прантля, (см. рис. 7.11) и допуская, что напряжения во всех фибрах

достигнут предела текучести, можно определить предельное значение момента шарнира пластичности. Эпюра напряжений такого состояния имеет вид двух прямоугольников с ординатами, равными пределу текучести (см. рис. 3.12, в). Предельный момент внутренних сил определяется из выражения

(И.4)

где S — статический момент половины сечения относительно нейтральной оси. Для симметричных сечений нейтральная ось проходит через центр тяжести сечения, в несимметричных сечениях нейтральная ось делит сечение на две равновеликие части и не совпадает с центром тяжести (рис. 3.12, г).

Сравнивая формулу (И.4) с обычной формулой М = sтW где М — предельный момент, определенный по упругой стадии работы материала, видим, что 2S играет роль пластического момента сопротивления; Wпл = 2S.

Пластический момент сопротивления Wпл больше упругого момента сопротивления W, и разница тем больше, чем больше материала расположено около нейтральной оси сечения. Для прямоугольного сечения Wпл=1,5W, для прокатных швеллеров и двутавров при изгибе в плоскости стенки Wпл=1,12W, при изгибе в плоскости, параллельной полкам, Wпл=1.2W.

Совместное воздействие нормальных и касательных напряжений ускоряет развитие пластичности и предельный момент МпрQ при наличии поперечной силы будет меньше Мпр при чистом изгибе.

При образовании шарнира пластичности прогибы в статически определимых системах нарастают беспредельно. В статически неопределимых при образовании шарнира только понижается степень статической неопределимости.

Однако, как мы с вами выяснили, при плоском изгибе (при наличии поперечной силы), эксплуатационные качества конструкции утрачиваются раньше, чем наступает беспредельное нарастание деформации.

В связи с этим проф. Н.С.Стрелецкий предложил принимать в качестве критерия предельного состояния по непригодности к эксплуатации ограниченную пластическую деформацию в сечении. В настоящее время это предложение используется в действующем СНиПе.

Для практических расчетов принята предельная относительная пластическая деформация в сечении

, где

Учет пластической работы стали допускается в балках сплошного сечения, несущих статическую нагрузку при касательных напряжениях в интервале 0.5Rs t 0.9Rs.

Проверка прочности таких балок выполняется по формуле

здесь с1 > 1– коэффициент, учитывающий развитие пластических деформаций по сечению в зависимости от относительной величины касательных напряжений и геометрических размеров и формы поперечного сечения. Формулы и таблицы для определения этого коэффициента приведены в СНиПе.

В случае косого изгиба условие прочности запишется выражением

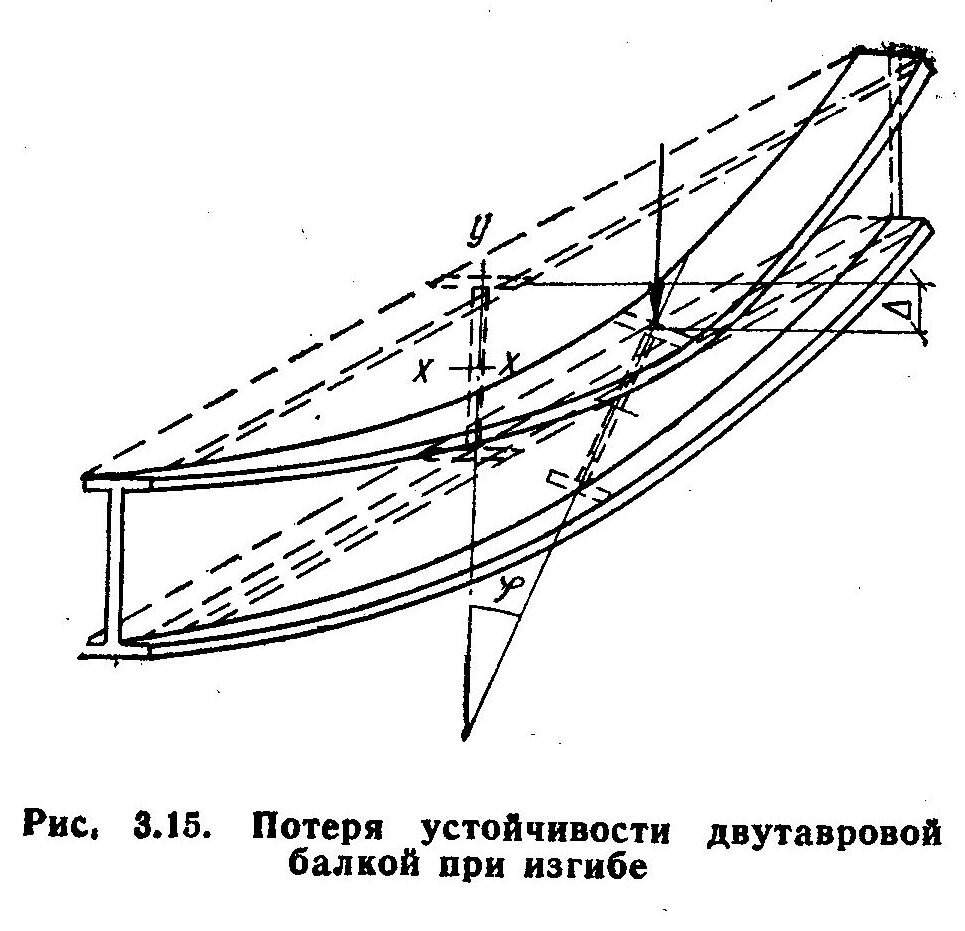
Проверка общей устойчивости изгибаемых элементов (первое предельное состояние). Изгибаемые элементы могут выйти из работы вследствие потери ими общей устойчивости. При потере устойчивости изгибаемый элемент (например, балка) при расположении нагрузки в плоскости главной оси инерции сначала изгибается в своей плоскости, затем при достижении нагрузкой критического значения начинает закручиваться и выходить из плоскости изгиба (рис. 3.15).

Проверка общей устойчивости балок сводится к сравнению возникающих напряжений с критическими. Расчетная формула этой проверки представима в виде:

где Wc – момент сопротивления для сжатого пояса;

jb = sкр/sу – коэффициент перехода от нормативных сопротивлений к критическим напряжениям потери общей устойчивости изгибаемыми элементами (обычно коэффициент jb называют балочным коэффициентом).

При определении значения jb за расчетную длину балки l еf следует принимать расстояние между точками закреплений сжатого пояса от поперечных смещений (узлами продольных или поперечных связей, точками крепления жесткого настила); при отсутствии связей l еf = l (где l — пролет балки); за расчетную длину консоли следует принимать: lеf = l при отсутствии закрепления сжатого пояса на конце консоли в горизонтальной плоскости (здесь l — длина консоли); расстояние между точками закреплений сжатого пояса в горизонтальной плоскости при закреплении пояса на конце и по длине консоли.

Устойчивость балок не требуется проверять:

а) при передаче нагрузки через сплошной жесткий настил, непрерывно опирающийся на сжатый пояс балки и надежно с ним связанный (плиты железобетонные из тяжелого, легкого и ячеистого бетона, плоский и профилированный металлический настил, волнистую сталь и т. п.);

б) при отношении расчетной длины балки lеf к ширине сжатого пояса b, не превышающем значений, определяемых по формулам табл. 8* для балок симметричного двутаврового сечения и с более развитым сжатым поясом, для которых ширина растянутого пояса составляет не менее 0,75 ширины сжатого пояса.

Проверка упругих деформаций, нарушающих нормальные условия эксплуатации (второе предельное состояние). В условиях нормального режима работы сооружения в балках могут появиться деформации, затрудняющие эксплуатацию конструкций. Эти деформации (прогибы) проверяют по упругой стадии работы конструкции от воздействия нормативных нагрузок. При этом возникающие максимальные прогибы не должны превышать предельных, приведенных в разделе 10 СНиП2.01.07-85*

f [f]

Расчет элементов стальных конструкций на центральное сжатие

Предельные состояния сжатых жестких стержней определяются развитием пластических деформаций при достижении напряжениями предела текучести, а гибких стержней — потерей устойчивости.

Расчет на прочность. Расчет на прочность центрально сжатых элементов выполняется так же, как и центрально растянутых, по формулам (Р.1) и (Р.3). Вместе с тем в этом случае могут быть учтены некоторые отличительные особенности работы материала на сжатие. Например, проверка прочности элементов с соединениями на болтах повышенной прочности может быть выполнена по сечению «брутто», т. е. без учета ослабления сечения отверстиями.

При малой длине выступающей части сжатого элемента (например, опорное ребро балки) его сечение определяется расчетом на местное смятие торцевой поверхности (при наличии пригонки

Требования по проверке устойчивости центрально-сжатых стержней установлены в действующем СНиП П-23-81* на основе расчета внецентренно-сжатых стержней с учетом влияния формы сечения, начального искривления оси, случайного эксцентриситета сжимающей силы, а также соединительных элементов (для сквозных стержней).

Начальные искривления или случайные эксцентриситеты приняты в соответствии с допускаемыми отклонениями, установленными в нормах на изготовление стальных конструкций.

При решении поставленной задачи был рассмотрен внецентренно-сжатый стержень, схема которого приведена на рис.3, а.

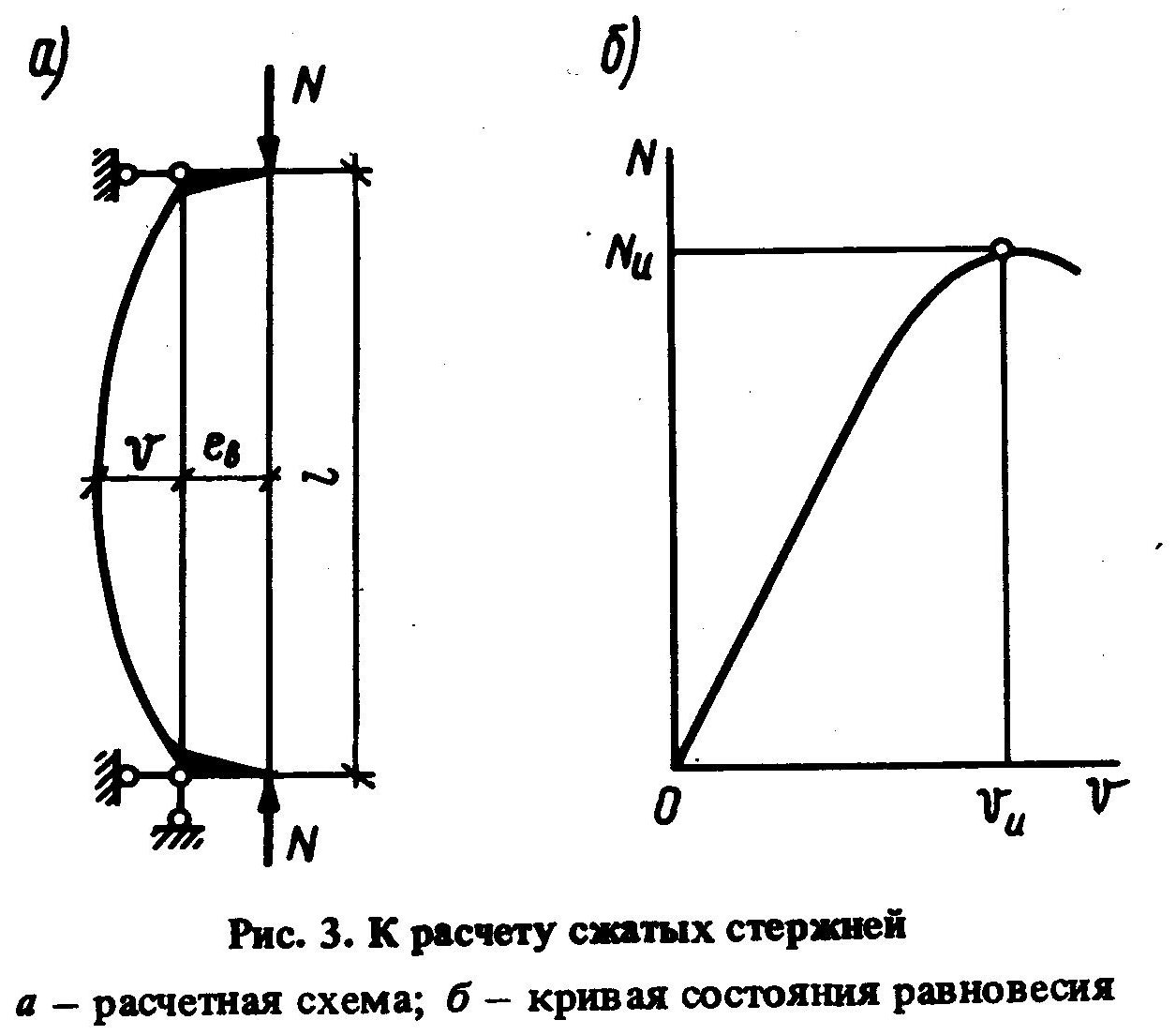
При этом решение выполнялось в предположении малости перемещений по деформированной схеме с учетом пластических деформаций, а значение расчетной несущей способности принято равным предельному значению сжимающей силы Nu, которая может быть воспринята элементом (рис. 3, б). Форма изогнутой оси принималась по полуволне синусоиды.

В СНиП П-23-81* методика практических расчетов центрально-сжатых элементов приведена с использованием коэффициентов устойчивости при центральном сжатии j (коэффициентов продольного изгиба), которые вычислены в зависимости от условной гибкости и приняты равными j = Nu/ (А Rу).

При вычислении значений коэффициентов j типы поперечных сечений сжатых элементов принимались в соответствии со значениями коэффициентами влияния формы сечения (табл.73 СНиП П-23-81*), а начальные несовершенства еb — по формуле

где i – радиус инерции сечения;

l – расчетная длина элемента.

При нормировании коэффициентов j определялась также критическая сила упругих идеальных стержней по методу Эйлера. Окончательные значения коэффициентов j принимались наименьшими из двух: вычисленных с учетом начальных несовершенств или по методу Эйлера с введением коэффициента надежности gе = 1.3 (). Это было сделано для ограничения прогибов сжатых стержней при относительно больших гибкостях, когда влияние начальных несовершенств становилось несущественным.

Полученные таким образом значения коэффициентов j для различных форм поперечных сечений были осреднены и аппроксимированы с помощью формул (8)-(10) СНиП П-23-81*, на основании которых для различных значений расчетных сопротивлений Rу, выраженных через приведенные гибкости была составлена табл. 72 СНиП П-23-81* коэффициентов продольного изгиба j для центрально-сжатых элементов.

Более точно эти величины можно определить по эмпирическим формулам.

В этом случае расчет на устойчивость сплошностенчатых элементов, подверженных центральному сжатию силой N следует выполнять по формуле

Работа и расчет элементов металлических конструкций