ОПТИМИЗАЦИЯ НА ГРАФАХ

Лекция №15

Многие прикладные задачи оптимизации могут быть сформулированы в форме той или иной задачи оптимизации на графах. Наряду с этим в теории графов многие интересные задачи связаны с решением задач оптимизации.

Из достаточно большого числа типовых задач оптимизации на графах можно выделить основные и в некотором смысле ставшие классическими для данного класса:

задача нахождения оптимальных покрывающих деревьев;
задача нахождения кратчайшего пути в графе;
задача нахождения критического пути в сетевом графе;
задача нахождения максимального потока в графе.

Для каждой из перечисленных задач поставлена в соответствие математическая постановка задачи в форме модели булева или целочисленного программирования. В то же время существуют специальные алгоритмы их решения, которые учитывают специфические особенности постановки этих задач.

Рассмотрим более подробно содержательную постановку задачи о максимальном потоке в сети. Данная задача имеет множество возможных вариантов постановки, один из которых может быть сформулирован следующим образом. Имеется система магистральных трубопроводов, связывающих источник добычи нефти или газа с предприятием по его промышленной переработке (рис. 15.1). Отдельные участки трубопроводов оснащены компрессорными установками для поддержания требуемого давления, необходимого для транспортировки продукта. Известны предельные значения пропускной способности каждого участка рассматриваемой системы. В предположении, что источник обладает достаточным запасами продукта, требуется определить количество транспортируемого продукта по каждому из участков трубопроводной системы так, чтобы количество доставленного на предприятие переработки продукта было максимальным.

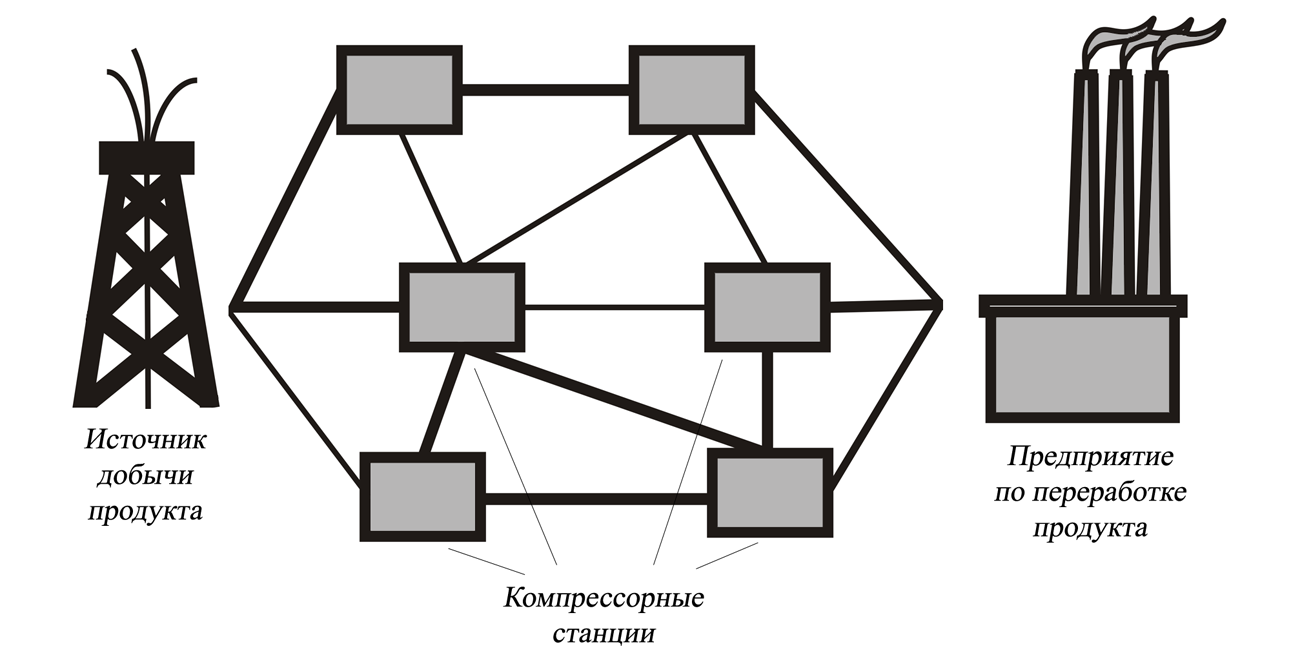
Рис. 15.1. Иллюстрация задачи о максимальном потоке в сети

Оценочной функцией в данной задаче является количество продукта, доставленного на предприятие переработки, а ограничениями служат предельные значения пропускной способности каждого участка рассматриваемой системы.

В бизнес-приложениях встречаются самые разнообразные варианты данной задачи, например, нахождение максимального пассажиропотока в транспортной системе мегаполиса, регулирование транспортных потоков на автомобильных магистралях и пр. Для наиболее эффективного анализа и решения подобных задач, их следует рассматривать в обобщенной постановке в форме задачи о максимальном потоке в сетевом графе или сети.

Чтобы в общем случае сформулировать задачу о максимальном потоке в сети, для рассматриваемой системы магистральных трубопроводов построим граф. В данном графе одна из вершин, называемая источником, будет соответствовать источнику добычи продукта, другая, называемая стоком, - предприятию по переработки этого продукта. Остальные вершины графа интерпретируются как компрессорные станции. Каждое ребро графа в этом случае будет соответствовать наличию участка трубопровода между парой компрессорных станций. Вес ребра равен пропускной способности соответствующего участка трубопровода.

Таким образом, задача о максимальном потоке в сети формулируется как задача нахождения переменных значений величин потока по каждому ребру графа, которые не превышают весов соответствующих ребер и максимизируют общий поток от источника к стоку.

Математическая постановка

В общем случае задачи оптимизации на графах не предполагают формулировку исходной задачи в форме задачи математического программирования, однако успех в решении соответствующих задач тесно связан с выбором удачной модели для ее математической постановки.

Математическая постановка задачи оптимизации на графах в общем случае может быть сформулирована в следующем виде:

или ,

где переменная x условно обозначает некоторый специальный объект графа, а множество допустимых альтернатив содержит все возможные специальные объекты рассматриваемого вида. При этом никаких дополнительных предположений о характере целевой функции или ограничений не делается. Однако, исходя из того факта, что в практических задачах оптимизации исходные графы являются конечными, множество допустимых альтернатив в типовых задачах оптимизации на графах также является конечным. Это обстоятельство позволяет в отдельных случаях находить решение той или иной конкретной задачи методом простого перебора всех специальных объектов того или иного вида.

Наряду с контролем вида множества допустимых альтернатив соответствующей задачи (для тех или иных задач может оказаться пустым) также необходимо указывать дополнительные свойства графа, которым он должен удовлетворять, чтобы соответствующая задача оптимизации имела допустимые решения.

Вернемся к рассмотрению задачи о максимальном потоке в сети и начнем с построения математической модели данной задачи.

Пусть G=(V, E, h) – ориентированный граф, в котором V={v1, v2,…,vn} – конечное множество вершин, E={e1, e2,…,en} – конечное множество дуг, h: EZ+ - весовая функция дуг, которая интерпретируется как пропускная способность дуги. Дополнительно в графе фиксируются две вершины: начальная вершина vs, которая называется исток, и конечная вершина vt, которая называется сток.

В предположении, что исходный граф G является связанным, т.е. вершина vt потенциально достижима из vs, и не содержит циклов, требуется определить поток максимального объема, протекающий из начальной вершины vs в конечную вершину vt.

Введем в рассмотрение следующие неотрицательные целочисленные переменные – xij, которые интерпретируются как величина потока, проходящего по дуге . Тогда математическая постановка задачи о максимальном потоке в сети может быть сформулирована следующим образом:

где множество допустимых альтернатив формируется следующей системой ограничений типа неравенств:

		(15.1)
		(15.2)
		(15.3)
		(15.4)

При этом первое ограничение (15.1) требует выполнения следующего условия: величина потока, выходящего из вершины vs (истока), должна быть равна величине потока, входящего в вершину vt (сток). Вторая группа ограничений (15.2) гарантирует выполнение следующего условия: любой частичный поток, входящий в каждую промежуточную вершину графа, должен быть равен потоку, выходящему из этой вершины. Общее количество ограничений (15.1) и (15.2) равно n-1. Третья группа ограничений (15.3) требует выполнения следующего условия: величина потока протекающего по дуге , должна быть неотрицательной и не должна превышать пропускной способности этой дуги cij. Наконец, последнее ограничение (15.4) требует, чтобы все переменные принимали только неотрицательные целочисленные значения.

Таким образом, нетрудно заметить, что задачу о максимальном потоке можно сформулировать как задачу целочисленного линейного программирования. Следует, однако, подчеркнуть, что решение сетевых задач симплекс методом едва ли целесообразно. С другой стороны, изучение формулировок сетевых задач линейного программирования помогает идентифицировать модели линейного программирования, которые на первый взгляд не являются сетевыми, но которые либо непосредственно, либо с некоторыми модификациями можно свести к сетевым.

Решение задачи о максимальном потоке в среде MS Excel

Рассмотрим задачу нахождения максимального поток в сети, которая представляет модель системы магистральных трубопроводов, связывающих источник добычи некоторого жидкого продукта (нефти, сжиженного газа) с предприятием по его промышленной переработке. Данная модель может быть представлена в виде схемы, формально представляющая собой ориентированный граф без циклов, состоящий из 6 вершин и 10 дуг (рис. 15.2). Предельные значения пропускной способности каждого участка рассматриваемой системы между двумя соседними компрессорными станциями, выраженные например в т/час, равны значению весовой функции для каждой дуги, которые указаны рядом с изображением этой дуги в графе.

В предположении, что источник, которому соответствует вершина v1=vs, обладает достаточными запасами продукта, требуется определить количество транспортируемого продукта по каждому из участков трубопроводной системы до стока, которому соответствует вершина v6=vt, так чтобы количество доставленного на сток продукта было максимальным.

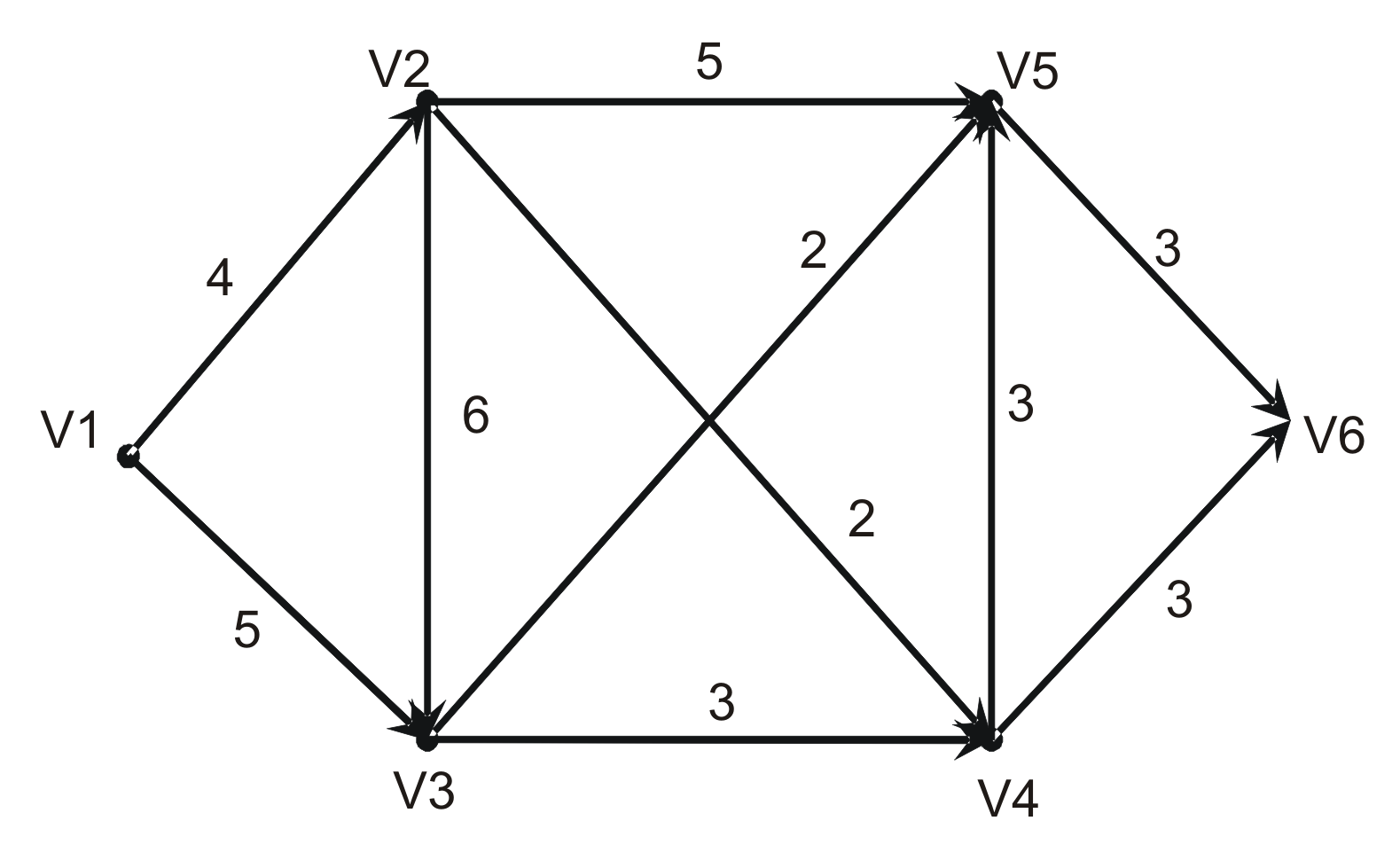
Рис.15.2. Исходный ориентированный граф индивидуальной задачи о

максимальном потоке в сети

Переменными математической модели данной индивидуальной задачи о максимальном потоке в сети являются 10 переменных: x12, x13, x23, x24, x25, x34, x35, x45, x46, x56. Каждая из этих переменных xij может принимать неотрицательные целочисленное значение, не превышающее пропускной способности дуги cij и соответствующее величине потока продукта, транспортируемого по отдельному трубопроводу, связывающему компрессорные станции – вершины сети. Тогда математическая постановка рассматриваемой индивидуальной задачи о максимальном потоке в сети может быть записана в следующем виде:

(15.5)

где множество допустимых альтернатив формируется следующей системой ограничений типа равенств и неравенств:

(15.6)

Заметим, что те переменные xij, для которых весовая функция дуг h не определена или равна 0, не входят в математическую постановку рассматриваемой задачи (15.5) - (15.6).

Для решения поставленной задачи воспользуемся программой электронных таблиц MS Excel – компонентом офисного пакета MS System Office. MS Excel позволяет выполнять быстрые расчеты и содержит встроенные средства для решения задач оптимизации. Также имеющиеся возможности MS Excel могут быть расширены за счет использования встроенного языка программирования VBA или вызова внешних функций из библиотек динамической компоновки, разработанных самим пользователем на таких языках программирования как Borland Delphi® и MS Visual C++®.

Для решения поставленной индивидуальной задачи нахождения максимального потока в сети с помощью программы MS Excel необходимо выполнить следующие действия.

Создать в книге «Оптимизация на графах» новый рабочий лист с именем «Максимальный поток».
Ввести необходимые надписи в ячейки A1:F1 (рис. 15.3). Конкретное содержание этих надписей не оказывает влияния на решение рассматриваемой задачи.
В ячейки A2:A11 ввести индексы начальных вершин, а в ячейки B2:B11 – индексы конечных вершин всех имеющихся дуг исходного графа.
В ячейки C2:C11 ввести значения пропускных способностей дуг исходного графа.
В ячейку F2 ввести формулу: =СУММ(D2:D3), которая представляет целевую функцию (15.5).
В ячейку E2 ввести формулу: =СУММ(D2:D3)-СУММ(D10:D11), которая представляет собой левую часть первого ограничения (15.6).
В ячейку E3 ввести значение левой части второго ограничения: D2-СУММ(D4: D6).
В ячейку E4 ввести значение левой части третьего ограничения: D3-СУММ(D7: D8).
В ячейку E5 ввести значение левой части четвертого ограничения: СУММ(D5; D7)-СУММ(D9: D10).
В ячейку E6 ввести значение левой части пятого ограничения: СУММ(D6; D8:D9)-D11.

Внешний вид рабочего листа с исходными данными для решения задачи о минимальном пути в графе имеет следующий вид (рис 15. 3).

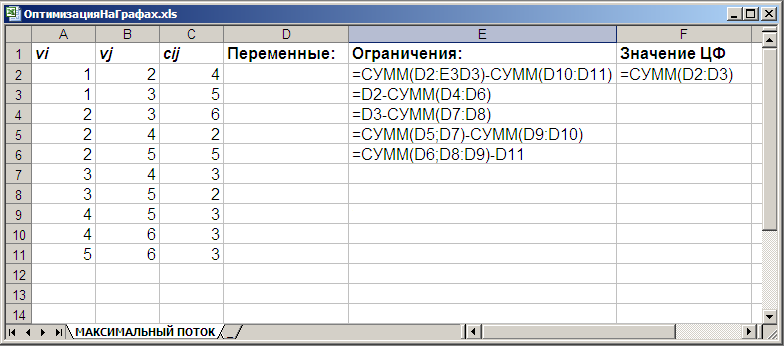
Рис. 15.3. Исходные данные для решения задачи о максимальном потоке в сети

Для дальнейшего решения задачи следует вызвать мастер поиска решений для чего необходимо выполнить операцию главного меню: Сервис | Поиск решения.

После появления диалогового окна Поиск решения следует выполнить следующие действия:

В поле с именем Установить целевую ячейку: ввести абсолютный адрес ячейки $F$2.
Для группы Равной: выбрать вариант поиска решения – максимальному значению.
В поле с именем Изменяя ячейки: ввести абсолютный адрес ячеек $D$2:$D$11.
Задать первых 5 ограничений для рассматриваемой задачи. С этой целью выполнить следующие действия:
- для задания этих ограничений в исходном диалоговом окне Поиск решения нажать кнопку с надписью Добавить;
- в появившемся дополнительном окне выбрать диапазон ячеек $E$2:$E$11, который должен отобразиться в поле с именем Ссылка на ячейку;
- в качестве знака ограничения из выпадающего списка выбрать равенство «=»;
- в качестве значения правой части ограничения ввести с клавиатуры значение 0;
- для добавления первого ограничения в дополнительном окне нажать кнопку с надписью Добавить.
Задать первое из 10 ограничений на пропускные способности дуг (15.6). С этой целью выполнить следующие действия:
- Для задания ограничения в исходном диалоговом окне Поиск решения нажать кнопку с надписью Добавить;
- В появившемся дополнительном окне выбрать ячейку $D$2, которая должна отобразиться в поле с именем Ссылка на ячейку;
- В качестве знака ограничения из выпадающего спуска выбрать нестрогое неравенство «<=».
- В качестве значения правой части ограничения в появившемся дополнительном окне выбрать ячейку $C$2, которая должна отобразиться в поле с именем Ссылка на ячейку;
- Для добавления первого ограничения в дополнительном окне нажать кнопку с надписью Добавить.
Аналогичным образом добавить остальные 9 ограничений (15.6), используя в качестве исходных ячеек $D$3: $D$11 и $C$3:$C$11.
Задать ограничение на целочисленные значения переменных. С этой целью выполнить следующие действия:
- В исходном диалоговом окне Поиск решения нажать кнопку с надписью Добавить;
- В появившемся дополнительном окне выбрать диапазон ячеек $D$2:$D$11, который должен отобразиться в поле с именем Ссылка на ячейку;
- В качестве знака ограничения из выпадающего списка выбрать строку «цел»;
- В качестве значения правой части ограничения в поле с именем Ограничение: оставить без изменения вставленное программой значение «целочисленные»;
- Для добавления первого ограничения в дополнительном окне нажать кнопку с надписью Добавить.
В окне дополнительных параметров поиска решения выбрать отметки Линейная модель и Неотрицательные значения.

Общий вид диалогового окна спецификации параметров мастера поиска решения показан на рис. 15.4.

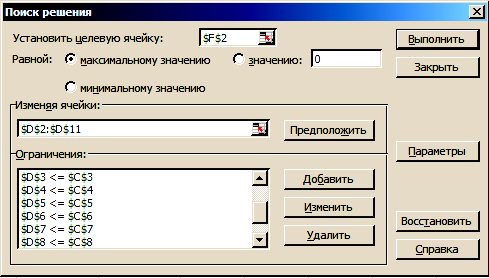
Рис. 15.4. Ограничения значений переменных и параметры мастера поиска решения для задачи о максимальном потоке в сети

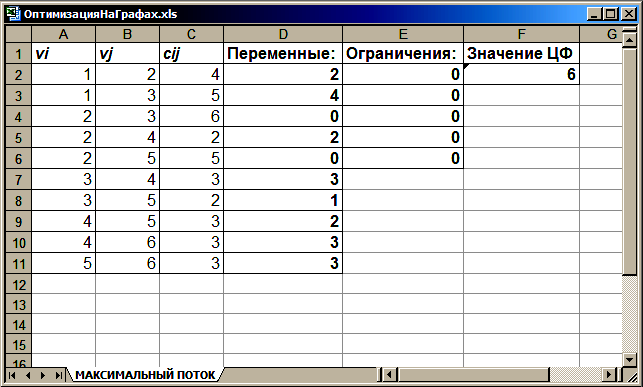
Рис. 15.5. Результат количественного решения задачи о максимальном

потоке в сети

После задания ограничений и целевой функции можно приступить к поиску численного решения, для чего следует нажать кнопку Выполнить. После выполнения расчетов программой MS Excel будет получено количественное решение, которое имеет следующий вид (рис. 15.5).

Результатом решения задачи о максимальном потоке в сети являются найденные оптимальные значения переменных: , , , , , , , , остальные переменные равны 0. найденному оптимальному решению соответствует значение целевой функции: .

Анализ найденного решения показывает, что максимальный поток в сети (рис. 15.2), проходящий из вершины 1 в вершину 6, протекает по следующим дугам: по дуге (1, 2) в количестве 2 т/час, по дуге (1, 3) в количестве 4 т/час, по дуге (2, 4) в количестве 2 т/час, по дуге (3, 4) в количестве 3 т/час, по дуге (3, 5) в количестве 1 т/час, по дуге (4, 5) в количестве 2 т/час, по дуге (4, 6) в количестве 3 т/час, по дуге (5, 6) в количестве 3 т/час.

Тем самым найден оптимальный план транспортировки продукта от пункта добычи до пункта переработки (рис. 15.6). При этом общая величина потока транспортируемого продукта для рассматриваемой сети будет максимальна и равна 6 т/час.

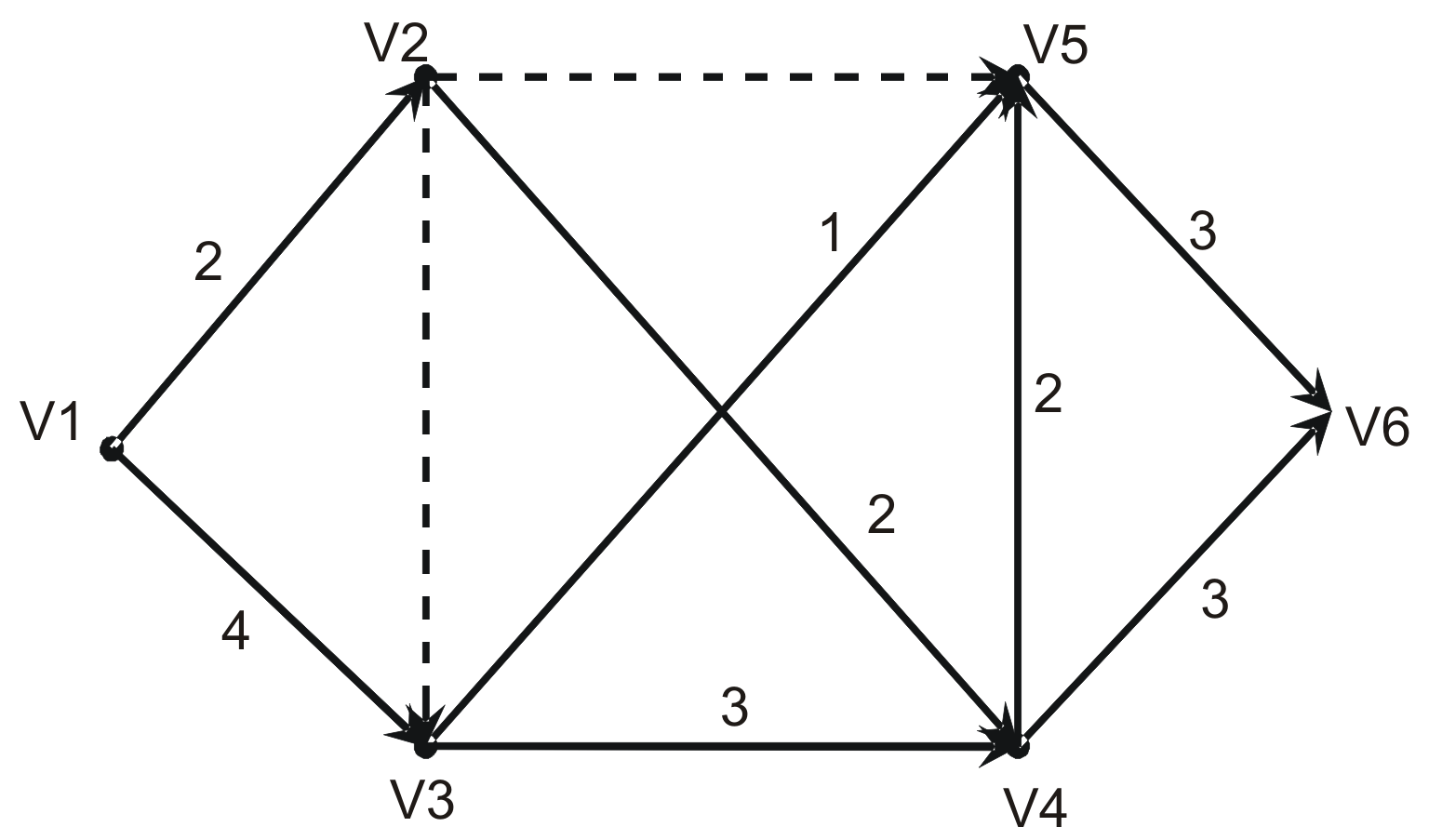
Рис. 15.6. Минимальный поток в исходной сети между вершинами 1 и 6.

Простейшая проверка найденного решения может быть связана с рассмотрением так называемых разрезов графа сети (рис. 15.6). Разрезом сети называется множество, которому принадлежит исток, и не принадлежит сток. Т.е. разрез - это минимальное (в смысле отношения включения) множество дуг, удаление которых “ разрывает” все пути, соединяющие исток и сток.

Пропускной способностью разреза называется число, равное сумме пропускных способностей дуг этого разреза. Разрез называется минимальным, если имеет наименьшую пропускную способность.

Например, применительно к найденному решению задачи о максимальном потоке в сети (рис. 15.6) множество дуг удовлетворяет определению минимального разреза и его пропускная способность равна 6, что в точности равно величине найденного максимального потока. Для дополнительной проверки получаемых с помощью программы MS Excel решений данной типовой задачи оптимизации на графах можно воспользоваться специальным алгоритмом пометок Форда - Фалкерсона.

Контрольные вопросы

1. В чем состоит особенность задач оптимизации на графах?

2. Приведите типовые примеры задач оптимизации на графах.

3. Приведите содержательную постановку задачи о максимальном потоке в сети.

4. Дать общую постановку задач оптимизации на графах.

5. Приведите математическую постановку задачи о максимальном потоке.

6. К какой из задач математического программирования сводится задача о максимальном потоке.

7. Приведите порядок действий при решении задачи о максимальном потоке в среде MS Office.

8. Опишите понятие разреза сети и его свойства.

9. Дайте определение понятию минимального разреза.

10. Использование какого метода решения задачи о максимальном потоке позволяет проверить решение данной задачи с помощью встроенных средств MS Excel.

PAGE 169

ОПТИМИЗАЦИЯ НА ГРАФАХ