ВЫПУКЛОЕ ПРОГРАММИРОВАНИЕ

Лекция №12

Широкий класс задач математического программирования связан с минимизацией выпуклых функций многих переменных, определенных на выпуклом множестве. Такие задачи называют задачами выпуклого программирования (ЗВП).

Задача математического программирования

(12.1)

называется задачей выпуклого программирования, если все функции являются выпуклыми функциями.

Остановимся на элементах выпуклого анализа – области математики, в которой изучаются свойства выпуклых множеств и выпуклых функций, и которая играет фундаментальную роль в теории и методах решения экстремальных задач.

Элементы выпуклого анализа

Приведем некоторые определения и рассмотрим конкретные примеры выпуклых множеств. Мы будем в дальнейшем иметь дело с функциями, определенными на множествах конечномерного евклидова пространства En.

Определение 12.1. Множество вида

(12.2)

называется отрезком, соединяющим точки и , и обозначаемым .

Очевидно, при точка X совпадет с одним из концов отрезка (), при – с другим (), а при - с некоторой внутренней точкой отрезка.

Определение 12.2. Множество называется выпуклым, если вместе с любыми двумя точками и ему принадлежит и отрезок их соединяющий.

Выпуклость множества означает, что из принадлежности и множеству следует, что принадлежит для всех .

Очевидно, в выпуклы отрезок, полупрямая, прямая, круг, треугольник, полуплоскость и вся плоскость.

Все пространство , очевидно, образует выпуклое множество. Пустое множество и множество, состоящее из одной точки, удобно считать выпуклыми.

Теорема 12.1. Теорема Фаркаша. Пусть заданы матрица размерности и вектор . Неравенство выполняется для всех в том и только том случае, если существует вектор такой, что .

Д о к а з а т е л ь с т в о. Достаточность. Пусть выполняются соотношения и . Тогда для любого вектора будет

Необходимость. Пусть для всех справедливо . Рассмотрим конус . Если , то теорема доказана. Предположим, что . Множество , по определению 12.2, выпукло и замкнуто, поэтому в силу теоремы отделимости существует вектор такой, что

(12.3)

для всех .

Так как при всех , то из (12.3) получаем, что при всех . Значит . С другой стороны . То есть и так как это имеет место для всех , то

. (12.4)

Но , поэтому из (12.3) следует

. (12.5)

Взяв , из (12.4) и (12.5) получаем противоречие условиям теоремы.

Замечание. Приведем геометрическое истолкование теоремы Фаркаша. Пусть

и . Конус есть совокупность всех векторов , которые образуют с каждым из векторов неострые углы. На рис 12.1 конус заштрихован вертикальными линиями, а конус - горизонтальными. Геометрический смысл теоремы таков. Чтобы для любого вектора угол между и был неострым, необходимо и достаточно, чтобы принадлежал конусу .

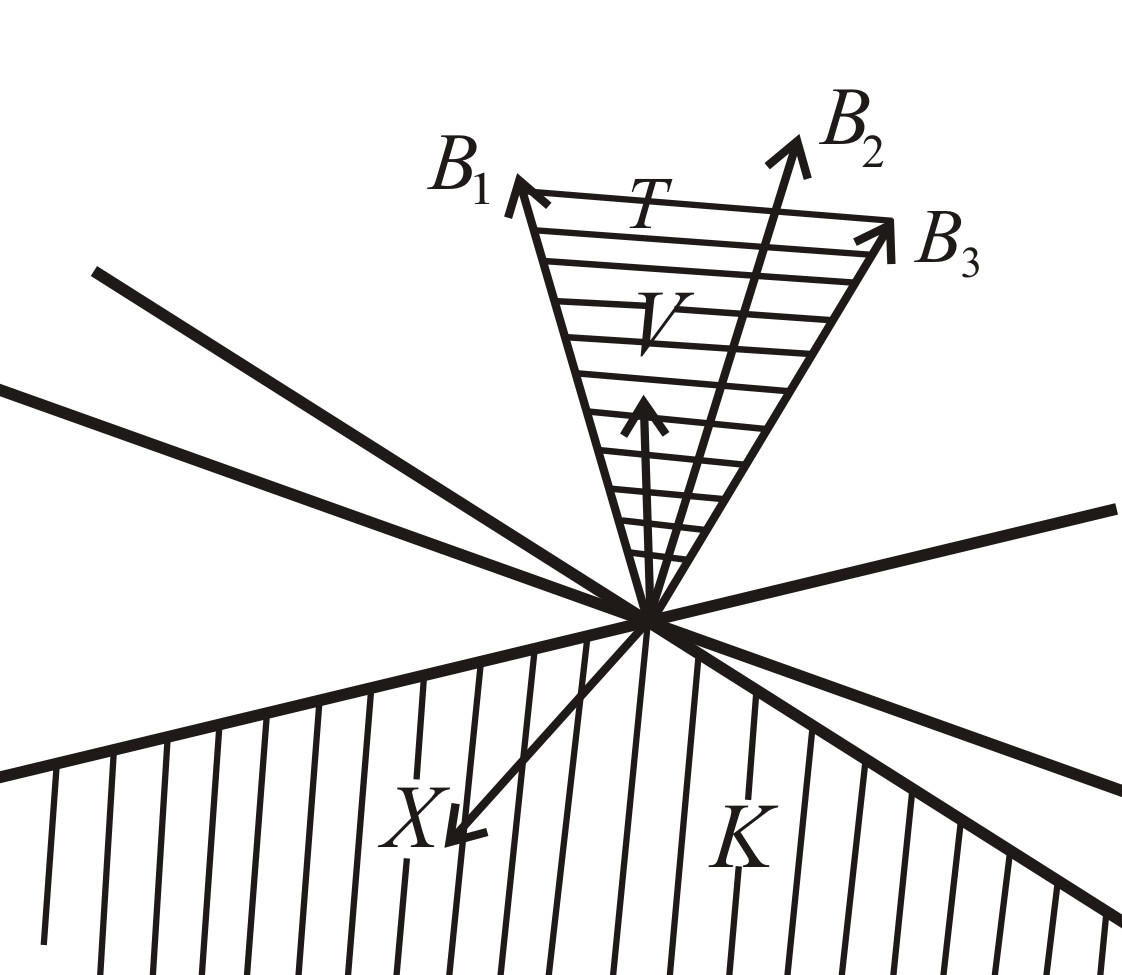
Рис 12.1

Определение 12.3. Функция , заданная на выпуклом множестве , называется выпуклой, если для любых точек и любого выполняется неравенство

(12.6)

Функция называется строго выпуклой, если для всех неравенство (12.6) выполняется как строгое. Функция называется сильно выпуклой, если существует такое число, (константа сильной выпуклости), что для всех и любого выполняется неравенство

(12.7)

Всякая сильно выпуклая функция является строго выпуклой и тем более выпуклой функцией, но не наоборот.

Примером выпуклой функции служит квадратичная функция с положительно определенной матрицей.

Теорема 12.2. Линейная комбинация с неотрицательными коэффициентами выпуклых на выпуклом множестве функций есть выпуклая функция на данном множестве.

Д о к а з а т е л ь с т в о. Пусть функции , определенные на выпуклом множестве , является выпуклым на . Покажем, что функция

, (12.8)

где выпукла на .

Для произвольных точек и из и любого числа имеем

В этой цепочке соотношений первое неравенство справедливо, поскольку функции выпуклые. Полученный результат показывает, что функция , определяемая формулой (12.8) является выпуклой на множестве .

Теорема 12.3. Если выпукла на выпуклом множестве , то для любых точек и любых чисел , таких что выполняется неравенство Йенсена

. (12.9)

Д о к а з а т е л ь с т в о (по индукции). При неравенство (12.9) очевидно. В самом деле, если , то и , т.е. (12.9) выполняется как равенство. Предположим, что (12.9) имеет место для , т.е. для выпуклой комбинации из точек. Покажем, что тогда оно справедливо и для выпуклой комбинации из точек множества , т.е.

. При этом, если , то и в (12.9) очевидно равенство. Если же . То из выпуклости и индуктивного предположения следует

Говорят, что множество удовлетворяет условию регулярности, если для каждого существует точка такая, что , т.е.

(12.10)

Нетрудно показать, что условию (12.10) эквивалентно другое условие, называемое условием регулярности Слейтера.

Теорема 12.4. Если для множества выполняется условие регулярности (12.10), то множество регулярно по Слейтеру, а именно существует точка , в которой все ограничения выполняются строго

. (12.11)

Д о к а з а т е л ь с т в о. Пусть выполняется условие регулярности (12.10). Выберем точку , являющуюся выпуклой комбинацией точек и, следовательно, принадлежащую . Тогда при любом будем иметь

т.е. . В этой цепочке соотношений первое неравенство справедливо в силу неравенства Йенсена, а второе – поскольку, по крайней мере, один член суммы, а именно строго меньше . Эти неравенства показывают, что для рассматриваемого имеет место условие регулярности Слейтера.

Приведем без доказательства следующее важное свойство выпуклых функций.

Выпуклая функция , определенная на выпуклом множестве непрерывна в каждой внутренней точке этого множества и имеет в каждой внутренней точке производную по любому направлению

Важное свойство выпуклых дифференцируемых функций, которым мы будем часто пользоваться, устанавливает следующая теорема.

Теорема 12.5. Функция , дифференцируемая на выпуклом множестве , выпукла тогда и только тогда, когда для любых и , принадлежащих выполняется неравенство

. (12.12)

Д о к а з а т е л ь с т в о. Необходимость. Пусть выпукла. Тогда для любых и , () и всех таких, что справедливо неравенство

или

откуда

Переходя к пределу в последнем неравенстве при , получим

Достаточность. Пусть теперь выполняется условие (12.12) для любых двух точек множества . Тогда для точки при , принадлежащей , справедливы неравенства

и .

Умножив первое неравенство на , второе - на и сложив полученные неравенства, имеем

или, учитывая, что имеем

т.е, что выпуклая функция на множестве .

Рассмотрим ряд экстремальных свойств выпуклых функций на выпуклом множестве, играющих существенную роль при решении задачи отыскания точки выпуклого множества , в которой выпуклая функция , определенная на достигает минимального значения: .

Теорема 12.6. Любая точка локального минимума функции на выпуклом множестве является точкой глобального минимума

Д о к а з а т е л ь с т в о. Пусть - точка локального минимума функции на . Тогда по определению точки локального минимума существует некоторая окрестность этой точки такая, что выполняется неравенство

. (12.13)

Предположим, что не является точкой глобального минимума функции , то есть что существует точка такая, что . Рассмотрим точки вида .

Так как множество выпукло, то . Далее из выпуклости и из предположения о следует

т.е. . Но это противоречит условию, что - точка локального минимума, поскольку при достаточно малых точка находится в окрестности , где имеет место (12.13).

Следовательно, - точка глобального минимума на .

Теорема 12.7. Множество точек минимума выпуклой функции на выпуклом множестве является выпуклым множеством.

Д о к а з а т е л ь с т в о. Пусть - множество точек минимума выпуклой функции на выпуклом множестве , т.е.

Выберем две любые точки и . Поскольку и - выпуклое множество, то для любого будет

а ввиду выпуклости функции имеем

То есть . Кроме того, поскольку - минимальное значение функции на , то . А, значит, , т.е. . Следовательно, - выпуклое множество.

Теорема 12.8. Строго выпуклая функция на выпуклом множестве достигает своего минимума не более чем в одной точке.

Д о к а з а т е л ь с т в о. Пусть - строго выпуклая функция на выпуклом множестве , т.е. для любых и всех выполнятся строгое неравенство

Пусть =.

Предположим, что найдется точка , такая, что

Тогда для любого точка принадлежит множеству и в силу строгой выпуклости функции будет

т.е. . Это противоречит условию, что - точка минимума. Следовательно, точка единственна.

Контрольные работы

1. Приведите постановку задачи выпуклого программирования.

2. Дайте определение выпуклого множества.

3.Приведите формулировку теоремы Фаркаша.

4. Дайте геометрическое истолкование теоремы Фаркаша.

5. Дайте определения выпуклой, строго выпуклой и сильно выпуклой функции на выпуклом множестве .

6. Приведите примеры выпуклых функций.

7. Сформулируйте условие регулярности множества .

8. Сформулируйте условие регулярности по Слейтеру, множества .

9. Приведите необходимое и достаточное условие выпуклости функции , дифференцируемой на выпуклом множестве .

10. Перчислите основные экстремальные свойства выпуклых функций на выпуклом множестве.

PAGE 131

ВЫПУКЛОЕ ПРОГРАММИРОВАНИЕ