Размах вариации. Среднее линейное отклонение. Дисперсия. Среднее квадратическое отклонение

Федеральное агентство по образованию

Сибирская Государственная Автомобильно-дорожная Академия

(СибАДИ)

Центр дополнительного образования

КОНТРОЛЬНАЯ РАБОТА

по дисциплине «Статистика»

Выполнил: студент 3 курса

Специальность: экономика и

управление на предприятии

транспорта

Белицкий А.А.

Проверил:

Калачинск

2010 г.

ВАРИАНТ 4

1. Размах вариации. Среднее линейное отклонение. Дисперсия. Среднее квадратическое отклонение.

Вариацию можно определить как количественное различие значений одного и того же признака у отдельных единиц совокупности. Термин «вариация» имеет латинское происхождение - variatio, что означает различие, изменение, колеблемость. Изучение вариации в статистической практике позволяет установить зависимость между изменением, которое происходит в исследуемом признаке, и теми факторами, которые вызывают данное изменение.

Для измерения вариации признака используют как абсолютные, так и относительные показатели.

К абсолютным показателям вариации относят:  размах вариации,  среднее линейное отклонение, среднее квадратическое отклонение,  дисперсию.

К относительным показателям вариации относят:  коэффициент осцилляции,  линейный коэффициент вариации,  относительное линейное отклонение и др.

Размах вариации R. Это самый доступный по простоте расчета абсолютный показатель, который определяется как разность между самым большим и самым малым значениями признака у единиц данной совокупности:

 

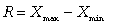
Размах вариации (размах колебаний) - важный показатель колеблемости признака, но он дает возможность увидеть только крайние отклонения, что ограничивает область его применения. Для более точной характеристики вариации признака на основе учета его колеблемости используются другие показатели.

Среднее линейное отклонение d, которое вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности. Эта величина определяется как средняя арифметическая из абсолютных значений отклонений от средней. Так как сумма отклонений значений признака от средней величины равна нулю, то все отклонения берутся по модулю.

Формула среднего линейного отклонения (простая)

 

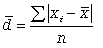
Формула среднего линейного отклонения (взвешенная)

 

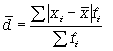
При использовании показателя среднего линейного отклонения возникают определенные неудобства, связанные с тем, что приходится иметь дело не только с положительными, но и с отрицательными величинами, что побудило искать другие способы оценки вариации, чтобы иметь дело только с положительными величинами. Таким способом стало возведение всех отклонений во вторую степень. Обобщающие показатели, найденные с использованием вторых степеней отклонений, получили очень широкое распространение. К таким показателям относятся среднее квадратическое отклонение  и среднее квадратическое отклонение в квадрате , которое называют дисперсией.

Средняя квадратическая простая

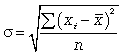
Средняя квадратическая взвешенная

 

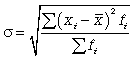
Дисперсия есть не что иное, как средний квадрат отклонений индивидуальных значений признака от его средней величины.

Формулы дисперсии взвешенной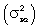  и простой :

 

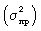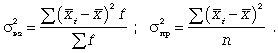
Расчет дисперсии можно упростить. Для этого используется способ отсчета от условного нуля (способ моментов), если имеют место равные интервалы в вариационном ряду.

Кроме показателей вариации, выраженных в абсолютных величинах, в статистическом исследовании используются показатели вариации (V), выраженные в относительных величинах, особенно для целей сравнения колеблемости различных признаков одной и той же совокупности или для сравнения колеблемости одного и того же признака в нескольких совокупностях.

Данные показатели рассчитываются как отношение размаха вариации к средней величине признака (коэффициент осцилляции), отношение среднего линейного отклонения к средней величине признака (линейный коэффициент вариации), отношение среднего квадратического отклонения к средней величине признака (коэффициент вариации) и, как правило, выражаются в процентах.

Формулы расчета относительных показателей вариации:

 (

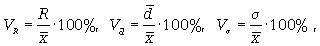
где VR - коэффициент осцилляции;  - линейный коэффициент вариации;  - коэффициент вариации.

Из приведенных формул видно, что чем больше коэффициент V приближен к нулю, тем меньше вариация значений признака.

В статистической практике наиболее часто применяется коэффициент вариации. Он используется не только для сравнительной оценки вариации, но и для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному).

2. Виды статистических таблиц. Основные правила их составления и оформления. Виды статистических графиков. Порядок их построения.

Статистические таблицы используются для оформления результатов статистических группировок.

Статистические таблицы - сводная числовая характеристика, исследующая совокупность по одному или несколько исследуемым признакам, взаимосвязанным логикой экономического анализа, т.е. это система строк и граф, которые в определенной последовательности и связи излагают результаты сводки и группировки статистической информации.

Статистическая таблица содержит подлежащее и сказуемое. Подлежащее располагается по строкам, а сказуемое - по графам.

В зависимости от подлежащего:

1. простая таблица (перечневая, хронологическая, территориальная),

2. групповая таблица по одному признаку,

3. комбинационная таблица делится на 2 и более групп.

Содержимое может быть простым и комбинационным. Каждая таблица должна иметь заголовок, место и время к которому относятся данные.

- отсутствие данных, --- - не располагаем данными.

Анализ таблиц:

1. структурный,

2. содержательный.

Таблицы сопряженности - это сводная числовая характеристика

изучаемой совокупности по 2 или более атрибутивным или качественным признакам.

Применяются при изучении общественного мнения, уровня и образа жизни,

общественно-политического строя и т.д.

Наиболее простым видом сопряженности - таблицы частот 2х2.

	В1	В2	Итого
А1
А2
Итого:

Графически статистические данные изображают:

1. диаграммы сравнения,

2. структурные диаграммы (круговые),

3. диаграммы динамики,

4. статистические карты.

Основные правила составления и оформления статистических таблиц:

1. Таблица должна быть по возможности небольшой по размерам, т.к. краткую таблицу легче проанализировать. Иногда целесообразнее построить 2-3 небольшие таблицы, чем одну большую.

2. Название таблицы, заглавие строк подлежащего и граф сказуемого должны быть сформулированы точно, кратко и ясно и, если это требуется, должны иметь единицы измерения. В названии таблицы следует указать территорию и период, к которым относятся приводимые данные. Не следует название показателей в таблице сопровождать инструктивными пояснениями, раскрывающими их содержание.

Лучше эти пояснения вынести в примечание.

3. Строки подлежащего и графы сказуемого обычно размещают по принципу от частного к общему, т.е. сначала показывают слагаемые, а в конце подлежащего или сказуемого приводят итоги. Если приводятся не все слагаемые, а выделяются наиболее важные из них, то сначала показывают общие итоги, а затем выделяют наиболее важные их составные части, для этого после итоговой строки дают пояснения «в том числе».

4. Строки в подлежащем и графы в сказуемом часто нумеруют для того, чтобы удобнее было ссылаться на цифры таблицы. При этом в сказуемом нумеруются только графы, в которые вписываются цифры. Графы подлежащего либо совсем не нумеруются, либо обозначаются литерами («А», «Б» и т.д.).

5. При заполнении таблицы пользуются следующими условными обозначениями: если данное явление совсем не имеет места, ставят тире, если сведения о данном явлении отсутствуют, ставят многоточие или пишут «нет сведений»; если сведения имеются, но числовые значения меньше принятой в таблице точности, ставят 0,0.

6. Округленные числа приводят в отдельных графах таблиц с одинаковой степенью точности (до 0,1, до 0,01 и т.д.). Когда показатели в процентах выражаются большими числами, то целесообразно заменить их выражением «во столько-то раз больше или меньше». Например, вместо 2486% лучше написать «в 24,9 раза больше».

7. Если приводятся не только отчетные данные, но и расчетные данные, то целесообразно сделать об этом оговорку в таблице или в примечании к ней.

8. Таблица может сопровождаться примечаниями, в которых указываются источники данных, более подробное содержание показателей и другие необходимые пояснения.

Графиками в статистике называются условные изображения статистических величин и их соотношений в виде различных геометрических образов: точек, линий, плоских фигур и т.п.

По способу построения графики делятся на:

- диаграммы - графическое изображение в системе координат статистических величин при помощи геометрических фигур или знаков; территория, к которой относятся эти величины, указана только словесно;

- картодиаграммы - диаграммы, наложенные на карту или план территории, к которой относятся изображаемые величины;

- картограммы - изображение величины показателя путем штриховки или раскраски соответствующей территории на карте или плане.

Наиболее простыми и наглядными графиками для сравнения величин одного статистического показателя, характеризующего разные объекты, являются столбиковые и полосовые диаграммы. Их построение требует соблюдения ряда правил.

Так, наиболее важным является соответствие столбиков по высоте, а полос по длине отображаемым цифрам. Поэтому, во-первых, нельзя допускать разрыв масштабной шкалы; во-вторых, нельзя начинать масштабную шкалу не от нуля, а от числа, близкого к минимальному в изображаемом ряду. Для построения диаграмм высоты столбиков или длины полос располагают в убывающем или возрастающем порядке.

При построении столбиковых диаграмм необходимо начертить систему прямоугольных координат. Основания столбиков одинакового размера размещаются на оси абсцисс, а высота столбика будет соответствовать величине показателя, нанесенного в соответствующем масштабе на ось ординат.

Каждый столбик посвящается отдельному объекту. Общее число столбиков равно числу сравниваемых объектов. Расстояние между столбиками берется одинаковое, а иногда столбики располагаются вплотную друг к другу.

Столбиковые диаграммы называются полосовыми, если столбики размещаются не по вертикали, а по горизонтали. В этом случае основание полос (объекты) располагается на оси ординат, а масштаб - на оси абсцисс.

Таким образом, столбиковые и полосовые диаграммы взаимозаменяемы.

При помощи столбиковых и полосовых диаграмм можно изобразить структуру явления и структурные сдвиги. Но чаще всего структура явлений характеризуется секторными диаграммами.

Секторная диаграмма представляет собой круг, разделенный радиусами на отдельные секторы, каждый из которых характеризует какую-то часть целого явления и занимает площадь круга пропорционально удельному весу этой части. Наглядность изображения достигается тем, что в круге глаз лучше улавливает удельные веса отдельных частей в целом.

Если начертить аналогичные графики за ряд лет, то можно наглядно увидеть не только структуру изучаемого явления, но и динамику структуры. Если же при построении графиков учесть и показатели роста (дать круги по размеру соответственно темпам роста), то можно отразить и динамику явлений.

Однако наиболее часто для изображения динамики применяют линейные графики. Их преимущество состоит в том, что динамика изображается в виде непрерывной линии, характеризующей непрерывность процесса.

Для построения линейных графиков используют систему прямоугольных координат. На оси абсцисс обычно откладывают периоды, а на оси ординат - показатели, характеризующие динамику.

На оси координат наносят масштабы. Особое внимание следует обратить на выбор масштабов, как на оси ординат, так и на оси абсцисс. От соотношения этих масштабов зависит общий вид графика.

Если масштаб для шкалы на оси абсцисс очень растянут по сравнению с масштабом на оси ординат, то колебания в динамике будит мало заметны. И наоборот, преувеличение масштаба на оси ординат по сравнению с масштабом на оси абсцисс даст слишком резкие колебания.

Если на графике изображаются показатели за различные периоды времени, то интервалы между периодами времени (длина отрезков) при нанесении шкалы на ось абсцисс должны быть пропорциональны величинам продолжительности периодов.

После нанесения шкалы определяют точки на поле графика, которые образуются пересечением двух прямых, проведенных перпендикулярно к соответствующим точкам на осях координат. Затем полученные точки соединяют отрезками и получают ломаные линии, характеризующие развитие изучаемого явления.

Линейные графики удобны тем, что на одном графике можно построить несколько кривых (ломаных) по разным показателям.

Графики применяются, чтобы сделать результаты статистического наблюдения, сводки и группировки статистических данных наглядными, более понятными и запоминающимися.

Главным достоинством графического метода является то, что он служит средством лаконичного, компактного и наглядного представления статистических данных. Статистический график в отличие от таблицы дает обобщающую картину состояния или развития того или иного явления, позволяет с одного взгляда подметить те закономерности, которые содержатся в цифровом статистическом материале.

Исключительно большое значение графического способа проявляется в том, что он служит мощным орудием обобщения и анализа статистических данных, а в некоторых случаях - единственным и незаменимым способом их исследования.

Графики дают целостную картину явлений и процессов, обобщающее представление о них и помогают осмыслить статистический материал. При графическом изображении статистических данных становятся особенно отчетливыми и наглядными взаимная связь между явлениями и процессами общественной жизни, основные тенденции их развития, степень распространенности их в пространстве и др.

Если рассматривать статистический график как плоскостное изображение, то в нем можно выделить графический образ и вспомогательные элементы.

Графический образ (основа графика) - это геометрические знаки, совокупность точек, линий и фигур, с помощью которых изображаются статистические величины. Правильный выбор графического образа имеет большое значение при построении статистического графика. Графический образ должен соответствовать цели графика и быть максимально выразительным, чтобы правильно изобразить статистические данные.

Вспомогательными элементами графика являются: поле графика, пространственные ориентиры, масштабные ориентиры, экспликация графика.

Поле графика - это пространство размещения знаков, имеющее определенные размеры и пропорции сторон. Размер поля зависит от назначения графика: в литературных источниках используются небольшие графики, а на стендах, витринах, выставках - довольно крупные. Что касается пропорций, то в этом отношении наиболее часто встречаются графики с неравными сторонами, но иногда они подаются и в виде квадратов.

Пространственные ориентиры определяют размещение геометрических знаков на поле. Они зависят от принятой системы координат. В статистических графиках наиболее часто применяется система прямоугольных (декартовых) координат.

Масштабные ориентиры дают геометрическим знакам количественную определенность. Сюда относятся эталоны знака, масштаб графика и масштабная шкала.

Эталоны знака отражают величину геометрических знаков, изображаются в виде кругов, прямоугольников, квадратов и обычно выносятся с поля графика. Особенно если на графике недостаточно места, а пояснения длинные.

Масштаб графика - условная мера перевода числовой величины в графическую.

Масштабная шкала - это линия, отдельные точки которой могут быть прочитаны как определенное значение статистического показателя. В статистических графиках обычно применяются:

- прямолинейные масштабные шкалы, которые, как правило, располагаются по осям координат;

- криволинейные масштабные шкалы, например, круговые, которые применяются в секторных диаграммах.

Масштабные шкалы бывают:

- равномерные, в которых отрезки пропорциональны числам;

- неравномерные, например, логарифмические масштабные шкалы, в которых отрезки пропорциональны не числам, а их логарифмам.

Экспликация графика - словесное объяснение содержания графика и значения каждого его геометрического знака. Она включает в себя:

- название графика - общий заголовок, кратко и точно раскрывающий основное содержание графика (тоже требование, что и к названию статистической таблицы);

- подписи вдоль масштабных шкал;

- пояснения к отдельным частям графика;

- числовые данные, которые дополняют или уточняют величину нанесенных на график показателей.

Размах вариации. Среднее линейное отклонение. Дисперсия. Среднее квадратическое отклонение