МЕТОДЫ ОПТИМИЗАЦИИ ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ

Лекция №8

Постановка и классификация задач математического

программирования

Многие практические задачи оптимизации сводятся к математическим моделям вида

, (8.1)

где допустимое множество не совпадает со всем пространством . В этих случаях говорят об условной минимизации функции переменных. В большинстве случаев допустимое множество определяется ограничениями-равенствами и (или) неравенствами, т.е. рассматривается задача

, , (8.2)

, (8.3)

, (8.4)

где - заданные множества индексов. Соотношения (8.2) - (8.4) представляют собой запись условий так называемой задачи математического программирования. Отметим несколько важных частных видов задач математического программирования.

Задача линейного программирования - в (8.2)-(8.4) все функции , - линейны, и все переменные удовлетворяют условию неотрицательности .
Задача нелинейного программирования - хотя бы одна из функций , в (8.2) - (8.4) не является линейной.
Задача на условный экстремум - отсутствуют ограничения-неравенства (8.3), т.е. .
Задача выпуклого программирования - все функции , в (8.2) - (8.4) - выпуклы, а ограничения-равенства отсутствуют, т.е. . Ее допустимое множество - выпукло.

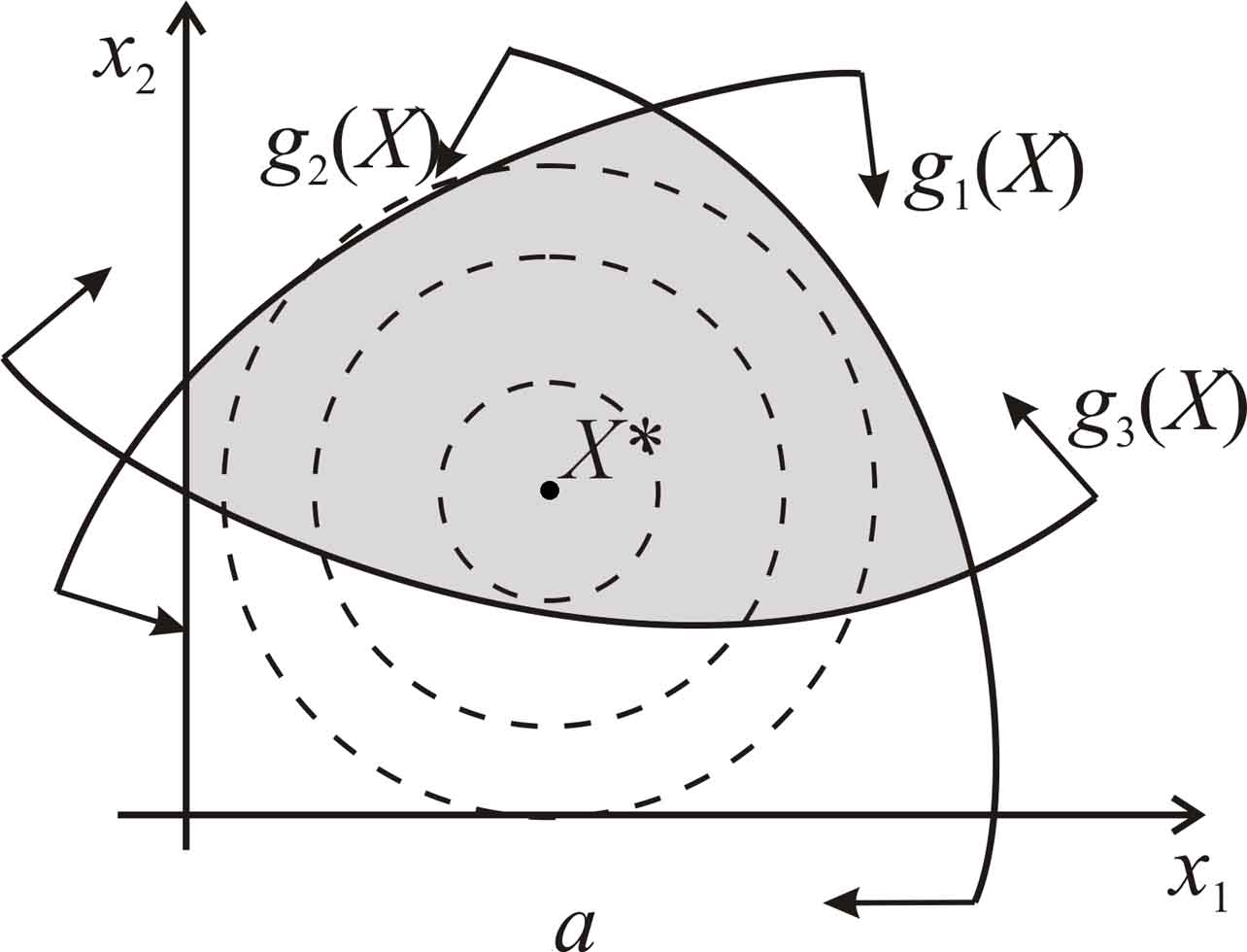
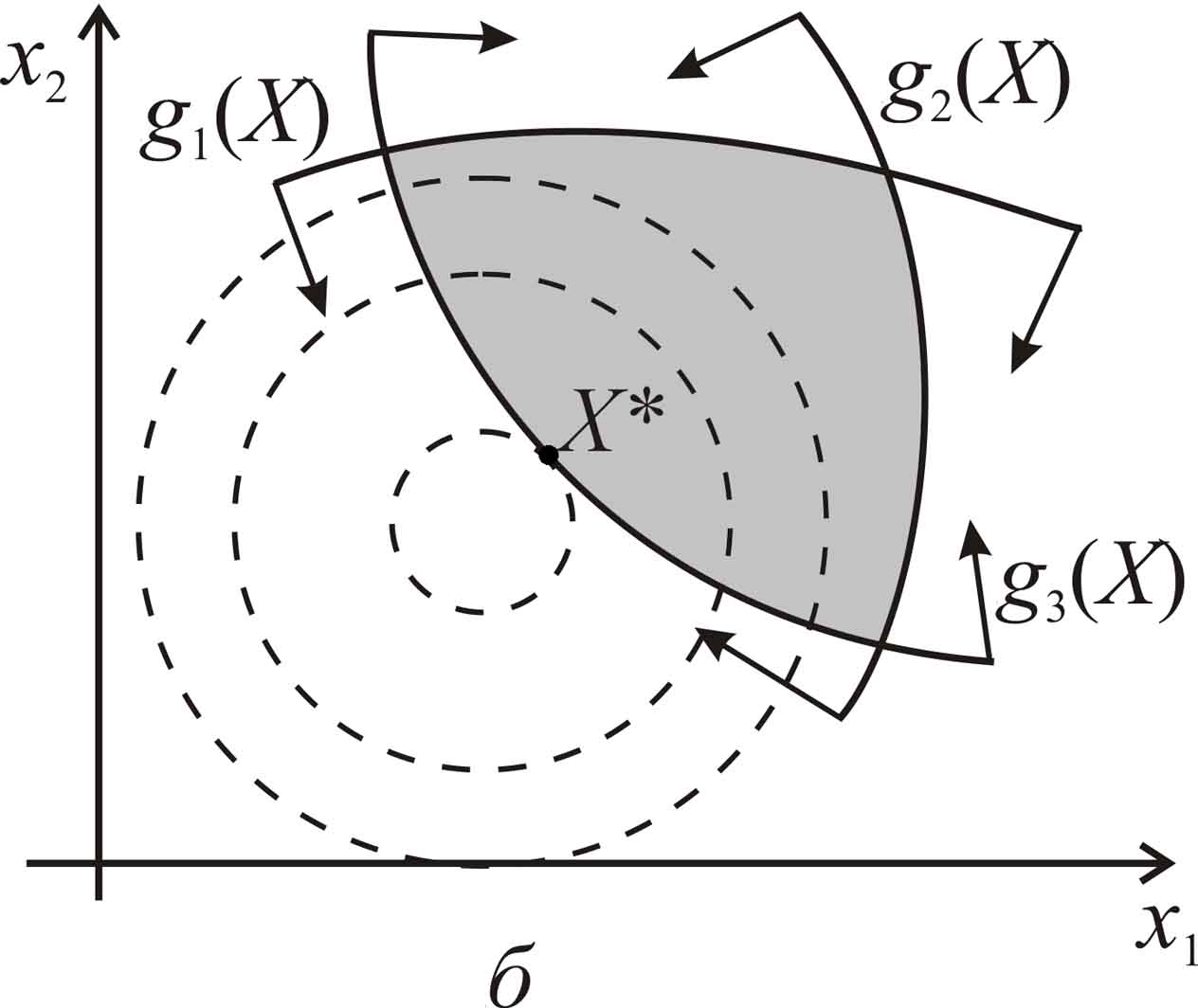
Решение задач математического программирования, как правило, связано со значительно большими трудностями, чем решение задач безусловной минимизации. На рис. 8.1 приведены возможные случаи расположения точки минимума в задаче математического программирования , , на допустимом множестве (множество окрашено). Пунктиром изображены линии уровня целевой функции.


Рис. 8.1. К задаче математического программирования для (, , ):а - точка совпадает с точкой безусловного минимума функции в ; б - не совпадает с точкой безусловного минимума

Для решения большинства практических задач используются приближённые численные методы. Рассмотрим некоторые из них, представляющие две группы методов.

1. Методы, использующие преобразование задачи условной оптимизации в эквивалентную последовательность задач безусловной оптимизации путём введения в рассмотрение вспомогательных функций. Эти методы называют методами последовательной безусловной оптимизации.

2. Методы решения задачи условной оптимизации, основанные на движении из одной допустимой точки, где выполняются все ограничения, к другой допустимой точке с меньшим значением целевой функции. Таким методом является, например, метод возможных направлений.

Основная идея методов первой группы состоит в том, чтобы аппроксимировать исходную задачу условной оптимизации некоторой вспомогательной задачей, решение которой менее сложно. Очевидно, что ограничившись лишь одной вспомогательной задачей, можно получить лишь приближённое решение. Если же использовать надлежащим образом построенную последовательность задач без ограничений, то искомое решение исходной задачи может быть найдено с требуемой точностью как предел соответствующей последовательности приближённых решений.

Методы непосредственного решения задачи условной оптимизации, образующие вторую группу, позволяют построить для целевой функции минимизирующую последовательность допустимых точек, сходящуюся к искомому точному решению поставленной задачи.

Классический метод решения задачи на условный экстремум

Пусть в задаче

(8.5)

, (8.6)

функции и , дифференцируемы в и ранг матрицы Якоби , равен в каждой точке допустимого множества , определенного системой (8.6). Последнее условие означает, что градиенты в точках не обращаются в нуль и линейно независимы. В этом случае равенства (8.6) задают связь между зависимыми к независимыми переменными из . Пусть, для определенности, этими зависимыми переменными являются и система (8.6) такова, что можно получить явные выражения

……………………

Подставляя их в формулу для целевой функции из (8.5), получим задачу минимизации

функции переменных без ограничений.

На практике решение системы (8.6) относительно зависимых переменных часто оказывается невозможным или весьма затруднительным, поэтому в классическом математическом анализе разработаны другие методы решения задачи (8.5) - (8.6), в частности метод множителей Лагранжа. Опишем этот метод.

Пусть - точка минимума в задаче (8.5)-(8.6). Будем рассматривать только допустимые в точке приращения , при которых , т.е. , . Для таких приращений с точностью до бесконечно малых более высокого порядка, чем , имеем:

(8.7)

Из равенств (8.7) видно, что независимых приращений ; существует только , а остальные могут быть выражены через них. Для определенности будем считать приращения с индексами зависимыми, а с номерами - независимыми.

Для рассматриваемых приращений разность , так как - точка минимума на множестве . Это возможно только при выполнении условия

. (8.8)

Из равенств (8.7) и (8.8) следует, что

(числа называют множителями Лагранжа). Поскольку приращения , при произвольны и независимы, из последнего равенства следует, что выражения в скобках для таких равны нулю. Выберем множители Лагранжа так, чтобы выражения в скобках обращались в нуль и при . Тогда для определения точки получим систему из уравнений:

, (8.9)

(8.10)

содержащую неизвестных .

Соотношения (8.9)—(8.10) являются необходимыми условиями минимума функции из (8.5) на множестве , заданном ограничениями (8.6). С другой стороны, они определяют стационарные точки так называемой функции Лагранжа задачи (8.5)—(8.6): , потому что равенства (8.9) можно интерпретировать как , а равенства (8.10) - как .

Сформулируем теорему о необходимых условиях локального условного экстремума в задаче (8.5) - (8.6), известную как правило множителей Лагранжа.

Теорема 8.1. Пусть в задаче (8.5) - (8.6) функции и , , дифференцируемы в . Тогда, если точка есть решение этой задачи и градиенты линейно независимы, то существует вектор такой, что

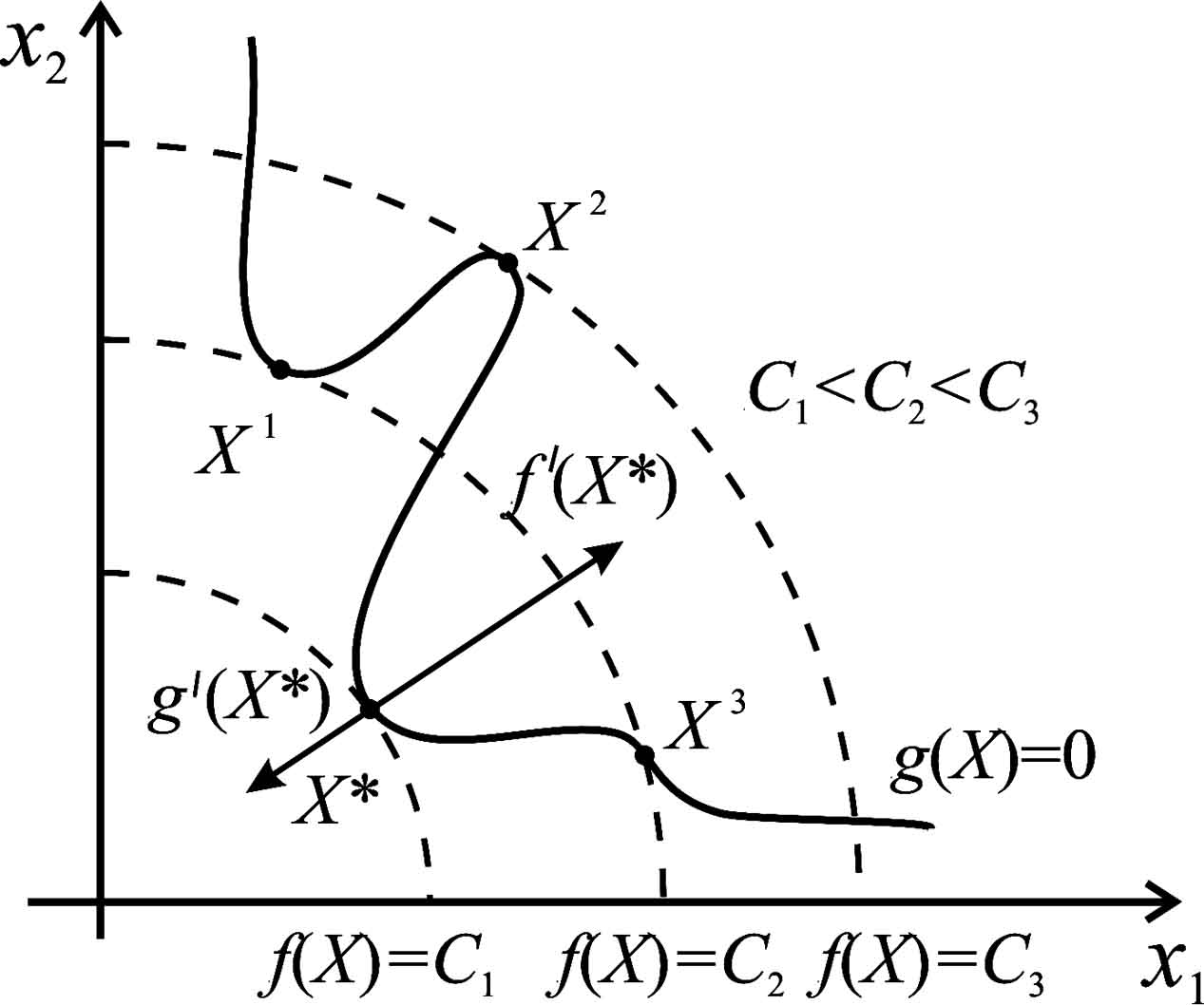
Рис. 8.2. Стационарные точки функции

Лагранжа задачи

Замечание. Последнее условие эквивалентно равенствам (8.9) и имеет простой геометрический смысл: в точке антиградиент целевой функции является линейной комбинацией градиентов (нормалей к поверхностям ). На рис. 8.2 приведена иллюстрация этого факта для задачи (8.5) - (8.6) при . Пунктиром изображены линии уровня целевой функции . В точке векторы и коллинеарны. В точках из достаточно малой окрестности точки , удовлетворяющих условию , выполняется неравенство . Очевидно, является точкой локального условного минимума, а - локального максимума при ограничении . Стационарная точка функции Лагранжа не является точкой локального условного экстремума, так как из нее можно сместиться, оставаясь на линии , так, что значение функции изменится в ту или иную сторону по сравнению с .

Отметим, что на допустимом множестве задачи (8.5) - (8.6) выполняются условия , поэтому для всех . Пусть - решение задач (8.5)—(8.6), а - множители Лагранжа, удовлетворяющие совместно с системе уравнений (8.9) - (8.10). Тогда

С учетом равенств (8.8) знак приращения функции Лагранжа в точке при фиксированном и малых приращениях - определяется ее вторым дифференциалом

Здесь, вообще говоря, , так как дифференциалы зависимы, однако с учетом (8.9) последняя сумма обращается в нуль, поэтому второй дифференциал функции Лагранжа в точке при является квадратичной формой дифференциалов и не зависит от вторых дифференциалов .

Сформулируем достаточные условия оптимальности в задаче (8.5) - (8.6) с использованием матрицы вторых производных по переменным функции Лагранжа:

Теорема 8.2. Пусть функции и , задачи (8.5)-(8.5) дважды дифференцируемы в , точка удовлетворяет системе уравнений (8.9)-(8.10), градиенты , , линейно независимы и квадратичная форма положительно определена при всех приращениях удовлетворяющих системе (8.7). Тогда является точкой локального минимума функции из (8.5) на множестве , определенном ограничениями (8.6).

Замечание. Если матрица положительно определена, то квадратичная форма при всех ненулевых векторах и проверка достаточного условия локального условного минимума значительно упрощается. В противном случае для такой проверки приходится из системы уравнений (8.6) выражать зависимые приращения и подставлять их в квадратичную форму для исследования ее положительной определенности.

Пусть в задаче (8.5) - (8.6) функция ограничена снизу на множестве . Опишем алгоритм решения этой задачи методом множителей Лагранжа.

Шаг 1. Составить функцию Лагранжа .

Шаг 2. Найти частные производные от по переменным и и приравнять их к нулю.

Шаг 3. Решить полученную систему уравнений, т.е. найти стационарные точки функции Лагранжа.

Шаг 4. С помощью достаточного условия (см. теорему 8.2) отобрать среди найденных стационарных точек точки локального условного минимума.

Шаг 5. Сравнить значения функции в точках локального условного минимума и найти точку глобального минимума.

Замечание 1. Система уравнений (8.9) - (8.10) представляет собой необходимые условия минимума функции Лагранжа в пространстве . Поэтому ее решения на шаге 3 можно искать численными методами, например, методом Ньютона, минимизируя .

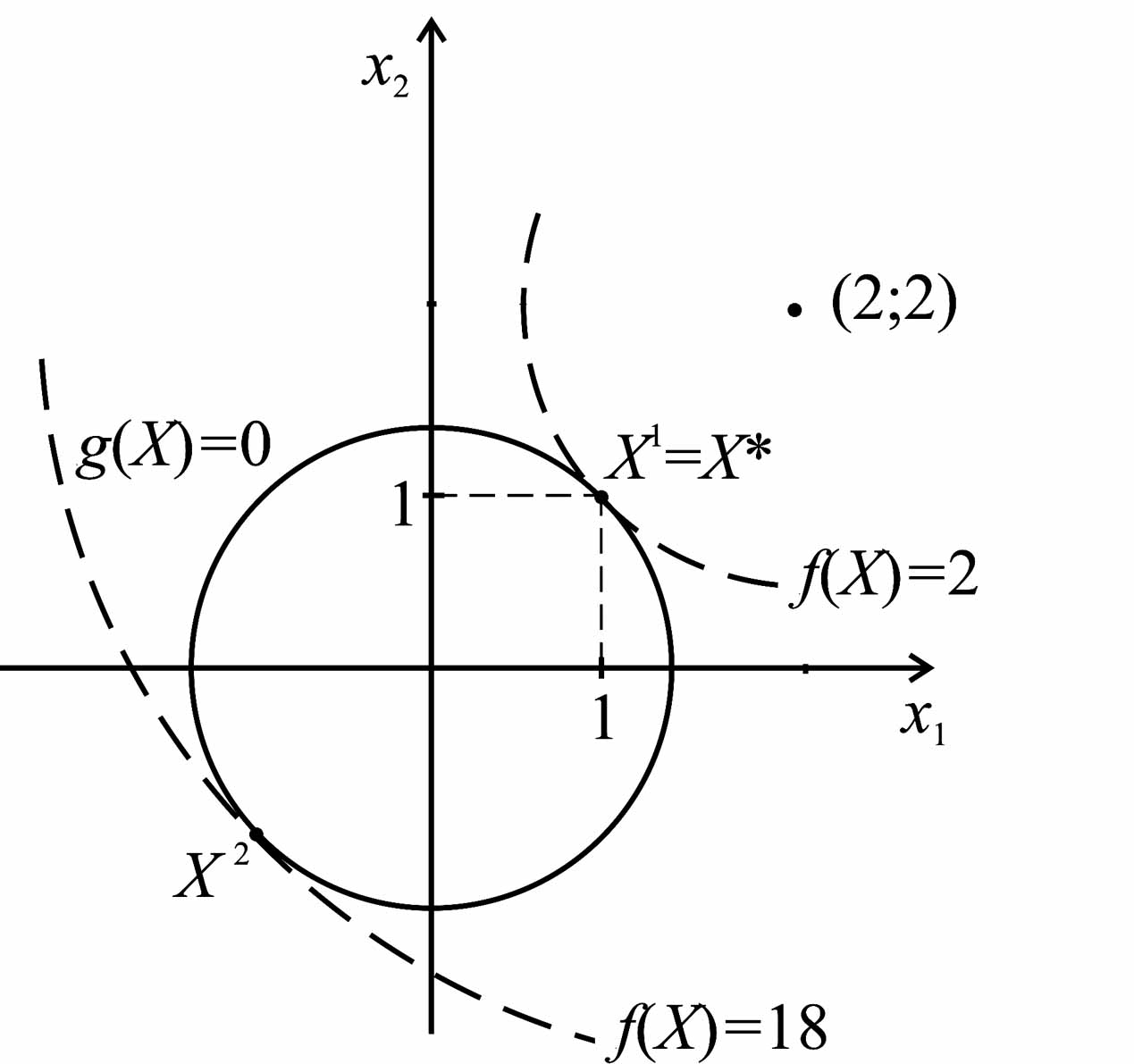
Пример 8.1. Решить задачу

Шаг 1.

Шаг 2.

Шаг 3. Эта система уравнений имеет два решения:

IIIаг 4. Составим матрицу вторых производных функции Лагранжа:

Для первого решения матрица положительно определена и, следовательно, - точка локального условного минимума.

Для второго решения требуется дополнительно учесть зависимость между приращениями и исследовать квадратичную форму . Для и имеем: при всех . Следовательно, вторая стационарная точка функции Лагранжа определяет точку локального условного максимума задачи.

Шаг 5. Окончательно находим: и (рис. 8.3).

Рис. 8.3. К примеру 8.1.

Контрольные вопросы

1. В чём заключается суть задач оптимизации при наличии ограничений.

2. Дать математическую постановку задачи математического программирования.

3. Перечислить основные виды задач математического программирования.

4. Пояснить классификацию задач математического программирования.

5. Опишите основные подходы, которые используются при решении большинства практических задач математического программирования.

6. Опишите классический метод решения задач на условный экстремум

7. Приведите правило множителей Лагранжа.

8. Сформулируйте необходимые условия минимума целевой функции на допустимом множестве, заданном ограничениями .

10. Сформулируйте достаточные условия оптимальности в задаче на условный экстремум.

11. Опишите алгоритм решения задачи на условный экстремум методом множителей Лагранжа.

PAGE 88

МЕТОДЫ ОПТИМИЗАЦИИ ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ