ПРЯМЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ
Лекция №5
ПРЯМЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ
Рассмотрим конкретнее вычислительные алгоритмы решения задачи безусловной минимизации, которые опираются только на вычисление значений функции , т.е. прямые методы минимизации. Важно отметить, что для их применения не требуется не только дифференцируемость целевой функции, но даже аналитическое ее задание. Нужно лишь иметь возможность вычислять или измерять значения в произвольных точках. Такие ситуации часто встречаются в практически важных задачах оптимизации.
Остановимся сначала на вычислительных процедурах вида (4.7), в которых выбор нового приближения к точке минимума определяется сравнением значений функции в нескольких точках пространства .
Минимизация по правильному симплексу
Поиск точки минимума функции с помощью правильных симплексов производится следующим образом. На каждой итерации поиска сравниваются значения функции в вершинах симплекса и выполняется процедура отражения для той вершины, в которой принимает наибольшее значение. Если в отраженной вершине получается меньшее значение функции, то переходят к новому симплексу. Иначе выполняют ещё одну попытку отражения для вершины со следующим по величине значением . Если и она не приводит к уменьшению функции, то сокращают длину ребра и строят новый симплекс с этим ребром. При этом в качестве базовой выбирают ту вершину старого симплекса, в которой функция принимает наименьшее значение. Поиск точки минимума заканчивают, когда либо ребро симплекса, либо разность между значениями функции в вершинах симплекса становятся достаточно малыми.
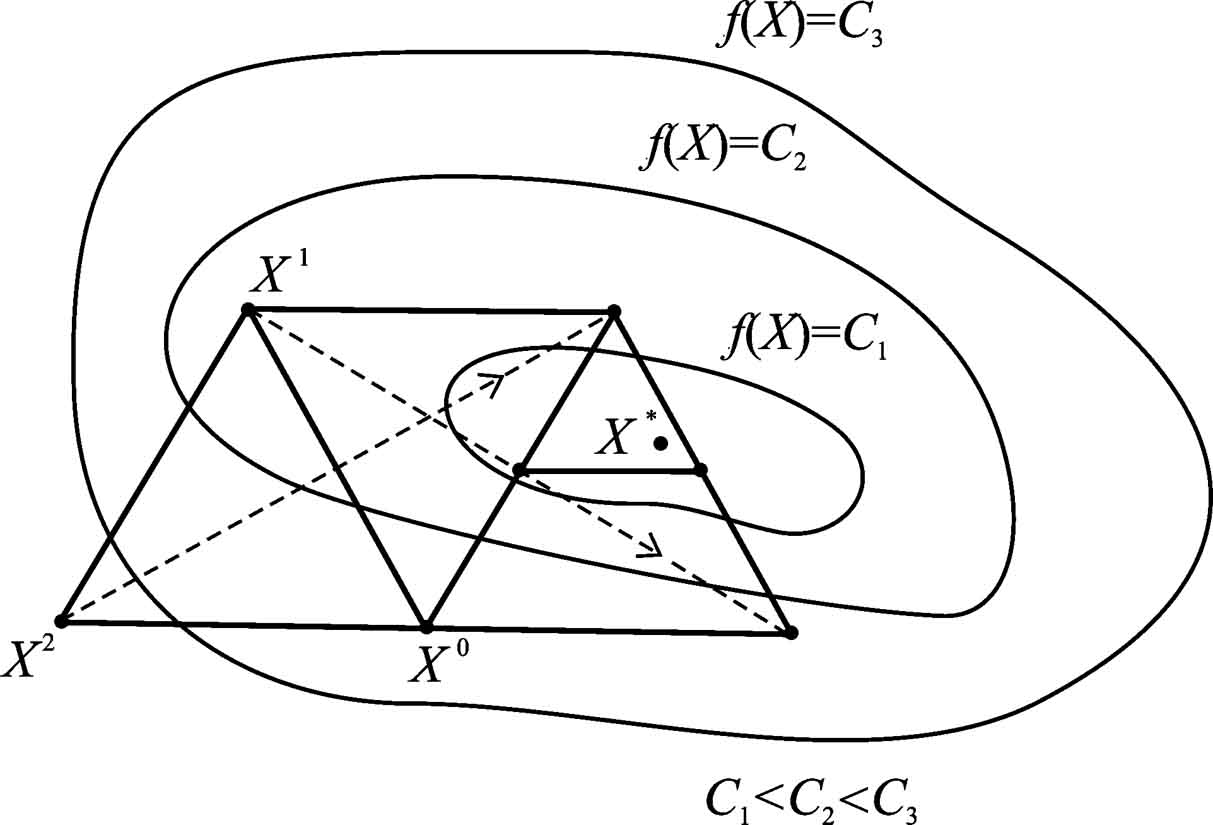
Геометрическая иллюстрация работы алгоритма в пространстве показана на рис. 5.1, где точки - вершины начального симплекса, а пунктиром указаны операции отражения.
|
|
|
Рис. 5.1. Поиск точки минимума функции с помощью
правильных симплексов в пространстве .
|
Замечание 1. Следует иметь в виду, что если функция многомодальна, то описанным методом может быть найдена точка локального, а не глобального минимума .
Замечание 2. Если ограниченность целевой функции не очевидна, то в алгоритм метода следует включить дополнительную процедуру останова.
Поиск точки минимума по деформируемому многограннику
Практические трудности, возникающие при реализации поиска по правильному симплексу, такие как постоянство величины шага, отсутствие ускорения поиска и трудности при проведении поиска на искривленных поверхностях уровня, привели к необходимости некоторых улучшений метода. Рассмотрим метод поиска, в котором симплекс может изменять свою форму и уже не остается симплексом. Более подходящим для него оказалось название “деформируемый многогранник”.
В методе деформируемого многогранника, как и в предыдущем методе, функция независимых переменных минимизируется с использованием вершин многогранника. Вершина, в которой значение функции максимально, проектируется через центр тяжести оставшихся вершин. Улучшенные значения функции находятся последовательной заменой точки с максимальным значением на более “хорошие” точки, пока не будет найден минимум .
Итак, пусть - вершины многогранника на некотором этапе поиска. Определим точки и , в которых функция имеет соответственно наибольшее и наименьшее значения:
.
Центр тяжести всех вершин, исключая , определим по формуле
Процедура отыскания вершины, в которой имеет лучшее значение, состоит из четырех операций.
1) Отражение – проектирование точки через центр тяжести в соответствии с соотношением
где – коэффициент отражения, - центр тяжести, вычисляемый по формуле (5.1).
2) Растяжение. Если , то вектор - растягивается в соответствии с соотношением
где –коэффициент растяжения. Если , то вершина заменяется на и начинается новый этап поиска снова с операции отражения. В противном случае заменяется на и также осуществляется переход к операции отражения нового этапа.
3) Сжатие. Если , любого : , то вектор сжимается в соответствии с формулой
где (0;1)- коэффициент сжатия. Вершина заменяется на и выполняется вновь операция отражения на новом этапе поиска.
4) Редукция. Если , то все векторы уменьшаются, например, в 2 раза с отсчетом от в соответствии с формулой
Далее возвращаемся к операции отражения для продолжения поиска на новом этапе.
Критерий окончания поиска может быть выбран в виде условия
где 0– достаточно малое число.
Геометрическая иллюстрация описанных процедур для пространства приведена на рис. 5.2. и 5.3.
|
|
|
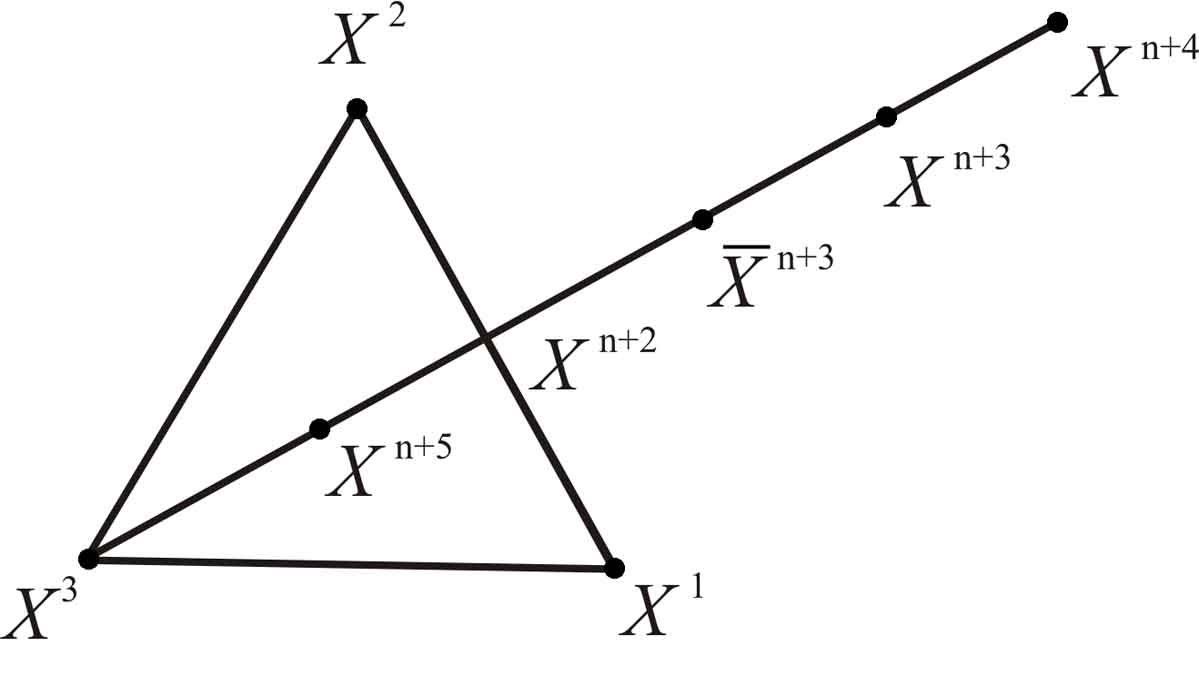
Рис. 5.2. Пробные точки , для
перехода к новому многограннику.
|
Так как величина, то выбор точек и соответствует отражению; , поэтому выбор точки соответствует сжатию, а и выбор точки приводит к растяжению симплекса.
|
|
|
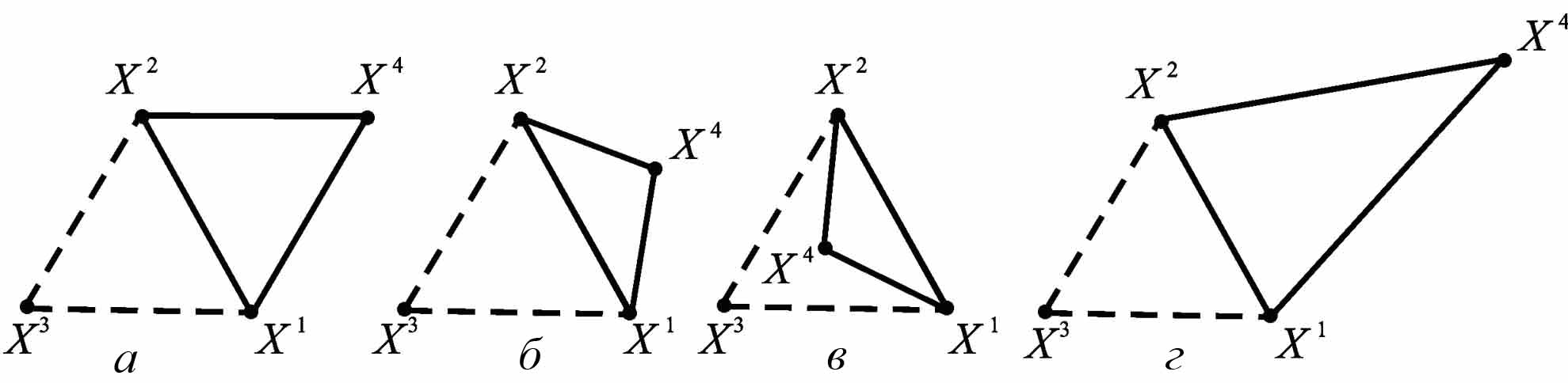
Рис.5.3. Новые многогранники, полученные в результате процедур отражения (а,б); сжатия (в); растяжения (г).
|
Деформируемый многогранник в отличие от жесткого симплекса адаптируется в процессе поиска к топографии целевой функции, вытягиваясь вдоль длинных наклонных плоскостей, изменяя направление в изогнутых впадинах и сжимаясь в окрестности минимума.
Метод циклического покоординатного спуска
Рассмотрим прямые методы решения задачи безусловной минимизации, использующие вместо итерационных процедур вида (4.7) простейшие вычислительные алгоритмы, основанные на рекуррентной формуле (4.13): , где - направление поиска точки из точки , а положительное число - величина шага в этом направлении.
Способ выбора и будет определять одну из трёх рассматриваемых далее модификаций метода покоординатного спуска.
Метод циклического покоординатного спуска заключается в последовательной минимизации целевой функции сначала по направлению первого базисного вектора , затем второго - и т.д. После окончания минимизации по направлению последнего базисного вектора цикл повторяется. Таким образом, метод циклического покоординатного спуска заключается в изменении каждый раз одной переменной, тогда как другие остаются постоянными.
Скорость сходимости данного метода невысока. Несмотря на это, метод циклического покоординатного спуска широко применяется на практике благодаря простоте реализации.
Заметим, что такой метод работает плохо, если в выражение минимизируемой функции входят произведения , т.е. если имеет место взаимодействие между
Указанного недостатка можно избежать с помощью следующей модификации метода покоординатного спуска, известной под названием метода Зейделя.
Метод Зейделя
Этот метод заключается в последовательной минимизации функции по направлению каждого из координатных векторов , всегда начиная из самой последней точки построенной последовательности. После завершения минимизации по направлению последнего координатного вектора цикл, называемый внешней итерацией, повторяется до тех пор, пока не выполнится одно из возможных условий окончания поиска:
где - заданный параметр точности.
Для приближенного решения вспомогательной задачи минимизации
на каждом внутреннем шаге внешней итерации целесообразно использовать изученный ранее метод поразрядного поиска.
3.4.6. Метод Пауэлла.
В основе этого метода лежит рассмотренный выше метод Зейделя, дополненный последовательным нахождением направлений убывания после завершения очередной внешней итерации и минимизацией функции по этим направлениям.
Пусть задана точка начального приближения . Выполним одну внешнюю итерацию метода покоординатного спуска Зейделя,т.е. найдем точку
где - единичный координатный вектор, у которого - я координата равна 1, остальные равны 0, . При этом величина шага определяется с помощью какой-либо процедуры одномерной оптимизации по
.
Далее выполняется “диагональный” шаг в направлении убывания функции по вектору: : , где величина шага определяется путем минимизации целевой функции в направлении вектора с помощью одномерного поиска по :
.
Полагая , приступаем к выполнению следующей внешней итерации. Описанная процедура повторяется до тех пор, пока не выполнится одно из условий (5.7).
Контрольные вопросы
1. Какие методы называют прямыми методами безусловной минимизации?
2. Перечислите основные прямые методы безусловной минимизации и укажите их достоинства и недостатки.
3. Какое условие используется в качестве критерия окончания поиска по деформируемому многограниику?
4. Опишите метод минимизации по правильному симплексу?
5. Поясните метод деформируемого многогранника.
6. Перечислите основные операции метода деформируемого многогранника, поясните их смысл?
7. Какая итерационная процедура лежит в основе метода покоординатного спуска?
8. Опишите метод Зейделя безусловной оптимизации?
9. Какие условия используются в качестве возможных условий окончания поиска в методах покоординатного спуска?
10. Поясните основные отличия в методах Зейделя и Пауэлла?
PAGE 62
ПРЯМЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ