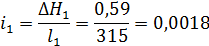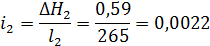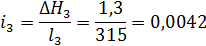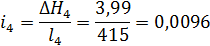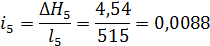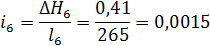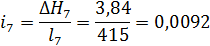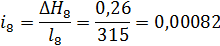Расчет коротких трубопроводов

содержание

[1] Задача №1. Расчет коротких трубопроводов.

[2] Заключение.

[3] Список использованной литературы.

Введение

Гидравлика — это наука о законах движения и равновесия жидкостей и способах приложения этих законов к решению конкретных технических задач.

Практическое значение гидравлики возросло в связи с потребностями современной техники в решении вопросов транспортирования жидкостей и газов различного назначения и использования их для разнообразных целей.

Трубопроводные системы представляют собой объединение труб с помощью различных соединений. Они являются основой системы обеспечения населения, производства и сельского хозяйства жизненно важными продуктами: чистым воздухом, питьевой и технологической водой, высоко- и низкопотенциальным теплоносителем (теплом), газом, нефтепродуктами.

Трубопроводы делятся на короткие и длинные. К первым относятся все трубопроводы, в которых местные потери напора превышают 5…10% потерь напора по длине. К ним относят, к примеру, системы водоснабжения, водоотведения, горячего водоснабжения внутри зданий. Ко вторым относятся трубопроводы, в которых местные потери меньше 5…10% потерь напора по длине. К таким трубопроводам относятся, например, магистральные водоводы, нефтепроводы. Целью расчета короткого трубопровода может быть определение напора или давления в начале трубопровода, потерь напора или потерь давления, а также определение расхода или диаметра трубопровода при известном напоре в его начале.

Длинные трубопроводы можно разделить также на простые и сложные. Простыми называются последовательно соединенные трубопроводы одного или различных сечений, не имеющих никаких ответвлений. К сложным трубопроводам относятся системы труб с одним или несколькими ответвлениями, параллельными ветвями и т.д. К сложным относятся и так называемые кольцевые трубопроводы.

Кольцевая сеть состоит из замкнутых колец и магистралей, присоединенных к водонапорной башне или резервуару. Кольцевые трубопроводы (системы водопровода) проектируются для подачи воды непосредственно потребителю на производственные нужды.

  1. Задача №1. Расчет коротких трубопроводов.

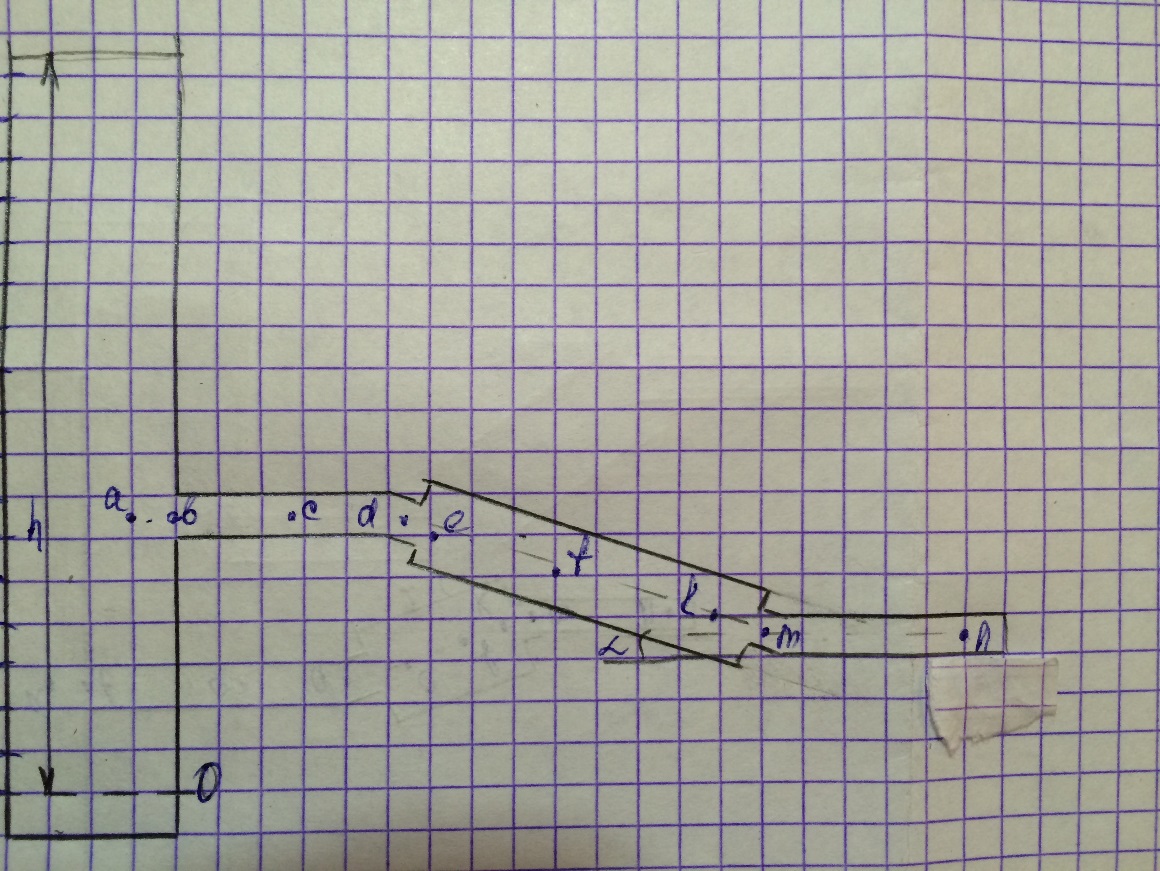Рис.1. Схема расположения трубопроводов.

При расчете коротких трубопроводов применяется уравнение Бернулли для двух выбранных сечений и уравнение неразрывности.

Уравнение Бернулли составляется относительно плоскости сравнения, которой может быть любая горизонтальная плоскость. Плоскость сравнения проведена по центру трубы в начале трубопровода.

Расчет необходимо начать с определения формы записи уравнения Бернулли. Для расчета систем водоснабжения и водоотведения обычно применяется уравнение Бернулли в форме напоров:

,

где высота z называется геометрической высотой, или высотой положения центра тяжести сечения струйки; – высота, определяемая величиной гидродинамического давления, или пьезометрическая высота; - коэффициент

Кориолиса; – скоростная высота, или скоростной напор; - потери напора.

Если трубопровод имеет участки с разными диаметрами, то потери напора h при движении жидкости от сечения 1-1 к сечению 3-3 складываются из потерь во всех участках трубопровода. В каждом участке потери разделяются на потери по длине и местные.

1. Скорости потоков в трубах

Скорость потоков в трубах:

2. Расчёт потерь напора в трубопроводах

Потери на выходе потока из бака определяется по формуле Вейсбаха:

выхода – коэффициент местного сопротивления

Потери напора по длине рассчитываются по формуле Дарси-Вейсбаха (труба 1):

Для определения потерь напора по длине трубы рассчитаем число Рейнольдса, по рассчитанному числу узнаем режим движения жидкости для всех участков с различными средними скоростями движения жидкости. Коэффициент гидравлического трения определяется по формулам, которые выбираются в зависимости от режима движения и области сопротивления.

Найдём число Рейнольдса

Число Рейнольдса определяет характер потока: ламинарный, промежуточный или турбулентный.

  • ламинарный , если Re <2300
  • промежуточный, если 2300 < Re <4000
  • турбулентный, если 4000 < Re

Зависимость коэффициента гидравлического сопротивления от числа Рейнольдса и эквивалентной шероховатости труб

Режим (зона)

Границы

Коэффициент гидравлического трения

Ламинарный

Re<2320

 (формула Стокса)

Турбулентный:

1.

Зона перехода турбулентного движения в ламинарное

2000<Re<3000

(формула Френкеля)

2.

Зона гидравлически гладких труб

2320<Re<10d/kэ

(формула Блазиуса)

(формула Конакова при Re<3*106)

3.

Зона смешанного трения или гидравлически шероховатых труб

10d/kэ<Re<500d/kэ

(формула Альтшуля)

4.

Зона квадратичного сопротивления (вполне шероховатого трения)

Re>500d/kэ

  (формула Никурадзе)

(формула Шифринсона)

Режим движения жидкости турбулентный, так как Re 4000. Трубопровод гидравлически шероховатый, 1- коэффициент гидравлического трения рассчитывается по формуле Шифринсона:

Потери напора на повороте:

пов.1 = 90° (1-cos20°)=0.06 м

Потери напора при внезапном расширении рассчитывается по формуле Борда:

Потеря напора по длине (труба 2):

Режим движения жидкости турбулентный, так как Re 2320.

Re ; 4000 < 194529 < 200000

Трубопровод гидравлически шероховатый.

Рассчитаем потери напора при внезапном сжатии:

n — коэффициент сжатия потока

Коэффициент сужения струи находим по формуле Альтшуля:

Потерю напора при внезапном сжатии находим по формуле Борда:

Потери напора на повороте:

Потери напора по длине (труба 3):

Найдем число Рейнольдса:

Режим движения жидкости турбулентный, так как Re 2320. Трубопровод гидравлически шероховатый, 3- коэффициент гидравлического трения рассчитывается по формуле Альтшуля. Потери напора по длине рассчитываются по формуле Дарси-Вейсбаха.

Рассчитаем суммарные потери напора:

= = 0,465+9,8+0,36+0,0078+0,0047+0,025+0,12+2,53=13,31м

3. Определение уровня воды в напорном баке

Составляем уравнение Бернулли и определяем уровень воды Н в напорном баке:

H = Z3 + + =-3,42 + + 13,31 = 10,29 м,

где Z3 – координата центра тяжести сечения III,

Z3 = = -3,42м

4. Расчёт и построение напорной линии

Полные напоры в сечениях трубопроводов:

На = Н = 10,29 м

Нв = На — hвых =10,29 — 0.465 = 9,8 м

Нс = Нв —=9,8 — 9,8 = 0 м

Нd = Нс —0 — 0,0078 = -0,0078 м

Не = Нd —=-0,0078 — 0.36 = -0,3678 м

Нf = Не —=-0,3678 — 0,0047 = -0,3725 м

Нk = Нf —=-0,3725 — 0,12 =-0,4925 м

Нm = Нk —= =-0,4925 — 0.025 = -0,5175 м

Нn = Нm —=-0,5175 — 2.53 = -3.02 м

Результаты расчётов наносим на рис.2

5. Расчёт и построение пьезометрической линии

Скоростные напоры в трубах:

Статические напоры в сечениях трубопроводов:

ha = На — = 10,29 — 0.93 =9,36 м

hв = Нв — = 9,8— 0.93 = 8,87 м

hс = Нс — = 0 — 0.93 = -0,93 м

hd = Нd — = -0,0078— 0.93 = -0,9378

hе = Не — = -0,3678 — 0.13 = -0,4978 м

hf = Нf — = -0,3725— 0.13 = -0,5025 м

hk = Нk — = -0,4925 — 0.13 = -0,6225 м

hm = Нm — =-0,5175 — 0.41 = -0,9275 м

hh = Нh — = -3,2— 0.41 = -3,61 м

Результаты расчётов наносим на рис. 2

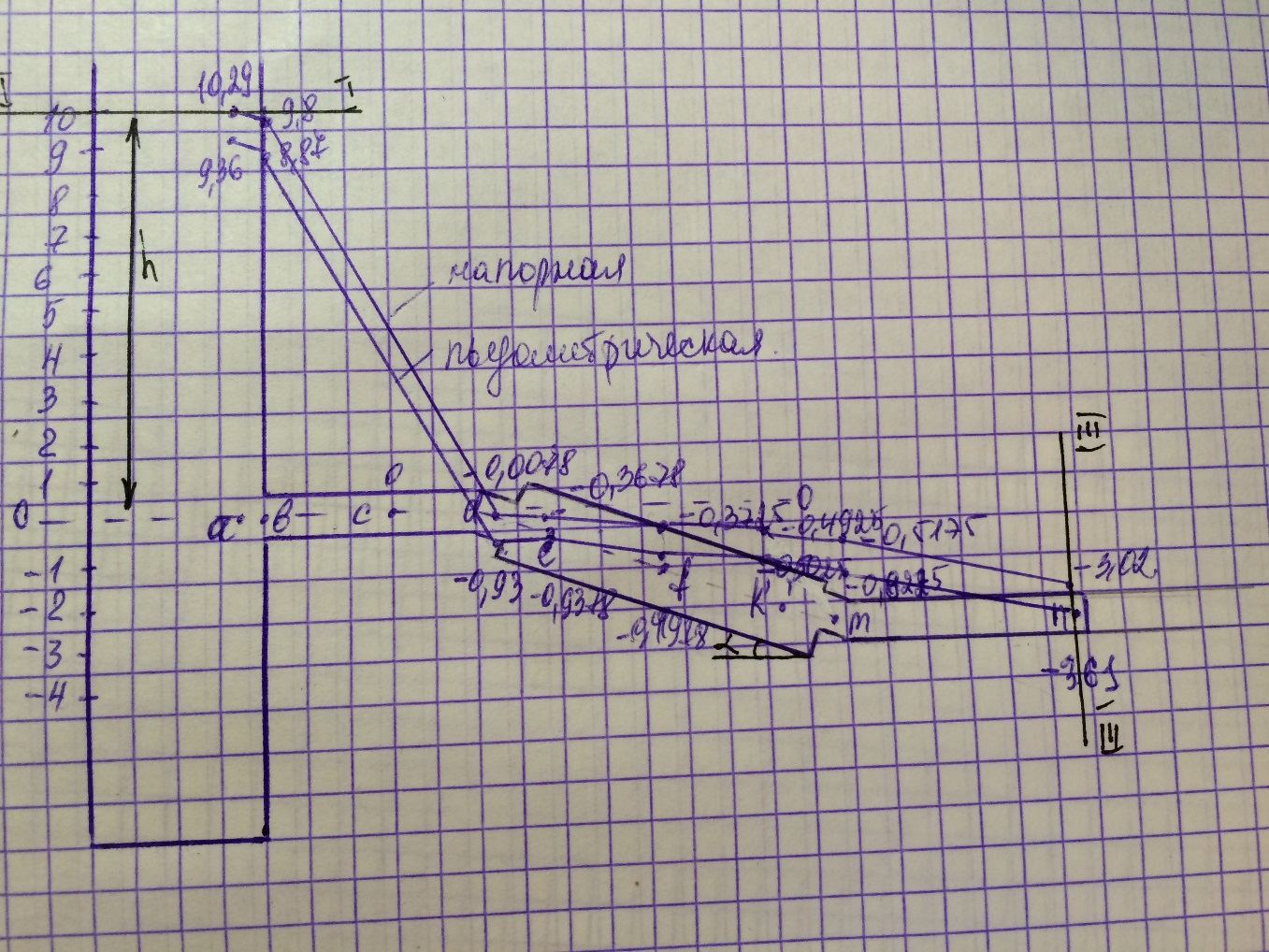
Рис. 2. Напорная и пьезометрическая линии.

6. Расчёт напорной характеристики

Потери в трубопроводах определяются его напорной характеристикой:

где

A - полное гидравлическое сопротивление трубопровода,

A1, A2, A3 – гидравлические сопротивления отдельных участков трубопроводов.

Отсюда =8.8*104+0.0623*104+4.6*104=13.4623*104

Напорная характеристики трубопровода =13.4623*104*(8*10-3)2=8.616м

Задача № 2:Определение высоты всасывания насоса

Определение диаметра, средняя скорость всасывающего трубопровода

Из формулы расхода выражаем диаметр трубы:

где Q – расход, – площадь сечения, v – скорость.

По ГОСТу при диаметре трубы меньшей или равной 250мм, скорость течения в ней воды варьируется от 0.6 до 1 м/с.

Принимаем диаметр трубопровода равный 100 мм, при заданном расходе вычислим скорость в трубопроводе:

При d = 100 мм

Геометрическая высота всасывания:

Для расчета предельной геометрической высоты установки (всасывания) центробежного насоса воспользуемся уравнением Бернулли для сечения 1-1 и 2-2

Определим области гидравлического сопротивления, для этого вычислим:

>500

Вычислим предельную высоту установки насоса:

Вычислим кавитационный запас:

  1. Задача №3:потокараспределения в кольцевой трубопроводной сети

Дана схема системы подачи и распределения воды:

Таблица №1

№

участка

Длина участка

l, м

Диаметр труб d, мм

Материал

Удельное гидравлическое сопротивление

,

(л/c)-2

Гидравлическое сопротивление участка

,

м·(л/c)-2

Расход

на

участке

x, л/с

Потери

напора

на участке x

H, м

1

315

400

чугун

0,2189·10-6

55.76·10-6

133

0,59

2

265

300

чугун

0,9485·10-6

168.7·10-6

133

0,59

3

315

250

чугун

2,528·10-6

665.2·10-6

70,91

1,3

4

415

200

чугун

8,092·-6

2615.5·10-6

48,91

3,99

5

515

150

чугун

37,11·10-6

10062·10-6

15

4,54

6

265

150

чугун

37,11·10-6

5869.5·10-6

5,63

0,41

7

415

200

чугун

8,092·10-6

2615.5·10-6

33,63

3,84

8

265

200

чугун

8,-92·10-6

1830.85·10-6

9,46

0,26

9

315

250

чугун

2,528·10-6

665.2·10-6

62,09

2,96

Таблица №2

Номер узла

Отбор в узле

Q, л/c

Давление в узле

P, Па

Геод. Отметка z, м

Напор в узле H, м

1

-133

117720

0

15

2

0

778914

0

79,95

3

22,0

759784

0

78,84

4

24,0

733101

0

76,97

5

25,0

618206

0

70,39

6

15,0

624995

0

66,08

7

28,0

687288

0

70,84

8

19,0

737225

0

77,47

Требуется:

1. Рассчитать расход на каждом участке; напор в узлах.

2. Рассчитать потери напора на участках; давление в каждом узле.

3. Рассчитать потери напора по каждому кольцу.

4. Построить напорную линию. Определить пьезометрические уклоны в каждом узле.

Схема системы подачи и распределения воды: в окружностях указаны номера узлов; над дугами – номера дуг; на дуге 1 – насосная станция; направление дуги указывает направление потока

Напорно-расходная характеристика насоса:

  1. Получение напоров в узлах и расходов по участкам Получение напоров в узлах и расходов по участкам.
    Составим уравнение баланса расходов в каждом узле нашей сети.


1. х1-Q1=0 х1=Q1 х1 Q1

2. x2+x9 +Q2-x1=0 x2+x9-x1=-Q2 x2 -Q2

3. x3-x2+Q3=0 x3-x2=-Q3 x3 -Q3

(1) 4. x4-x3-x8+Q4=0 x4-x3-x8=-Q4 x4 b= -Q4

5. x5-x4-x6+Q5=0 x5-x4-x6=-Q5 x= x5 -Q5

6. -x5+Q6=0 -x5=-Q6 x6 -Q6

7. x6-x7 +Q7=0 x6-x7=-Q7 x7 -Q7
8. x7+x8+x9+Q8=0 x7+x8+x9=-Q8 x8 -Q8
x9

Построение математической модели кольцевого трубопровода.
Составим матрицу полученной системы А (матрица инцинденций).

А

участок
узел

1

2

3

4

5

6

7

8

9

1

1

0

0

0

0

0

0

0

0

2

-1

1

0

0

0

0

0

0

1

3

0

-1

1

0

0

0

0

0

0

4

0

0

-1

1

0

0

0

-1

0

5

0

0

0

-1

1

-1

0

0

0

6

0

0

0

0

-1

0

0

0

0

7

0

0

0

0

0

1

-1

0

0

8

0

0

0

0

0

0

1

1

-1

Ах=b

Система линейно-зависима, т.к. Qi=0 и при сложении всех уравнений системы (1) получили 0=0, поэтому одно уравнение можно вычеркнуть. Получаем усеченную матрицу А и усеченный вектор b.

А

участок
узел

1

2

3

4

5

6

7

8

9

1

1

0

0

0

0

0

0

0

0

2

-1

1

0

0

0

0

0

0

1

3

0

-1

1

0

0

0

0

0

0

4

0

0

-1

1

0

0

0

-1

0

5

0

0

0

-1

1

-1

0

0

0

6

0

0

0

0

-1

0

0

0

0

7

0

0

0

0

0

1

-1

0

0

Q1

-Q2

-Q3

b= -Q4

-Q5

-Q6

-Q7

Тогда уравнение баланса расходов примет вид: Ax=b. (2)

  1. Составляем уравнение Бернулли для каждого участка гидравлической системы, например, для первого участка.

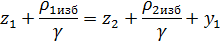
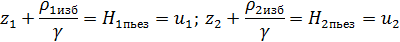
На первом участке получаем следующее уравнение:

u1-u2=y1,

где u1, u2 – пьезометрические напоры в 1 и 2 узлах; y1 - потери напора на первом участке, y1=y1длина+y1насос=S1|x1|x1-H0-SH|x1|x1=(S1+Sн)|x1|x1-H0 (потери напора для насоса берутся со знаком «-», т.к. дуга моделирует насос).

Аналогично, составляя уравнения Бернулли для всех остальных участков, получим систему уравнений (3).

1. u1-u2=y1; y1= (S1+Sн)|x1|x1-H0 u1 y1

2. u2-u3 =y2; y2=S2|x2|x2 u2 y2

3. u3-u4 =y3; y3=S3|x3|x3 u3 y3

4. u4-u5 =y4; y4=S4|x4|x4 u4 y4

(3) 5. u5-u6 =y5; y5=S5|x5|x5 u= u5 y= y5

6. u7-u5 =y6; y6=S6|x6|x6 u6 y6

7. u8-u7 =y7; y7=S7|x7|x7 u7 y7

8. u8-u4 =y8; y8=S8|x8|x8 u8 y8

9. u2-u8 =y9; y9=S9|x9|x9 y9

(S1+Sн)|x1|x1

S2|x2|x2

S3|x3|x3

S4|x4|x4

f(x)= S5|x5|x5

S6|x6|x6

S7|x7|x7

S8|x8|x8

S9|x9|x9

Матрица системы (3) является транспонированной матрицей матрицы А.

Выпишем матрицу AT – транспонированную матрицу.

AT

участок
узел

1

2

3

4

5

6

7

8

1

1

-1

0

0

0

0

0

0

2

0

1

-1

0

0

0

0

0

3

0

0

1

-1

0

0

0

0

4

0

0

0

1

-1

0

0

0

5

0

0

0

0

1

-1

0

0

6

0

0

0

0

-1

0

1

0

7

0

0

0

0

0

0

-1

1

8

0

0

0

-1

0

0

0

1

9

0

1

0

0

0

0

0

-1

Тогда в матричном виде получаем:

ATu=f(x). (4)

  1. Для нахождения неизвестных u и x имеем следующую систему нелинейных уравнений:

Ax=b (2)
ATu=f(x). (4)

Из составленных уравнений мы получили 9 переменных x и 8 переменных u, всего 9+8=17 – переменных и 7+9=16 - уравнений. Для решения системы уравнений (2) и (4) необходимо задать значение одной из переменных, в данном случае по условию задан напор в первом узле, равный Н1=25 м. Воспользовавшись программой ИСИГР, находим искомые значения расхода на участке x, потерь напора на участке x, давления в узле и напора в узле и заносим данные в таблицы 1 и 2.

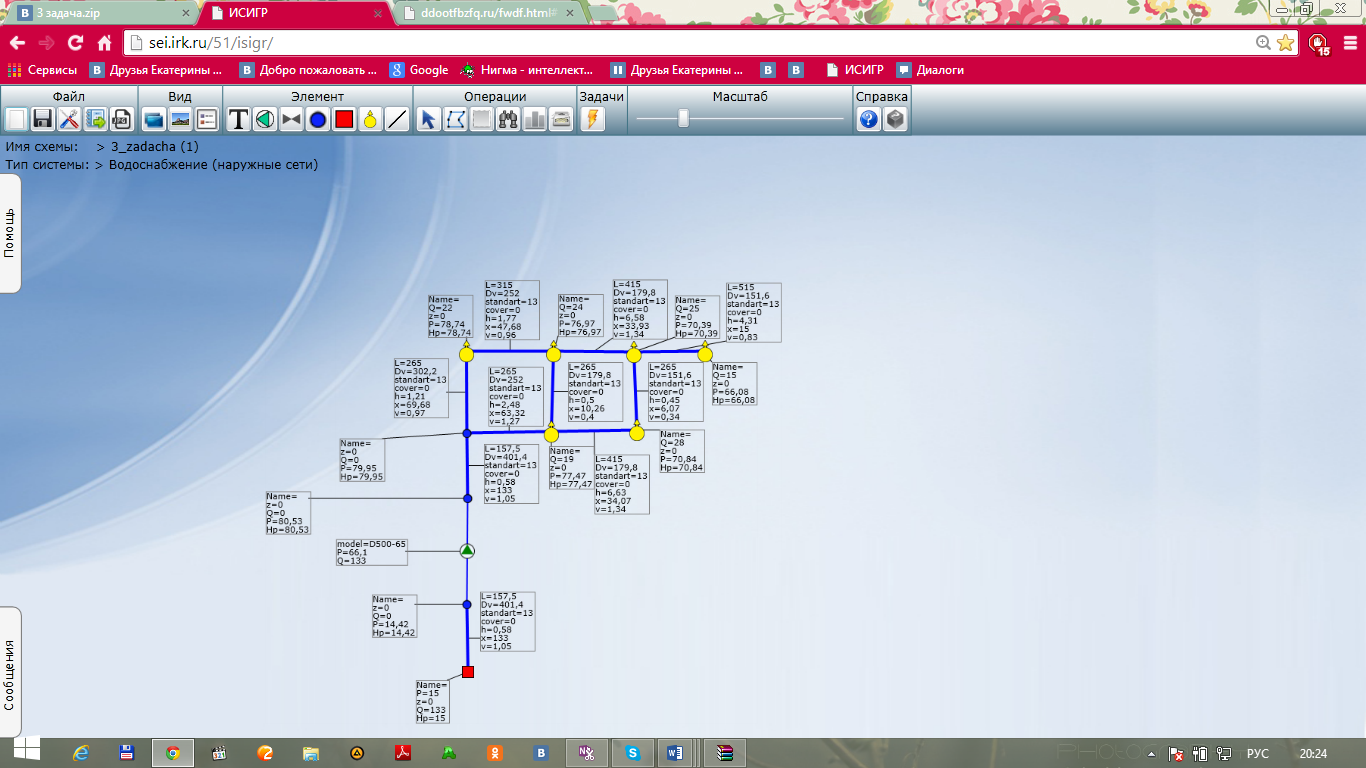
Рис. 6. Схема задачи, решённой в программе ИСИГР

4.Строим пьезометрическую линию трубопровода с 1 до 6 узла, воспользовавшись программой ИСИГР

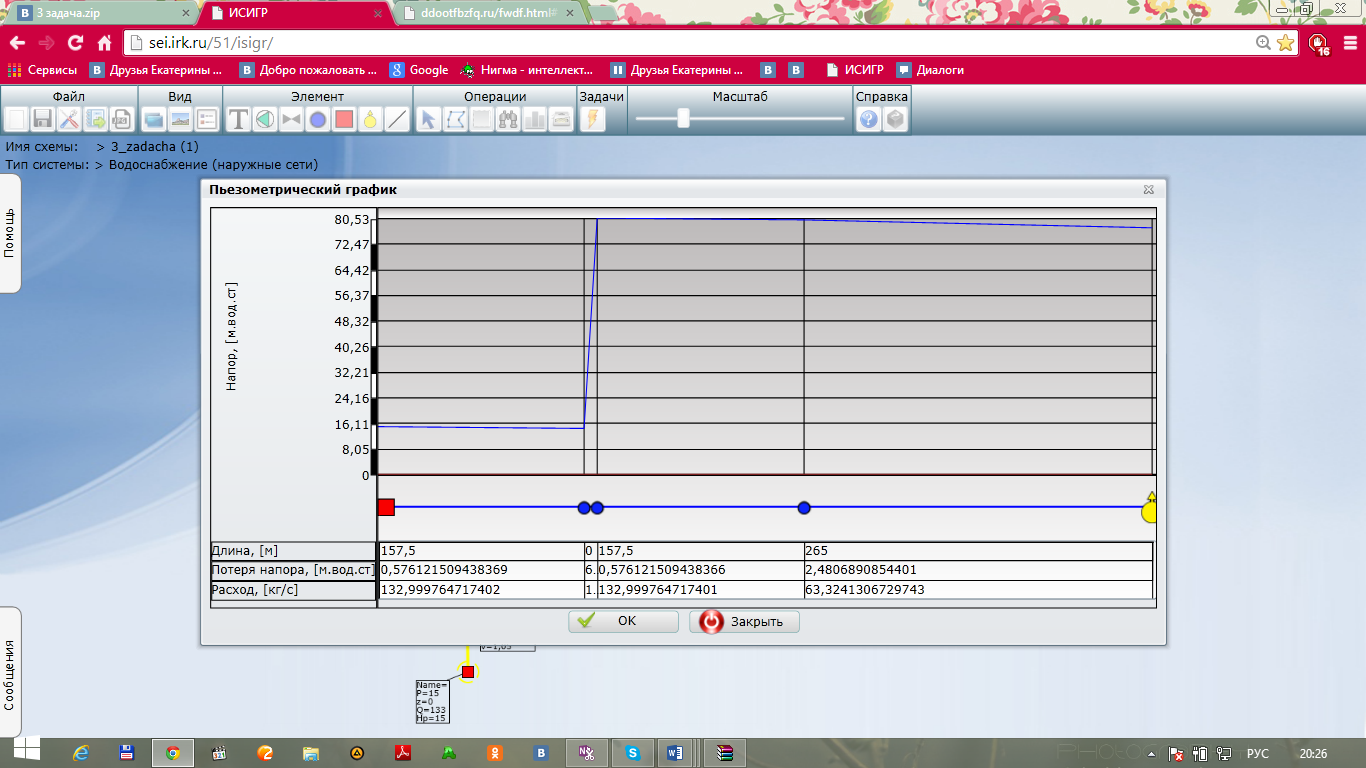
Рис. 7. Напорная характеристика трубопровода с 1 до 6 узла

5. Потери напора по кольцу. Находим алгебраическую сумму потерь напора в кольцах, которая должна быть равна нулю: . Сеть считается рассчитанной, если при данных расходах по ветвям кольцевой сети потери напора по одной ветви кольца равны потерям напора по другой его ветви.

В нашей сети мы можем выделить три кольца, по которым делаем расчеты.

  1. Рассчитаем потери напора по кольцу 2-3-4-8.

Поток в точке 2 разделяется на два направления, а в точке 4 эти потоки сходятся. Отсюда следует, что сумма потерь напора от точки 2 до точки 4 по правой ветви должна быть равна сумме потерь напора между этими точками по левой ветви:

Нкольцо1 = (Н2–Н3) + (Н3–Н4) – (Н8–Н4) – (Н2–Н8) = 0.

Т.е. при рассмотрении движения воды относительно кольца мы принимаем положительными потери напора, возникающие при движении воды по ходу часовой стрелки, а отрицательными – против часовой стрелки.

  1. Рассчитаем потери напора по кольцу 4-5-7-8.

Поток в точке 8 разделяется на два направления, а в точке 5 эти потоки сходятся. Отсюда следует, что сумма потерь напора от точки 8 до точки 5 по правой ветви должна быть равна сумме потерь напора между этими точками по левой ветви:

Нкольцо2 = (Н8–Н4) + (Н4–Н5) – (Н7–Н5) – (Н8–Н7) = 0.

  1. Рассчитаем потери напора по кольцу 2-3-4-5-7-8.

Поток в точке 2 разделяется на два направления, а в точке 5 эти потоки сходятся. Отсюда следует, что сумма потерь напора от точки 2 до точки 5 по правой ветви должна быть равна сумме потерь напора между этими точками по левой ветви:

Нкольцо3 = (Н2–Н3) + (Н3–Н4) + (Н4–Н5) – (Н7–Н5) – (Н8–Н7) – (Н2–Н8) = 0.

Сумма потерь напора по каждому кольцу равна нулю.

  1. Определение давления в узлах кольцевой цепи

Избыточное давление определяется из определения полного напора:

,

где Hn – напор в соответствующем узле, zn геометрическая высота соответствующего узла, удельный вес (= 9,81 103, Н/м3).

= 9,81 103 (15,00 0) = 117720 Па;

= 9,81 103 (84.93 0) = 778914 Па;

= 9,81 103 (83.63 0) = 759784 Па;

= 9,81 103 (81.71 0) = 733101 Па;

= 9,81 103 (77.72 0) = 618206 Па;

= 9,81 103 (73.18 0) = 624995Па;

= 9,81 103 (78.13 0) = 687288 Па;

= 9,81 103 (81.97 0) = 737225 Па.

  1. Гидравлический уклон

Гидравлический уклон выражает потерю полной удельной энергии (гидродинамического напора), приходящуюся на единицу длины потока.