Множества. Массивы. Генерация подмножеств

ЛЕКЦИЯ 3.

Множества.

Существуют разные подходы к представлению множества:

1.Хранится каждый элемент, присутствующий в множестве. Это может быть смежное представление (например, массив элементов) или связанное размещение элементов в памяти (в дальнейшем рассмотрим организацию связанных списков).

2.Определяются все потенциально возможные злементы множества А: А={а0, а1, . . . . .аn-2, аn-1}. Всего n элементов. Затем для каждого подмножества X из А определяется для каждого элемента, принадлежит ли он этому подмножеству. Для этого каждому множеству сопоставляется бинарная (т.е. состоящая из 0 и 1) последовательность b0,b1,…bn-1, определяемая так:

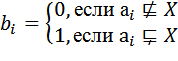i=0,1,2, . . .n-1

Наилучший метод представления множеств существенно зависит от операций, которые планируется выполнять над множествами. Это типичные операции: выяснить, имеется ли конкретный элемент в данном множестве, добавить в множество новые элементы, удалить из множества элементы, выполнить обычные теоретико-множественные операции, например объединение или пересечение двух множеств.

Вектор b= {b0,b1,…bn-1} называется характеристическим вектором из n элементов. Это представление удобнее тем, что основные операции над множествами можно выполнять как побитовые операции над двоичными векторами. Однако для больших n использование таких векторов практически невыполнимо.

Рассмотрим задачу формирования различных подмножеств заданного массивом множества А={а0, а1, . . . . .аn-2, аn-1}. Заводят некоторую строку битов и устанавливают взаимно-однозначное соответствие между битами строки b и числами из А: bi <=> а [i].

b: а[n-1] а[n-2] . . . . а[2] а[1] а[0]

.......

n-1 n-2 2 1 0

Описать переменную b можно, например, так

unsigned int b; // если n<32

или

unsigned char b [NN] ; // если n<NN*8

Рассмотрим такое описание b:

unsigned int b;

Пусть в переменной b записана информация о некотором подмножестве СА:

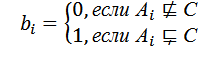i=0,1,2, . . .n-1

n-1 n-2 . . . . . . . .. . . . . 3 2 1 0

.. .

. . . . .

Содержимое b есть некоторое целое число

r=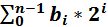, где 0 r 2n-1,

т.е. для множества А={а[0], а[1], а[2], . . . . а[n-2],а[n-1]}

возможны 2n различных подмножеств.

Как, имея b, получить подмножество элементов из А?

Просматриваем все биты от 0-го до (n-1)-го из b, выводим элементы а[i], соответствующие единичным битам.

Void f1 (int A[], int n, unsigned int b)

{//вывод элементов подмноджества, заданного строкой b

cout<<’\n’;

.. .

. . . . .

int m=1;

n-1 n-2 . . . . . . . .. . . . . 3 2 1 0

for (int i=0; i<n; i++)

{if (b&m) cout<<а[i]<<” ”;

m<<=1;

}

cout<<’\n’;

}

Void f2 (int а[ ], int n, unsigned char b [ ] )

{//вывод элементов подмножества, заданного массивом b.

int j=0, m=0;

cout<<’\n’;

for (int i=0; i<n; i++)

if (b[j] & 1<<m)

{ cout<<а[i]<<” ”;

m++;

if (m==8){m=0; j++;}

}

cout << ’\n’;

}

Как сформировать все подмножества из А?

Так как представление в строке b есть всегда некоторое целое число, то для формирования всех подмножеств можно формировать числа от нуля до 2n-1(начать с нуля и добавлять по 1 на каждом шаге), их двоичные представления дадут все подмножества n-элементного множества.

unsigned int b=0, k=(1<<n)-1; //k=0000…..0111111111

while (b<k) // n

{b=b+1;

//обработка подмножества, заданного битовой строкой b

. . . . . . . . . .

}

В этом алгоритме последовательно получаемые подмножества могут сильно отличаться друг от друга: после (n-1)-элементного множества (которому соответствует число 01111…..1) идёт одноэлементное множество(отвечающее числу 1000……0). Это часто неудобно.

. . . .000 . . . .000001

. . . .000. . . . 000010

. . . .000. . . . 000011

. . . . . . . . . . . . . . . .

. . . .000. . . . 011111

. . . .000. . . .100000

. . . . 000 . . . .100001

. . . . 000. . . . 100010

. . . . . . . . . . . . . . . . . .

. . . . 000. . . 1001111

. . . . 000. . . 1010111

. . . . . . . . . . . . . . . . . .

. . . . 000. . . .1111100

. . . .000. . . 10000000

. . . .000. . . 10001111 и т.д.

, , , , , , , , , , , , , , , , , ,

. . . .00001111100000

. . . .00010000001111

Пример 1.

Рассмотрим алгоритм генерации k-элементных подмножеств множества из n элементов, т.е. последовательного формирования возрастающих по значению битовых строк с k единицами.

//Nelset.cpp k-элементные подмножества,

// маска - слово

#include <iostream>

#include <fstream>

#include <iomanip>

#include <math.h>

using namespace std;

//Дана совокупность не более n целых чисел

//и число k. Выбрать все подмножества из k

// простых чисел.

//Все подмножества (k –элементные) записать в файл.

const int L=32; // n=31 элемент +1 ( 0 – 30)+1

ifstream fin;

ofstream fout;

// прототипы функций

void print (ofstream &fout, int a[], int n, unsigned int b);

bool prost (int a);

int main ()

{int i;

unsigned int b,n,k, nn;

int a[L];

fin.open("danN_el.txt");

if (fin.fail()){cout<<"error open danN.txt\n"; return(1);}

fout.open("rezNK_el.txt",ios::app);

if (fout.fail()){cout<<"error open rezNK.txt\n";return(1);}

cout<<"k--> "; //кол-во эл-ов в подмножестве

cin>>k;

i=0;

fout<<"Данное множество: "<<endl;

while (fin>>a[i])

{fout<<setw(6)<<a[i];

i++;

if ((i%10)==0)fout<<endl;

}

fout<<endl;

fout<<k<<"- элементные подмножества простых чисел: "<<endl;

n=i; //cчитано n элементов: 0-ой, 1-й,... , (n-1)-ый

//выделение подмножеств, b – битовая строка (маска)

b=(1<<k)-1; //в маске k единиц 000...011...1 (1-ое подмножество)

nn=1<<n; //здесь единица n-го разряда

{print (fout, a, n, b); //обработка 1-го подмножества

//получение следующей маски из n единиц

unsigned int m;

m=1;

while ((b&m)==0) // пропуск крайних нулей

{ m=m<<1;}

int bb=0; //счетчик единиц

while ( (b&m)!=0) //пока не нуль, обработка единиц

{ bb++; //подсчёт единиц

b=b^m; //обнуление единиц

m=m<<1;

}

b=b|m; // первый 0 после единиц заменяем на 1

//установка bb-1 единиц в конец маски

b=b | ((1<<(bb-1))-1); //новая маска

}

while (b<nn);

fin.close(); fout.close();

return 0;

}

// запись в файл подмножеств из k простых элементов

void print (ofstream &fout, int a[ ], int n, unsigned int b)

{unsigned int m; int i, t;

int B[L];

bool p=true;

i=0; m=1; t=0;

for (i=0; i<n && p; i++)

{if (b&m) //не нуль

{B[t]=a[i]; t++;

if (!prost(a[i])){p=false;}

}

m<<=1;

}

if (p)

{for (i=0;i<t;i++)

fout<<setw(6)<<B[i];

fout<<endl;

}

// проверка числа на простоту

bool prost (int a)

{int d,q;

bool p;

a=abs(a);

p=(a==2) || (a%2!=0);

if (p)

{d=3; q=int( sqrt (double(a)));

while (d<=q && a%d !=0)

d=d+2; //d+=2;

p=d>q;

}

return p;

}

danN_el.txt

123 13 5 7 43 17

11 33 41

rezNK_el.txt

Данное множество:

13 5 7 43 17 29 11 33 41

- элементные подмножества простых чисел:

5 7 43 17

5 7 43 29

5 7 17 29

5 43 17 29

7 43 17 29

5 7 43 11

5 7 17 11

5 43 17 11

7 43 17 11

5 7 29 11

5 43 29 11

7 43 29 11

5 17 29 11

7 17 29 11

43 17 29 11

5 7 43 41

5 7 17 41

5 43 17 41

7 43 17 41

5 7 29 41

5 43 29 41

7 43 29 41

5 17 29 41

7 17 29 41

43 17 29 41

5 7 11 41

5 43 11 41

7 43 11 41

5 17 11 41

7 17 11 41

43 17 11 41

5 29 11 41

7 29 11 41

43 29 11 41

17 29 11 41

Данное множество:

13 5 7 43 17 29 11 33 41

- элементные подмножества простых чисел:

5 7 43 17 29 11 41

Замечание. Сформировать новую битовую строку из k единиц можно с помощью следующих операторов:

s=b & (– int(b));

r=s + b;

b=r | (((b^r)>>2) / s);

где b- предыдущая битовая строка c k единицами, s,r –переменные.

unsigned int x, s,r;

Пример 2. Решето Эратосфена.

Используя алгоритм “Решето атосфена” записать в файл все простые числа, не превышающие заданного N.

Решето представляет битовую строку для чисел от 0 до N. Сами числа не хранятся. Во все биты строки (кроме 0-го и 1-го,где -0) записываются 1. Выбирается самое маленькое число, из решета удаляются все кратные ему числа (их биты обнуляются), само число помещается в файл.Таким образом из решета удаляются все числа, не являющиеся простыми, остаются единичными только биты, соответствующие простым числам, а сами числа собираются в файле.

Для заданного числа n строится битовая строка s в виде массива из q элементов типа unsigned int (32 бита).

//Resh1.cpp

#include <iostream>

#include <fstream>

#include <iomanip>

using namespace std;

//Решето Эратосфена

const int n=1000; //N

const int q=(n>>5)+1; // это равно (n/32+1), но быстрее!

ofstream fout;

unsigned int u(unsigned int t)

//элемент из s c 1 в бите для t

{return 1<<(t&31);} //=(1<<(t%32);

unsigned int w(unsigned int t)

//номер элемента s с битом для t

{return t>>5;} // = t/32;

int main ()

{unsigned int s[q], z;

unsigned int a, c, i, j, t;

for (i=0;i<q-1;i++)

s[i]=0xFFFFFFFF;

z=1<<(n&31); // z=1<<(n%32);

s[q-1]=z-1;

s[0]=0xFFFFFFFC; // обнуление 0-го и 1-го битов

fout.open("Rezresh.txt");

if (fout.fail()){cout<<"error open rezresh.txt\n" ; return(1);}

a=1; c=0;

while (a<n)

{a++; // выбрано число а

i=u(a); j=w(a);

if ((s[j]&i)!=0) // а соответствует i-ый бит

{fout<<setw(5)<<a; // запись а в файл

c++; if(c%10==0)fout<<endl;

t=a;

while (t<=n-a)

{t+=a;

i=u(t); j=w(t);

s[j]=s[j]&(s[j]^i); }

}

} fout.close();

return 0;

}

Rezresh.txt

2 3 5 7 11 13 17 19 23 29

31 37 41 43 47 53 59 61 67 71

79 83 89 97 101 103 107 109 113

131 137 139 149 151 157 163 167 173

181 191 193 197 199 211 223 227 229

239 241 251 257 263 269 271 277 281

293 307 311 313 317 331 337 347 349

359 367 373 379 383 389 397 401 409

421 431 433 439 443 449 457 461 463

479 487 491 499 503 509 521 523 541

557 563 569 571 577 587 593 599 601

613 617 619 631 641 643 647 653 659

673 677 683 691 701 709 719 727 733

743 751 757 761 769 773 787 797 809

821 823 827 829 839 853 857 859 863

881 883 887 907 911 919 929 937 941

953 967 971 977 983 991 997

Задачи

Задание на тему «Массивы. Генерация подмножеств.»

В массиве из N целых чисел найти все К–элементные подмножества, состоящие из простых чисел.
В массиве из N целых чисел найти все К–элементные подмножества, состоящие из чисел, сумма цифр которых равна заданному числу S.
В массиве из N целых чисел найти все К–элементные подмножества, состоящие из простых чисел.
В массиве из N целых чисел найти все К–элементные подмножества, состоящие из чисел, имеющих одинаковые множества простых делителей.
Для заданного массива из N чисел построить все подмножества, определить суммы элементов каждого подмножества.
Для заданного массива из N чисел построить все подмножества, определить НОД элементов каждого подмножества.
Для заданного массива из N чисел построить все подмножества, определить подмножества с заданной суммой элементов.
Для заданного массива из N чисел построить все подмножества, определить подмножества, состоящие из чисел, кратных 3.
Дано N произвольных однозначных чисел и произвольное число M. Расставить между каждой парой чисел, записанных в данном порядке, знаки ‘+’и ‘-‘, так чтобы значением получившегося выражения было число M. Сообщить, если требуемая расстановка невозможна.{Cчастливый билет}
В массиве из N целых чисел найти все К–элементные подмножества, состоящие из чисел, имеющих одинаковые множества цифр в записи чисел.
Для заданного массива из N чисел построить все подмножества, определить подмножества, сумма элементов которых есть простое число.
В массиве из N целых чисел найти все К–элементные подмножества, состоящие из чисел, в записи которых есть одинаковые цифры.
Для заданного массива из N чисел построить все подмножества, определить подмножества, сумма элементов которых не содержит одинаковых цифр.

14. Из файла вводится пара А и B целых положит.

чисел, создаётся множество используемых цифр

для каждого числа. Определить общие цифры,

все цифры, используемые в A и B, цифры А, которых

нет в B,цифры B, которых нет в A.

Множества. Массивы. Генерация подмножеств