Основы теории погрешностей
1.Основы теории погрешностей
2.Численные методы решения нелинейных уравнений с одним неизвестным
3.Численные методы решения систем линейных уравнений
4.Интерполирование функций
5.Численное дифференцирование
6.Численное интегрирование
7.Численное решение обыкновенных дифференциальных уравнений
1.Основы теории погрешностей
Основные вопросы, рассматриваемые на лекции:
- Неустранимая погрешность.
- Ошибки арифметических действий.
- Основные задачи теории приближённых вычислений.
При решении конкретной задачи источником погрешностей окончательного результата могут быть неточность начальных данных, округления в процессе счета, а также приближённый метод решения. В соответствии с этим будем разделять погрешности на:
- погрешности из-за начальной информации (неустранимая погрешность);
- погрешности вычислений;
- погрешности метода.
- Неустранимая погрешность
Неустранимая погрешность - это погрешность, связанная с ошибками в исходной информации.
Причинами этих ошибок может быть, например, неточность измерений, невозможность представить данную величину конечной дробью.
Различают абсолютную и относительную погрешности. Пусть x - истинное значение величины, 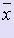 - её приближенное значение, принимаемое в расчетах.
- её приближенное значение, принимаемое в расчетах.
Величина 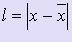 называется абсолютной погрешностью числа
называется абсолютной погрешностью числа 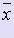 .
.
Точная верхняя грань множества значений 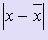 , которое определяется найденным ,
, которое определяется найденным , 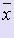 и имеющейся информацией относительно x, называется предельной абсолютной погрешностью величины
и имеющейся информацией относительно x, называется предельной абсолютной погрешностью величины 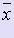 .
.
Относительной погрешностью величины 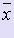 называется отношение её абсолютной погрешности к величине
называется отношение её абсолютной погрешности к величине 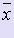 :
: 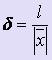 .
.
Аналогично можно определить предельную относительную погрешность x числа 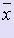 :
: 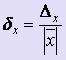
Относительные погрешности чисел принято выражать в процентах, поэтому: 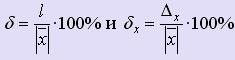
При записи приближённых чисел желательно указывать их точность, сообщая те границы, в которых это число может находиться: 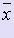 ± x.
± x.
Значащая цифра числа считается верной в узком смысле, если абсолютная погрешность (предельная) не превосходит половины единицы того разряда, в котором стоит данная цифра.
В противном случае цифра считается сомнительной.
Значащая цифра числа считается верной в широком смысле, если абсолютная погрешность (предельная) не превосходит единицы того разряда, в котором стоит данная цифра.
При записи чисел руководствуются следующим правилом: все цифры числа должны быть верными.
Поэтому округление чисел, записанных в десятичной системе, производится по правилу первой отбрасываемой цифры:
- Если первая из отбрасываемых цифр меньше 5, то оставляемые десятичные знаки сохраняются без изменения;
- Если первая из отбрасываемых цифр больше 5, то последняя оставляемая цифра увеличивается на 1;
- Если первая из отбрасываемых цифр равна 5, а за ней идут не нули, то последняя оставляемая цифра увеличивается на 1;
- Если первая из отбрасываемых цифр равна 5, и все цифры, идущие за ней - нули, то последняя оставляемая цифра увеличивается на 1, если она нечетная, и остаётся без изменения, если - четная.
· Ошибки арифметических действий
Если f (x, y) = x + y, то x + y = x + y.
Если f (x, y) = x - y, то x - y = x + y.
Если f (x, y) = x · y, то xy = 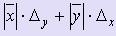 .
.
Если f (x, y) =  , то
, то 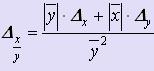 .
.
Из формул для абсолютных погрешностей суммы, разности, произведения и частного выводятся формулы для соответствующих относительных погрешностей. 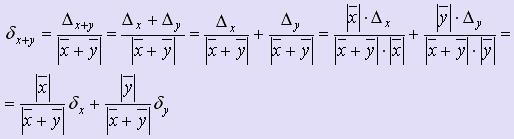
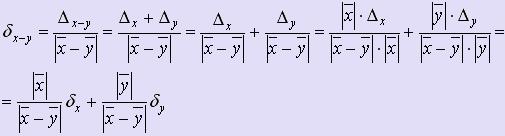
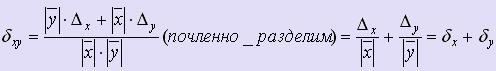
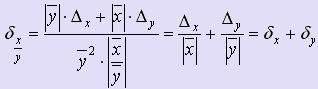
Если f (x) = x n , то xn = 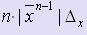 .
.
Если 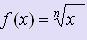 , то
, то 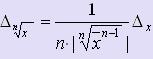 .
.
xn = n · x. 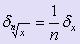 .
.
· Основные задачи теории приближённых вычислений
Прямая задача: указаны действия, которые нужно выполнить и заданы предльные погрешности. Требуется оценить погрешность результата.
Обратная задача: указаны действия, которые нужно выполнить, задана погрешность, которая допустима для результата. Требуется установить, какими должны быть погрешности исходных данных, чтобы полученный результат имел заданную точность.
2.Численные методы решения нелинейных уравнений с одним неизвестным
Основные вопросы, рассматриваемые на лекции:
- Метод половинного деления (метод дихотомии).
- Метод хорд.
- Метод касательных (метод Ньютона).
- Комбинированный метод хорд и касательных.
- Метод простой итерации.
Для большинства уравнений вида f (x) = 0 (1), где f (x) - нелинейная функция одной переменной, не существует аналитических выражений (формул) для вычисления их корней. Поэтому приходится применять различные численные методы для отыскания корней уравнения f (x) = 0.
Задача нахождения корней уравнения (1) обычно состоит из двух этапов:
- отделение корня, т.е. установление промежутка, в котором находится корень, причём единственный.
- уточнение корня, т.е. вычисление приближённого значения корня с заданной точностью.
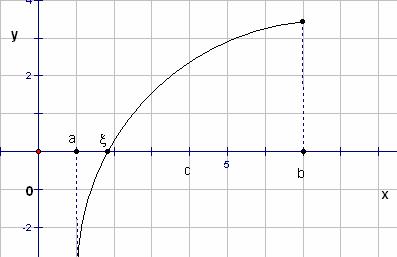
Для существования корня уравнения (1) на замкнутом промежутке достаточно, чтобы выполнялись условия теоремы Больцано-Коши.
Теорема Больцано-Коши: если функция f(x) определена и непрерывна на замкнутом промежутке [a; b] и на концах его принимает значение разных знаков, f(a) · f(b) < 0, то между a и b найдётся по крайней мере один корень функции f(x), т.е. найдётся точка с, a < c < b, для f (с) = 0.
Для единственности корня функции на замкнутом промежутке, если он существует, достаточно, чтобы функция f(x) была монотонной, т.е. f ' (x) сохраняет свой знак на промежутке.
Отделение корня можно произвести графически или аналитически. Таким образом, на 1 этапе нужно найти такой промежуток [a; b], чтобы f(a) · f(b) < 0 и
f ' (x) сохраняла свой знак на [a; b].
Уточнение корня можно произвести одним из следующих методов.
- Метод половинного деления (метод дихотомии).
Пусть на отрезке [a; b] имеется только один корень уравнения (1). Найдем середину отрезка 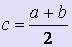 . Если f (с) = 0, то корень найден. В противном случае из двух отрезков [a; c] и [c; b] выбираем тот, в котором содержится корень.
. Если f (с) = 0, то корень найден. В противном случае из двух отрезков [a; c] и [c; b] выбираем тот, в котором содержится корень.
|
|
С выбранным промежутком делаем то же, что с исходным и т.д. |
Как только |bn - an| < E, где Е - заданная точность, то в качестве приближённого значения корня можно взять середину этого отрезка: 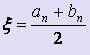 .
.
· Метод хорд.
Пусть на отрезке [a; b] имеется единственный корень, т.е. f(a) · f(b) < 0;
f ' (x) сохраняет свой знак на [a; b];
f '' (x) сохраняет свой знак на [a; b].
Заменим дугу кривой y = f (x) на отрезке [a; b] хордой, проходящей через точки (a; f (a)) и(b; f (b)). Абсцисса точки пересечения хорды с осью Ох есть приближение к корню уравнения (1). Обозначим её через x1.
|
Корень уравнения (1) будет находиться между x1и одним из концов отрезка [a; b] в зависимости от свойств функции. |
|
Если f ' (x) · f '' (x) > 0 для любого x [a; b], то для вычисления х1, х2, ... , хi, ... используются следующие формулы:
[a; b], то для вычисления х1, х2, ... , хi, ... используются следующие формулы: 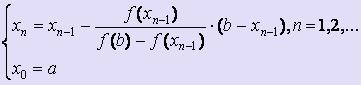
Если f ' (x) · f '' (x) < 0 для любого x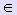 [a; b], то для вычисления х1, х2, ... , хi, ... используются следующие формулы:
[a; b], то для вычисления х1, х2, ... , хi, ... используются следующие формулы: 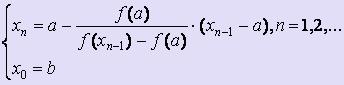
или 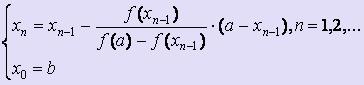
Заканчиваем процесс уточнения корня, когда расстояние между очередными приближениями хnи xn-1 станет меньше заданной погрешности E: |хn - xn-1| < E или когда значение функции |f (xn)| < E.
· Метод касательных (метод Ньютона)
Пусть на отрезке [a; b]:
- Уравнение f (x) = 0 имеет единственный корень, т.е. f (a) · f (b) < 0;
- f ' (х) и f '' (х) сохраняют свои знаки.
|
Заменим дугу кривой y = f (x) на [a; b] касательной, проведённой к графику функции y = f (x) в одной из точек (a; f (a)) и (b; f (b)). Эту точку следует выбирать так, чтобы точка пересечения касательной с осью Ox не вышла за пределы отрезка [a; b]. |
|
В результате получим последовательность приближённых значений {xn}, монотонно сходящуюся к точному значению корня с.
При этом корень уравнения f (x) = 0 находится между xi и одним из концов промежутка [a; b] в зависимости от свойств функции y = f (x).
Если f ' (x) · f '' (x) > 0 для любого x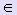 [a; b], то для вычисления х1, х2, ... , хi, ... используются следующие формулы:
[a; b], то для вычисления х1, х2, ... , хi, ... используются следующие формулы: 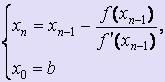
Если f ' (x) · f '' (x) < 0 для любого x [a; b], то для вычисления х1, х2, ... , хi, ... используются следующие формулы:
[a; b], то для вычисления х1, х2, ... , хi, ... используются следующие формулы: 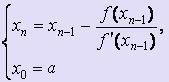
Процесс уточнения корня заканчивается, когда выполняется условие |хn - xn-1| < E, где E - допустимая погрешность вычисления или когда |f (xn)| < E.
· Комбинированный метод хорд и касательных
Соединяя метод хорд с методом касательных, получаем метод, на каждом шаге которого находим приближённые значения корня с по недостатку и по избытку: xn < c < 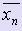 , причем каждое значение xn и
, причем каждое значение xn и 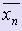 стремится к с.
стремится к с.
Если f ' (x) · f '' (x) < 0 для любого x [a; b], то для вычисления значений по недостатку и по избытку используются следующие формулы:
[a; b], то для вычисления значений по недостатку и по избытку используются следующие формулы: 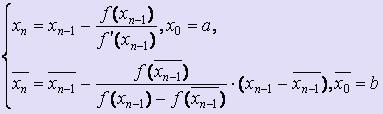
Если f ' (x) · f '' (x) > 0 для любого x [a; b], то для вычисления значений по недостатку и по избытку используются следующие формулы:
[a; b], то для вычисления значений по недостатку и по избытку используются следующие формулы: 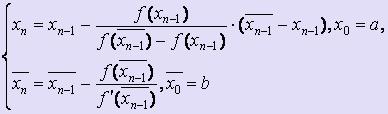
Процесс уточнения корня заканчивается, когда выполняется условие 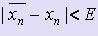 , где E - допустимая погрешность вычисления. При этом в качестве приближённого значения корня принимается середина промежутка [xn,
, где E - допустимая погрешность вычисления. При этом в качестве приближённого значения корня принимается середина промежутка [xn, 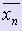 ]:
]: 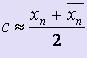 .
.
· Метод простой итерации
По функции f (x) строят функцию (x) такую, что уравнение x = (x) (2) эквивалентно уравнению f (x) = 0 (1). При этом корень c уравнения (1) является корнем уравнения (2).
Затем строят последовательность {xk} по формуле (3) xk = (xk-1), k = 1, 2, : начиная с некоторого приближения x0.
Сходимость последовательности {xk} обеспечивается выбором функции (x) и выбором начального значения x0. Выбирая различными способами функцию , будем получать различные итерационные методы.
Опишем один из способов получения уравнения (2): 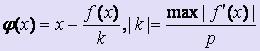 , где р - произвольное число. При этом число k имеет тот же знак, что и производная функции f на отрезке [a; b] и | ' (x)|
, где р - произвольное число. При этом число k имеет тот же знак, что и производная функции f на отрезке [a; b] и | ' (x)|  q < 1.
q < 1.
3. Численные методы решения систем линейных уравнений
Основные вопросы, рассматриваемые на лекции:
- Метод простой итерации.
- Метод Зейделя.
- Метод исключения Гаусса.
- Метод простой итерации
Пусть дана система линейных уравнений 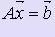 (1),
(1),
где 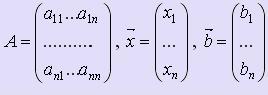
Предполагая, что aii 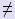 0 (i = 1, :,n) разрешим её относительно x1, x2,:, xn:
0 (i = 1, :,n) разрешим её относительно x1, x2,:, xn: 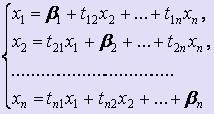 (2),
(2),
где i = bi / aii, tij = -aij / aii, при i 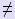 j, tij = 0 при i = j.
j, tij = 0 при i = j.
Систему (2) можно записать в виде 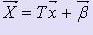 ( 2' ).
( 2' ).
Теорема. Если матрица Т удовлетворяет одному из условий:
с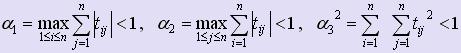 ,
,
то система уравнений (2) имеет единственное решение, которое может быть получено как предел последовательности, построенной по формулам 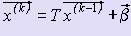 , k = 1, 2, :, начиная с произвольного x(0) = ( x1(0), x2(0), :, xn(0) ).
, k = 1, 2, :, начиная с произвольного x(0) = ( x1(0), x2(0), :, xn(0) ).
Процесс уточнения корня заканчивается, когда выполняется условие 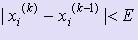 ,i = 1, :, n, где E - допустимая погрешность вычисления. При этом x(k) = ( x1(k), x2(k), :, xn(k) ) - решение системы (1).
,i = 1, :, n, где E - допустимая погрешность вычисления. При этом x(k) = ( x1(k), x2(k), :, xn(k) ) - решение системы (1).
· Метод Зейделя
Пусть дана система линейных уравнений (1). Сведём систему (1) к системе (2). Зададим некоторые начальные приближения неизвестных x1(0) = 1, x2(0) = 2, :, xn(0) = n.
Подставим их в правые части системы и вычислим новые приближения, при этом будем использовать приближения к решениям, найденные при выполнении текущей итерации, т.е.
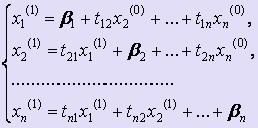
Аналогичным образом проводим вторую итерацию и т.д.
Процесс уточнения корня заканчивается, когда выполняется условие 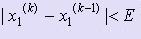 ,k = 1, :, n, где E - допустимая погрешность вычисления.
,k = 1, :, n, где E - допустимая погрешность вычисления.
Замечание: при решении системы линейных уравнений методом Зейделя итерационный процесс будет сходящимся лишь в случае, если для каждого уравнения выполняется условие 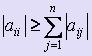 , i = 1, :, n, однако в сумму не входит слагаемое aij c равными i и j. При этом хотя бы одно неравенство должно выполняться строго. Это условие является достаточным условием сходимости метода Зейделя.
, i = 1, :, n, однако в сумму не входит слагаемое aij c равными i и j. При этом хотя бы одно неравенство должно выполняться строго. Это условие является достаточным условием сходимости метода Зейделя.
· Метод исключения Гаусса
(рассматривается решение систем уравнений данным методом и вычислений обратной матрицы с помощью метода Гаусса).
Метод исключения Гаусса относится к прямым методам решения систем линейных уравнений.
Идея этого метода заключается в том, чтобы исходную систему линейных уравнений 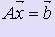 (1) с произвольной матрицей А свести некоторыми эквивалентными преобразованиями к системе вида
(1) с произвольной матрицей А свести некоторыми эквивалентными преобразованиями к системе вида 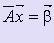 (2), где - треугольная матрица.
(2), где - треугольная матрица.
Затем из последнего уравнения системы (2) находится xn, из предыдущего - xn-1 и т.д.
Вычисление обратной матрицы с помощью метода Гаусса:
Пусть xi - i-ый столбец искомой обратной матрицы, ei - i-ый столбец единичной матрицы.
Т.к. A · A-1 = E, то 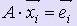 , при i = 1, 2, :, n. Задача нахождения обратной матрицы сводится к задаче решения n систем n линейных уравнений с одной и той же матрицей A, но с разными правыми частями.
, при i = 1, 2, :, n. Задача нахождения обратной матрицы сводится к задаче решения n систем n линейных уравнений с одной и той же матрицей A, но с разными правыми частями.
4. Интерполирование функций
Основные вопросы, рассматриваемые на лекции:
- Основные понятия интерполяции, задача, приводящая к приближению функции, геометрический смысл интерполирования
- Интерполяционный многочлен Лагранжа
- Схема Эйткена
- Оценка погрешности интерполяционной формулы Лагранжа
- Конечные разности
- Интерполяционные формулы Ньютона
- Первая интерполяционная формула Ньютона
- Вторая интерполяционная формула Ньютона
- Оценка погрешностей первой и второй интерполяционных формул Ньютона
- Обратное интерполирование
- Интерполяция сплайнами
- Основные понятия интерполяции, задача, приводящая к приближению функции
Интерполяция (от лат. interpolation - изменение, переделка) - в математике и статистике, отыскание промежуточных значений величины по некоторым известным её значениям [Сов. энциклопедический словарь].
Задача, приводящая к приближению функции, заключается в следующем. Известны значения функции f (x) в точках x1, x2, :, xn; требуется восстановить её значения при других х.
Интерполяционный полином, передающий свойства функции f (x) будем строить в виде:
Pn(x) = c11(x) + c22(x) + : + cnn(x), где 1(x), 2(x), :, n(x) - класс линейно-независимых функций, при этом Pn(xi) = f (xi), i = 1, 2, :, n.
Таким образом, Pn(x)  f(x).
f(x).
Точки x1, x2, :, xn называются узлами интерполяции.
· Интерполяционный многочлен Лагранжа
Пусть известны значения функции f (x) в (n+1) точке x0, x1, :, xn. Тогда многочлен Лагранжа, передающий свойства функции f (x), можно записать так: 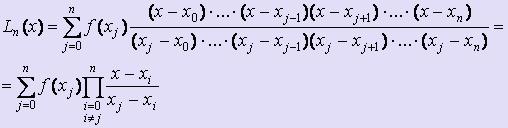
· Схема Эйткена
Схема Эйткена предлагает более удобную форму нахождения полинома Лагранжа.
Основная идея данного метода заключается в следующем.
На первом этапе вычисляются многочлены L0,1(x), L1,2(x), :, Ln-1,n(x), построенные на каждой паре соседних узлов 0,1; 1,2; :; n-1,n соответственно.
При этом 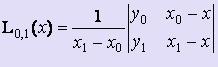 ,
, 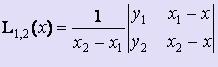 , :,
, :,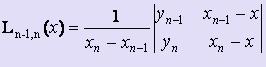 .
.
Таким образом, многочлены, построенные на паре соседних узлов, вычисляются по формулам: 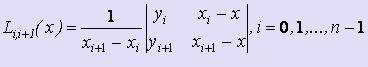 .
.
Затем на основе этих многочленов вычисляются многочлены, построенные на тройках соседних узлов: 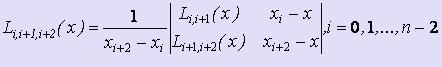 .
.
И т.д. пока не получится один многочлен, построенный на всех узлах интерполяции: 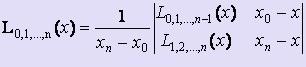 .
.
Полученный многочлен L0, 1, ..., n(x)  Ln(x).
Ln(x).
· Оценка погрешности интерполяционной формулы Лагранжа
Имеем yj = f ( xj ), Ln(x). Многочлен Ln(x) построен так, что Ln( xj ) = f ( xj ).
Вычисляя погрешность Rn(x) таким образом: Rn(x) = f (x) - Ln(x), можно получить следующую формулу для оценки погрешности интерполяционной формулы Лагранжа: 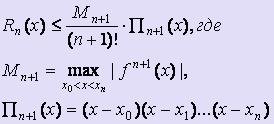 .
.
Такая оценка возможна только в том случае, когда известно аналитическое выражение для f. Если же f задана таблично, то производные заменяются конечными разностями.
· Интерполяционные формулы Ньютона
- Первая интерполяционная формула Ньютона
Пусть yi = f ( xi ), xi = x0 + ih, i = 1, 2, :, n.
Нужно построить Pn(x), удовлетворяющий двум условиям:
- Степень полинома не должна превышать n.
- Pn( xi ) = yi.
Формула Pn(x) для первой интерполяционной формулы Ньютона имеет вид: 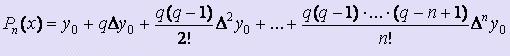 ,
,
где q = ( x - x0 ) / h.
Первая интерполяционная формула Ньютона применяется тогда, когда x находится вначале таблицы. Тогда в качестве x0 следует брать ближайшее слева к заданному x табличное значение.
- Вторая интерполяционная формула Ньютона
Когда значение аргумента находится ближе к концу отрезка интерполяции, применять первую интерполяционную формулу становится невыгодно.
Для этого применяется вторая интерполяционная формула Ньютона: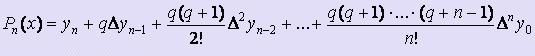 ,
,
где q = ( x - xn ) / h.
Здесь в качестве xn следует брать ближайшее справа к заданному x табличное значение.
· Оценка погрешностей первой и второй интерполяционных формул Ньютона
Используя подстановки q = ( x - x0 ) / h и q = ( x - xn ) / h и заменяя соответствующим образом выражение для Пn+1(x) в формуле оценки погрешности интерполяционной формулы Лагранжа, получим формулы для оценки погрешности интерполирования по первой и второй интерполяционной формуле Ньютона соответственно: 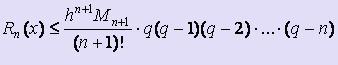 ,
, 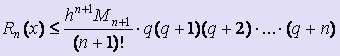 .
.
· Обратное интерполирование
Задача обратного интерполирования заключается в следующем. Если значения {yi} в таблице упорядочены по возрастанию или убыванию, то функция y = f (x) монотонна на [ x0 , xn ], и эту же таблицу можно интерпретировать как задание дискретного образа функции x = (y), обратной по отношению к функции y = f(x). Для этой обратной функции также может быть поставлена задача интерполирования: найти значение x* по заданному значению y*.
Пусть {xi} равноотстоящие узлы, расположенные на расстоянии h друг от друга и построен один из полиномов Ньютона (для определённости - первый): 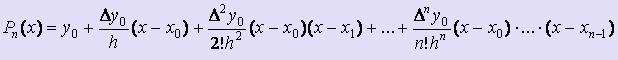 .
.
При решении задачи обратного интерполирования с помощью этого полинома в его левой части возникает известное значение y*, а сама формула становится алгебраическим уравнением относительно х. Если числа {yi} упорядочены по возрастанию или убыванию, то это уравнение имеет единственное решение на [ x0 , xn ].
Его решение следует искать любым из изученных ранее методов для решения нелинейных уравнений.
В рассматриваемом нами случае наиболее естественным способом для решения уравнения является метод простой итерации.
Подставим y = y* в вышепредставленную формулу и преобразуем получившееся равенство к виду: 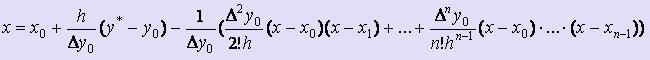 .
.
Это уравнение имеет структуру x = (x), т.е. по виду пригодно для применения метода простой итерации.
В качестве начального приближения можно взять значение x(0) = xi, ближайшее к искомому х*. Имея начальное приближение x(0), строим итерационный процесс для решения полученного уравнения пока не будет достигнута заданная точность: 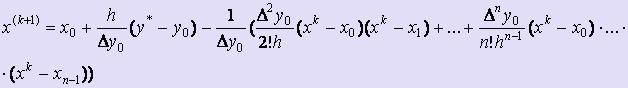
· Интерполяция сплайнами
При большом количестве узлов интерполяции сильно возрастает степень интерполяционных многочленов, что делает их неудобными для вычислений.
В этом случае удобно пользоваться особым видом кусочно-полиномиальной интерполяции - интерполяции сплайнами.
Суть этого подхода заключается в следующем.
Определение. Пусть отрезок [a, b] разбит точками на n частичных отрезков [xi , xi+1],i = 0, 1, :, n-1. Сплайном порядка m называется функция Sm (x), обладающая следующими свойствами:
1) Функция Sm (x) непрерывна на отрезке [a, b] вместе со своими производными до некоторого порядка р.
2) На каждом отрезке [xi , xi+1] функция совпадает с некоторым алгебраическим многочленомPm,i (x) степени m.
Разность m - p между степенью сплайна и наивысшим порядком непрерывной на отрезке [a, b] производной называют дефектом сплайна.
Будем рассматривать сплайны, дефект которых равен 1.
Наиболее широкое распространение получили кубические сплайны S3 (x).
Итак, для осуществления интерполяции необходимо построить такой сплайн, что S(xi ) = yi, i = 0, 1, :, n.
Согласно определению кубический сплайн можно представить в виде: 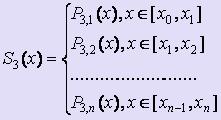 ,
,
где каждый из P3, i (x) - многочлен третьей степени: 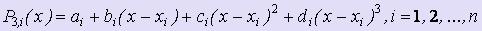 .
.
При этом коэффициенты ai = yi.
Можно показать, что коэффициенты сi вычисляются по формулам: 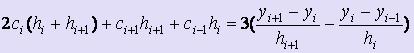 .
.
Для вычисления коэффициентов di используются формулы: 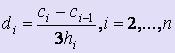 .
.
Для вычисления коэффициентов bi - формулы: 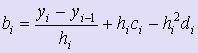 .
.
5. Численное дифференцирование
Основные вопросы, рассматриваемые на лекции:
- Постановка задачи численного дифференцирования
- Численное дифференцирование на основе интерполяционных формул Ньютона
- Оценка погрешности дифференцирования с помощью многочлена Ньютона
- Численное дифференцирование на основе интерполяционной формулы Лагранжа
- Оценка погрешности численного дифференцирования с помощью многочлена Лагранжа
- Постановка задачи численного дифференцирования
Функция y = f(x) задана таблицей:
|
x |
x0 |
x1 |
... |
xn |
|
y |
y0 |
y1 |
... |
yn |
на отрезке [a; b] в узлах a = x0 < x1 < x2 < : <xn =b</x. Требуется найти приближенное значение производной этой функции в некоторой точке х* 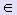 [a; b]. При этом х* может быть как узловой точкой, так и расположенной между узлами.
[a; b]. При этом х* может быть как узловой точкой, так и расположенной между узлами.
- Численное дифференцирование на основе интерполяционных формул Ньютона
Считая узлы таблицы равноотстоящими, построим интерполяционный полином Ньютона. Затем продифференцируем его, полагая, что f '(x)  '(x) на [a; b]:
'(x) на [a; b]:
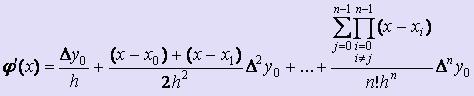 (1)
(1)
Формула значительно упрощается, если производная ищется в одном из узлов таблицы:х* = xi = x0 + ih: 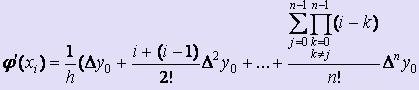 (2)
(2)
Подобным путём можно получить и производные функции f (x) более высоких порядков. Однако, каждый раз вычисляя значение производной функции f (x) в фиксированной точке х в качестве х0 следует брать ближайшее слева узловое значение аргумента.
- Численное дифференцирование на основе интерполяционной формулы Лагранжа
Запишем формулу Лагранжа для равноотстоящих узлов в более удобном виде для дифференцирования: 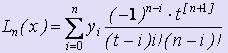
Затем, дифференцируя по х как функцию от t, получим: 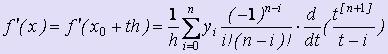
Пользуясь этой формулой можно вычислять приближённые значения производной таблично-заданной функции f (x) в одном из равноотстоящих узлов.
Аналогично могут быть найдены значения производных функции f(x) более высоких порядков.
6. Численное интегрирование
Основные вопросы, рассматриваемые на лекции:
- Постановка задачи численного интегрирования
- Квадратурные формулы Ньютона-Котеса
- Формулы прямоугольников
- Формула трапеций
- Формула Симпсона
- Квадратурные формулы Гаусса
- Метод Монте-Карло
- Постановка задачи численного интегрирования
Требуется вычислить определённый интеграл вида 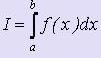 , причём функция может быть задана как в виде формулы, так и в виде таблицы.
, причём функция может быть задана как в виде формулы, так и в виде таблицы.
- Квадратурные формулы Ньютона-Котеса
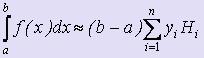 ,
,
где 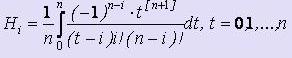 - коэффициенты Котеса.
- коэффициенты Котеса.
Эти формулы дают на одном участке интегрирования различные представления для различного числа n отрезков разбиения.
- Формулы прямоугольников
Пусть требуется вычислить интеграл 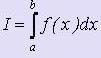 .
.
Если отрезок интегрирования [a; b] достаточно велик, то нужно разбить его на более мелкие отрезки равной длины 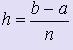 , где n - число отрезков, и заменяя на каждом из отрезков криволинейную трапецию прямоугольником, вычислить площади этих прямоугольников. Затем полученные площади нужно сложить, эта сумма и будет принята за приближённое значение искомого интеграла.
, где n - число отрезков, и заменяя на каждом из отрезков криволинейную трапецию прямоугольником, вычислить площади этих прямоугольников. Затем полученные площади нужно сложить, эта сумма и будет принята за приближённое значение искомого интеграла.
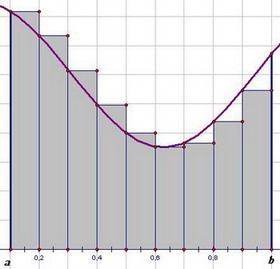
Что касается построения прямоугольников, то их можно строить по-разному: можно проводить перпендикуляр до пересечения с кривой f (x) из правого конца каждого отрезка (Рис. 1), можно - из левого конца (Рис. 2)
|
|
|
В зависимости от этого формулы для вычисления несколько различны и носят название формулы прямоугольников с правыми или левыми ординатами соотвественно:
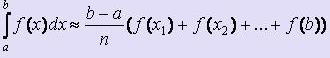
(формула "правых" прямоугольников)
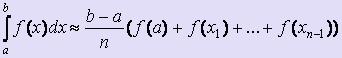
(формула "левых" прямоугольников)
Существует ещё формула "средних" прямоугольников: 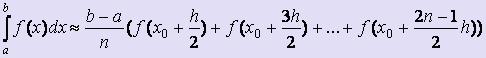 , для которой построение прямоугольников осуществляется через середины каждого из отрезков разбиения:
, для которой построение прямоугольников осуществляется через середины каждого из отрезков разбиения: 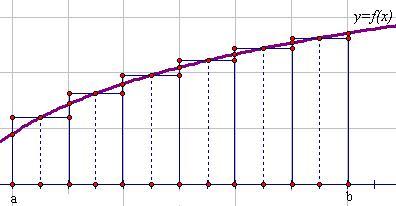
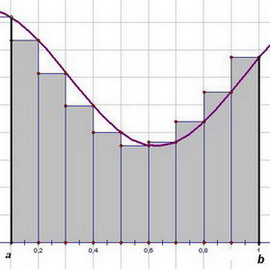
- Формула трапеций
|
Идея метода аналогична той, что представлена в методе прямоугольников. Отличие заключается в том, что на каждом отрезке разбиения криволинейная трапеция заменяется на обычную трапецию, площадь которой вычисляется по формуле |
|
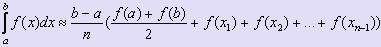
- Формула Симпсона
Заменяя на каждом отрезке разбиения часть кривой y = f (x) на параболическую кривую, вычисляя площади получившихся фигур и суммируя их, получим формулу Симпсона:
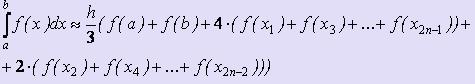 ·
·
- Квадратурные формулы Гаусса
Традиционно при получении квадратурных формул Гаусса в исходном интеграле выполняется замена переменной, переводящая интеграл по отрезку [a; b] в интеграл по отрезку [-1; 1]:
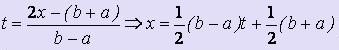 .
.
Тогда 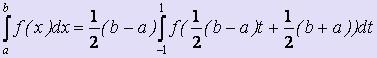 .
.
Будем использовать линейную интерполяцию подынтегральной функции.
Если вместо отрезка [-1; 1] взять в качестве узлов интерполяции подвижные узлы t1, t2, то нужно выбрать эти значения так, чтобы площадь трапеции, ограниченнной сверху прямой, проходящей через точки A1 (t1, (t1) ) и A2 (t2, (t2) ) была равной интегралу от любого многочлена некоторой наивысшей степени.
Полагая, что это многочлен третьей степени, вычислим t1, t2, которые получаются равными 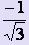 и
и 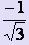 , отличаясь лишь нумерацией значений.
, отличаясь лишь нумерацией значений.
Далее разбивая отрезок интегрирования на n частей, применяя к каждому из них описанную выше идею, можно получить формулу Гаусса: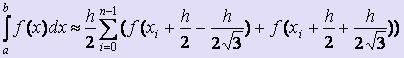
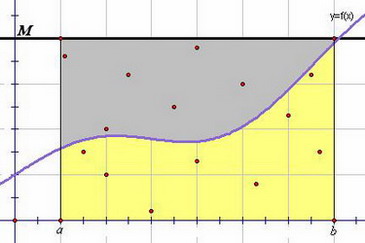
- Метод Монте-Карло
|
Идея метода: Пусть f (x) > 0 (для простоты рассуждений). |
|
- отрезком [a; b] оси Ох
- отрезком, принадлежащим прямой y = M длины b-a
- отрезками, принадлежащими прямым х = a и x = b, заключёнными между осью Ох и прямой y = M.
Координаты таких точек вычисляются по формулам: 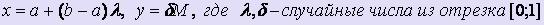 .
.
Если найдено таким образом n точек и k из них принадлежит криволинейной трапеции, ограниченной кривой y = f (x), прямыми x = a, x = b и осью Ох, то, с учётом того, что при больших n распределение точек по прямоугольнику близко к равномерному, то отношение k / nприближённо равно отношению площади криволинейноё трапеции к площади прямоугольника: 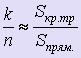
При этом
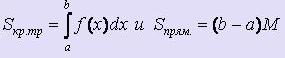
Подставляя значения площадей и выражая интеграл, получаем: 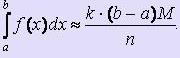
7. Численное решение обыкновенных дифференциальных уравнений
Основные вопросы, рассматриваемые на лекции:
- Постановка задачи
- Метод Эйлера
- Методы Рунге-Кутта
- Многошаговые методы
- Решение краевой задачи для линейного дифференциального уравнения 2 порядка
- Численное решение дифференциальных уравнений в частных производных
- Постановка задачи
Простейшим обыкновенным дифференциальным уравнением (ОДУ) является уравнение первого порядка, разрешённое относительно производной: y ' = f (x, y) (1). Основная задача, связанная с этим уравнением известна как задача Коши: найти решение уравнения (1) в виде функции y (x), удовлетворяющей начальному условию: y (x0 ) = y0 (2).
ДУ n-ого порядка y (n) = f (x, y, y',:, y(n-1) ), для которого задача Коши состоит в нахождении решения y = y(x), удовлетворяющего начальным условиям:
y (x0 ) = y0 , y' (x0 ) = y'0 , :, y(n-1)(x0 ) = y(n-1)0 , где y0 , y'0 , :, y(n-1)0 - заданные числа, можно свести к системе ДУ первого порядка.
- Метод Эйлера
В основе метода Эйлера лежит идея графического построения решения ДУ, однако этот же метод даёт одновременно и численную форму искомой функции. Пусть дано уравнение (1) с начальным условием (2).
Получение таблицы значений искомой функции y (x) по методу Эйлера заключается в циклическом применении формулы: 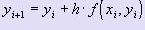 , i = 0, 1, :, n. Для геометрического построения ломаной Эйлера (см. рис.) выберем полюс A(-1,0) и на оси ординат отложим отрезок PL=f(x0 , y0 ) (точка P - это начало координат). Очевидно, что угловой коэффициент луча AL будет равен f(x0 , y0 ), поэтому чтобы получить первое звено ломаной Эйлера достаточно из точки М провести прямую MM1 параллельно лучу AL до пересечения с прямой х = х1 в некоторой точке М1(х1, у1). Приняв точку М1(х1, у1) за исходную откладываем на оси Оу отрезок PN = f (x1, y1) и через точку М1 проводим прямую М1М2 | | AN до пересечения в точке М2(х2, у2) с прямой х = х2 и т.д.
, i = 0, 1, :, n. Для геометрического построения ломаной Эйлера (см. рис.) выберем полюс A(-1,0) и на оси ординат отложим отрезок PL=f(x0 , y0 ) (точка P - это начало координат). Очевидно, что угловой коэффициент луча AL будет равен f(x0 , y0 ), поэтому чтобы получить первое звено ломаной Эйлера достаточно из точки М провести прямую MM1 параллельно лучу AL до пересечения с прямой х = х1 в некоторой точке М1(х1, у1). Приняв точку М1(х1, у1) за исходную откладываем на оси Оу отрезок PN = f (x1, y1) и через точку М1 проводим прямую М1М2 | | AN до пересечения в точке М2(х2, у2) с прямой х = х2 и т.д. 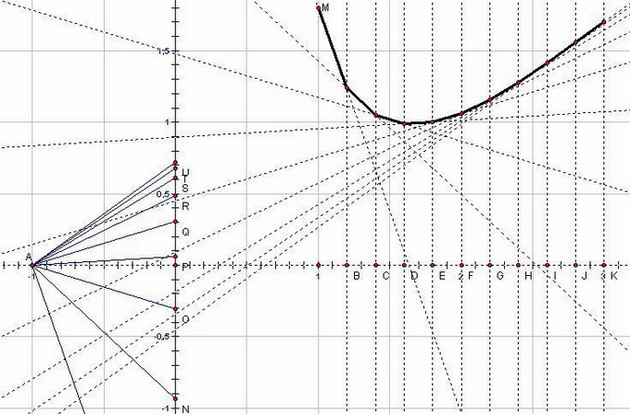
Недостатки метода: малая точность, систематическое накопление ошибок.
- Методы Рунге-Кутта
Основная идея метода: вместо использования в рабочих формулах частных производных функции f (x, y) использовать лишь саму эту функцию, но на каждом шаге вычислять её значения в нескольких точках. Для этого будем искать решение уравнения (1) в виде: 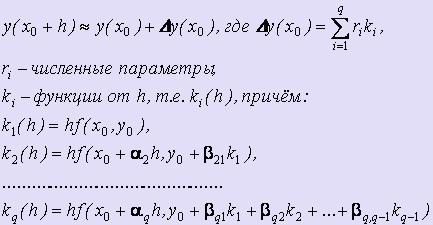
Меняя , , r, q, будем получать различные варианты методов Рунге-Кутта.
При q=1 получаем формулу Эйлера.
При q=2 и r1=r2= получаем, что , = 1 и, следовательно, имеем формулу: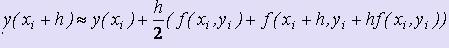 , которая называется усовершенствованный метод Эйлера-Коши.
, которая называется усовершенствованный метод Эйлера-Коши.
При q=2 и r1=0, r2=1 получаем, что , = и, следовательно, имеем формулу: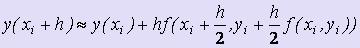 - второй усовершенствованный метод Эйлера-Коши.
- второй усовершенствованный метод Эйлера-Коши.
При q=3 и q=4 также существуют целые семейства формул Рунге-Кутта. На практике они применяются наиболее часто, т.к. не наращивают ошибок.
Рассмотрим схему решения дифференциального уравнения методом Рунге-Кутта 4 порядка точности. Расчёты при использовании этого метода ведутся по формулам: 
Их удобно вносить в следующую таблицу:
|
x |
y |
y' = f (x,y) |
k=h · f(x,y) |
y |
|
x0 |
y0 |
f(x0,y0) |
k1(0) |
k1(0) |
|
x0 + ·h |
y0 + ·k1(0) |
f(x0 + ·h, y0 + ·k1(0)) |
k2(0) |
k2(0) |
|
x0 + ·h |
y0 + ·k2(0) |
f(x0 + ·h, y0 + ·k2(0)) |
k3(0) |
k3(0) |
|
x0 + h |
y0 + k3(0) |
f(x0 + h, y0 + k3(0)) |
k4(0) |
k4(0) |
|
|
|
|
|
y0 = / 6 |
|
x1 |
y1 = y0 + y0 |
f(x1,y1) |
k1(1) |
k1(1) |
|
x1 + ·h |
y1 + ·k1(1) |
f(x1 + ·h, y1 + ·k1(1)) |
k2(1) |
k2(1) |
|
x1 + ·h |
y1 + ·k2(1) |
f(x1 + ·h, y1 + ·k2(1)) |
k3(1) |
k3(1) |
|
x1 + h |
y1 + k3(1) |
f(x1 + h, y1 + k3(1)) |
k4(1) |
k4(1) |
|
|
|
|
|
y1 = / 6 |
|
x2 |
y2 = y1 + y1 |
и т.д. |
до получения всех искомых |
значений y |
- Многошаговые методы
Рассмотренные выше методы - это так называемые методы пошагового интегрирования дифференциального уравнения. Они характерны тем, что значение решения на следующем шаге ищется с использованием решения, полученного лишь на одном предыдущем шаге. Это так называемые одношаговые методы.
Основная идея же многошаговых методов заключается в использовании при вычислении значения решения на следующем шаге нескольких предыдущих значений решения. Также эти методы носят название m-шаговых по числу m используемых для расчётов предыдущих значений решения.
В общем случае для определения приближённого решения yi+1 m-шаговые разностные схемы записываются таким образом (m 1):
1): 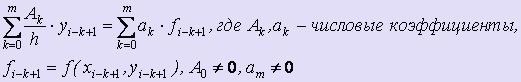
Рассмотрим конкретные формулы, реализующие простейшие явный и неявный методы Адамса.
Явный метод Адамса 2 порядка (2-шаговый явный метод Адамса)
Имеем a0 = 0, m = 2.
Таким образом, 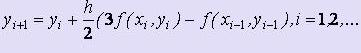 - расчётные формулы явного метода Адамса 2-ого порядка.
- расчётные формулы явного метода Адамса 2-ого порядка.
При i = 1 имеем неизвестное y1, которое будем находить по методу Рунге-Кутта при q = 2 илиq = 4.
При i = 2, 3, : все необходимые значения известны.
Неявный метод Адамса 1 порядка
Имеем: a0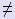 0, m = 1.
0, m = 1.
Таким образом, 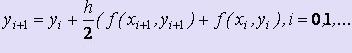 - расчётные формулы неявного метода Адамса 1-ого порядка.
- расчётные формулы неявного метода Адамса 1-ого порядка.
Основная проблема неявных схем заключается в следующем: yi+1 входит и в правую и в левую часть представленного равенства, поэтому имеем уравнение для поиска значения yi+1. Данное уравнение является нелинейным и записано в форме, подходящей для итерационного решения, поэтому будем использовать метод простой итерации для его решения: 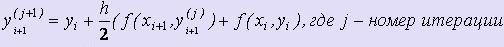
Если шаг h выбран удачно, то итерационный процесс быстро сходится.
Данный метод также не является самостартующимся. Так для вычисления y1 надо знать y1(0). Его можно найти по методу Эйлера.
- Решение краевых задач для ОДУ методом конечных разностей
Рассмотрим линейную краевую задачу y'' + p(x)·y' + q(x) = f(x), a  x
x  b, где p (x), q (x) и f (x)непрерывны на [a; b] и y0 = 1y1 + 1, yN = 2yN-1 + 2
b, где p (x), q (x) и f (x)непрерывны на [a; b] и y0 = 1y1 + 1, yN = 2yN-1 + 2
Для решения этого уравнения:
- Разобъём отрезок [a; b] на n равных частей длины, или шага
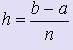 .
.
Точки разбиения xi = x0 + ih, i = 0, 1, :, n, x0 = a, xn = b называются узлами, а их совокупность - сеткой на отрезке [a; b]. - Значения в узлах искомой функции y = y (x) и её производных y' = y' (x), y'' = y'' (x)обозначим соответственно через yi = y(xi ), y'i = y'(xi ), y''i = y''(xi ).
Введём обозначения: pi = p(xi ), qi = q(xi ), fi = f(xi ). - Заменим производные конечно-разностными отношениями:
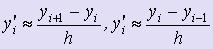 ,
, 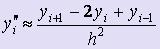 .
.
Эти формулы приближённо выражают значения производных во внутренних точках интервала [a; b]. - Для граничных точек положим:
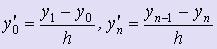
- Используя конечно-разностные отношения данное дифференциальное уравнение при х = хiприближённо можно заменить линейной системой уравнений:
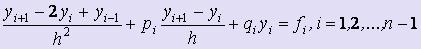
Кроме того, краевые условия дают ещё два уравнения.
Таким образом, получена линейная система n+1 уравнений c n+1 неизвестными y0, y1, :, yn, представляющими собой значения искомой функции y(x) в узлах сетки.
Полученная система уравнений называется разностной схемой.
Она решается методом прогонки или каким-либо общим численным методом (например, методом итерации).
 [a1; b1]
[a1; b1] 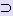 ...
... 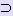 [an; bn], длины которых стремятся к нулю.
[an; bn], длины которых стремятся к нулю.
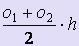 , где o1 и o2 - основания трапеции.
, где o1 и o2 - основания трапеции. 
 M для любого x из отрезка [a; b]. На графике - это прямая y = M.
M для любого x из отрезка [a; b]. На графике - это прямая y = M.