АНАЛИЗ СИСТЕМЫ ЭЛЕКТРОПРИВОДА

PAGE 2

Министерство образования и науки Российской Федерации

ФГБОУ ВПО

ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра Электропривода и электрического транспорта

Допускаю к защите

Руководитель Гоппе Г.Г.

АНАЛИЗ СИСТЕМЫ ЭЛЕКТРОПРИВОДА

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

к курсовой работе по дисциплине

Теория автоматического регулирования

1.215.00.00.ПЗ

Выполнил студент группы ЭАПБ-11-1 Ясенский И.А.

подпись И.О. Фамилия

Нормоконтроль Гоппе Г.Г.

подпись И.О. Фамилия

Курсовая работа защищена с оценкой

Иркутск 2013 г.

Министерство образования и науки Российской Федерации

ФГБОУ ВПО

ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ЗАДАНИЕ

НА КУРСОВОЕ ПРОЕКТИРОВАНИЕ

По курсу ____ Теория автоматического регулирования _

Студенту ______________________ Ясенский И.А.

(фамилия, инициалы)

Тема проекта _АНАЛИЗ СИСТЕМЫ ЭЛЕКТРОПРИВОДА

Исходные данные: выполнить проектирование согласно данному варианту.

Схема 2.

№ варианта	Передаточные функции (ПФ)	Параметры ПФ	Дополнительные данные
2.15	Wп1=Кп1; Wон=Кос	Кп1=10, Кп2=13 Тп2=0.05, Кос=0.15 Тя=0.16, Ктг=0.03184 Ке=0.7, Км=0.7 Rя=1, J=1	о=314 с-1 Мс=10 Нм

Рекомендуемая литература:

1. Теория автоматического управления. Методические указания и варианты заданий для практических занятий. [Электронный ресурс] /Сост. Г.Г. Гоппе, З.А. Федорова. - Иркутск: Изд-во НИ ИрГТУ, 2012.- 42 с.- Электрон. опт. диск (CD-ROM).
2. Теория автоматического управления. Методические указания для самостоятельной работы студентов. [Электронный ресурс] /Сост. Г.Г. Гоппе, З.А. Федорова. - Иркутск: Изд-во НИ ИрГТУ, 2012.- 71 с.- Электрон. опт. диск (CD-ROM).
3. Гоппе Г.Г., Федорова З.А.Теория автоматического управления. Методическое пособие и варианты заданий для курсового проектирования студентам специальностей: 1804 – Электропривод и автоматика промышленных и технологических комплексов; 1807 – Электрический транспорт– Иркутск, Изд-во ИрГТУ, 2003 г.- 26 c.

Графическая часть на _2_ листах.

Дата выдачи задания “_06_” _______сентября___________________2013 г.

Дата представления проекта руководителю “_17__” ____декабря___2013 г.

Руководитель курсового проектирования

СОДЕРЖАНИЕ КУРСОВОЙ РАБОТЫ

Введение …………………………………………………………………………. 4

1. Определение передаточных функций по задающему и по возмущающему воздействию …………………………………………………………………..... 5

2. Проверка САУ на устойчивость …..……………………………………….... 9

3. Определение переходной функции по задающему воздействию аналитически и на ЭВМ ………………………………………………………………….23

4. Определение переходной функции САУ по возмущающему воздействию

на ЭВМ ………………………………………………………………...…..............………28

5. Определение на ЭВМ способом структурного моделирования переходного процесса САУ при одновременном действии задающего и возмущающего воздействий ………………………………………....................................... .…..29

Заключение ……………………………………………………………………...30

Список литературы ……………………………………………………………..31

ВВЕДЕНИЕ

Современная теория автоматического регулирования является основной частью теории управления. Система автоматического регулирования состоит из регулируемого объекта и элементов управления, которые воздействуют на объект при изменении одной или нескольких регулируемых переменных. Под влиянием входных сигналов (управления или возмущения), изменяются регулируемые переменные. Цель же регулирования заключается в формировании таких законов, при которых выходные регулируемые переменные мало отличались бы от требуемых значений. Решение данной задачи во многих случаях осложняется наличием случайных возмущений (помех). При этом необходимо выбирать такой закон регулирования, при котором сигналы управления проходили бы через систему с малыми искажениями, а сигналы шума практически не пропускались.

Теория автоматического регулирования прошла значительный путь своего развития. На начальном этапе были созданы методы анализа устойчивости, качества и точности регулирования непрерывных линейных систем. Затем получили развитие методы анализа дискретных и дискретно-непрерывных систем.

Опираясь на существующие методы теории связи и теории колебаний, ТАУ создала собственные методы анализа и синтеза автоматических систем управления.

Современные тенденции в автоматизации технических систем и технологи-ческих процессов характеризуются широким применением ЭВМ для управления, созданием машин и оборудования со встроенными микропроцессорными средствами, обеспечивающими управление, информацию, защиту и диагностику.

1. Определение передаточных функций по задающему и по

возмущающему воздействию

1.1. Вывод передаточных функций разомкнутой системы и замкнутой системы по задающему (управляющему) воздействию

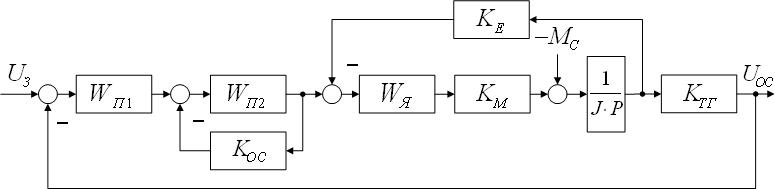
Рисунок 1.1 - Заданная структурная схема

Введено обозначение .

Если ставиться задача определить функцию по задающему воздействию, то все остальные воздействия принимаются равными нулю.

а) Эквивалентная передаточная функция контура с обратной связью по напряжению

Поделим числитель и знаменатель на , получим

=;

где =4,40678;

=0,0169;

б) Передаточная функция двигателя (при Мс=0).

.

Помножим числитель и знаменатель на и введем обозначение , получим .

Структурная схема примет вид, приведенный на рис. 1.2.

Рисунок 1.2 – Преобразованная структурная схема после свертывания 2-х контуров

Передаточная функция разомкнутой системы:

По варианту задания

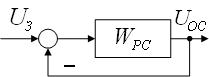
Рисунок 1.3 – Упрощенная структурная схема

Передаточная функция замкнутой системы по управляющему (задающему) воздействию (рис. 1.3)

.

,

где

;

;

=;

.

Передаточная функция разомкнутой системы:

Передаточная функция замкнутой системы по управляющему (задающему) воздействию

.

1.2. Вывод передаточной функции замкнутой системы по возмущающему воздействию

При получении передаточной функции по возмущающему воздействию все остальные воздействия принимаются равными нулю, а структурная схема принимает вид (рис. 1.4)

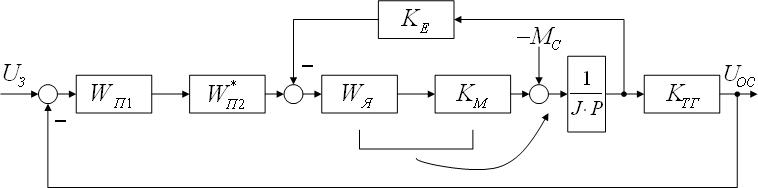
Рисунок 1.4 – Структурная схема после свертывания 1-го контура в пункте 1.1

Преобразуем схему, перенеся 2 звена через суммирующий узел (см. рис. 1.4) и введем компенсацию в подходящую к узлу ветвь (см. рис. 1.5).

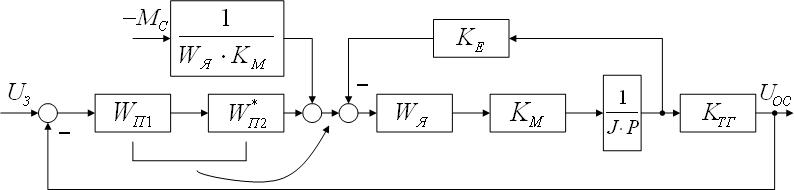
Рисунок 1.5 – Схема после переноса 2-х звеньев через суммирующий узел

Снова перенесем 2 звена через суммирующий узел (см. рис. 1.5) и введем компенсацию в подходящую к узлу ветвь (см. рис. 1.6).

Рисунок 1.6 – Схема после еще одного переноса 2-х звеньев через суммирующий узел

В итоге получаем преобразованную схему (рис. 1.7):

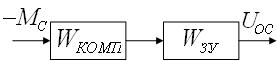
Рисунок 1.7 – Преобразованная схема

Найдем передаточную функцию замкнутой системы по возмущающему воздействию:

,

где

По заданию

Найдем искомую передаточную функцию по возмущающему воздействию

.

,

где ,

,

.

2. Проверка САУ на устойчивость

2.1. Проверка устойчивости по алгебраическому критерию

Гурвица

Поскольку порядок характеристического уравнения замкнутой системы равен 3-ем или 4-ем, то наиболее удобным для оценки устойчивости оказывается алгебраический критерий Гурвица. Тем более он позволяет определить предельный коэффициент усиления разомкнутой системы и коэффициент запаса устойчивости.

Характеристическое уравнение замкнутой системы 3-го порядка имеет вид

, где .

В соответствии с критерием Гурвица замкнутая САУ будет устойчива, если при все определители Гурвица, составленные по коэффициентам характеристического уравнения САУ, будут больше нуля – .

Получим главный определить (определитель третьего порядка) и другие определители Гурвица как:

Пользуясь, критерием Гурвица, определим предельный коэффициент усиления – или такое значение коэффициента, при котором САУ находится на границе устойчивости. Для этого главный определитель Гурвица должен быть равен нулю, а это возможно, если – система на границе апериодической устойчивости и если – система на границе колебательной устойчивости.

Приравняем к нулю определитель (n-1)го порядка:

Определяем

и коэффициент запаса устойчивости .

2.2. Проверка устойчивости по корням характеристического уравнения

Для того чтобы провести проверку устойчивости, мы используем программу “Определения корней характеристического уравнения. xls”, введя в нее коэффициенты.

Характеристическое уравнение САУ 3-го порядка запишем в виде:

, где .

Введя эти коэффициенты в программу определения корней характеристического уравнения, получим:

Вещественная часть всех корней меньше нуля, поэтому замкнутая система устойчива.

Замкнутая система коэффициентом =2,004455

Вещественная часть всех корней меньше нуля, поэтому разомкнутая система устойчива.

Система на границе устойчивости с коэффициентом =133,2692

Система на границе устойчивости, потому что вещественная часть двух

корней равна нулю

Система на границе неустойчивости с коэффициентом 1,5* =199,904

Система не устойчивости, потому что вещественная часть двух корней положительна

2.3. Проверка устойчивости САУ по критерию (годографу)

Михайлова

Этот критерий позволяет судить об устойчивости замкнутой САУ по поведению годографа.

Если годограф Михайлова при изменении от 0 до +, начинаясь на положительной вещественной полуоси, последовательно пройдет n квадрантов комплексной плоскости в положительном направлении, то замкнутая САУ устойчива.

В этом пункте используется программа “Частотные характеристики. xls”, куда вводится передаточная функция замкнутой системы, но для проверки правильности решения мы находим точки пересечения с осями.

Построение годографа Михайлова для системы 3-го порядка проводится по выражению, полученному из характеристического полинома замкнутой системы при подстановке в него .

,

где , .

1). Точки пересечения с действительной осью можно найти из условия .

Частоты, при которых годограф Михайлова пересекает действительную ось, равны

, 19,28302,

а значение при этих частотах:

2). Точку пересечения с мнимой осью находят из условия .

Частота, при которой годограф Михайлова пересекает мнимую ось, равна

=2,88449

а значение при этой частоте

.

Для построения годографа Михайлова введем в программу “Частотные характеристики.xls” параметры передаточной функции замкнутой системы по управляющему воздействию

Пример выполнения программы для системы 3-го порядка приведен ниже

Рисунок 2.1 - Годограф Михайлова замкнутой системы при Крс=2.004455

Система 3-го порядка устойчива, т.к. годограф Михайлова проходит в положительном направлении 3 квадранта.

Рисунок 2.2 – Годограф Михайлова замкнутой системы при Крс пред= 133,2692

Система 3-го порядка на границе устойчивости, т.к. годограф Михайлова проходит через через нуль.

Рисунок 2.3 – Годограф Михайлова замкнутой системы при 1,5*Крс пред=199.9038

Система 3-го порядка не устойчива, т.к. последовательность прохождения квадрантов

2.4. Проверка устойчивости САУ по критерию Найквиста

Этот критерий позволяет судить об устойчивости замкнутой САУ по виду АФХ разомкнутой САУ. Если разомкнутая САУ устойчива, то замкнутая система устойчива, если АФХ разомкнутой системы не охватывает критическую точку с координатами (-1,j0).

В программу “Частотные характеристики. xls” вводим передаточную функцию разомкнутой системы, а для проверки правильности решения находим точки пересечения с осями.

Вариант 1: система 3-го порядка

а) Построение АФХ разомкнутой системы

АФХ разомкнутой системы строим по выражению, полученному из передаточной функции разомкнутой системы при подстановке в нее и приведения полученного комплексного выражения к алгебраической форме записи

.

1). Точки пересечения с действительной осью можно найти из условия .

Частоты, при которых АФХ разомкнутой системы пересекает действительную ось, равны:

, = 19,2824

а значение при этих частотах:

2). Точки пересечения с мнимой осью находят из условия

Частота, при которой АФХ разомкнутой системы пересекает мнимую ось, равна =2.1026, а значение при этой частоте .

Исследование устойчивости по критерию Найквиста
“”	“P()”	“Q()”
0	2,004455	0
19,28244	-0,01504	9,664E-19
1,664078	0	-0,589757

Для построения АФХ разомкнутой системы введем в программу “Частотные характеристики.xls” параметры передаточной функции разомкнутой системы

А) Система коэффициентом Крс=2.004455

.

Пример выполнения программы для системы 3-го порядка приведен ниже

Рисунок 2.4 – АФХ системы Kpc=2.004455

Система устойчива, т.к. АФХ разомкнутой системы не охватывает точку с координатами ().

б)Система с коэффициентом Крс пред=133,2692

Рисунок 2.5 – АФХ системы при Крс пред=133,2692

Система на границе устойчивости с коэффициентом Крс пред=133,2692, т.к. АФХ разомкнутой системы проходит через точку с координатами (-1,j0)

c) Система неустойчива с коэффициентом 1,5* Kpc пред=199,9038

Рисунок 2.6 – АФХ системы при 1,5*Кpc пред=199,9038

Система неустойчива, т.к. АФХ разомкнутой системы охватывает точку с координатами ()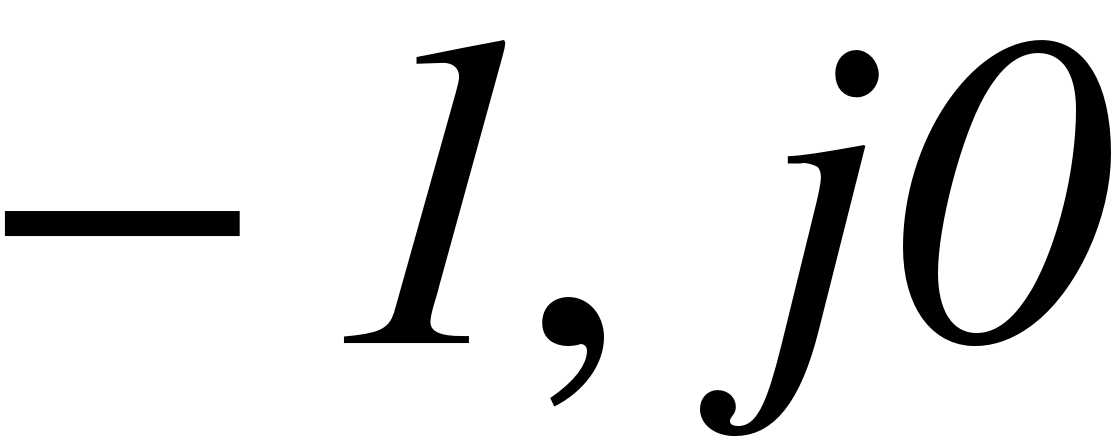

б) Построения ЛАХ и ЛФХ разомкнутой системы

Корни характеристического уравнения и корни

Из Пункта 2.2

1)Корни характеристического уравнения

,

Все корни действительные

Тогда можно записать

.

Сопрягающие частоты для асимптотической ЛАХ:

Выражение для действительной ЛАХ

.

Асимптотическая ЛАХ состоит из 4-х асимптот. 1-ая асимптота с нулевым

наклоном до частоты , далее до частоты с наклоном , затем до с наклоном

и после того

Выражение для ЛФХ

Для построения ЛАХ и ЛФХ разомкнутой системы введем в программу “Частотные характеристики.xls” параметры передаточной функции:

А)Система с коэффициентом

.

Рисунок 2.7 – ЛАХ и ЛФХ разомкнутой системы

Система устойчива, если при частоте среза ЛАХ, ЛФХ проходит выше линии .

б)Система с коэффициентом

Рисунок 2.8 – ЛАХ и ЛФХ системы при Кпред=133,2692

Система на границе устойчивости с коэффициентом, потому что

c)Система неустойчива с коэффициентом

Рисунок 2.9 – ЛАХ и ЛФХ системы при 1,5*Крс пред=132,2884

Система неустойчива с коэффициентом , потому что

3. Определение переходной функции по задающему

воздействию аналитически и на ЭВМ

Переходной функцией называется переходный процесс в САУ, который получается при подаче на вход единичного ступенчатого воздействия.

При выполнении этого пункта очень часто возникают трудности, т.к. существует несколько случаев для систем 3го порядка: 1) все корни действительные; 2) один действительный и два комплексно-сопряженные. Для систем 4го порядка 3 случая: 1)две пары комлексно-сопряженных корней; 2) два действительных и пара комплексно-сопряженных; 3) случай не встречается, когда 4 действительных корня.

Рассмотрим четыре случая: два для системы 3го и два для системы 4го

3.1. Определение аналитического выражения переходной

функции

функция характеристического уравнения замкнутой системы

исходными данными является передаточная функция по управляющему воздействию

И корни характеристического уравнения

Система 3-го порядка, корни комплексно-сопряженные и один действительный .

Корни характеристического уравнения получаем с помощью программы “Определение корней характеристического уравнения. xls” на ЭВМ.

Чтобы записать выражение для переходной функции во временной области, необходимо получить обратное преобразование Лапласа от изображения переходной функции

.

Из равенства изображений

,

приведя правую часть к общему знаменателю, можно приравнять числители

,

а из их равенства формируем условия для определения коэффициентов А, В, С и D, приравнивая коэффициенты при р с одинаковой степенью в обеих частях равенства:

при ;

при

;

при ;

при .

Из первого уравнения определяем коэффициент А

=1; (3.1)

Получим систему алгебраических уравнений для определения :

(3.2)

Подставив полученное значение и значения корней характеристического уравнения в систему уравнений (3.2) можно определить коэффициенты

B=-1,11935

C=0,119345

D=-0,05958

по методу Гаусса в программе ” пункт 3.1 (р1, al, bt).xls” и построить h(t) по выражению

3.2. Построение графика переходной функции на ЭВМ

Для построения графика при управляющем воздействии введем в программу “Временные характеристики.xls” параметры передаточной функции замкнутой системы

.

Рассмотрим на примере:

Пример (схема 2 задание 2.16):

График приведен на рис. 3.1.

Замкнутая система при =12,04455

Рисунок 3.1 - График при

Рисунок 3.2 Замкнутая система при =133,2692

Рисунок 3.3 Замкнутая система при = 199,9038

4. Определение переходной функции САУ по возмущающему

воздействию на ЭВМ

Для построения графика при возмущающем воздействии введем в программу “Временные характеристики.xls” параметры передаточной функции замкнутой системы.

.

Рассмотрим на примере:

Пример (схема 2 задание 2.16):

График приведен на рис. 4.1.

Рисунок 4.1 - График при возмущающем воздействии

5. Определение на ЭВМ способом структурного моделирования переходного процесса САУ при одновременном действии

задающего и возмущающего воздействий

Структурное моделирование проводим по заданной структурной схеме, изображенной на рис. 5.1.

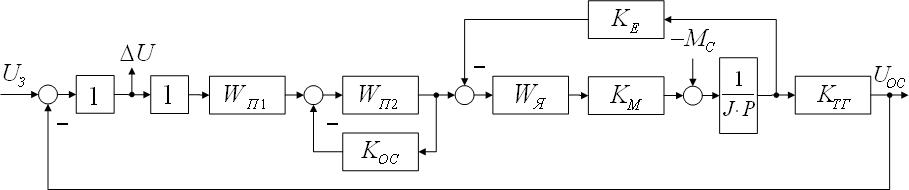
Рисунок 5.1. - Схема 2

Листинг рабочих подпрограмм для 2 ой схемы

Sub PR100() '........... Определение U(I) по уравнениям связи ...........

' Ubx=fnUbx(TS): F=fnF(TS)

'........................ Уравнения связи .....................

Select Case I

Case 1: U(I) = U3 - Y(9)

Case 2: U(I) = Y(1)

Case 3: U(I) = Y(2) ' - Y(4)

Case 4: U(I) = Y(3) - Koc * Y(4)

Case 5: U(I) = Y(4) - Y(8)

Case 6: U(I) = Y(5)

Case 7: U(I) = Y(6) - Mc

Case 8: U(I) = Y(7)

Case 9: U(I) = Y(7)

End Select

End Sub

Sub PR150() '......... Определение Y(I) для звена 0-го типа ...........

End Sub

Sub PR200() '............ Определение параметров звеньев ..............

'==============================================================

N = 9: ' <=== Количество звеньев

U3 = 10: Mc = 10

Kp1 = 10: Kp2 = 13: Koc = 0.15

Ke = 0.7: Km = 0.7: Ktg = 0.03184:

Tp1 = 0: Tp2 = 0.05: Te = 0.16: Jd = 1: Re = 1:

'==============================================================

I = 1: TYP(I) = 3: H0(I) = 1

I = 2: TYP(I) = 3: H0(I) = 1

' I = 2: TYP(I) = 2: B0(I) = 2418.342: B1(I) = 4935.391: B2(I) = 987.0782: B3(I) = 0: B4(I) = 0: ' A0(I) = 1: A1(I) = 44.73636: A2(I) = 9.199036: ' <== A2(I)<>0

I = 3: TYP(I) = 3: H0(I) = Kp1:

' I = 3: TYP(I) = 1: B0(I) = Kp1: B1(I) = 0: B2(I) = 0: B3(I) = 0:

' A0(I) = 1: A1(I) = Tp1:

I = 4: TYP(I) = 1: B0(I) = Kp2: B1(I) = 0: B2(I) = 0: B3(I) = 0:

A0(I) = 1: A1(I) = Tp2:

I = 5: TYP(I) = 1: B0(I) = 1 / Re: B1(I) = 0: B2(I) = 0: B3(I) = 0:

A0(I) = 1: A1(I) = Te:

I = 6: TYP(I) = 3: H0(I) = Km

I = 7: TYP(I) = 1: B0(I) = 1: B1(I) = 0: B2(I) = 0: B3(I) = 0:

A0(I) = 0: A1(I) = Jd:

I = 8: TYP(I) = 3: H0(I) = Ke

I = 9: TYP(I) = 3: H0(I) = Ktg

'----------------------------------------------------------------

For I = 1 To N

If TYP(I) = 4 Then B21(I) = B2(I) - B1(I): A21(I) = A2(I) - A1(I)

Next I

End Sub

(по задающему воздействию)

Рисунок 5.2 – Графики и при задающем воздействии

(по возмущающему воздействию)

Рисунок 5.3 - Графики и при возмущающем воздействии

(при совместном действии двух входных воздействий)

Рисунок 5.4 - Графики и при совместном действии

двух входных воздействий