Электрогидравлический следящий дроссель управления
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра «Тракторы»
группа 101010
КУРСОВАЯ РАБОТА
по дисциплине
«Теория автоматического управления»
Тема: Электрогидравлический следящий дроссель управления
Выполнил: Ковриков Е.Е.
Проверил: Вашкевич Ю.Ф.
Минск 2014
Содержание
- Описание устройства и работы автоматической системы ,
разработка ее функциональной схемы………………………………3
- Разработка математической модели и структурной схемы
заданной системы……………………………………………………..6
- Оценка устойчивости системы……………………………………..8
- Расчет и построение частотных характеристик системы…………..9
- Построение желаемой ЛАЧХ системы ………………………………14
6. Определение ЛАЧХ корректирующего устройства и расчет его
параметров …………………………………………………………......16
- Построение структурной схемы и определение передаточной
функции скорректированной САР…………………………………...17
- Расчет переходной характеристики и оценка качества
скорректированной САР.…………………………………………..…18
9. Заключение…………………………………………………………......23
10. Литература……………………………………………………………24
1. Описание устройства и работы автоматической системы, разработка ее функциональной схемы
В данной курсовой работе рассматривается электрогидравлический следящий привод с дроссельным управлением. Электрогидравлический следящий привод с дроссельным управлением служит для обеспечения пропорциональной связи между положением объекта управления и электрическим сигналом управления.
Привод (Рисунок 1) состоит из электрического усилителя-сумматора 1, электромеханического преобразователя(ЭМП) 3, двухкаскадного дросселирующего распределителя, гидроцилиндра 11, электрического датчика положения (потенциометра) 13. Дросселирующий гидрораспределитель сопло-заслонка является первым каскадом гидравлического усилителя и состоит из заслонки 4, двух сопел 5 и двух постоянных дросселей 6. Золотниковый дросселирующий гидрораспределитель 7 с центрирующими пружинами 8 является вторым каскадом гидравлического усиления. ЭМП в совокупности с
двухкаскадным дросселирующим распределителем образуют электроусилитель(ЭГУ).
Шток 9 гидроцилиндра жестко связан с объектом управления 10.Поршень 12 под действием разности давлений в полостях ГЦ перемещается до тех пор, пока
управляющее напряжение не будет скомпенсировано напряжением , подводимым к усилитель-сумматору1 с выхода потенциометра 13 обратной связи. Для улучшения динамических свойств привода применяется последовательное корректирующее устройство (КУ) 2.
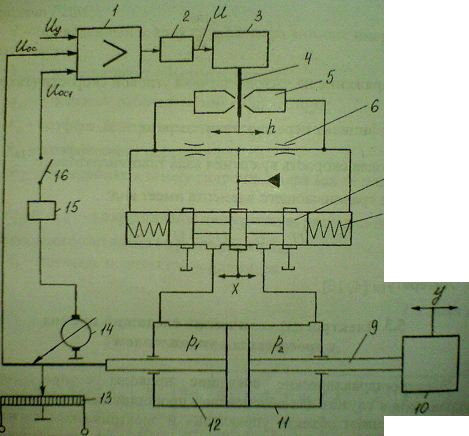
Рисунок 1— Принципиальная схема электрогидравлического привода с дроссельным управлением
Исходные данные:
Уравнения движения динамических звеньев привода:
1.Гидроцилиндр, управляемый золотниковым распределителем(ГИМ)
2.ЭГУ:
3.Усилитель постоянного тока:
4.Датчик положения:
5.Сравнивающий элемент:
Постоянные времени и коэффициенты передач в уравнениях движения:

Рисунок 2—Функциональная схема электрогидравлического привода с дроссельным управлением
2. Разработка математической модели и структурной схемы
заданной системы
На основание имеющейся функциональной схемы электрогидравлического следящего привода с дроссельным управлением составим структурную схему:
-

Рисунок 3—Структурная схема электрогидравлического привода с дроссельным управлением
Запишем передаточные функции звеньев:
1.Усилитель постоянного тока:
— безинерционное звено;
2.Электрогидроусилитель:
—апериодическое звено 1-го порядка;
3.ГИМ:
— последовательное соединение интегрирующего и апериодического звена 2-го порядка ;
4.Датчик положения:
—безинерционное звено;
Рассчитаем постоянные времени и коэффициенты передачи:
Передаточные функции системы:
1. Передаточная функция разомкнутой системы:
2. Главная передаточная функция системы:
3. Передаточная функция замкнутой САР для ошибки:
3. Оценка устойчивости системы
Устойчивость замкнутой системы определим по критерию Гурвица.
Характеристическое уравнение системы имеет вид:
Т.к. исследуемая САР 4-го порядка, то запишем для нее характеристическое уравнение в общем виде:
Получим следующие коэффициенты:
Для устойчивости системы 4-го порядка по критерию Гурвица необходимо и достаточно:
Тогда
Система неустойчива параметрически.
4. Определение частотных характеристик системы
Построение АЧХ и АФЧХ замкнутой САР.
Запишем выражение для главной передаточной функции, подставив в него постоянные все коэффициенты:
Подставим и перепишем предыдущее выражение в виде:
Помножив на комплексно сопряженное выражение, получим
Расчет сведем в таблицу:
|
|
0
|
0,02
|
0,06
|
0,1
|
0,12
|
0,14
|
0,16
|
0,18
|
0,2
|
0,22
|
0,25
|
|
|
-
|
-1,69
|
-1,22
|
-1
|
-0,9
|
-0,85
|
-0,79
|
-0,74
|
-0,69
|
-0,65
|
-0,6
|
|
|
0,129
|
0,102
|
0,089
|
0,047
|
0,0092
|
0,0065
|
0,0038
|
0,00298
|
0
|
-0,0042
|
-0,016
|
|
|
0
|
-0,000023
|
-0,000054
|
-0,000067
|
-0,0000723
|
-0,00093
|
-0,000105
|
-0,00022
|
-0,000182
|
-0,000092
|
-0,000023
|
|
|
0,123
|
0,147
|
0,239
|
0,038
|
0,024
|
0,017
|
0,013
|
0,009
|
0,0078
|
0,0064
|
0,005
|
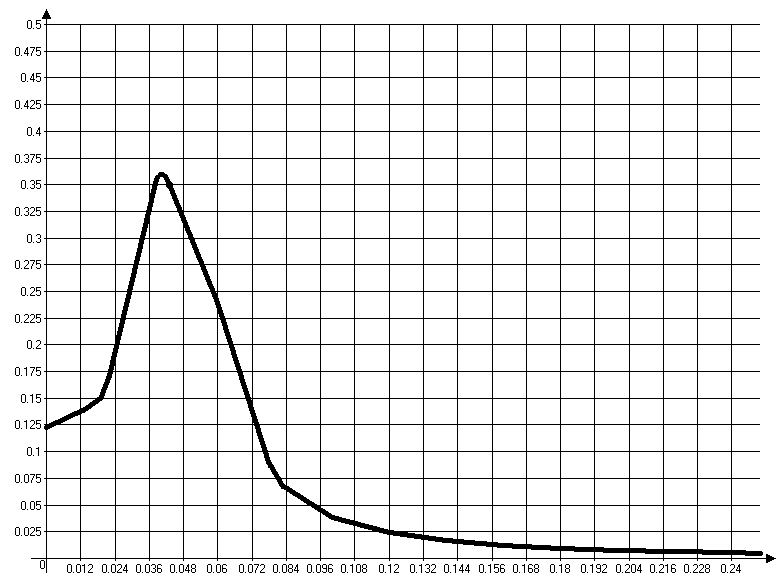
Рисунок 2 - АЧХ замкнутой САР
Построение ЛАЧХ и ЛФЧХ разомкнутой САР.
Для построения выражение для передаточной функции разомкнутой системы :
Для расчета ЛФЧХ будем учитывать, что:
- безинерционное звено
- апериодическое звено 1-го порядка
- апериодическое звено 2-го порядка
- безинерционное звено
Результаты снесем в таблицу:
|
|
0,1
|
0,5
|
1
|
5
|
10
|
20
|
35
|
50
|
|
|
-1
|
-0,3
|
0
|
0,7
|
1
|
1,3
|
1,54
|
1,7
|
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
|
-1,1
|
-5,48
|
-10,85
|
-43,79
|
-62,45
|
-75,38
|
-81,52
|
-84,04
|
|
|
-90,61
|
-93,31
|
-96,61
|
-120,09
|
-139,21
|
-156,67
|
-166,15
|
-170,21
|
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
|
-91,71
|
-98,79
|
-107,46
|
-163,88
|
-201,66
|
-232,05
|
-247,67
|
-254,25
|
При кривая асимптотически приближается к
Для расчета ЛАЧХ будем учитывать, что:
- безинерционное звено
- апериодическое звено 1-го порядка
- апериодическое звено 2-го порядка
- безинерционное звено
Значит
Результаты снесем в таблицу:
|
|
0,1
|
0,5
|
1
|
5
|
10
|
20
|
35
|
50
|
|
|
-1
|
-0,3
|
0
|
0,7
|
1
|
1,3
|
1,54
|
1,7
|
|
|
45,11
|
45,11
|
45,11
|
45,11
|
45,11
|
45,11
|
45,11
|
45,11
|
|
|
-87,95
|
-87,95
|
-87,96
|
-88
|
-88,12
|
-88,55
|
-89,57
|
-90,79
|
|
|
-7,08
|
-21,06
|
-27,08
|
-41,06
|
-47,08
|
-53,1
|
-57,96
|
-61,06
|
|
|
18,06
|
18,06
|
18,06
|
18,06
|
18,06
|
18,06
|
18,06
|
18,06
|
|
|
-31,86
|
-45,84
|
-51,87
|
-65,89
|
-72,03
|
-78,48
|
-84,36
|
-88,68
|
Рисунок 4 - ЛАЧХ разомкнутой САР
Рисунок 5 - ЛФЧХ разомкнутой САР
5. Построение желаемой ЛАЧХ системы и оценка качества САР
- Построение низкочастотной области желаемой ЛАЧХ
Определяем добротность желаемой системы по ускорению:
Из точки проводим прямую с наклоном , т.к. исходная САР является астатической 1-го порядка.
Определяем первую сопрягающую частоту , принимая, что низкочастотная асимптота имеет однократный излом:
При частоте на прямой с наклоном находим точку B, а затем из нее проводим прямую с наклоном . Таким образом получена низкочастотная область желаемой ЛАЧХ.
- Построение среднечастотной области желаемой ЛАЧХ
Определяем частоту среза:
Принимаем ,
Через проводим прямую с наклоном до пересечения слева с прямой и получаем точку пересечения C.
- Нахождение границы среднечастотной области ЛАЧХ
По графику рисунка 2 из методического пособия находим запасы устойчивости по фазе и амплитуде () в зависимости от :
Откладываем координаты и проводим линии параллельные оси частот. Находим , при которой и , при которой :
- Построение высокочастотной области желаемой ЛАЧХ
Для построения высокочастотной области желаемой ЛАЧХ и сопряжения ее со среднечастотной области нужно построить ЛАЧХ исходной САР в разомкнутом состоянии. Высокочастотная асимптота желаемой ЛАЧХ мало влияет на свойства САР. Поэтому для упрощения корректирующего устройства ее нужно совмещать с высокочастотной асимптотой ЛАЧХ исходной САР.
Для построения асимптотической ЛАЧХ исходной САР определим сопрягающие частоты:
Откладываем сопрягающие частоты:
При частоте ЛАЧХ исходной САР проходит через точку с ординатой . Через и проводим прямую с наклоном до сопрягающей частоты , т.к. исходная САР астатическая 1-го порядка. Затем до частоты проводим прямую с наклоном , а после нее с наклоном . В результате построения получим ломаную , которая является асимптотической ЛАЧХ исходной САР. При построении высокочастотной асимптоты желаемой ЛАЧХ принимаем такие же наклоны как для ЛАЧХ исходной САР на тех же сопрягающих частотах. Получаем ломаную ABCDЕF, которая является асимптотической ЛАЧХ желаемой ЛАЧХ .
- Проверка правильности построения желаемой ЛАЧХ.
Для проверки оценим избыток фазы в точках при и .
Избыток фазы при частоте определим по формуле:
- порядок астатизма
Избыток фазы на частоте подсчитаем по приближенной формуле:
6. Определение ЛАЧХ корректирующего устройства и расчет его параметров
Для определения ЛАЧХ последовательного корректирующего устройства необходимо из ординат желаемой ЛАЧХ вычесть ординаты ЛАЧХ для всех сопрягающих частот.
Так как ЛАЧХ последовательного корректирующего устройства имеет сложную конфигурацию, то приходится использовать два последовательно соединенных корректирующих устройства. По полученной характеристике из таблицы 8.2 («Линейные автоматические системы» И.М.Макаров, Б.М.Менский) находим схемы электрических корректирующих устройств:
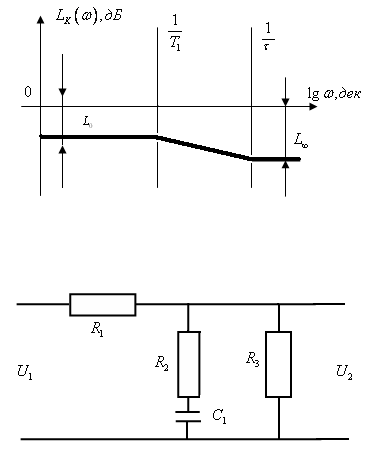
Из построенного графика ЛАЧХ КУ имеем:
Задаемся значением
Получим КУ со следующими параметрами:
; ; ; ;
7. Построение структурной схемы и определение передаточной функции скорректированной САР
Структурная схема скорректированной САР имеет вид:
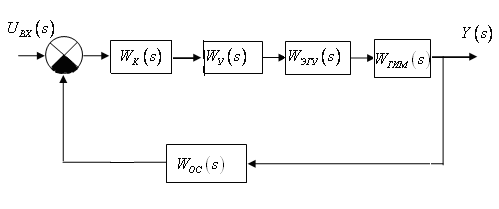
где передаточная функция корректирующего устройства
Главная передаточная функция системы
8. Расчет переходной характеристики и оценка качества скорректированной САР
Рассчитывать переходную характеристику скорректированной САР будем пользуясь методам трапециидальных вещественных частотных характеристик.
Для этого построим график ВЧХ. В выражении для главной передаточной функции скорректированной САР делаем подстановку
Расчеты сведем в таблицу:
|
|
0
|
0,001
|
0,004
|
0,006
|
0,008
|
0,01
|
0,012
|
0,014
|
0,016
|
|
|
0,125
|
0,1239
|
0,1235
|
0,13679
|
0,08535
|
0,232
|
0,00657
|
0,0022
|
0,00094
|
|
|
0,018
|
0,02
|
0,022
|
0,024
|
0,026
|
0,028
|
0,03
|
0,032
|
0,034
|
|
|
0,000438
|
0,000223
|
0,00012
|
0,0000923
|
0,000043
|
0,000027
|
0,0000178
|
0,000012
|
0,0000082
|
|
|
0,036
|
0,038
|
0,04
|
0,042
|
0,044
|
0,046
|
0,047
|
0,049
|
0,05
|
|
|
0,00000586
|
0,0000042
|
0,0000036
|
0,0000023
|
0,00000199
|
0,0000017
|
0,0000014
|
0,0000009
|
0,00000078
|
По данным таблицы строим ВЧХ скорректированной САР.
Рисунок 7 - ВЧХ скорректированной САР
После построения ВЧХ скорректируем ее трапециями (рисунок 7). При этом в окрестностях экстремумов прямолинейные участки располагаются параллельно оси частот . Вычерчиваем полученные трапеции так, чтобы основание каждой трапеции легло на ось частот (рисунок 8).
Для каждой i-ой трапеции определяем частоты . .
Результаты снесем в таблицу:
|
|
Параметры
|
|
|
|
|
|
|
|
1
|
-0,123
|
0
|
0,008
|
0
|
|
2
|
0,106
|
0,008
|
0,0175
|
0,45
|
|
3
|
0,017
|
0,0175
|
0,045
|
0,39
|
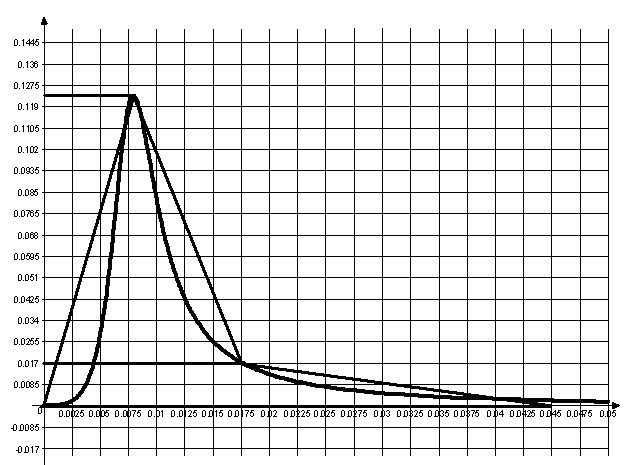
Рисунок 8.
Рисунок 9.
Проверка:
Определяем составляющие переходной характеристики. По табл. -функций для каждой i-ой трапеции находим столбец соответствующий значению коэффициента . Из этого столбца для ряда значений табличного время выписываем значение . Затем для каждой выбранной точки табличного времени определяем действительное время , а по значению определяем ординаты составляющей переходной характеристики, которая соответствует i-ой трапеции: .
Расчет проведем в таблицах:
|
|
|
|
|
|
|
|
|
|
|
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
1
|
0,31
|
125
|
-0,0372
|
1
|
0,447
|
57,14
|
0,0474
|
|
3
|
0,755
|
375
|
-0,069
|
3
|
1,038
|
171,43
|
0,11
|
|
4
|
0,857
|
500
|
-0,103
|
4
|
1,127
|
228,57
|
0,1195
|
|
5
|
0,895
|
625
|
-0,1074
|
5
|
1,112
|
285,71
|
0,11787
|
|
6
|
0,903
|
750
|
-0,1084
|
6
|
1,062
|
342,85
|
0,1126
|
|
8
|
0,91
|
1000
|
-0,1092
|
8
|
0,982
|
457,14
|
0,104
|
|
10
|
0,939
|
1250
|
-0,1127
|
10
|
0,985
|
571,4
|
0,1044
|
|
12
|
0,95
|
1500
|
-0,114
|
12
|
0,99
|
685,7
|
0,1049
|
|
15
|
0,956
|
1875
|
-0,1147
|
15
|
0,998
|
857,14
|
0,1058
|
|
20
|
0,967
|
2500
|
0,116
|
20
|
1,001
|
1142,85
|
0,1061
|
|
25
|
0,975
|
3125
|
0,951
|
25
|
0,996
|
1428,57
|
0,1056
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0
|
0
|
0
|
0
|
|
|
1
|
0,432
|
22,22
|
0,0073
|
|
|
3
|
1,013
|
66,66
|
0,0017
|
|
|
4
|
1,11
|
88,88
|
0,0189
|
|
|
5
|
1,112
|
111,11
|
0,0189
|
|
|
6
|
1,068
|
133,33
|
0,018
|
|
|
8
|
0,998
|
177,77
|
0,0169
|
|
|
10
|
0,994
|
222,22
|
0,0168
|
|
|
12
|
0,989
|
266,66
|
0,0168
|
|
|
15
|
0,991
|
333,33
|
0,0169
|
|
|
20
|
1,004
|
444,44
|
0,017
|
|
|
25
|
0,999
|
555,55
|
0,01698
|
|
По данным таблицы строим график составляющих переходной характеристики (Рис. 8). Затем суммируем ординаты всех составляющих в выбранные моменты времени и определяем ординаты переходной характеристики САР.
Определим показатели качества САР:
- Перерегулирование:
- Время переходного процесса:
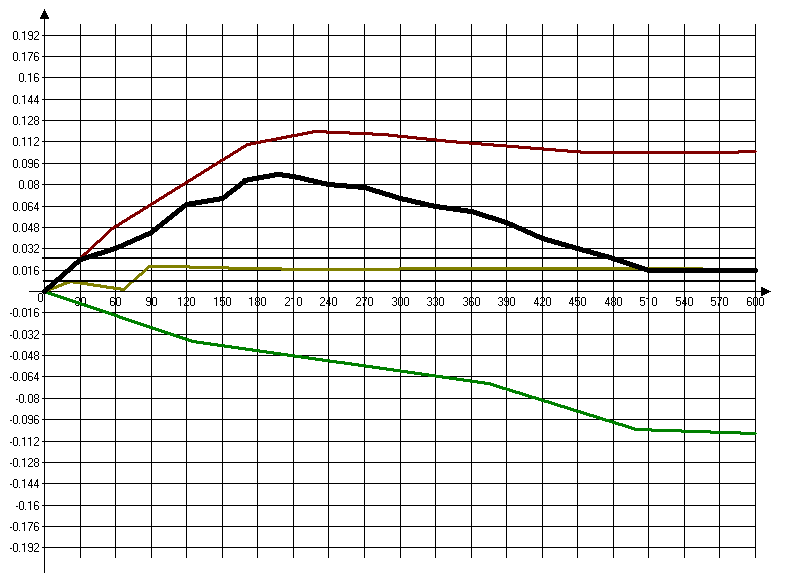
Рисунок 10 - Переходная характеристика САР
Заключение
В ходе выполнения данной курсовой работы были разработаны функциональная схема автоматической системы, математическая модель и структурная схема. Было установлено, что система является астатической 2-го порядка. Были построены АЧХ, АФЧХ замкнутой САР и ЛАЧХ, ЛФЧХ разомкнутой САР. Была построена желаемая ЛАЧХ. При этом избыток фаз составлял и . Было подобрано корректирующее устройство и рассчитаны все ее параметры. Была построена переходная характеристика скорректированной САР методом В.В. Солодовникова по ВЧХ САР. Определены перерегулирование и время переходного процесса.
Литература
- Автушко В.П.: Методические указания к выполнению курсовой работы по курсу «Теория автоматического управления». Минск, БНТУ, 2006, 52 стр.
- «Линейные автоматические системы» И.М.Макаров, Б.М.Менский, учебное пособие для вузов. М., «Машиностроение», 1977, 464 стр.
Электрогидравлический следящий дроссель управления