Расчет теплообменного аппарата

Содержание

Введение 5

1 Термодинамические процессы с идеальными углеводородными смесями 6

1.1 Исходные данные для термодинамических расчетов 6

1.2 Определение параметров газовой смеси одинаковых для всех термодинамических процессов 6

1.3 Политропный процесс с показателем политропы 7

1.4 Политропный процесс с показателем политропы 10

1.5 Политропный процесс с показателем политропы 13

1.6 Политропный процесс с показателем политропы 16

1.7 Политропный процесс с показателем политропы 19

1.8 Политропный процесс с показателем политропы 22

Выводы 25

2 Расчет теплообменного аппарата 26

2.1 Исходные данные 26

2.2 Конструктивный тепловой расчет теплообменного аппарата 27

2.3 Рекуперативный теплообменник с трубчатой поверхностью теплообмена (противоток) 34

Выводы 35

Список использованных источников 36

Введение

В термодинамике рассматриваются обратимые процессы. Все реальные процессы необратимы, они протекают с конечной скоростью (при наличии трения и диффузии) и при значительной разности температур РТ и источников теплоты.

Термодинамическим процессом называется изменение состояния термодинамической системы, характеризующееся изменением ее параметров. В качестве термодинамических систем могут рассматриваться некоторые объемы газов.

В основных технологических установках и устройствах нефтяной и газовой промышленности наиболее часто встречающимися газами являются углеводородные или их смеси с компонентами воздуха и небольшим количеством примесей других газов. Это могут быть процессы в газгольдерах, пропан- бутановых хранилищах, сырьевых и товарных парков нефтеперерабатывающих заводов, нефтебаз, нефтеперекачивающих станций, а также в газораспределительных сетях газоснабжения населенных пунктов.

Целью термодинамического расчета является определение основных параметров газовой смеси в конечном состоянии

Теплообменным аппаратом (теплообменником) называется устройство, в котором осуществляется теплообмен между двумя или несколькими теплоносителями.

В рекуперативных теплообменниках теплоносители непрерывно омывают разделяющую стенку (поверхность теплообмена) с двух сторон и обмениваются при этом теплотой. В рекуперативном трубчатом теплообменнике один из теплоносителей протекает внутри труб, а второй омывает их наружные поверхности.

Цель конструктивного расчета состоит в определении величины поверхности теплообмена по известному количеству передаваемой теплоты и температурам теплоносителей на входе и выходе аппарата.

1 ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ С ИДЕАЛЬНЫМИ УГЛЕВОДОРОДНЫМИ СМЕСЯМИ

1.1 Исходные данные для термодинамических расчетов

1 кг газовой смеси в распределительной газовой сети в зависимости от состава совершает термодинамические процессы от состояния 1 до состояния 2 с показателями .

Объем газовой смеси во всех процессах изменяется в раз.

Смесь обладает свойствами идеального газа.

Начальное (в состоянии 1) давление . Начальная температура .

Определить основные параметры газовой смеси в состоянии 1 () и состоянии 2 (), изменение внутренней энергии, энтальпии, энтропии смеси, работу, внешнюю теплоту процесса, коэффициент распределения энергии в процессах.

Состав газовой смеси по объему:

Vв - 80%

1.2 Определение параметров газовой смеси одинаковых для всех термодинамических процессов

1.2.1 Определение кажущейся молекулярной массы смеси

1.2.2 Массовые доли смеси

1.2.3 Газовая постоянная смеси

1.2.4 Объем газовой смеси в начальном состоянии

1.2.5 Объем газовой смеси в конечном состоянии

1.3 Политропный процесс с показателем политропы

1.3.1 Давление газовой смеси в конечном состоянии

1.3.2 Температура газовой смеси в конечном состоянии

1.3.3 Средняя температура процесса

1.3.4 Средняя изобарная теплоёмкость компонентов газовой смеси

1.3.5 Средняя массовая изобарная теплоёмкость газовой смеси

1.3.6 Средняя массовая изохорная теплоёмкость газовой смеси

1.3.7 Термодинамическая работа процесса

1.3.8 Потенциальная работа процесса

1.3.9 Изменение внутренней энергии

1.3.10 Изменение энтальпии

1.3.11 Изменение энтропии

1.3.12 Теплота процесса

1.3.13 Коэффициент распределения энергии

1.3.14 Проверка правильности расчетов

1.4 Политропный процесс с показателем политропы

1.4.1 Давление газовой смеси в конечном состоянии

1.4.2 Температура газовой смеси в конечном состоянии

1.4.3 Средняя температура процесса

1.4.4 Средняя изобарная теплоёмкость компонентов газовой смеси

1.4.5 Средняя массовая изобарная теплоёмкость газовой смеси

1.4.6 Средняя массовая изохорная теплоёмкость газовой смеси

1.4.7 Показатель адиабаты

1.4.8 Термодинамическая работа процесса

1.4.9 Потенциальная работа процесса

1.4.10 Изменение внутренней энергии

1.4.11 Изменение энтальпии

1.4.12 Политропная теплоёмкость

1.4.13 Теплота процесса

1.4.14 Изменение энтропии

1.4.15 Коэффициент распределения энергии

1.4.16 Проверка правильности расчетов

1.5 Политропный процесс с показателем политропы

1.5.1 Давление газовой смеси в конечном состоянии

1.5.2 Температура газовой смеси в конечном состоянии

1.5.3 Средняя температура процесса

1.5.4 Средняя изобарная теплоёмкость компонентов газовой смеси

1.5.5 Средняя массовая изобарная теплоёмкость газовой смеси

1.5.6 Средняя массовая изохорная теплоёмкость газовой смеси

1.5.7 Термодинамическая работа процесса

1.5.8 Потенциальная работа процесса

1.5.9 Изменение внутренней энергии

1.5.10 Изменение энтальпии

1.5.11 Изменение энтропии

1.5.12 Теплота процесса

1.5.13 Коэффициент распределения энергии

1.5.14 Проверка правильности расчетов

1.6 Политропный процесс с показателем политропы

1.6.1 Давление газовой смеси в конечном состоянии

1.6.2 Температура газовой смеси в конечном состоянии

1.6.3 Средняя температура процесса

1.6.4 Средняя изобарная теплоёмкость компонентов газовой смеси

1.6.5 Средняя массовая изобарная теплоёмкость газовой смеси

1.6.6 Средняя массовая изохорная теплоёмкость газовой смеси

1.6.7 Показатель адиабаты

1.6.8 Термодинамическая работа процесса

1.6.9 Потенциальная работа процесса

1.6.10 Изменение внутренней энергии

1.6.11 Изменение энтальпии

1.6.12 Политропная теплоёмкость

1.6.13 Теплота процесса

1.6.14 Изменение энтропии

1.6.15 Коэффициент распределения энергии

1.6.16 Проверка правильности расчетов

1.7 Политропный процесс с показателем политропы

Принимаем k=1,29

1.7.1 Давление газовой смеси в конечном состоянии

1.7.2 Температура газовой смеси в конечном состоянии

1.7.3 Средняя температура процесса

1.7.4 Средняя изобарная теплоёмкость компонентов газовой смеси

1.7.5 Средняя массовая изобарная теплоёмкость газовой смеси

1.7.6 Средняя массовая изохорная теплоёмкость газовой смеси

1.7.7 Термодинамическая работа процесса

1.7.8 Потенциальная работа процесса

1.7.9 Изменение внутренней энергии

1.7.10 Изменение энтальпии

1.7.11 Теплота процесса

1.7.12 Изменение энтропии

1.7.13 Коэффициент распределения энергии

1.7.14 Проверка правильности расчетов

1.8 Политропный процесс с показателем политропы

1.8.1 Давление газовой смеси в конечном состоянии

1.8.2 Температура газовой смеси в конечном состоянии

1.8.3 Средняя температура процесса

1.8.4 Средняя изобарная теплоёмкость компонентов газовой смеси

1.8.5 Средняя массовая изобарная теплоёмкость газовой смеси

1.8.6 Средняя массовая изохорная теплоёмкость газовой смеси

1.8.7 Показатель адиабаты

1.8.8 Термодинамическая работа процесса

1.8.9 Потенциальная работа процесса

1.8.10 Изменение внутренней энергии

1.8.11 Изменение энтальпии

1.8.12 Политропная теплоёмкость

1.8.13 Теплота процесса

1.8.14 Изменение энтропии

1.8.15 Коэффициент распределения энергии

1.8.16 Проверка правильности расчетов

Выводы

Проведенное исследование позволяет разбить все политропные процессы с от до при расширении газа на три группы:

I группа:. В этой группе , а следовательно, и ; здесь , а следовательно, . Так как , то теплоемкость в этой группе процессов положительна. Подведенная к газу теплота расходуется на увеличение внутренней энергии и на совершение им работы расширения;

II группа: . Для этой группы , а следовательно, и ; и, следовательно, ; теплоемкость в процессах отрицательная, так как . Термодинамические процессы второй группы характерны тем, что работа расширения совершается как за счет подведенной к газу теплоты, так и за счет внутренней энергии;

III группа: . Здесь при расширении газа все параметры состояния уменьшаются (), но теплоемкость , т.е. положительная. В процессах этой группы расширение газа происходит с уменьшением его внутренней энергии и отдачей теплоты в окружающую среду.

2 ТЕПЛОВОЙ РАСЧЁТ ТЕПЛООБМЕННОГО АППАРАТА

Задание. В одноходовом кожухотрубном теплообменном аппарате горячий теплоноситель движется в межтрубном пространстве и охлаждается от температуры = 130 °С до = 53 °С.

Внутренний диаметр кожуха аппарата D=252·10-3 м. Холодный теплоноситель движется внутри металлических трубок. Холодный теплоноситель нагревается от = 30 °С до = 55 °С.

Число трубок в теплоносителе n = 62. Трубки теплообменника с внутренней стороны покрыты отложениями (накипью) толщиной нак = 0,6·10-3 м. Тепловая мощность, вносимая в ТОА Qвн = 550 кВт. Потери теплоты в окружающую среду составляют (1-)100 %.

Определить поверхность нагрева F и число секций N теплообменника. Длина секций lс = 5 м.

Расчёт провести для прямоточного и противоточного направлений теплоносителей, а также при наличии накипи на трубах и при её отсутствии.

Известно также:

Внутренний диаметр трубок dв = 16·10-3 м;

Коэффициент теплопроводности

материала трубок с = 110·10-3 кВт/(м·К);;

холодный теплоноситель нефть

наружный диаметр трубок dн = 18·10-3 м;

Коэффициент теплопроводности

накипи нак = 0,7·10-3 кВт/(м·К);;

горячий теплоноситель вода

Коэффициент использования

теплоты = 0,98;

Ориентация трубного пучка в

пространстве горизонтальная.

Конструктивный тепловой расчёт ТОА

1. Тепловая мощность, полученная холодным теплоносителем:

Графики изменения температуры теплоносителей по длине аппарата:

а) прямоток б) противоток

Из графиков видим, что прямоток невозможен, дальнейшие расчеты ведем только для противотока.

2. Температурный перепад между теплоносителями на концах аппарата, противоток :

3. Температурные напоры для противотока:

при : ;

при : .

В данном случае для противотока :

;

следовательно

4. Изменение температуры по длине аппарата:

;

5. Средние температуры горячего и холодного теплоносителей:

;

6. Теплофизические свойства горячего и холодного теплоносителей выписываем из приложений 1 и 2, используя при необходимости линейную интерполяцию.

Горячий теплоноситель – вода

Выписываем значения параметров при найденной средней температуре 91,5°С:

средняя плотность

коэффициент теплопроводности

удельная теплоёмкость Ср1 = 4,2098 кДж/(кг·К);

кинематическая вязкость

коэффициент объёмного расширения

число Прандтля Pr1 =

Холодный теплоноситель – нефть

Выписываем значения параметров при найденной средней температуре 42,5°С:

средняя плотность

коэффициент теплопроводности

удельная теплоёмкость

Ср2 = 2,0 кДж/(кг·К);

кинематическая вязкость

коэффициент объёмного расширения

число Прандтля

Pr2 = Ср2 / = 8002,0103 / 0,18 = 133,3.

7. Проходные сечения горячего и холодного теплоносителей:

8. Скорости движения теплоносителей:

9. Эквивалентные диаметры:

;

10. Число Рейнольдса для горячего и холодного теплоносителя:

;

11. Температура стенки (в первом приближении):

12. Найдём числа Прандтля для теплоносителей при температуре стенки. Теплофизические свойства теплоносителей выписываем из приложений 1 и 2, используя при необходимости линейную интерполяцию.

Горячий теплоноситель – вода.

Выписываем значения параметров при температуре стенки 67°С:

средняя плотность = 978 кг/м3;

коэффициент теплопроводности

удельная теплоёмкость Срст1 = 4,1783 кДж/(кг·К);

кинематическая вязкость

коэффициент объёмного расширения

число Прандтля Prст1 = 2,693

Холодный теплоноситель – нефть

Выписываем значения параметров при найденной средней температуре 42,5°С:

средняя плотность

коэффициент теплопроводности

удельная теплоёмкость

Ср2 = 2,0 кДж/(кг·К);

кинематическая вязкость

коэффициент объёмного расширения

число Прандтля

Pr2 = Ср2 / = 8002,0103 / 0,18 = 133,3.

13. Температурный напор:

14. Числа Грасгофа для теплоносителей:

для горячего теплоносителя

для холодного теплоносителя

15. Определим режимы течения и выберем формулу для числа Нуссельта:

Горячий теплоноситель

при Re1 = 5177,349

Так как 2300 < Re1 < 104 , режим течения – переходный, число Нуссельта вычисляется по формуле:

где - коэффициент, определяемый по величине числа Рейнольдса (табл. 4.3).

В данном случае = 17,121.

Холодный теплоноситель

При Re2 = 1222,4

Так как Re2 < 2300, Gr2Pr2 < 8105, режим течения – ламинарно вязкостное, число Нуссельта вычисляется по формуле:

;

Динамическая вязкость связана с кинематической формулой , где - плотность вещества. Отсюда :

при t = tж = 42,5 С, ;

при t = tст = 67 С, (т.к. нефть)

16. Коэффициенты теплоотдачи для горячего и холодного теплоносителей:

17. Коэффициенты теплопередачи:

Толщина стенки трубок:

Без накипи:

С накипью:

18. Определим поверхности теплообмена:

Противоток, без накипи

Противоток, с накипью

19. Поверхность теплообмена одного погонного метра пучка:

20. Длина теплообменника:

L=F/f

21. Число секций:

Оно вычисляется по формуле N = L / lc, где L - длина теплообменника, вычисленная в п.20.

Противоток, без накипи

N = 35,58 / 5 = 7,116. Принимаем N = 8;

Противоток, с накипью

N = 35,67 / 5 = 7,134. Принимаем N = 8.

22. Сводная таблица результатов теплового расчёта:

Наименование величины	Схема движения теплоносителя
	прямоток	противоток
Средний температурный напор, °С	—	43,993
Коэффициент теплопередачи К, кВт/(м2·К)	Без накипи	0,104
	С накипью	0,1037
Поверхность нагрева F, м2	Без накипи	—	117,81
	С накипью	—	118,102
Длина теплообменника, м	Без накипи	—	35,58
	С накипью	—	35,67

2.3 Рекуперативный теплообменник с трубчатой поверхностью теплообмена (противоток)

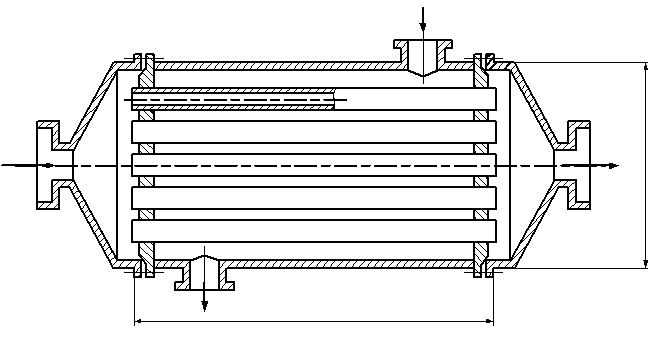
Рисунок 2.3.1 – Эскиз секции с основными размерами

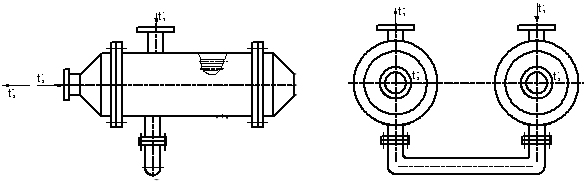
Рисунок 2.3.2 – Схема соединения секций в теплообменном аппарате

Выводы

Теплообменные аппараты могут иметь самое разнообразное назначение – паровые котлы, конденсаторы, пароперегреватели, воздухонагреватели, радиаторы и т.д. Теплообменные аппараты в большинстве случаев значительно отличаются друг от друга как по своим формам и размерам, так и по применяемым в них рабочим телам.

Руководствуясь данным расчетом теплообменного аппарата можно произвести выбор типа аппарата и его конструктивные размеры. Также на основе результатов расчета можно составить конструктивную схему аппарата.

Литература

В.В. Кузнецова, В.А. Симаков, В.В.Репин. Тепловой расчёт теплообменного аппарата. Методические указания к расчётно – графической работе по курсу «Теплопередача» для студентов дневной, вечерней и заочной формы обучения. – Уфимс. нефт. институт, 1991 – 30 с.
Ф.Ф.Абузова, Р.А.Молчанова, М.А.Гиззатов Термодинамические процессы с идеальными углеводородными смесями: Учеб. Пособие. –Уфим. нефт. институт, 1990 – 59 с.
Исаченко В.П., Осипова В.А., Сукомол А.С. Теплопередача. – М.: Высшая школа, 1964 – 459с.
Я.М. Вильнер, Я.Т. Ковалев, Б.Б. Некрасов. Справочное пособие по гидравлике, гидромашинам и гидроприводам. – Минск: Высшая школа, 1976 – 416с.

EMBED Equation.3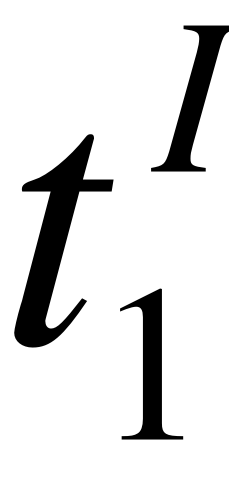

L( F)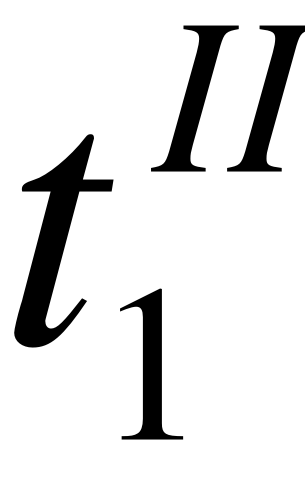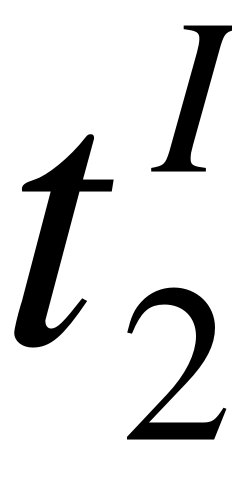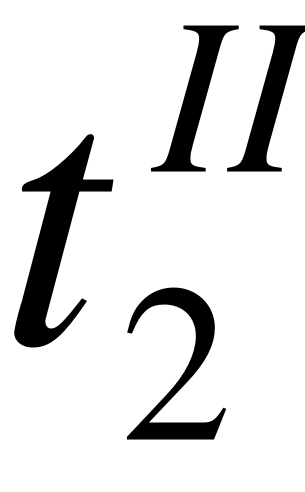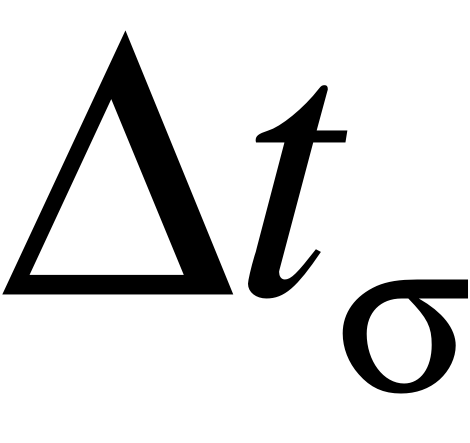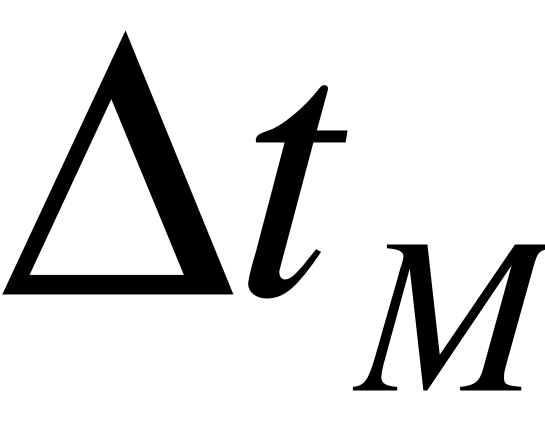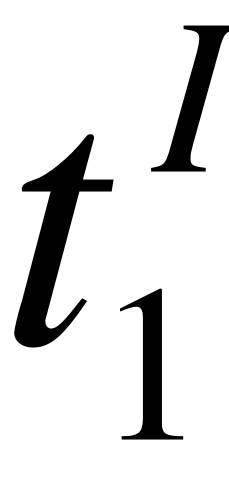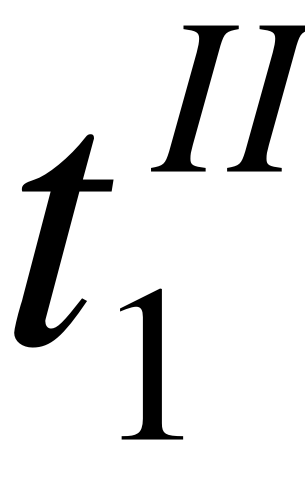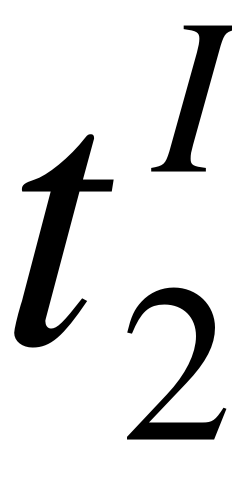

EMBED Equation.3

L( F)

Расчет теплообменного аппарата