Основные методы построения и преобразования схем САУ

Введение

Автоматика - это область науки и техники, охватывающая теорию и принципы построения систем управления, действующих без непосредственного участия человека.

Первые автоматы, т.е. машины, работающие без участия человека, были созданы ещё греческим учёным Героном Александрийским.

Первые автоматические устройства промышленного назначения были разработаны в связи с появлением паровых машин. Во второй половине XIX века появились автоматические устройства, основанные на использовании электрической энергии. Первоначально работы по созданию автоматических систем в механике, электротехнике, теплотехнике и других научных отраслях велись независимо друг от друга.

В настоящее время автоматические системы широко применяются во всех областях деятельности человека - в промышленности, на транспорте, в устройствах связи, при научных исследованиях и др.

Широкое развитие систем автоматического управления, систем и средств автоматизации во всех областях техники и отраслях современного производства связано с разработкой, модернизацией и выпуском в больших количествах разнообразных технических средств автоматики, к которым относятся функциональные элементы и различные автоматические устройства.

Постоянное развитие науки и техники и интенсивное внедрение научно-технических достижений в производство обеспечивают непрерывное пополнение арсенала технических средств автоматики, вытесняя устаревшие элементы новыми, более современными конструкциями.

Главной задачей данной работы является ознакомление с основными методами построения и преобразования схем САУ, а также освоение методов технического расчета, проведения анализа устойчивости и выбора оптимального регулятора.

1 Исследование режимов системы автоматического управления

1.1 Определение передаточной функции замкнутой системы

В качестве исследуемой системы нам была предложена система изображённая на рисунке 1.1:

Рисунок 1.1. Функциональная схема системы регулирования температуры

где UЗ – задающее напряжение;

УС – усилитель;

U – отклонение напряжения;

U1 – входное напряжение регулирования двигателя;

ДВ – двигатель;

1 – угол поворота вала двигателя;

Р – редуктор;

2 – угол поворота вала редуктора;

РО – регулирующий орган;

t1 – температура на входе объекта;

ОР – объект регулирования;

t2 – температура на выходе объекта;

ЧЭ – чувствительный элемент;

UИЗ – измеренное напряжение.

Для того чтобы найти передаточную функцию всей системы, необходимо определить передаточные функции каждого ее элемента.

1. Уравнение регулируемого объекта

Wр.об.(р)=(1 + T1p)t2 = k1t1p= , (1.1)

где k1 – коэффициент передачи;

T1 – постоянная времени ОР;

2. Уравнение регулирующего органа

Wр.ор.(p)= t1 = k22,= k2 , (1.2)

где k2 – коэффициент передачи.

3. Уравнение двигателя вместе с редуктором

Wдв.(p)=(1 + T2p) p2 = k3U1 , (1.3)

где T2 – постоянная времени двигателя;

k3 – коэффициент передачи.

4. Уравнение усилителя

Wус.(p)=U1 = k4 U , (1.4)

5. Уравнение чувствительного элемента

Uиз = k5 t2 , (1.5)

Так как рассматриваемая система содержит обратную связь, то общая передаточная функция будет рассчитываться:

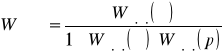
(1.6)

,

Передаточная функция прямой цепи (связи) определяется как функция цепочки последовательно соединенных звеньев. Она будет рассчитываться следующим образом:

(1.7)

,

Подставим данные нам значения в полученные уравнения:

k1 = 0,5

k2 = 1 (С/рад)

k3 = 0,09 (рад/В)

k4 = 4

k5 = 1

T1 = 18 с

T2 = 0,2 с

Uиз = 20 В

T1=1,75; T2=15,4.

Для того чтобы определить тип элементарных звеньев, определим значение коэффициента затухания:

Т.к. >1, следовательно, звено является апериодическим звеном второго порядка.

1.2 Построение логарифмической амплитудной частотной характеристики

Апериодическое звено второго порядка не относится к числу элементарных звеньев, его можно представить как последовательное соединение двух апериодических звеньев первого порядка. Для этого:

Передаточная функция апериодического звена второго порядка:

(1.8)

,

Уравнение асимптотической ЛАЧХ для апериодического звена второго порядка имеет вид:

L()

Построение:

1. Вычисление сопрягающих частот и определение значения 20lgk.

20lg0,15 = 16,5;

1 = = 0,066; lg1 = -1,18;

2 = = 5; lg2 = 0,7

2. Первая асимптота начинается в точке 20lgk и продолжается до точки сопрягающей частоты 1=1/ T3 – начало второй асимптоты, которая откладывается с наклоном – 20дБ/дек. Третья асимптота начинается в точке сопрягающей частоты 2=1/ T4 и имеет наклон уже – 40дБ/дек.

Рисунок 1.2. Амплитудная частотная характеристика апериодического звена второго порядка

1.3 Построение логарифмической фазовой частотной характеристики

Общая ЛФЧХ () будет представлять собой сумму фазовых частотных характеристик апериодических звеньев первого порядка.

() = -arctg T3 - arctg T4 , (1.10)

() = -arctg ·15,2 - arctg ·0,2015 ,

ЛФЧХ в этом случае при 0 асимптотически стремится к оси частот, а при – к прямой = =–2

Таблица 1.1

Данные для построения ФЧХ

	0,001	0,005	0,01	0,05	0,1	1	5
lg	-3	-2,3	-2	-1,3	-1	0	0,69
()	-0,88	-4,4	-8,76	-37,8	-57,8	-97,63	-134,46

10	15	20	25	30	50	75	100
1	1,176	1,3	1,398	1,477	1,7	1,86	2
-153,23	-161,44	-165,87	-168,62	-170,48	-174,26	-176,16	-177,12

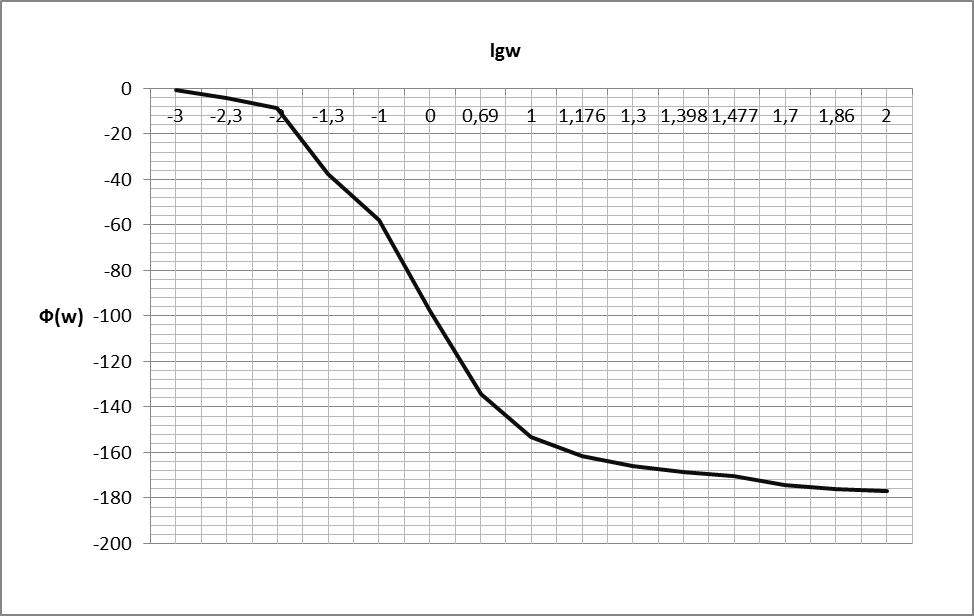
Рисунок 1.3. Фазовая частотная характеристика апериодического звена второго порядка

1.4 Временные характеристики САУ

Важной характеристикой автоматических систем (звеньев) является переходные и импульсные переходные функции и их графики – временные характеристики.

Переходная функция h(t) есть функция, описывающая реакцию системы (звена) на единичное ступенчатое воздействие при нулевых начальных условиях.

При построении переходной характеристики апериодического звена второго порядка используется зависимость:

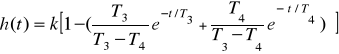
(1.11)

,

Таблица 1.2

Данные для построения переходной характеристики

t	0	1	10	20	30	40
h(t)	0	0,0077	0,0713	0,1092	0,1289	0,139

50	60	70	80	90	100
0,14435	0,147	0,148	0,149	0,1496	0,14979

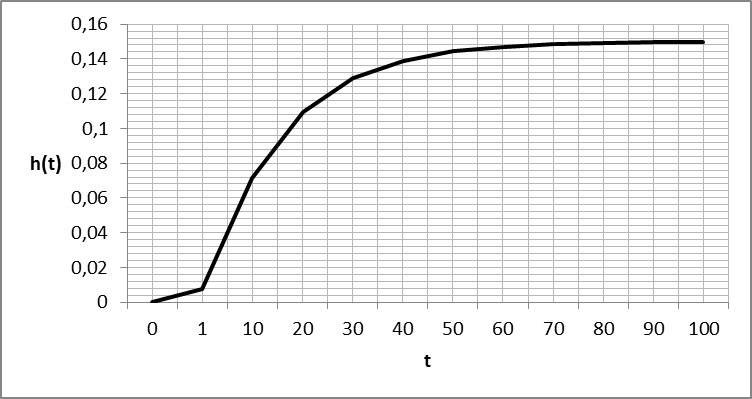
Рисунок 1.4. Переходная характеристика апериодического звена второго порядка

Импульсной переходной, или весовой, функцией системы (звена) называют функцию, описывающую реакцию системы (звена) на единичное импульсное воздействие при нулевых начальных условиях.

Весовая и переходная функции связаны между собой следующим образом:

(t)=h(t)' , (1.12)

Таким образом, дифференцируя выражение (1.11), можно найти весовую функцию апериодического звена второго порядка звена.

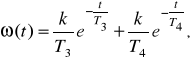
(1.13)

где Т3 и Т4 корни характеристического уравнения передаточной функции.

Таблица 1.3

Данные для построения весовой характеристики

t	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9
(t)	0,754	0,463	0,286	0,178	0,112	0,072	0,047	0,033	0,023	0,018

1	1,2	1,5	1,7	2	2,2	2,5	2,7	3
0,015	0,0111	0,009	0,009	0,0087	0,0093	0,0079	0,0083	0,0081

Рисунок 1.5. Весовая характеристика апериодического звена второго порядка

1.5 Исследование устойчивости САУ

Устойчивость – это свойство системы возвращаться в исходный или близкий к нему установившийся режим после всякого выхода из него в результате какого-либо воздействия.

Для суждения об устойчивости системы практически не требуется находить корней ее характеристического уравнения в связи с тем, что разработаны косвенные признаки, по которым можно судить о знаках действительных частей этих корней и тем самым об устойчивости системы, не решая самого характеристического уравнения. Эти косвенные признаки называются критериями устойчивости.

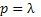
Так как коэффициенты 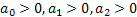, а также определитель Гурвица больше 0, следовательно, САУ устойчива.

2 Синтез системы «объект-регулятор»

2.1 Анализ и синтез оптимальной системы «объект-регулятор». Определение оптимальных параметров настройки П, ПИ, ПИД – регуляторов.

Для различных видов объектов регулирования передаточная функция физически реализуемой оптимальной системы автоматического регулирования является одинаковой (унифицированной). При этом передаточная функция регулятора является «зеркальным отображением» минимально-фазовой части передаточной функции объекта регулирования, а звено чистого запаздывания корректируется интегральной компонентой.

Для объектов регулирования второго порядка с запаздыванием близким к оптимальному является пропорционально-интегрально-дифференциальный (ПИД-) регулятор. Для объектов регулирования первого порядка с запаздыванием близким к оптимальному является пропорционально-интегральный (ПИ-) регулятор.

Согласно заданию, передаточная функция объекта управления имеет вид:

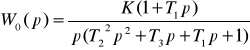
(2.1)

,

К0 = 50;

Т1 = 0,33;

Т2 = 7,4;

Т3 = 8;

= 0,99.

После подстановки числовых значений передаточная функция примет вид:

Далее, находится выражение инверсной расширенной амплитудной - фазовой характеристики объекта.

Согласно формуле:

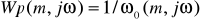
(2.2)

,

получаем:

Так как заданное значение = 0,99, то по формуле (2.2) определяется значение m (m = 0,733) и подставляем его в предыдущее выражение для расширенной амплитудно-фазовой характеристики.

(2.3)

,

Из расширенной амплитудно-фазовой характеристики находятся действительная и мнимая части:

Перед тем, как определить оптимальные параметры настройки П, ПИ, ПИД регуляторов необходимо определить частоту среза объекта, которая находится из выражения для амплитудно-фазовой характеристики объекта управления. АФХ объекта получается после замены оператора р на j в заданной передаточной функции объекта.

Таким образом, АФХ примет вид:

Далее находится АЧХ объекта, на основании которой определяется частота среза.

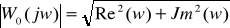
(2.4)

,

АЧХ объекта управления имеет вид:

При нулевой частоте значение амплитуды равно 50. Следовательно, w=wс, откуда по формуле

= 0,03*50 = 1,5.

Таким образом, необходимо решить уравнение:

.

Корни этого уравнения можно найти любым удобным методом, но при этом необходимо учитывать только положительные вещественные корни.

В данном случае для определения корней уравнения используется математический редактор Mathcad, результат расчета приведен на рисунке 2.1.

Рисунок 2.1. Результаты расчета корней уравнения в редакторе Mathcad.

Так как необходимо учитывать только положительные вещественные корни, то решением исходного уравнения являются следующий параметр w=wc = 0,847 с-1.

Для определения оптимальных параметров регулятора необходимо решить уравнение (2.5). Приравняв вещественные и мнимые части в уравнении (2.5) к соответствующим параметрам регулятора.

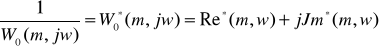
(2.5)

,

Расчет оптимальных параметров настройки для П-регулятора производится по формуле:

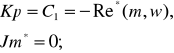
(2.6)

Таким образом, имеем:

Из второго уравнения системы определяется w любым удобным способом с учетом положительных вещественных корней и подставляется в первое уравнение системы. В данном случае w = 0,061 с-1 и оптимальным параметром настройки П – регулятора является значение Кропт = - 0,0008.

Для ПИ-регулятора расчет оптимальных значений параметров настройки производится следующим образом.

Для каждого значения частот от 0 до частоты среза определяются точки С1С0 и С1, соответствующие требуемой степени затухания . Оптимальным параметром является точка на линии, равной степени затухания С1С0 = f(С1), лежащая справа от глобального максимума.

Таким образом, для ПИ – регулятора по формуле (2.7) находятся параметры настройки:

(2.7)

Подставив рассчитанные значения, получаем:

Данные для построения графика зависимости С1С0=f(С1) для ПИ-регулятора приведены в таблице 2.1:

Таблица 2.1

Данные для определения параметров оптимальной настройки ПИ-регулятора

w	C0	C1	C0*C1
0	0	0	0
0,01	-2,74*10-6	-2,85*10-4	7,81*10-10
0,02	-9,88*10-6	-5,57*10-4	5,50*10-9
0,03	-2,03*10-5	-8,20*10-4	1,66*10-8
0,04	-3,37*10-5	-1,08*10-3	3,63*10-8
0,05	-5,03*10-5	-1,34*10-3	6,74*10-8
0,06	-7,13*10-5	-1,60*10-3	1,14*10-7
0,07	-9,86*10-5	-1,87*10-3	1,84*10-7
0,08	-1,35*10-4	-2,16*10-3	2,92*10-7
0,09	-1,83*10-4	-2,47*10-3	4,52*10-7
0,1	-2,48*10-4	-2,80*10-3	6,94*10-7
0,11	-3,35*10-4	-3,19*10-3	1,07*10-6
0,12	-4,50*10-4	-3,60*10-3	1,62*10-6
0,13	-5,98*10-4	-4,07*10-3	2,43*10-6
0,14	-7,88*10-4	-4,58*10-3	3,61*10-6
0,15	-1,03*10-3	-5,16*10-3	5,31*10-6
0,16	-1,33*10-3	-5,82*10-3	7,74*10-6
0,17	-1,70*10-3	-6,54*10-3	1,11*10-5
0,18	-2,15*10-3	-7,36*10-3	1,58*10-5
0,19	-2,70*10-3	-8,27*10-3	2,23*10-5
0,2	-3,34*10-3	-9,28*10-3	3,10*10-5

График зависимости С1С0=f(С1) для ПИ-регулятора приведен на рисунке 2.2.

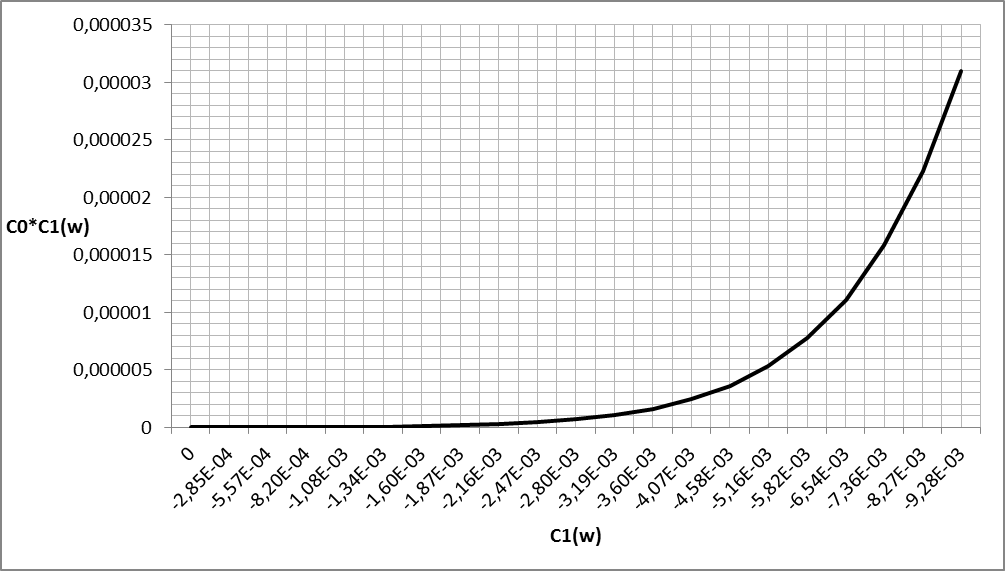
Рисунок 2.2. График зависимости С1С0 = f(C1) для ПИ – регулятора

Необходимо выбрать точку правее глобального максимума. Следовательно можно взять С1 = -2,7*10-2, С1С0 = 5,13*10-4. В результате решения системы уравнений определяются оптимальные параметры настройки,

Оптимальные параметры настройки для ПИД–регулятора в соответствии с формулой (2.8):

, (2.8)

с учетом того, что =0,1, определяются следующим образом:

;

;

Данные для построения графика зависимости С1С0=f(С1) для ПИД-регулятора приведены в таблице 2.2:

Таблица 2.2

Данные для определения параметров оптимальной настройки ПИД-регулятора

w	C0	C1	C0*C1
0,001	0,012349	0,011875	0,000147
0,0025	0,019526	0,018749	0,000366
0,005	0,027613	0,026474	0,000731
0,0075	0,033819	0,032385	0,001095
0,01	0,03905	0,03736	0,001459
0,0125	0,04366	0,041734	0,001822
0,015	0,047825	0,045684	0,002185
0,0175	0,051656	0,049311	0,002547
0,02	0,055221	0,052684	0,002909
0,025	0,061737	0,058838	0,003632
0,03	0,067627	0,064392	0,004355

Продолжение таблицы 2.2.

0,035	0,073042	0,069491	0,005076
0,04	0,07808	0,074229	0,005796
0,045	0,082813	0,078673	0,006515
0,05	0,08729	0,082869	0,007234

График зависимости С1С0=f(С1) для ПИД-регулятора приведен на рисунке 2.3.

Рисунок 2.3. График зависимости С1С0 = f(C1) для ПИД-регулятора

Необходимо выбрать точку правее глобального максимума. Следовательно, можно взять С1 = 0,0907, С1С0 = 0,0087.

В результате решения системы уравнений определяются оптимальные параметры настройки:

,

,

.

2.2 Построение переходных характеристик синтезированной системы «объект – регулятор» в среде MATLAB

В соответствии с заданием курсовой работы необходимо выполнить проверку рассчитанных параметров регуляторов в программах электронного моделирования. С помощью пакета Simulink программы MATLAB строится модель исследуемой системы с различными типами регуляторов и по виду переходной характеристики выбирается оптимальный регулятор.

Модель исследуемой системы с П-регулятором приведена на рисунке 2.4.

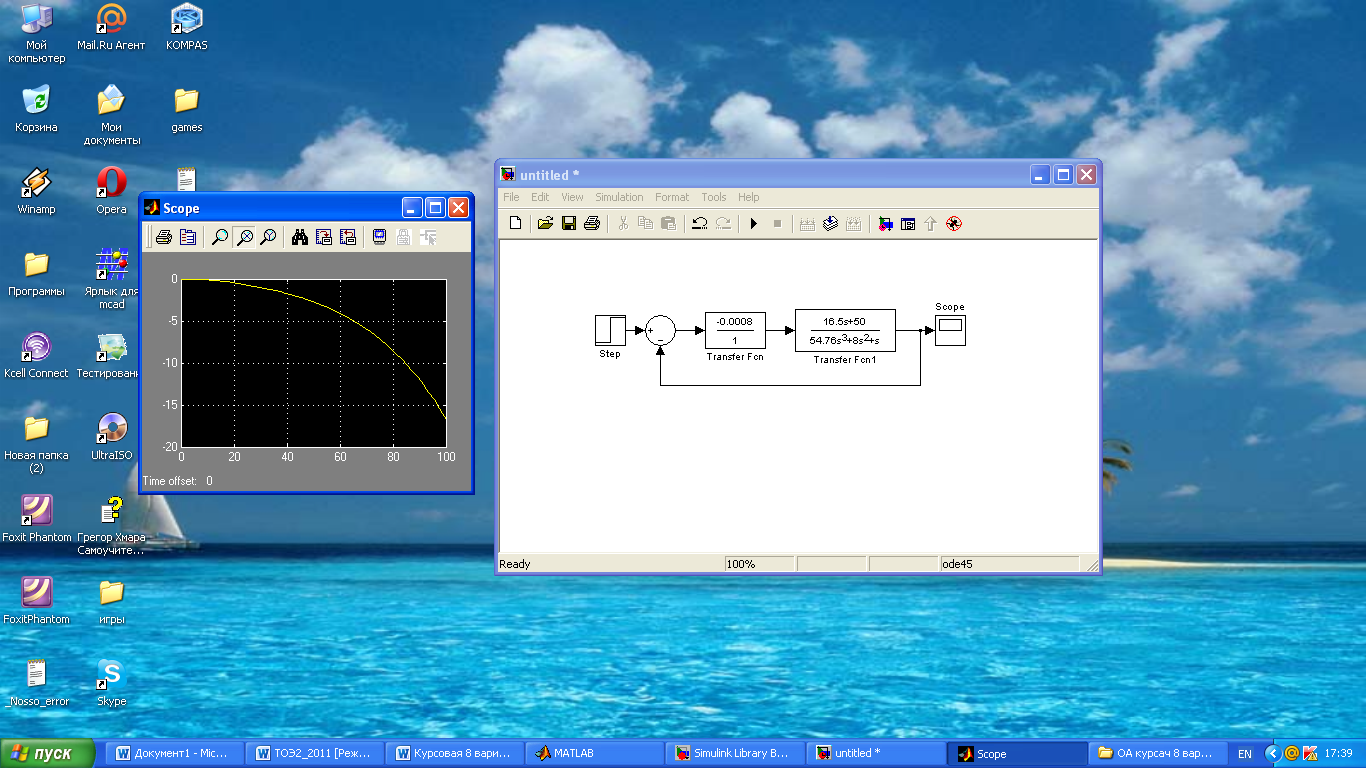
Рисунок 2.4. Модель системы с П-регулятором

Переходная характеристика системы с П-регулятором приведена на рисунке 2.5.

Рисунок 2.5. Переходная характеристика с П-регулятором

ПИ-регулятор можно представить как параллельное соединение пропорционального и интегрирующего звеньев. Коэффициент передачи пропорционального звена в соответствии с расчетом, приведенным выше, равен -0,027 коэффициент передачи интегрирующего звена равен .

Таким образом, модель исследуемой системы с ПИ-регулятором приведена на рисунке 2.6.

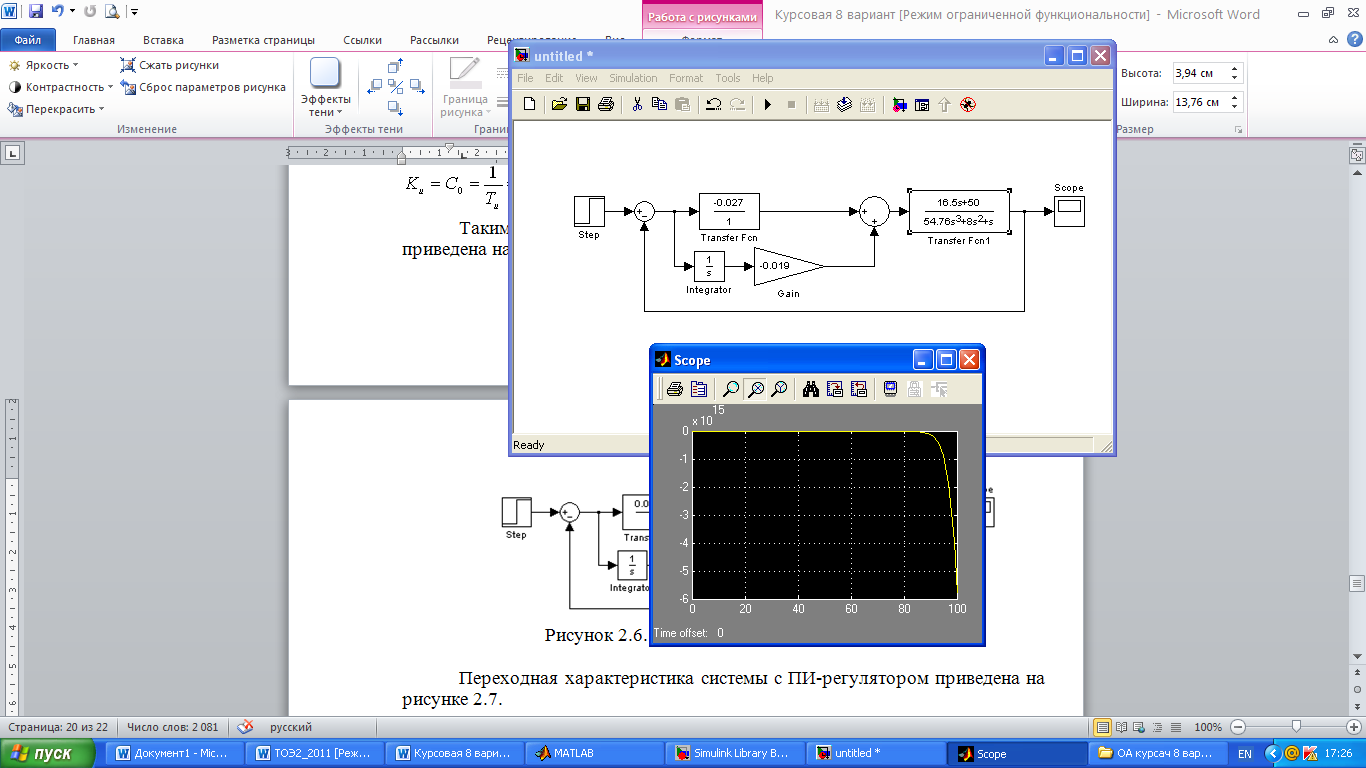
Рисунок 2.6. Модель системы с ПИ-регулятором

Переходная характеристика системы с ПИ-регулятором приведена на рисунке 2.7.

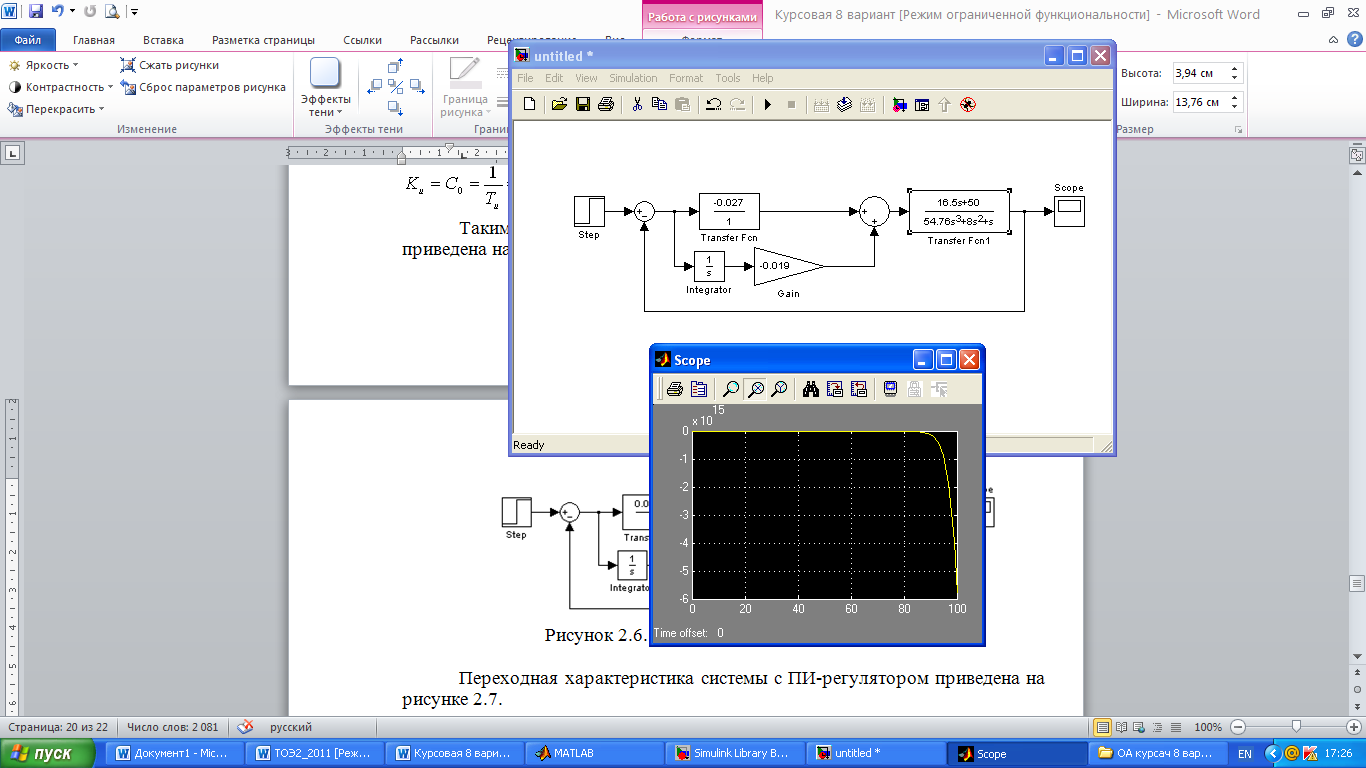
Рисунок 2.7. Переходная характеристика системы с ПИ-регулятором

ПИД-регулятор можно представить как параллельное соединение пропорционального, интегрирующего и дифференцирующего звеньев. Коэффициент передачи пропорционального звена в соответствии с расчетом, приведенным выше, равен 0,168 коэффициент передачи интегрирующего звена равен , коэффициент передачи дифференцирующего звена равен .

Модель исследуемой системы с ПИД-регулятором приведена на рисунке 2.8.

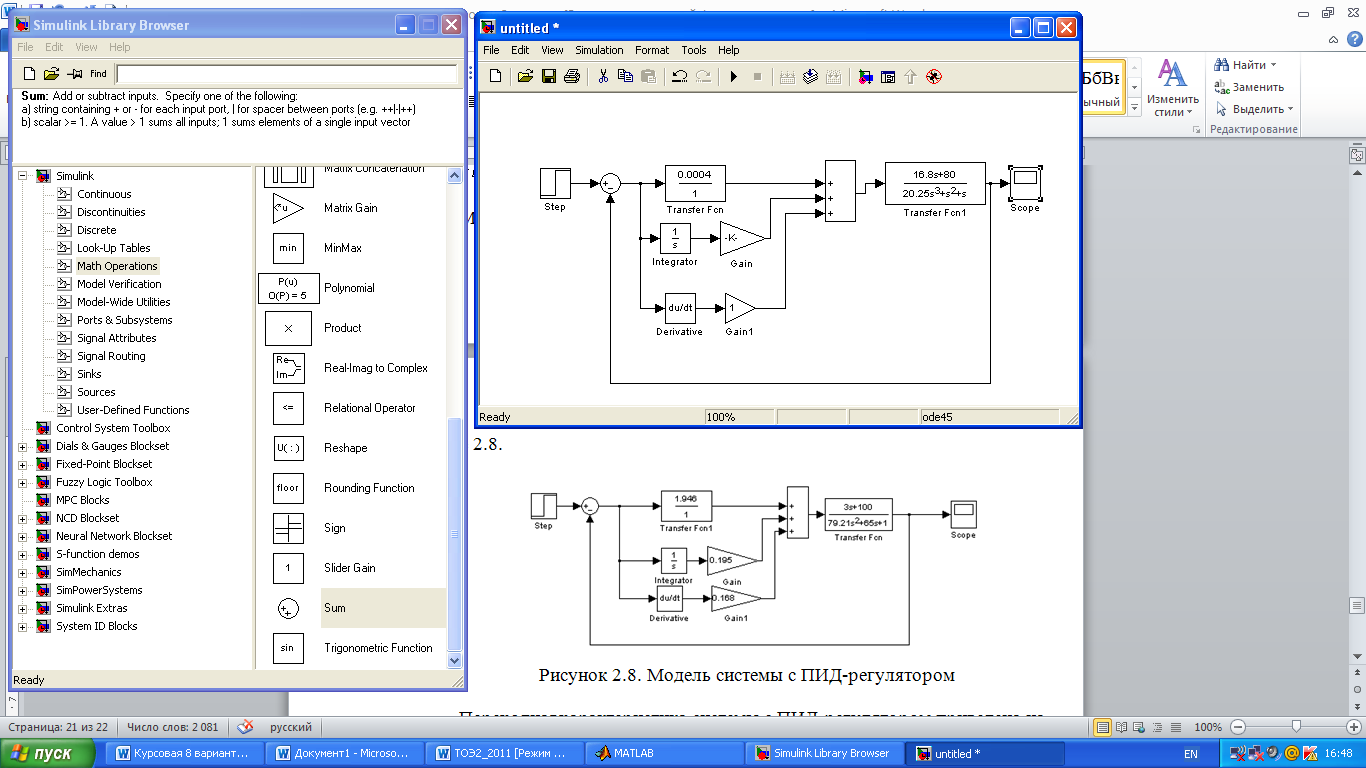
Рисунок 2.8. Модель системы с ПИД-регулятором

Переходная характеристика системы с ПИД-регулятором приведена на рисунке 2.9.

Рисунок 2.9. Переходная характеристика системы с ПИД-регулятором

Заключение

В ходе выполнения данной работы исследования режимов автоматического управления, построены: временные, логарифмические и фазовые характеристики. Определены оптимальные параметры настройки П, ПИ, ПИД-регуляторов. На основании полученных характеристик можно сделать вывод, что для заданного объекта управления оптимальным является П-регулятор, так как у ПИ-регулятора наблюдается малое время переходного процесса, но достаточно большая статическая ошибка, а у ПИД-регулятора, перерегулирование.

Список литературы