Теорія автоматичного керування (ТАК)

1 ВСТУП

Технічний прогрес характеризується неперервним ростом автоматизації виробництва в усіх галузях народного господарства.

Від автоматизації окремих установок і агрегатів в наш час переходять до комплексної автоматизації і створенню автоматичних цехів та заводів-автоматів, які забезпечують максимальне підвищення продуктивності праці, зниження собівартості продукції і підвищення культури виробництва.

Тільки завдяки автоматизації стало можливим здійснення ряду найбільш прогресивних технологічних процесів, створення нових сучасних видів повідомлень і засобів зв’язку.

Для розробки та ефективної експлуатації автоматичних систем регулювання (АСР) необхідно знати загальні закони їх побудови і дії, методи дослідження і настройки. Ці питання вивчає наука про автоматичні системи керування.

Теорія автоматичного керування (ТАК) – наукова дисципліна, предметом вивчення якої є системи, які складаються з об’єкта та пристрою керування (автоматичного регулятора) і допоміжних елементів. ТАК виявляє загальні закономірності функціонування, які притаманні автоматичним системам різної природи і на основі цього розробляє принципи побудови ефективних систем для керування об’єктами різного призначення. При вивченні процесів керування в ТАК абстрагуються від фізичних та конструктивних особливостей систем і замість реальних систем розглядаються їх адекватні математичні моделі. За допомогою цих моделей розв’язуються основні задачі ТАК – аналізу та синтезу автоматичних систем. При цьому широко використовуються математичні методи – теорія диференціальних рівнянь, теорія функцій комплексної змінної, перетворення Лапласа і Фур’є, матриці і т.д.

Головними задачами теорії автоматичного керування є дві – задачі аналізі та синтезу. В першому випадку задається система та її параметри і необхідно визначити властивості системи, в другому випадку задаються вимоги і необхідно створити систему, яка відповідала б цим вимогам. Друга задача є більш складною і, як правило, немає однозначного розв’язку. Названі задачі розв’язуються на основі математичного опису елементів та системи в цілому,

що дає можливість дослідити усталені та перехідні процеси в них. Одним з підходів отримання математичного опису системи є розбиття її на окремі ланки, для кожної з них визначаються закономірності перетворення вхідного сигналу у вихідний. При цьому виділення ланок здійснюється, виходячи із зручності математичного опису.

2 ДОСЛІДЖЕННЯ ОБ’ЄКТА РЕГУЛЮВАННЯ

Дослідження об’єкта регулювання представляє собою визначення його статичних та динамічних характеристик за каналами керувальних та збурювальних діянь. Для проведення даного дослідження потрібно визначити еквівалентні передаточні функції кожної ємності заданого об’єкта за каналами різних діянь, скласти структурну схему об’єкта та визначити його передаточні функції за каналами збурення та управління.

2.1 ЗАВДАННЯ ОБ’ЄКТА УПРАВЛІННЯ

Властивості об’єкта за каналами збурювальних та керувальних діянь аналізуються моделюванням на ЕОМ. За потреби спочатку виконуються структурні перетворення.

В даній курсовій роботі об’єкт задається у вигляді системи диференціальних рівнянь:

(2.1.1)

де індекси і = 1,2,3 відносяться до першої, другої та третьої ємностей об’єкта;

- стала часу і – ї ємкості;

- відхилення вихідної величини і – ї ємкості від початку;

- коефіцієнт передачі і – ї ємності об’єкта за каналом управління;

- зміна клерувального діяння, прикладена до і – ї ємності об’єкта;

- коефіцієнт передачі і – ї ємності за каналом збурення;

- зміна збурю вального діяння, прикладеного до і – ї ємності об’єкта;

- коефіцієнт передачі відповідно від попередньої та наступної

ємностей;

- час.

Коефіцієнти рівнянь мають такі значення

T1=30 T2=50 T3=30 K1U=0,6 K2U=0 K3U=0

K1Z=0.4 K2Z=0 K3Z=0.2 K12=0.8 K21=0 K23=0.9

К32=0.3 Z1=30 Z2=0 Z3=20

Підставимо в систему (1) значення коефіцієнтів, що дорівнюють 0 і отримаємо систему (2)

2.2 Визначення передаточних функцій

об’єкта регулювання

За пишемо систему рівнянь (2) в операторному вигляді

Визначимо значення

З системи рівнянь (4) визначимо передаточні функції ланок системи

Структурна схема об’єкту регулювання показана на рисунку 1.

Рисунок 1 – Вихідна структурна схема об’єкта

Визначимо передаточні функції об’єкту за каналами управління і збурення:

Після підстановки значень в рівняннях (12) значень передаточних функцій отримаємо рівняння (13):

(13)

2.3 Визначення статичних та динамічних

характеристик об’єкта регулювання

Статичні характеристики об’єкта визначимо за передаточними функціями. Для визначення статичних характеристик замінимо зображення похідних нулями.

Статичні характеристики матимуть такий вигляд:

Управляючий та збурюючий впливи вимірюються у відсотках ходу регулюючого органу. Повний діапазон зміни від повного закриття до повного відкриття становить 100%. Графіки статичних характеристик показані на рисунку 2.

Графік кривої розгону – це залежність вихідної величини від часу, що минув від моменту подачі стрибкоподібного одиничного сигналу на вхід каналу. Графіки кривих розгону показано на рисунках 3, 4,5.

Рисунок 2 – Графіки статичних характеристик.

Рисунок 3 – Графік кривої розгону по каналу управління U1.

=22 с, Ті=223 с, k=0.7529.

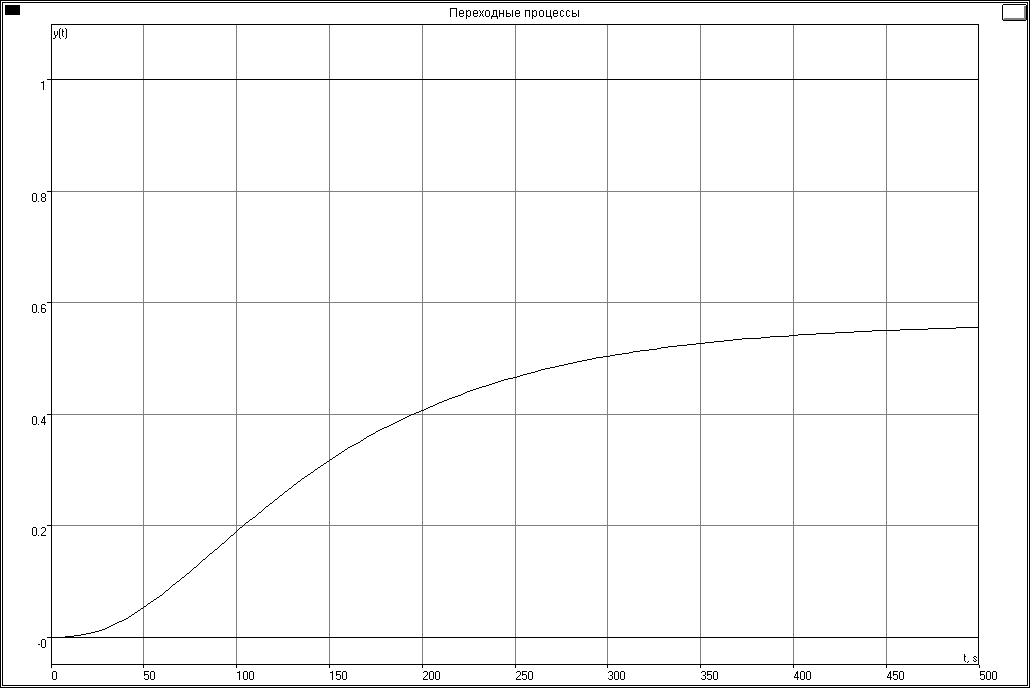
Рисунок 4 – Графік кривої розгону по каналу збурення Z1.

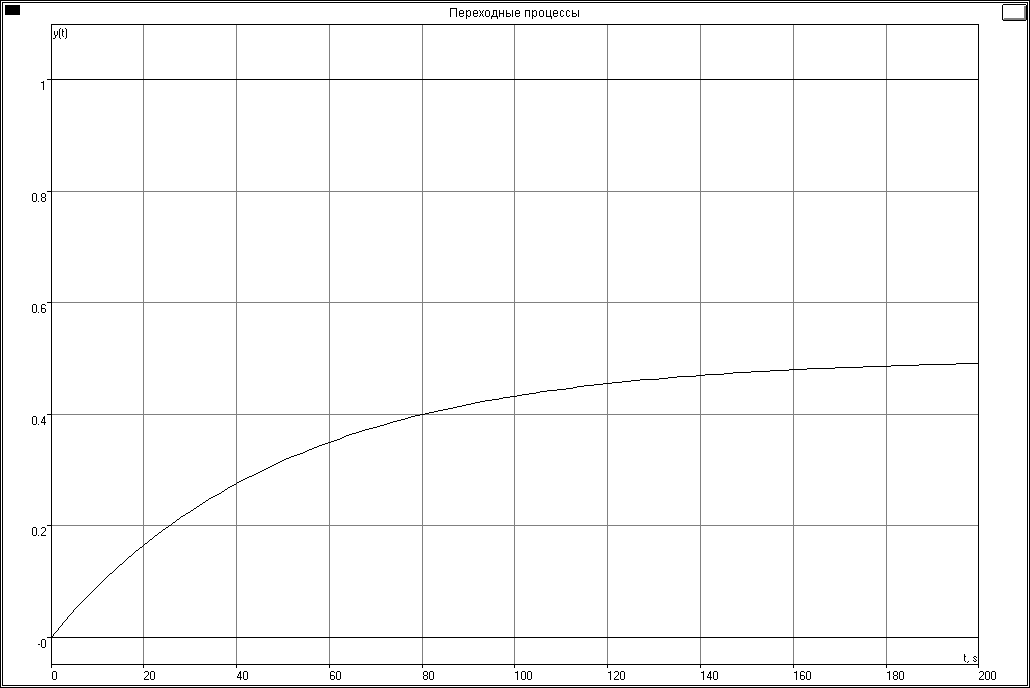
Рисунок 5 – Графік кривої розгону по каналу збурення Z3.

Для побудови амплітудно-фазної характеристики об’єкта необхідно зробити заміну в передаточній функції р на j. Після такого перетворення отримують частотну характеристику W(j).

або

Помнижимо всі дроби (16) на число спряжене з знаменником

Після цього необхідно виділити дійсну та уявну частини.

(18)

Амплітудну частотну характеристику будують за формулою

Фазову частотну характеристику будують за формулою

Підставимо значення змінних в формули (19) та (20)

Графіки частотних характеристик об’єкта показані нижче на рисунках 6,7,8,9,10,11.

Рисунок 6 – Графіки АЧХ і ФЧХ каналу U1.

Рисунок 7 – Графік АФХ по каналу U1.

Рисунок 8 – Графіки АЧХ і ФЧХ каналу Z1.

Рисунок 9 – Графіки АФХ каналу Z1.

Рисунок 10 – Графіки АЧХ і ФЧХ по каналу Z3.

Рисунок 11 – Графік АФХ по каналу Z3.

3 РОЗРОБЛЕННЯ ТА ДОСЛІДЖЕННЯ СИСТЕМИ АВТОМАТИЧНОГО РЕГУЛЮВАННЯ

3.1 Вибір закону регулювання

Закон регулювання вибирається на основі вимог до якості процесу регулювання. Оцінюють можливість використання стандартних регуляторів в одноконтурній САР.

Структурна схема одноконтурної САР має вигляд, зображений на рисунку 12.

Рисунок 12 – Структурна схема одноконтурної САР за відхиленням.

Синтез системи регулювання починається з перевірки відповідності статичної похибки, що виникає в статичних системах її допустимому значенню. Похибка в САР має дві складові

Хзад ()– похибка відтворення завдання,

XZ() – похибка створена збуренням.

Об’єкт має властивість самовирівнювання. Для стабілізації значення вихідного сигналу обираємо П-регулятор.

За кривою розгону по каналу управління визначимо значення Тоб=223 с, об=22 с, Коб=0.7529.

Відношення . За графіком визначимо значення . Оскільки Коб=0.7529 то .

Схема об’єкта регулювання з П-регулятором зображена на рисунку 13, а графік перехідного процесу зображений на рисунку 14.

Рисунок 13 – Схема САР з П-регулятором

Рисунок 14 – Процес регулювання з П-регулятором.

3.2 Аналіз стійкості системи та її корекція

Розроблена САР перевіряється на стійкість. Для цього використовуються частотний критерій стійкості – годограф Михайлова.

Для визначення стійкості за критерієм Михайлова використовується аналіз характеристичного полінома системи.

Вираз можна подати у вигляді суми дійсної та уявної частини:

UD() – дійсна частина, складена з членів з парними степенями .

VD() – уявна частина, яка утримує члени з непарними степенями .

Характеристичний поліном визначений з передаточної функції системи автоматичного регулювання має вигляд

Для стійкості системи необхідно щоб при зміні частоти від нуля до безкінечності кут повороту визначається за формулою =n/2. Так як n=6 то необхідний кут =6/2=3. Для стійкості системи достатньо щоб серед всіх n коренів рівняння не було розвязків на уявній комплексній площині і перетворюючих в нуль комплексний поліном D(j). Критерій стійкості зображено на рисунках 15-16. З рисунків видно, що система стійка, так як кут повороту годографа Михайлова =3, графік виходить з точки (0,68;0) на додатній півосі дійсної осі і огинає точку (0,0).

Рисунок 15 – Годограф Михайлова.

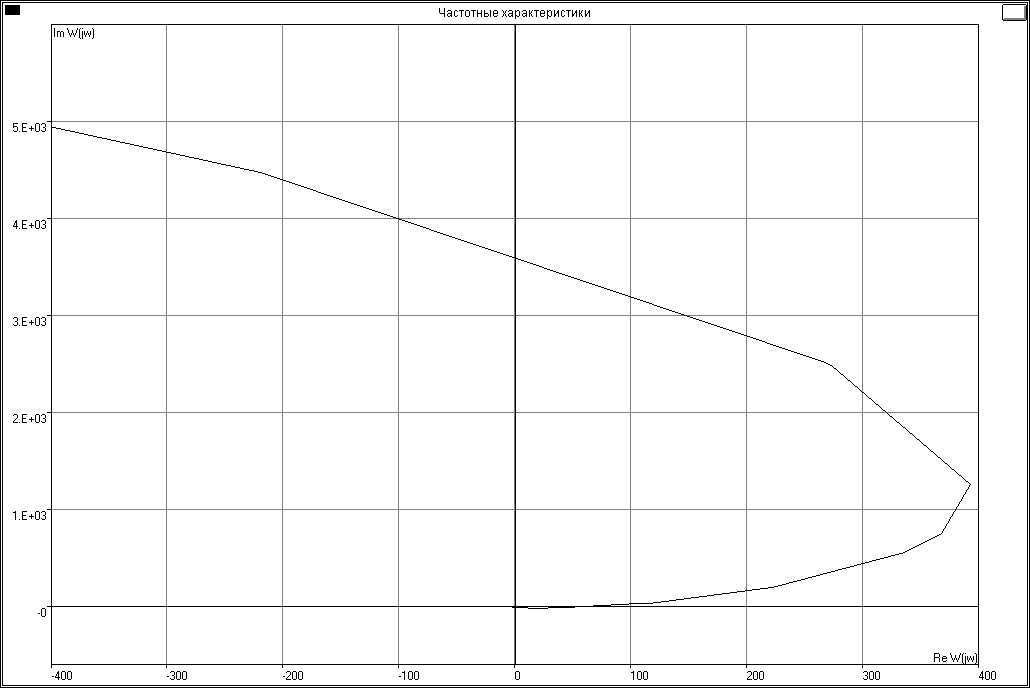
Рисунок 16 – Годограф Михайлова збільшено

3.3 Параметрична оптимізація системи

Параметрична оптимізація розробленої АСР полягає в знаходженні оптимальних параметрів настройки регулятора, що забезпечують найкраще значення критерія якості перехідного процесу. Залежно від поставлених перед автоматичною системою регулювання задач критеріями якості можуть бути час регулювання, інтегральні оцінки.

При пропорційному законі регулювання і коефіцієнті підсилення Кр=10.6 кінцеве значення вихідної величини Х3=20,7729 статична похибка регулювання =20-20.7729=-0.7729. Для покращення процесу регулювання необхідно використати регулятор, що відпрацьовує пропорційно-інтегральний закон регулювання.

Визначення оптимальних параметрів настройки ПІ – регулятора проводять в наступній послідовності. Визначимо відношення Tоб/об. Для даного об’єкта регулювання це відношення становить . За графіком значення Тиз.опт/об=3.5 оскільки об=22 с, то Тиз.опт.=3.522=77 с. По кривій КобКр знаходимо КобКр.опт=6. Знаючи, що Коб=0.7529 знаходимо Кр.опт=6/0.7529=7.926. На рисунку 19 показано процес регулювання.

Схема об’єкта регулювання з ПІ-регулятором зображена на рисунку 17, а графік перехідного процесу зображений на рисунку 18.

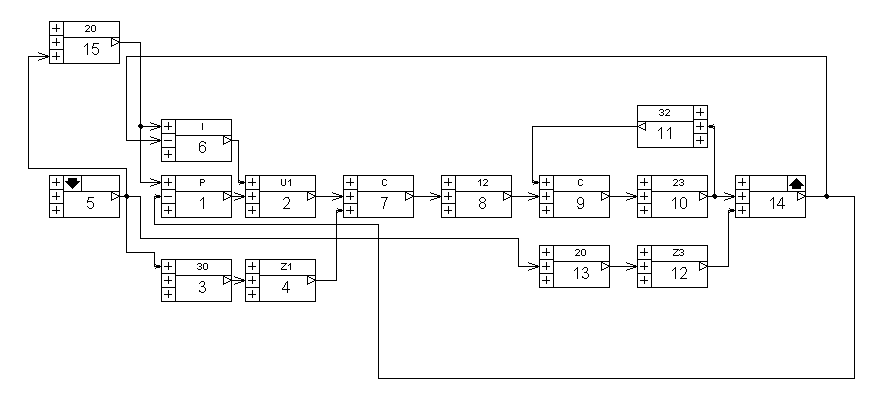
Рисунок 17 – Схема САР з ПІ-регулятором

Рисунок 18– Процес регулювання при оптимальних параметрах настройки

3.4 Оцінка чутливості системи

Для оцінки чутливості системи до зміни параметрів настройки регулятора необхідно проаналізувати вплив на перехідні процеси зміни параметрів настройки регулятора. Процес регулювання з ПІ-регулятором при змінених на 20% настройках наведено на рисунках 19 та 20.

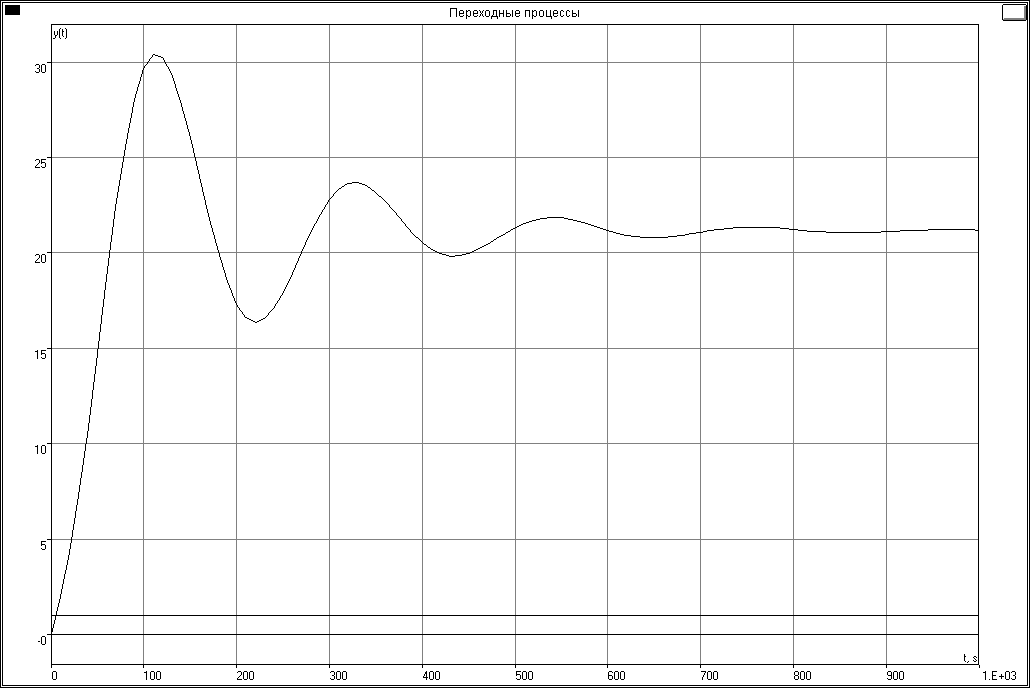
Рисунок 19 – Процес регулювання при параметрах настройки зменшених на 20%

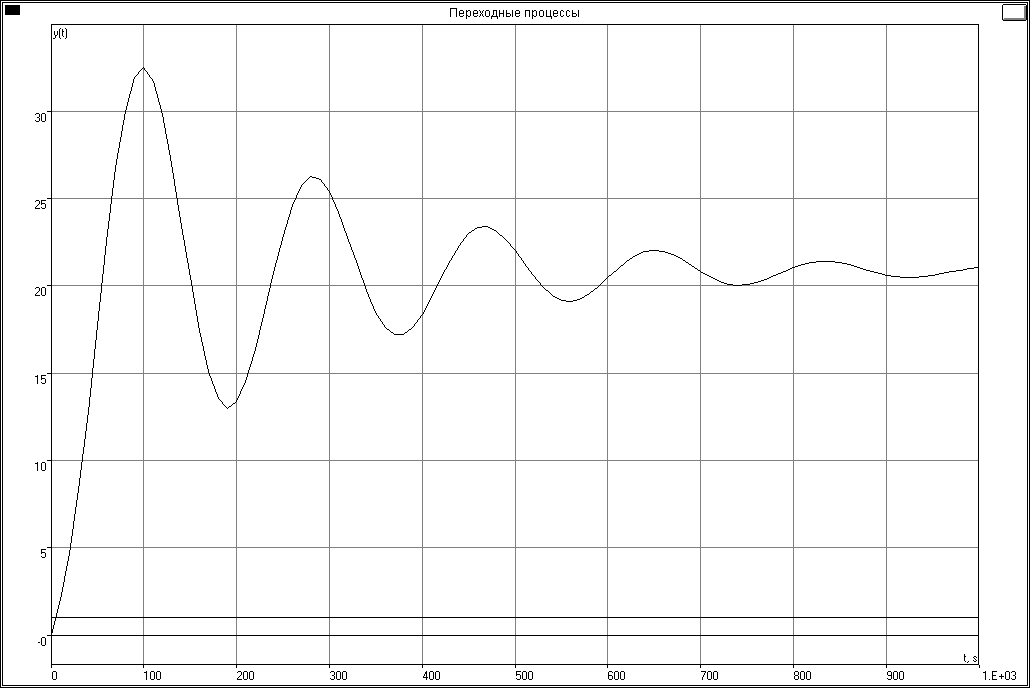
Рисунок 20 – Процес регулювання при параметрах настройки збільшених на 20%

4 ВИСНОВОК

При виконанні курсової роботи визначено передаточні функції динамічних ланок, сукупність яких представляє собою об’єкт регулювання. На основі визначених передаточних функцій і побудованої структурної схеми об’єкта визначені його статичні та динамічні характеристики: визначені крива розгону об’єкта за каналами управління та регулювання, фазо – частотна, амплітудо-частотна, амплітудно-фазна характеристики. Вибраний П-закон регулювання і система автоматичного регулювання з П – регулятором досліджена на стійкість за критерієм Михайлова. Отримана система стійка, але точність не задовольняє поставленим вимогам, тому замість П регулятора використано ПІ регулятор для якого знайдені оптимальні параметри настройки. Також проведено оцінку чутливості системи до збурюючих впливів та змін параметрів настройки регулятора.

СПИСОК ЛІТЕРАТУРИ

1 Ладанюк А.П. теорія автоматичного керування: Курс лекцій – частина перша – К.:НУХТ, 2004. – 184 с.

2 Автоматизація технологічних процесів і виробництв харчової промисловості: Підручник/Ладанюк А.П., Трегуб В.Г., Ельперін І.В., Цюцюра В.Д. – К.:Аграрна освіта, 2001. – 224 с

3 Гордин Е.М., Стародуб К.Я. Автоматическое регулирование. Учеб. Пособие для техникумов. М., «Высш. школа», 1976. 352 с. с ил.

4 Конспект лекцій.

Арк.

Дата

Підпис

№ докум.

Арк.

Змн.

Арк.

Дата

Підпис

№ докум.

Арк.

Змн.

Арк.

Дата

Підпис

№ докум.

Арк.

Змн.

Арк.

Дата

Підпис

№ докум.

Арк.

Змн.

Арк.

№ докум.

Підпис

Дата

Арк.

Змн.

Арк.

№ докум.

Підпис

Дата

Арк.

Дата

Підпис

№ докум.

Арк.

Змн.

Арк.

Дата

Підпис

№ докум.

Арк.

Змн.

Арк.

Дата

Підпис

№ докум.

Арк.

Змн.

Арк.

№ докум.

Підпис

Дата

Арк.

Змн.

Арк.

№ докум.

Підпис

Дата

Арк.

Дата

Підпис

№ докум.

Арк.

Змн.

Арк.

Дата

Підпис

№ докум.

Арк.

Змн.

Арк.

№ докум.

Підпис

Дата

Арк.

Змн.

Арк.

№ докум.

Підпис

Дата

Арк.

Дата

Підпис

№ докум.

Арк.

Змн.

Арк.

Дата

Підпис

№ докум.

Арк.

Змн.

Арк.

Дата

Підпис

№ докум.

Арк.

Дата

Підпис

№ докум.

Арк.

Змн.

Арк.

№ докум.

Підпис

Дата

Арк.

Дата

Підпис

№ докум.

Арк.

Змн.

Арк.

Дата

Підпис

№ докум.

Арк.

Змн.

Арк.

№ докум.

Підпис

Дата

Арк.

Змн.

Арк.

№ докум.

Підпис

Дата

Арк.

Дата

Підпис

№ докум.

Арк.

Змн.

Арк.

№ докум.

Підпис

Дата

Арк.

Дата

Підпис

№ докум.

Арк.

Змн.

Арк.

Дата

Підпис

№ докум.

Арк.

Змн.

Теорія автоматичного керування (ТАК)