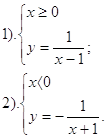Графіки та їх функції
Новомосковський колегіум №11
Реферат по геометрії
«Графіки та їх функції»
Учня 9-А класу
Зінченко Даниїла
Зміст.
Глава I. Історія виникнення.
1.1 Виникнення і поняття функції в стародавньому світі.
1.2 Виникнення і поняття функції в стародавньому Єгипті.
1.3 Виникнення і поняття функції в Стародавньому Вавилоні.
1.4 Виникнення і поняття функції в Стародавній Греції.
1.5 Графічне зображення залежностей, історія виникнення.
1.6 Внесок у розвиток графіків функцій Рене Декартом.
Глава II. Визначення функцій.
2.1 Основні поняття про функції.
2.2 Способи завдання функцій.
Глава III. Дослідження функцій та їх графіків.
3.1 Найпростіші функції та їх графіки.
3.2 Тригонометричні функції.
3.3 Криві другого порядку.
Глава IV. Методи побудови графіків функцій.
4.1 Паралельний перенос.
4.1.1 Перенесення уздовж осі ординат.
4.1.2 Перенесення уздовж осі абсцис.
4.2 Відображення.
4.2.1 Побудова графіка функції виду y = f (-x)
4.2.2 Побудова графіка функції виду y = - f (x)
4.2.3 Побудова графіків парної і непарної функцій.
4.2.4 Побудова графіка оберненої функції.
4.3 Деформація.
4.3.1 Деформація графіка вздовж осі ординат.
4.3.2 Деформація графіка вздовж осі абсцис.
4.4 Алгебраїчні операції над графіками функцій.
4.4.1 Графік суми (різниці) функцій.
4.4.2 Графік твори функцій.
4.4.3 Графік функції виду.
4.4.4 Графік приватного двох функцій.
4.5 Побудова графіків складних функцій.
4.5.1 Графік функції у = [f (x)] k.
4.5.2 Графік функції у = af (x)
Глава V: Графіки нетрадиційних функцій.
Глава I. Історія виникнення
1.1 Виникнення і поняття функції в стародавньому світі
Поняття функції сягає своїм корінням в ту далеку епоху, коли люди вперше зрозуміли, що оточуючі їх явища взаємопов'язані. Вони ще не вміли рахувати, але вже знали, що, чим більше оленів вдасться вбити на полюванні, тим довше плем'я буде позбавлено від голоду, чим довше горить багаття, тим тепліше буде в печері.
З розвитком скотарства і землеробства, ремесла та обміну збільшилася кількість відомих людям залежностей між величинами. Багато хто з них виражалися за допомогою чисел. Це дозволило формулювати їх словами "більше на", "менше на", "більше в стільки-то разів". Якщо за одного бика давали 6 овець, то двох биків обмінювали на 12 овець, а трьох биків на 18 овець. Такі розрахунки призвели до виникнення поняття про пропорційність величин.
1.2 Виникнення і поняття функції в стародавньому Єгипті
Але коли виникли перші цивілізації, утворилися великі (за тодішніми масштабами), армії, почалося будівництво гігантських пірамід, то знадобилися писарі, які враховували надходять податки, визначали кількість цегли, потрібне для зведення палаців, підраховували, скільки продовольства треба заготовити для далеких походів. Від одного покоління переписувачів до іншого переходили правила вирішення завдань, щоб вирішити такі завдання, треба було знати, як залежать обсяги геометричних фігур від їх розмірів, вміти враховувати нахил насипу. Деякі єгипетські завдання показують, що в той час вміли навіть обчислити об'єм піраміди
1.3 Виникнення і поняття функції в Стародавньому Вавілоні
Високого рівня досягла математика в Стародавньому Вавілоні. Щоб полегшити обчислення, вавилоняни склали таблиці зворотних значень чисел, таблиці квадратів і кубів чисел і навіть таблиці для суми квадратів чисел їх кубів. Говорячи сучасною мовою, це було табличное завдання функцій y = 1 / x, y = x2, y = x3, y = x2 + x3
Користуючись такими таблицями, вавилоняни могли вирішувати і зворотні завдання - за заданим обсягом куба знаходити довжину його сторони, тобто Витягувати кубічні корені. Вони вміли навіть розв'язувати рівняння виду x2 + x3 = a. Були у вавилонян і таблиці функцій двох змінних, наприклад таблиці додавання і множення. Користуючись різними таблицями, вони могли вирахувати і довжину гіпотенузи по довжинах катетів, тобто Знаходити значення функції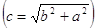
Зрозуміло, шлях від появи таблиць до створення загального поняття функціональної залежності був ще дуже довгий, але перші кроки по цьому шляху вже були зроблені.
1.4 Виникнення і поняття функції в Стародавній Греції
У Стародавній Греції наука прийняла інший характер, ніж в Єгипті та в Вавилоні. З'явилися професійні вчені, які вивчали саму математичну науку, займалися строгими логічними висновками одних тверджень з інших. Багато чого з того, що робили давньогрецькі математики, теж могло призвести до виникнення поняття про функції. Вони вирішували завдання на побудову і дивилися, при яких значеннях задача має рішення, вивчали, скільки рішень може мати ця задача, і т.д. Стародавні греки знайшли багато різних кривих, невідомих переписувачам Єгипту і Вавилона, вивчали залежності між відрізками діаметрів і хорд в колі, еліпсі та інших лініях. Але все ж давньогрецькі математики не створили загального поняття функції.
1.5 Графічне зображення залежностей, історія виникнення
Дослідження загальних залежностей почалося в 14 столітті. Середньовічна наука була схоластичної. Для доказу своєї правоти вчені вдалися чи не до досвіду, а до цитат з Аристотеля і Платона або до посилань на біблійні оповіді. При такому характері "наукових дискусій" не залишалося місця вивченню кількісних залежностей, йшлося лише про якості предметів та їх зв'язках один з одним. Але серед схоластів виникла школа, що стверджувала, що якості можуть бути більш або менш інтенсивними (плаття людини, який звалився в річку, мокріша, ніж у того, хто лише потрапив під дощ)
Французький вчений Микола Оресм став зображати інтенсивність довжинами відрізків. Коли він мав у своєму розпорядженні ці відрізки перпендикулярно деякої прямої, їх кінці утворювали лінію, названу ним "лінією інтенсивностей" або "лінією верхнього краю". Сучасний читач відразу впізнає в ній графік відповідної функціональної залежності. Оресм вивчав навіть "площинні" і "тілесні" якості, тобто функції, залежні від двох або трьох змінних.
Важливим досягненням Оресма була спроба класифікувати отримані графіки. Він виділив три типи якостей: рівномірні (з постійною інтенсивністю), рівномірно-нерівномірні (з постійною швидкістю зміни інтенсивності) і нерівномірно-нерівномірні (всі інші), а також характерні властивості графіків таких якостей.
Ідеї Оресма на багато обігнали тодішній рівень науки. Щоб розвивати їх далі, потрібно було вміти висловлювати залежності між величинами не тільки графічно, але і за допомогою формул, а буквеній, алгебри в той час не існувало. Лише після того, як протягом 16 століття була поступово створена буквена алгебра, вдалося зробити наступний крок у розвитку поняття функції.
1.6 Внесок у розвиток графіків функцій Рене Декартом
Щоб створити математичний апарат для вивчення графіків функцій, знадобилося поняття змінної величини. Це поняття було введено в науку французьким філософом і математиком Рене Декартом (1596-1650). Саме Декарт прийшов до ідей про єдність алгебри і геометрії і про роль змінних величин, він зруйнував прірву, що лежала з часів давньогрецької математики, між геометрією і арифметикою.
Щоб звільнити алгебру від невластивого їй геометричного мови, Декарт ввів фіксований одиничний відрізок і став розглядати відносини інших відрізків до нього.
При записи залежностей між величинами Декарт став застосовувати літери. При цьому операціями над величинами відповідали операції над буквами. Тепер уже для перетворення однієї залежності в іншу не треба було писати громіздких пропорцій, вивчати подібні трикутники і перетворювати геометричні фігури. Досить було по твердо, встановленим правилам робити алгебраїчні перетворення, причому всі ці перетворення проводилися загалом, вигляді.
Таким чином, графіки функцій за весь час свого існування пройшли через ряд фундаментальних перетворень, що привели їх до того виду, до якого ми звикли. Кожен етап або щабель розвитку графіків функцій - невід'ємна частина історії сучасної алгебри та геометрії.
Глава II. визначення функцій
2.1 Основні поняття про функції
Величини, що беруть участь в одному і тому ж явищі, можуть бути взаємопов'язані, так що зміна одних з них тягне за собою відповідну зміну інших. Наприклад, збільшення (або зменшення) радіусу кола веде до обов'язкового збільшення (або зменшення) його площі. У таких випадках кажуть, що між змінними величинами існує функціональна залежність, причому одну величину називають функцією, або залежною змінною (е часто позначають буквою у), а іншу - аргументом, або незалежної змінної (її позначають буквою х). Функціональну залежність між х і у прийнято позначати символом y = f (x). Якщо значенню х відповідає більше, ніж одне значення у. то така функція називається багатозначною. Дослідження багатозначних функцій зазвичай зводиться до дослідження однозначних.
Змінна величина у є функція аргументу х, тобто y = f (x), якщо кожному можливому значенню х відповідає одне певне значення у.
Графіком функції називається сукупність всіх точок на площині, прямокутні координати яких х і у задовольняють рівняння y = f (x). Горизонтальну вісь Ох називають віссю абсцис, вертикальну вісь Оу - віссю ординат. Графічне зображення функції має важливе значення для її вивчення. На графіку функції часто безпосередньо видно такі її особливості, які можна було б встановити лише шляхом тривалих обчислень. Якщо між величинами х і у існує функціональний зв'язок, то байдуже, яку з цих величин вважати аргументом, а яку - функцією.
2.2 Способи завдання функцій
Функціональна залежність, що встановлює відповідність між значеннями аргументу х і функції у, може бути різними способами:
1). Табличний спосіб. При цьому способі ряд окремих значень аргументу х1, х2, ..., хk і відповідний йому ряд окремих значень функції у1, у2, ..., уk задаються у вигляді таблиці. Незважаючи на простоту, такий спосіб завдання функції володіє істотним недоліком, оскільки не дає повного уявлення про характер функціональної залежності між х і у і не є наочним.
2). Словесний спосіб. Зазвичай цей спосіб завдання ілюструють прикладом функції Дирихле у = D (х): якщо х - раціональне число, то значення функції D (х) дорівнює 1, а якщо число х - ірраціональне, то значення функції D (х) дорівнює нулю. Таким чином, щоб знайти значення D (x0) при заданому значенні х = х0, необхідно будь - яким способом встановити, раціонально або ірраціонально число х0.
3). Графічний спосіб. Функціональна залежність може бути задана за допомогою графіка функції у = f (x). Перевагою такого способу завдання є наочність, що дозволяє встановити важливі риси поведінки функції. Недолік графічного способу полягає в неможливості застосування математичного апарату для більш детального дослідження функції.
4). Аналітичний спосіб. При аналітичному способі завдання відома формула, за якою за заданим значенням аргументу х можна знайти відповідне значення функції у. У математиці найчастіше використовується саме аналітичний спосіб завдання функцій. Перевагами такого способу завдання є компактність, можливість підрахунку значення у при будь-якому значенні х і можливість застосування математичного апарату для більш детального дослідження поведінки функції. Однак аналітичному способу завдання функції притаманна недостатня наочність і можлива трудність обчислення значень функції.
Короткий розгляд різних способів завдання функції показує, що для докладного вивчення її поведінки найкраще поєднувати дослідження аналітичного виразу функції з побудовою її графіка.
Нарешті, ще раз підкреслимо наступне: з визначення функції випливає, що для її завдання необхідно лише вказати закон відповідності між величинами х і у. Спосіб же завдання цього закону не має значення.
Глава III. Дослідження функцій та їх графіків
3.1 Найпростіші функції та їх графіки
Пропорційні величини. Якщо змінні величини у і х (прямо) пропорційні, то функціональна залежність між ними виражається рівнянням y = kx, де k є деяка постійна величина (коефіцієнт пропорційності). Графік прямої пропорційності є пряма лінія 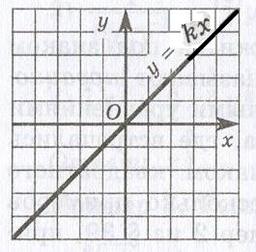 , що проходить через початок координат і утворює з віссю абсцис кут , тангенс, якого дорівнює постійної k; tg = k. Тому коефіцієнт пропорційності k називається також кутовим коефіцієнтом.
, що проходить через початок координат і утворює з віссю абсцис кут , тангенс, якого дорівнює постійної k; tg = k. Тому коефіцієнт пропорційності k називається також кутовим коефіцієнтом.
Лінійна функція. Лінійної називається функція виду: y = kx + b, в аналітичний вираз, якій змінні х і у входять в першого ступеня. Графік лінійної функції представляє пряму лінію 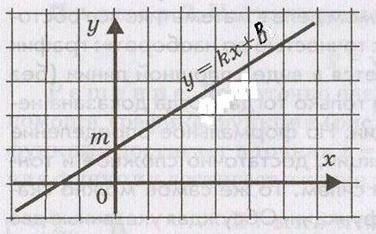 , розташовується відносно координатних осей різним чином, залежно від постійних коефіцієнтів, k і b, які можуть приймати позитивні чи негативні значення або бути рівним нулю. Для побудови графіка лінійної функції можна скористатися геометричним змістом коефіцієнтів k і b або знайти дві точки прямої на площині, наприклад, точки перетину з осями координат.
, розташовується відносно координатних осей різним чином, залежно від постійних коефіцієнтів, k і b, які можуть приймати позитивні чи негативні значення або бути рівним нулю. Для побудови графіка лінійної функції можна скористатися геометричним змістом коефіцієнтів k і b або знайти дві точки прямої на площині, наприклад, точки перетину з осями координат.
Властивості функції y = kx + b:
D (f) = (-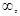 +
+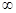 );
);
Зростає, якщо k> 0, убуває, якщо k <0;
Не обмежена ні зверху, ні знизу;
Немає ні найбільшого, ні найменшого значень;
Функція неперервна;
E (f) = (-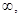 +
+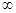 );
);
Зворотній пропорційність. Якщо змінні величини у і х обернено пропорційні, то функціональна залежність між ними виражається рівнянням 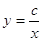 , де з є деяка постійна величина. Графік зворотній пропорційності є крива лінія
, де з є деяка постійна величина. Графік зворотній пропорційності є крива лінія 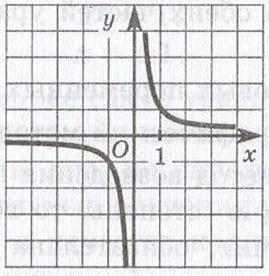 , звана гіперболою, що складається з двох гілок.
, звана гіперболою, що складається з двох гілок.
Властивості функції: 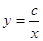
D (f) = (-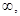 0) U (0, +
0) U (0, +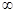 );
);
Якщо з> 0, то функція спадає на відкритому промені (-0) і на відкритому промені (0, +); якщо з <0, то функція зростає на (-0) і на (0, +);
Не обмежена ні знизу, ні зверху;
Немає ні найменшого, ні найбільшого значень;
Функція неперервна на відкритому промені (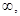 -0) і на відкритому промені (0, +
-0) і на відкритому промені (0, +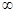 );
);
Е (f) = (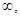 -0) U (0, +
-0) U (0, +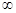 );
);
Якщо з> 0, то функція опукла вгору при х <0, тобто на відритому промені (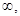 -0), і опукла вниз при х> 0, тобто на відкритому промені (0, +
-0), і опукла вниз при х> 0, тобто на відкритому промені (0, +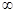 ). Якщо з <0, то функція опукла вгору при х> 0 і опукла вниз при х <0;
). Якщо з <0, то функція опукла вгору при х> 0 і опукла вниз при х <0;
Функція має асимптоти y = 0 і x = 0 /
Квадратична функція. Функція y = ax2 + bx + с (a, b, с - постійні величини; а 0) називається квадратичною. У найпростішому випадку y = ax2 (b = с = 0) графік є крива лінія, що проходить через початок координат. Крива, що служить графіком функції y = ax2, є парабола 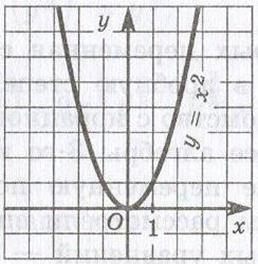 . Кожна така парабола має вісь симетрії (OY), звану віссю параболи. Точка О перетину параболи з її віссю називається вершиною параболи. Графік функції y = ax2 + bx + з має ту ж формулу, що і графік функції y = ax2 (при тому ж значенні а), тобто також є парабола. Вісь цієї параболи і раніше вертикальна, але вершина лежить не на початку координат, а в точці
. Кожна така парабола має вісь симетрії (OY), звану віссю параболи. Точка О перетину параболи з її віссю називається вершиною параболи. Графік функції y = ax2 + bx + з має ту ж формулу, що і графік функції y = ax2 (при тому ж значенні а), тобто також є парабола. Вісь цієї параболи і раніше вертикальна, але вершина лежить не на початку координат, а в точці 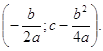
Властивості функції ax2 + bx + з:
Для випадку, а> 0
D (f) = (-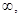 +
+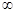 );
);
Убуває на промені 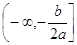 , зростає на промені
, зростає на промені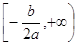 ;
;
Обмежена знизу, не обмежена зверху;
унаім. = Y0, yнаіб. Не існує;
неперервна;
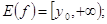
Опукла вниз.
Для випадку, а <0
D (f) = (- +);
Убуває на промені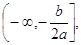 зростає на промені
зростає на промені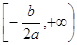 ;
;
Не обмежена знизу, обмежена зверху;
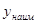 не існує, yнаіб. = Y0;
не існує, yнаіб. = Y0;
неперервна;
6. 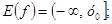
Опукла вгору.
Властивості функції y = ax2:
Для випадку, а> 0
D (f) = (-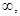 +
+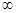 );
);
Убуває на промені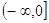 , зростає на промені
, зростає на промені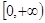 ;
;
Обмежена знизу, не обмежена зверху;
унаім. = 0, yнаіб. Не існує;
неперервна;
E (f) =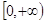 ;
;
Опукла вниз.
Для випадку, а <0
D (f) = (-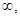 +
+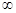 );
);
Убуває на промені зростає на промені;
Не обмежена знизу, обмежена зверху;
унаім. Не існує, yнаіб. = 0;
неперервна;
E (f) =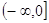
Опукла вгору.
Статечна функція. Зазвичай статечними функціями називають функції виду 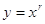 , де r - будь-яке дійсне число. Так, якщо r - натуральне число (r = n), то отримуємо функцію
, де r - будь-яке дійсне число. Так, якщо r - натуральне число (r = n), то отримуємо функцію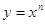 .
.
Графік статечної функції y = xn у разі парного n (n = 4, 6,8, ...) схожий на параболу, а графік статечної функції y = xn у разі непарного n (n = 5, 7, 9, ...) схожий на кубічну параболу.
Якщо r = - n, то отримуємо функцію y = x - n, тобто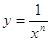 .
.
Нарешті, якщо r = 0, тобто мова йде про функції y = x0, то в результаті виходить звичайна функція у = 1, де х 0; графік цієї функції
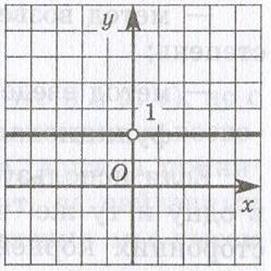
Тепер розглянемо функцію y = xr, де r - позитивне чи негативне дробове число. Розглянемо як приклад функцію y = x2,5. Область її визначення - промінь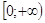 . Побудуємо на цьому промені графіки функцій у = х2 (гілка параболи) і у = х3 (гілка кубічної параболи) - ці графіки зображені. Варто зауважити, що на інтервалі (0;
. Побудуємо на цьому промені графіки функцій у = х2 (гілка параболи) і у = х3 (гілка кубічної параболи) - ці графіки зображені. Варто зауважити, що на інтервалі (0;
1) кубічна парабола розташовується нижче, а на відкритому промені (1; + ) вище параболи. Неважко переконатися в тому, що графік функції у = х2,5 проходить через точки (0; 0) і (1;
1), як і графіки функцій у = х2, у = х3. При інших значеннях аргументу х графік функції у = х2,5 знаходиться між графіками функцій у = х2 і у = х3 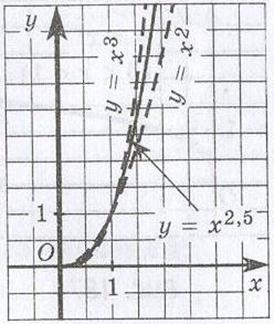 .
.
Чому так відбувається? подивимося:
1). Якщо 0 <х <1, то 2). Якщо х> 1, то
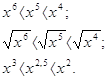
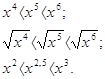

Приблизно так само йде справа для будь-якої статечної функції виду у = хr, де -неправильно дріб (чисельник більше знаменника). Її графіком є крива 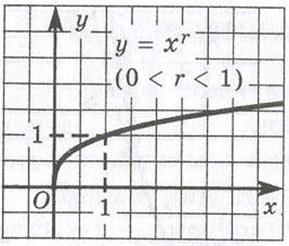 , схожа на гілку параболи. Чим більше показник r, тим "крутіше" спрямована ця крива вгору.
, схожа на гілку параболи. Чим більше показник r, тим "крутіше" спрямована ця крива вгору.
Властивості функції 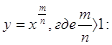
D (f) =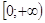 ;
;
не є ні парною, ні непарною;
зростає на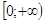 ;
;
не обмежена зверху, обмежена знизу;
не має найбільшого значення; у наим. = 0;
неперервна;
E (f) =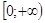 ;
;
опукла вниз.
Розглянемо ступеневу функцію 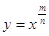 для випадку, коли
для випадку, коли 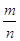 - правильна дріб
- правильна дріб 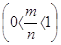 . Все розглянуте в цій главі відносно функції
. Все розглянуте в цій главі відносно функції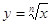 , або, що те ж саме
, або, що те ж саме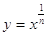 , має і стосовно будь-якої статечної функції виду у = хr, де
, має і стосовно будь-якої статечної функції виду у = хr, де 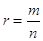 - правильна дріб. Графік цієї функції:
- правильна дріб. Графік цієї функції:
Властивості функції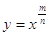 , де:
, де: 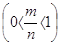
D (f) =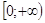 ;
;
не є ні парною, ні непарною;
зростає на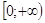 ;
;
не обмежена зверху, обмежена знизу;
не має найбільшого значення; у наим. = 0;
неперервна;
E (f) =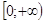 ;
;
опукла вгору.
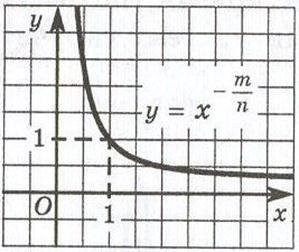
Нам залишилося розглянути ступеневу функцію виду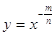 . Область її визначення - відкритий промінь
. Область її визначення - відкритий промінь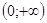 . Вище ми побудували графік статечної функції y = x - n, де n - натуральне число. При
. Вище ми побудували графік статечної функції y = x - n, де n - натуральне число. При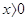 графік функції y = x - n схожий на гілку гіперболи. Точно так само справа йде для будь статечної функції виду
графік функції y = x - n схожий на гілку гіперболи. Точно так само справа йде для будь статечної функції виду 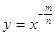 графік, якій зображений. Відзначимо, що графік даної функції має горизонтальну асимптоту y = 0 і вертикальну асимптоту x = 0.
графік, якій зображений. Відзначимо, що графік даної функції має горизонтальну асимптоту y = 0 і вертикальну асимптоту x = 0.
Властивості функції: 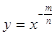
D (f) =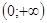 ;
;
не є ні парною, ні непарною;
зростає на;
не обмежена зверху, обмежена знизу;
не має ні найбільшого значення, ні найменшого значення;
неперервна;
E (f) =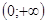 ;
;
опукла вниз.
Функція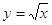 . Графіком функції є гілка параболи
. Графіком функції є гілка параболи 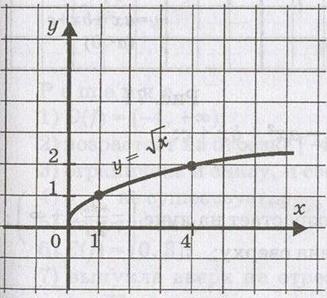 .
.
Властивості функції:
D (f) =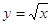
зростає;
Обмежена знизу, не обмежена зверху;
у наим. = 0, yнаіб. = Не існує;
неперервна;
E (f) =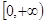 ;
;
Опукла вгору.
7. Функція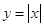 . Графіком функції є об'єднання двох променів: у = х, х0 і
. Графіком функції є об'єднання двох променів: у = х, х0 і
у = - х, х0 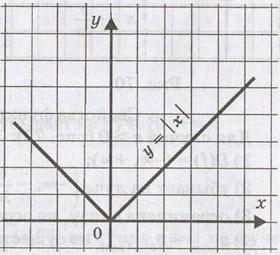 .
.
Властивості функції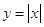 .
.
D (f) = (-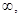 +
+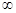 );
);
Убуває на промені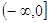 , зростає на промені
, зростає на промені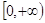 ;
;
Обмежена знизу, не обмежена зверху;
унаім. = 0, yнаіб. Не існує;
неперервна;
E (f) =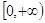 ;
;
Опукла вниз.
3.2 Тригонометричні функції
Унаслідок того, що тригонометричні функції вивчаються у шкільній програмі, в рефераті на них приділено мінімум уваги. Всі основні положення вказані в таблиці
|
Функция |
Область определения |
Множество значений |
Четность |
Участки монотонности |
|
Sin x |
- < x < + |
[-1 ; 1] |
нечетная |
Возрастает при x((4p-1)p/2; (4p+1)p/2) Убывает при x((4p+1)p/2; (4p+3)p/2) |
|
Cos x |
- < x < + |
[-1 ; 1] |
четная |
Возрастает при х((2p-1)p;2pn) Убывает при x(2pn;(2p+1)p) |
|
Tg x |
x p/2 + pn |
(- ; + ) |
нечетная |
Возрастает при x((2p-1)p/2;(2p+1)p/2) |
|
Ctg x |
x pn |
(- ; + ) |
нечетная |
Убывает при x(pn;(n+1)p) |
|
Sec x |
x p/2 + pn |
(- ;-1] [1 ; + ] |
четная |
Возрастает при x(2pn;(2n+1)p) Убывает при x(2pn;(2n+1)p) |
|
Cosec x |
x pn |
(- ;-1] [1 ; + ] |
нечетная |
Возрастает при x((4p+1)p/2; (4p+3)p/2) Убывает при x((4p-1)p/2; (4p+1)p/2) |
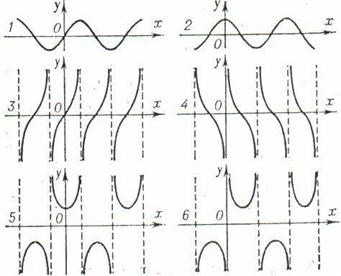
3.3 Криві другого порядку
У попередньому параграфі було встановлено, що всяка пряма в прямокутній системі координат Оху визначається рівнянням першого ступеня щодо змінних х і у. Так само було встановлено, всяке рівняння першого ступеня ах + bу + с = 0 в прямокутній системі координат визначає пряму і притому єдину, якщо а + b 0. У цій главі ми займемося вивченням ліній визначаються рівняннями другого ступеня щодо поточних координат х і у :
ах + 2bху + су + 2dх + 2eу + f = 0 (1)
Такі лінії називають лініями (кривими) другого порядку. Коефіцієнти рівняння (1) можуть приймати різні дійсні значення, виключаючи одночасне рівність а, b і c нулю (в іншому випадку рівняння (1) не буде рівнянням другого ступеня).
Еліпс.
Еліпсом називають безліч всіх точок площини, сума відстаней від кожної з яких до двох даних точок тій же площині, званих фокусами, є величина постійна, більша, ніж відстань між фокусами.
Складемо рівняння еліпса з фокусами в даних точках F1 і F2. Для цього виберемо прямокутну систему координат так, щоб вісь Ох проходила через фокуси, а початок координат ділило відрізок F1F2 навпіл 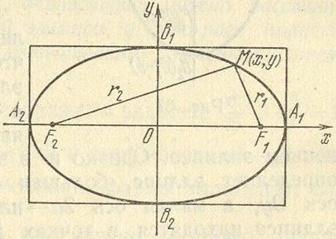 . Позначивши F1F2 = 2с, отримаємо F1 (с; 0) і F2 (-с; 0). Нехай М (х; у) - довільна точка еліпса.
. Позначивши F1F2 = 2с, отримаємо F1 (с; 0) і F2 (-с; 0). Нехай М (х; у) - довільна точка еліпса.
Відстань r1 = F1M і r2 = F2M називаються фокальними радіусами точки М.
Покладемо r1 + r2 = 2а; (1)
Тоді згідно з визначенням еліпса 2а - величина постійна, причому 2а> 2с, тобто а> c.
За формулою відстані між двома точками знаходимо
r1 = 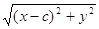 та r2 =
та r2 = 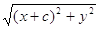
Підставами знайдені значення r1 і r2 в рівність (1) отримаємо рівняння еліпса
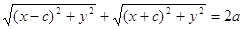
Після нескладних перетворень рівняння прийме вид
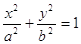 (2)
(2)
Рівняння (2) називається канонічним рівнянням еліпса.
дослідження:
Координати точки О (0; 0) не задовольняють рівняння (2), тому еліпс, який визначається цим рівнянням, не проходить через початок координат.
Знайдемо точки перетину еліпса з осями координат. Поклавши в рівнянні (2) у = 0, знайдемо х = ± а. Отже, еліпс перетинає вісь Ох в точках А1 (а; 0) і А2 (-а; 0). Аналогічно отримуємо точки перетину еліпса з віссю Оу: В1 (0; b) і B2 (0; - b)
D (y) [-a; a]
E (y) [-b; b]
При зростанні х від 0 до а величина у убуває від b до 0, а при зростанні уот 0 до b величина х убуває від а до 0.
Окремим випадком еліпса є коло, де а = b.
Окружність
Як відомо, окружністю називають безліч всіх точок площини, однаково віддалених від даної точки, званої центром.
Нехай дана окружність радіусом r з центром в точці О1 (a; b) 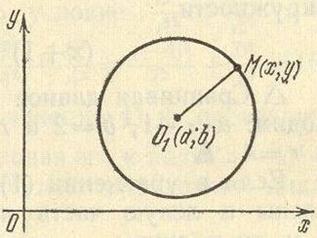 ;
;
потрібно скласти її рівняння.
Візьмемо на даній окружності довільну точку М (х; у)
Маємо: О1М = r, тобто 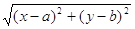 = r
= r
Звідки (х-а) + (у - b) = r (1)
Отже, рівняння (1) задовольняють координати довільної точки кола. Більше того, цього рівняння не задовольняють координати жодної точки, що не лежить на колі, так як якщо
О1М <r, то (х-а) + (у - b) <r,
і якщо
О1М> r, то (х-а) + (у - b) > r.
Отже, (1) Є рівняння кола радіусом r з центром в точці О1 (a; b). Якщо центр кола знаходиться на осі Ох, тобто якщо b = 0, то рівняння (1) набуде вигляду
(х-а) + у = r
Якщо центр кола знаходиться на осі Ох, тобто якщо b = 0, то рівняння (1) набуде вигляду
х + (у - b) = r
Нарешті, якщо центр кола знаходиться на початку координат, тобто якщо а = b = 0, то рівняння прийме (1) вид
х + у = r
Якщо в рівнянні (1) розкрити дужки, перенести всі члени в ліву частину і розташувати їх за ступенями х і у, то отримаємо
x + y - 2ax - 2by + a + b - r = 0
Звідси випливає, що рівняння кола є рівнянням другого ступеня щодо змінних х і у, як би вона не була розташована в площині Оху.
У цьому розділі були розглянуті основні найпростіші функції, криві другого порядку і тригонометричні функції, так само представлені їх графіки.
Глава IV. Методи побудови графіків функцій
Дослідження функції дає можливість знайти область визначення і область зміни функції, області її зменшення чи збільшення, асимптоти, інтервал знакопостоянства та ін. Однак при розгляді графіків багатьох функцій часто можна уникнути проведення подібного дослідження, використовуючи ряд методів, що спрощують аналітичний вираз функції і полегшують побудову графіка . Викладу саме таких методів присвячується ця глава, яка може служити практичним керівництвом при побудові багатьох функцій.
4.1 Паралельний перенос
4.1.1 Перенесення уздовж осі ординат
f (x) => f (x) - b
Нехай потрібно побудувати графік функції у = f (х) - b. Неважко помітити, що ординати цього графіка для всіх значень x на b одиниць менше відповідних ординат графіка функцій у = f (х) при b> 0 і на b одиниць більше - при b <0. Отже, графік функції у = y (х) - b можна отримати паралельним перенесенням уздовж осі ординат графіка функції у = f (х) на bедініц вниз при b> 0 або вгору при b <0. Переміщення графіка пов'язане з його перемальовування, що буває важко, особливо у випадку складних графіків. Перенесення ж графіка на bедініц вниз або вгору вздовж осі ординат еквівалентний відповідному протилежного переносу осі абсцис настільки ж одиниць. Саме цим способом ми будемо користуватися. Тоді представивши вихідну функцію у вигляді у + b = f (х), сформулюємо наступне правило.
Для побудови графіка функції y + b = f (x) слід побудувати графік функції y = f (x) і перенести вісь абсцис на b одиниць вгору при b> 0 або наb одиниць вниз при b <0. Отриманий в новій системі координат графік є графіком функції y = f (x) - b.
4.1.2 Перенесення уздовж осі абсцис
f (x) => f (x + a)
Нехай потрібно побудувати графік функції у = f (x + a). Розглянемо функцію y = f (x), яка в деякій точці x = x1 приймає значення у1 = f (x1). Очевидно, функція у = f (x + a) прийме таке ж значення в точці x2, координата якої визначається з рівності x2 + a = x1, тобто x2 = x1 - a, причому розглядається рівність справедливо для сукупності всіх значень з області визначення функції. Отже, графік функції у = f (x + a) може бути отриманий паралельним переміщенням графіка функції y = f (x) уздовж осі абсцис вліво наa одиниць при a> 0 або вправо на a одиниць при a <0. Паралельне ж переміщення уздовж осі абсцис на a одиниць еквівалентно переносу осі ординат на стільки ж одиниць, але в протилежний бік. Таким чином, отримуємо наступне правило.
Для побудови графіка функції y = f (x + a) слід побудувати графік функції y = f (x) і перенести вісь ординат на a одиниць вправо при a> 0 або наa одиниць вліво при a <0. Отриманий в новій системі координат графік є графіком функції y = f (x + a).
4.2 Відображення
4.2.1 Побудова графіка функції виду y = f (-x)
f (x) => f (-x)
Очевидно, що функції y = f (-x) і y = f (x) приймають рівні значення в точках, абсциси яких дорівнюють за абсолютною величиною, але протилежні за знаком. Інакше кажучи, ординати графіка функції y = f (-x) в області позитивних (негативних) значень х будуть рівні ординатам графіка функції y = f (x) при відповідних по абсолютній величині негативних (позитивних) значеннях х. Таким чином, отримуємо наступне правило.
Для побудови графіка функції y = f (-x) слід побудувати графік функції y = f (x) і відобразити його відносно осі ординат. Отриманий графік є графіком функції y = f (-x)
4.2.2 Побудова графіка функції виду y = - f (x)
f (x) => - f (x)
Ординати графіка функції y = - f (x) при всіх значеннях аргументу рівні за абсолютною величиною, але протилежні за знаком ординатам графіка функції y = f (x) при тих же значеннях аргументу. Таким чином, отримуємо наступне правило.
Для побудови графіка функції y = - f (x) слід побудувати графік функції y = f (x) і відобразити його відносно осі абсцис.
4.2.3 Побудова графіків парної і непарної функцій
Як уже зазначалося, для парної функції y = f (x) у всій області зміни її аргументу справедливе співвідношення f (x) = f (-x). Отже, функція такого роду приймає однакове значення при всіх значеннях аргументу, рівних за абсолютною величин, але протилежних за знаком. Графік парної функції симетричний щодо осі ординат.
Для побудови графіка парної функції y = f (x) слід побудувати гілку графіка цієї функції тільки в області позитивних значень аргументу (х0). Графік функції y = f (x) в області негативних значень аргументу симетричний побудованої гілки щодо осі ординат і виходить відображенням її відносно цієї осі.
Для непарної функції y = f (x) в області всіх значень аргументу справедливо рівність f (-x) = - f (x). Таким чином, в області негативних значень аргументу ординати графіка непарної функції рівні за величин, але протилежні за знаком ординатам графіка тієї ж функції при відповідних позитивних значеннях х. Графік непарної функції симетричний відносно початку координат.
Для побудови графіка непарної функції y = f (x) слід побудувати гілку графіка цієї функції тільки в області позитивних значень аргументу (х0). Графік функції y = f (x) в області негативних значень аргументу симетричний побудованої гілки відносно початку координат і може бути отриманий відображенням цієї гілки щодо осі ординат з подальшим відображенням у області негативних значень відносно осі абсцис.
4.2.4 Побудова графіка оберненої функції
Як уже зазначалося, пряма і зворотна функції виражають одну і ту ж залежність між змінними х і у, з тією лише відмінністю, що в зворотної функції змінні помінялися ролями, що рівносильно зміні позначень осей координат. Тому графіком зворотної функції симетричний графіку прямої функції щодо бісектриси I і III координатних кутів, тобто відносно прямої y = x. Таким чином, отримуємо наступне правило.
Для побудови графіка функції y = j (x), зворотної по відношенню до функції y = f (x), слід побудувати графік y = f (x) і відобразити його відносно прямої y = x.
4.3 Деформація
4.3.1 Деформація графіка вздовж осі ординат
f (x) => A · f (x)
Розглянемо функцію виду y = A · f (x), де A> 0. Неважко помітити, що при рівних значеннях аргументу ординати графіка цієї функції будуть в A разів більше ординат графіка функції у = f (x) при A> 1 або 1 / A разів менше ординат графіка функції y = f (x) при A <1. Таким чином, отримуємо наступне правило.
Для побудови графіка функції y = A · f (x) слід побудувати графік функції y = f (x) і збільшити його ординати в A раз при A> 1 (призвести розтягнення графіка вздовж осі ординат) або зменшити його ординати в 1 / A раз при A <1 (провести стиснення графіка вздовж осі ординат). Отриманий графік є графіком функції y = A · f (x).
4.3.2 Деформація графіка вздовж осі абсцис
f (x) => f (x).
Нехай потрібно побудувати графік функції y = f (x), де > 0. Розглянемо функцію y = f (x), яка в довільній точці x = x1 приймає значення y1 = f (x1). Очевидно, що функція y = f (x) приймає таке ж значення в точці x = x2, координата якої визначається рівністю x1 = x2, причому це рівність справедливо для сукупності всіх значень х з області визначення функції. Отже, графік функції y = f (x) виявляється стислим (при <1) або розтягнутим (при > 1) вздовж осі абсцис щодо графіка функції y = f (x). Таким чином, отримуємо правило.
Для побудови графіка функції y = f (x) слід побудувати графік функції y = f (x) і зменшити його абсциси в раз при > 1 (провести стиснення графіка вздовж осі абсцис) або збільшити його абсциси в 1 / раз при <1 (призвести розтягнення графіка вздовж осі абсцис). Отриманий графік є графіком функції y = f (x).
4.4 Алгебраїчні операції над графіками функцій
Розглянемо основні алгебраїчні дії над функціями і їх графіками, такі як додавання і віднімання (y = f (x) ± g (x)), множення (y = f (x) · g (x)), ділення (y = f (x) / g (x)). При побудові такого типу графіків слід враховувати, що область визначення функції y є спільною частиною областей визначення кожної з функцій f (x) і g (x). Використання викладених нижче методів побудови графіків особливо доцільно у випадку, коли f (x) і g (x) є елементарними функціями різних типів.
4.4.1 Графік суми (різниці) функцій
y = f (x) ± g (x)
Графік слід будувати по точках, складаючи або віднімаючи ординати графіків функцій f (x) і g (x), відповідні одному і тому ж значенню аргументу (зрозуміло, спочатку будуються графіки функцій f (x) і g (x)).
При побудові графіка різниці функцій зазвичай не вдаються до віднімання графіків, а будують спочатку графік функції - g (x) і потім складають графіки f (x) і - g (x).
4.4.2 Графік твори функцій
y = f (x) · g (x).
Для побудови графіка даної функції треба побудувати графіки функцій f (x) і g (x) і перемножити значення ординат, відповідні одним і тим же значенням аргументу.
4.4.3 Графік функції виду
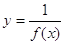
Для побудови такого графіка слід побудувати графік функції y1 = f (x) і, ділячи, одиницю на чисельні значення ординат цієї функції з урахуванням знака, по точках побудувати графік даної функції.
При цьому областю визначення функції у є область визначення функції y1 = f (x), за винятком тих значень х, при яких f (x) = 0. У цих точках функція y = 1 / f (x) не визначена (як правило, тут є вертикальні асимптоти). f(x) ± у0, при f(x) = ±1 у=±1 (тобто значення заданої функції у і функції y1 = f (x) збігаються)
4.4.4 Графік приватного двох функцій
y = f (x) / g (x).
Дану функцію можна представити у вигляді
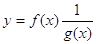
Побудова графіка функції зводиться до побудови графіків функцій y1 = f (x) і y2 = 1 / g (x) і подальшого перемножування по точках значень відповідних ординат цих графіків з урахуванням знака.
4.5 Побудова графіків складних функцій
Перш, ніж приступити до побудови графіка складної функції j [f (x)], необхідно спочатку побудувати графік функції f (x), а потім по точках будувати графік складної функції, проводячи операцію взяття функції від функції. Розглянемо ряд найважливіших приватних випадків.
4.5.1 Графік функції у = [f (x)] k
Для побудови графіка функції у = [f (x)] k слід побудувати графік y1 = f (x) і, звівши значення ординат побудованого графіка в ступінь k, по точках побудувати графік заданої функції.
Відзначимо, що в загальному випадку число k може бути як цілим, так і дробовим. Якщо зведення в ступінь k зводиться до операції витягання кореня парному ступеня (наприклад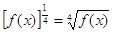 , чи
, чи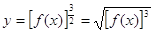 , то функція y визначена тільки там, де f (x) 0 (відповідно графік потрібно будувати тільки в цій області).
, то функція y визначена тільки там, де f (x) 0 (відповідно графік потрібно будувати тільки в цій області).
4.5.2 Графік функції у = af (x)
Для побудови графіка функції у = af (x) слід побудувати графік y1 = f (x), а потім, звівши підставу в ступінь, рівну значенню ординат графіка, по точках побудувати графік заданої функції.
При цьому в точках, де f (x) = 0, у = 1, в точках, де f (x) = 1, у = а. Для випадку а> 1 f(x) y , а при f(x) - y 0; для випадку а<1 при f(x) y 0, а при f(x) - y На практиці при побудові графіків випадок а <1 зручно зводити до випадку а> 1 (наприклад, 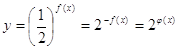 )
)
У цьому розділі були розглянуті найбільш відомі і повсюдно використовувані в математиці методи побудови графіків складних функцій. Так само ця глава насичена найбільш цікавими і корисними потенційними знаннями для учня.
Глава V: Графіки нетрадиційних функцій
1. Графік функції 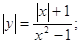
Нам дана функція:
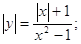
Знайдемо область допустимих значень для цієї функції:
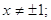
У знаменнику ми бачимо формулу різниці квадратів, розкриємо її і представимо у вигляді:
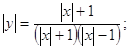
Після скорочення ми отримали наступний результат:
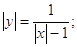
Розкриємо модуль і отримаємо:
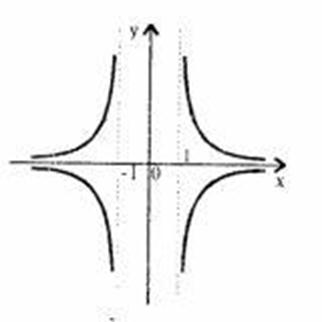
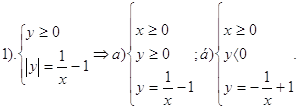
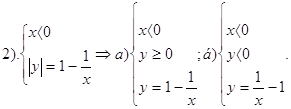
2. Графік функції
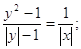
Нам дана функція:
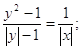
Знайдемо область допустимих значень для цієї функції:
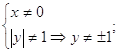
У чисельнику бачимо формулу різниці квадратів, розкриємо її і представимо у вигляді:
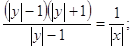
Після скорочення ми отримали наступний результат:
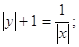
Зберемо доданки, що містять змінну "у" ліворуч, а доданки, що містять змінну "x" і вільні члени праворуч, отримаємо:
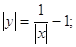
Розкриємо модуль і отримаємо:
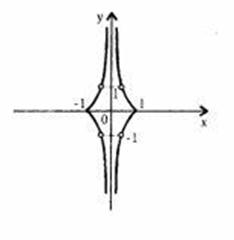
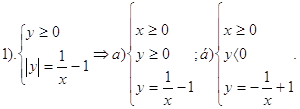
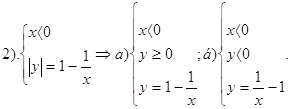
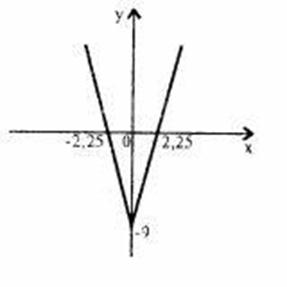
3. Графік функції 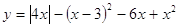
Графік заданий функцією:
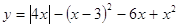
Побудуємо графік, розкриваючи модуль.
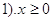 , Від сюди слід, що
, Від сюди слід, що
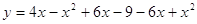 ,
,
Привівши подібні, отримаємо:
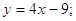
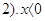 , То від сюди витікає наступне:
, То від сюди витікає наступне: 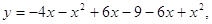
Після приведення подібних і застосування відповідних дій над ними, ми отримаємо нижче наведене:
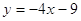 .
.
4. Графік функції 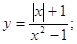
Графік заданий функцією:
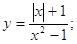
Знайдемо область допустимих значень для цієї функції.
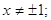
У знаменнику функції помітна формула різниці квадратів, розкриємо її наступним чином:
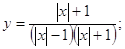
Після неважких скорочень отримуємо:
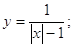
Розкриємо модуль, що міститься в знаменнику дробу функції, нижче наведеними чином: