Количественное исследование влияния на погрешность восстановления реального сигнала частоты его дискретизации и характеристик реального восстанавливающего фильтра
Вве�де�ние
Целью данной курсовой работы является количественное исследование влияния на погрешность восстановления реального сигнала частоты его дискретизации и характеристик реального восстанавливающего фильтра. В процессе выполнения работы необходимо осуществить дискретизацию заданного видеосигнала с последующим его восстановлением, а также проанализировать спектры сигнала на этапах дискретизации и восстановления. Кроме этого необходимо сделать выводы о влиянии на погрешность восстановления дискретизированного сигнала частоты дискретизации, длительности исходного сигнала и частоты среза фильтра, а так же определить значения вышеуказанных величин, при которых погрешность восстановления сигнала будет удовлетворять указанной в техническом задании.
При выполнении курсовой работы предполагается использовать математический пакет MathCAD 2001 для численных расчётов и построения графиков. Виртуальный эксперимент будет произведён в симуляторе Electronics Workbench 5.12 Pro.
1 Спек�траль�ный ана�лиз дис�кре�ти�зиро�вано�го сиг�на�ла
В данной курсовой работе сигнал S(t), является импульсом. Для анализа таких сигналов необходимо определить их амплитуду и длительность Тs.Чтобы использовать теорему Котельникова необходимо сигнал подвергнуть дискретизации.
Сиг�нал S(t), рас�смат�ри�вае�мый в дан�ной кур�со�вой ра�бо�те опи�сы�ва�ет�ся фор�му�лой:
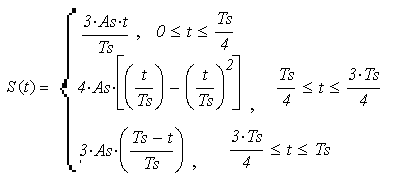 (1)
(1)
Максимальное значение сигнала As=1 В, длительность сигнала Ts=1 мс.
Гра�фик ис�ход�но�го ви�део�сиг�на�ла изо�бра�жен на ри�сун�ке 1. Рас�чет это�го гра�фи�ка, а так�же всех дру�гих за�ви�си�мо�стей, про�из�во�дил�ся с по�мо�щью спе�ци�аль�ной про�грам�мы IKURA па�ке�та MathCAD Professional 2001.
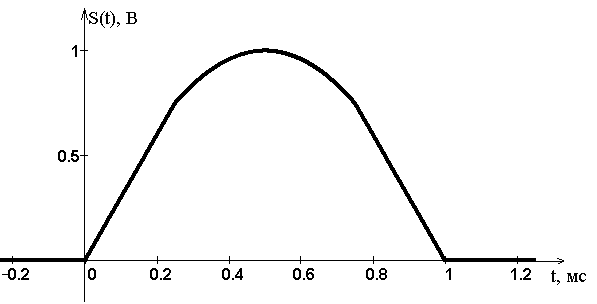
Ри�су�нок 1 – Ис�ход�ный ви�део�сиг�нал S(t)
Так как исходный сигнал ограничен во вре�ме�ни в про�ме�жут�ке от 0 мс до 1 мс, сле�до�ва�тель�но, он име�ет бес�ко�неч�ный спектр, оп�ре�де�ляю�щий�ся с по�мо�щью пре�об�ра�зо�ва�ния Фу�рье по фор�му�ле:
(2)
Гра�фик спек�тра ис�ход�но�го сиг�на�ла при�ве�ден на ри�сун�ке 2.
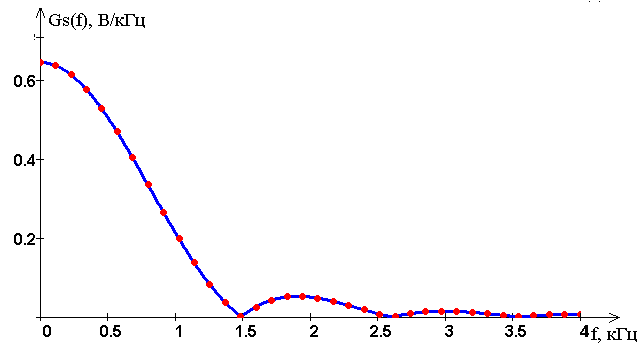
Ри�су�нок 2 – Спек�траль�ная плот�ность ис�ход�но�го ви�део�сиг�на�ла
Спектральная плотность представленная на рисунке 2, не имеет конечной частоты про которой она обратиться в 0. Сигнал не удастся восстановить без погрешности, так как спектр бесконечен. Делаем вывод, что теорему Котельникова нельзя использовать для данного сигнала. Если взять спектральную плотность и ограничить её, так что практическая ширина спектра составила от 95% до 99% энергии, то дискретизировать сигнал удаться.
Для того чтобы продискретизировать такой сигнал нам нужно определить практическую ширину спектра, то есть частоту Fm, которая ограничивает участок спектра, в котором содержится 95% энергии. Эту частоту можно определить из равенства Парсеваля:
(3)
Энер�гия Es оп�ре�де�ля�ет�ся по фор�му�ле :
(4)
В ре�зуль�та�те вычислений по�лу�че�на за�ви�си�мость гра�нич�ной час�то�ты Fm прак�ти�че�ской ши�ри�ны спек�тра ис�ход�но�го сиг�на�ла, от ве�ли�чи�ны q (q - до�ля пол�ной энер�гии сиг�на�ла, при�хо�дя�щая�ся на спек�траль�ные со�став�ляю�щие с час�то�та�ми
от 0 до Fm ) .
Затем, определим частоту дискретизации, руководствуясь критерием:
(5)
Пред�ва�ри�тель�но вы�бе�рем час�то�ту дис�кре�ти�за�ции рав�ной уд�во�ен�но�му зна�че�нию мак�си�маль�ной час�то�ты спек�тра, т.е. 2.1 кГц.
2 Рас�чет ха�рак�те�ри�стик сиг�на�ла на вы�хо�де дис�кре�ти�за�то�ра
Сиг�нал, опи�сы�вае�мый не�пре�рыв�ной ин�тег�ри�руе�мой с квад�ра�том функ�ци�ей S(t), спектр ко�то�рой ог�ра�ни�чен час�то�той Fm, пол�но�стью и од�но�знач�но оп�ре�де�ля�ет�ся свои�ми дис�крет�ны�ми от�счё�та�ми, взя�ты�ми че�рез ин�тер�вал вре�ме�ни T1/2Fm, и мо�жет быть пред�став�лен в ви�де:
(6)
Если дискретизацию производить идеальным дискретизатором (т.е. дискретизатором с нулевой длительностью отсчетных импульсов, по сути дельта- импульсами ), то сигнал на выходе его можно описать следующей зависимостью:
S(t)= (7)
На ри�сун�ке 3 пред�став�ле�ны гра�фик ис�ход�ной функ�ции и дис�кре�ти�зи�ро�ван�но�го сиг�на�ла при час�то�те дис�кре�ти�за�ции 2.1 кГц.
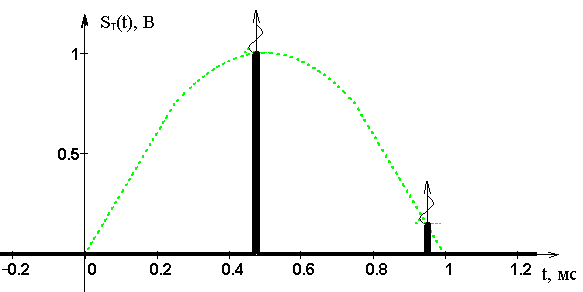
Ри�су�нок 3 – Дис�кре�ти�зи�ро�ван�ный ви�део�сиг�нал и ис�ход�ный сиг�нал
При рас�смот�ре�ние ри�сун�ка 3, мы мо�жем убедиться, что дис�кре�ти�зи�ро�ван�ный сиг�нал пол�но�стью по�вто�ря�ет по оги�баю�щей ис�ход�ный сиг�нал.
Спек�траль�ная плот�ность дис�кре�ти�зи�ро�ван�но�го сиг�на�ла оп�ре�де�ля�ет�ся по фор�му�ле:
(8)
где N – чис�ло от�сче�тов.
На ри�сун�ке 4 при�ве�ден спектр дис�кре�ти�зи�ро�ван�но�го сиг�на�ла при вы�бран�ной час�то�те дис�кре�ти�за�ции F=2.1 кГц.
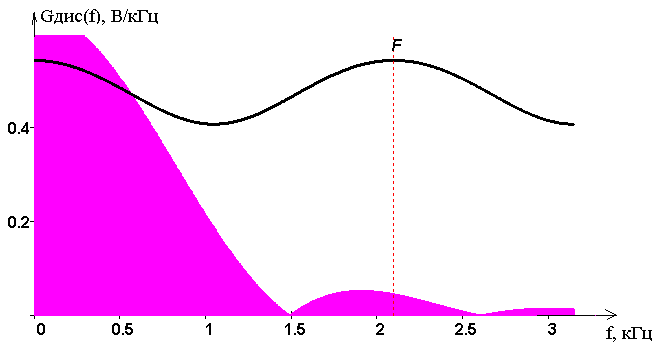
Ри�су�нок 4 – Спек�траль�ная плот�ность дис�кре�ти�зи�ро�ван�но�го сиг�на�ла и ис�ход�но�го ви�део�сиг�на�ла
Спектр дискретизированого сигнала не похож на спектр исходного. Видимо, частота дискретизации выбрана не верно. Это означает, что необходимо увеличить число отчётов до того когда спектры начнут совпадать по форме.
На сле�дую�щем ри�сун�ке 5 пред�став�лен спектр фаз ис�ход�но�го и �ди�ск�ре�ти�зи�ро�ван�но�го ви�део�сиг�на�ла.
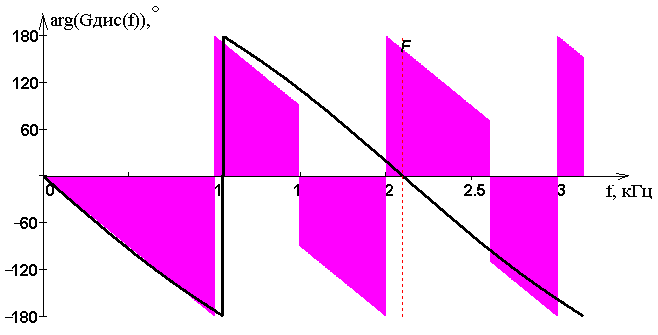
Ри�су�нок 5 – Спектр фаз ис�ход�но�го и про�ди�ск�ре�ти�зи�ро�ван�но�го ви�део�сиг�на�ла
Вывод: во-первых, мы выяснили, что спектр дискретизтрованного сигнала представляет собой похожую форму с частотой дискретизации копий спектра исходного сигнала; во-вторых, мы наблюдаем значительные искажения в спектре дискретизированого сигнала, вызванные тем, что мы ограничили спектр исходного сигнала.
3 Ана�лиз час�тот�ных и вре�мен�ных ха�рак�те�ри�стик вос�ста�нав�ли�ваю�ще�го фильт�ра
Для вос�ста�нов�ле�ния не�пре�рыв�но�го сиг�на�ла по дис�крет�ным от�сче�там пред�по�ла�га�ет�ся ис�поль�зо�вать фильтр низ�ких час�тот Баттерворта-Томсона 4-го по�ряд�ка. Пе�ре�да�точ�ная функ�ция фильт�ра пред�став�ля�ет�ся в ви�де:
(9)
Где Ko – ко�эф�фи�ци�ент уси�ле�ния на ну�ле�вой час�то�те, – ко�эф�фи�ци�ент, обес�пе�чи�ваю�щий при Ko=1 еди�нич�ную пе�ре�да�чу на ну�ле�вой час�то�те.
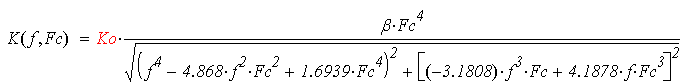
ФЧХ фильт�ра пред�став�ле�на фор�му�лой:
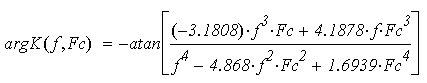 (10)
(10)
По�строе�ние гра�фи�ков про�из�во�дит�ся для пред�ва�ри�тель�но вы�бран�ной час�то�ты сре�зы рав�ной мак�си�маль�ной час�то�те сре�за 1 кГц.
Рас�чет час�тот�ной, им�пульс�ной ха�рак�те�ри�сти�ки, а так�же вре�ме�ни за�держ�ки фильт�ра при�во�дит�ся в при�ло�же�нии А.
АЧХ и ФЧХ фильт�ра име�ет вид пред�став�лен�ный на ри�сун�ках 6 и 7.
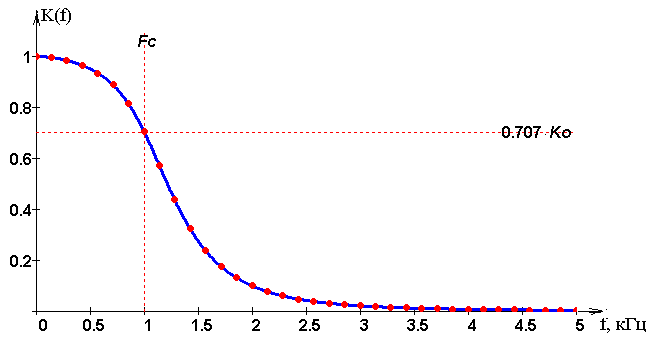
Ри�су�нок 6 – АЧХ вос�ста�нав�ли�ваю�ще�го фильт�ра ниж�них час�тот
АЧХ является фильтром Баттерворта-Томсона четвёртого порядка. ФНЧ очень сильно далёк от идеального, так как его полоса пропускания неравномерна, а полоса затухания плавно уходит в бесконечность. Это обусловлено небольшим порядком, а так же тем что фильтры Баттерворта-Томсона имеют неравномерность в полосе пропускания.
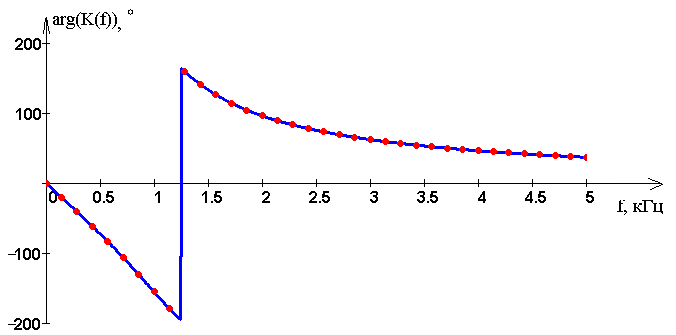
Ри�су�нок 7 – ФЧХ вос�ста�нав�ли�ваю�ще�го фильт�ра ниж�них час�тот
Сигнал, проходя через фильтр Баттерворта-Томсона четвёртого порядка, как и при прохождении через любое электронное устройство, будет задерживаться на некоторое время. Эта задержка определяется по формуле:
(11)

Гра�фик за�держ�ки пред�став�лен на ри�сун�ке 8.
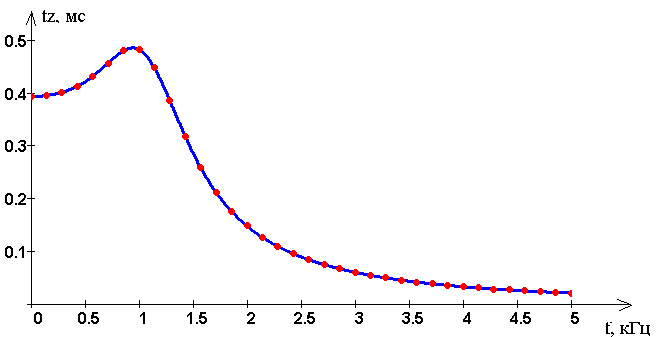
Ри�су�нок 8 – За�ви�си�мость вре�ме�ни за�держ�ки от час�то�ты
Из рисунка 8 наблюдается не равномерность вре�ме�ни за�держ�ки от час�то�ты. Это означает, что ФНЧ на разных частотах имеет разную задержку времени выхода со входом. Самая максимальная задержка будет на низких частотах, а с ростом частоты она стремиться к 0. Это обусловлено, реактивностью элементов фильтра.
В ка�че�ст�ве кон�крет�но�го зна�че�ния вре�ме�ни за�держ�ки сиг�на�ла, вос�ста�нов�лен�но�го фильт�ром по дис�крет�ным от�сче�там, це�ле�со�об�раз�но взять за�держ�ку фильт�ра на ну�ле�вой час�то�те. После предварительных расчетов получим время задержки равное 0,39 мс.
Так же важ�ной ха�рак�те�ри�сти�кой фильт�ра яв�ля�ет�ся его им�пульс�ная ха�рак�те�ри�сти�ка, так как она по�зво�ля�ет рас�счи�тать сиг�нал на вы�хо�де фильт�ра и оп�ре�де�ля�ет�ся по фор�му�ле:
(12)
Импульсная характеристика фильт�ра пред�став�ле�на на ри�сун�ке 9.
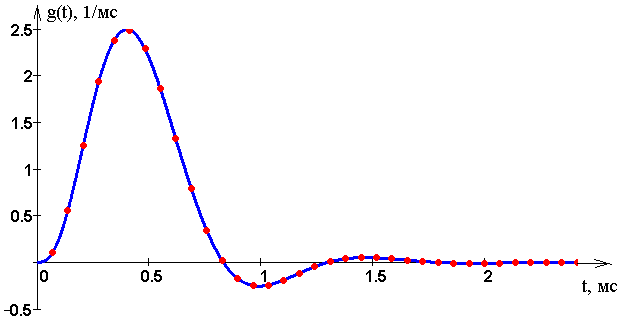
Ри�су�нок 9 – Им�пульс�ная ха�рак�те�ри�сти�ка вос�ста�нав�ли�ваю�ще�го фильт�ра
Им�пульс�ная ха�рак�те�ри�сти�ка это есть отклик фильтра на дельта функцию, то есть на импульс бесконечно малый по времени и бесконечно большой по амплитуде. Из рисунка 9 видно, что в нулевой момент времени индуктивность представляет собой разрыв, поэтому и не наблюдается сигнал. Затем заряжается конденсатор, после чего он разряжается плавно из за того что нагрузка представляет собой резистор, который имеет не маленькое сопротивление. Колебание наблюдается из за того что ёмкость и индуктивность представляют собой колебательный контур.
4 Рас�чет сиг�на�ла, вос�ста�нов�лен�но�го по дис�крет�ным от�сче�там за�дан�ным ФНЧ
Не�пре�рыв�ный сиг�нал на вы�хо�де вос�ста�нав�ли�ваю�ще�го ФНЧ с импульсной характеристикой при воз�дей�ст�вии на его вхо�де иде�аль�но�го дис�кре�ти�зи�ро�ван�но�го сиг�на�ла Sk(t) оп�ре�де�ля�ет�ся по фор�му�ле:
(13)
На ри�сун�ке 10 пред�став�ле�ны за�ви�си�мо�сти ис�ход�но�го сиг�на�ла и вос�ста�нов�лен�но�го, сме�щен�но�го на вре�мя за�держ�ки фильт�ра.
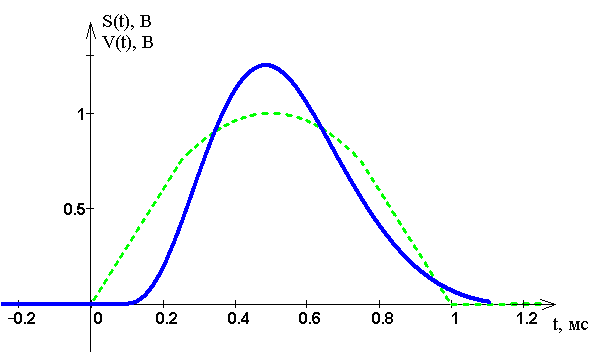
Ри�су�нок 10 – Вос�ста�нов�лен�ный и ис�ход�ный сиг�на�лы
На ри�сун�ках 11 и 12 пред�став�ле�ны спек�траль�ная плот�ность и спектр фаз ис�ход�но�го и вос�ста�нов�лен�но�го сиг�на�лов.
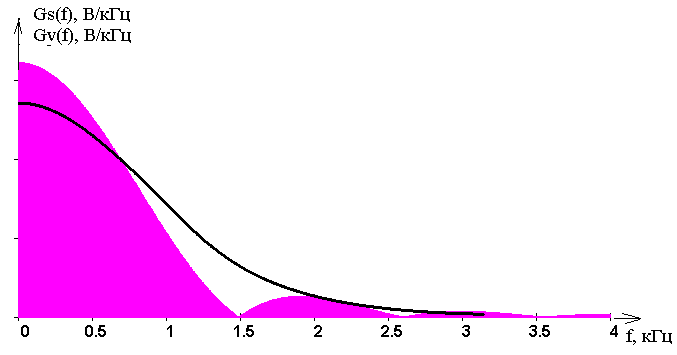
Ри�су�нок 11 – Спек�траль�ная плот�ность ис�ход�но�го (за�ли�тая се�рым) и вос�ста�нов�лен�но�го сиг�на�лов
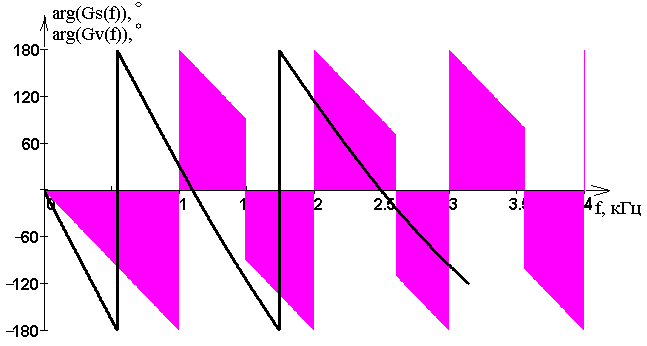
Ри�су�нок 12 – Спектр фаз ис�ход�но�го и вос�ста�нов�лен�но�го сиг�на�лов
Раз�ность спек�траль�ных плот�но�стей ис�ход�но�го и вос�ста�нов�лен�но�го сиг�на�лов обу�слов�ле�на тем, что по�сле вос�ста�нов�ле�ния сиг�на�ла из-за пе�ре�кры�тия спек�тров и ис�поль�зо�ва�ния ФНЧ по�те�ря�на (за�хва�че�на) часть спек�тра дис�кре�ти�зи�ро�ван�но�го сиг�на�ла.
Ана�ли�зи�руя по�лу�чен�ные за�ви�си�мо�сти, при�хо�дим к вы�во�ду, что вос�ста�нов�лен�ный сиг�нал не удов�ле�тво�ря�ет по�греш�но�сти вос�ста�нов�ле�ния, тре�бу�ет�ся про�вес�ти ис�сле�до�ва�ния по вы�бо�ру оп�ти�маль�ных зна�че�ний час�то�ты дис�кре�ти�зац�ии и час�то�ты сре�за фильт�ра.
5 Ис�сле�до�ва�ние влия�ния на по�греш�ность вос�ста�нов�ле�ния сиг�на�ла час�то�ты дис�кре�ти�за�ции и час�то�ты сре�за ФНЧ
Из пре�ды�ду�щих пунк�тов вид�но, что вос�ста�нов�лен�ный сиг�нал при тех час�то�тах дис�кре�ти�за�ции и сре�за не удов�ле�тво�ря�ет тре�бо�ва�ни�ям, по�это�му про�ве�дем ис�сле�до�ва�ния по вы�бо�ру оп�ти�маль�ных зна�че�ний час�тот.
Сна�ча�ла про�ве�дем рас�чет за�ви�си�мо�сти по�греш�но�сти вос�ста�нов�ле�ния d, оп�ре�де�ляе�мой по фор�му�ле сиг�на�ла от ве�ли�чи�ны час�то�ты дис�кре�ти�за�ции F,из�ме�няю�щей�ся в дос�та�точ�но ши�ро�ких пре�де�лах и определяемой по формуле:
(14)
где Ev – энер�гия вос�ста�нов�лен�но�го сиг�на�ла, оп�ре�де�ляе�мая как и для ис�ход�но�го сиг�нала.
По по�лу�чен�ным дан�ным по�стро�ен гра�фик 13.
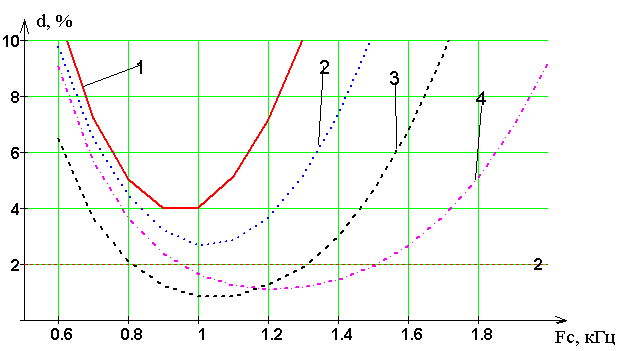
1 – F=2.5 кГц, 2 – F=2.7 кГц, 3 – F=3 кГц, 4 – F=3.5 кГц.
Ри�су�нок 13 – За�ви�си�мость по�греш�но�сти вос�ста�нов�ле�ния от час�то�ты дис�кре�ти�за�ции и частоты среза фильтра
Из рисунке 13 можно легко определить по�греш�но�сть вос�ста�нов�ле�ния от час�то�ты дис�кре�ти�за�ции и частоты среза фильтра. Как видно из графика наибольший интерес для нас представляет кривая 3, так как она пересекает область 2% погрешность при восстановлении.
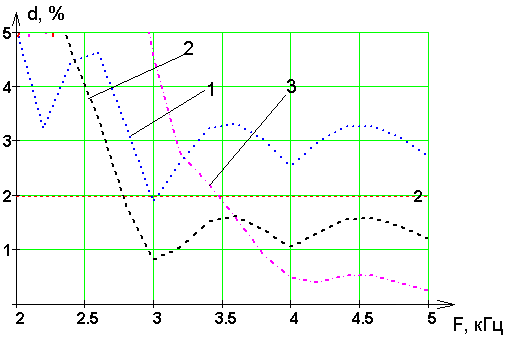
1 – Fc=0.81 кГц, 2 - Fc=1 кГц, 3 - Fc=1.5 кГц.
Рисунок 14 – Зависимость погрешности восстановления от частоты дискретизации
Из рисунке 14 можно легко определить по�греш�но�сть вос�ста�нов�ле�ния от час�то�ты дис�кре�ти�за�ции и частоты среза фильтра. Как видно из графика наибольший интерес для нас представляет кривая 1, так как она пересекает область 2% погрешность при восстановлении.
Таким образом следует что при 2% погрешности при восстановлении Fc = 0.81кГц, а F = 3кГц.
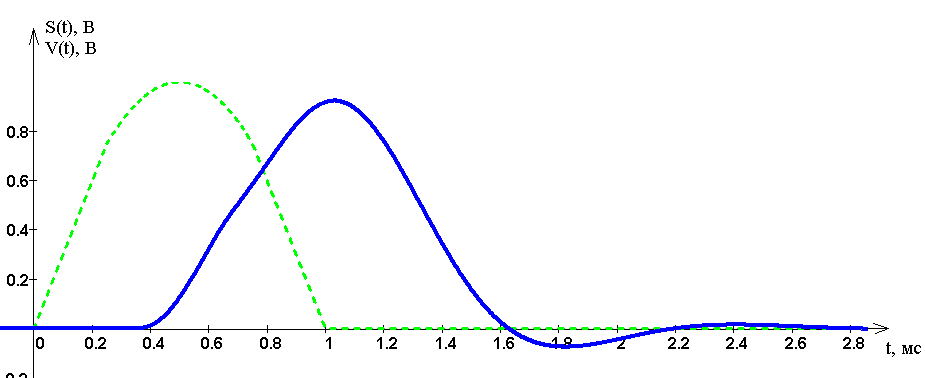
Ри�су�нок 15 – Ис�ход�ный и вос�ста�нов�лен�ный ре�аль�ным ФНЧ сиг�на�лы
6 Срав�ни�тель�ный ана�лиз ка�че�ст�ва вос�ста�нов�ле�ния сиг�на�ла за�дан�ным ре�аль�ным ФНЧ с иде�аль�ным ФНЧ
Про�ве�дем ис�сле�до�ва�ние по вос�ста�нов�ле�нию ви�део�сиг�на�ла иде�аль�ным фильт�ром низ�ких час�тот. Возь�мем в ка�че�ст�ве ис�ход�ных дан�ных час�то�ты со�от�вет�ст�вую�щие оп�ти�маль�но�му вы�бо�ру, т.е. F=3 кГц, Fc=0,81 кГц. Рас�чет сиг�на�ла на вы�хо�де ИФНЧ про�ве�дем по фор�му�ле:
(15)
Ис�ход�ный, вос�ста�нов�лен�ный ре�аль�ным ФНЧ и ИФНЧ сиг�на�лы при час�то�тах дис�кре�ти�за�ции 3 кГц и час�то�те сре�за 0,81 кГц пред�став�ле�ны на ри�сун�ке 16.
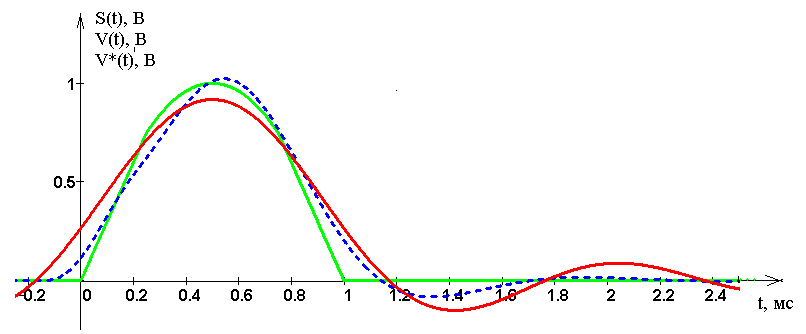
Ри�су�нок 16 – Ис�ход�ный (1), вос�ста�нов�лен�ный ре�аль�ным ФНЧ (2) и ИФНЧ сиг�на�лы
По�греш�ность вос�ста�нов�ле�ния при этих час�то�тах ИФНЧ рав�на 7.45%, у ре�аль�но�го 1.99 %. Получается, что идеальный фильтр при данной частоте среза восстанавливает дискретизированный сигнал хуже (с большей погрешностью восстановления). Это вызвано тем, что практическая ширина спектра сигнала 1,5 кГц, а идеальный фильтр обрезает спектр на частоте 0.81 кГц, т.е. обрезается нужная часть спектра, а АЧХ реального фильтра не заканчивается на частоте среза и нужная часть спектра проходит через фильтр, хотя и с затуханием.
7 Исследование качества восстановления сигнала при разных значениях длительности исходного сигнала