Волновые поля, возбуждаемые гармоническим источником, движущимся по поверхности изотропного слоя

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

(ФГБОУ ВПО «КубГУ»)

Кафедра математического моделирования

ДОПУСТИТЬ К ЗАЩИТЕ В ГАК

Заведующий кафедрой академик РАН,

д-р физ.-мат наук, профессор

_________________ В.А. Бабешко

(подпись) (инициалы, фамилия)

_______________________2014г.

ВЫПУСКНАЯ КВАЛИФИКАЦИОННАЯ РАБОТА

Бакалавра

Волновые поля, возбуждаемые гармоническим источником, движущимся по поверхности изотропного слоя

Работу выполнила К.М.Пеньковская

(подпись, дата) (инициалы, фамилия)

Факультет компьютерных технологий и прикладной математики

Направление 010500.62 – Прикладная математика и информатика

Научный руководитель

канд. физ.-мат наук, доцент _________________________ П.В.Сыромятников

(подпись, дата) (инициалы, фамилия)

Нормоконтролер

доцент, канд. физ.-мат наук, _____________________________ М.С.Капустин

(подпись, дата) (инициалы, фамилия)

Краснодар 2014

РЕФЕРАТ

Выпускная квалификационная работа 41 с., 35 рис., 3 источника.

ТЕОРИЯ УПРУГОСТИ, ВОЛНОВЫЕ ПОЛЯ, ГАРМОНИЧЕСКИЙ ИСТОЧНИК, ИЗОТРОПНЫЙ СЛОЙ, ПРИНЦИП ПРЕДЕЛЬНОГО ПОГЛОЩЕНИЯ, ПРЕОБРАЗОВАНИЕ ФУРЬЕ

Объектом исследования являются «частичные» смещения, вызванные нагрузками с осцилляциями и без осцилляций.

Цель работы – произвести численный расчет частичных нагрузок в подвижной системе координат, сравнить полученные результаты при разных диапазонах скоростей.

Решение задачи осуществляется путем использования интегральных преобразований Фурье и численного решения с использованием программ пакета NAG. В качестве математической модели взят бесконечно протяженный изотропный слой некоторой толщины и нагрузка в прямоугольной области поверхности слоя, связанная с подвижной системой координат.

При реализации расчетов использовались средства Compaq Visual Fortran 6.5.0 и библиотеки NAG.

Подобные задачи представляют интерес при изучении проблем касающихся транспорта, строительства придорожной инфраструктуры, а также эффектов, связанных с высокой скоростью передвижения и т.д.

СОДЕРЖАНИЕ

ВВЕДЕНИЕ

Анализу волновых полей, вызванных движущимися по поверхности твердого тела источниками, посвящено немалое число исследований [1,2].

Во многих случаях подобного рода задачи связаны с проблемами транспорта и строительства придорожной инфраструктуры, но исследование связанных с высокой скоростью передвижения по упругой поверхности эффектов представляет и самостоятельный научный интерес.

К подобным задачам, как правило, применимы те же методы, что и для динамических и статических задач теории упругости [1,2], но они имеют и свою специфику, которая приводит к необходимости модификаций имеющихся методов.

Данная работа посвящена расчету и численному исследованию поверхностных возмущений изотропного слоя в плоском случае, вызванных поверхностной гармонической нагрузкой, перемещающейся в фиксированном направлении с постоянной скоростью.

Задача решается с помощью техники интегральных преобразований Фурье [1,2] и численного интегрирования с применением программ пакета NAG [3]. Специфика задачи заключается в появлении т.н. наведенной анизотропии, определяемой направлением движения и величиной скорости.

Для модельных параметров среды в плоской постановке исследуются трансформации всех компонент поверхностных возмущений в «дозвуковом» диапазоне скоростей ( - скорость релеевской волны) и в «сверхзвуковом» диапазоне (- скорость продольной волны).

Актуальность данной задачи определяется качественными изменениями упругой поверхности при вариациях скорости, частоты и параметров источника.

1 Постановка задачи

Рассматривается изотропный упругий слой в декартовой системе координат , который занимает объем , , где - толщина слоя.

В подвижной системе координат , где

, (1.1)

- скорость движения, - время, на поверхности слоя, в прямоугольной области со сторонами :

(1.2)

приложена векторная гармоническая нагрузка (общий экспоненциальный множитель в дальнейшем опускается)

, (1.3)

которая движется без вращения вдоль прямой Ox с постоянной скоростью v.

Вне области механические напряжения равны нулю:

. (1.4)

Слой лежит на жестком основании при :

. (1.5)

Требуется определить (в общем случае комплексные) смещения в подвижной системе координат , связанной с источником.

2 Символ матрицы Грина изотропного слоя для гармонического источника в подвижной системе координат

В начале приведем без вывода вид символа Фурье матрицы Грина изотропного слоя , лежащего на жестком основании [1,2], при возбуждении гармонических колебаний поверхностным источником в неподвижной системе координат.

Произвольные колебания изотропной среды в случае отсутствия объемных сил описывается системой уравнений Ляме [1]:

, (2.1)

где - оператор Лапласа, - вектор-функция, описывающая смещение точки упругой среды с координатами , коэффициенты Ляме, характеризующие упругие свойства материала, - плотность.

Установившиеся гармонические колебания изотропной среды описываются следующей системой уравнений Ляме [1]:

, (2.2)

где - круговая частота. Обычно при рассмотрении гармонических колебаний общий множитель опускается и рассуждения ведутся относительно комплексных амплитуд искомых величин. Граничные условия для задачи с неподвижным источником имеют вид:

, (2.3)

(2.4)

Далее применяется стандартная техника интегральных преобразований Фурье. Для нахождения символа смещений используется преобразование Фурье по двум пространственным переменным :

(2.5)

Вектор (2.5) может быть представлен через символ Фурье матрицы Грина и символ вектора поверхностной нагрузки [1,2]:

,(2.6)

где

(2.7)

Функции , входящие в состав матрицы Грина, в случае слоя на жестком основании имеют вид:

(2.8)

где

(2.9)

Рассмотрим вторую производную по времени, входящую в уравнения движения Ляме (2.1):

(2.10)

Согласно (2.10) в образах Фурье получаем соответствие :

(2.11)

Последнее соотношение означает, что в образах Фурье уравнений Ляме для неподвижного источника квадрат частоты заменяется в случае подвижной системы координат на выражение:

(2.12)

Отличие символа матрицы Грина для подвижного источника от случая неподвижного источника ограничивается только выражением (2.12). Символ матрицы Грина для подвижного источника, соответствующий подстановке (2.12), обозначим . Непосредственно данная замена сказывается только на величинах (2.9), содержащих частоту . После подстановки (2.12) получаем:

(2.13)

При этом среда приобретает анизотропию, обусловленную направлением движения и скоростью источника , как в плоском, так и в пространственном случае.

3 Интегральное представление решения задачи для гармонического поверхностного подвижного источника.

Решение задачи для подвижного гармонического источника может быть представлено в виде обратного преобразования Фурье [1,2], полностью аналогичного случаю неподвижного источника: (3.1)

Здесь представляет собой контуры в комплексных плоскостях , которые отклоняются при обходе вещественных полюсов матрицы в соответствии с принципом предельного поглощения [1,2].

Для задач в плоской постановке двойной интеграл переходит в однократный интеграл следующего вида:

(3.2)

Считая для простоты , интегралы от отдельных компонент матрицы (3.2), которые в дальнейшем будем называть «частичными» смещениями , запишем в виде:

(3.3)

В данной работе основное внимание было уделено вертикальным смещениям , вызванным вертикальной нагрузкой , и определяемым элементом матрицы Грина (2.8):

(3.4)

4 Численные результаты для плоской задачи режима движения без осцилляций.

В данном пункте последовательно и однотипно рассмотрены частичные смещения (3.3) для режима движения без осцилляций в плоском случае (для - в антиплоском).

Скорость движения рассматривалась в четырех диапазонах 1) - 4):

1) - дозвуковой диапазон, (4.1)

2) - первый сверхзвуковой диапазон,

3) - второй сверхзвуковой диапазон,

4) - третий сверхзвуковой диапазон.

В подвижной системе координат (1.1), в качестве поверхностного подвижного источника рассматривался «длинный» источник :

, (4.2)

При этом Фурье-образ подвижного источника имеет вид:

(4.3)

Графики частичных смещений представляют собой интегралы (3.3) от соответствующих произведений элементов символа матрицы Грина и нагрузки . Интегралы (3.3) рассчитывались численно при введении комплексной частоты :

, , (4.4)

по ограниченному вещественному контуру , где R - достаточно большое положительное число. Для численного интегрирования использовались программы вычисления интегралов от осциллирующих функций пакета NAG [3].

При расчетах брались следующие модельные безразмерные значения толщины слоя , плотности , констант Ляме :

, , , (4.5)

Данным значениям безразмерных параметров соответствуют следующие безразмерные скорости:

, , (4.6)

4.1 Численные результаты для смещений u11.

Результаты расчетов смешений , определяемых элементом матрицы и вызываемых горизонтальной нагрузкой вида (4.3) в диапазонах скоростей 1) - 4) (4.1), представлены ниже.

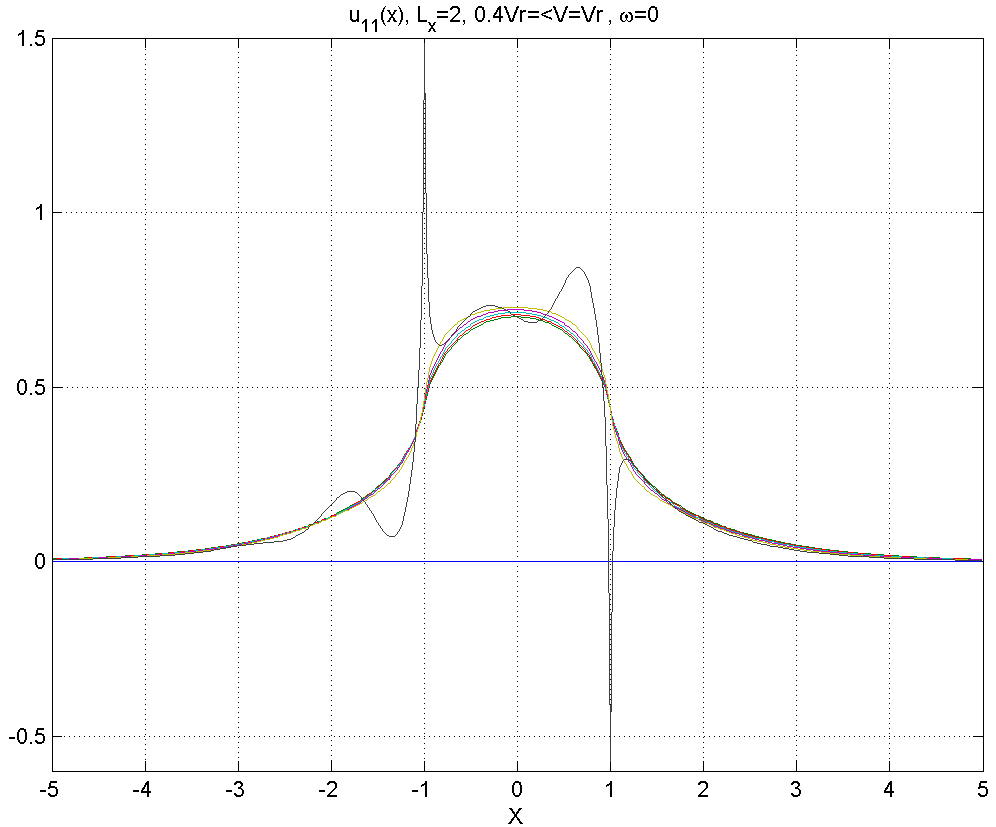
Рисунок 4.1.1 – Вид смещений в диапазоне скоростей .

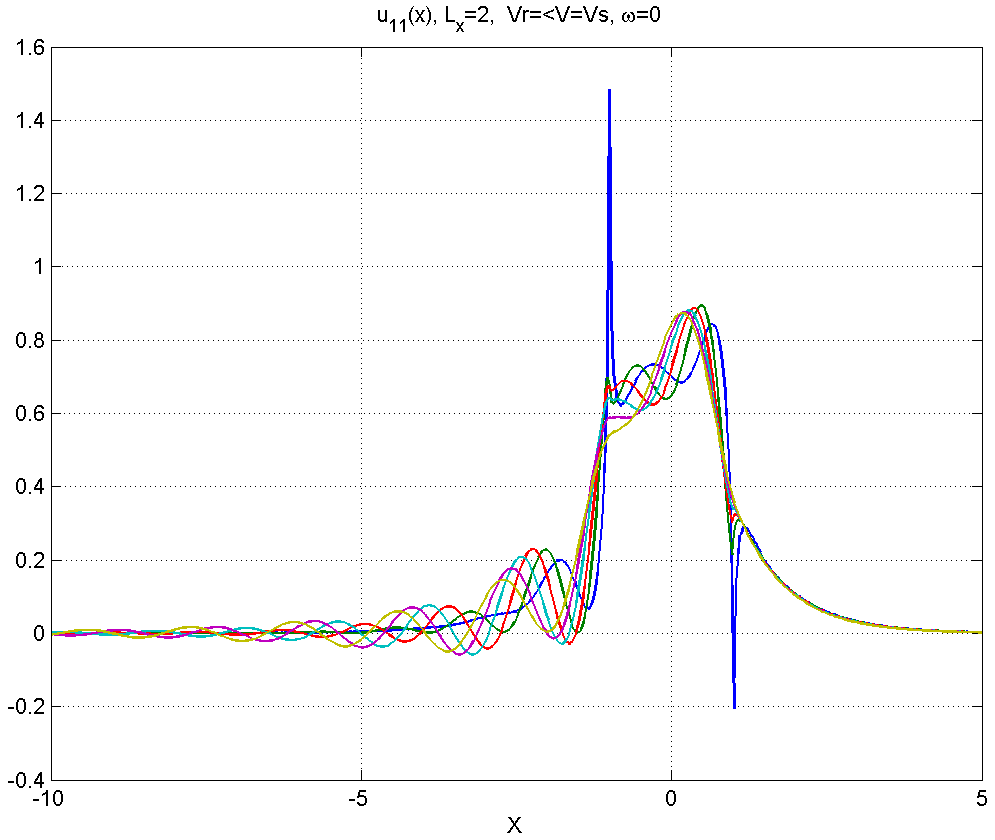
Рисунок 4.1.2 – Вид смещений в диапазоне скоростей .

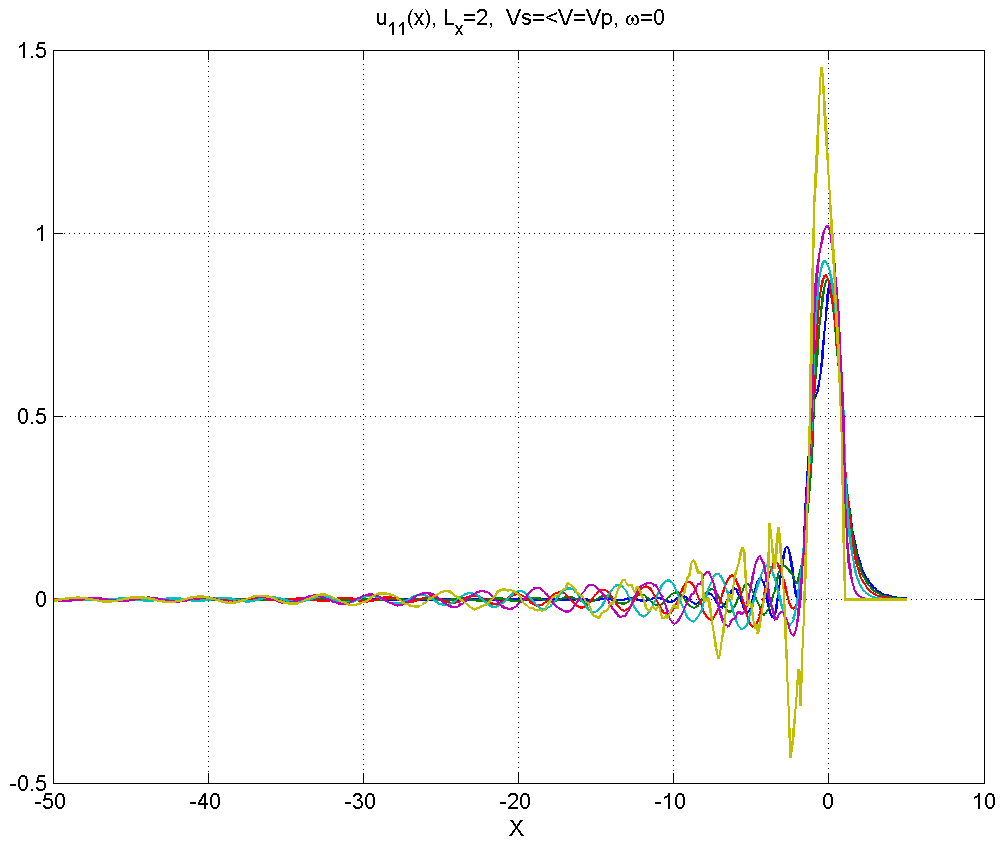
Рисунок 4.1.3 – Вид смещений в диапазоне скоростей .

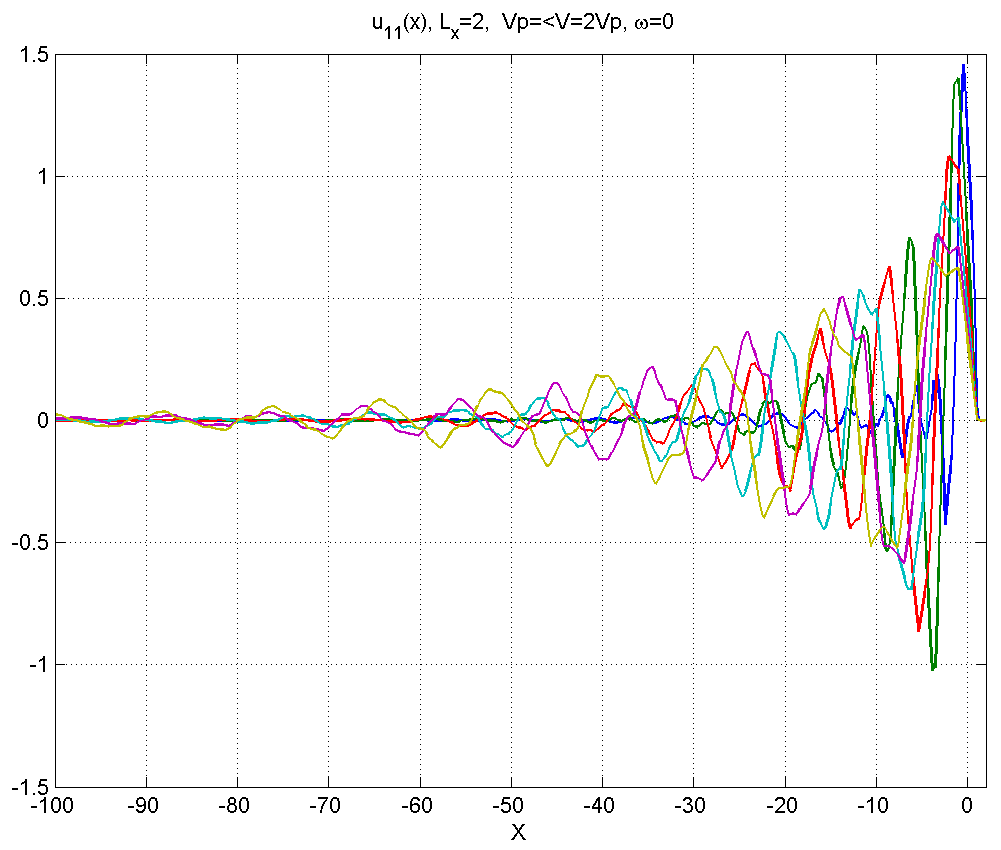
Рисунок 4.1.4 – Вид смещений в диапазоне скоростей .

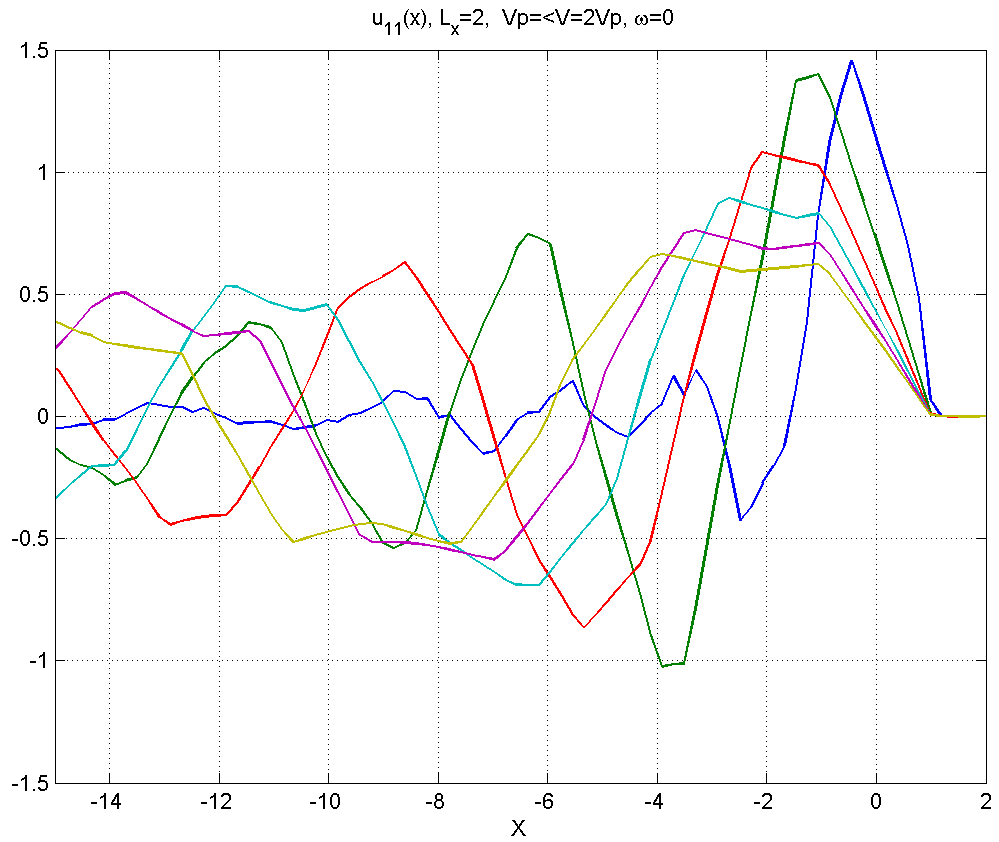
Рисунок 4.1.5 – Вид смещений в диапазоне скоростей .

На рис. 4.1.6 представлена зависимость и координат максимума в зависимости от скорости движения в диапазоне .

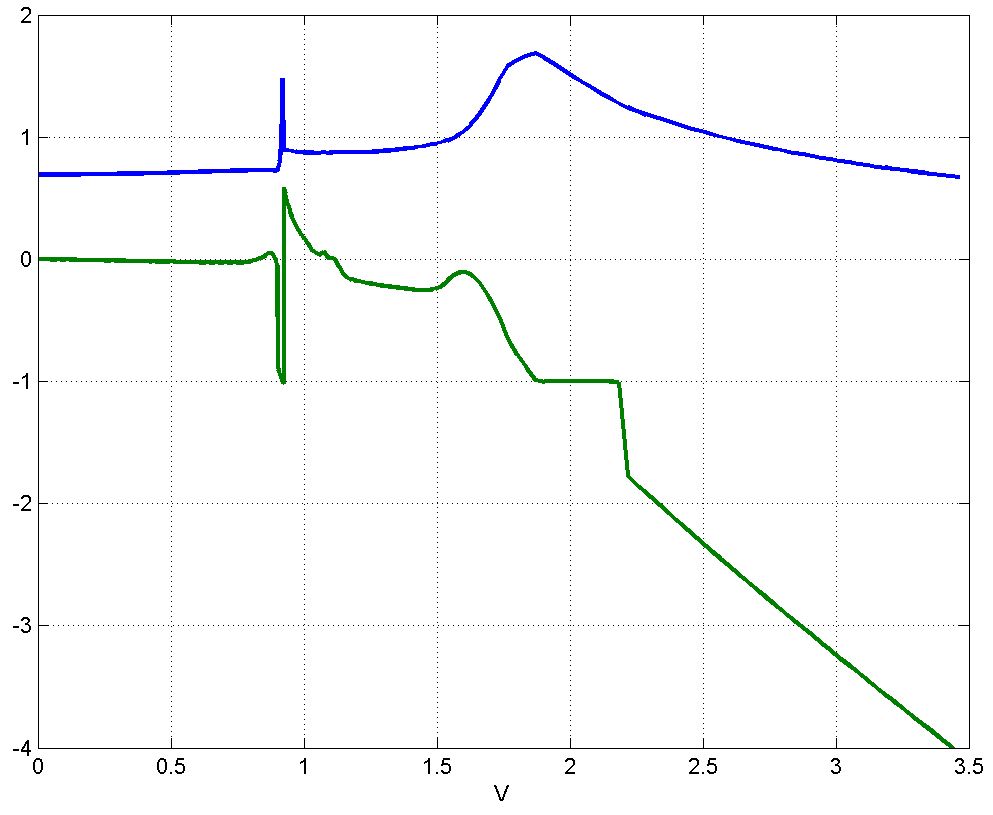
Рисунок 4.1.6 – Вид (синий цвет, верхний график) и координат максимума (зеленый цвет, нижний график) в зависимости от скорости движения в диапазоне .

Как видно из данной серии расчетов, в диапазоне 1) смещения мало отличаются от статического решения, заметные изменения появляются только при .

В диапазоне 2) позади источника появляется синусоидальный шлейф.

В диапазоне 3) шлейф значительно растягивается.

В диапазоне 4) вблизи источника смещения приобретают сложный несинусоидальный характер, при удалении от источника шлейф асимптотически приобретает характер синусоиды.

Амплитудная зависимость от скорости, представленная на рис. 4.1.6, позволяет сделать следующие выводы.

Имеется два максимума , первый из которых связан с релеевской скоростью, второй максимум достигается при , т.е. при значениях скорости, близких к скорости продольной волны .

Максимум смещений при нулевой скорости , при скорости удвоенной продольной волны . При этом выполняются соотношения:

.

В диапазоне 1) находится примерно в центре источника , при приближении скорости к координаты резко изменяются от до .

В диапазоне скоростей координаты смещаются к заднему краю источника , при максимум выходит за пределы источника и наблюдается нарастающее отставание , имеющее кусочно-линейный характер.

4.2 Численные результаты для смещений u22.

В данном пункте представлены результаты расчетов смешений , определяемых элементом матрицы и вызываемых горизонтальной нагрузкой вида (4.3). Для данного источника характерными являются несколько иные, чем (4.1) диапазоны скоростей, а именно, диапазон 1) и 2) (4.1) теперь можно объединить в один «дозвуковой» диапазон, 3) и 4) остаются без изменений.

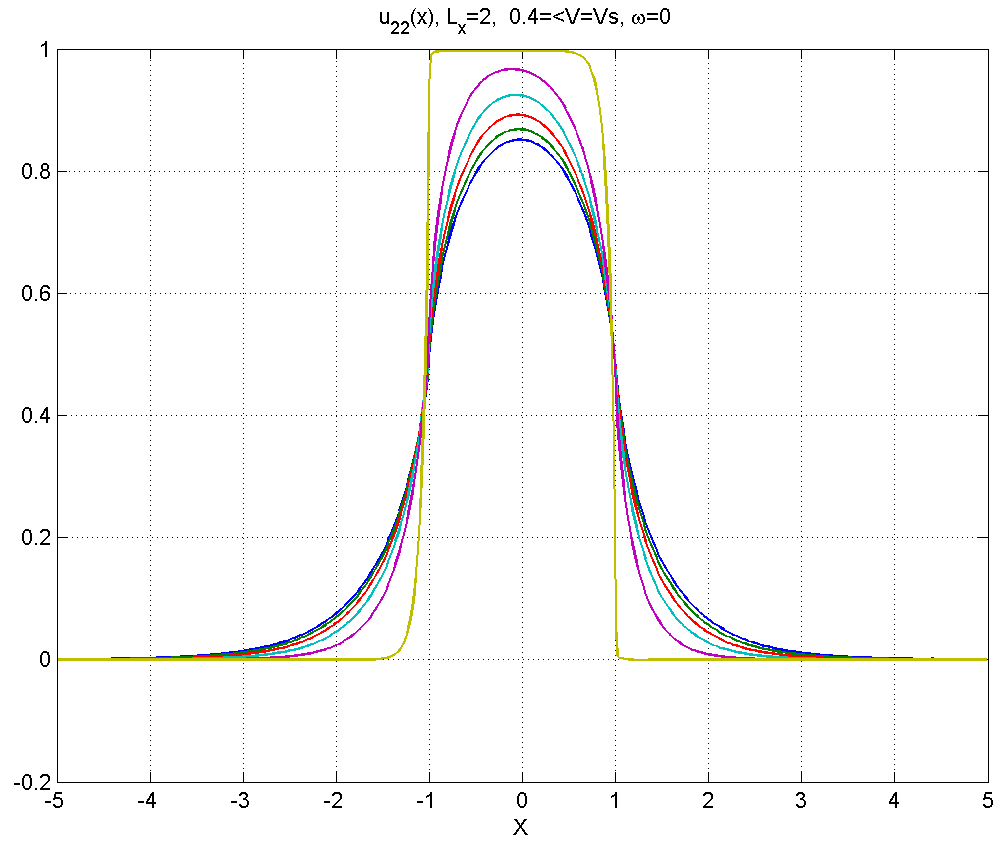
Рисунок 4.2.1 – Вид смещений в диапазоне скоростей .

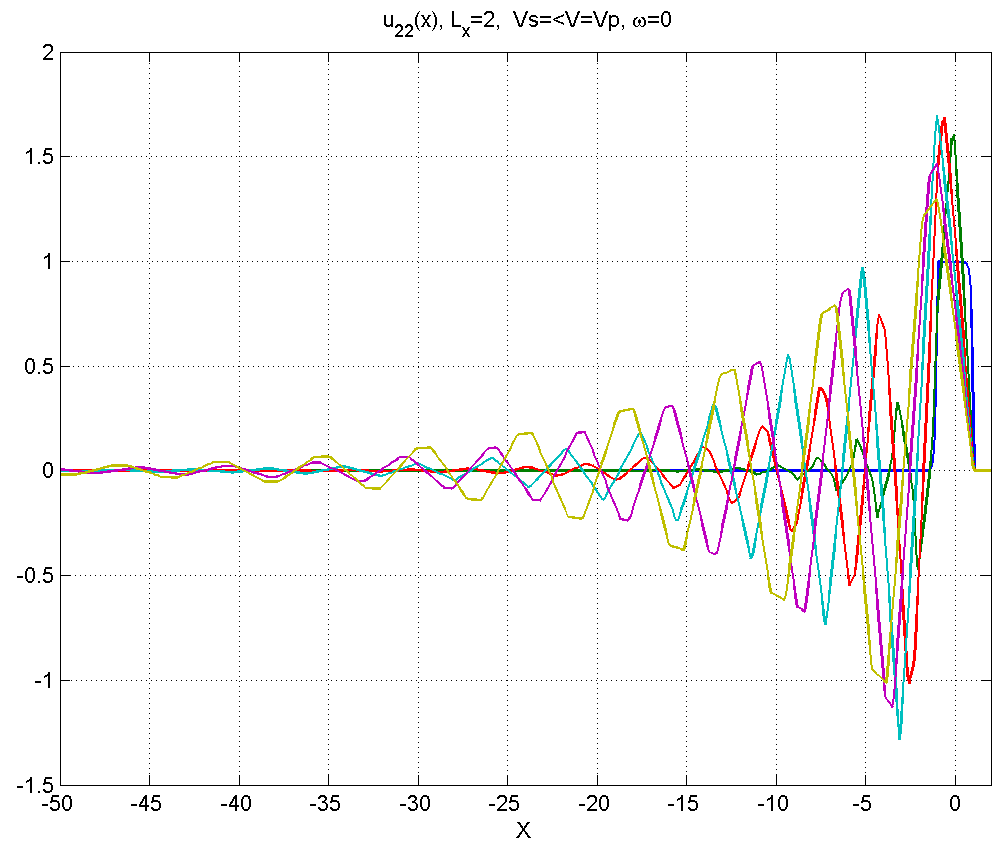
Рисунок 4.2.2 – Вид смещений в диапазоне скоростей .

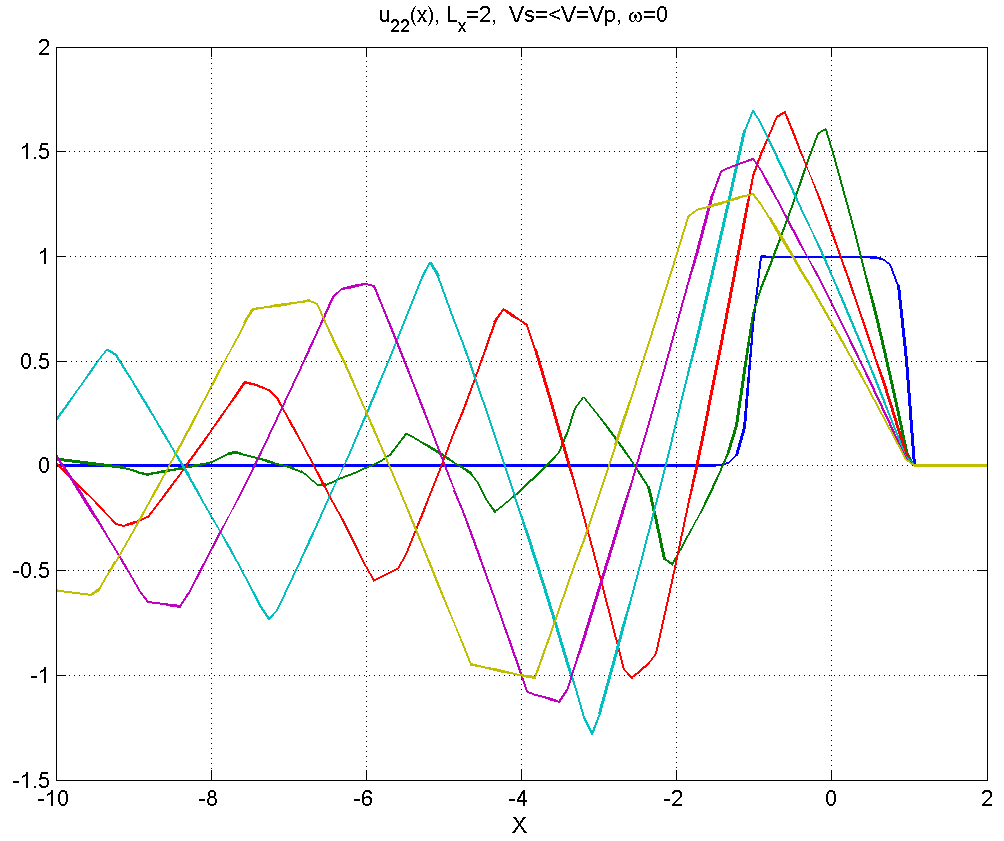
Рисунок 4.2.3 – Вид смещений в диапазоне скоростей .

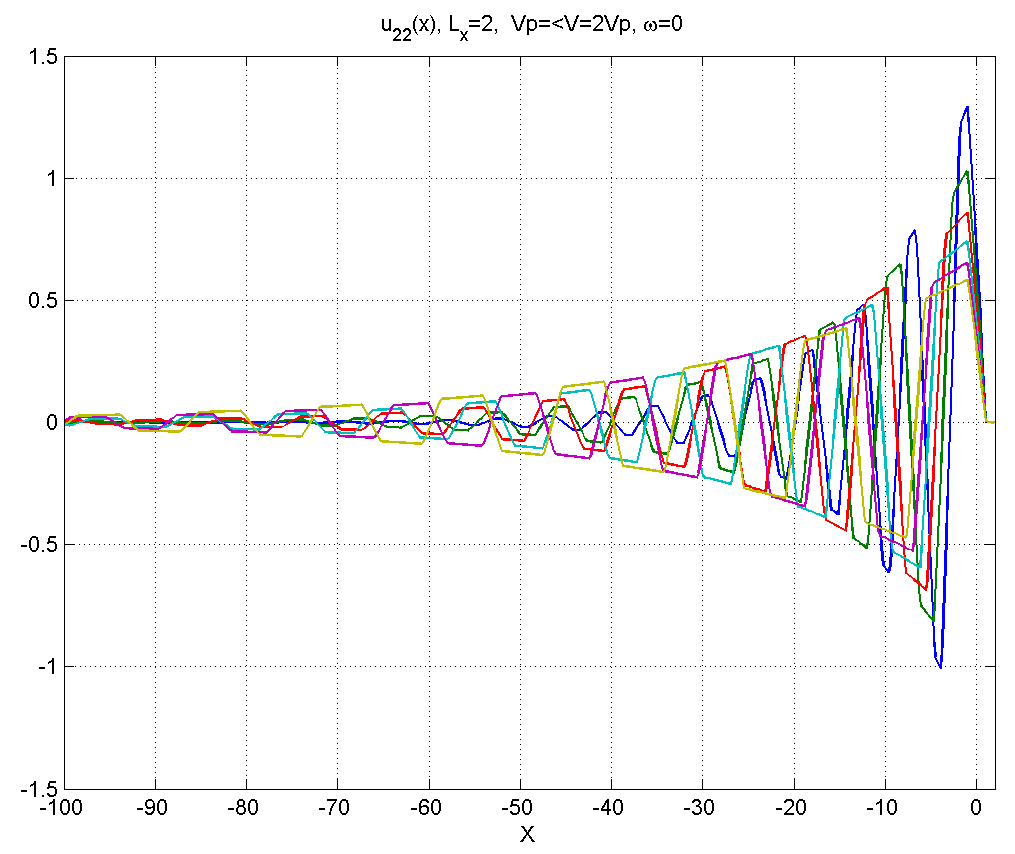
Рисунок 4.2.4 – Вид смещений в диапазоне скоростей .

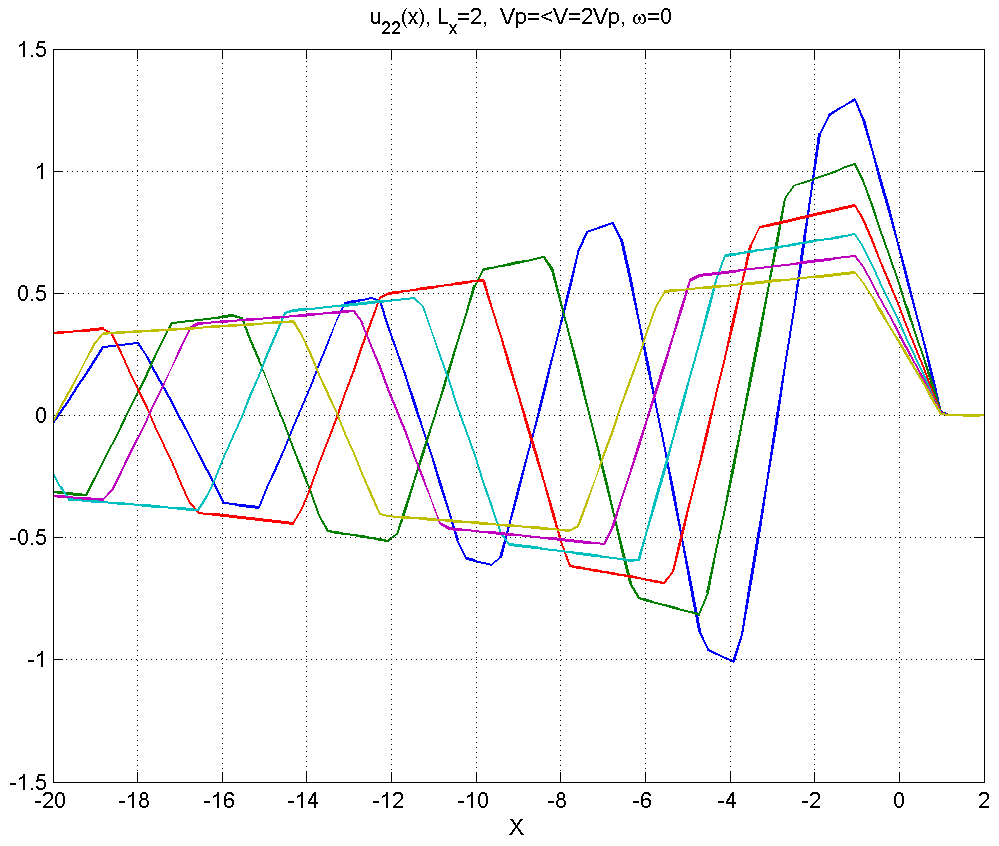
Рисунок 4.2.5 – Вид смещений в диапазоне скоростей .

На рис. 4.2.6 представлена зависимость и координат максимума в зависимости от скорости движения в диапазоне .

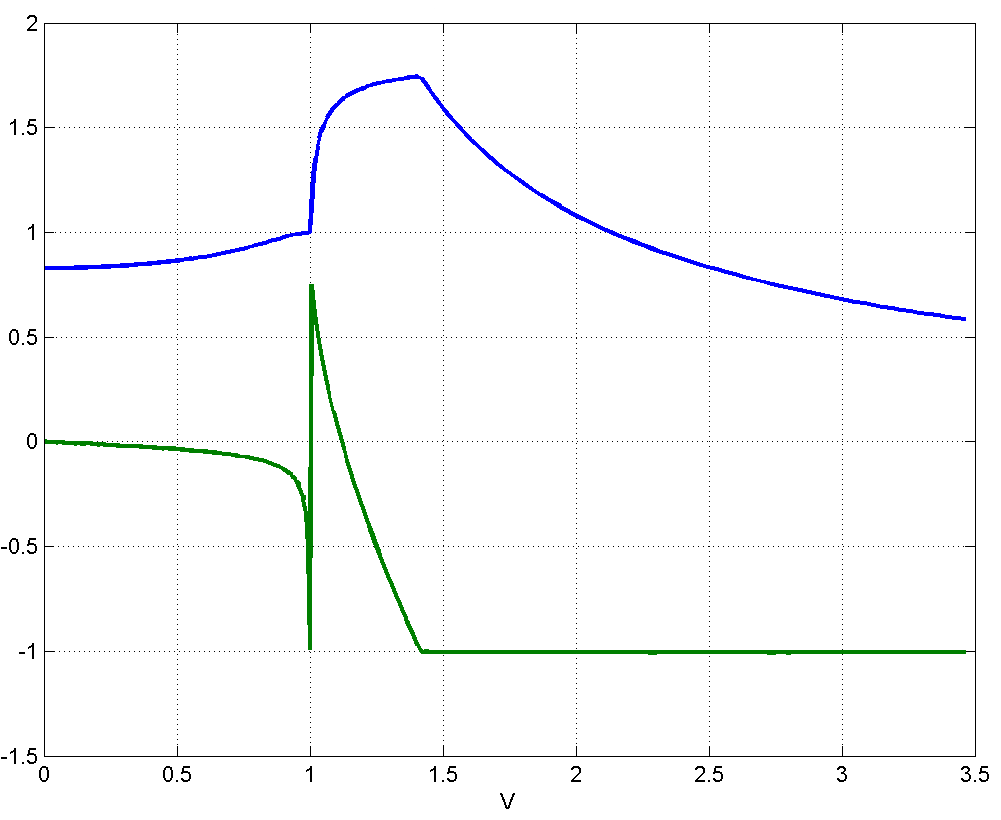
Рисунок 4.2.6 – Вид (синий цвет, верхний график) и координат максимума (зеленый цвет, нижний график) в зависимости от скорости движения в диапазоне .

Как видно из данной серии расчетов, в диапазоне (диапазон 1)-2)) смещения мало отличаются от статического решения, заметные изменения появляются только при . При профиль приобретает почти прямоугольный вид. Скорость релеевской волны не является критической для данного источника.

В диапазоне 3) позади источника появляется линейно-треугольный шлейф.

В диапазоне 4) шлейф значительно растягивается, сохраняя линейно-треугольный вид даже в дальней зоне.

Имеется один максимум , который не связан ни с одной из характерных скоростей , поскольку максимум приходится на , что соответствует примерно середине интервала . Резкий рост амплитуды наблюдается при достижении , в этой же точке происходит резкая смена координат максимума: от до .

Максимальные смещения при нулевой скорости , при скорости удвоенной продольной волны . При этом выполняются соотношения:

.

В диапазоне находится примерно в центре источника , при приближении скорости к координаты резко смещаются к .

В диапазоне скоростей координаты смещаются от к заднему краю источника . При максимум очень незначительно выходит за пределы источника и остается в районе .

4.3 Численные результаты для смещений u31.

Ниже представлены результаты расчетов вертикальных смешений , определяемых элементом матрицы и вызываемых горизонтальной нагрузкой вида (4.3) в диапазонах скоростей 1)-4) (4.1).

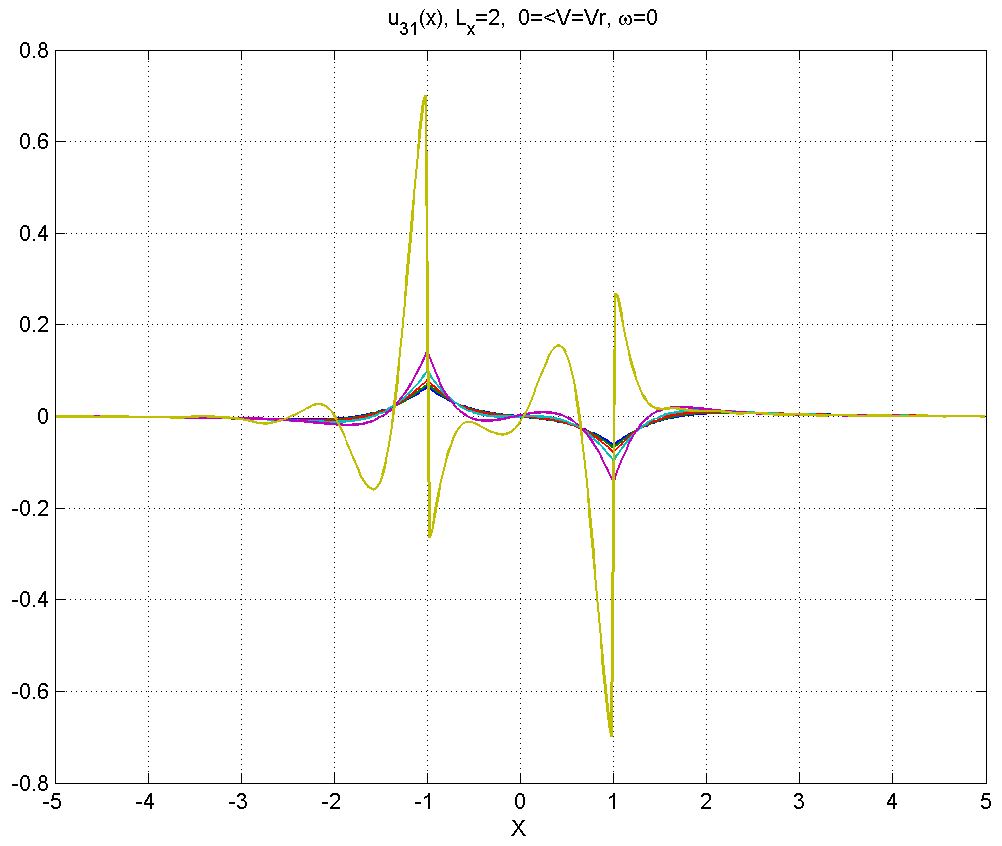
Рисунок 4.3.1 – Вид смещений в диапазоне скоростей .

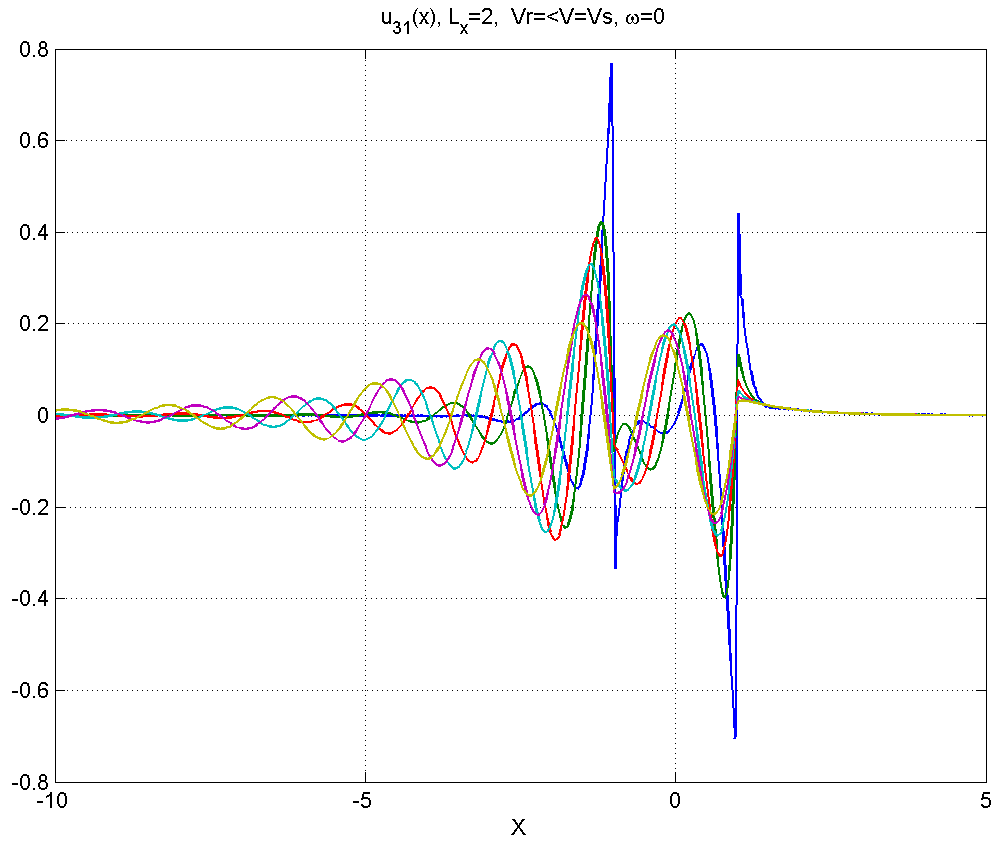
Рисунок 4.3.2 – Вид смещений в диапазоне скоростей .

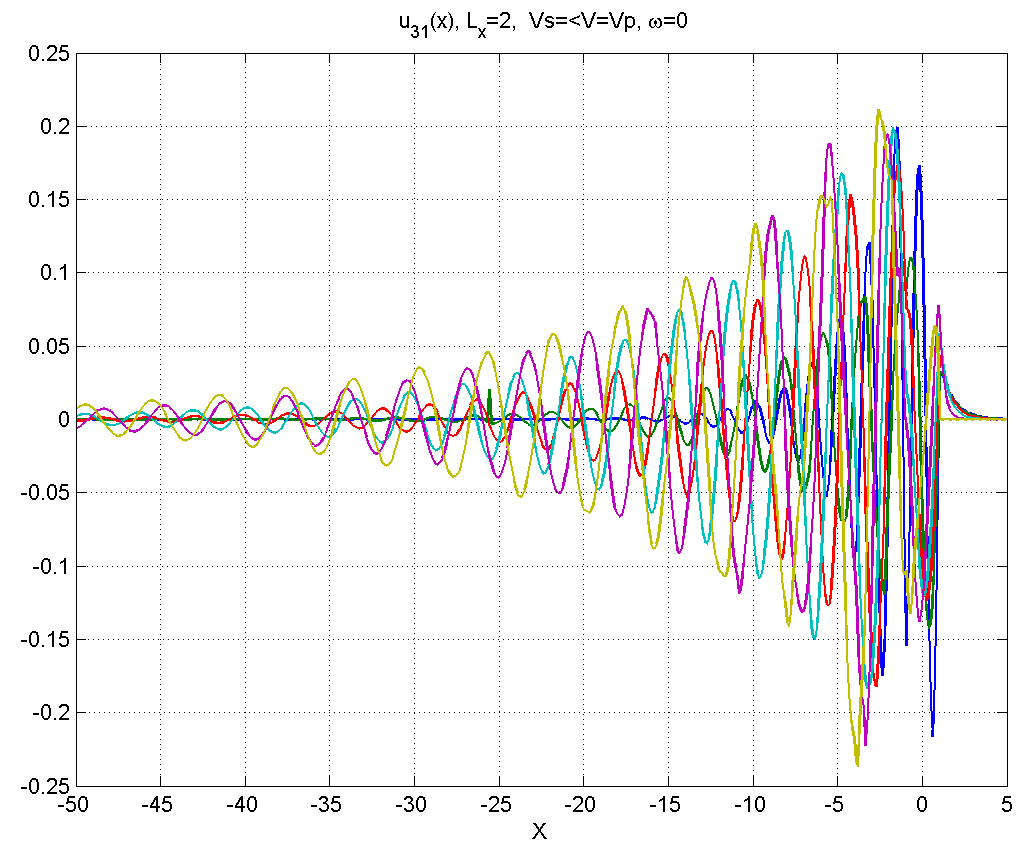
Рисунок 4.3.3 – Вид смещений в диапазоне скоростей .

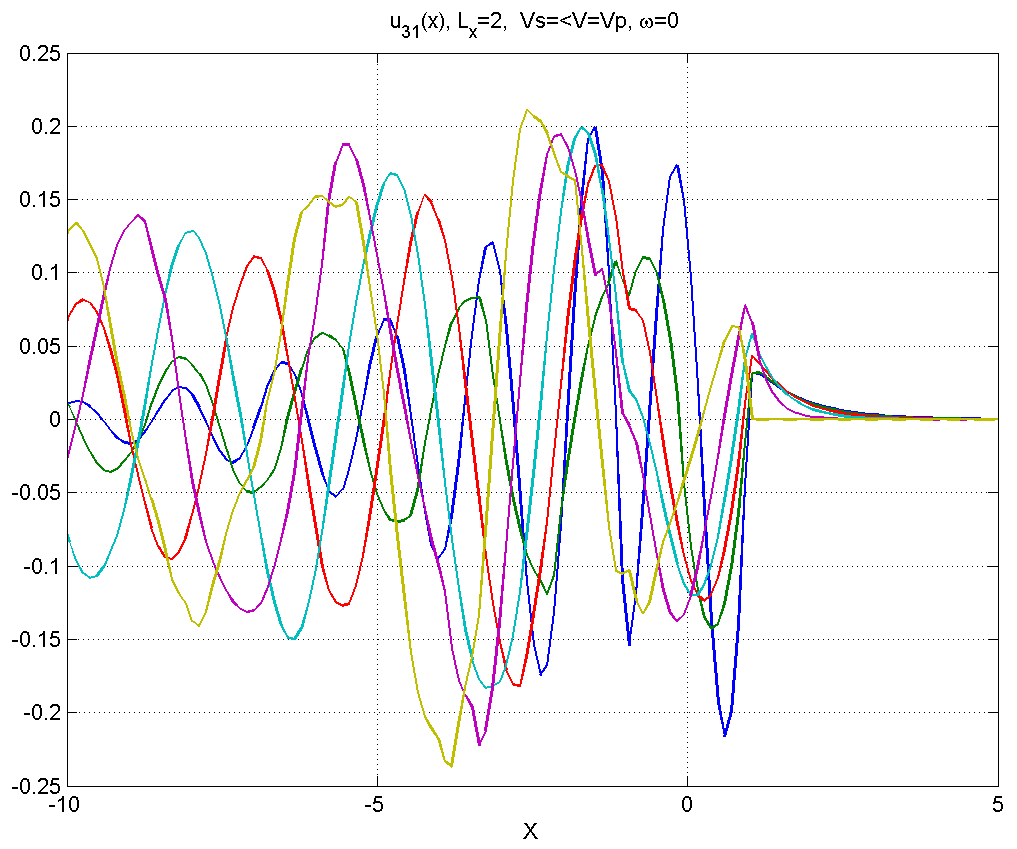
Рисунок 4.3.4 – Вид смещений в диапазоне скоростей .

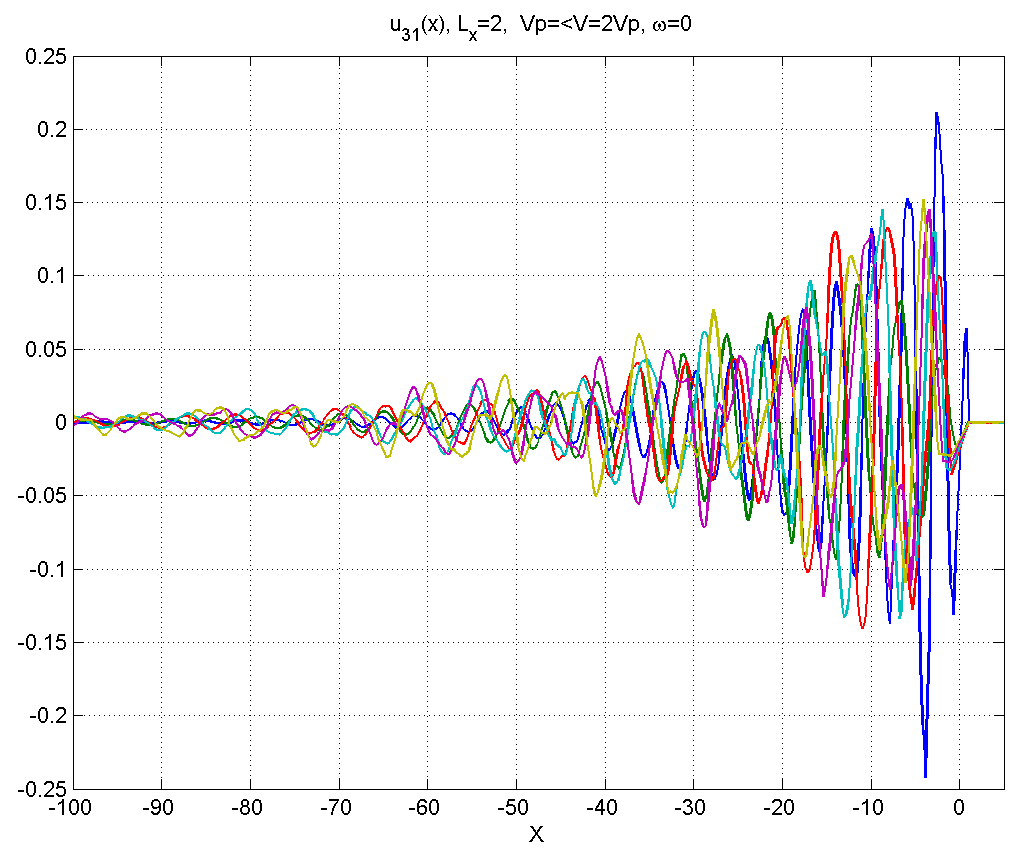
Рисунок 4.3.5 – Вид смещений в диапазоне скоростей .

Рисунок 4.3.6 – Вид смещений в диапазоне скоростей .

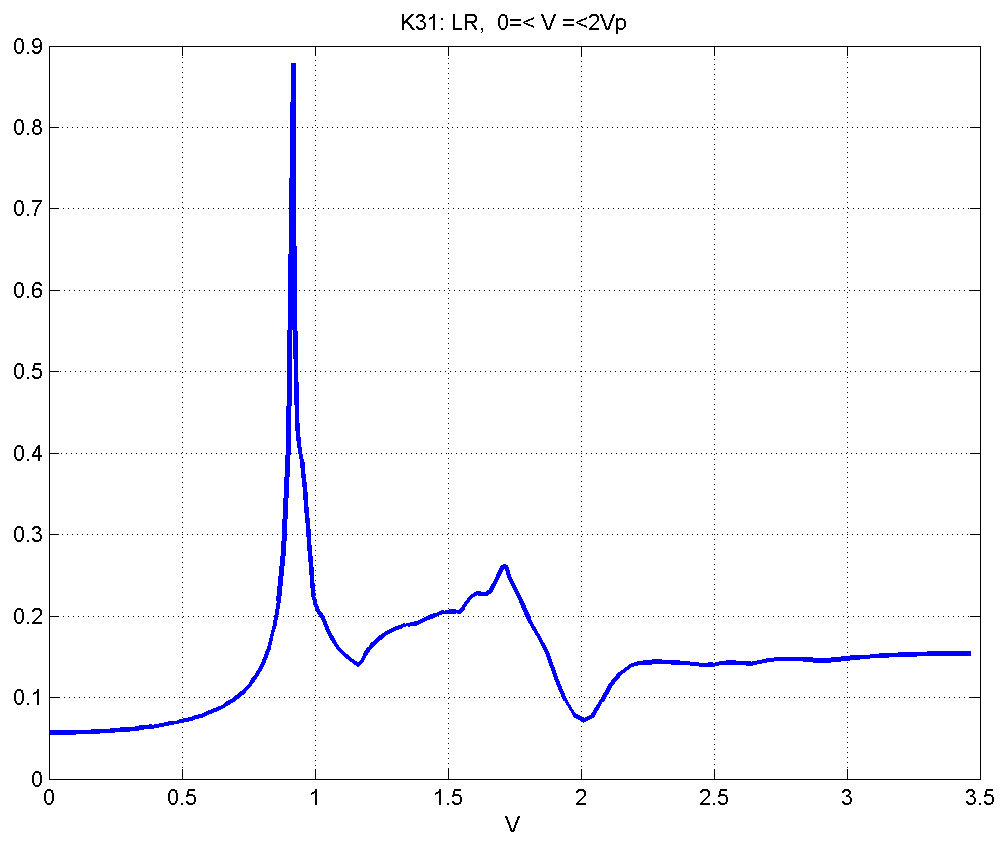
Рисунок 4.3.7 – Вид в зависимости от скорости движения в диапазоне .

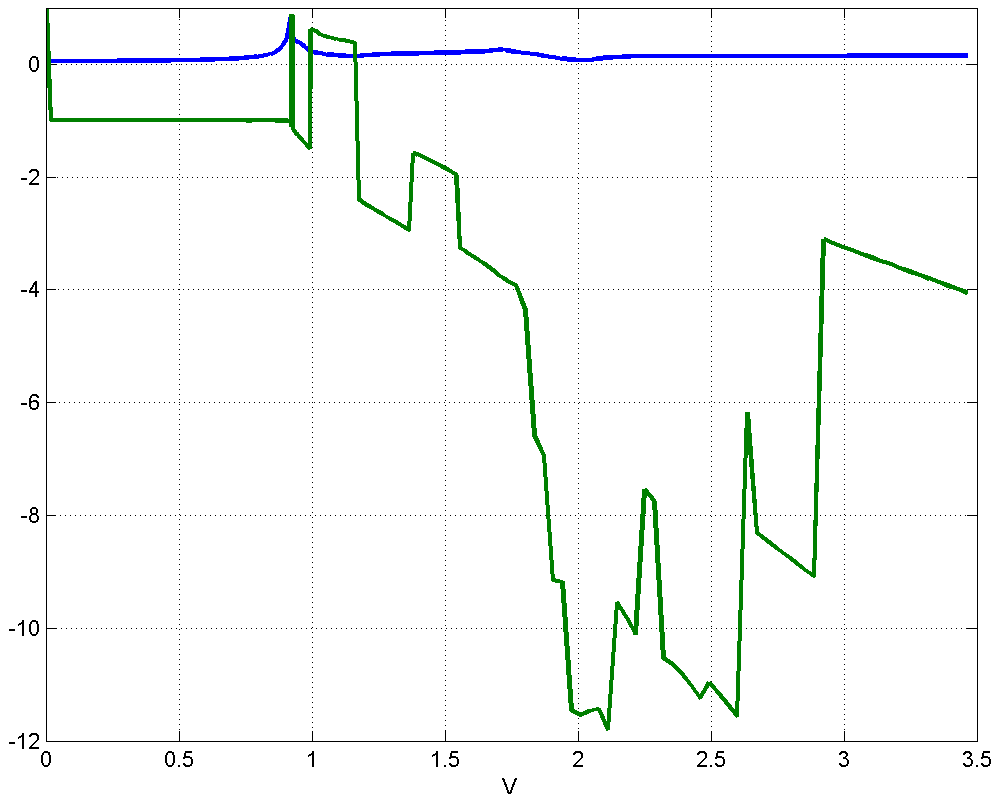
Рисунок 4.3.8 – Вид (синий цвет, верхний график) и координат максимума (зеленый цвет, нижний график) в зависимости от скорости движения в диапазоне .

Как видно из данной серии расчетов, в диапазоне 1) смещения мало отличаются от статического решения, заметные изменения появляются только при .

В диапазоне 2) позади источника появляется синусоидальный шлейф.

В диапазоне 3) шлейф значительно растягивается.

В диапазоне 4) вблизи источника смещения приобретают сложный несинусоидальный характер, при удалении от источника шлейф асимптотически приобретает характер синусоиды.

Имеется два максимума , первый их которых связан с , второй максимум достигается при .

Максимальные смещения при нулевой скорости , при скорости удвоенной продольной волны . При этом выполняются соотношения:

В отличие от предыдущих случаев, при максимум почти монотонно растет.

В диапазоне 1) находится сначала на правой границе источника , затем перемещается в крайнюю левую точку источника , остается в окрестности до достижения . При координаты изменяются в широком диапазоне значений кусочно-линейным образом.

4.4 Численные результаты для смещений u13.

Результаты расчетов и качественные выводы для горизонтальных смешений , определяемых элементом матрицы и вызываемых вертикальной нагрузкой вида (4.3) в диапазонах скоростей 1)-4) (4.1), буквально совпадают с результатами для .

4.5 Численные результаты для смещений u33.

В данном пункте представлены результаты расчетов вертикальных смешений , определяемых элементом матрицы и вызываемых вертикальной нагрузкой вида (4.3) в диапазонах скоростей 1)-4) (4.1).

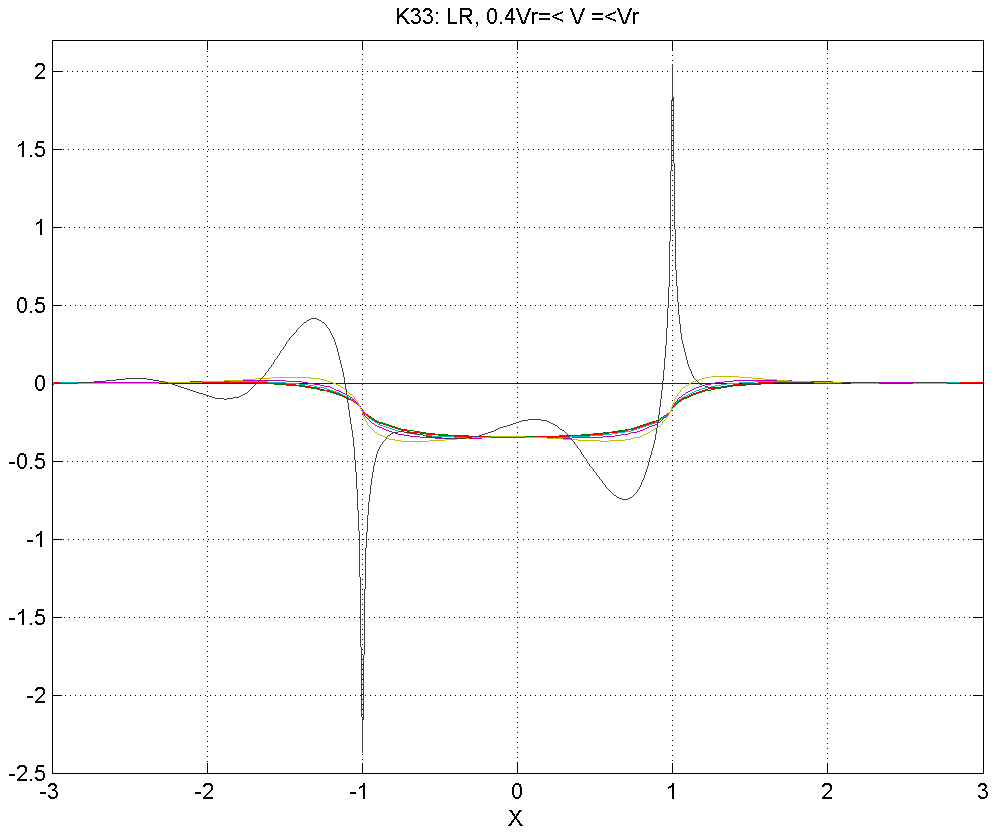
Рисунок 4.5.1 – Вид смещений в диапазоне скоростей .

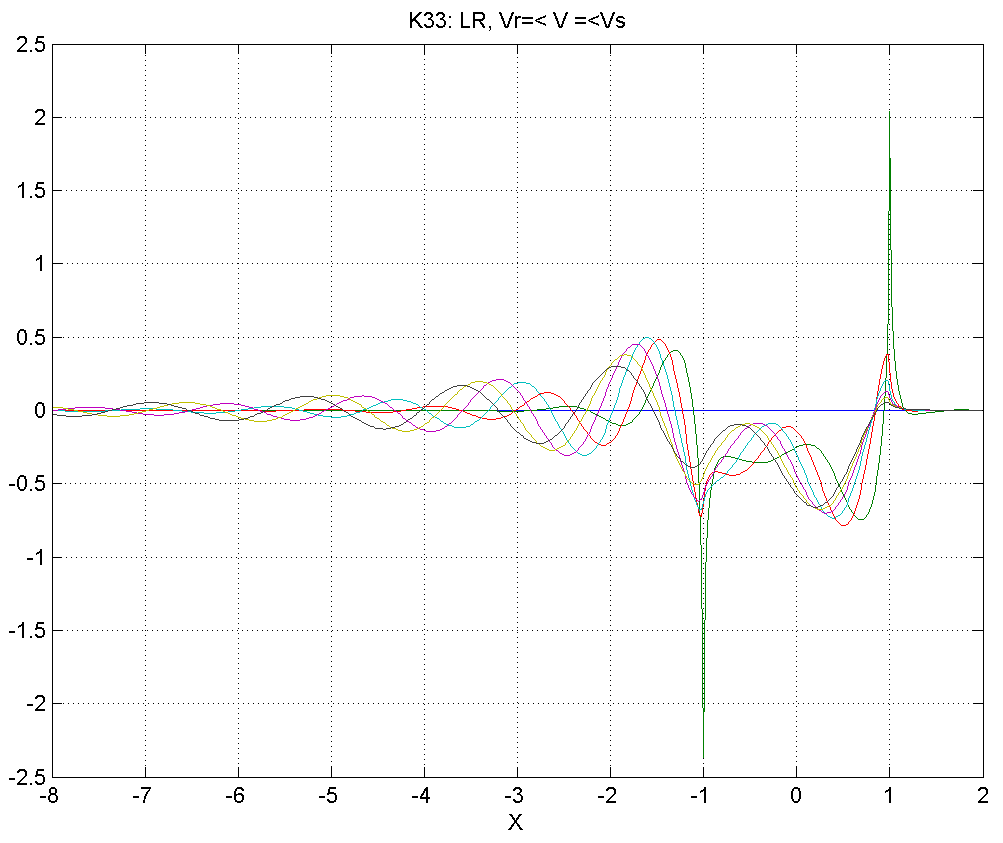
Рисунок 4.5.2 – Вид смещений в диапазоне скоростей .

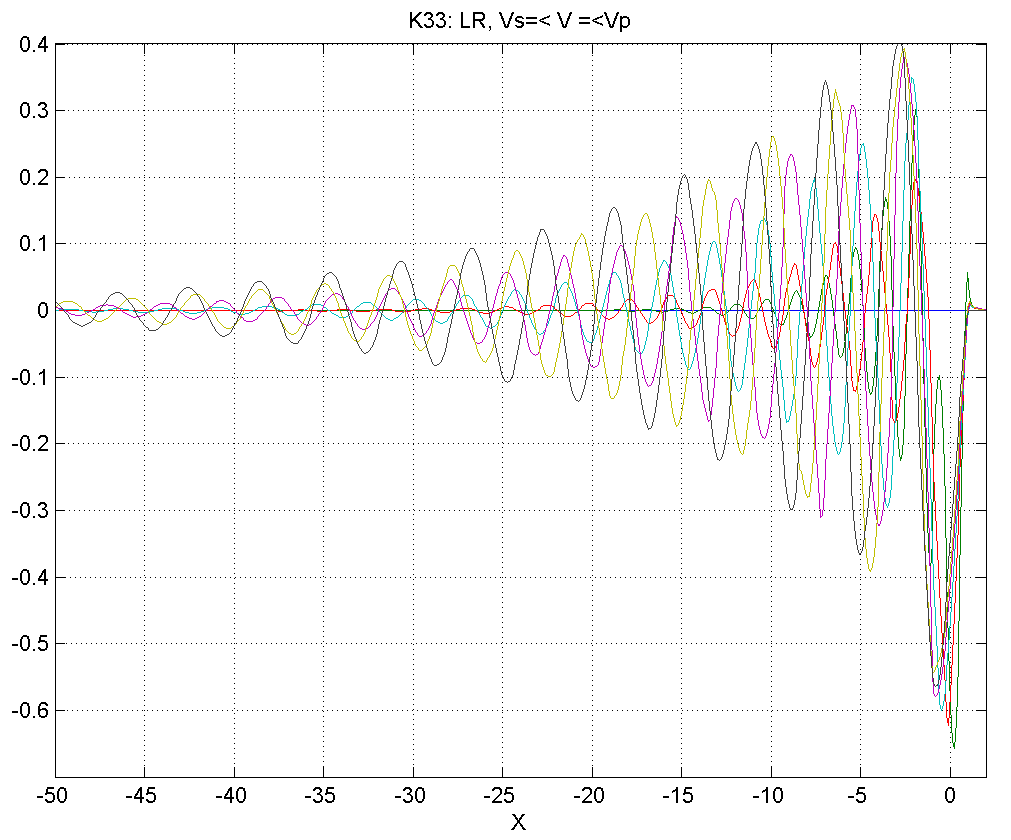
Рисунок 4.5.3 – Вид смещений в диапазоне скоростей .

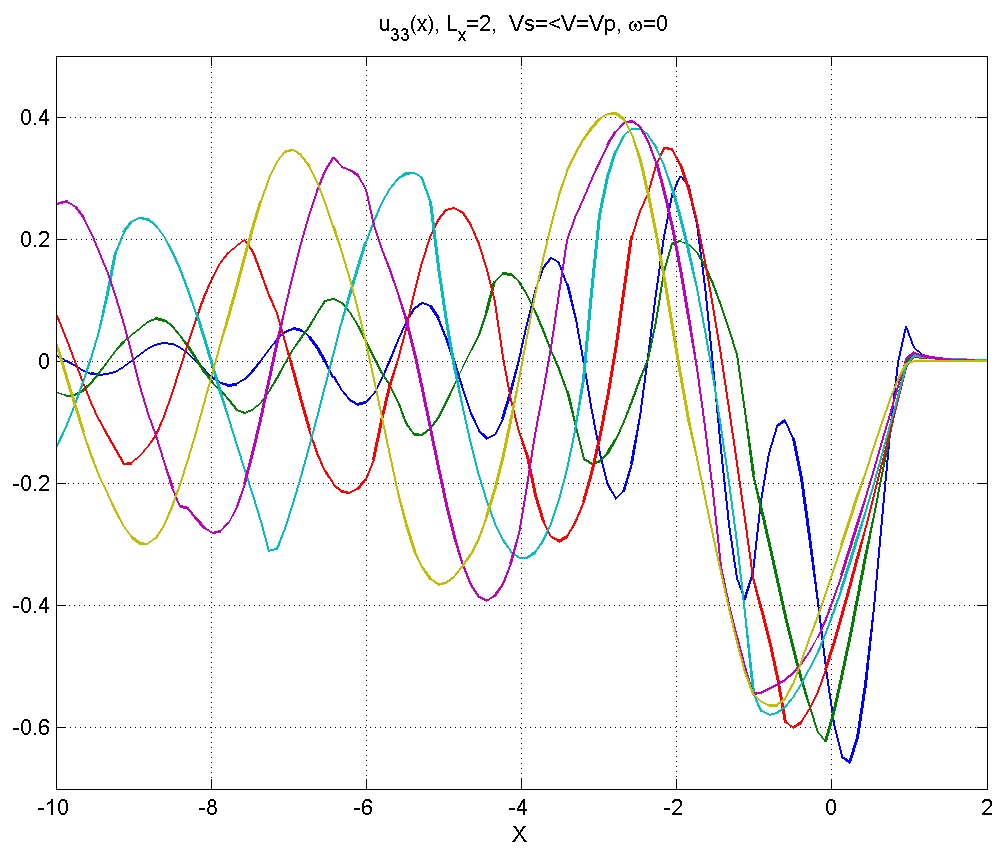
Рисунок 4.5.4 – Вид смещений в диапазоне скоростей .

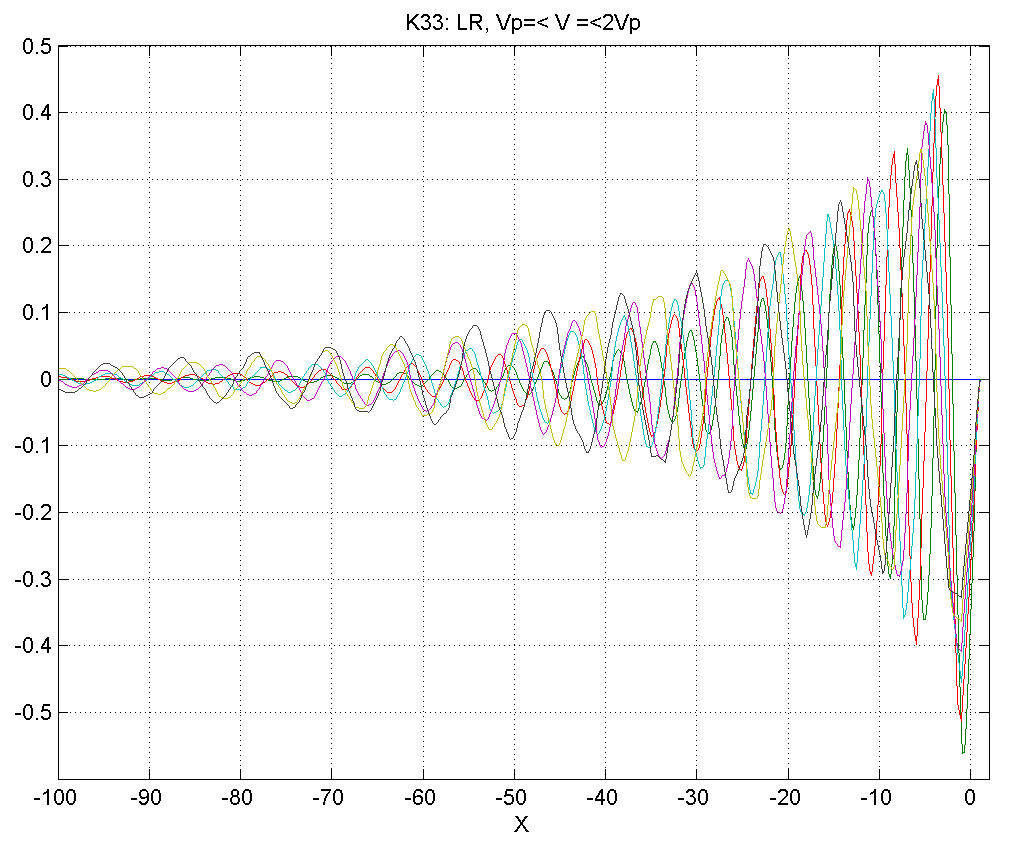
Рисунок 4.5.5 – Вид смещений в диапазоне скоростей .

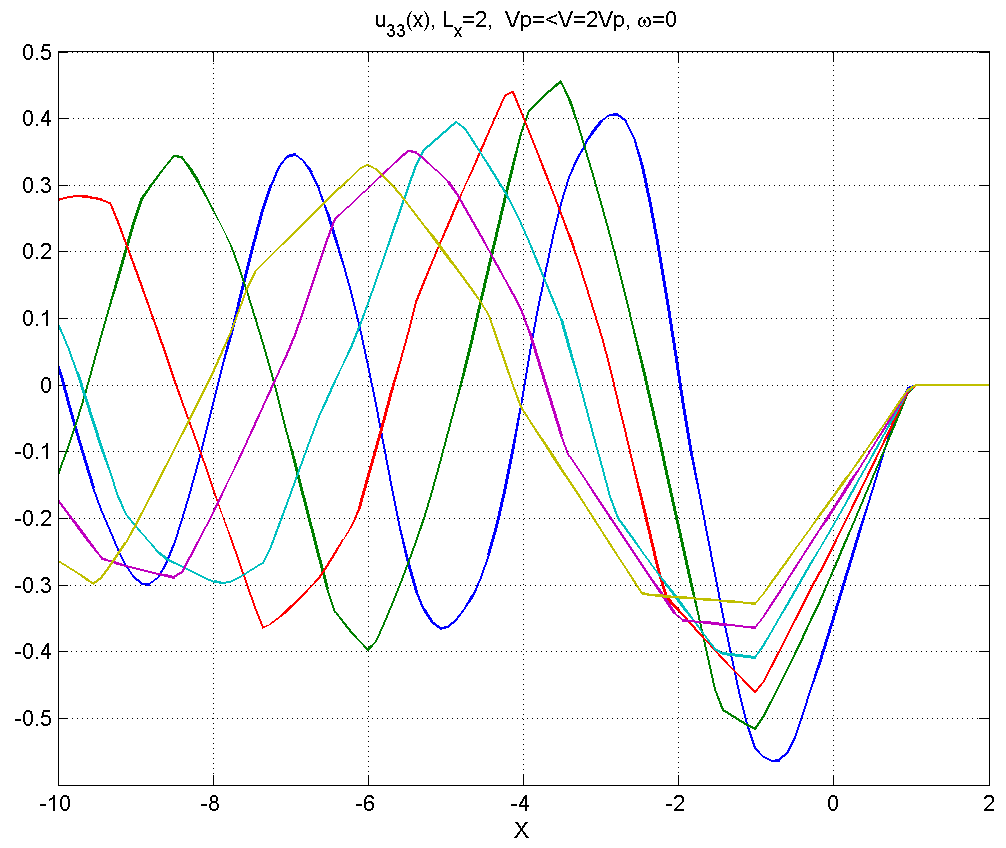
Рисунок 4.3.6 – Вид смещений в диапазоне скоростей .

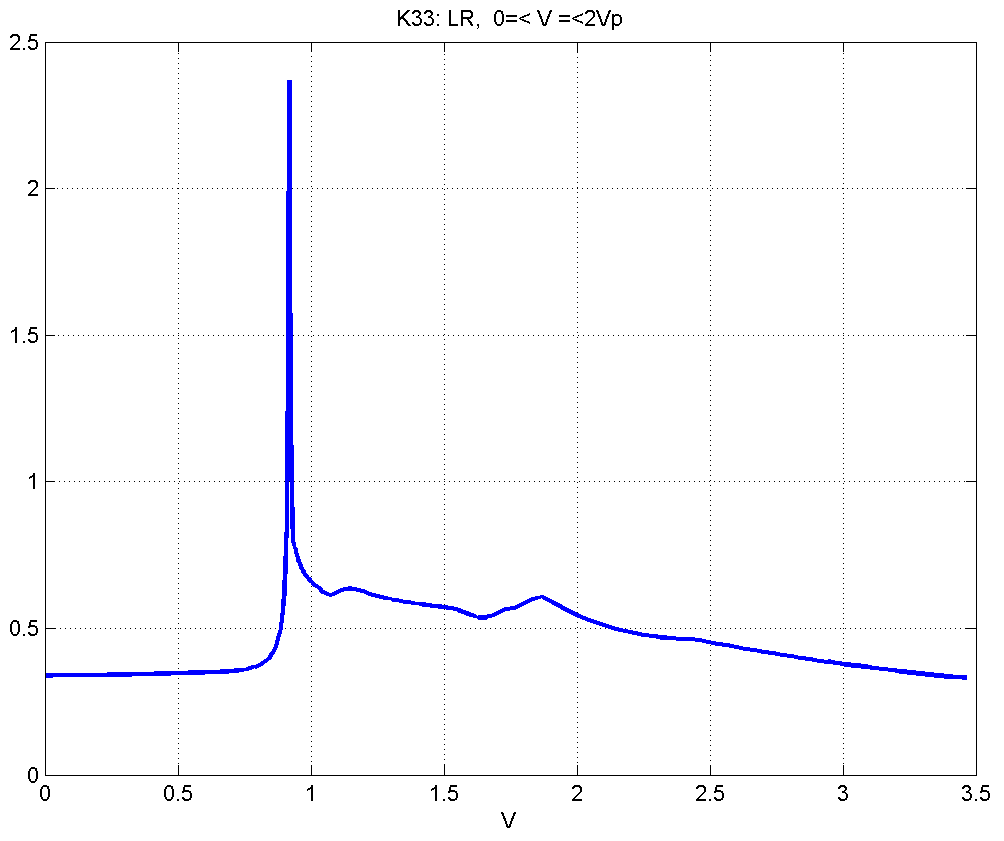
Рисунок 4.3.7 – Вид в зависимости от скорости движения в диапазоне .

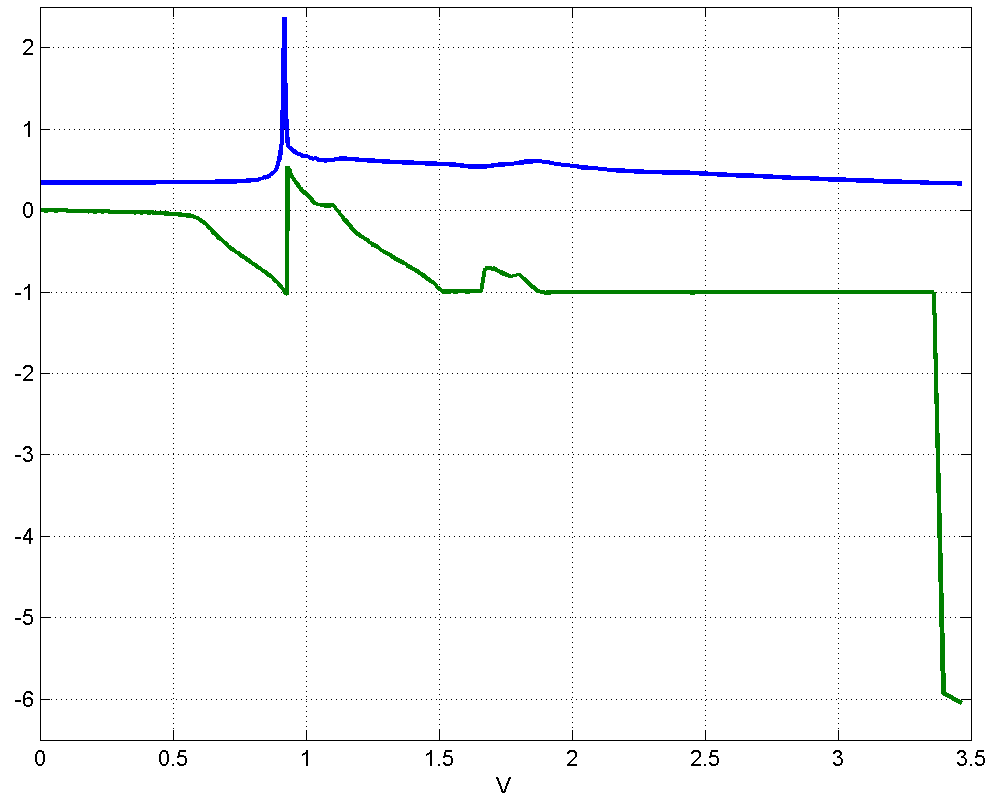
Рисунок 4.3.8 – Вид (синий цвет, верхний график) и координат максимума (зеленый цвет, нижний график) в зависимости от скорости движения в диапазоне .

Как видно из данной серии расчетов, в диапазоне 1) смещения мало отличаются от статического решения, заметные изменения появляются только при .

В диапазоне 2) позади источника появляется синусоидальный шлейф.

В диапазоне 3) шлейф значительно растягивается.

В диапазоне 4) вблизи источника смещения приобретают несинусоидаль-ный характер, при удалении от источника шлейф асимптотически приобретает характер синусоиды.

Имеется три максимума , первый их которых связан с релеевской скоростью, второй максимум достигается при ,

третий максимум достигается при , т.е. в окрестности скорости продольной волны .

Максимум смещений при нулевой скорости , при скорости удвоенной продольной волны . При этом выполняются соотношения:

В диапазоне находится примерно в центре источника , в диапазоне координаты монотонно приближаются к заднему краю источника , в окрестности координаты изменяются от до .

В диапазоне скоростей координаты снова смещаются к заднему краю источника , при максимум остается в окрестности , при максимум выходит далеко за пределы источника , далее наблюдается нарастающее отставание , имеющее линейный характер.

5 Численные результаты для плоской задачи режима движения источника при наличии осцилляций

При наличии осцилляций, когда , характер поверхностных возмущений существенно отличается от случая движения без осцилляций, рассмотренного выше.

В данном пункте расчеты производились только для вертикальных смещений , определяемых и вертикальной нагрузкой вида (4.3). Проведены расчеты величин для серии безразмерных частот при фиксированной скорости .

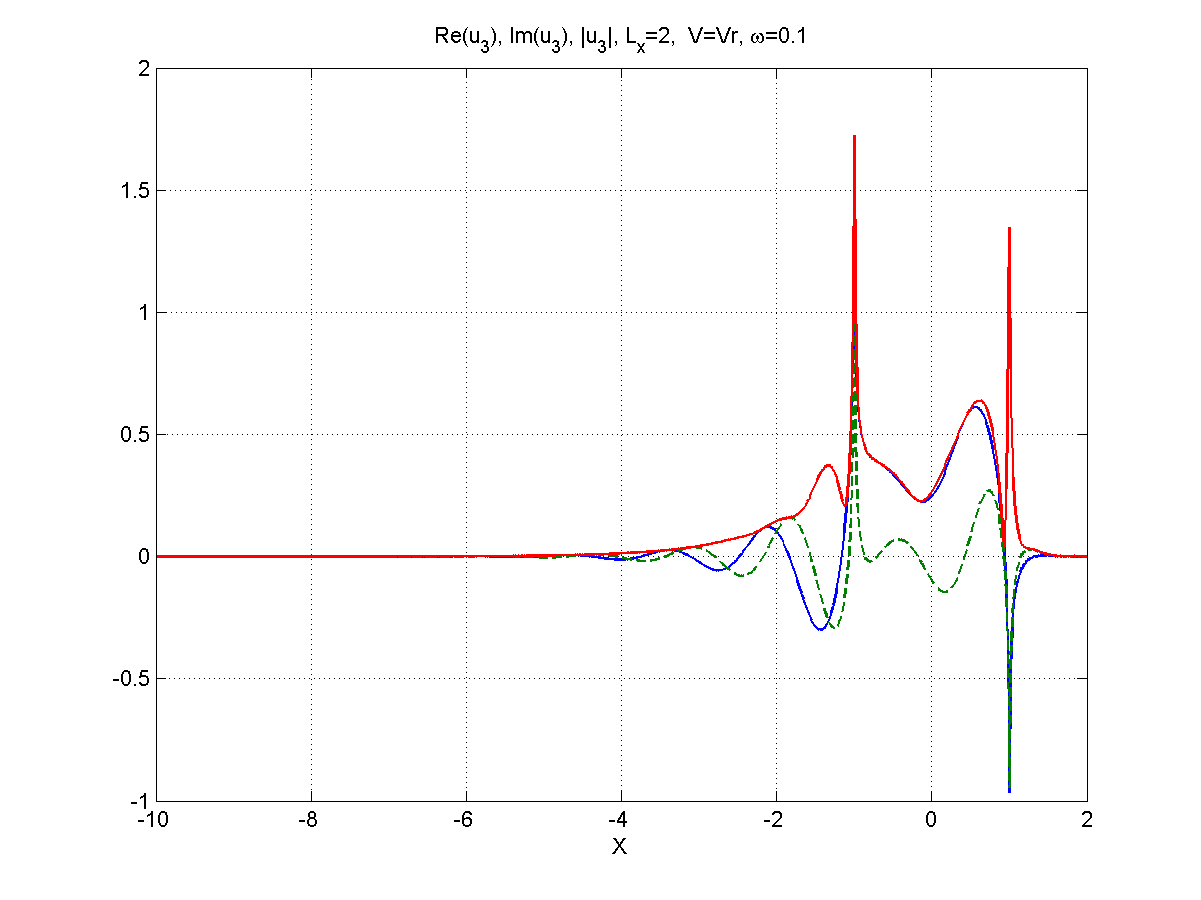
Рисунок 5.1 – Вид (синий),(зеленый), (красный), частота .

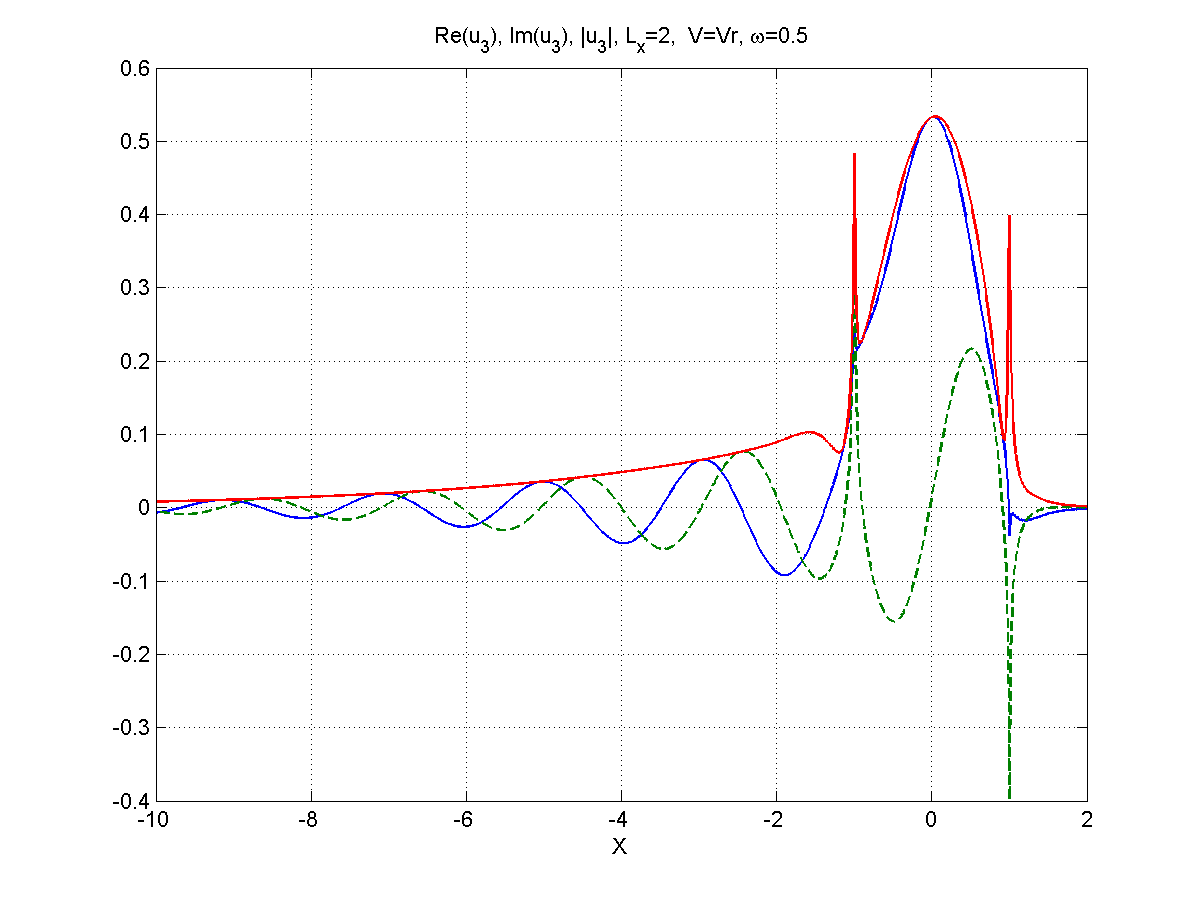
Рисунок 5.2 – Вид (синий),(зеленый), (красный), частота .

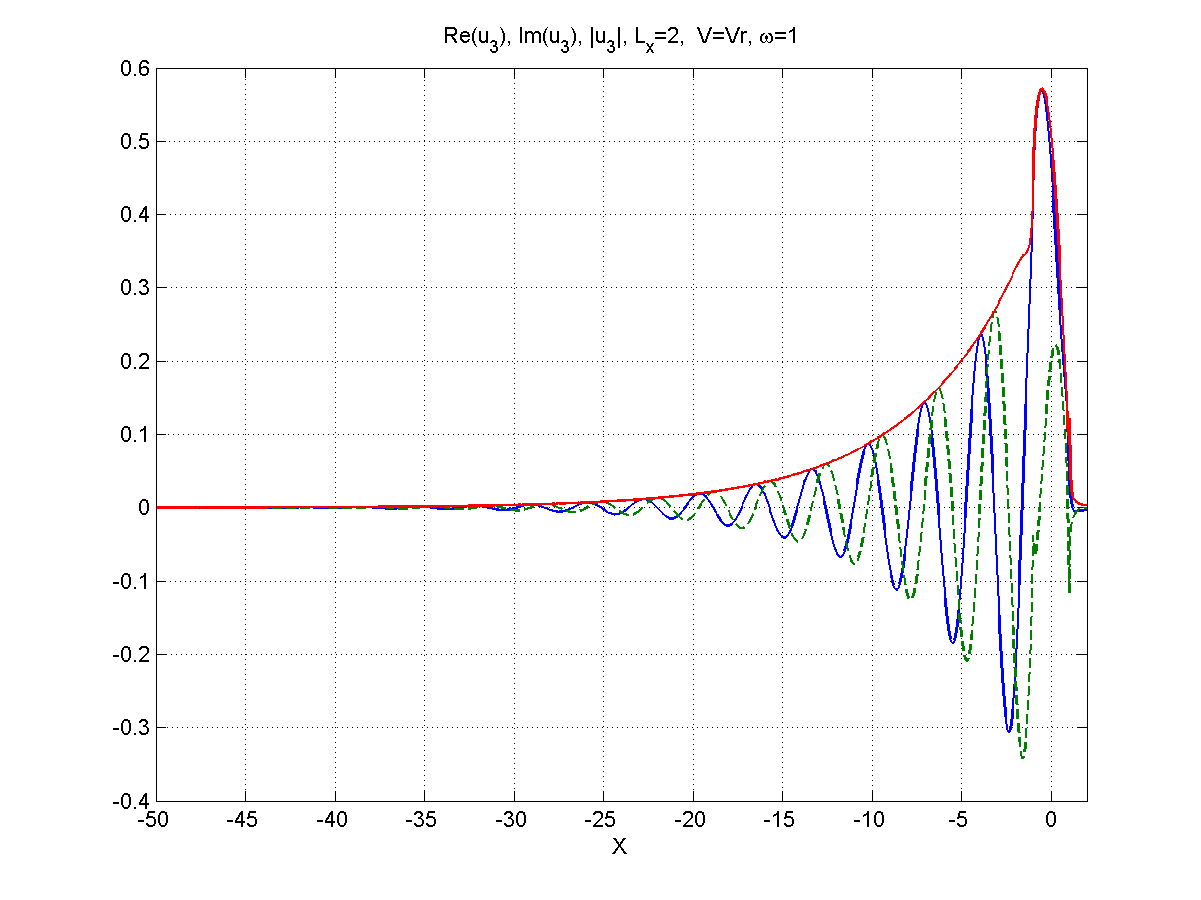
Рисунок 5.3 – Вид (синий),(зеленый), (красный), частота .

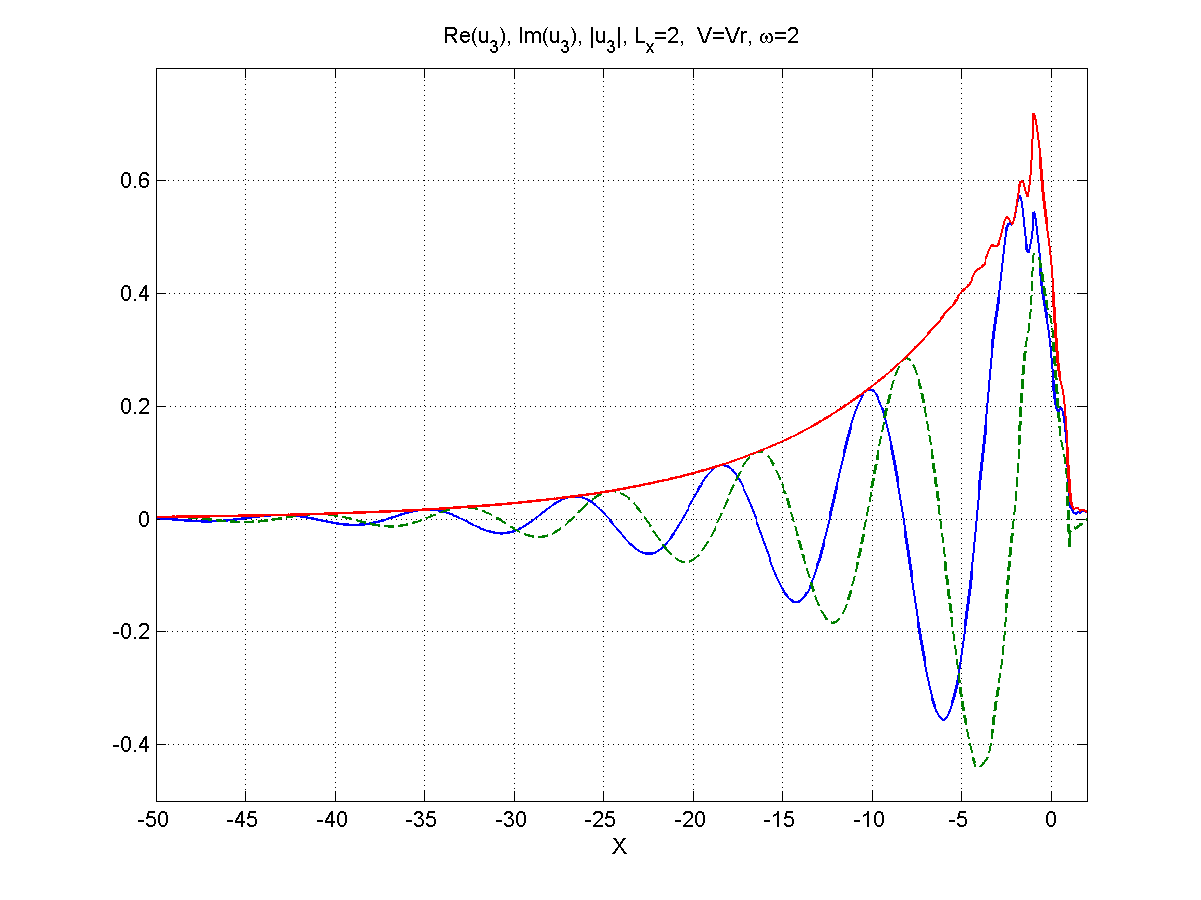
Рисунок 5.4 – Вид (синий),(зеленый), (красный), частота .

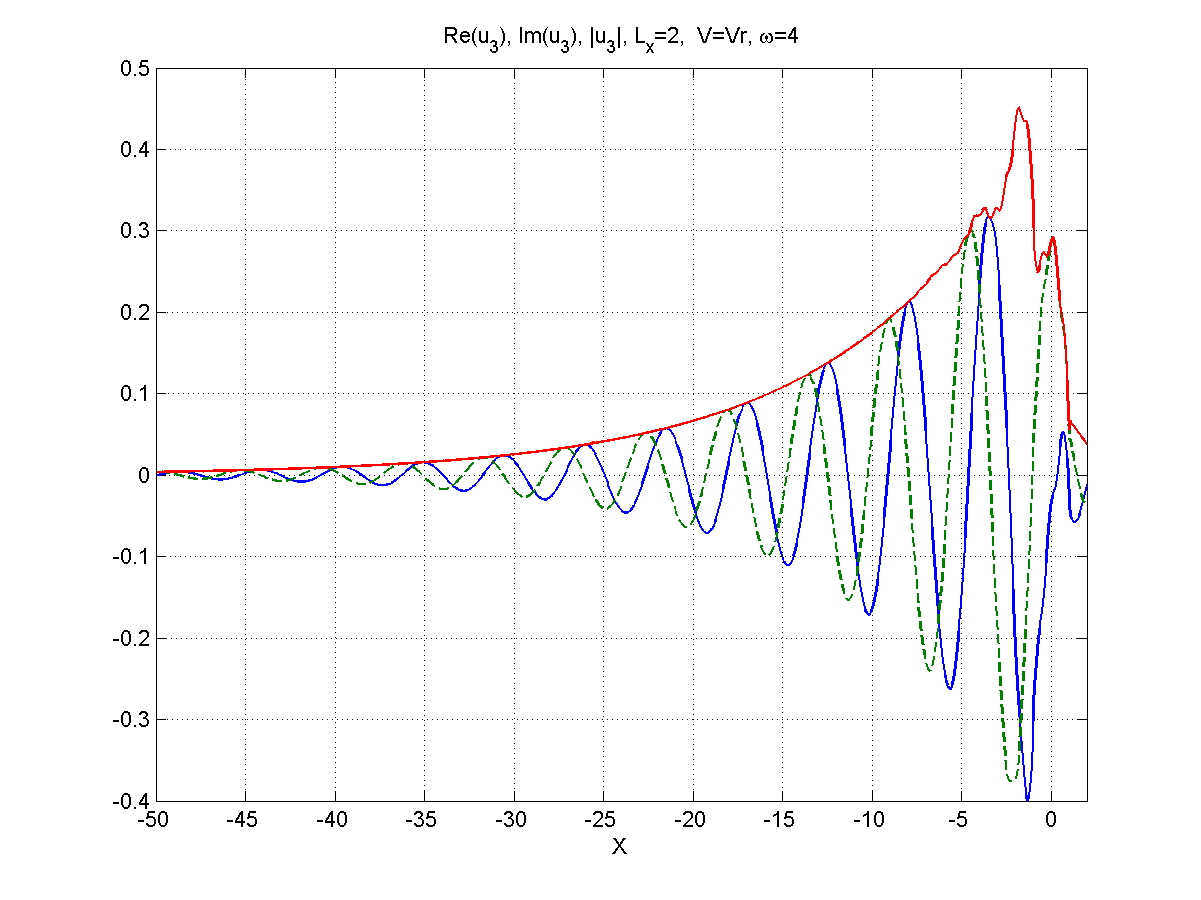
Рисунок 5.5 – Вид (синий),(зеленый), (красный), частота .

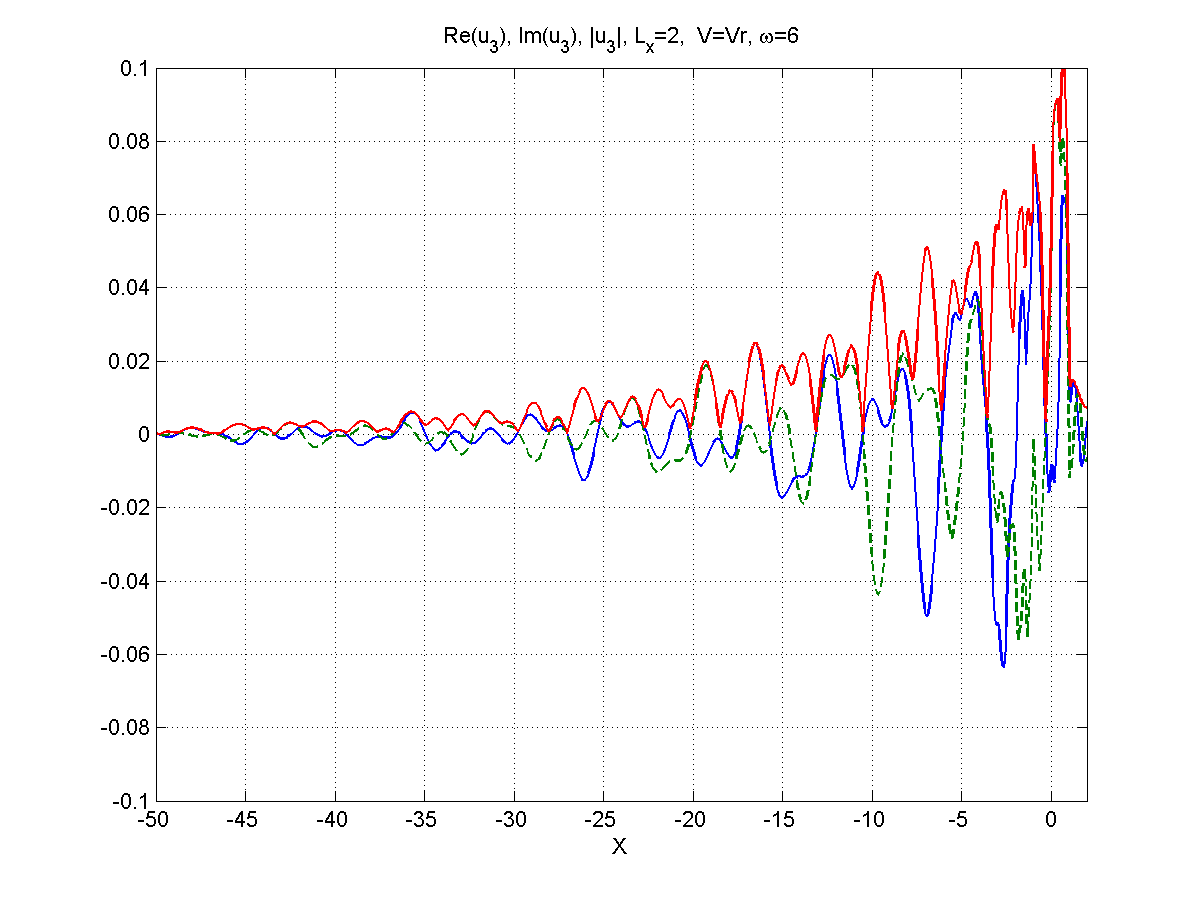
Рисунок 5.6 – Вид (синий),(зеленый), (красный), частота .

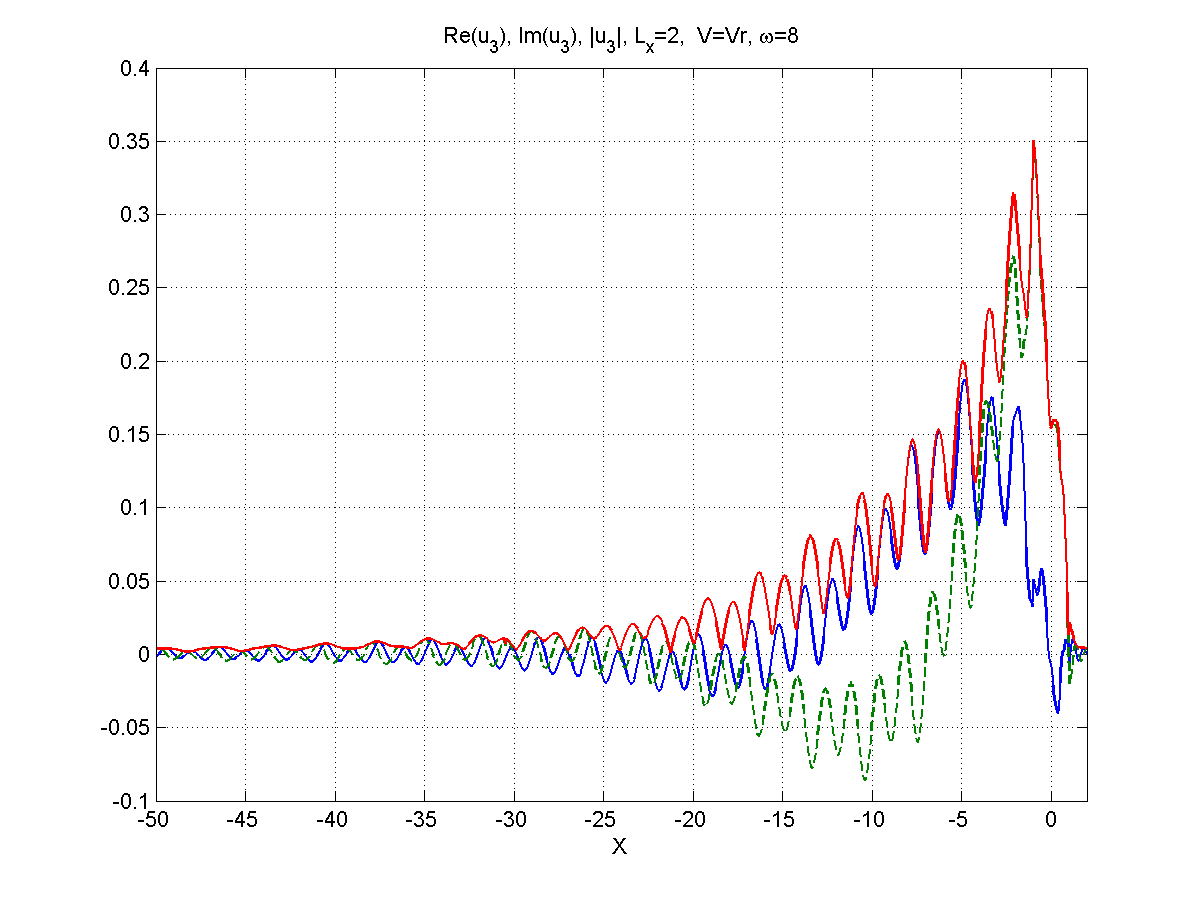
Рисунок 5.7 – Вид (синий),(зеленый), (красный), частота .

По серии расчетов п. 5 составим таблицу максимальных амплитуд в зависимости от безразмерной частоты при фиксированной скорости :

Таблица 5.1

Частота	0.1	0.5	1	2	4	6	8
Максимум амплитуды	1.72	0.533	0.572	0.719	0.451	0.104	0.35
Координаты максимума амплитуды	-1.0	0.024	-0.496	-0.964	-1.796	0.648	-0.964

По таблице 5.1 можно сделать очевидный вывод, что максимальная амплитуда наблюдается при частоте (), второй по величине максимум достигается при частоте ().

При этом максимум амплитуды находится в пределах источника, близко к заднему краю источника .

Отметим, что на всех частотах, кроме (), точка максимума находится в пределах границ источника: .

ЗАКЛЮЧЕНИЕ

По результатам проведенных расчетов можно сделать следующие выводы.

1. Режим движения без осцилляций.

Для величин можно сделать однотипные выводы:

1. При скоростях источника в диапазоне картина смещений на поверхности слоя несущественно меняется с увеличением скорости и мало отличается от случая статической нагрузки в неподвижной системе координат.
   1. Заметные несимметричные деформации поверхности начинаются при скоростях порядка .
   2. В диапазоне скоростей за источником формируется синусоидальный быстро убывающий шлейф.
   3. В диапазоне скоростей шлейф значительно растягивается, при этом существенных изменений синусоидального шлейфа не происходит.
   4. В диапазоне скоростей синусоидальный шлейф продолжает растягиваться и значительно деформируется в ближней от источника зоне.
   5. Для величины характер изменений заметно отличается от соответствующих изменений для величин . В диапазоне смещения мало отличаются от статического решения, заметные различия появляются только при . При профиль приобретает почти прямоугольный вид. Скорость релеевской волны не является критической для данной величины. В диапазоне позади источника появляется линейно-треугольный шлейф. В диапазоне шлейф значительно растягивается, сохраняя линейно-треугольный вид даже в дальней зоне.
   6. Величины и тождественны качественно и количественно.
   7. Для величин при скорости существует единственный максимум амплитуды во всем диапазоне .
   8. Для величины в диапазоне имеется несколько локальных максимумов, наибольший из которых соответствует скорости , второй по величине максимум соответствует скорости релеевской волны.
   9. Для величины в диапазоне имеется единственный максимум, соответствующий скорости , что находится примерно на середине интервала .
   10. Для смещений наблюдается монотонное убывание максимальной амплитуды при , для смещений , напротив, наблюдается почти монотонный рост амплитуды в этом же диапазоне.
   11. Для величин выполняются следующие соотношения максимальных амплитуд к максимальным амплитудам при нулевой скорости:

,,,.

1. Максимальное соотношение для амплитуд, равное 15.55, наблюдается у смещений , второе по величине, равное 6.99, – соответствует , третье, равное 2.98, - , наименьшее, равное 2.43,- .
   1. Соотношения (п.п.1.12) означают, что даже при очень плавном наборе скорости достижение критической скорости может сопровождаться динамическим ударом, величина которого определяется отношением соответствующих амплитуд (от 2.43 до 15.55 при наборе скорости). Аналогично, при торможении также возникает динамический удар, величина которого может быть и меньше, и больше удара при разгоне, поскольку графики амплитуд несимметричны относительно критических скоростей.
2. Режим движения при наличии гармонических осцилляций.
   1. Для рассмотренного набора частот максимум амплитуды при скорости приходится на частоту (), второй максимум приходится на частоту ().
   2. Наибольший максимум значительно меньше, чем соответствующий максимум для режима движения без осцилляций ().
   3. Точка максимума амплитуды для первых двух максимумов находится в пределах границ источника, совпадает или находится близко к заднему краю источника .
   4. На всех частотах, кроме (), точка максимума находится в пределах границ источника: .
3. Характер возмущений поверхности при наличии осцилляций.

существенно зависит от частоты и от скорости, поэтому исследование амплитудно-частотных характеристик источников необходимо рассматривать в зависимости от этих двух параметров. Режим движения без осцилляций и режим движения при наличии осцилляций качественно различаются, что позволяет рассматривать эти режимы как самостоятельные задачи

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Бабешко, В.А. Динамика неоднородных линейно-упругих сред / В.А. Бабешко, Е.В. Глушков, Ж.Ф. Зинченко - М.: Наука, 1989 г. -344с.
2. Калинчук В.В. Динамика поверхности неоднородных сред / В.В. Калинчук, Т.И. Белянкова - М.: Физматлит, 2009 г. -312с.
3. D01AKF Subroutine NAG Fortran Library [Электронный ресурс]. URL: http://www.nag.co.uk (дата обращения 15.05.2014)

PAGE

PAGE \* MERGEFORMAT 41

Волновые поля, возбуждаемые гармоническим источником, движущимся по поверхности изотропного слоя