КОЛЕБАНИЯ РОТОРОВ
III. ВИБРАЦИЯ И УДАР
13. КОЛЕБАНИЯ РОТОРОВ
13.1. Динамика простейшего ротора
Рассмотрим изгибные колебания простейшего ротора, состоящего из невесомого вала, на котором закреплён диск массой m (рис. 13.1).
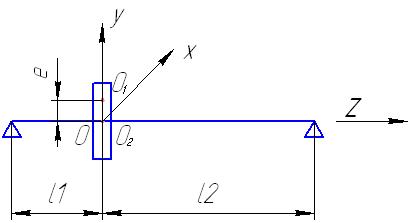
Рис. 13.1. Простейший ротор
Вал вращается на 2-х шарнирных опорах. Допустим, что опоры абсолютно жесткие, и диск расположен посередине вала (). Точку пересечения оси вала со срединной плоскостью диска (точку крепления диска к валу) обозначим О2. Смещение этой точки будет являться прогибом вала в месте расположения диска. Будем считать, что центр масс диска расположен в точке О1 и смещён относительно оси вала (точки О2) на величину эксцентриситета e. Будем рассматривать только изгибные колебания ротора. Колебания ротора будем рассматривать в глобальной системе координат OXYZ, начало которой расположено на недеформируемой оси опор в точке ее пересечения со срединной плоскостью диска.
Ось Z совпадает с осью опор и направлена так, как это показано на рисунке, оси X, Y находятся в срединной поверхности диска (X – горизонтально; Y – вертикально).
Прогиб вала, т.е. смещение точки О2 от оси недеформируемого вала будем обозначать как . Проекции этого вектора на оси будем обозначать как , .
Здесь и далее знак «~» обозначает, что данная величина является функцией от времени.
Опоры ротора могут деформироваться, и в этом случае точка О2 будет смещаться не только за счёт прогиба вала, но и за счёт опор. Полное смещение точки О2 будем описывать вектором . Проекции этого вектора на оси обозначим как и .
В рассматриваемом случае опоры являются абсолютно жёсткими: .
Смещение центра масс диска (точки О1) от оси опор будем обозначать вектором . Его проекции соответственно: .
Поскольку центр масс диска смещён относительно оси, то говорят, что имеет место массовая неуравновешенность. Из-за ее наличия при вращении ротора с угловой скоростью возникает центробежная сила, в результате действия которой вал деформируется. Это приведёт к тому, что вал начнёт не только вращаться относительно своей оси, но и совершать круговое движение вокруг оси опор.
Примем, что в начальный момент времени (t=0) точка О1 располагалась в горизонтальной плоскости, т.е. находилась на оси Х. В произвольный момент времени t точки О1 и О2 расположены так, как показано на рисунке 13.2.
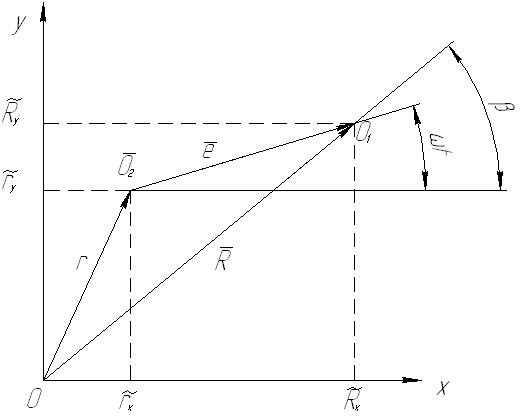
Рис. 13.2. Колебания ротора в плоскости ОXY
Из рисунка находим:
(13.1)
. (13.2)
Запишем условие равновесия для диска:
(13.3)
Здесь - сила упругости, возникающая в вале при его прогибе; - сила инерции.
Сила упругости зависит от прогиба вала и от жесткости вала c:
(13.4)
Сила инерции в соответствии с принципом Даламбера
, (13.5)
Подставив (13.4) и (13.5) в (13.3) с учетом (13.1) и (13.2), получим:
(13.6)
. (13.7)
Разделим все слагаемые уравнений (13.6), (13.7) на массу m, введем обозначение (это собственная частота колебаний вала) и продифференцируем по t. Получим:
(13.8)
Решение системы (1.8) имеет вид:
(13.9)
Здесь , , , - любые линейно независимые частные решения однородной системы дифференциальных уравнений
, (13.10)
С1…4 – неизвестные постоянные, которые определяются из начальных условий, , - любые частные решения неоднородной системы (13.8).
В соответствии с этим можно записать решение (13.9) в виде:
. (13.11)
Первые два слагаемых в каждом решении описывают свободные колебания вала, которые происходят с собственной частотой вала p и быстро затухают вследствие трения. Поэтому будем рассматривать только вынужденные колебания с частотой , представленные третьими слагаемыми.
(13.12)
Подставим (13.12) в (13.8). Получим:
. (13.13)
Отсюда , (13.14)
и колебания ротора будут описываться выражениями
; . (13.15)
Проследим за движением ротора в течение промежутка времени, за который вал совершит один полный оборот вокруг своей деформированной оси. Примем, что в момент начала наблюдения t=0. Тогда за указанный промежуток времени фаза колебаний изменится от 0 до . Положение сечения вала для различных значений фазы колебаний изображено на рис. 13.3. Видно, что за один полный оборот вокруг деформированной оси вал также совершит один полный оборот вокруг оси опор.
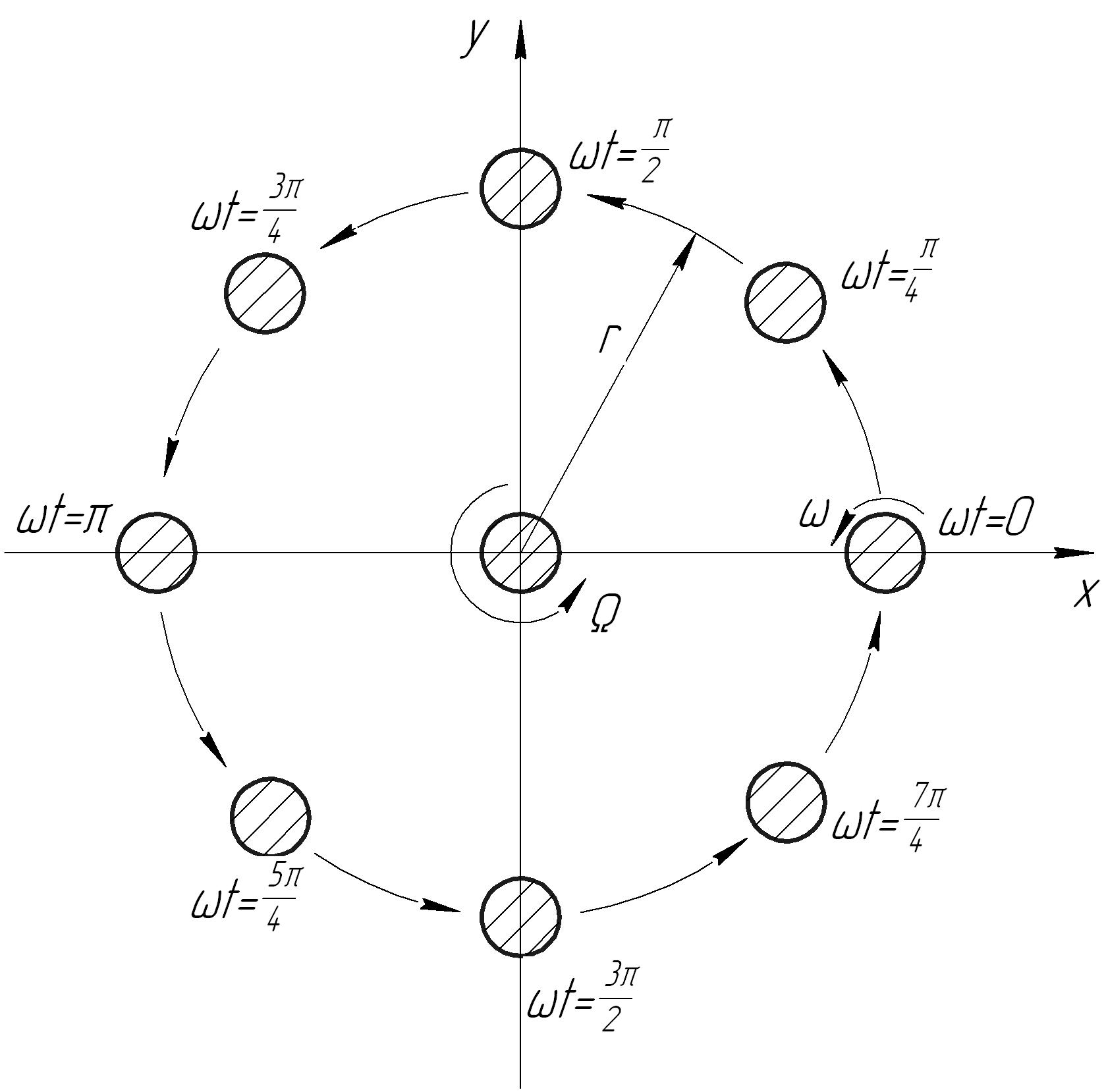
Рис. 13.3. Прецессия ротора
Вращение вала относительно своего положения равновесия называется прецессионным движением, или прецессией ротора. Частоту прецессионного вращения будем обозначать . В рассматриваемом случае частота прецессии равна частоте вращения вала вокруг своей оси, т.е.
= (13.16)
В общем случае и могут не совпадать как по величине, так и по направлению. При соблюдении условия (13.16) прецессия называется синхронной. Если и совпадают по направлению, то прецессия называется прямой, а если прецессионное движение и вращение вала происходит в разные стороны, то прецессия называется обратной.
Определим прогиб вала.
. (13.17)
Как видно, он является постоянным и не зависит от времени, то есть прецессионное движение происходит по окружности. Прецессия с постоянной амплитудой и угловой скоростью называется регулярной.
Видно, что при происходит . Резонансное увеличение амплитуды колебаний будет продолжаться до тех пор, пока вся энергия колебаний не будет уходить на преодоление сил трения, или пока вал не разрушится. Частота вращения ротора, на которой он вступает в резонанс, называется его критической частотой вращения.
Рассмотрим, что происходит с центром масс ротора при прохождении резонанса. В соответствии с формулами (13.1) и (13.2)
(13.18)
. (13.19)
Из (13.18), (13.19) видно, что ; из (13.15) видно, что также .
Т.о. точки О1 и О2 расположены на одной прямой.
Если , то (рис.13.4).

Рис. 13.4. Колебания ротора при
Если , то (рис. 13.5).

Рис.13.5. Колебания ротора при
Если , . Это явление называется самоцентрированием ротора.
В рассмотренной расчетной схеме вал имеет только одну степень свободы (прогиб диска). Реальный ротор ГТД имеет бесконечное множество степеней свободы, а следовательно, собственных частот колебаний и критических вращения. Низшую из них называют первой критической частотой вращения, следующую по возрастанию – второй, и так далее. Критические частоты будем обозначать как
Форма колебаний – это относительное распределение перемещений по колеблющемуся телу. Каждой критической частоте соответствует одна и только одна форма колебаний (рис. 13.6). Точки, в которых амплитуда колебаний равна нулю, называются узловыми.
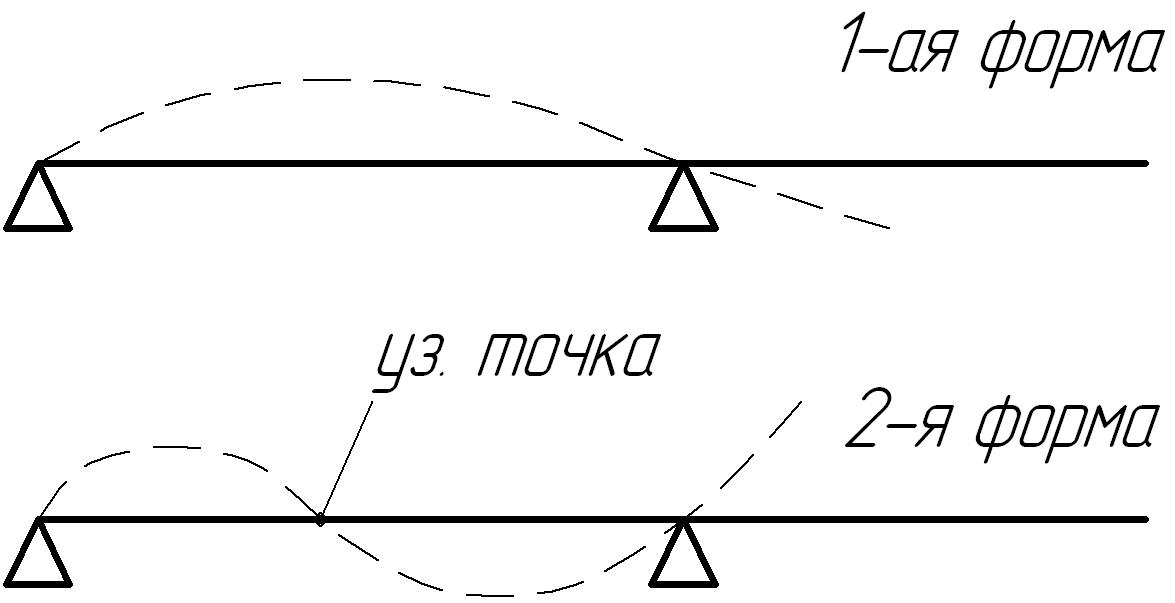
Рис.13.6. Колебания ротора на жестких опорах.
Амплитуда колебаний зависит от соотношения силы, вызывающей колебания (в данном случае, центробежная сила, зависящая от массы ротора, эксцентриситета и угловой скорости вращения) и силы трения. Однако соотношения амплитуд между собой сохраняются для каждой формы колебаний (рис. 13.7).
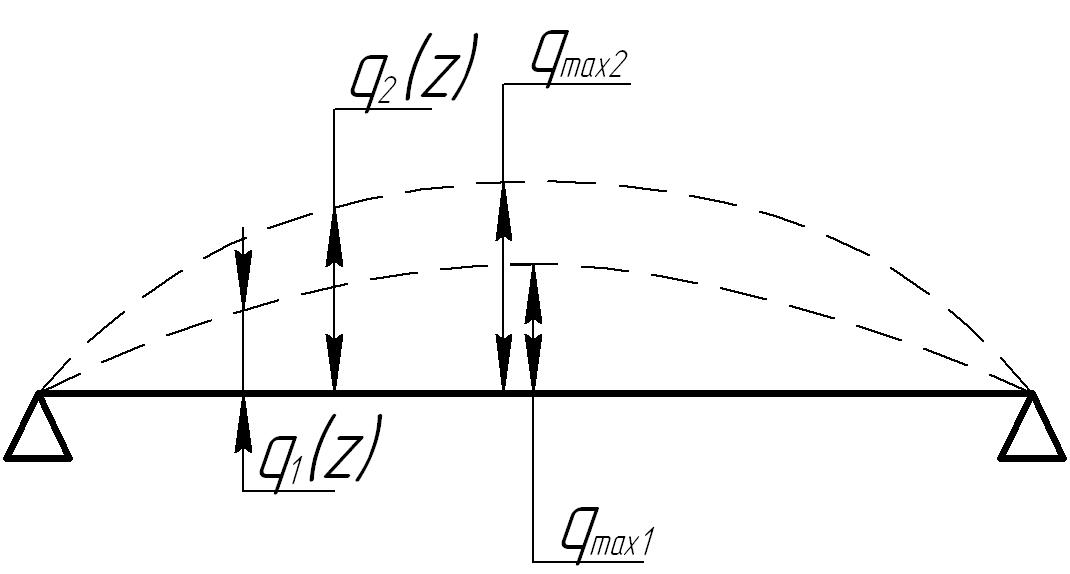
Рис. 13.7. Первая форма колебаний ротора при различных амплитудах
Роторы ГТД, делятся на жёсткие и гибкие. Ротор называется жестким, если его максимальная частота вращения меньше 0,5…0,7 . Если уравнение не выполняется, то ротор называется гибким. Преимуществом гибкого ротора, у которого <, является то, что после прохождения критической частоты вращения он самоцентрируется. К его недостаткам относится то, что при запуске и остановке двигателя ротор проходит через резонанс. Чтобы при этом избежать разрушения ротора, обычно используются демпферы колебаний, которые будут рассмотрены далее.
13.2. Влияние податливости опор на критическую частоту вращения ротора
Податливость опор оказывает существенное влияние на величину собственных частот колебаний ротора, и как следствие, на величину его критических частот вращения. Если жёсткости опор сопоставимы с жёсткостью вала ротора, то пренебрежение ими приводит к существенным ошибкам в расчетах. Проанализируем влияние податливости опор на динамику простейшего ротора. Пусть ротор вращается на упругих опорах, жесткость которых будем обозначать как Со. Для упрощения уравнений будем считать, что диск расположен посредине вала (рис. 13.8).
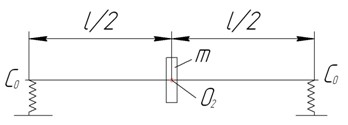
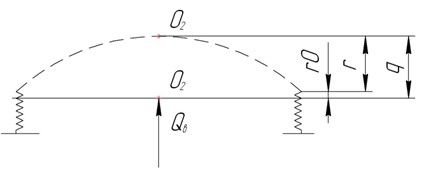
Рис. 13.8. Ротор на податливых опорах
Условие равновесия ротора имеет вид
(13.20)
где сила упругости . Здесь cp – жесткость ротора в месте закрепления диска с учетом податливости опор.
Для определения этой жесткости приложим к валу в точке О2 в произвольном направлении некоторую статическую силу . Под действием этой силы вал прогнётся, опоры ротора деформируются. В результате точка О2 сместится. Это смещение обозначим вектором . Представим это смещение как сумму двух векторов
(13.21),
где - смещение за счет прогиба вала, - смещение за счет деформирования опор. Так как сила приложена посередине вала, то каждая из опор будет деформироваться под действием силы . Найдем связь между смещением и силой . В точке приложения силы должно выполняться условие равновесия
,
где упругая сила . Тогда
.
Поскольку каждая из опор ротора будет деформироваться под действием силы :
.
Подставляя выражения для r и r0 в (13.21) получим:
.
Откуда находим:
. (13.22)
Проецируя равенство (13.20) на оси глобальной системы координат, получим
(13.23)
Обозначая (собственная частота колебаний ротора с учетом податливости его опор), и учитывая выражения (13.1) и (13.2), получим
(13.24)
Решая эту систему так же, как (13.8), получим, что собственная частота ротора на упругих опорах определяется выражением
. (13.25)
Из анализа этого выражения видно, что собственная частота колебания ротора существенно зависит от жёсткости опор Со. Если Со=0, то p=0. Если , то , то есть к собственной частоте ротора на абсолютно жёстких опорах. Зависимость критической частоты ротора от жесткости опор имеет вид (рис.13.9):
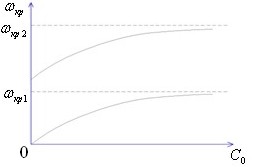
Рис. 13.9. Зависимость критической частоты ротора от жесткости опор
При рассмотрении модели с несколькими степенями свободы можно показать, что при Со=0 обращается в ноль только первая критическая частота, остальные уменьшаются, но не до нуля.
Зависимость критической частоты ротора от жесткости опор позволяет управлять критической частотой в широких пределах при помощи изменения жесткости опор.
13.3. Критические частоты вращения ротора на анизотропных упругих опорах
Из-за особенностей конструкции корпуса двигателя опоры вала могут обладать неодинаковой жёсткостью в горизонтальной и вертикальной плоскостях. (Например, если есть продольный разъем корпуса компрессора, то в плоскости фланца разъема жесткость больше, в перпендикулярной плоскости меньше. Различные ребра опор могут иметь различные жесткости из-за различного диаметра отверстий для подвода и отвода смазки и так далее.) Если такое различие существенно, то в динамике ротора появляются особенности, которые необходимо учитывать при проектировании и доводке двигателя. Рассмотрим динамку простейшего ротора, вращающегося на упругих анизотропных опорах. Пусть жёсткость опор в горизонтальной плоскости Cox, а в вертикальной Coy. Как и в предыдущем случае считаем, что диск расположен посредине вала, а его центр масс смещён на величину эксцентриситета e. Моментами инерции диска и демпфированием в роторе пренебрегаем.
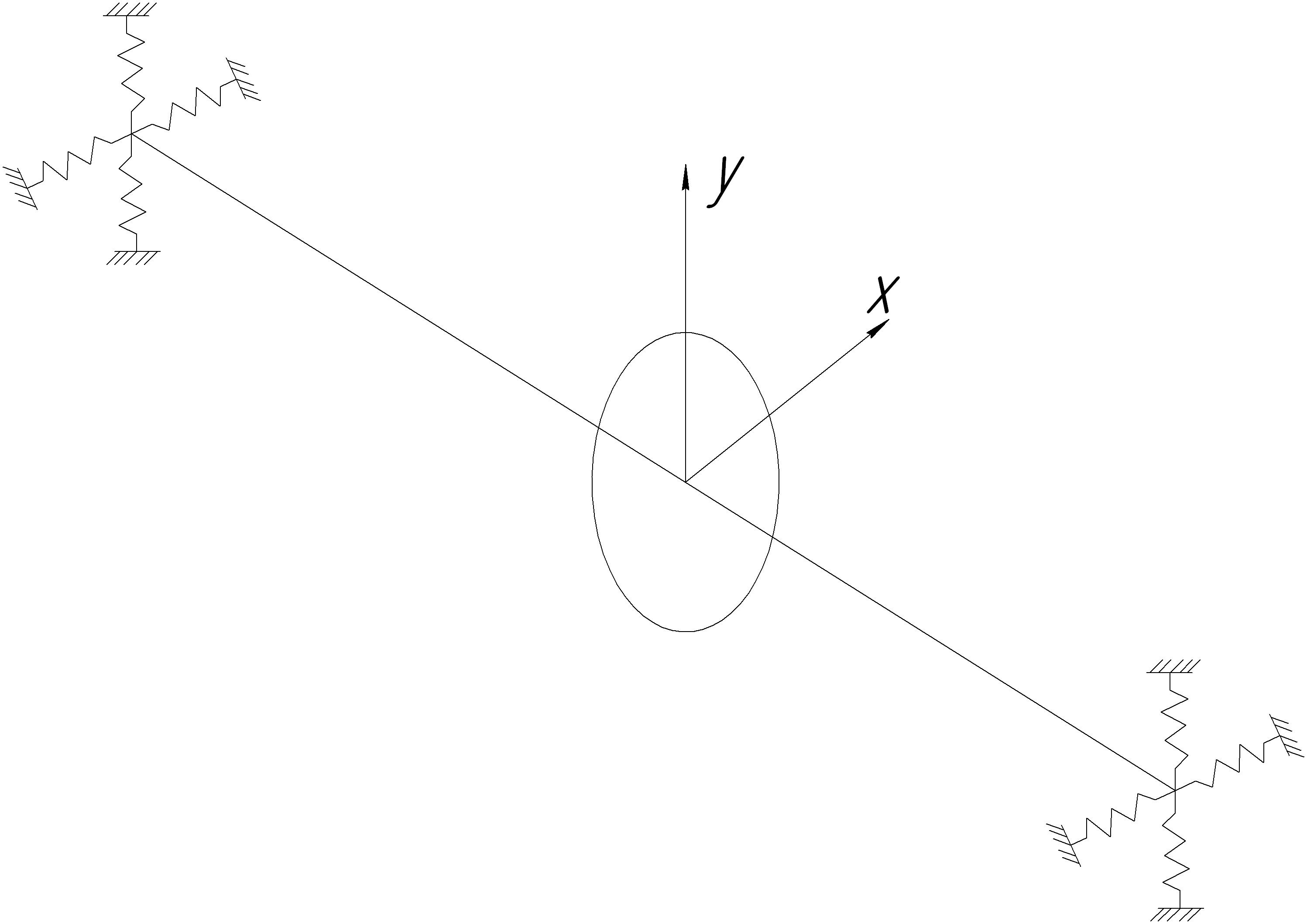
Рис. 13.10. Ротор на анизотропных опорах
Т.к. опоры имеют разную жёсткость в направлениях Х и Y, ротор в точке О2 так же обладает жёсткостями, отличными в горизонтальной и вертикальной плоскостях. По аналогии с (13.22) можно записать
В этом случае уравнения равновесия (13.3) для диска в проекциях на оси глобальной системы координат принимают вид:
(13.26)
Обозначим собственную частоту ротора в горизонтальной плоскости:
в вертикальной плоскости:
Учитывая выражения для определения и (13.1) и (13.2), преобразуем (13.26) к следующему виду:
(13.27)
Решение (13.27), как и системы (13.8), будем искать в виде вынужденных колебаний:
(13.28)
Подставляя (13.28) в (13.27) получаем выражения для амплитуд колебаний:
Таким образом, если опоры ротора анизотропные, и в роторе имеется массовая неуравновешенность , то при вращении вала вокруг своей собственной оси возникает прецессионное движение, которое будет описываться уравнениями:
(13.29)
Из анализа (13.29) можно сделать следующие выводы:
1. Ротор имеет две отличные по величине резонансные частоты колебаний, и, следовательно, две критические частоты вращения . Примем для определенности, что .
2. Амплитуда прецессии будет переменной:
Следовательно, прецессия является нерегулярной. Движение вала происходит по эллипсу.
Рассмотрим поведение ротора при прохождении через критические частоты вращения. Будем рассматривать движение ротора в течение промежутка времени, за который вал совершает один полный оборот, т.е. .
Разделим весь диапазон частоты вращения ротора на несколько интервалов, и рассмотрим на каждом из них прецессионное движение ротора.
а) (рис. 13.11):
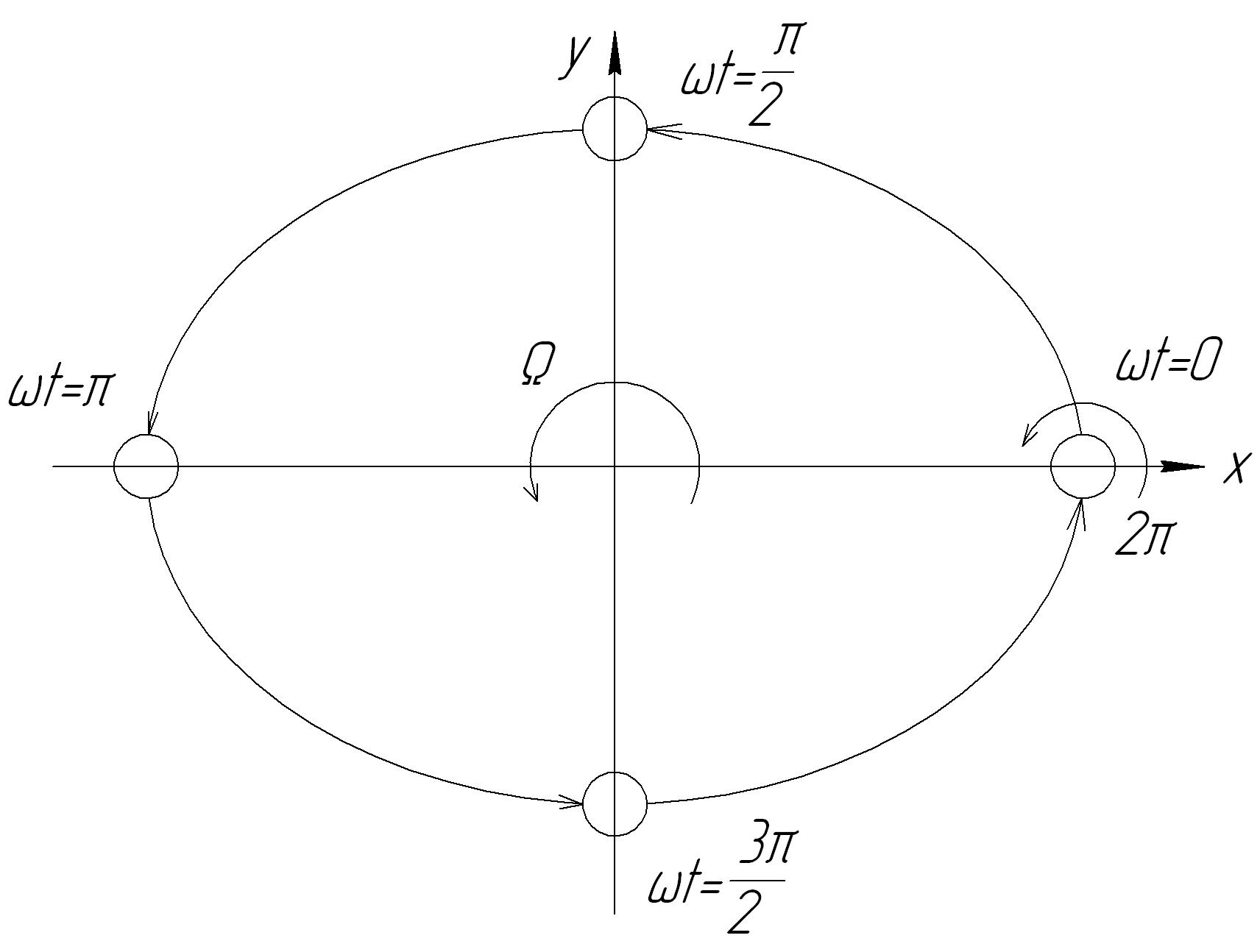
Рис. 13.11. Колебания ротора при
Положения сечения вала при изменении фазы колебаний от 0 до изображены на рисунке. Поскольку , амплитуда , то есть движение происходит по эллипсу, вытянутому вдоль оси Х. Так как , прецессия является синхронной. Направление вращения при прецессии совпадает с направлением вращения вала вокруг своей оси, следовательно, прецессия является прямой.
б) (рис. 13.12):
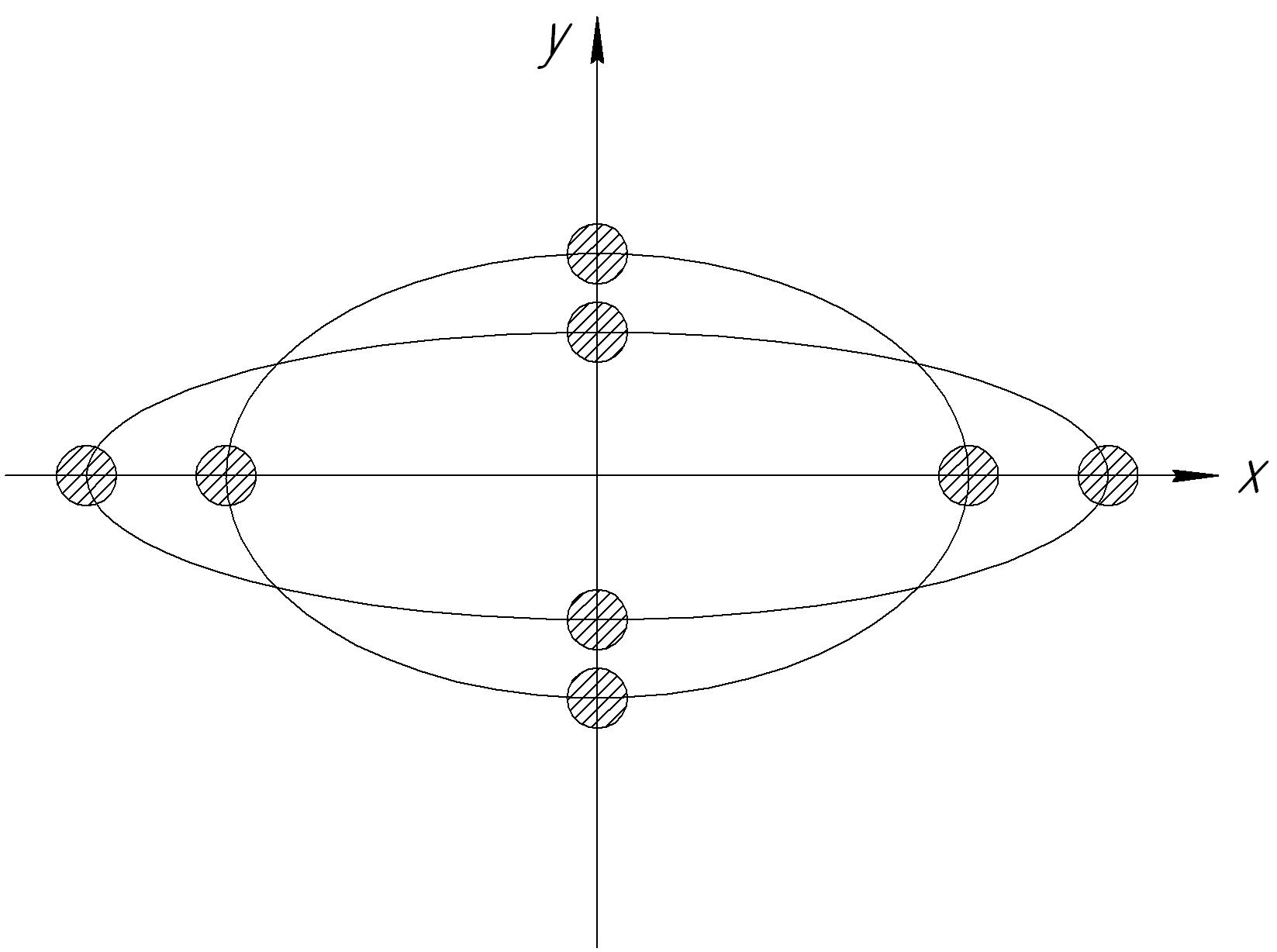
Рис. 13.12. Колебания ротора при
При траектория начинает вырождаться в эллипс, вытягиваться вдоль оси X. При движение фактически превращается в колебания в горизонтальной плоскости.
в) (рис. 13.13):
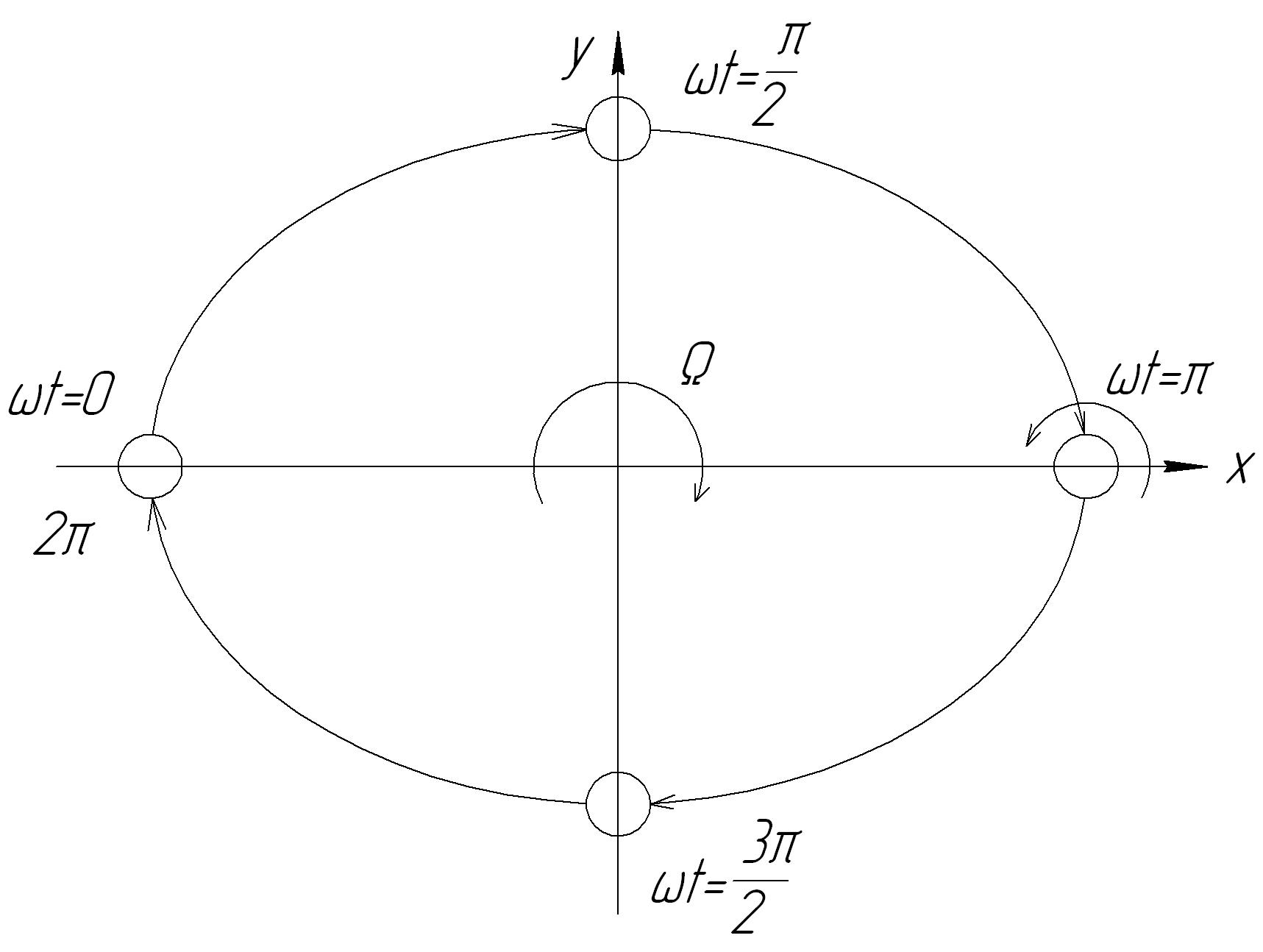
Рис. 13.13. Колебания ротора при
Из рисунка видно, что ротор совершает обратную нерегулярную синхронную прецессию.
г) (рис. 13.14). При траектория начинает вырождаться в эллипс, вытягиваться вдоль оси Y. При движение фактически превращается в колебания в вертикальной плоскости.
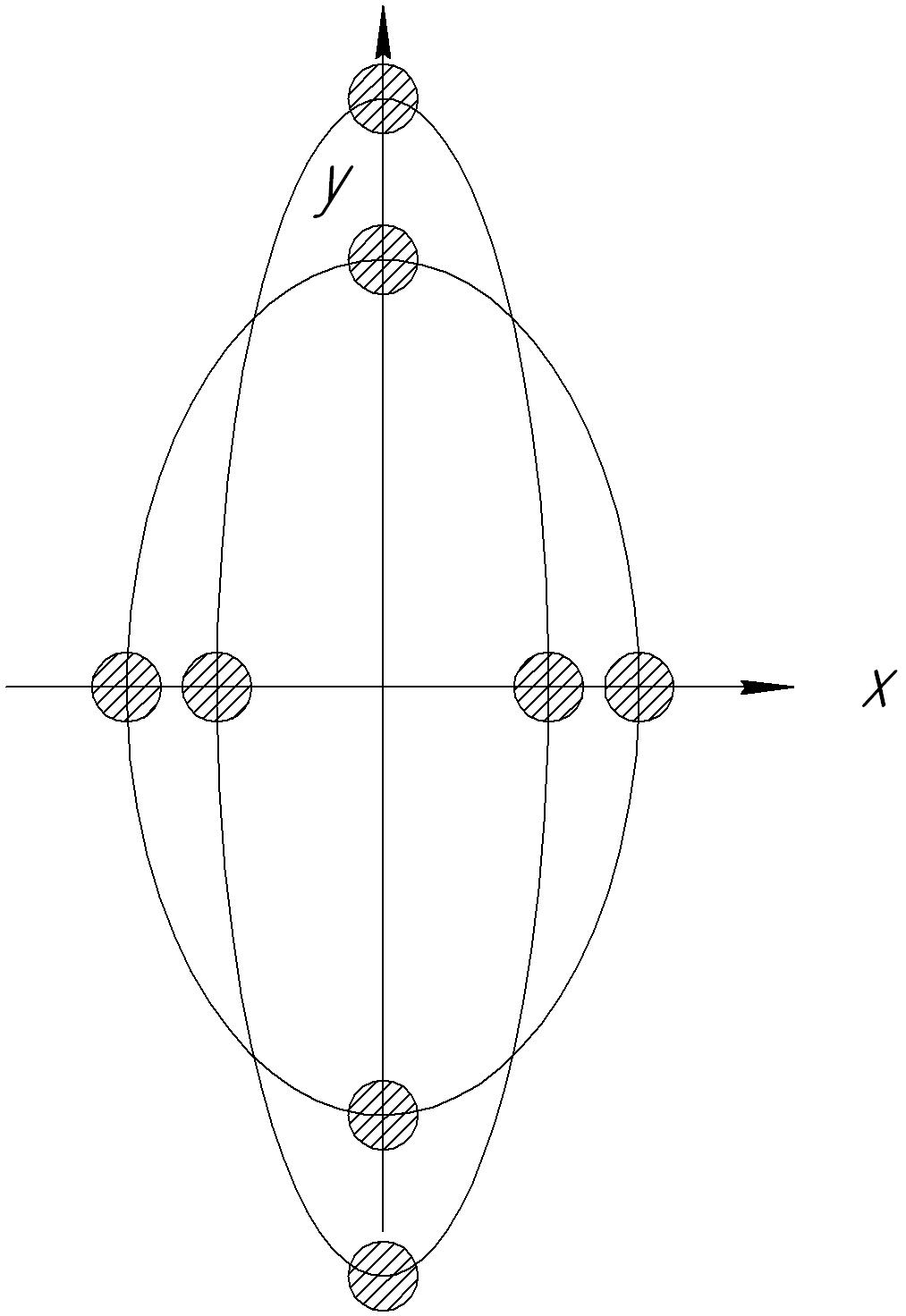
Рис. 13.14. Колебания ротора при
д) (рис. 13.15):
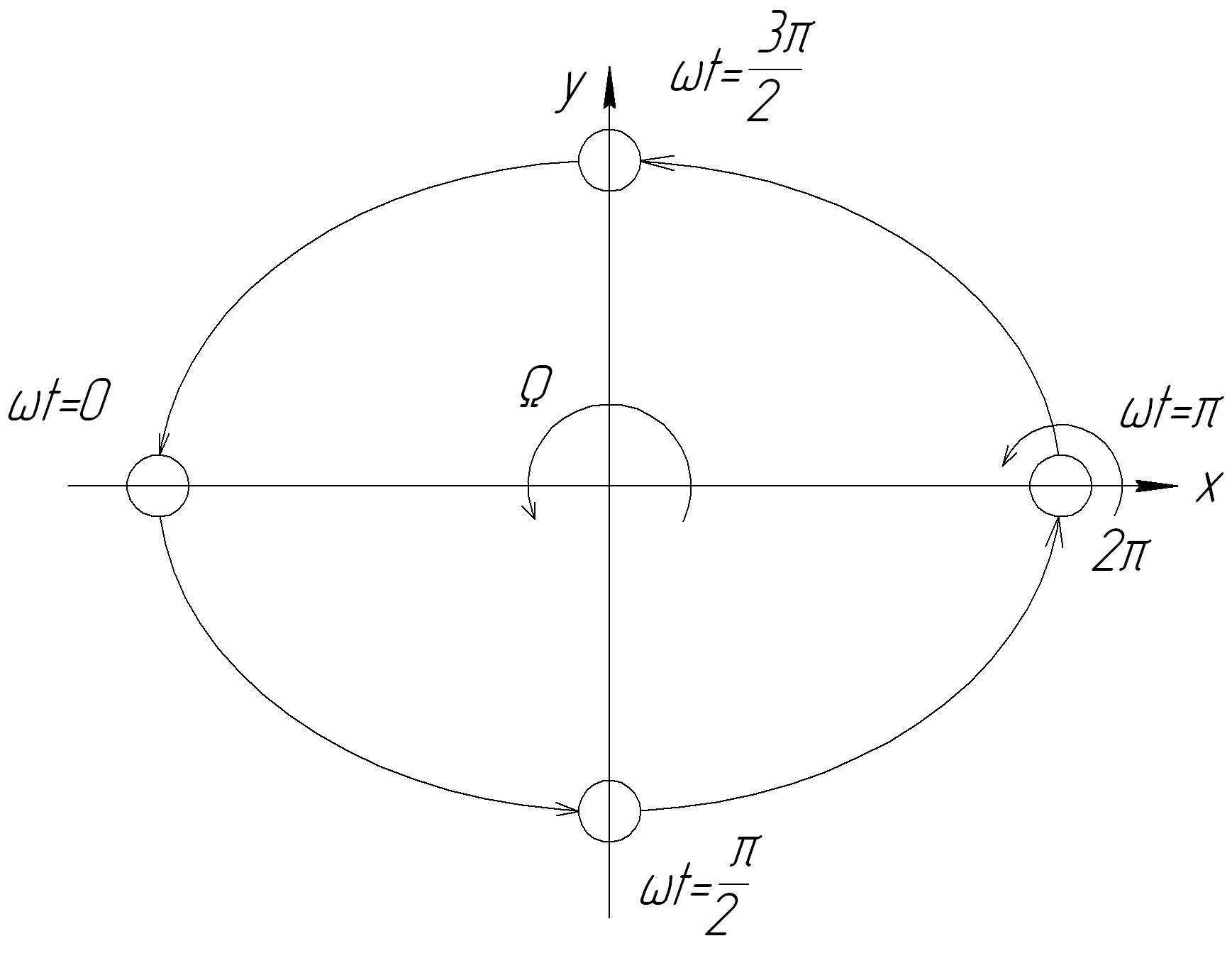
Рис. 13.15. Колебания ротора при
Из рисунка видно, что ротор вновь совершает прямую нерегулярную синхронную прецессию.
13.4. Влияние гироскопического момента на собственные частоты колебаний ротора
Пусть простейший ротор вращается на абсолютно жестких шарнирных опорах вокруг собственной оси с угловой скоростью и одновременно совершает прецессию вокруг оси опор с угловой скоростью . Считаем, что в данном случае диск с моментом инерции J расположен не посередине вала. При прогибе вала диск ротора повернётся на некоторый угол (рис. 13.16). При прецессии он всегда нормален плоскости, в которой происходит изгиб вала, и, следовательно, к вектору прогиба вала .
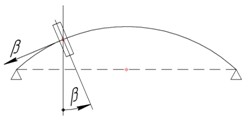
Рис. 13.16. Колебания ротора с диском, расположенным не посередине вала
При прецессионном движении на ротор действует гироскопический момент . Из теоретической механики известно, что ; , где - угол между векторами и . Вектор гироскопического момента направлен таким образом, что со стороны его стрелки кратчайший поворот вектора к вектору виден против часовой стрелки. Из рисунка (13.17) видно, что при прямой прецессии гироскопический момент стремится вернуть диск в исходное положение, т.е. он увеличивает возвращающий момент, что эквивалентно увеличению жёсткости. Таким образом, гироскопический момент при прямой прецессии увеличивает жёсткость вала и, как следствие, все его собственные частоты колебания и критические частоты.
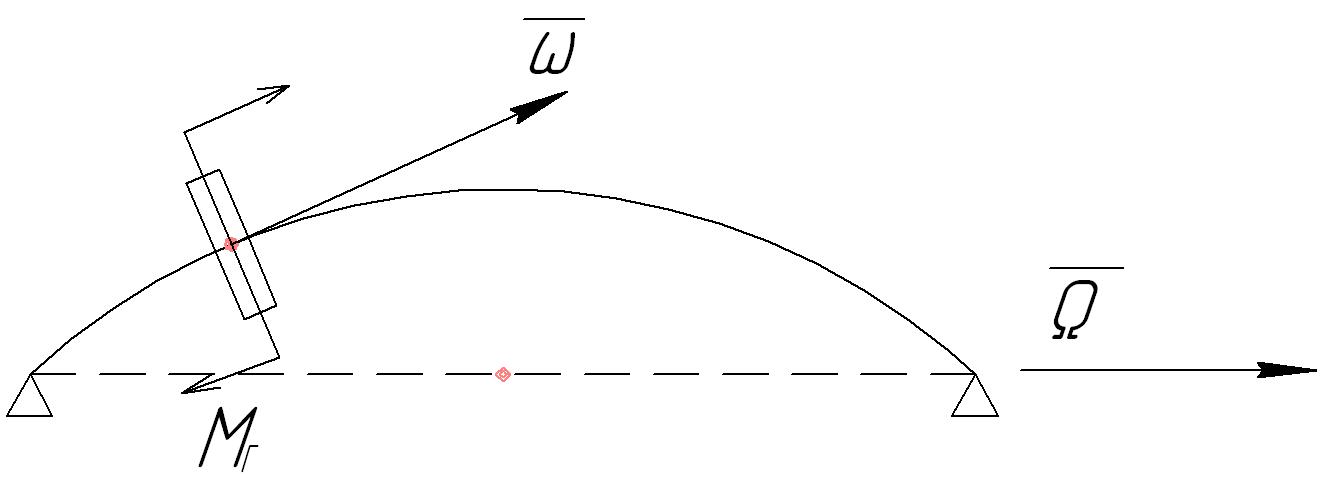
Рис. 13.17. Случай прямой прецессии
При обратной прецессии (рис. 13.18) гироскопический момент уменьшает упругий возвращающий момент, что эквивалентно уменьшению жесткости системы.
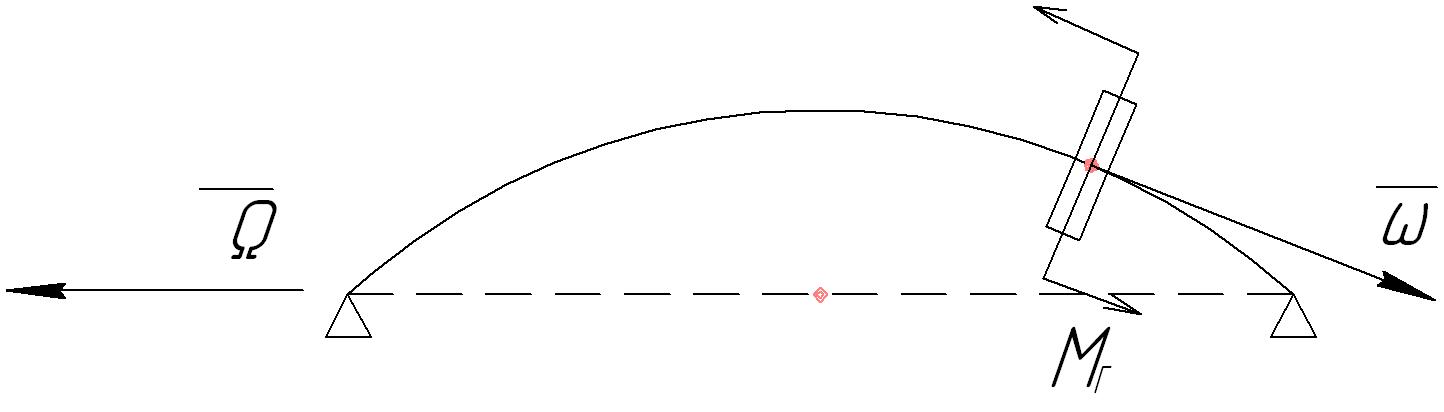
Рис. 13.18. Случай обратной прецессии
Графически зависимость собственной частоты колебаний ротора от частоты прецессии имеет вид (рис. 13.19.):
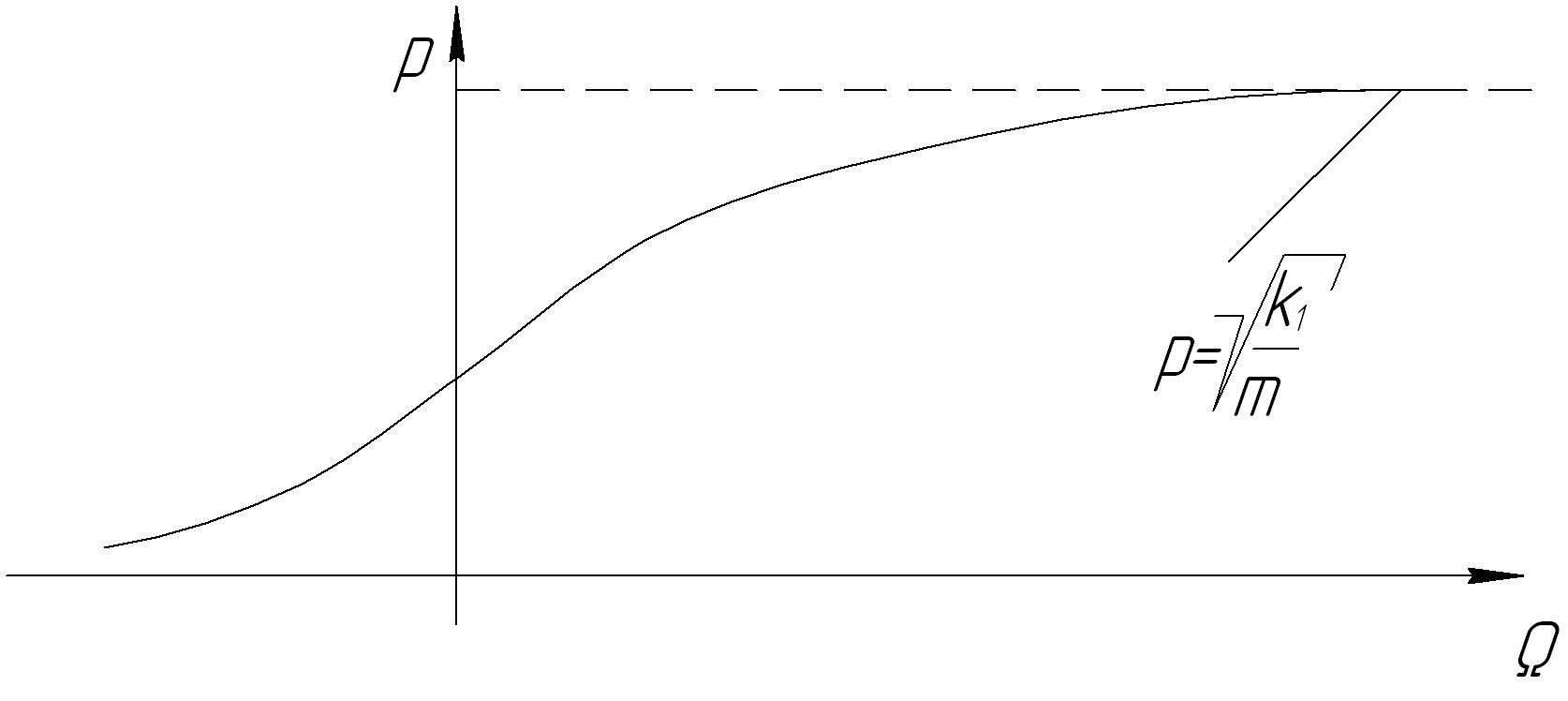
Рис. 13.19. Зависимость собственной частоты колебаний ротора от частоты прецессии
При .
13.5. Критические частоты анизотропного вала
Вал может иметь различную жесткость и в направлении осей Х и Y вследствие различных канавок, пазов, а также из-за погрешностей изготовления. Можно показать, что в диапазоне частот
(13.30)
ротор теряет устойчивость. Движение ротора происходит с непрерывным нарастанием амплитуды, до тех пор, пока вся энергия колебаний не будет уходить на преодоление сил трения, или пока вал не разрушится. Все частоты, лежащие в диапазоне (13.30), являются критическими.
6.6. Методы борьбы с опасными изгибными колебаниями роторов
Существует три способа снижения уровня поперечных вибраций ротора:
- уравновешивание ротора (балансировка);
- отстройка от опасных резонансных режимов (частотная отстройка)
- введение в конструкцию опор специальных гасителей колебаний (демпферов).
Балансировка
Главным источником возбуждения изгибных колебаний ротора является его массовая неуравновешенность. Чем больше неуравновешенность, тем больше уровень вибрации. Уровень вибрации зависит от частоты вращения. Он особенно велик на резонансе.
Для того, чтобы ротор находился в состоянии динамического равновесия, необходимо, чтобы выполнялось два условия:
1) - главный вектор всех неуравновешенных сил равен нулю.
2) - главный момент всех неуравновешенных сил равен нулю, где
- сила от неуравновешенной массы, - момент от неуравновешенной силы.
Этого добиваются, подвешивая ротор на специальном балансировочном станке и добавляя в необходимых местах небольшие грузы (обычно в турбине) или убавляя массу в необходимых местах (для этого обычно сошлифовывается часть периферии диска компрессора).
Частотная отстройка
Частотная отстройка – это смещение критической частоты вращения ротора за пределы рабочего диапазона частот вращения ротора (рис. 13.20).
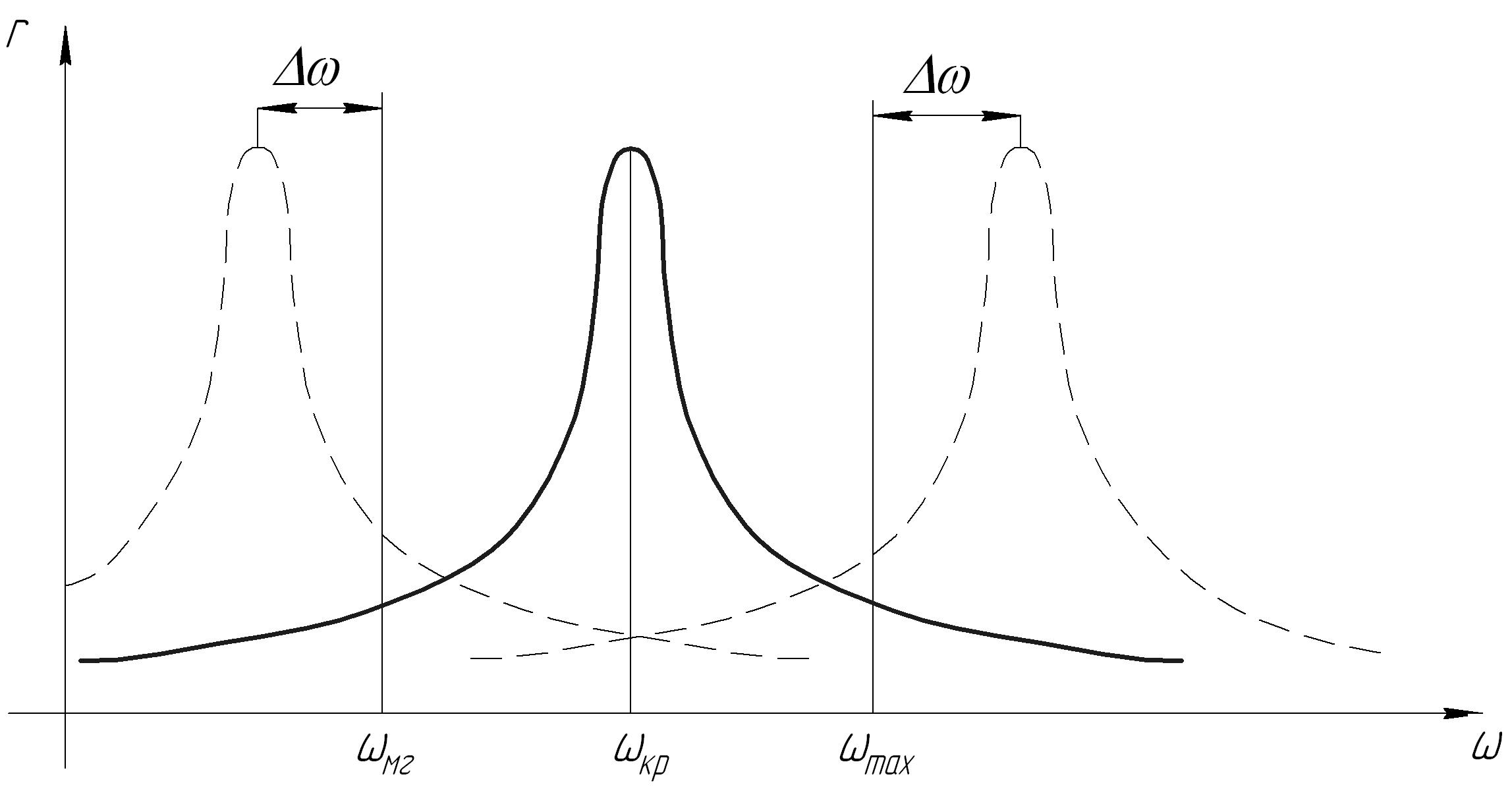
Рис. 13.20. Частотная отстройка
Если вывод критической частоты осуществляется за , то это отстройка называется отстройкой вверх, если отстройка осуществляется за , то это отстройка вниз.
Отстройка должна осуществляться с некоторым запасом , который должен быть не менее 10 %, а в некоторых случаях достигает 50 %.
При отстройке вверх ротор не проходит резонанс, но отстройка вверх сопровождается увеличением массы, и ротор является жестким, не используя преимуществ самоцентрирования. При отстройке вниз при запуске ротор проходит через резонанс, что приводит к повышенным вибрациям. Для борьбы с ними обычно необходим демпфер.
Изменение критической частоты вала обычно производится не за счет изменения толщины вала (уменьшение толщины ведет к потере валом статической прочности, увеличение толщины ведет к чрезмерному росту массы), а за счет изменения жесткости опор.
Демпфирование
Демпфер – это специальное устройство, рассеивающее энергию колебаний на трение. Существуют гидродинамические демпферы, в которых энергия колебаний рассеивается на вязкое трение в жидкости (рис. 13.21), и демпферы сухого трения (пластинчатые), в которых энергия колебаний рассеивается на трение пластин (рис. 13.22).
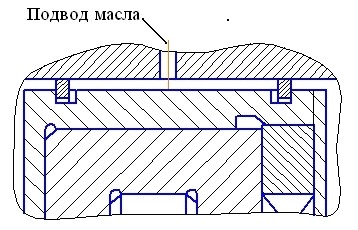
Рис. 13.21. Гидродинамический демпфер
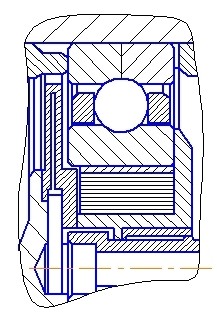
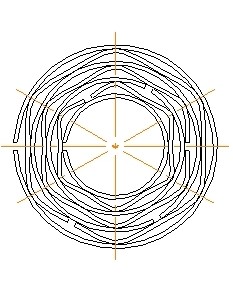
Рис. 13.22. Демпфер сухого трения
Введение в опоры ротора демпферов позволяет снизить прогиб вала при прохождении через резонанс за счёт рассеяния энергии колебания. Амплитудно-частотная характеристика ротора с различной степенью демпфирования показана на рис. 6.23.
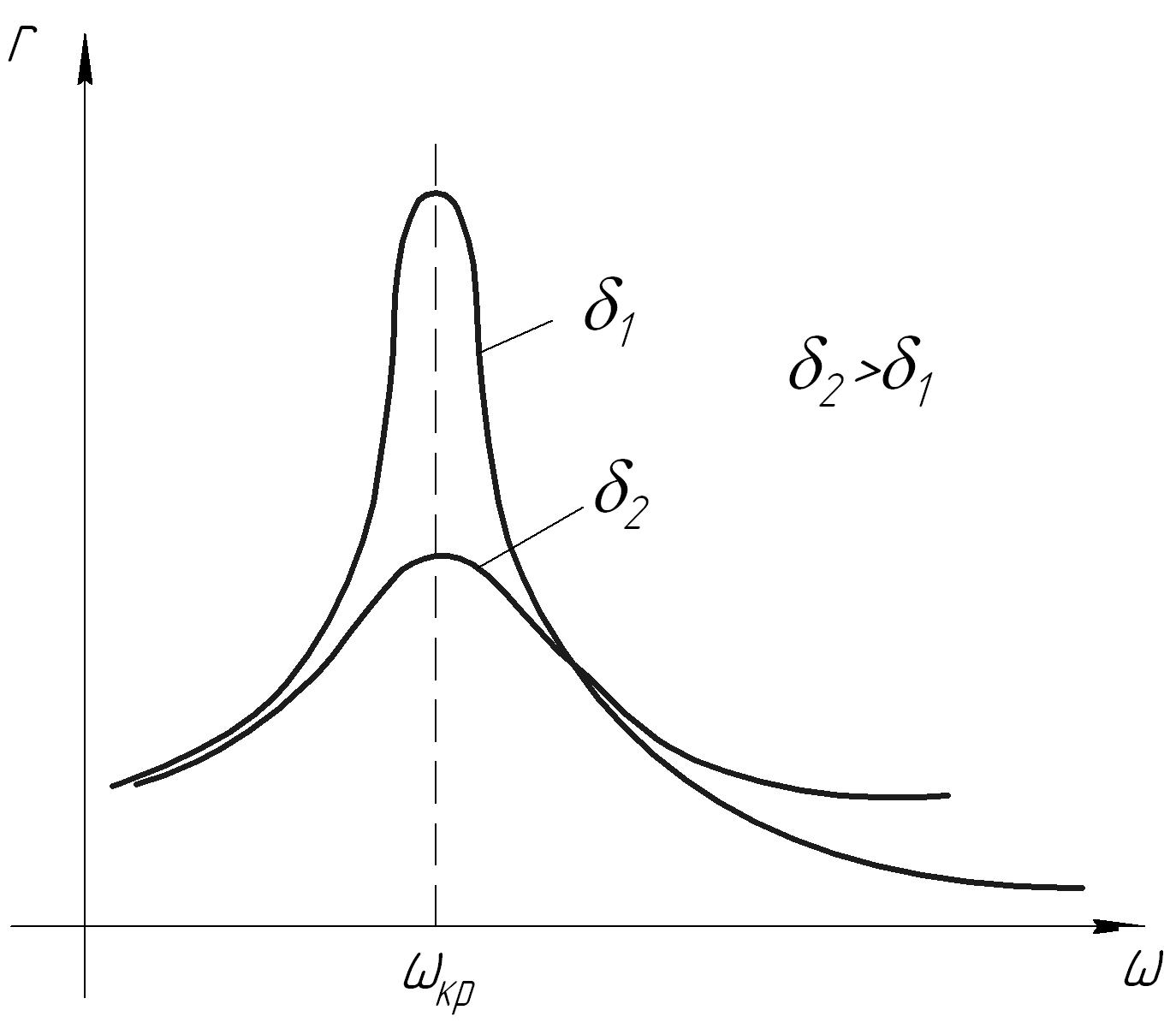
Рис. 13.23. Влияние демпфирования на колебания
14. КОЛЕБАНИЯ ЛОПАТОК
14.1. Изгибные колебания. Получение системы дифференциальных уравнений
Допущения:
- лопатку рассматриваем как закрученный стержень переменного сечения;
- отсутствует связь изгибных и крутильных колебаний;
- ось лопатки проходит через центры тяжести всех сечений и нерастяжима;
- при колебаниях все сечения остаются плоскими и перпендикулярными упругой линии (гипотеза Кирхгофа – Лява).
Примем систему координат OXYZ, начало которой O расположено в центре тяжести корневого сечения, оси X и Y совпадают с главными центральными осями инерции корневого сечения (пусть ), ось Z направлена по оси лопатки. Оси вспомогательной системы координат параллельны осям главной системы координат, начало находится в центре тяжести текущего сечения. Выделим в лопатке бесконечно малый элемент высотой dz (рис. 14.1).
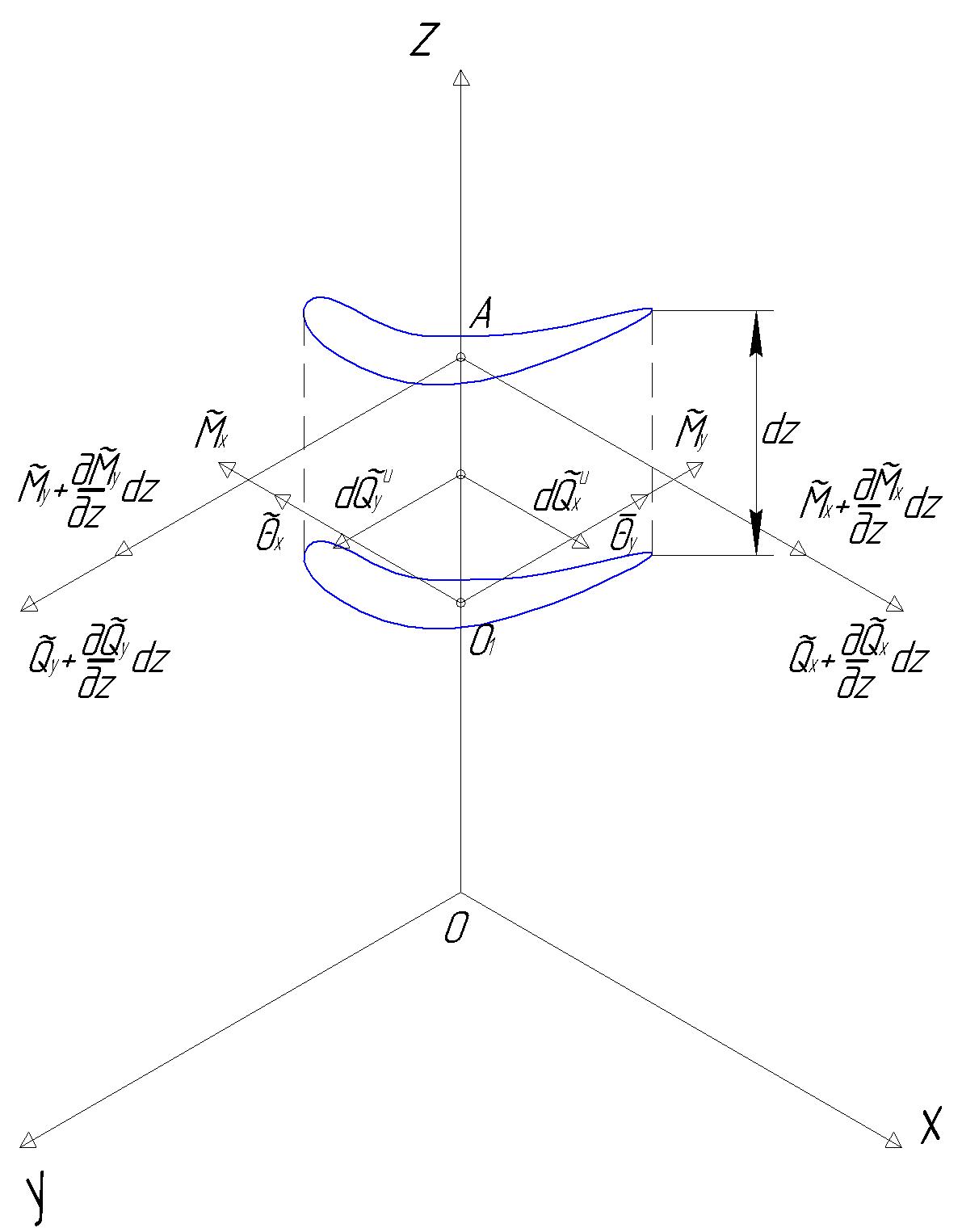
Рис.14.1. Бесконечно малый элемент лопатки
и динамические силы, приложенные к нему при изгибных колебаниях
Рассмотрим условия равновесия элемента с учетом сил инерции
и
,
где и - упругие смещения в направлении осей X и Y. Знак волны над переменной означает то, что она зависит от времени.
В направлении оси
, откуда
(14.1)
Из условия равновесия в направлении оси аналогично получаем
(14.2)
Вокруг оси :
.
Приводя подобные и пренебрегая бесконечно малыми второго порядка, получаем
. (14.3)
Вокруг оси :
.
Приводя подобные и пренебрегая бесконечно малыми второго порядка, получаем
. (14.4)
Установим связь моментов и углов поворота сечений. В плоскости OXZ (рис. 14.2)
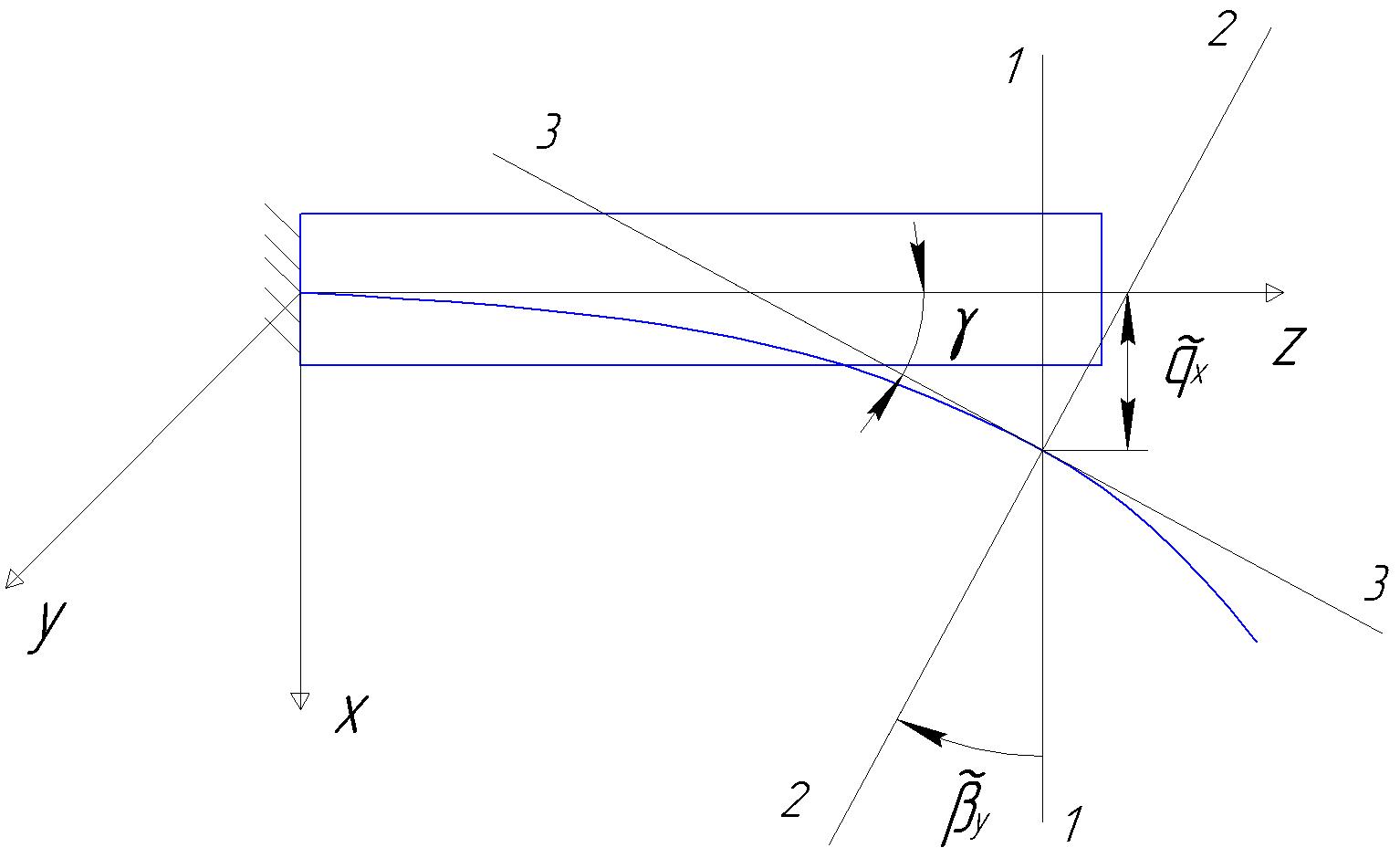
Рис.14.2. Изгиб оси лопатки в плоскости OXZ
1 – положение сечения в равновесном состоянии; 2 - положение изогнутой оси лопатки;
3 - касательная к изогнутой оси лопатки в месте расположения сечения.
Из рис. 14.2 видно, что
С учетом знаков момента и угла поворота
(14.5)
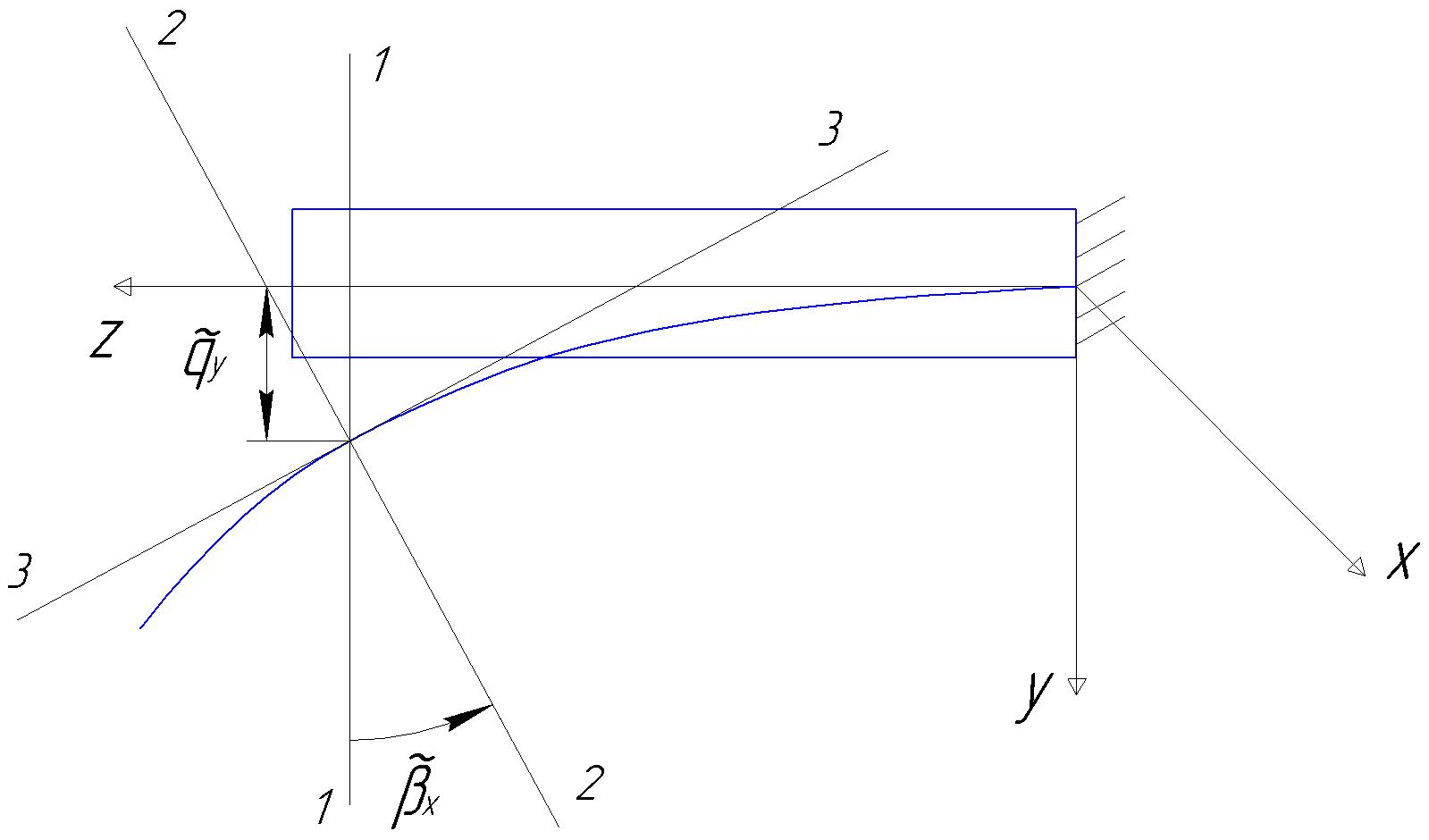
Рис.14.3. Изгиб оси лопатки в плоскости OYZ
1 – положение сечения в равновесном состоянии; 2 - положение изогнутой оси лопатки;
3 - касательная к изогнутой оси лопатки в месте расположения сечения.
В другой плоскости из рис. 14.3 видно
(14.6) .
Сечение лопатки поворачивается вокруг осей X и Y. Из рис. 14.4 видно, что (с учетом знаков углов поворота) перемещение произвольной точки сечения в направлении оси Z вследствие поворота сечения вокруг оси X составляет
,
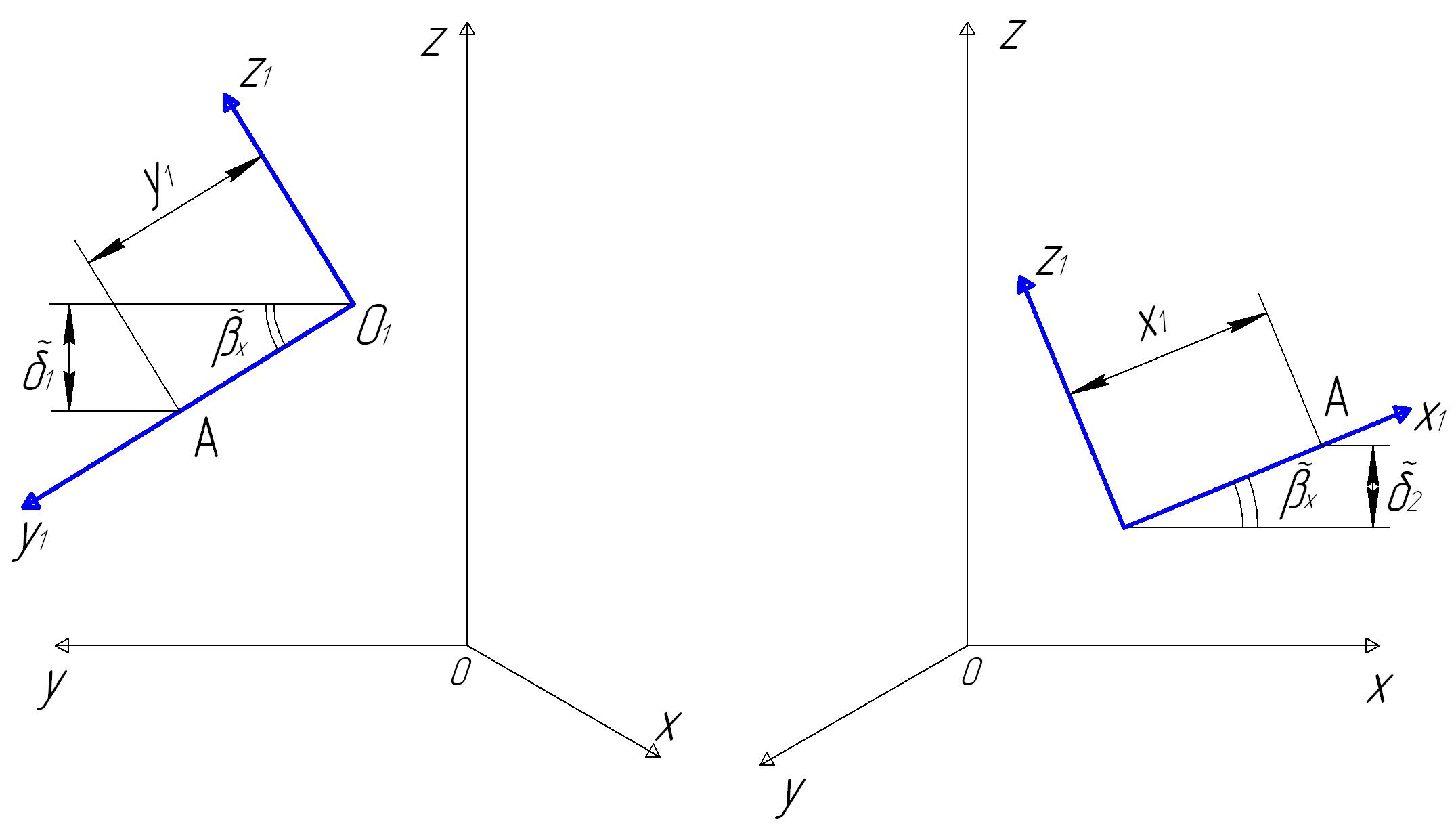
Рис.14.4. Поворот сечения лопатки в плоскостях OXZ и OYZ
вследствие поворота сечения вокруг оси Y составляет
.
Есть также перемещение в направлении оси Z сечения в целом, связанное с перемещением его центра, точки О1 . Полное перемещение точки в направлении оси Z
.
Согласно формулам Коши
.
Тогда напряжение в окрестности точки
.
Это напряжение создает бесконечно малые моменты вокруг осей (рис. 14.5)

Рис. 14.5. Определение знаков моментов сил от напряжения на бесконечно малой площади dF
,
.
Полный момент
В первое слагаемое входит статический момент вокруг оси . Поскольку – главная ось инерции, этот момент равен нулю. Во второе слагаемое входит момент инерции относительно оси , в третье – центробежный момент инерции. Таким образом,
Аналогично:
Поскольку деформации лопатки при колебаниях малы, будем считать, что оси главной и вспомогательной систем координат приблизительно параллельны. Тогда
; , моменты инерции тоже приблизительно одинаковы.
Запишем два последних уравнения в матричной форме.
.
Обозначив матрицу как [A] , получим
.
Пусть матрица имеет вид . Тогда
(14.7)
(14.8)
Уравнения (14.1)…(14.8) образуют систему дифференциальных уравнений, описывающих изгибные колебания лопатки:
Параметры в первых четырех уравнениях, а именно: qx ; y ; My ; Qx имеют отношение к плоскости OXZ, поэтому первые четыре уравнения описывают колебания в плоскости OXZ, а последние четыре – определяют колебания в плоскости OYZ. Связь между колебаниями в этих плоскостях осуществляется через коэффициент axy при Mx и My. Если лопатка не слишком закрученная, то оси и приблизительно совпадают с главными осями инерции во всех сечениях, в таком случае центробежные моменты инерции близки к нулю, коэффициент axy = 0 и связь между колебаниями в плоскостях OXZ и OYZ отсутствует. В этом случае
; .
Рассмотрим колебания в плоскости OXZ, т. е. только первые четыре уравнения. Их решение будем искать в гармоническом виде (где p – собственная частота колебаний):
После подстановки в дифференциальные уравнения получаем:
Из первого уравнения . Подставим это во второе уравнение, получим . Подставив в третье уравнение, получим . Подставив в четвертое уравнение, получим . Окончательно получили дифференциальное уравнение четвертого порядка
.
Обозначим
. Тогда
,
.
Решение уравнения четвертого порядка - сумма четырех линейно независимых частных решений.
Частными решениями уравнения являются , , а также гиперболические косинус и синус
В решение будем подставлять их суммы, которые называются функциями Крылова.
,
,
,
.
Преимущество этих функций состоит в том, что при дифференцировании они переходят друг в друга: dS/dz = V ; dT/dz = S ; dU/dz = T; dV/dz = U.
При этом S(0)=1; T(0) = U(0) = V(0) = 0.
Подставим решение вида в полученные уравнения.
,
,
.
Неизвестные постоянные С1, С2, С3, С4 определяются из граничных условий.
14.2. Колебания консольно закрепленной лопатки
Система имеет по две степени свободы (перемещение и угол поворота) на каждой из границ, соответственно, необходимы по 2 граничных условия на каждую границу.
При z=0 при консольном абсолютно жестком закреплении qx=0; y=0 .
;
;
откуда следует
.
Также
,
откуда следует
.
При z=l на свободном краю лопатки ; . Подставив в решение, получим
.
Или
.
Эта однородная система уравнений имеет решения, если ее определитель равен нулю.
Это имеет место при , где
K1=1,875 ,
K2=4,69 ,
K3=7,8
и т.д.
Поскольку i=Ki/l ,
.
Это уравнение определяет бесконечное количество собственных частот колебаний, каждой из которых соответствует своя форма колебания (форма колебания – это распределение относительных перемещений по колеблющемуся телу). Первая, вторая и третья формы изгибных колебаний приведены на рис. 14.6.
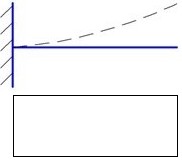
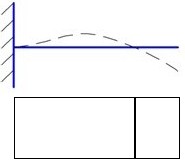
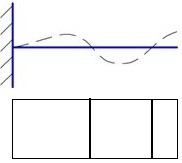
Рис.14.6. Первая, вторая и третья формы изгибных колебаний
14.3. Влияние податливости консольного закрепления на собственные частоты колебаний лопатки
Рассмотрим случай, когда закрепление исключает линейные перемещения, но податливо с жесткостью Cm для угловых перемещений.
На краю z=0 имеет место qx=0, откуда C1=0.
Закрепление создает момент .
Поскольку ,
,
получаем
.
При z=l на свободном краю лопатки My(l)=0; Qx(l)=0 . Подставив в решение, получим
.
Объединив эти уравнения с предыдущим, получим систему из трех уравнений для определения С2;C3;C4.
Если Cm=0 (это соответствует шарнирному замку лопатки), то частота первой изгибной формы равна нулю, то есть первая изгибная форма колебаний отсутствует. В этом состоит преимущество применения шарнирного замка (который, однако, имеет больший вес). Остальные формы изгибных колебаний сохраняются, но частоты их уменьшаются (рис. 14.7).
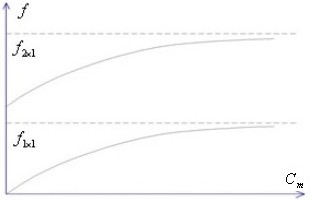
Рис. 14.7. Влияние податливости консольного закрепления
на собственные частоты колебаний лопатки
14.4. Крутильные колебания лопаток
Лопатку будем рассматривать как стержень постоянного сечения. Допустим, что центр тяжести и центр жесткости во всех сечениях лопатки совпадают, и кручение не зависит от изгиба.
Крутящий момент вокруг оси z
,
откуда , (14.9)
где G – модуль сдвига, а момент инерции на кручение
,
где b – длина хорды лопатки, функция описывает корытце лопатки, а - спинку (рис. 14.8). Если сечение близко к круглому, - полярному моменту инерции.
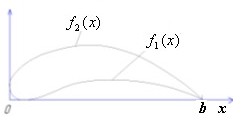
Рис. 14.8. Расчет момента инерции на кручение
На бесконечно малый элемент лопатки действует также момент от сил инерции
,
где массовый момент инерции
.
Тогда
Рассмотрим равновесие бесконечно малого элемента лопатки (рис. 14.9):
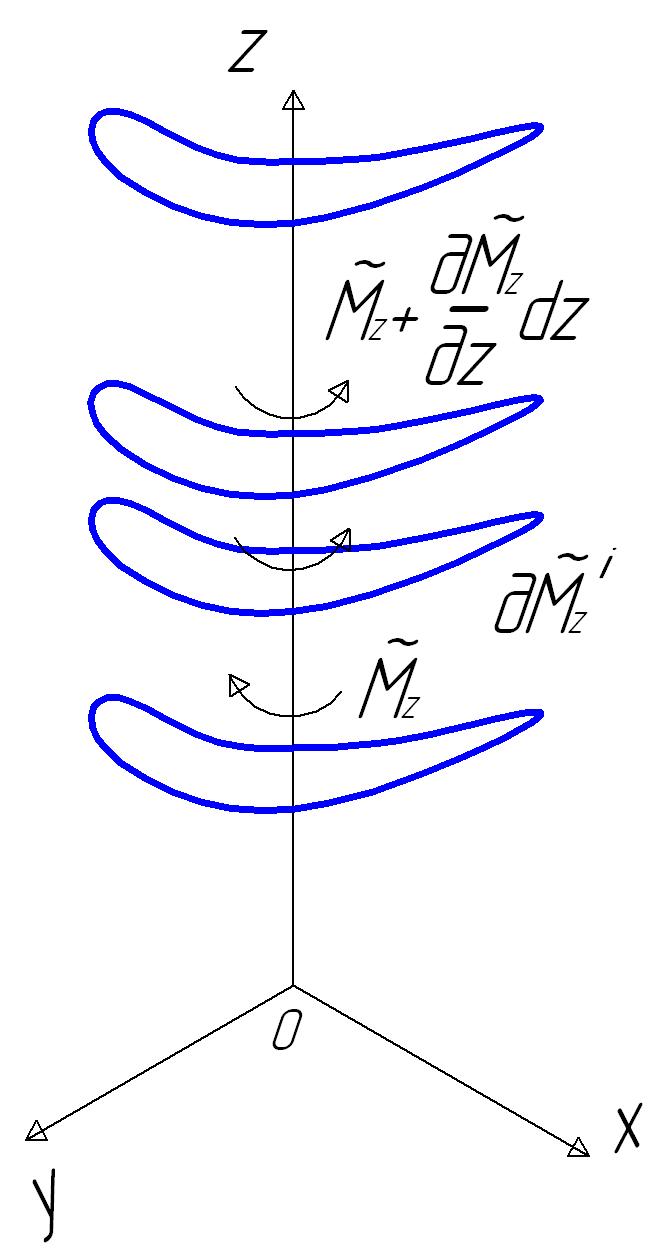
Рис.14.9. Бесконечно малый элемент лопатки
и приложенные к нему динамические силы при крутильных колебаниях
,
откуда
(14.10)
Уравнения (1.9) и (1.10) образуют систему дифференциальных уравнений, описывающих крутильные колебания лопатки. Решение будем искать в гармоническом виде
,
.
Подставив решение в уравнения (14.9) и (14.10), продифференцировав и сократив на , получим
,
.
Выразив из первого уравнения и подставив его во второе, получим
.
Обозначим , тогда , и
.
Это однородное дифференциальное уравнение второго порядка. Его решение имеет вид
.
Постоянные найдем из граничных условий.
В каждом сечении лопатка имеет одну степень свободы, поэтому получаем по одному граничному условию на каждой границе лопатки.
При z=0 при консольном абсолютно жестком закреплении , откуда следует
.
При z=l на свободном краю лопатки .
.
Это эквивалентно условию , , где n=1,2,3…
Значению соответствует частота колебаний и распределение углов поворота по лопатке вида (рис. 1.10, вверху). Это – первая крутильная форма колебаний. Ее узловая линия расположена вдоль лопатки.
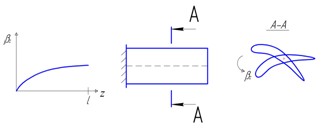
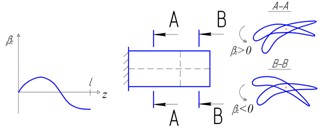
Рис. 14.10. Узловые линии при крутильных колебаниях лопатки
Значению соответствует частота колебаний и распределение углов поворота по лопатке вида (рис. 14.10, внизу). Это – вторая крутильная форма колебаний. Ей соответствует еще одна узловая линия поперек лопатки. По разные стороны этой линии колебания происходят в противоположных направлениях.
14.5. Классификация форм колебаний лопаток
Лопатка имеет бесконечное количество собственных частот и форм колебаний. Для их качественного описания используются числа и . При движении, описываемом числом , все точки поперечного сечения одновременно смещаются в одну сторону (рис. 14.11 слева). Число характеризует распределение смещений в поперечном сечении лопатки. При =1 все точки смещаются в одну сторону. Это соответствует чисто изгибным колебаниям. При

Рис. 14.11. Изгибные, крутильные и оболочечные колебания
=2 часть точек сечения смещается в одну сторону, часть в другую. Это соответствует крутильным колебаниям (рис. 14.11 в центре). При =3 происходят более сложные колебания, которые называют оболочечными (рис.14.11 справа). Формы колебаний можно представить в виде таблицы (рис.14.12). Частоты колебаний увеличиваются вправо и вниз:
;
Реальная лопатка закручена и имеет различную толщину в различных сечениях, ее узловые линии могут быть не прямыми и не перпендикулярными относительно её оси.
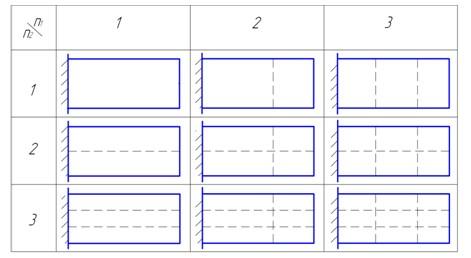
Рис.14.12. Таблица форм колебаний консольно закрепленной лопатки
14.6. Влияние различных факторов на собственные частоты колебаний лопаток
1. Влияние материала проявляется через сомножитель . Для используемых в двигателестроении металлических материалов (с точностью три - пять процентов), и изменение материала на собственную частоту лопатки не влияет. Для композитных материалов это не так, и для них нужно также учитывать анизотропию свойств, то, что ExEy.
2. Влияние центробежной силы связано с тем, что при отклонении лопатки от положения равновесия при колебаниях у центробежной силы появляется плечо, и появляется момент, возвращающий лопатку в положение равновесия (рис.14.13). Поэтому для вывода лопатки из положения равновесия необходимо преодолеть не только жесткость лопатки, но и действие момента центробежной силы. Это эквивалентно увеличению жесткости лопатки, поэтому частота колебаний при этом увеличивается.
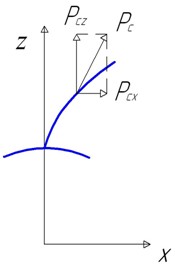
Рис.14.13. Плечо центробежных сил
Различают статическую частоту лопатки на неподвижном роторе и динамическую частоту , которая растет с увеличением оборотов. Для первой изгибной формы
,
где n – обороты ротора,
,
здесь - средний диаметр рабочего колеса, - средний угол установки лопатки.
Влияние центробежной силы наибольшее на низшие формы колебаний. На крутильные колебания центробежная сила не влияет, так как при кручении у нее не появляется плечо.
3. Влияние температуры происходит вследствие уменьшения модуля жесткости Е с ростом температуры. Температурная поправка
,
где - модуль жесткости нагретой лопатки, - модуль жесткости при нормальной температуре.
Поскольку при увеличении оборотов двигателя растет и температура, влияние температуры накладывается на влияние центробежной силы. Температура лопаток компрессора меняется незначительно, поэтому их динамическая частота только увеличивается. В турбине при больших температурах влияние температуры сильнее, поэтому динамическая частота лопаток на малых оборотах увеличивается, а на больших уменьшается.
4. Влияние геометрических параметров (рис. 14.14) при равномерном изменении по длине лопатки можно оценить, пользуясь приближенными формулами для площади сечения
и момента инерции профиля
(здесь - хорда лопатки, - максимальная толщина ее профиля, – максимальный подъем средней линии, см. рис. 14.14).
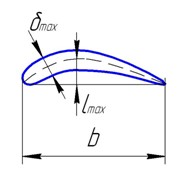
Рис. 14.14. Геометрические параметры профиля лопатки
.
Видно, что хорда лопатки на частоту не влияет, увеличение длины существенно уменьшает частоту, увеличение и – увеличивает частоту.
5. При неодинаковом изменении геометрических параметров по длине лопатки жесткость лопатки определяется теми участками, где имеются большие относительные деформации (вблизи мест закрепления или узловых линий), а инерционные свойства – теми участками, где имеются большие перемещения (вдали от мест закрепления или узловых линий). Например, при увеличении толщины лопатки в корневом сечении, увеличится ее жесткость и вырастет частота первой изгибной формы (рис. 14.15, первый рисунок). При увеличении толщины лопатки на периферии увеличатся ее инерционные свойства, и частота первой изгибной формы уменьшится (рис. 14.15, второй рисунок).
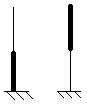
Рис. 14.15. Утолщение различных сечений лопатки
При подрезке уголка (рис. 14.16) уменьшатся инерционные свойства периферии, что также вызовет увеличение частоты первой изгибной формы.
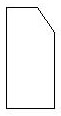
Рис. 14.16. Лопатка со срезанным уголком
15. КОЛЕБАНИЯ ДИСКА РАБОЧЕГО КОЛЕСА
Диск будем рассматривать как круглую пластину переменной толщины в рамках модели Тимошенко. Для пластины в цилиндрической системе координат:
, (15.1)
, (15.2)
, (15.3)
, (15.4)
, (15.5)
где D – цилиндрическая жесткость, k учитывает характер распределения напряжений.
- крутящий момент, который образуется от касательных напряжений на площадке с нормалью r. - погонная перерезывающая сила, которая возникает от касательных напряжений. Она действует в направлении оси Z на площадке с нормалью r. - скручивающий момент, который возникает от нормальных напряжений на площадке с нормалью . - крутящий момент от касательных напряжений на площадке с нормалью . - погонная перерезывающая сила от касательных напряжений , действующая в направлении оси Z на площадке с нормалью .
Выделим элемент диска двумя радиальными плоскостями, расположенными под углом , и двумя цилиндрическими поверхностями с радиусами r и dr (рис.15.1).
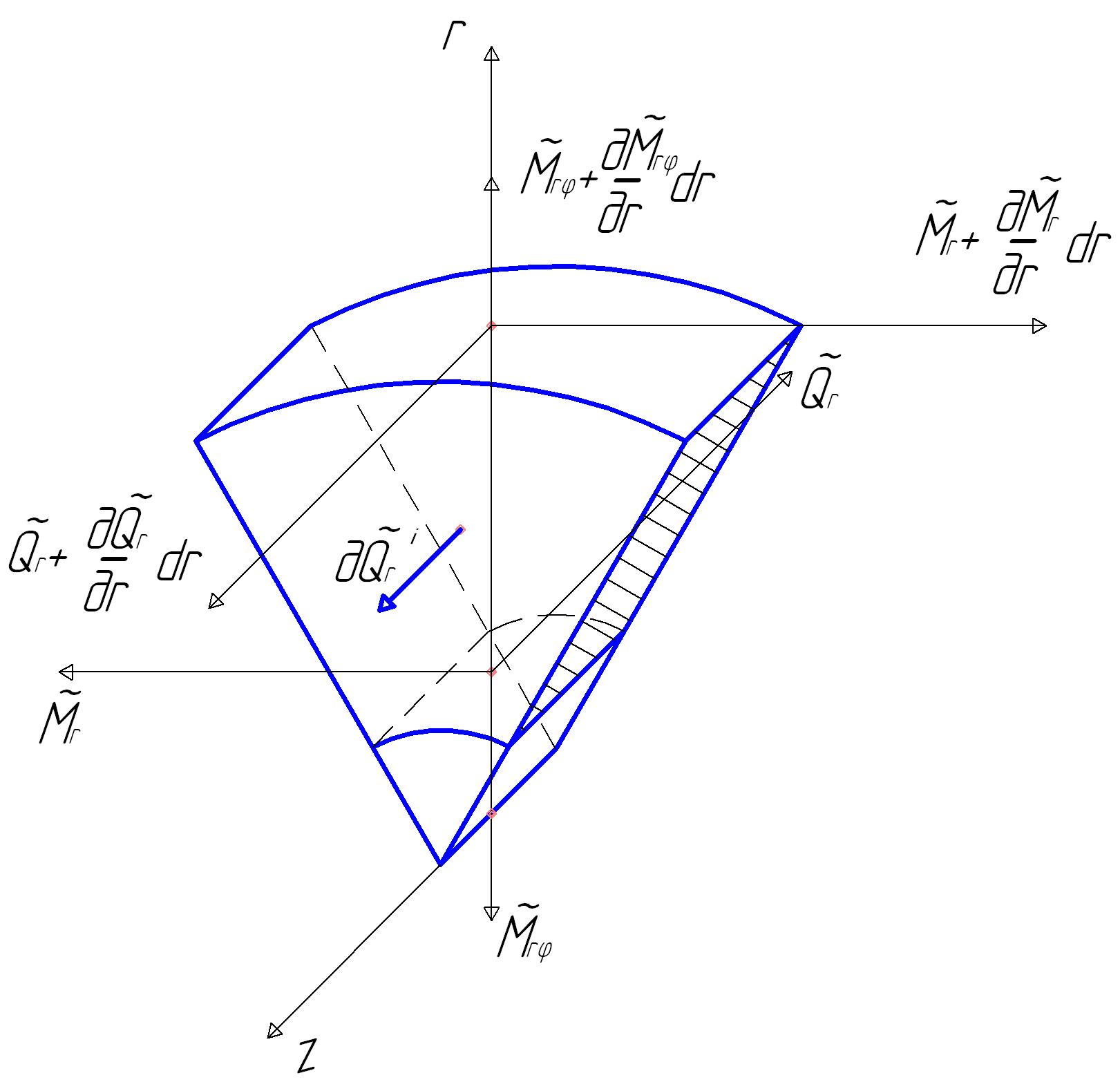
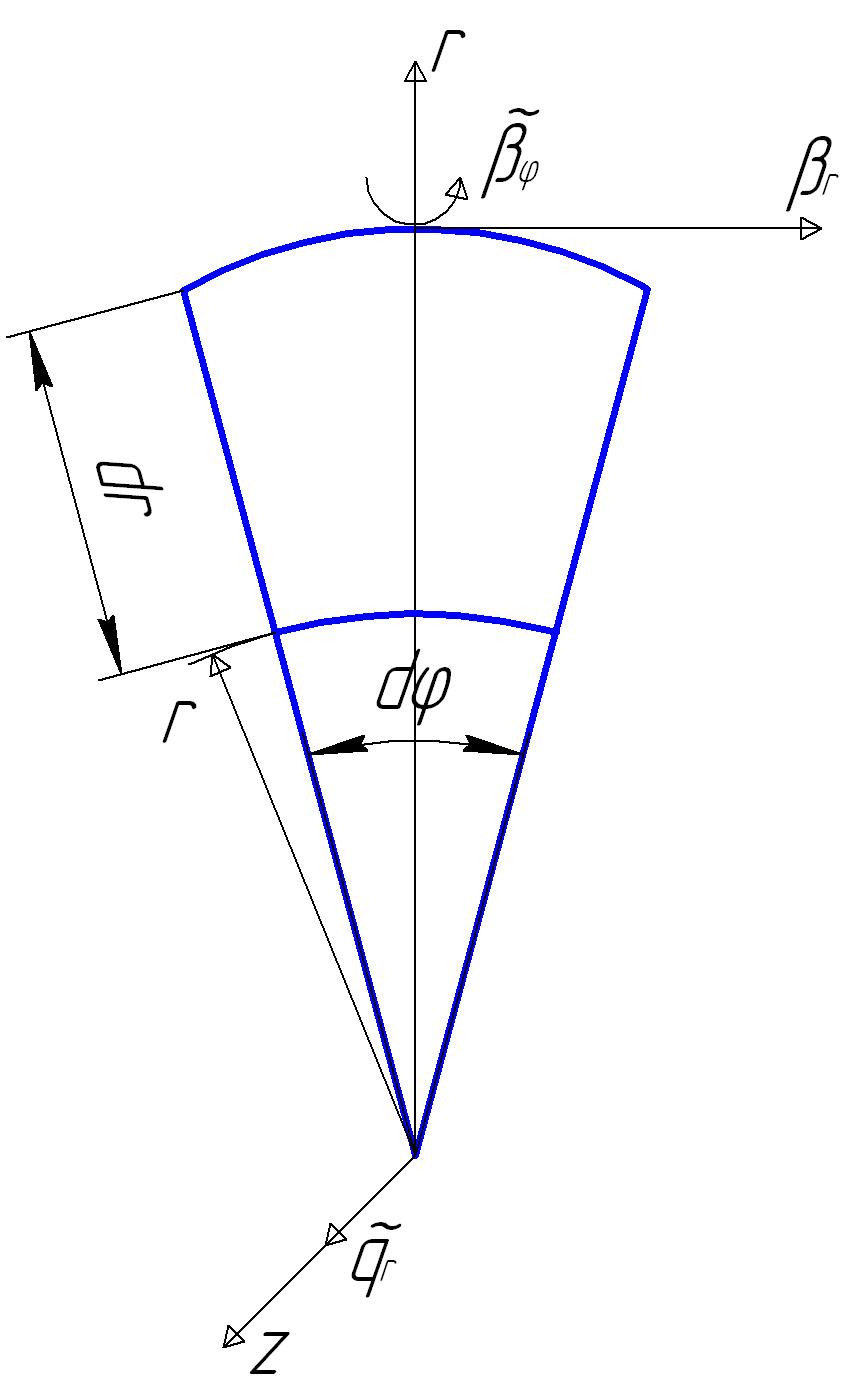
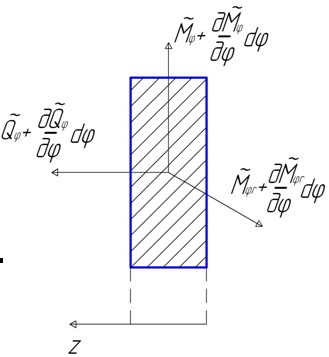
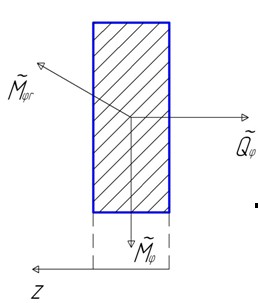
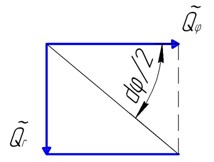
Рис.15.1. Бесконечно малый элемент диска и действующие на него динамические силы
Получим систему дифференциальных уравнений, описывающую колебания диска, из рассмотрения уравнений (15.1) – (15.5) и условий равновесия элемента диска.
Из (15.1) (также умножив и разделив на r) получим
. (15.6)
Из (15.3) получим
(15.7)
Из (3.2)
(15.8)
Преобразуем (15.4), подставив из (15.6):
(15.9)
Сила инерции
(15.10)
Рассмотрим равновесие элемента. Проекции сил на ось Z:
(15.11)
Преобразуем
(15.12)
С учетом (15.12), (15.11) примет вид
,
.
Поделив на , получим
. (15.13)
Продифференцируем (15.5) по :
.
Подставив это в (15.13), получим
(15.14)
Сумма моментов относительно оси r :
Пренебрегая бесконечно малыми второго порядка, полагая и , получаем
.
Разделив на и учтя =, а также умножив и разделив на r, получим:
.
Подставив и из (15.9) и (15.5), получим
(15.15)
Проекции моментов на окружное направление:
Раскроем скобки аналогично (15.12):
.
Разделив на , а также умножив и разделив на r, получим:
.
Подставив из (15.9), получим
. (15.16)
Уравнения (15.8), (15.6), (15.7), (15.14), (15.16), (15.15) образуют систему (15.17) относительно 6 переменных
, , , , , .
(15.17)
Решение системы (15.17) должно быть периодическим по .
.
Поэтому решение будем искать в виде:
(15.18)
Здесь p – собственная частота, t – время, - сдвиг фазы колебаний.
Подставив (15.18) в (15.17), взяв производные по и сократив на , получим систему дифференциальных уравнений первого порядка.
(15.19)
Общее решение системы имеет вид
,
где - любые линейно независимые частные решения (15.19).
Частные решения находим численным методом. На радиусе начала интегрирования примем
……………..
.
Постоянные определим из граничных условий.
Рассмотрим определение собственных частот колебаний диска переменного сечения, закрепленного на внутреннем радиусе и свободного на периферии .
Граничные условия на радиусе :
, , .
, отсюда .
Аналогично получаем .
Граничные условия на радиусе :
, , . Из этого получаем систему уравнений:
(15.20)
Система имеет решения, если ее определитель равен нулю.
Приведем алгоритм расчета собственных частот колебаний диска:
1. Задается m=0.
2. Принимается начальная частота колебаний .
3. Интегрируется три раза система (15.19) с начальными значениями
.
4. Вычисляется определитель системы (15.20) и сравнивается со значением на предыдущем шаге. Если его знак изменился, перейти к п.6. Если не изменился – к п.5.
5. Частота увеличивается на шаг . Перейти к п.3.
6. Меняется шаг . Перейти к п.5.
7. Дробление шага продолжается до тех пор, пока не выполнится (погрешности расчета).
8. Определяется собственная частота .
9. Принимается начальная частота . Перейти к п.3.
10. Если найдены все собственные частоты колебаний для заданного m (в пределах рассматриваемого диапазона частот), то m= m+1. Перейти к п. 1.
После расчета собственных частот рассчитываются собственные формы колебаний диска. В выражении первые два сомножителя определяют распределение амплитуды колебаний по диску.
При m=0 амплитуды во всех точках окружности одинаковы.
При m=1 имеются две линии, на которых амплитуда колебаний равна нулю. Эти линии образуют узловой диаметр (рис. 15.2).
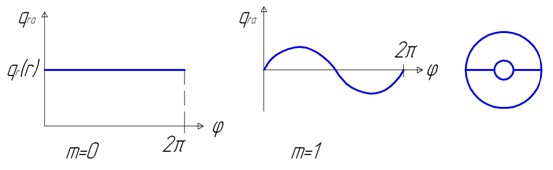
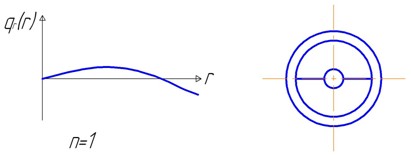
Рис.15.2. Колебания диска с узловыми диаметрами и узловыми окружностями
При m=2 имеются четыре линии, на которых амплитуда колебаний равна нулю. Эти линии образуют два узловых диаметра. И т.д.
Функция также может менять знак по радиусу диска. При n=0 все значения в один и тот же момент времени имеют одинаковый знак. Амплитуды колебаний с ростом m в центре убывают. При большом значении m колеблется только обод диска.
При n=1 функция имеет одну перемену знака по радиусу диска. При этом появляется узловая окружность (см. рис. 15.2). При n=2 функция имеет две перемены знака по радиусу диска. При этом появляются две узловых окружности. И т.д.
Формы колебаний с m=0 и различным количеством узловых окружностей называют зонтичными.
С увеличением m и n частота колебаний растет, за единственным исключением:
.
Формы колебаний диска можно представить в виде таблицы (рис.15.3).
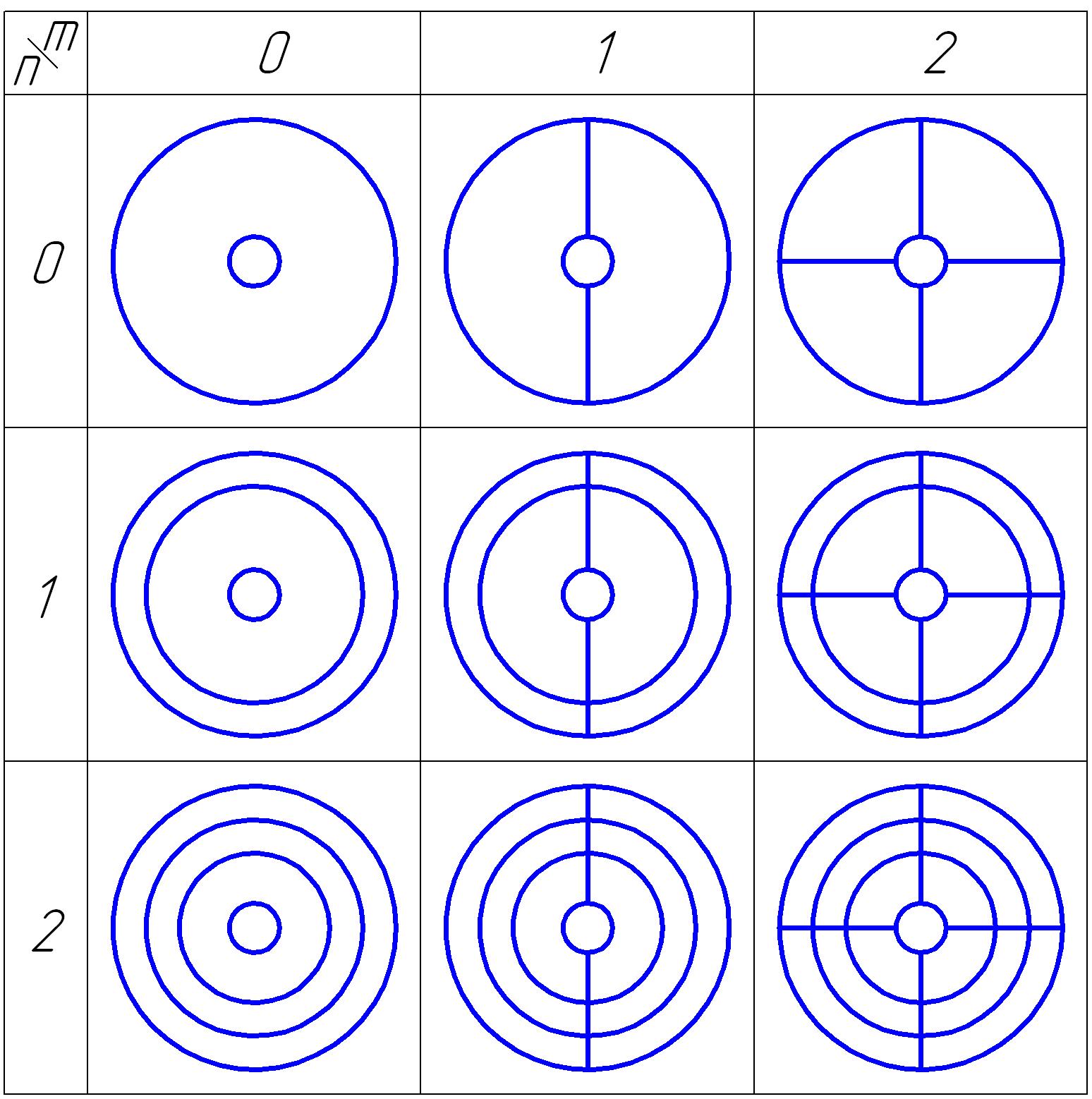
Рис. 15.3. Таблица форм колебаний центрально закрепленного диска
Удобно представить частоты колебаний в виде единого графика в зависимости от количества узловых диаметров m. Такой график называют спектром колебаний диска (рис. 15.4).
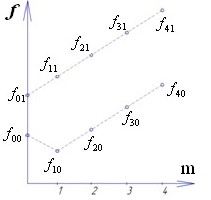
Рис. 15.4. Спектр колебаний диска
Поскольку лопатки увеличивают массу на ободе диска, собственные частоты колебаний диска с лопатками уменьшаются. Узловые диаметры могут проходить только между лопатками, поэтому их количество у диска с лопатками не бесконечно, а ограничено числом z/2, если количество лопаток z четное, и (z-1)/2, если количество лопаток нечетное.
Узловые окружности зонтичных форм колебаний диска с лопатками могут проходить по лопаткам (рис. 15.5).
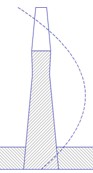
Рис. 15.5. Форма колебаний диска с лопатками
Все незонтичные (m>1) формы колебаний являются парными. Кроме решения (15.18) существует решение
(15.21)
Его подстановка в систему (15.17) приводит к системе, аналогичной (15.19). Частоты колебаний при этом будут те же самые, но распределение смещений будет сдвинуто на 1/4 волны, то есть на угол . Парные формы колебаний не зависят друг от друга. Пусть
,
,
где , , , - соответственно, амплитуды и сдвиги фаз, которые зависят от начальных условий, - распределение смещений по радиусу диска (. При колебаниях диска возбуждаются обе парные формы, результатом является их суперпозиция. Рассмотрим частные случаи.
1. . Результирующее движение
.
Здесь , .
Видно, что диск имеет m узловых диаметров. Их положение определяется из условия
при . Отсюда
,
.
Положение узловых линий в этом случае не зависит от времени. Это – колебания со стоячими волнами.
Положение узловых линий зависит от соотношения и , которое зависит от начальных условий и может быть любым – следовательно, положение узловых линий произвольное.
2. Пусть ==D, возбуждение колебаний приложено к точке 1 диска и перемещается по окружности (рис. 15.6). Для формы m=1 узловая линия имеет вид диаметра. Если для формы она проходит через точку 1, форма возбуждаться не будет (энергия передается посредством работы, а работа при нулевом перемещении равна нулю). Будет возбуждаться перпендикулярная узловая линия формы . Когда источник возбуждения колебаний перейдет в точку 3 (под углом 900), перестанет возбуждаться форма , но появится форма . При положении источника в промежуточной точке 2, возбуждается суперпозиция форм и , линия, противоположная точке 2.
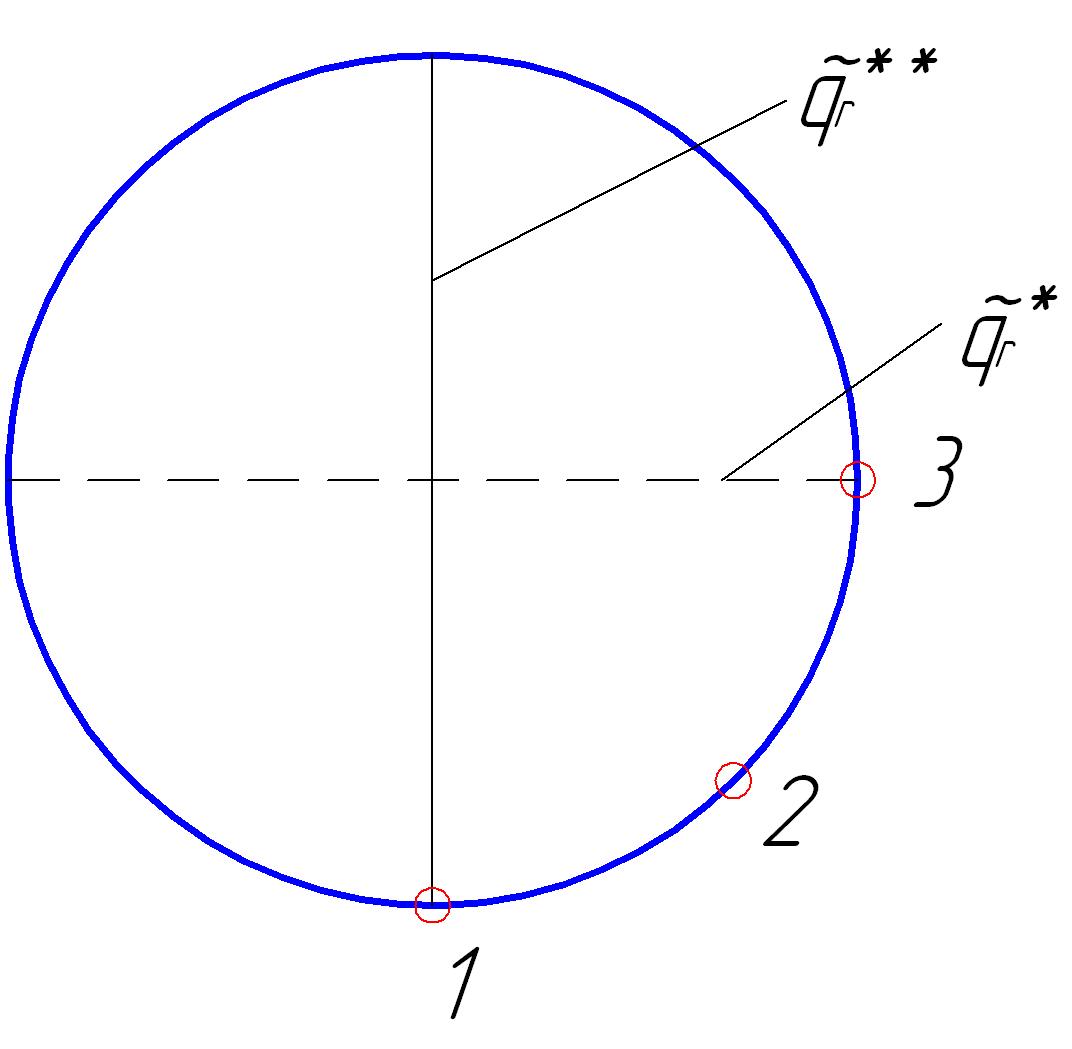
Рис.15.6. Возбуждение парных форм колебаний
Таким образом, узловые линии стоячих волн перемещаются по диску при перемещении источника возбуждения колебаний.
3. Возможны также колебания диска с бегущими волнами. Пусть , , . Результирующее колебание
.
Узловые линии определяются выражением , откуда
, .
Видно, что положение узловых линий зависит от времени. Это – колебания с бегущей волной. Угловая скорость вращения узловых линий
,
так как она отрицательна, это – колебания с назад бегущей волной.
4. Если ==D, , , то
.
Узловые линии определяются выражением , откуда
, , .
Это – колебания с вперед бегущей волной.
В ГТД все резонансные колебания происходят с назад бегущей волной. Автоколебания – в 90% случаев с вперед бегущей волной.
16. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ РАБОЧИХ КОЛЕС ГТД
16.1. Понятие о возбуждающих гармониках
Основной источник колебаний РК – окружная неравномерность поля давлений и поля скоростей в газовом потоке перед и за РК. Действующая на лопатку газовая сила неодинакова и зависит от условий на входе в двигатель, от обтекания всех элементов проточной части до РК и непосредственно за РК. Так как периодическая по окружности, ее можно разложить в ряд Фурье:
. (16.1)
Угол определяет положение лопатки в неподвижной системе координат, угол - в системе координат, вращающейся вместе с РК (рис.16.1).
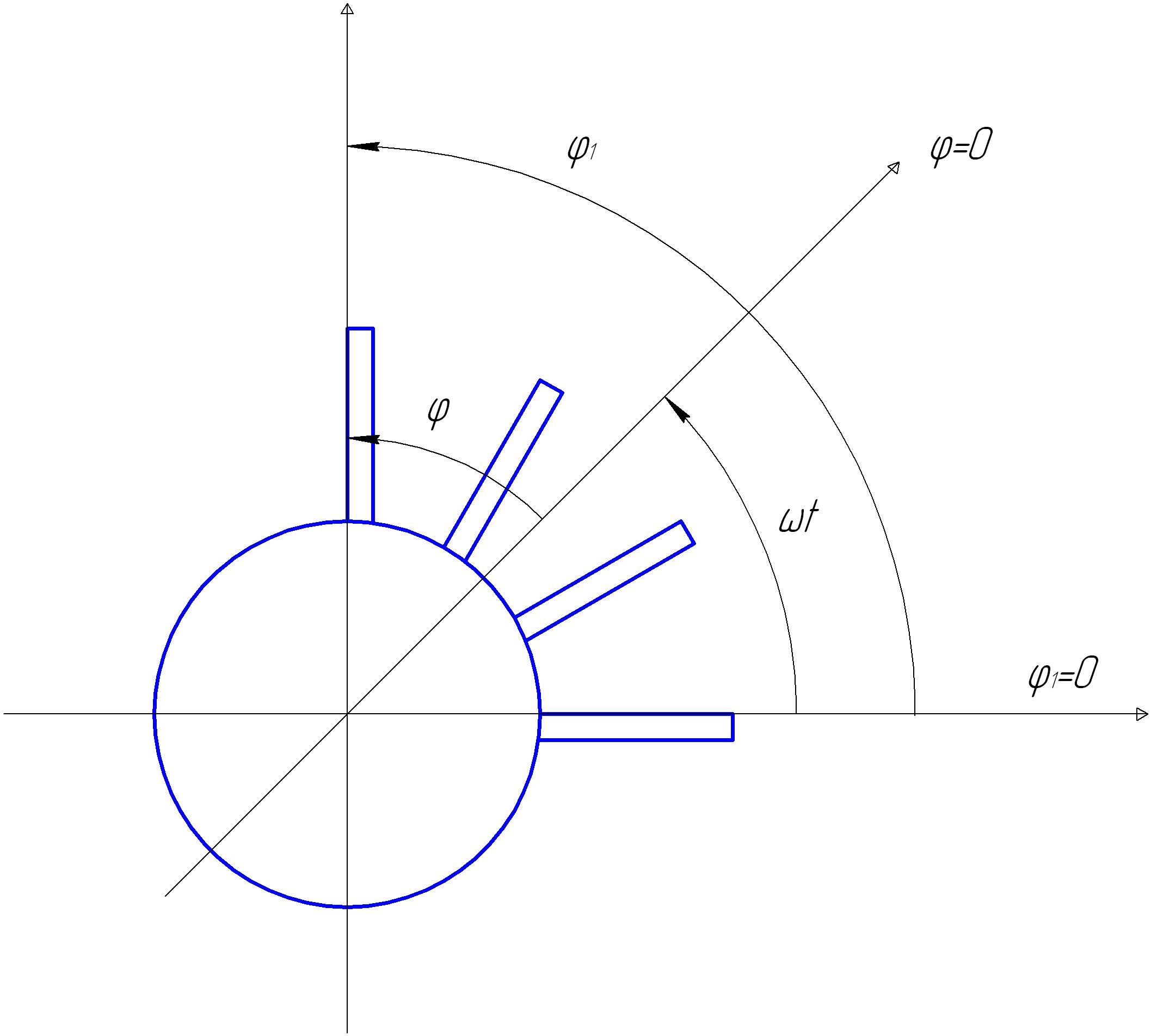
Рис. 16.1. Подвижная и неподвижная системы координат
Отсюда
Одно из слагаемых разложения (16.1) имеет вид
.
То есть каждое слагаемое разложения эквивалентно двум нагрузкам с частотой и сдвигом по фазе на 1/4 периода. Это соответствует колебаниям с назад бегущей волной.
Так как каждое слагаемое разложения (16.1) может возбуждать колебания, его называют возбуждающей гармоникой. Так как
,
частота возбуждающей гармоники линейно зависит от частоты вращения ротора . m называют номером гармоники. Гармоника с номером m возбуждает только колебания, кратные m. Амплитуда зависит от условий обтекания элементов проточной части перед и за РК. Гармонический анализ неоднородностей полей давлений по окружности показывает, что наибольшей интенсивностью обладает 1-я гармоника. С увеличением номера гармоники интенсивность возбуждения падает. Если принять интенсивность 1-й гармоники за 100 %, то интенсивность 2-й составляет 30%, 3-й 10%, интенсивность 4-й гармоники уже пренебрежимо мала. Но если есть конструктивные элементы (лопатки НА, ребра и т.д.) с количеством m, то амплитуда гармоники с номером m будет значительно больше.
16.2. Резонансная диаграмма
Диаграмма, отражающая зависимость собственных частот колебаний РК и частот возбуждающих гармоник от частоты вращения ротора и позволяющая находить режимы работы двигателя, на которых происходят резонансные колебания РК, называется резонансной диаграммой (рис.16.2). На резонансной диаграмме отображаются:
- частотная линия рабочего колеса, показывающая изменение той или иной собственной частоты в зависимости от режима работы двигателя (реально из-за небольшого различия геометрических характеристик лопатки, жесткости закрепления и т.д. это не линия, а полоса шириной около 3% в обе стороны от скелетной линии);
- линии возбуждающих гармоник (прямые с угловым коэффициентом m);
- линии продолжительных рабочих режимов двигателя: максимального, крейсерского, малого газа и т.д. (реально из-за погрешности работы регулятора оборотов это также диапазоны шириной около 3% в обе стороны).
Рис. 16.2. Резонансная диаграмма
Там, где линия возбуждающей гармоники пересекается с частотной линией, имеет место резонанс. Однако опасны только резонансы, совпадающие с продолжительными рабочими режимами. Другие резонансные частоты двигатель достаточно быстро проходит, и опасные колебания не успевают развиться.
16.3. Автоколебания
Автоколебания – это незатухающие колебания, происходящие без воздействия возбуждающих гармоник и других переменных во времени сил. Для возникновения автоколебаний необходим источник энергии и механизм превращения ее в энергию колебаний.
Источником энергии для рабочего колеса является газовый поток. Механизм передачи энергии связан с обтеканием лопаток. Рассмотрим плоскопараллельные автоколебания незакрученной лопатки в незакрученном потоке. Пусть поток набегает на лопатку со скоростью под углом атаки . Пусть в результате случайного воздействия лопатка вышла из положения равновесия и стала совершать гармонические колебания с частотой p.
.
Разложим движение на перпендикулярное скорости потока и параллельное . Соответствующие этим движениям скорости равны и . Таким образом, относительная скорость потока становится равной и угол атаки изменяется на величину (рис. 16.3), причем при изменение угла атаки <0. параллельное рное скорости потока коростью под углом атаки . е случайного воздействия лопатка вышла из положения равновесия и
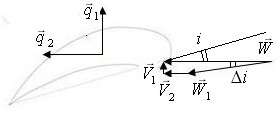
Рис. 16.3. Изменение угла атаки
.
Так как и малы, , , .
На лопатку действует аэродинамическая сила . Здесь - плотность потока, - хорда лопатки, - коэффициент подъемной силы. Он зависит от угла атаки (рис. 16.4).
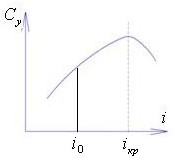
Рис. 16.4. Зависимость коэффициента подъемной силы от угла атаки
Разложим в ряд Тейлора в окрестностях :
Оставив два первых слагаемых разложения, получаем
Соответственно аэродинамическая сила будет переменной во времени:
.
Найдем работу аэродинамической силы на перемещении лопатки.
.
Работа за период колебаний Т
Если (докритическое обтекание, см. рис. 4.4), то A<0, энергия колебаний лопатки рассеивается. Рассеивание энергии колебаний за счет взаимодействия с набегающим потоком называется аэродинамическим демпфированием.
Если (закритическое обтекание), то A>0 , газовый поток добавляет лопатке энергию, и амплитуда ее колебаний будет увеличиваться до разрушения.
По нормам прочности автоколебания недопустимы. При их возникновении необходим перерасчет течения газа в двигателе, чтобы не допускать закритического обтекания лопаток.
16.4. Борьба с опасными колебаниями рабочих колес
Борьба с колебаниями рабочих колес – сложная задача, не имеющая универсальных решений. Всякое предлагаемое мероприятие может быть, с одной стороны, недостаточно эффективным, а с другой стороны, ухудшает какие-то иные параметры двигателя. Борьба с колебаниями ведется по трем направлениям.
- Уменьшение силы, вызывающей колебания.
Поскольку источником колебаний является окружная неравномерность газовой силы, меры борьбы с колебаниями направлены на уменьшение этой неравномерности. Неравномерность газового потока за лопаткой уменьшается очень быстро, пропорционально (где - расстояние до источника неравномерности), поэтому небольшое увеличение расстояния между рабочим колесом и направляющим аппаратом (рис. 16.5) дает значительный эффект. Величину осевого зазора для обеспечения минимального уровня возбуждения удобно задавать в относительных величинах как:
= а/b, или в виде: К=А/Сm,
где а - средний осевой зазор между вен цами,
b - хорда возбуждающего венца;
А - расстояние между положениями максимальной толщины - Сm - возбуждаемой и возбуждающей лопатки или стойки опоры.
На основе экспериментальных исследований установлено, что при = 0.5 или К=6 уровень переменных напряжений в лопатках стабилизируется на минимальном уровне. Однако увеличение зазора увеличивает габариты и вес двигателя.
Рис. 16.5. Влияние осевого зазора между рабочей лопаткой и возбудителем колебаний (стойками опор, лопатками направляющих аппаратов)
В случае применения наклонного направляющего аппарата (рис. 16.6) рабочая лопатка попадает в зону неравномерности потока, вызванную направляющим аппаратом, не одновременно по всей своей высоте, а только в окрестностях точки А, которая к тому же перемещается по высоте лопатки по мере ее поворота вокруг оси двигателя. Однако наклоненный направляющий аппарат тяжелее обычного.
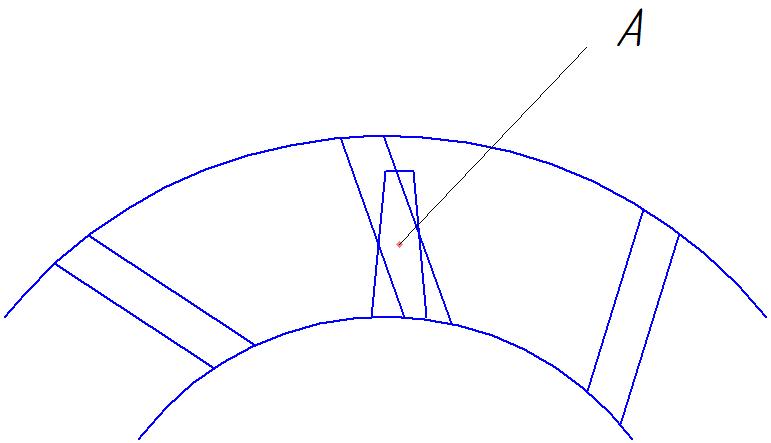
Рис. 16.6. Наклонный направляющий аппарат
Для уменьшения сил, вызывающих колебания, желательно неравномерное расположение стоек опор, ребер и т.д. (так, на рис. 16.7 желательно ). Однако при этом жесткость конструкции будет различна в различных направлениях, а анизотропия опор нежелательна при колебаниях валов двигателя.
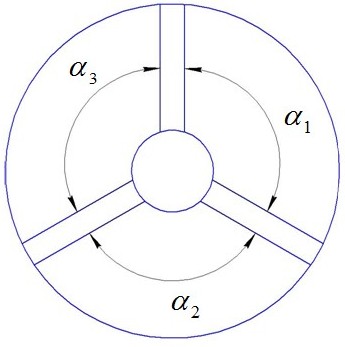
Рис. 16.7. Неравномерное расположение ребер
Нежелательно применение конструкций, увеличивающих неравномерность газового потока. Например, если клапан перепуска установлен непосредственно на проточную часть, при его открытии возникнет очень значительная окружная неравномерность. Поэтому обычно в проточной части выполняется много маленьких отверстий по окружности, выводящих в ресивер, а клапан перепуска размещается на ресивере против того места на окружности, где отверстия отсутствуют. Выпуск воздуха через много распределенных по окружности малых отверстий искажает газовый поток не так сильно, как могло бы исказить одно большое отверстие к перепускному клапану. По этой же причине порой применяются ленты перепуска, открывающие щель для выхода воздуха почти по всей окружности.
- Частотная отстройка.
Частотная отстройка является наиболее распространенным способом борьбы с колебаниями лопаток.
Необходимость отстройки определяется на этапе проектирования при помощи резонансной диаграммы. Как и для роторов ГТД, применяется частотная отстройка вверх или вниз. Поскольку собственные частоты лопаток имеют небольшие индивидуальные различия, а регулятор двигателя также поддерживает обороты с некоторой индивидуальной погрешностью, отстройка от резонанса должна быть не менее, чем на 10% по оборотам двигателя.
Изменение собственной частоты лопатки обычно производится при помощи изменения толщины ее сечений в требуемых местах (применение шарнирного замка, устраняющего первую изгибную форму колебаний, также можно рассматривать как способ частотной отстройки). Если изменение толщины сечения превышает 20%, необходимо перепрофилировать лопатку, произведя новый расчет течения газа через лопаточную решетку. В качестве экстренного способа частотной отстройки применяется подрезка уголков лопатки (например, турбина двигателя Р11-300), но это нежелательно, так как рассчитанное оптимальное течение газа в таком случае будет искажено.
После частотной отстройки необходим повторный расчет статической прочности лопатки, так как ее сечения были изменены.
Частотную отстройку затрудняет то, что, уходя от одного резонанса, можно попасть на другой. Против автоколебаний частотная отстройка бесполезна.
Для дисков ГТД частотная отстройка также является наиболее распространенным способом борьбы с колебаниями (тем более, что применение демпферов в дисках не всегда возможно). Изменение собственных частот диска осуществляется за счет изменения его сечения.
- Демпфирование.
Для борьбы с колебаниями лопаток и дисков применяются, как правило, демпферы сухого трения.
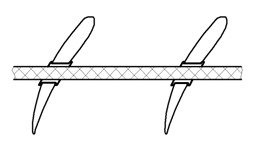
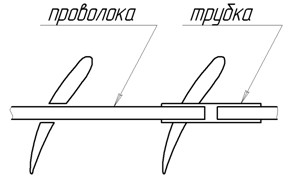
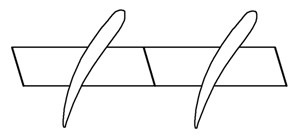
Энергия колебаний может рассеиваться при трении проволок внутри троса, пропущенного через отверстия в пере лопатки (рис. 16. 8, а). Трос может быть заменен трубкой (рис. 16. 8, б), при этом трение реализуется между поверхностями трубки и отверстия в пере лопатки. Трение может осуществляться между боковыми поверхностями антивибрационных (рис. 16. 8, в) или бандажных полок. Однако все эти демпферы, расположенные в проточной части, ведут к некоторым газодинамическим потерям на их обтекание.
а б в
Рис. 16.8. Демпферы лопаток, устанавливаемые в проточной части
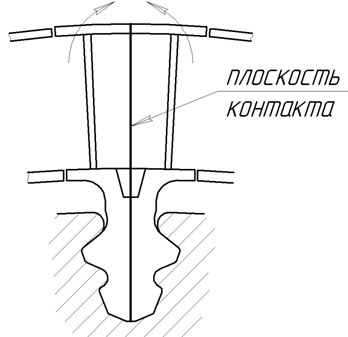
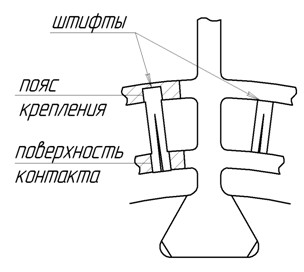
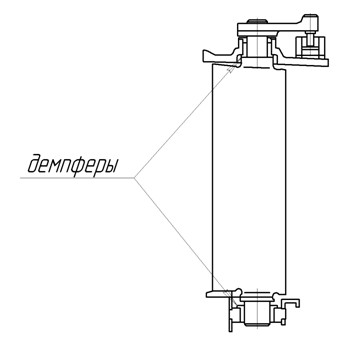
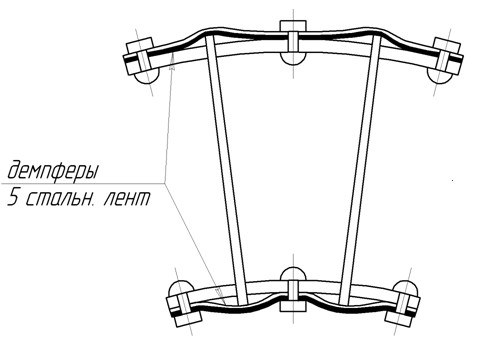
Поверхность трения может быть образована разрезом замка или пера лопатки (рис. 16.9, а). На лопатки устанавливаются штифты (рис. 16.9, б), демпфирующие втулки (рис. 16,9, в), многослойные пакеты металлических лент (рис. 16.9, г).
а б
в г
Рис. 16.9. Демпферы колебаний в замках лопаток
Детали из композиционных материалов обладают большим рассеиванием энергии при внутреннем трении в материале (в десятки раз больше, чем у стали). В этом одна из важных причин стремления к применению композиционных материалов.
Демпфирование за счет рассеивания энергии уменьшает амплитуду колебаний на резонансе. Частота при этом изменяется незначительно (на несколько процентов даже при большом демпфировании). В отличие от этого частотная отстройка изменяет собственную частоту колебаний, практически не меняя амплитуду колебаний на резонансе.
17. ЗАЩИТА ОТ ВИБРАЦИИ
Виброизоляция является действенным средством уменьшения динамических нагрузок на агрегаты двигателя и увеличения их работоспособности.
17.1.Необходимые данные для проектирования виброзащитной системы
Для проектирования виброизоляции какого-либо объекта необходимы:
а) чертежи объекта с указанием возможного расположения мест крепления виброизоляторов;
б) данные:
- о весе агрегата m,
- о положении центра тяжести агрегата, обычно принимаемом за начало координат при расчете виброзащитной системы (координаты центра тяжести агрегата определяются по формулам:
(17.1)
где Qi — вес i-того элемента агрегата; xi, yi, zi, — координаты центра тяжести i-того элемента агрегата в системе координат X, Y, Z; п— число элементов агрегата);
- о моментах инерции агрегата относительно k-ой оси системы координат;
- о воздействующей вибрации (ее частоте и амплитуде в направлении k-ой оси системы координат);
в) характеристика различных подводок (трубопроводов, кабелей и т.д. - их назначение, материал, форма, размеры и др.) с указанием мест их присоединения к объекту;
г) требования, предъявляемые к виброизоляции:
- допускаемые амплитуды перемещения и ускорения защищаемого объекта (допускаемое перемещение связано обычно с возможностью разрыва подведенных к объекту трубопроводов и кабелей, с возможностью удара защищаемого объекта о соседние конструкции, с точностью работы агрегата; допускаемое ускорение обычно связано с тем, какие инерционные нагрузки может выдержать объект, не теряя работоспособности);
- эффективность виброзащиты на рабочей частоте, определяемая коэффициентом передачи вибрации (где - амплитуда перемещения защищаемого объекта в направлении k-ой оси);
д) сведения о возможности воздействия на виброизоляторы различных агрессивных веществ (топлива, масла и т. п.) и температуре в местах установки виброизоляторов;
е) требуемый ресурс виброзащитной системы.
17.2. Расчет характеристик виброзащитной системы
Виброизолятор, как любое упругое тело, при деформации несет потенциальную энергию деформирования П. В виброизоляторе также, как правило, существует трение, благодаря которому рассеивается энергия колебаний. При колебаниях направление деформирования виброизолятора меняется, при этом изменяется также направление силы трения, поэтому в координатах «перемещение - реакция виброизолятора » процесс нагрузки виброизолятора не совпадает с процессом его разгрузки. Эти процессы вместе образуют петлю гистерезиса виброизолятора, площадь которой равна энергии, рассеиваемой за один цикл деформации виброизолятора (рис. 17.1).
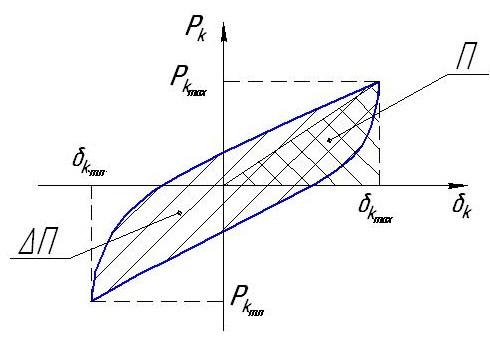
Рис. 17.1. Петля гистерезиса виброизолятора
По петле гистерезиса легко определить экспериментально коэффициент рассеивания энергии виброизолятора
. (17.2)
Рассмотрим случай возбуждения колебаний в направлении k-ой оси переменной гармонической силой с амплитудой и частотой («силовое» возбуждение). В этом случае дифференциальное уравнение движения линейной виброзащитной системы имеет вид
(17.3)
Здесь - жесткость системы, - перемещение, - коэффициент демпфирования, все параметры в направлении k-ой оси, t - время. Это уравнение можно преобразовать в вид
, (17.4)
где , и - частота собственных колебаний системы.
Общее решение этого уравнения имеет вид
,
где - сдвиг фазы колебаний системы относительно колебаний внешней силы. Первые два слагаемых описывают свободные колебания системы, которые быстро прекращаются вследствие действия трения. Подставим в уравнение (17.4) только третье слагаемое решения, описывающее вынужденные колебания. Заменим также
. Получим
(17.5).
Это уравнение должно выполняться при любом значении t. Поэтому коэффициенты при и должны быть равны между собой.
и (17.6).
Возведем оба уравнения (17.6) в квадрат и сложим.
,
отсюда амплитуда вынужденных колебаний
. (17.7)
Если учесть , получим
. (17.8)
Если , то . Это случай статической деформации.
Амплитуда колебаний максимальна при . В этом случае амплитуда колебаний равна . Это случай резонанса. Величину
называют коэффициентом демпфирования.
Коэффициент усиления колебаний на резонансе
. (17.9)
Коэффициент передачи вибрации на любой частоте
. (17.10)
Максимальное ускорение при резонансе
. (17.11)
В случае, если источником колебаний является перемещение основания с амплитудой («кинематическое» возбуждение колебаний), уравнение (17.3) принимает вид
, (17.12)
где
(17.13)
- перемещение центра масс системы в абсолютных координатах ( в этом случае – относительное перемещение). После дифференцирования и деления на m уравнение (17.12) принимает вид
(17.14).
Решение аналогично (17.4). С учетом (17.13) амплитуда деформации виброизолятора
, (17.15)
откуда коэффициент передачи вибрации
. (17.16)
На резонансе амплитуда деформации равна
. (17.17)
Амплитуда абсолютного ускорения на резонансе
. (17.18)
Резонансная частота виброзащитной системы с учетом демпфирования равна
. (17.19)
Из (17.14) – (17.18) видно, что отличие «силового» и «кинематического» возбуждения связано с величиной . Для большинства виброзащитных систем < 0.1, поэтому различие результатов невелико.
Линейная система имеет петлю гистерезиса в виде эллипса. Петли гистерезиса многих виброизоляторов (особенно сухого трения) имеют другую форму. Чтобы иметь возможность использовать для расчета таких систем уравнения (17.3) или (17.14), применяется линеаризация – определяется эквивалентный коэффициент демпфирования , при котором площадь петли гистерезиса виброизолятора равна площади эллиптической петли с такими же амплитудой деформации и .
При подстановке в (17.3) решения видно, что максимальная сила трения равна . Площадь эллиптической петли гистерезиса с амплитудой деформации в этом случае равна .
Потенциальная энергия деформированного до амплитуды упругого тела равна
. В таком случае коэффициент рассеивания энергии
.
Значение коэффициента рассеивания энергии любого виброизолятора можно определить по его петле гистерезиса по уравнению (17.2). Тогда эквивалентный коэффициент демпфирования
(17.20)
Поскольку , то . В случае резонанса ()
и амплитуда колебаний равна.
Если агрегат установлен на n виброизоляторов, вместо следует использовать суммарную жесткость виброзащитной системы в направлении k-ой оси , где - жесткость i-того виброизолятора в направлении этой же оси.
Если пренебречь трением, коэффициент передачи вибрации на частоте равен
. (17.21)
Видно, что ослабление вибрации () происходит в случае и будет тем больше, чем больше различие и . Диапазон частот после называется диапазоном вибрационной защиты. Однако чрезмерное уменьшение для его увеличения (т.е. суммарной жесткости виброзащитной системы) недопустимо, так как мягкая виброзащитная система будет иметь амплитуду колебаний на резонансе, превышающую предельно допустимую. Чрезмерной будет и деформация системы под действием статической нагрузки . Поскольку , получаем . Так, например, чтобы обеспечить собственную частоту объекта 10 Гц, необходимо разместить его на виброизоляторах такой жесткости, чтобы их статическое перемещение составляло 2,5 мм. При собственной частоте 5 Гц статическое перемещение виброизоляторов будет составлять 10 мм, а для собственной частоты объекта в 1 Гц необходимы виброизоляторы с перемещением 250 мм, что невозможно по соображениям как компоновки агрегатов, так и конструкции виброизоляторов.
Из анализа уравнения (17.10) для коэффициента передачи вибрации с учетом трения видно, что при слишком больших значениях ослабление виброизолятором вибрации в диапазоне вибрационной защиты очень мало, и виброзащитная система неэффективна. Но при слишком малых значениях будет велика амплитуда колебаний виброзащитной системы на резонансе, и защищаемый агрегат может выйти из строя при прохождении резонанса.
Силы трения целесообразно учитывать, если выполняется условие
0,05 . (17.22)
Жесткость виброизолятора может быть так же, как и коэффициент рассеивания энергии, экспериментально определена по петле гистерезиса. Если максимальная и минимальная деформация виброизолятора в направлении k-ой оси и , максимальная и минимальная реакция и соответственно (рис. 17.1), то
. (17.23)
Поскольку жесткость и коэффициент рассеивания энергии виброизолятора зависят от формы петли гистерезиса, они в общем случае нелинейных характеристик виброизолятора зависят от амплитуды деформации виброизолятора и от деформации виброизолятора под действием статической нагрузки.
17.3. Оптимальное размещение виброизоляторов
При поступательном перемещении основания, возбуждающем колебания агрегата, агрегат может совершать также и вращательные колебания. Приближенную оценку наибольших амплитуд колебаний виброизолированного объекта в какой-либо i-ой точке можно производить по формулам:
(17.24)
(17.25)
(17.26)
где x0i, y0i, z0i координаты i-ой точки в системе осей Х0, Y0, Z0 с началом в центре тяжести установки, a0x, a0y, a0z – амплитуды поступательного перемещения центра тяжести агрегата в направлении соответствующих осей, , , - амплитуды вращательных колебаний агрегата вокруг соответствующих осей. Видно, что в точках, удаленных от центра тяжести агрегата, амплитуды колебаний могут быть велики, что может повести к разрыву подведенных к агрегату трубопроводов и кабелей, удару агрегата о соседние конструкции. Ресурс виброизоляторов также снижается при больших амплитудах деформации. Поэтому оптимальным является такое размещение виброизоляторов, при котором вращательные колебания отсутствуют.
Если агрегат, установленный на n виброизоляторов, совершает поступательные колебания в направлении оси Z с амплитудой a0z, то в i-ом виброизоляторе возникает реакция Czi a0z, которые ведут к появлению момента вокруг оси Х, равного yviCzi a0z, где yvi – координата точки крепления i-ого виброизолятора (рис. 17.2).
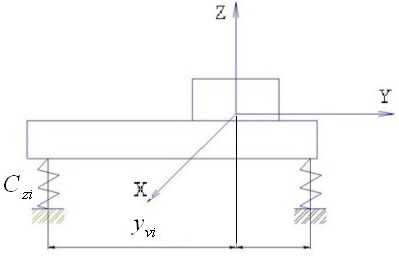
Рис. 17.2. Определение условий отсутствия вращательных колебаний
Для того, чтобы вращательные колебания вокруг оси Х отсутствовали, сумма моментов должна быть равна нулю, то есть , или, сократив на одинаковый сомножитель a0z ,
. (17.27)
Из условия равенства нулю моментов относительно оси Y получаем
. (17.28)
Если рассмотреть поступательные колебания агрегата в направлении оси Х, получим условие
. (17.29)
Если рассмотреть поступательные колебания агрегата в направлении оси Y, получим условие
. (17.30)
Условия (17.27) – (17.30) определяют оптимальное размещение виброизоляторов. Точка, относительно которой они выполняются, называется центром жесткости виброзащитной системы. Для отсутствия вращательных колебаний стремятся совместить центр жесткости с центром масс агрегата, или хотя бы расположить центр жесткости и центр масс на одной прямой, вдоль которой действует возбуждающая вибрация.
Исходя из этого, можно рассмотреть различные схемы размещения виброизоляторов на защищаемом объекте (рис. 17.3).
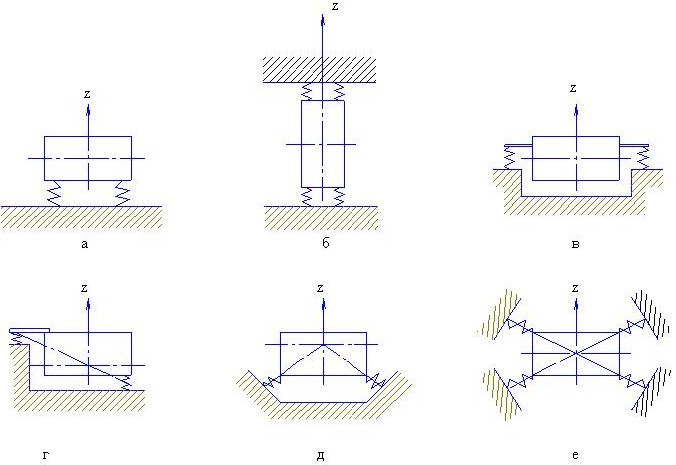
Рис. 17.3. Различные схемы размещения виброизоляторов
Схема (а) проста для монтажа, но неоптимальна при воздействии вибрации в боковом направлении. В схеме (б) центр масс совмещен с центром жесткости, но для этого требуется дополнительная плоскость размещения виброизоляторов, что увеличивает вес системы. Недостаток схемы (в) – увеличение габаритов виброзащитной системы в ширину. При размещении виброизоляторов по схеме (г) вращательные колебания будут отсутствовать, но агрегат будет иметь перекос в статическом состоянии. Схемы (д) и (е) очень хорошо уравновешены, но требуются специальные наклонные кронштейны для монтажа виброизоляторов.
Виброизоляторы, кроме того, следует располагать так, чтобы был удобен их монтаж и замена, а также была бы возможность наблюдения за их состоянием в процессе эксплуатации. Для этого необходимо предусмотреть зазоры или проходы, обеспечивающие доступ ко всем виброизоляторам.
17.4. Конструкции виброизоляторов для агрегатов ГТД
Известно большое количество типов виброизоляторов, каждый из которых обладает своими преимуществами и недостатками.
1. Стальные пружины. Обладают значительной прочностью, невысокой стоимостью, их характеристики линейны, что упрощает расчет виброзащитной системы. Однако они обладают слишком низким рассеиванием энергии колебаний – коэффициент передачи на резонансе достигает 100 и более, что может повести к разрушению оборудования при переходе через резонанс.
2. Эластомерные виброизоляторы. Стоимость их невысока, рассеивание энергии колебаний связано с внутренним трением в материале (резина, иные полимеры) и существенно больше, чем в пружинах (коэффициент передачи на резонансе около 10 или менее), вес существенно меньше, чем у стальных виброизоляторов. Но они обладают низкой способностью выдерживать воздействие окружающей среды (высокие и низкие температуры, масло, топливо, кислоты, вакуум, радиация, свет и т.д.), недостаточной прочностью.
3. Гидравлические и пневматические виброизоляторы и демпферы. Обладают высокой нагрузочной способностью (десятки и сотни тонн, например, амортизаторы, гасящие удар самолета при посадке). Рассеивание энергии колебаний связано в них с протеканием жидкости или газа через малые отверстия с высоким гидравлическим сопротивлением. Оно достаточно велико (коэффициент передачи на резонансе может быть не более 3). Однако конструкция таких виброизоляторов сложна, они часто нуждаются для своей работы в сложных системах, обеспечивающих давление жидкости или газа (насосы, фильтры и т.д.), а также чувствительны к засорению рабочих органов. Их характеристики зависят от частоты колебаний (для гидравлических виброизоляторов) или от квадрата частоты колебаний (для пневматических виброизоляторов), что затрудняет расчет виброзащитной системы.
4. Виброизоляторы сухого трения, как правило, цельнометаллические (пластинчатые, тросовые, из прессованной проволочной сетки, в частности, разработанного в КуАИ/СГАУ проволочного материала МР). Рассеивание энергии колебаний связано в них с внешним трением элементов конструкции друг о друга. Они обладают очень высоким рассеиванием энергии (коэффициент передачи на резонансе до 1,5), высокой прочностью и стойкостью к воздействию окружающей среды. Но технология изготовления этих виброизоляторов сложнее, что определяет их более высокую стоимость. Характеристики их нелинейны, что затрудняет расчет виброзащитной системы.
Исходя из вышеизложенного, для защиты неприводных агрегатов применяются, как правило, виброизоляторы сухого трения в зоне высоких температур и воздействия топлива и масла, и виброизоляторы на основе эластомеров там, где это позволяет температура и отсутствие агрессивной среды.
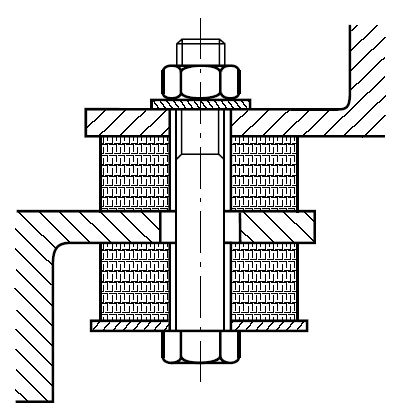
Виброизоляторы могут иметь различную форму упругодемпфирующих элементов. На рис. 17.4 приведены виброизоляторы с упругодемпфирующим элементом втулочного типа – бескорпусной (а) и корпусной (б). К втулочным виброизоляторам относятся, например, виброизоляторы из материала МР типа ВВ, ВП. На рис. 17.5 приведены виброизоляторы с упругодемпфирующим элементом кольцевого типа (АМГ, АК). На рис. 17.6 - виброизоляторы с упругодемпфирующим элементом колокольчикового типа (ДКА, ДКУ). В качестве упругодемпфирующего элемента может применяться трос (рис. 17.7).
а б
Рис. 17.4. Виброизоляторы втулочного типа: а – бескорпусной, б - корпусной
а б
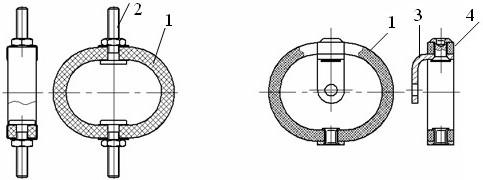
Рис. 17.5. Виброизоляторы втулочного типа: АМГ (а) и АК (б):
1 – упругодемпфирующий элемент, 2 – болт, 3 – кронштейн, 4 - заклепка
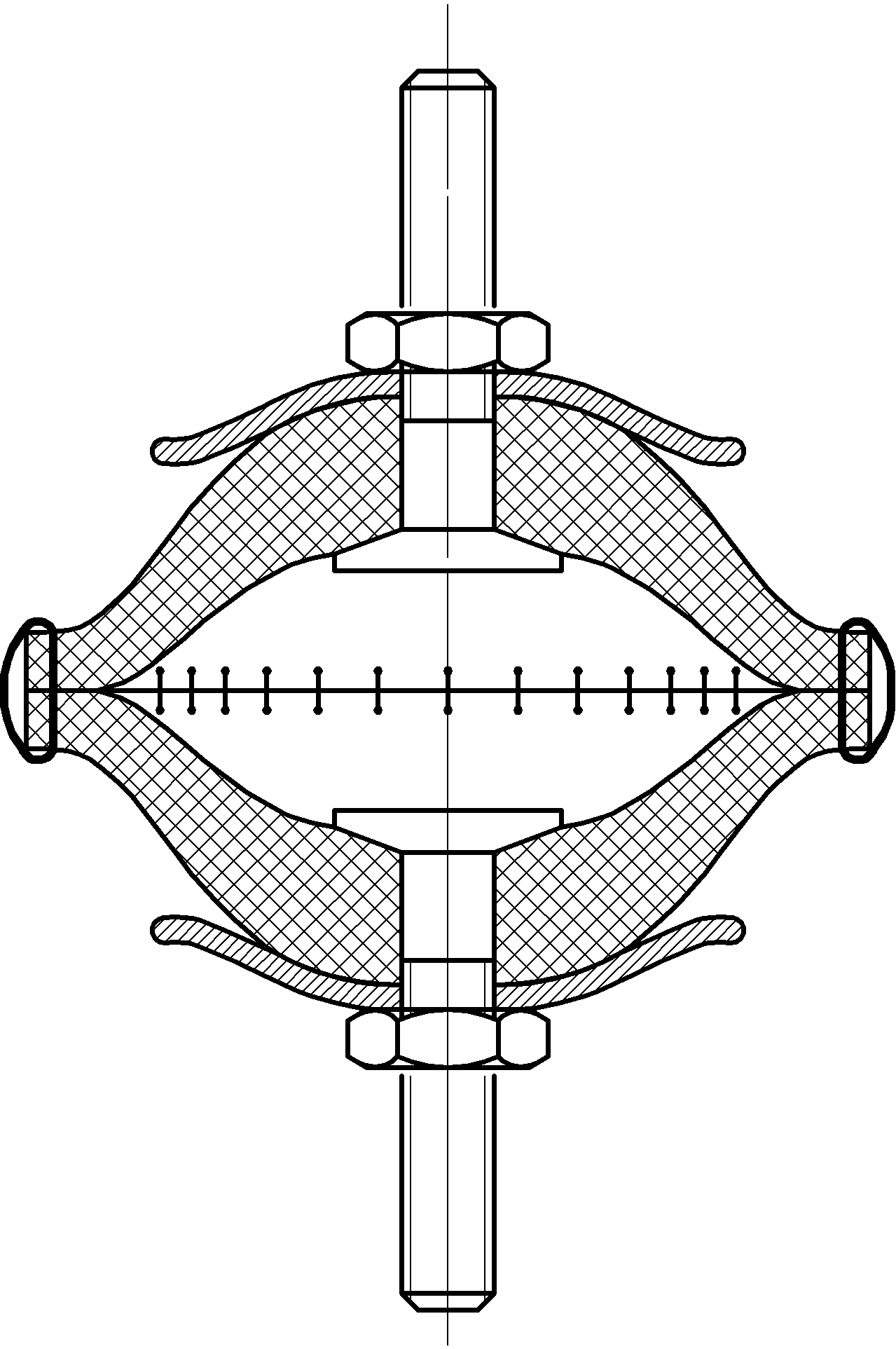
Рис. 17.6. Виброизолятор колокольчикового типа
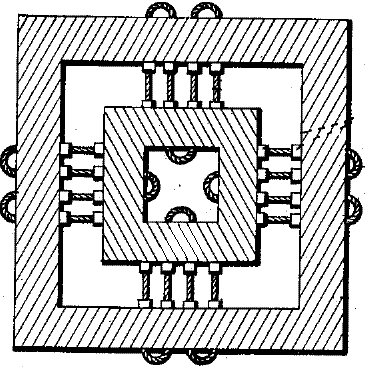
Рис. 17.7. Тросовые виброизоляторы
Виброизолятор может иметь упругодемпфирующий элемент из эластомера или прессованной проволоки, и одновременно пружину для дополнительной жесткости (рис. 17.8).

Рис. 17.8. Виброизолятор втулочного типа с пружиной
На рис. 17.9, 17.10, 17.11 приведены некоторые виброизоляторы с упругодемпфирующими элементами из резины (типов АКСС, АР, АРМ).
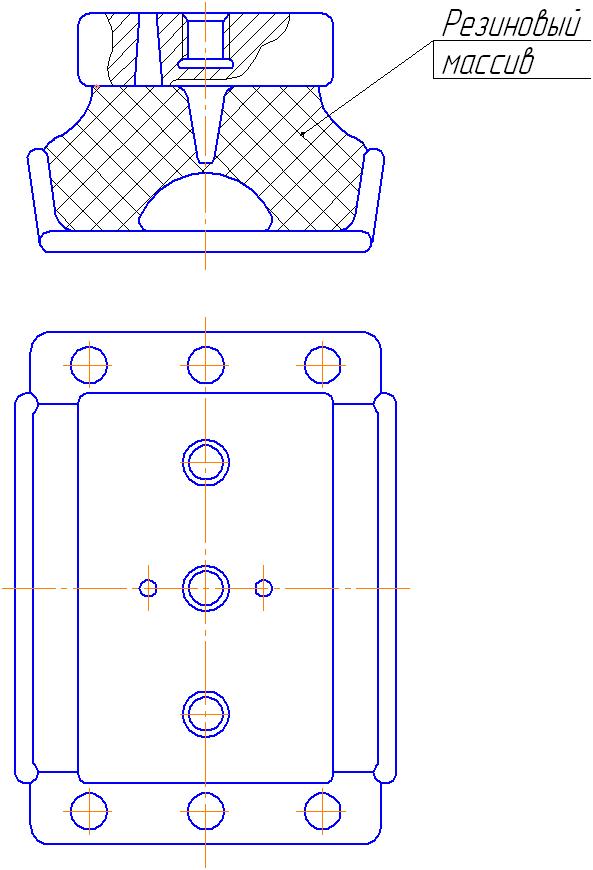
Рис. 17.9. Виброизолятор типа АКСС Рис. 17.10. Виброизолятор типа АР
Рис. 17.11. Виброизолятор типа АРМ
17.5. Защита от случайной вибрации
Во многих случаях действующая на объект сила изменяется не по гармоническому закону, а случайно. Один из примеров этого – вибрация при транспортировке (неровности дороги расположены случайно и имеют случайную высоту). Другой пример – наложение очень большого количества возбуждающих колебания сил, каждая из которых изменяется по своему сложному закону.
Ускорение не может служить характеристикой случайной вибрации, так как его математическое ожидание для случайного процесса равно нулю (рис. 17.12).
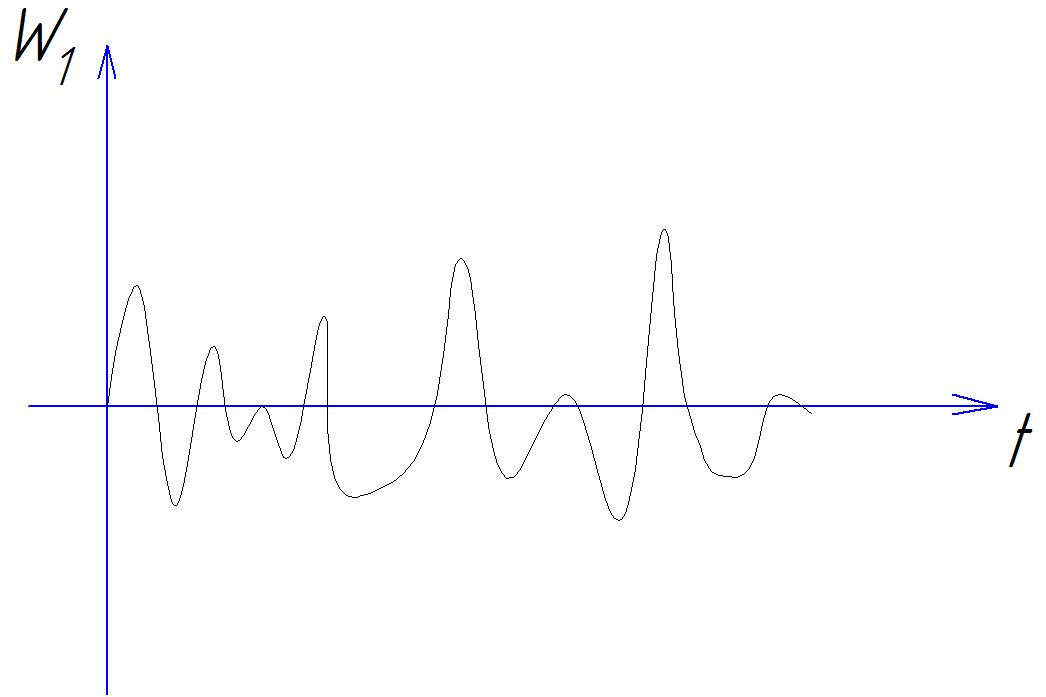
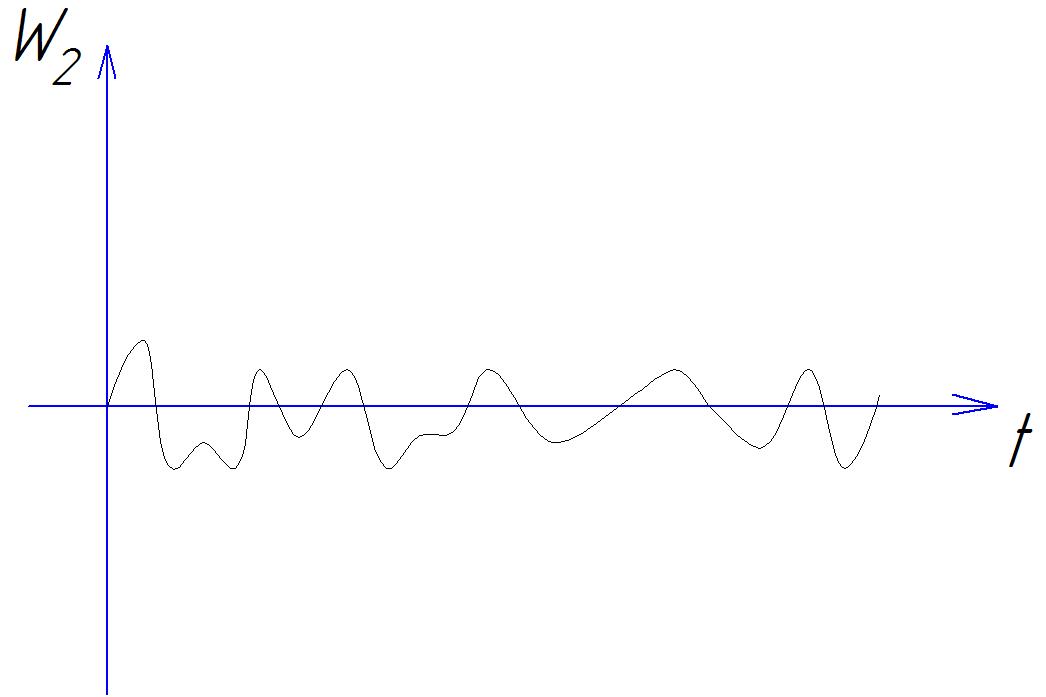
Рис. 17.12. Случайное воздействие с различной амплитудой
В качестве характеристики случайной вибрации применяется квадрат ускорения, отнесенный к ширине частотного диапазона, в котором задана случайная вибрация (рис. 17.13). Эта величина называется спектральной плотностью случайной вибрации и измеряется в величинах .
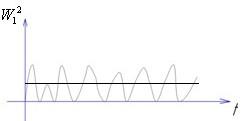

Рис. 17.13. Средние квадратичные значения случайного воздействия
Среднее значение ускорения, действующего на защищаемый объект,
,
среднее значение перемещения защищаемого объекта
.
Максимальное перемещение с доверительной вероятностью 0,95 равно , максимальное ускорение защищаемого объекта . По найденному максимальному значению ускорения определяется максимальная инерционная нагрузка на защищаемое оборудование, и сравнивается с допустимой. Значение максимального перемещения позволяет оценить целостность подведенных к объекту трубопроводов и кабелей, отсутствие ударов защищаемого оборудования о соседние конструкции. По среднему значению ускорения оценивается комфортность подвески для человека.
18. СИСТЕМЫ ЗАЩИТЫ ОТ УДАРА
Ударом в технике называют кинематическое или силовое возмущение относительно большой интенсивности и относительно малой продолжительности. При кинематическом возмущении удар определяется законом изменения ускорения основания w, на котором расположен защищаемый объект, от времени t.
Наибольшее значение имеют максимальное ускорение основания , время удара и полный импульс ударного воздействия на тело с массой m
. (18.1)
Для упрощения при расчетах форму ударного импульса рассматривают как прямоугольную, треугольную, полусинусоидаль-ную, пилообразную и т.д. (рис.18.1).
В некоторых случаях рассматривают длительность удара на уровне , понимая под этим промежуток времени длительностью , при котором .
Расчетная модель системы защиты от удара с одной степенью свободы состоит из тела, движущегося вдоль оси Х, виброизолятора, создающего силу , и основания. При силовом возмущении внешняя сила приложена к телу в направлении оси Х, основание при этом считается неподвижным и является объектом защиты.
1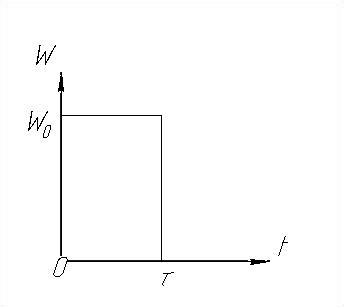 2
2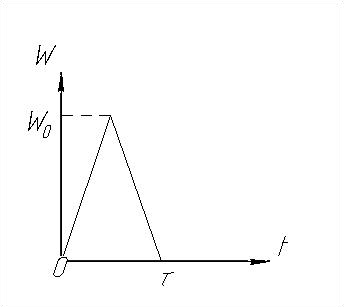
3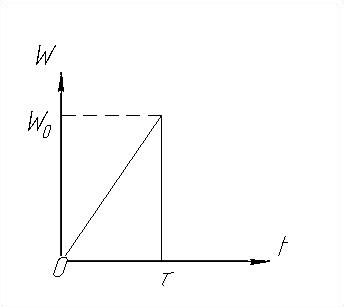 4
4
Рис.18.1. Формы ударного импульса. 1 – прямоугольная, 2 – треугольная, 3 – пилообразная, 4 – полусинусоидальная
Уравнение движения тела при этом имеет вид
, (18.2)
где , , – абсолютная координата тела.
При кинематическом возмущении основание движется по закону , объектом защиты от удара является тело, которое подвергается воздействию со стороны виброизолятора, создающего силу , где – относительная координата тела. Уравнение движения тела при этом имеет вид
, (18.3)
где . Уравнения (18.2) и (18.3) совпадают с точностью до обозначений, поэтому расчет силового и кинематического ударного возбуждения одинаков.
Рассмотрим вначале простейшую линейную модель системы защиты от удара с виброизолятором с постоянной жесткостью k (рис.2). Поскольку длительность удара мала, предположим, что его энергия почти не успевает рассеяться в виброизоляторе, и демпфированием можно пренебречь. В таком случае уравнение движения имеет вид
, (18.4)
где – собственная частота системы.
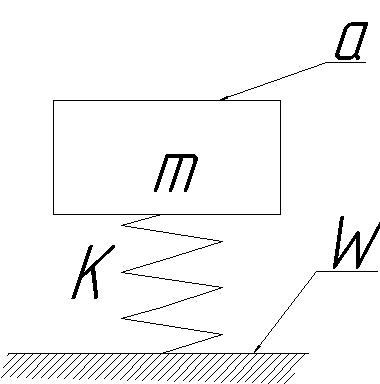
Рис.18.2. Линейная модель системы защиты от удара.
Движение такой системы после воздействия мгновенного импульса в момент происходит согласно уравнению
.
При начальных условиях , , это уравнение принимает вид . Рассматривая воздействие на систему как серию импульсов , приходим к интегралу
(18.5a)
при или
(18.5b)
при (в этом случае действие удара уже прекратилось и система совершает свободные колебания).
Из (18.4) абсолютное ускорение защищаемого объекта
(18.6)
Поскольку основная цель расчета на удар состоит в определении максимальных абсолютного ускорения и относительного перемещения защищаемого объекта, соотношения (18.5) и (18.6) удобно представить в виде:
, (18.7)
, (18.8)
где , ,
, .
При
, , , .
В соответствии с (18.7) и (18.8), процессы и можно рассматривать как модулированные по амплитуде колебания с частотой , причем функции и можно рассматривать как огибающие. Наибольшие значения перемещения и ускорения не могут быть больше их.
Зависимости ускорений основания и защищаемого объекта от времени показаны на рис. 3. Пусть в момент отклонение объекта наибольшее. Если , удар называется коротким, в противном случае – длинным.
Рис.18.3. Зависимости ускорений основания и защищаемого объекта от времени
Для простейшего случая удара с постоянным ускорением (ударный импульс прямоугольной формы) получаем решение:
. (18.9)
Наибольшее значение перемещения объекта в этом случае
, (18.10)
ускорение защищаемого объекта равно
. (18.11)
Видно, что эффективность защиты от удара зависит от значения безразмерного параметра (или , где Т – период собственных колебаний системы). Коэффициент передачи удара
. (18.12)
Защита от удара () обеспечивается при .
Приведем решения для некоторых других простейших форм ударного импульса:
Полусинусоидальная форма:
при ; (18.13a)
при
(18.13b)
Треугольная форма:
при ; (18.14a)
при; (18.14b)
при . (18.14c)
Уменьшение параметра необходимо и в этих случаях. В частности, из (18.13a) можно получить, что для защиты от короткого удара полусинусоидальной формы требуется
.
Наибольшее возможное значение коэффициента передачи удара для линейной системы при ударе прямоугольной формы можно получить из (18.11). Поскольку прямоугольная форма удара имеет наибольшее значение импульса S, для всех других форм удара наибольшее возможное значение коэффициента передачи удара меньше. Так, для пилообразной формы , для полусинусоидальной формы .
Рассеивание энергии несколько уменьшает значение. Коэффициент передачи удара с учетом демпфирования можно оценить:
, (18.15)
где – коэффициент рассеивания энергии.
Ударным спектром системы называют зависимость коэффициента передачи удара от отношения длительности удара к периоду собственных колебаний системы (или, что то же самое, от произведения длительности удара на собственную частоту системы).
На рис. 18.4 приведен ударный спектр линейной демпфированной системы при ударе полусинусоидальной формы. Он получен при помощи уравнений (18.13) с учетом (18.15).
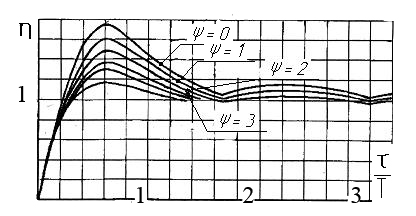
Рис.18.4. Ударный спектр линейной демпфированной системы защиты от удара
при ударе полусинусоидальной формы
Нагрузочные характеристики P(x) (где P – сила, x – перемещение) виброизоляторов, применяемых в системах защиты от удара (в частности, из материала МР), часто существенно нелинейны. Различают жесткую нелинейную характеристику, в которой сила увеличивается больше, чем в линейной, и мягкую нелинейную характеристику, в которой сила увеличивается меньше, чем в линейной (рис.18.5).
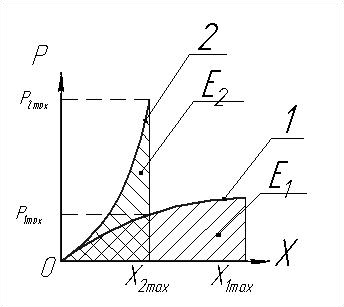
Рис.18.5. Мягкая (1) и жесткая (2) нелинейные характеристики виброизолятора
Допуская, что время удара мало, и пренебрегая демпфированием, получаем, что скорость объекта после удара равна
. (18.16)
Кинетическая энергия, вносимая ударом в систему
. (18.17)
Эта энергия равна потенциальной энергии деформирования виброизолятора . Если максимальные деформации виброизоляторов с мягкой и жесткой характеристикой равны и , а максимальные их реакции, соответственно, и (см. рис.18.5), то площади и должны быть одинаковы и равны K.
Метод расчета воздействия удара на систему с нелинейными виброизоляторами ясен из рис.18.5. По уравнениям (18.16) и (18.17) рассчитывается значение энергии удара. Далее с последовательным увеличением x численно интегрируется площадь под нагрузочной характеристикой виброизолятора. Равенство интеграла значению K означает, что получены значения и . Наибольшее ускорение защищаемого объекта
.
Характеристика виброизолятора может быть несимметричной (как, например, у виброизоляторов из МР типов ДК, ДКУ, АК, АМГ) (см. рис.17.5, 17.6). В таком случае необходимо интегрировать как участок сжатия, так и участок растяжения виброизолятора. Возможно, что значенияи будут достигнуты порознь при деформации виброизолятора в разных направлениях.
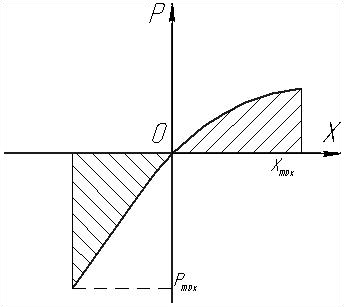
Рис.18.6. Несимметричная характеристика системы защиты от удара
Упругие опоры объекта, как правило, используются для защиты не только от удара, но и от вибрации. Поскольку перемещения при вибрации значительно меньше, чем при ударе, жесткость системы в диапазоне малых деформаций может быть выбрана оптимальной для защиты от вибрации и равной, а в диапазоне больших деформаций – оптимальной для защиты от удара (рис.18.7).

Рис.18.7. Билинейная характеристика системы защиты от удара
Уравнение для такой билинейной системы может быть получено для прямоугольного удара из условия равенства энергии удара K площади под нагрузочной характеристикой системы.
.
После расчета необходимо оценить период собственных колебаний системы . Поскольку момент достижения максимальных ускорения и перемещения , если , удар является длинным, допущение о малости времени его действия не выполняется и вышеизложенный расчет некорректен.
Если удар является длинным, рассматривать его как мгновенный импульс, вносящий энергию в систему, нельзя. Более корректным будет замена импульсом прямоугольной формы той же площади, той же длительности и интенсивности .
Под действием квазипостоянного ускорения система получает квазистатическое перемещение , рассчитываемое при помощи нагрузочной характеристики:
Относительно нового положения равновесия (;) система совершает свободные колебания (рис. 18.8, а, б). Их энергия равна
Пренебрегая рассеиванием энергии, получаем, что такова же энергия системы при колебании в противоположную сторону
Это уравнение решается численным интегрированием для определения и .
а б
Рис.18.8. Воздействие длинного удара на нелинейную систему:
а – в координатах (t; P), б – в координатах (x; P)
19. РАСЧЕТ НЕПРОБИВАЕМОСТИ КОРПУСОВ
При разрушении элементов ротора последствия вторичных разрушений могут быть более опасными для самолета, чем первичное разрушение. Защита фюзеляжа от фрагментов разрушения ротора осуществляется постановкой бронезащиты.
Толщина бронезащиты определяется из условия равенства кинетической энергии фрагментов разрушения и работы, необходимой для разрушения защиты:
Wк = Ln . (19.1).
Кинетическая энергия оборвавшегося фрагмента разрушения определяется по формуле:
, (19.2)
где m - масса фрагмента разрушения ротора;
- частота вращения ротора;
R - радиус центра масс.
Работа, необходимая для разрушения изотропной металлической преграды может быть определена по формуле:
L = l h2 ср (к + n ), (19.3)
где l - периметр фрагмента разрушения, соприкасающийся с преградой;
h - толщина преграды (бронезащиты);
ср = 0.65 в - динамический предел сопротивления срезу;
- коэффициент увеличения прочности материала при ударе (для скоростей вращения роторов ГТД = 1.3);
в - предел прочности материала бронезащиты;
к 2,5 - эмпирический коэффициент, учитывающий работу, затраченную на изгиб оболочки защиты;
n = 2/3 - эмпирический коэффициент, учитывающий работу, затраченную на срез оболочки;
Из (19.2) и (19.3) следует, что толщина изотропной металлической бронезащиты может быть определена по формуле:
Из проведенных экспериментов следует, что фрагменты разрушения могут разлетаться под углом 150 от плоскости вращения. Поэтому ширину бронезащиты определяют как: S = 2Dtg150, где D - расстояние от центра масс фрагмента разрушения до бронезащиты.
Для лопаток с бандажной полкой при попадании посторонних предметов в двигатель наиболее вероятно разрушение надполочной части лопаток. Поэтому в таких случаях часто толщину бронезащиты устанавливают только из условия удержания надполочной части лопатки.
Пример расчета толщины кольцевой бронезащиты из титанового сплава ВТ-20 от обрыва части лопастей вентилятора над бандажной полкой приведен в табл. 19.1.
Таблица 19.1.
|
Ступень вентилятора |
1 |
2 |
3 |
|
Максимально возможная частота вращения ротора в эксплуатации, n, об/мин |
5430 |
5430 |
5430 |
|
Максимально возможная частота вращения ротора в эксплуатации, =(n/30), c-1 |
568,6 |
568,6 |
568,6 |
|
Масса надполочной части лопатки, m, кг |
0,411 |
0,153 |
0,118 |
|
Радиус центра масс надполочной части лопаток, Rц.м., м |
0,643 |
0,617 |
0,589 |
|
Кинетическая энергия надполочной части лопатки, Ек, Дж |
77459 |
35860 |
23076 |
|
Центробежная сила надполочной части лопатки, С, Н |
85112 |
30411 |
22406 |
|
Центробежная сила всей лопатки, С, Н |
318442 |
139312 |
92940 |
|
Толщина бронезащиты для удержания надполочной части лопатки, h, мм |
8,9 |
4,8 |
4.8 |
20. ОСНОВЫ ВИБРОДИАГНОСТИКИ
Вибродиагностика – это определение состояния двигателя по его вибрации. Преимущества вибродиагностики – своевременное обнаружение дефекта (до того, как он приведет к отказу двигателя), возможность узнавать о состоянии двигателя непосредственно при его эксплуатации, а не при разборке на заводе. Применение вибродиагностики позволило перейти от эксплуатации двигателей по ресурсу к эксплуатации по техническому состоянию. При эксплуатации по ресурсу двигатель после исчерпания назначенного ресурса необходимо было снять с самолета, отправить на завод, разобрать, осмотреть – и в большинстве случаев убедиться в том, что двигатель работоспособен, и все эти операции являются излишними. При эксплуатации по техническому состоянию известно состояние данного конкретного двигателя на самолете – может ли он далее безопасно эксплуатироваться или нуждается в ремонте.
Вибрационный сигнал от двигателя можно подвергнуть гармоническому анализу (разложению по частотам ) и получить спектр вибрации двигателя (рис. 20.1).
Рис. 20.1. Спектр вибрации двигателя
Эталонный спектр вибрации – это спектр исправного двигателя. С ним сравнивается спектр вибрации данного конкретного двигателя. Некоторые дефекты (например, развитие трещин) могут повести к уменьшению вибрации, поэтому внезапное уменьшение уровня вибрации также является опасным. На первых этапах вибродиагностики в качестве критерия уровня вибрации использовалось среднеквадратичное значение амплитуд вибрации. Если эта величина изменялась на 20 % за один полет или на 40 % за три полета (неважно – в сторону увеличения или уменьшения), считалось, что двигатель следует вывести из эксплуатации.
Современное компьютерное оборудование позволяет сравнивать непосредственно спектры вибраций и определять, какое отклонение от эталонного является допустимым, а какое недопустимо. Если в базе данных есть спектры вибрации двигателей с известными дефектами, по спектру вибрации данного конкретного двигателя можно предположить, какой именно дефект развивается в этом двигателе.
По вибрации обнаруживаются отказы в самых важных узлах двигателя – турбокомпрессоре, трансмиссиях, форсажной камере.
Система эксплуатации двигателя по техническому состоянию, кроме вибродиагностики, должна включать систему осмотра внутренних частей двигателя (в первую очередь лопаток, дисков и жаровых труб) при помощи авиаскопов, системы контроля давления и температуры в различных сечениях газового потока (причем должно контролироваться не только значение величины, но и его равномерность в различных точках сечения), системы контроля температуры масла и стружки в масле, системы контроля температуры подшипников и так далее.
Учебное издание
Уланов Александр Михайлович
ВИБРАЦИЯ И ПРОЧНОСТЬ АВИАЦИОННЫХ ДВИГАТЕЛЕЙ
И ЭНЕРГЕТИЧЕСКИХ УСТАНОВОК
Учебное пособие
Редактор
Доверстка
Подписано в печать . Формат 60х84 1/16.
Бумага офсетная. Печать офсетная.
Печ. л. .
Тираж экз. Заказ ___ ____ . Арт. С - /2011
Самарский государственный
аэрокосмический университет.
443086 Самара, Московское шоссе, 34.
_____________________________________________________________
Изд-во Самарского государственного
аэрокосмического университета.
443086 Самара, Московское шоссе, 34.
max
К=6 ( = 0.5)
а
b
А