Инженерная геодезия, Т.Е. Миркина
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Южно-Уральский государственный университет
Кафедра «Градостроительство»
528(07)
М636
Т.Е. Миркина
инженернАЯ геодезиЯ
Учебное пособие
Челябинск
Издательство ЮУрГУ
2007
УДК 528.48 (076.5) + 528,4 (075.8)
М636
Одобрено
учебно-методической комиссией
архитектурно-строительного факультета.
Рецензенты:
Рецензенты: Проценко Г.Г., Игнатьев В.Ф.
|
М636 |
Миркина, Т.Е. Инженерная геодезия: учебное пособие. Конспект лекций для студентов I курса специальности 270115 «Экспертиза и оценка недвижимости» /Т.Е. Миркина. Че лябинск: Изд. ЮУрГУ, 2007. 96 с. |
|
ISBN Пособие составлено в соответствии с учебным планом и рабочей про граммой для специальности 270115 при изучении дисциплины “Инженерная геоде зия”, и является помощью студентам и преподавателям в части подготовки к лекционному и лабораторно-практическому курсам, а также к зачетам по дисциплине. УДК 528.48 (076.5) + 528,4(075,8) |
ISBN © Издательство ЮУрГУ, 2007
Оглавление
Тема 1. Введение……………………………………………………………………… 5
1.1. Предмет и задачи геодезии……………………………………………………. 5
1.2. Общие сведения о форме и размерах Земли…………………………………. 6
1.3. Математические модели поверхности Земли, применяемые в геодезии…… 7
Тема 2. Системы координат
2.1. Система географических (астрономических) координат……………………. 9
2.2. Система геодезических координат……………………………………………. 9
2.3. Прямоугольная система координат Гаусса – Крюгера………………………10
Тема 3. Ориентирование……………………………………………………………… 12
3.1. Ориентирование линий в геодезии…………………………………………… 12
3.2. Прямая и обратная геодезические задачи. Их применение в геодезическом
производстве……………………………………………………………………………16
Тема 4. Масштабы. Сведения из теории погрешностей
4.1. Масштабы……………………………………………………………………… 18
4.2. Основы математической обработки геодезических измерений…………… 20
Тема 5. Топографические карты и планы
5.1. Геодезические планы, карты………………………………………………… 22
5.2. Условные знаки на планах, картах, геодезических
и строительных чертежах……………………………………………………………. 22
5.3. Номенклатура топографических планов и карт…………………………… 24
5.4. Понятие о рельефе местности……………………………………………….. 35
5.5. Задачи, решаемые по карте…………………………………………………… 40
Тема 6. Плановые и высотные геодезические сети………………………………… 42
6.1. Плановая геодезическая сеть………………………………………………… 42
6.2. Высотная геодезическая сеть………………………………………………… 44
Тема 7. Линейные измерения………………………………………………………… 46
7.1. Приборы для измерения расстояний………………………………………… 46
7.2. Измерение линий лентой……………………………………………………. 46
7.3. Измерения расстояния нитяным дальномером…………………………….. 47
7.4. Дальномерные определения расстояний…………………………………… 49
7.5. Измерение линий оптическими дальномерами…………………………….. 50
Тема 8. Теодолитные работы………………………………………………………… 51
8.1. Принцип измерения горизонтальных и вертикальных углов……………… 51
8.2. Основные части теодолита…………………………………………………… 52
8.3. Изучение устройства и поверки теодолита типа Т30……………………….. 54
8.4. Измерение горизонтальных и вертикальных углов………………………… 59
8.5. Теодолитные работы………………………………………………………….. 63
8.6. Топографические съемки…………………………………………………….. 67
Тема 9. Нивелирные работы
9.1. Нивелирование. Назначение. Методы нивелирования…………………….. 70
9.2. Системы высот………………………………………………………………… 72
9.3. Нивелиры, рейки, принадлежности, классификация………………………. 72
9.4. Геодезические работы при проектировании и строительстве трасс желез-
ных и автомобильных дорог, проектировании трасс трубопроводов, ЛЭП и дру-
гих линейных сооружений……………….………………………………………….. 79
Тема 10. Геодезические работы, связанные со строительством
10.1. Основные элементы разбивочных работ…………………………………… 87
10.2. Геодезические работы при вертикальной планировке строительной пло-
щадки………………………………………………………………………………….. 91
10.3. Передача отметок на дно котлована и на этаж…………………………….. 94
Библиографический список………………………………………………………….. 96
Тема 1. Введение
Краткая историческая справка о развитии Геодезии
Возникновение геодезии относится к глубокой древности. Известно, что в государствах Ближнего Востока за несколько тысячелетий до н.э. была создана сложная ирригационная система. За 2150 лет до н.э. был построен тоннель длиной 0,9 км под рекой Евфрат, при этом река была отведена в новое русло. На территории многих государств сохранились остатки древних подземных сооружений, свидетельствующие о высоком уровне строительного искусства тех времен. Эти работы нельзя было выполнить без геодезических измерений соответствующей точности.
В середине XV – XVI вв. оживляется торговля, расширяется мореплавание, открываются новые земли – все это вызвало потребность в картах и планах.
В конце XVII столетия учеными был сделан вывод, что Земля имеет форму шара, сплюснутого у полюсов. Перед геодезистами встала задача определить форму и размеры Земли. Появлялись новые инструменты. Возникали новые задачи, стоящие перед геодезической службой. В 1919 г. 15 марта был подписан декрет о создании Высшего геодезического управления (позже ГУГК, позже Роскартография), которое взяло на себя функции руководства всеми общегосударственными и ведомственными геодезическими работами. Значительное развитие получили инженерно-геодезические работы, выполняемые многочисленными ведомствами в целях обеспечения изысканий, проектирования, строительства и эксплуатации различных объектов народного хозяйства.
1.1. Предмет и задачи геодезии
Геодезия – наука об измерениях на земной поверхности, проводимых для определения формы и размеров Земли, изображения земной поверхности в виде планов, карт и профилей, для решения инженерных и народнохозяйственных задач.
Геодезия в процессе своего развития разделилась на ряд научных и научно-технических дисциплин:
- высшая геодезия (с разделом Морская геодезия) занимается изучением формы и размеров Земли, ее внешнего гравитационного поля, определяет координаты и высоты отдельных точек земной поверхности в единой системе на территории всей страны;
- геодезия (топография) изучает методы детальных измерений и изображения участков земной поверхности на топографических планах и картах;
- картография изучает методы изображения земной поверхности или ее частей в виде карт и планов (в различных проекциях);
- фототопография занимается изучением приборов и методов фотографирования местности с воздуха или с земли и преобразования фотоснимков в планы и карты;
- космическая геодезия решает основные задачи геодезии, а также задачи геодезического обеспечения космических съемок поверхности Земли, Луны и планет с помощью космических летательных аппаратов;
- маркшейдерия изучает методы и средства геодезических измерений, выполняемых в условиях горных выработок (карьерах, шахтах), а также при строительстве подземных сооружений (тоннели, метро).
- прикладная (инженерная) геодезия занимается изучением методов и средств производства геодезических работ, связанных с решением задач изысканий, проектирования, строительства и эксплуатации всех видов и типов инженерных сооружений, монтажа, выверки и наладки технологического оборудования, включая наблюдения за осадками и деформациями этих сооружений.
Геодезия использует достижения целого ряда наук: математики, физики, астрономии, географии, геоморфологии, фотографии, механики. В геодезии используют современные методы и средства вычислений, счетные машины, программные комплексы, позволяющие получать картографический материал в электронном виде.
Велика роль геодезии в народном хозяйстве и обороне страны. Большое значение имеет прикладная геодезия при изысканиях и строительстве газовых, водопроводных, канализационных сетей и сооружений. Инженерно-геодезические измерения необходимы при разработке проекта инженерных коммуникаций для перенесения их на местность, для возведения и эксплуатации сооружений. Геодезическими измерениями и построениями осуществляется беспрерывный контроль за соблюдением проектной геометрической формы и размеров сооружения и его стабильностью. В процессе строительства и эксплуатации сооружений методами и средствами прикладной геодезии производят наблюдения за осадками и деформациями сооружений. Широкое развитие землеустроительных работ, направленных на наиболее рациональное использование земли, учет качества сельскохозяйственных земель, проведение оросительных и осушительных мероприятий невозможно без геодезических измерений.
1.2. Общие сведения о форме и размерах Земли
Физическая поверхность Земли имеет сложную форму, суша занимает 29%, моря и океаны – 71% всей поверхности. Чтобы изобразить земную поверхность на плане, надо знать фигуру Земли. Это позволит выбрать такой метод проектирования изображения земной поверхности, которая бы позволила спроектировать неправильную форму Земли в виде математической модели.
Прежде всего, дадим понятие «уровенной поверхности». Уровенная поверхность (рис.1.1) – поверхность, перпендикулярная в каждой точке к направлению силы тяжести (отвесной линии).
Уровенных поверхностей можно провести сколько угодно, т.к. Земля неоднородна и состоит из слоев, плотность которых различна. За фигуру Земли принимается уровенная поверхность, совпадающая с поверхностью океанов и морей при спокойном состоянии водных масс и мысленно продолженная под материками. Такая уровенная поверхность называется геоидом.
Рис. 1.1. Понятие уровенной поверхности
1.3. Математические модели поверхности Земли, применяемые в геодезии
- Если бы Земля была бы однородной, неподвижной и подвержена только действию внутренних сил тяготения, она имела бы форму шара (рис.1.2).
Рис. 1.2. Шар
- Под действием центробежной силы, вызванной вращением вокруг оси с постоянной скоростью, Земля приобрела форму сфероида или эллипсоида вращения (рис.1.3).
Рис. 1.3. Эллипсоид вращения
- На самом деле, из-за неравномерного распределения масс внутри Земли, эллипсоидальная фигура Земли сдеформирована и имеет форму геоида (рис.1.4). Наибольшие отступления геоида от эллипсоида не превышают 100 – 150 м.
Т.о. специальными инструментами с физической поверхности Земли геодезические измерения проектируют на геоид, фигура которого не изучена. Фигуру геоида заменяют правильной математической фигурой, к которой можно применять математические законы. Размеры земного эллипсоида составляют:
большая полуось а = 6378245 м,
малая полуось b = 6356863 м,
полярное сжатие = 1: 298,3.
Рис. 1.4. Геоид
- Для того, чтобы земной эллипсоид ближе подходил к геоиду, его располагают в теле Земли, ориентируя определенным образом. Такой эллипсоид с определенными параметрами и определенным образом ориентированный в теле Земли, называется референц-эллипсоидом (рис.1.5).
Рис. 1.5. Референц-эллипсоид
- Геоид не может быть строго изучен из-за незнания распределения плотности масс внутри Земли. Было предложено вместо геоида принять фигуру квазигеоида (рис.1.6), которая может быть определена точно на основании астрономо-геодезических и гравиметрических измерений на поверхности Земли без учета внутреннего строения и плотности масс внутри Земли. Поверхность квазигеоида отклоняется от поверхности геоида максимально 2 м в горных районах, на океанах и морях их поверхности совпадают.
Рис. 1.6. Квазигеоид
Тема 2. Системы координат
2.1. Система географических (астрономических) координат
Рис. 2.1. Географическая система координат
Географическая (астрономическая) широта – угол, составленный отвесной линией в данной точке и плоскостью экватора (рис.2.1);
Географическая (астрономическая) долгота – двугранный угол между плоскостью астрономического меридиана, проходящего через данную точку и плоскостью начального меридиана (Гринвича) (рис.2.1);
Астрономический азимут а – двугранный угол, составленный плоскостью астрономического меридиана, проходящего через данную точку и плоскостью, проходящей через данную линию и отвесную линию данной точки (рис.2.1).
Широта может принимать значения 0 90 и называются “северные и южные широты”;
Долгота может принимать значения 0 180 и называются “западные и восточные долготы”;
Азимут а может принимать значения 0 а 360, иногда пользуются не азимутами, а румбами, тогда румбы имеют названия.
2.2. Система геодезических координат
Рис. 2.2. Геодезическая система координат
Геодезическая широта В – угол, составленный нормалью к поверхности эллипсоида в данной точке и плоскостью экватора (рис.2.2);
Геодезическая долгота L – двугранный угол между плоскостью геодезического меридиана, проходящего через данную точку и плоскостью начального меридиана (Гринвича) (рис.2.2);
Геодезический азимут А – двугранный угол, составленный плоскостью геодезического меридиана, проходящего через данную точку и плоскостью, проходящей через данную линию и нормаль в данной точке (рис.2.2).
Широта В может принимать значения 0 В 90 и называются “северные и южные широты”;
Долгота L может принимать значения 0 L 180 и называются “западные и восточные долготы”;
Азимут А может принимать значения 0 А 360.
Связь между двумя системами координат:
В = ; L = sec; А = а + (L ) sin, (1.1)
где и – уклонения отвесной линии в плоскостях меридиана и первого вертикала.
2.3. Прямоугольная система координат Гаусса – Крюгера
Рис. 2.3. Поперечно-цилиндрическая проекция ГауссаКрюгера
Земной шар (рис.2.3) вписывают в цилиндр такого же диаметра. Линия касания шара и цилиндра называется осевым меридианом. Территория, расположенная вправо и влево от осевого меридиана принимается за плоскость, в пределах которой искажения изображаемых на плоскости элементов поверхности эллипсоида минимальны.
Поверхность земного эллипсоида делят меридианами, отстоящими друг от друга по долготе на 6, на двуугольники, называемые зонами (рис.2.4). Таких зон всего 60. Каждая зона имеет свою систему координат.
Рис. 2.4. Шестиградусные зоны
Территория России находится выше экватора, поэтому отрицательных абсцисс на нашей территории нет. Чтобы избавиться от отрицательных ординат (для удобства работы с числами), осевой меридиан мысленно переносят на 500 км влево (рис.2.5). Точки, лежащие вправо от перенесенного меридиана, будут иметь положительные ординаты. Значения ординат у для точек, лежащих справа от настоящего осевого меридиана, больше 500 км, для точек, лежащих влево – меньше 500 км. Чтобы отличить точки, имеющие одинаковые координаты, но расположенные в разных зонах, перед значением ординат у ставится номер зоны, а преобразованная ордината вычисляется по формуле у = 500 000 м + у.
Примеры: зона № 15
Для точки К: хк = 4 560 200 м;
ук = + 214 356 м;
хк = 4 560 200 м;
= 15 714 356 м;
№ зоны ордината 500 000 м + 214 356 м.
Для точки Д: хд = 6 340 500 м;
уд = – 186 653 м;
хд = 6 340 500 м;
= 15 313 347 м;
Тема 3. Ориентирование
Ориентирование линий в геодезии. Дирекционный угол, истинный и магнитный азимуты, румбы. Сближение меридианов и магнитные склонения, их использование при вычислении азимутов. Прямая и обратная геодезические задачи. Применение их в геодезическом производстве.
3.1. Ориентирование линий в геодезии
Ориентировать – значит найти направление заданной линии относительно другого направления, принятого за исходное.
За исходное направление в геодезии принимают:
а) Астрономический (истинный меридиан)
Рис. 3.1. Истинный азимут
А – астрономический (истинный) азимут линии – горизонтальный угол, отсчитываемый в данной точке от северного конца истинного меридиана по ходу часовой стрелки до направления ориентируемой линии (рис.3.1).
А – прямой истинный азимут, Аобр – обратный.
б) Магнитный меридиан
Рис. 3.2. Магнитный азимут
Ам – магнитный азимут линии – горизонтальный угол, отсчитываемый в данной точке от северного конца магнитного меридиана по ходу часовой стрелки до направления ориентируемой линии (рис.3.2),
А – истинный азимут,
– склонение магнитной стрелки – угол между истинным и магнитным меридианами.
со знаком «+» при положении магнитного меридиана вправо от истинного меридиана, и со знаком «–» при положении влево.
Ам = А – (3.1)
Пример 1:
Ам = 30833, = 6 27. Найти А.
А = Ам + = 30833 6 27 = 30206.
в) Осевой меридиан зоны
Рис. 3.3. Дирекционный угол
– дирекционный угол линии – горизонтальный угол, отсчитываемый в данной точке от северного конца осевого меридиана или линии, ему параллельной, по ходу часовой стрелки до направления ориентируемой линии (рис.3.3).
– дирекционный угол линии LN, обр – дирекционный угол линии NL.
Связь прямого и обратного дирекционных углов можно выразить уравнением:
обр = 180. (3.2)
Связь истинного азимута и дирекционного угла выражается формулой
А = + , (3.3)
где – сближение меридианов – угол между истинным и осевым меридианами.
имеет знак «+», если осевой меридиан расположен вправо от истинного меридиана, и знак «–»,если осевой меридиан расположен влево от истинного меридиана.
Пример 2: = 2 35, = 168 47. Вычислить А.
А = + = 168 47 + (2 35) = 166 12.
Пример 3: = + 4 11, А = 312 56. Вычислить .
А = + ; = А = 312 56 4 11 = 308 45.
г) Румбы
Иногда вместо дирекционных углов используют румбы. Румб – острый угол, отсчитываемый от ближайшего (северного или южного) конца осевого меридиана до направления определяемой линии (рис.3.4).
Связь между дирекционными углами и румбами:
СВ: r = ;
ЮВ: r = 180 , = 180 r;
ЮЗ: r = 180, = 180 + r;
СЗ: r = 360 , = 360 r.
Рис. 3.4. Румбы
А = + ;
Ам = А – ; (3.5)
Ам = + – .
Пример 4:
r = ЮЗ: 5641, = 180 + 5641 = 23641.
Пример 5:
= 9211, = 4 30, = 9 42. Найти А и Ам.
А = 9211 4 30 = 8741,
Ам = 8741 + 9 42 = 9723.
3.2. Прямая и обратная геодезические задачи. Их применение в геодезическом производстве
а) Прямая геодезическая задача
Рис. 3.5. Прямая геодезическая задача
Дано: координаты точки 1 х1, у1; горизонтальное проложение линии 1 – 2: d1,2;
дирекционный угол линии 1 – 2: 1,2 (рис.3.5).
Найти: координаты точки 2: х2, у2.
Решение: координаты точки 2: х2 = х1 + х; у2 = у1 + у, (3.6)
где приращения координат х = d · cos ; у = d · sin , (3.7)
откуда х2 = х1 + d · cos ; у2 = у1 + d · sin . (3.8)
Знаки приращений координат х и у зависят от знаков функций sin и cos .
б) Обратная геодезическая задача
Рис. 3.6. Обратная геодезическая задача
Дано: координаты точек 1 и 2: х1, у1; х2, у2 (рис.3.6).
Найти: горизонтальное проложение линии 1 – 2: d1,2; дирекционный угол линии 1 – 2: 1,2.
Решение: х = х2 – х1; у = у2 – у1; (3.9)
; (3.10)
. (3.11)
По значению tg определяется румб линии. По знакам приращений координат определяется четверть, а по четверти определяется дирекционный угол линии.
Рис. 3.7. Знаки приращений координат
в зависимости от четверти
Прямая геодезическая задача применяется при вычислении координат в теодолитном ходе. Обратная геодезическая задача применяется в тех случаях, когда по известным координатам 2-х точек определяют расстояние между ними и дирекционный угол линии.
Тема 4. Масштабы. Сведения из теории погрешностей
4.1. Масштабы
Масштаб – отношение длины линии на плане к соответствующей проекции этой линии на местности.
а) Численный масштаб – число, правильная дробь, в числителе – единица, знаменатель – степень уменьшения изображения.
Пример: Масштаб 1:1 000 – 1 сантиметру карты (плана) соответствует 1 000 сантиметров на местности или 10 метров. Масштаб 1:100 000 – 1 см карты соответствует 100 000 см местности или 1 000 м.
б) Линейный масштаб – графический чертеж (рис.4.1). Расстояние между большими отрезками постоянное и называется основанием масштаба. Обычно выбирают основанием отрезок в 2 см.
Масштаб 1: 10 000
Рис. 4.1. Линейный масштаб
Для масштаба 1: 10 000: в 1 см 100 м, в 2 см 200 м.
Левая часть делится на 10 частей, каждая часть делится еще пополам. Для данного масштаба одно маленькое деление соответствует 10 метрам.
Для определения расстояний по карте (плане) циркулем переносят на линейный масштаб (рис. 4.2) расстояние и оценивают его.
Пример: 400 + 90 = 490 м
Рис. 4.2. Пример определения расстояния по карте
в) Поперечный масштаб – применяют для более точного определения длин отрезков
Рис. 4.4. Принцип определения наименьшего деления поперечного масштаба
На прямой линии (рис.4.3) откладывают отрезки по 2 см (основание масштаба). Вверх по перпендикуляру откладывают на равном расстоянии 10 равных частей. Левая часть полученного прямоугольника делится 10 наклонными линиями (трансверсалями). Наименьшее деление поперечного масштаба (рис.4.4) равен 1/10 части левой шкалы.
Пример 1: для масштаба 1:10 000, в 1 см 100 м, в 2 см 200 м. Одно деление слева от 0 20 м, одно деление при подъеме вверх по трансверсали 2 м.
Расстояние АВ: по 200 м – 3 деления, по 20 м – 3 деления, по 2 м – 4 деления. Итого: 600 м + 60 м + 8 м = 668 м.
Пример 2: для масштаба 1:25 000, в 1 см 250 м, в 2 см 500 м. Одно деление слева от 0 50 м, одно деление при подъеме вверх по трансверсали 5 м.
Расстояние АВ: по 500 м – 3 деления, по 50 м – 3 деления, по 5 м – 4 деления. Итого: 1500 м + 150 м + 20 м = 1670 м.
Наименьшее расстояние, различаемое глазом, 0,1 мм. Точностью масштаба называют горизонтальное расстояние на местности, соответствующее в данном масштабе 0,1 мм плана. Так для масштаба 1:5 000 в 1 см – 50 м, в 1 мм – 5 м, в 0,1 мм – 0,5 м. Для 1:5 000 точность масштаба 0,5 м.
Предельная точность масштаба 0,2 мм (точность, различаемая глазом 0,1 мм, и точность применяемых измерительных приборов 0,1 мм), т.е. для масштаба
1:5 000 это 1 м.
4.2. Основы математической обработки геодезических измерений
Геодезические измерения определяют относительное положение точек земной поверхности.
Различают следующие виды измерений:
- линейные – получают наклонные и горизонтальные расстояния между точками. Инструменты: мерные ленты, рулетки, проволоки, оптические свето- и радиодальномеры;
- угловые – определяют величины горизонтальных и вертикальных углов. Инструменты: эклиметры, буссоли, теодолиты;
- высотные – получают разности высот отдельных точек. Инструменты: баронивелиры, теодолиты-тахеометры, нивелиры.
Измерения бывают:
- непосредственные (прямые);
- косвенные.
Измерения бывают:
- равноточные (один объект наблюдения, один наблюдатель, один мерный прибор, одна методика наблюдений, одинаковые условия внешней среды);
- неравноточные (когда не соблюдаются выше перечисленные условия).
Измерения сопровождаются погрешностями (ошибками): грубыми (из-за невнимательности наблюдателя), систематическими (из-за несовершенства приборов) и случайными (зависящими от многих причин и неподдающимися никаким прогнозам).
Грубые погрешности исключают повторными наблюдениями. Систематические погрешности можно учесть, вводя поправки в измеренные величины за длину ленты, длину метра реек, за погрешности прибора и т.д. Случайные погрешности исключить нельзя, но можно ослабить их влияние на измеренные величины путем многократных наблюдений.
Имеем ряд измерений 1, 2 ….n одной и той же величины, истинное значение которой Х. Случайные погрешности этих измерений i = i Х. Ряд случайных погрешностей 1, 2 …. n имеет свойства:
- свойство ограниченности – все случайные погрешности должны быть меньше заранее известного предела
пред;
- свойство симметричности – число положительных и отрицательных погрешностей должно быть одинаковым
– + ;
- свойство унимодальности – малые по абсолютной величине погрешности должны встречаться чаще, чем большие
;
- свойство компенсации – при неограниченном числе измерений предел среднего значения погрешностей стремится к нулю
.
Виды погрешностей:
- случайная (абсолютная) погрешность = – Х;
- вероятнейшая погрешность v;
- средняя квадратическая погрешность m;
- относительная погрешность ;
- предельная погрешность пред = 2m.
Тема 5. Топографические карты и планы
5.1. Геодезические планы, карты
План – чертеж, представляющий собой уменьшенное и подобное изображе ние ее проекции на горизонтальную плоскость (рис. 5.1, а).
На плане длины линий, углы, площади контуров участков местности не иска жаются, а степень уменьшения ее линейных элементов (масштаб изображения) постоянна для всех частей плана.
Планы, на которых изображена только ситуация местности, называются кон турными (ситуационными).
Планы, на которых кроме предметов местности изображен еще и рельеф, на зываются топографическими.
Карта – построенное по определенным математическим законам уменьшенное изображение на плоскости всей Земли или ее частей с учетом кривизны Земли (рис. 5.1, б).
Карты делятся на крупномасштабные – 1:100 000 и крупнее, среднемасштаб ные – от 1:200 000 до 1:1 000 000, мелкомасштабные – мельче 1:1 000 000.
При создании карт строят сетку меридианов и параллелей – картографическую сетку. Кроме того, для удобства на картах изображают километровую сетку – линии, параллельные экватору и осевому меридиану.
а) б)
Рис. 5.1. План а), карта б)
5.2. Условные знаки на планах, картах, геодезических и строительных чертежах
Для обозначения на планах и картах различных предметов местности применяют специально разработанные условные знаки.
Условные знаки делятся на:
а) контурные (масштабные), изображающие предметы местности с соблюдением масштаба карты и дающие представление о местоположении предмета и его размерах (рис. 5.2);
Рис. 5.2. Контурные условные знаки
б) внемасштабные, дающие представление о том, что это за объект, его местоположение, но не дающие представления об истинных размерах объекта (рис. 5.3);
Рис. 5.3. Внемасштабные условные знаки
в) линейные, по ширине не отображаются в масштабе карты, а по длине отображаются (рис. 5.4);
Рис. 5.4. Линейные условные знаки
г) пояснительные, указывающие географические названия, качественные и количественные характеристики (рис. 5.5).
Рис. 5.5. Пояснительные условные знаки
5.3. Номенклатура топографических планов и карт
Номенклатура – система разграфки и обозначений топографиче ских планов и карт.
В основу номенклатуры карт на территории Российской Федерации положена международная разграфка листов карты масштаба 1:1 000 000 (рис.5.6). Для получения одного листа карты этого масштаба земной шар делят меридианами и параллелями на колонны и ряды (пояса).
Меридианы проводят через каждые 6. Счет колонн от 1 до 60 идет от 180 меридиана от 1 до 60 с запада на восток, против часовой стрелки. Колонны совпадают с зонами прямоугольной разграфки, но их номера отличаются ровно на 30. Так для зоны 12 номер колонны 42 (табл. 5.1).
Параллели проводят через каждые 4. Счет поясов от А до W идет от экватора к северу и югу (табл. 5.2).
В пересечении таких колонн и рядов (поясов) образуются листы карт масштаба 1:1 000 000. Номенклатура одного из таких листов складывается из буквы ряда и номера колонны: T44, S48. Размеры такого листа 6 по долготе и 4 по широте.
Рис. 5.6. Номенклатура карт масштаба 1:1 000 000
Таблица 5.1
Номера колонн
|
колонна |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
|
от |
0 |
6 |
12 |
18 |
24 |
30 |
36 |
42 |
48 |
54 |
60 |
|
до |
6 |
12 |
18 |
24 |
30 |
36 |
42 |
48 |
54 |
60 |
66 |
|
колонна |
42 |
43 |
44 |
45 |
46 |
47 |
48 |
49 |
50 |
51 |
52 |
|
от |
66 |
72 |
78 |
84 |
90 |
96 |
102 |
108 |
114 |
120 |
126 |
|
до |
72 |
78 |
84 |
90 |
96 |
102 |
108 |
114 |
120 |
126 |
132 |
Таблица 5.2
Номера рядов
|
ряд |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
|
от |
0 |
4 |
8 |
12 |
16 |
20 |
24 |
28 |
32 |
36 |
40 |
|
до |
4 |
8 |
12 |
16 |
20 |
24 |
28 |
32 |
36 |
40 |
44 |
|
ряд |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
|
от |
44 |
48 |
52 |
56 |
60 |
64 |
68 |
72 |
76 |
80 |
84 |
|
до |
48 |
52 |
56 |
60 |
64 |
68 |
72 |
76 |
80 |
84 |
88 |
Для получения карты масштаба 1:500 000 лист миллионной карты делят на четыре листа и обозначают прописными буквами русского алфавита А. Б, В, Г (рис.5.7). Номенклатура такого листа складывается из номенклатуры листа масштаба 1:1 000 000 и буквы листа 1:500 000 (Т–44–Б). Размеры такого листа 3 по долготе и 2 по широте.
T44 (1:1 000 000)
Рис. 5.7. Номенклатура карт масштаба 1:500 000
Для получения карты масштаба 1:300 000 лист карты масштаба 1:1 000 000 делят на 9 частей и обозначают римскими цифрами I – IX (рис.5.8). Номенклатура такого листа складывается из цифры листа 1:300 000 и номенклатуры листа масштаба 1:1 000 000 (III–Т–44). Размеры такого листа 2 по долготе и 1 20 по широте.
III–Т–44
(1:300 000)
Рис. 5.8. Номенклатура карт масштаба 1:300 000
Для получения карты масштаба 1:200 000 лист карты масштаба 1:1 000 000 делят на 36 частей и обозначают римскими цифрами I – XXXVI (рис.5.9). Номенклатура такого листа складывается из номенклатуры листа масштаба 1:1 000 000 и цифры листа 1:200 000 (Т–44–ХХXVI). Размеры такого листа 1 по долготе и 40 по широте.
Т–44–ХХXVI
(1:200 000)
Рис. 5.9. Номенклатура карт масштаба 1:200 000
Для получения карты масштаба 1:100 000 лист карты масштаба 1:1 000 000 делят на 144 части и обозначают арабскими цифрами 1 – 144 (рис.5.10). Номенклатура такого листа складывается из номенклатуры листа масштаба 1:1 000 000 и цифры листа 1:100 000 (Т–44–25). Размеры такого листа 30 по долготе и 20 по широте.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
13 |
24 |
||||||||||
|
25 |
36 |
||||||||||
|
37 |
48 |
||||||||||
|
49 |
60 |
||||||||||
|
61 |
72 |
||||||||||
|
73 |
84 |
||||||||||
|
85 |
96 |
||||||||||
Рис. 5.10. Номенклатура карт масштаба 1:100 000
Дальнейшее деление карт на более крупный масштаб ведется на основе листа карты масштаба 1:100 000 (рис.5.11).
Для получения карты масштаба 1:50 000 лист карты масштаба 1:100 000 делят на 4 части и обозначают прописными буквами русского алфавита А. Б, В, Г. Номенклатура такого листа складывается из номенклатуры листа масштаба 1:100 000 и буквы листа 1:50 000 (Т–44–25–Б). Размеры такого листа 15 по долготе и 10 по широте.
Для получения карты масштаба 1:25 000 лист карты масштаба 1:50 000 делят на 4 части и обозначают строчными буквами русского алфавита а, б, в, г. Номенклатура такого листа складывается из номенклатуры листа масштаба 1:50 000 и буквы листа 1:25 000 (T–44–25–А–а). Размеры такого листа 730 по долготе и 5 по широте.
Лист карты масштаба 1:10 000 получается делением листа карты масштаба 1:25 000 на 4 части и обозначают цифрами 1, 2, 3, 4. Номенклатура такого листа складывается из номенклатуры листа масштаба 1:25 000 и цифры листа 1:10 000
(T–44–25–А–г–4). Размеры такого листа 345 по долготе и 230 по широте.
T44–25 (1:100 000)
Рис. 5.11. Номенклатура карт масштабов 1:50 000 1:10 000
Для получения карты масштаба 1:5 000 лист карты масштаба 1:100 000 делят на 256 части и обозначают цифрами 1256 (рис.5.12). Номенклатура такого листа складывается из номенклатуры листа масштаба 1:100 000 и в скобках цифры листа 1:5 000, например T4425 (252).
Для получения карты масштаба 1:2 000 лист карты масштаба 1:5000 делят на 9 частей и обозначают строчными буквами русского алфавита а и (рис.5.13). Номенклатура такого листа складывается из номенклатуры листа масштаба 1:5 000 и буквы листа 1:2 000, например T4425 (252а).
T4425 (1:100 000)
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
17 |
32 |
||||||||||||||
|
33 |
48 |
||||||||||||||
|
49 |
64 |
||||||||||||||
|
65 |
80 |
||||||||||||||
|
81 |
96 |
||||||||||||||
|
97 |
112 |
||||||||||||||
|
113 |
128 |
||||||||||||||
|
129 |
144 |
||||||||||||||
|
145 |
160 |
||||||||||||||
|
161 |
176 |
||||||||||||||
|
177 |
192 |
||||||||||||||
|
193 |
208 |
||||||||||||||
|
209 |
224 |
||||||||||||||
|
225 |
240 |
||||||||||||||
|
241 |
256 |
Рис. 5.12. Номенклатура карт масштаба 1:5000
T4425 (252) (1:5000)
Рис. 5.13. Номенклатура карт масштаба 1:2 000
Для топографических планов, создаваемых на участках площадью менее 20 км2, применяется прямоугольная разграфка. В основу этой разграфки положен планшет 1:5000 с размерами рамок 4040 см, обозначаемый арабскими цифрами, например 6 (рис.5.14). Ему соответствует 4 листа 1:2000, каждый из которых обозначается присоединением к номеру масштаба 1:5000 одной из четырех заглавных букв А, Б, В, Г, например 6Г.
6 (1:5000)
Рис. 5.14. Номенклатура планов масштабов 1:5 0001:500
План масштаба 1:2000 делится на четыре плана масштаба 1:1000, они обозначаются римскими цифрами I, II, III и IV, например 6БII.
План масштаба 1:2000 делится на 16 листов масштаба 1:500, они обозначаются арабскими цифрами 1 – 16, например 6В15.
Для масштабов 1:2000, 1:1000 и 1:500 размеры рамок 5050 см.
Задачи
- Какому масштабу соответствуют номенклатуры?
К–42 1:1 000 000
К–42–А 1:500 000
IX–К–42 1:300 000
К–42–IX 1:200 000
К–42–144 1:100 000
К–42–144–В 1:50 000
К–42–144–В–б 1:25 000
К–42–144–В–б–2 1:10 000
К–42–144–(250) 1:5000
К–42–144–(250–ж) 1:2000
10 1:5000
10–В 1:2000
10–В–IV 1:1000
10–А–14 1:500
- Определить номенклатуры карт, граничащих с 8-и сторон с картой К–42–133.
- Определить географические координаты карты с номенклатурой
К–42–144–В–б–2.
Колонна 42 (табл.5.1): 66 – 72;
ряд К (табл.5.2): 40 – 44.
К–42 (1:1 000 000)
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
13 |
24 |
||||||||||
|
25 |
36 |
||||||||||
|
37 |
48 |
||||||||||
|
49 |
60 |
||||||||||
|
61 |
72 |
||||||||||
|
73 |
84 |
||||||||||
|
85 |
96 |
||||||||||
|
|
|||||||||||
Ответ:
- Найти номенклатуру листа масштаба 1:10 000, внутри которого расположена точка с географическими координатами:
= 491833;
= 931609.
Ряд М: 48 52; колонна 46: 90 96.
М–46 (1:1 000 000)
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
13 |
24 |
||||||||||
|
25 |
36 |
||||||||||
|
37 |
48 |
||||||||||
|
49 |
60 |
||||||||||
|
61 |
72 |
||||||||||
|
73 |
84 |
||||||||||
|
85 |
96 |
||||||||||
|
97 |
|||||||||||
|
|
В пересечении по горизонтали и вертикали по получен 103 лист с номенклатурой М–46–103 масштаба 1:100 000.
В пересечении по вертикали и по горизонтали получен лист Б масштаба
1:50 000 с номенклатурой М–46–103–Б.
В пересечении по вертикали и по горизонтали получен лист а масштаба
1:25 000 с номенклатурой М–46–103–Б–а.
В пересечении по вертикали и по горизонтали получен лист 1 масштаба
1:10 000 с номенклатурой М–46–103–Б–а–1.
Ответ: М–46–103–Б–а–1.
5.4. Понятие о рельефе местности
Рельеф – совокупность неровностей физической поверхности Земли (рис.5.15).
Рис. 5.15. Рельеф:
d – заложение горизонталей (расстояние между соседними горизонталями на плоскости);
h – высота сечения рельефа (разность высот двух соседних горизонталей);
– крутизна склона;
– горизонталь;
– бергштрих (направление понижения скатов).
5.4.1. Основные формы рельефа
а) Гора, холм (рис. 5.16) – куполообразная или коническая возвышенность земной поверхности
Рис. 5.16. Гора
Небольшая гора – холм (сопка), искусственный холм – курган.
б) котловина (рис. 5.17) – чашеобразное замкнутое со всех сторон углубление
Рис. 5.17. Котловина
в) хребет (рис. 5.18) – возвышенность, вытянутая в одном направлении и образованная двумя противоположными скатами
Рис. 5.18. Хребет
г) лощина (рис. 5.19) – вытянутое в одном направлении желобообразное углубление с наклоном в одну сторону
Рис. 5.19. Лощина
Широкая лощина – долина; узкая лощина – балка; в горах узкая лощина – ущелье.
д) седловина (рис. 5.20) – понижение между двумя соседними горными вершинами или возвышенностями
Рис. 5.20. Седловина
5.4.2. Горизонтали
Горизонталь замкнутая кривая линия, все точки которой имеют одну и ту же высоту над начальной уровенной поверхностью
Свойства горизонталей:
- точки, лежащие на одной и той же горизонтали, имеют одинаковую высоту;
- все горизонтали должны быть непрерывны;
- горизонтали не могут пересекаться или раздваиваться;
- расстояния между горизонталями в плане характеризуют крутизну ската – чем меньше расстояние (заложение), тем круче скат;
- кратчайшее расстояние между горизонталями соответствует направлению наибольшей крутизны ската;
- водораздельные линии и оси лощин пересекаются горизонталями под прямыми углами;
- горизонтали, изображающие наклонную плоскость, имеют вид параллельных кривых.
Когда расстояние между горизонталями на плане превышает 2 см, для уточнения форм рельефа применяют дополнительные горизонтали – полугоризонтали (рис.5.21).
Рис. 5.21. Полугоризонталь
5.4.3. Уклон линии. Графики заложений
Уклон i линии – отношение превышения h к заложению линии d (рис. 5.22). Уклон – мера крутизны ската.
Например, h = 1 м, d = 20 м. i = 1/20 = 0,05.
Уклоны выражаются в процентах i = 5% или в промиллях i = 50 ‰. Чем больше d, тем меньше крутизна .
уклон линии ; (5.1)
крутизна ската .
Рис. 5.22. Уклон линии
График заложений по уклонам
График строится по формуле ,
где h – константа для данной карты; i – задается.
Пример: Масштаб 1:10 000, h = 1 м, i = 0,001 (табл. 5.2). Подставляя в формулу, получим = 1000 м, что на карте масштаба 1:10 000 составляет 10 см.
Таблица 5.2
|
h, м |
1 |
1 |
1 |
1 |
1 |
1 |
|
i ‰ |
0,001 |
0,002 |
0,003 |
0,004 |
0,005 |
0,006 |
|
d, м |
1000 |
500 |
333 |
250 |
200 |
167 |
|
на карте, см |
10 |
5 |
3,33 |
2,5 |
2,0 |
1,67 |
Рис. 5.23. График заложений по уклонам
График заложений по углам
График строится по формуле ,
где h – константа для данной карты;
– задается.
Пример: Масштаб 1:10 000, h = 2,5 м (табл. 5.3). Для = 030; d = 2,5 · ctg 030 = 286,5 м, что на карте составляет 2,86 см и т.д. для углов 1, 2, 3… 10.
Таблица 5.3
|
h, м |
2,5 |
2,5 |
2,5 |
2,5 |
2,5 |
2,5 |
2,5 |
|
, град. |
030 |
1 |
2 |
3 |
5 |
… |
10 |
|
ctg |
114.59 |
57.29 |
28.64 |
19.08 |
11.43 |
… |
5.67 |
|
d, м |
286.47 |
143.22 |
71.59 |
47.70 |
28.58 |
… |
14.18 |
|
На карте, см |
2,86 |
1,43 |
0,72 |
0,48 |
0,29 |
… |
0,14 |
Рис. 5.24. График заложений по углам
5.5. Задачи, решаемые по карте
Рис. 5.25 Фрагмент топографической карты
Задачи, которые можно решать по карте, следующие:
1. Определение по карте географических координат т. а (рис. 5.25):
т. а г. Малиновская = 544021;
= 180503.
2. Определение по карте прямоугольных координат т. б (см. рис. 5.25):
т. б т.148,1 х = 6065 300 м;
у = 4312 800 м.
3. Определение направления аб (см. рис. 5.25):
= 60;
А = + = 60 + (222) = 5738;
Ам = А = 5738 (612 + 102) = 5024.
4. Определение крутизны ската по линии а – б (табл. 5.4): 1 = 1,8 и т.д.
Таблица 5.4
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
|
1,8 |
1,6 |
1,6 |
0,40 |
0,50 |
1,2 |
5. Построение линии заданного уклона (рис. 5.26):
i = h d; d = h i; h = 2,5 м; i = 0,035; d = 2,5 0,035 = 71 м.
Для масштаба 1 10000: в 1 см – 100 м;
х см 71 м; х = 0,71 см или 7 мм.
Раствором циркуля в 7 мм (или более) шагают от горизонтали до горизонтали, выбирая наиболее рациональный ход:
Рис. 5.26. Построение линии заданного уклона
6. Построение продольного профиля по линии а – б (рис. 5.27):
Рис. 5.27. Продольный профиль
7. Определение расстояния аб (см. рис. 5.25): d = 1053 м.
Тема 6. Плановые и высотные геодезические сети
Государственная геодезическая сеть – совокупность пунктов с известными координатами (х, у) и высотой (Н), равномерно расположенных на всей территории страны.
6.1. Плановая геодезическая сеть
6.1.1. Методы, схемы, точность и плотность пунктов при создании сети
- триангуляция (рис. 6.1) применяется в открытой местности:
Рис. 6.1. Триангуляция
- полигонометрия (рис. 6.2) применяется в закрытой местности:
Рис. 6.2. Полигонометрия
- трилатерация (рис. 6.3) применяется в особых случаях и выполняется по особой программе:
Рис. 6.3. Трилатерация
Точность сетей:
- главное геодезическое обоснование 1 – 4 классов;
- сети сгущения 1 и 2 р.;
- съемочное обоснование.
Плотность пунктов:
- для съемок в масштабах 1:10 000 и 1: 25 000 1 пункт на 50 – 60 км2;
- для 1:5 000 1 пункт на 20 – 30 км2;
- для 1:2 000 1 пункт на 5 – 15 км2.
- для крупномасштабных съемок в застроенной территории 4 пункта на 1 км2;
в незастроенной территории 1 пункт на 1 км2;
Для уменьшения продольного и поперечного сдвига ряда сети выполняют базисные и астрономические измерения широты , долготы и азимута а (рис. 6.4).
6.1.2. Типы знаков и типы центров
Для обеспечения видимости между геодезическими пунктами над центрами устанавливают различные типы знаков, конструкция и высота которых зависят от физико-географических условий местности, а также целесообразности применения материалов, дающих наибольший экономический эффект.
сигнал пирамида насадка надстройка на здании
Рис. 6.5. Типы знаков
Для сохранности геодезических пунктов на длительное время, возможности их дальнейшего использования и исходя из физико-географических условий местности, глубины промерзания почвы, наличия зданий и сооружений закладывают центры различных типов. Существует специальный альбом типов центров.
фундаментальный грунтовый стенной стенная временный
репер репер репер марка репер
Рис. 6.6. Типы центров
6.2. Высотная геодезическая сеть
Высотная (нивелирная) геодезическая сеть предназначена для создания единой системы высот на территории государства, для решения научных и прикладных задач. В настоящее время наряду с традиционными методами нивелирования применяются современные методы определения высотного положения геодезических пунктов с помощью спутниковых и лазерных приборов, что позволяет сократить время и средства на выполнение данной работы.
6.2.1. Схемы, методы, точность и плотность пунктов при создании сети
Схемы создания сети:
Рис. 6.7. Схема нивелирования I – IV классов:
Линии нивелирования I класса
Линии нивелирования II класса
Линии нивелирования III класса
Линии нивелирования IV класса
Стенная марка
Временный репер
Фундаментальный репер
Грунтовый репер
Стенной репер
Методы построения: геометрическое, тригонометрическое, физическое, автоматическое (подробно рассматриваются в теме 9).
Точность сетей:
- нивелирование I, II, III и IV классов (со средней квадратической погрешностью на 1 км хода от ± 0,5 мм до ± 8 мм);
- техническое нивелирование;
- тригонометрическое нивелирование.
Плотность пунктов:
- периметр полигона I класса составляет 1200 1600 км в обжитой и 2400 км в необжитой местности;
- полигон II класса составляет 400 600 км в обжитой и 800 км в необжитой местности;
- полигон III класса составляет 150 200 км;
- длина хода IV класса не более 50 км;
- в техническом нивелировании длина хода зависит от высоты сечения рельефа и колеблется от 1 до 16 км;
- в тригонометрическом нивелировании число сторон хода должно быть не более 5, в горных районах не более 7 – 8.
6.2.2. Типы нивелирных центров
Все линии нивелирования закрепляют марками или реперами через 5 км, в сейсмической зоне через 3 4 км, в труднодоступной территории через 6 7 км. Через 50 60 км закладывают фундаментальные реперы. В стенах зданий и сооружений закладывают стенные марки или реперы, в скальных породах устанавливают скальные реперы и марки.
фундаментальный грунтовый стенной временный стенная
репер репер репер репер марка
Рис. 6.8. Типы нивелирных центров
Тема 7. Линейные измерения
Линейные измерения бывают непосредственные и косвенные:
- непосред ственные – измерения с помощью приборов для измерения длин линий;
- кос венные – расстояния вычисляются по другим, непосредственно измерен ным величинам.
7.1. Приборы для измерения расстояний
- рулетки 5, 10, 20, 30, 50 м;
- ленты 20,24,50,100 м;
- нитяной дальномер;
- дальномеры двойного изображения
- светодальномеры; ;
- радиодальномеры; ;
- инварные проволоки, жезлы; .
7.2. Измерение линий лентой
- провешивание линий
Рис. 7.1. Измерение линии лентой
Измеренное расстояние вычисляется по формуле
, (7.1)
где Д – расстояние между точками,
– длина ленты,
m – число шпилек в комплекте,
k – число передач комплекта шпилек,
n – число шпилек у заднего мерщика,
r – остаток.
В длину линии, измеренной лентой (рулеткой), вводят поправки:
- поправка за компарирование (за длину мерного прибора):
к = (поправка за компарирование одной ленты), (7.2)
(поправка во всю линию). (7.3)
- поправка за температуру:
(7.4)
где – линейный коэффициент расширения стали,
t – температура измерения,
tо – температура компарирования,
- поправка за угол наклона (всегда со знаком “” (рис. 7.2):
(7.5)
где угол наклона линии.
Рис. 7.2. Введение поправки за угол наклона
Окончательно длина линии вычисляется по формуле
d = Д + Дк + Дt +Д. (7.6)
Пример.
Даны измерения: о = 20 м; m = 11; n = 4; k = 2; r = 15,37 м; = 19,95 м;
t = +20; tо = +15; = 0,0000125; = 2о 30.
Вычислить окончательную длину линии и выполнить оценку точности изме рения линии.
Д = 20 (11 – 1) 2 + 20 4 + 15,37 = 495,37 м.
Вычисляем поправки:
- за компарирование = 19,95 – 20 = 0,05 м; Дк = .
- за температуру Дt = 0,0000125 (20-15) 495,37 = +0,031 м.
- за угол наклона Д = 2 495,37 0,02182 = 0,47 м.
Окончательно длина линии равна
d1 = 495,37 – 1,24 + 0,031 – 0,47 = 493,69 м.
При измерении во второй раз остаток r = 15,84 м, d2 = 493,84 м.
Разность двух измерений d = 493,84 – 493,69 = 0,15 м – абсолютная ошибка измерений. Среднее значение измеренной линии dср = 493,765 м.
Относительная ошибка измерений .
7.3. Измерения расстояния нитяным дальномером
Рис. 7.3. Нитяной дальномер
Расстояние, измеренное нитяным дальномером, вычисляется по формуле
Д = d + f + , (7.7)
где d – расстояние от рейки до фокуса,
f – фокусное расстояние объектива зрительной трубы,
– расстояние от объектива до основной оси теодолита,
ав – расстояние между дальномерными нитями,
АВ = – количество делений на рейке между А и В.
Из подобия АВF и авf:
где – коэффициент дальномера, обычно равен 100;
f + = с – постоянная дальномера, обычно равна 0,10 м.
С учетом выше изложенного Д = . (7.8)
Для удобства работы подкрашивают рейки таким образом, чтобы К = 100, а с = 0.
Рис. 7.4. Приведение линий к горизонту
Приведение к горизонту расстояний, измеренных дальномером:
- если рейка перпендикулярна визирной оси ( = МN): Д = ;
- если рейка отвесна ( = МN): Д = ;
- если необходимо вычислить горизонтальное проложение:
d = . (7.9)
7.4. Дальномерные определения расстояний
- измерения дальномером с постоянным базисом и переменным параллактиче ским углом
Рис. 7.5. Линия, измеренная дальномером с постоянным базисом
и переменным параллактиче ским углом: Д =
- измерения дальномером с постоянным параллактическим углом и переменным базисом
Рис. 7.6. Линия, измеренная дальномером с постоянным
параллактическим углом и переменным базисом: Д =
7.5. Измерение линий оптическими дальномерами (на основе светодальномера)
Электронный тахеометр 3Та5 (рис. 7.7) применяется как для линейных, так и для угловых измерений. Средняя квадратическая погрешность измерения горизонтальных углов тахеометром составляет 5.
Дальномерная часть прибора выполнена на основе светодальномера. В при боре генерируются электромагнитные колебания высокой частоты, которые мо дулиру ются. Образуется сигнал в виде модулированных колебаний или импуль сов, кото рый с помощью оптической системы прибора направляется на отража тель. Отража тель (рис. 7.8) возвращает сигнал к прибору. Измеренные углы и расстояния поступают в блок обработки. Высотное поло же ние снятых точек определяется по измеренным углам наклона и расстояниям мето дом тригонометрического нивелирования.
Рис. 7.8. Одно- и шести призменные отражатели
Тема 8. Теодолитные работы
Принцип измерения горизонтальных и вертикальных углов. Изучение устройства и поверки теодолита типа Т30. Измерение горизонталь ных и вертикальных углов. Теодолитные работы
8.1. Принцип измерения горизонтальных и вертикальных углов
Угловые измерения необходимы при развитии триангуляционных се тей, про кладывании полигонометрических, теодолитных и высотных ходов, выполнении то пографических съемок и решении многих геодезических за дач при строительстве сооружений.
Рис. 8.1. Принцип измерения горизонтального угла
Расположим над вершиной измеряемого угла параллельно горизон тальной плоскости градуированный круг, центр которого совмещен с точ кой от весной ли нии Вв (рис. 8.1). Тогда угол измеряемый горизонтальный угол. Деления на круге под писаны по ходу часовой стрелки, а и с – отсчеты по градуированной ок ружности круга, горизонтальный угол = а с.
Рис. 8.2. Принцип измерения вертикального угла
Измерение вертикальных углов – углов наклона производят с помощью вертикального круга (рис. 8.2). Вертикальный круг жестко скреплен с осью трубы и вращается вместе с ней. Алидада расположена на оси вращения трубы, но не скреплена с ней и при вращении трубы остается неподвижной.
Зрительную трубу наводят на наблюдаемую точку, отсчет по вертикальному кругу даст значение угла наклона (при соблюдении условия, что значение М0 = 0).
Угломерный инструмент, позволяющий измерять горизонтальные, вертикальные углы и расстояния, на зывается теодолитом.
По назначению выделяют теодолиты маркшейдерские, проектировочные и др.
По материалам изготовления кругов и по устройству отсчетных приспособле ний теодолиты подразделяются на две группы:
- с металлическими лимбами;
- со стеклянными лимбами – оптические теодолиты.
По конструкции теодолиты делятся на повторительные и простые. У повтори тельных теодолитов лимб и алидада имеют независимое и совместное вращение.
Теодолит, имеющий вертикальный круг, устройство для измерения расстоя ний (дальномер) и буссоль, называется теодолитом–тахеометром.
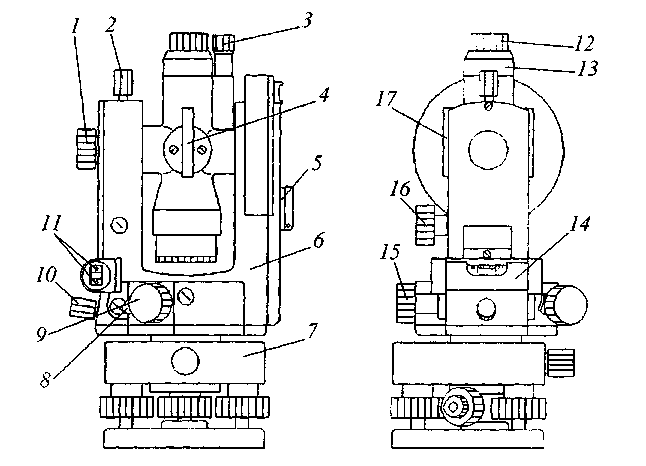
8.2. Основные части теодолита
Основными частями теодолита являются: лимб или горизонтальный круг, алидада, зрительная труба, цилинд рический уровень, подставки, вертикальный круг, подъемные винты.
Лимб (рис.8.3) является одной из основных частей всех геодезических приборов и представляет собой проградуированный от 0 до 360 круг, изготовленный из стекла или металла (в настоящее время применяют только стеклянные лимбы).
Алидада (см. рис. 8.3) соосна с лимбом, изготовлена также из стекла и представляет собой круг, на который нанесен штрих или шкала.
Рис. 8.3. Лимб, алидада
Зрительная труба (рис. 8.4) состоит из ряда линз, как выпуклых так и вогнутых и применяется для визирования на наблюдаемый предмет.
1 2 3 4 5 6
Рис. 8.4. Зрительная труба:
1 – предмет, 2 – объектив, 3 – фокусирующая линза,
4 – сетка нитей, 5 – окуляр, 6 – глаз
Сетка нитей (рис. 8.5) представляет собой стеклянную пластинку, на которую гравировкой нанесены нити сетки. Она служит для точного наведения на наблюдаемый предмет, а также снабжена дальномерными нитями для измерения расстояния.
Рис. 8.5. Сетки нитей:
1 – вертикальная нить, 2 – горизонтальная нить, 3 – дальномерные нити
Уровни (рис. 8.6) в теодолите позволяют установить прибор в строго вертикальное положение. Существует две конструкции уровней: цилиндрический и круглый.
Рис. 8.6. Уровни:
а) цилиндрический уровень: 0 – нульпункт уровня,
uu – ось цилиндрического уровня;
б) круглый уровень: 0 – нульпункт уровня,
uu – ось круглого уровня
Ось цилиндрического уровня – касательная к внутренней поверхности ампулы уровня в его нульпункте.
Ось круглого уровня – нормаль, проходящая через нульпункт 0, перпендикулярно к плоскости, касательной внутренней поверхности ампулы уровня в его нульпункте.
Поле зрения отсчетного микроскопа (для горизонтального и вертикального кругов) индивидуально для разных типов теодолитов и представлено на рис. 8.7 и
рис. 8.8.
а) б)
а) б)
Рис. 8.8. Поле зрения теодолита Т30:
а) ВК: 3°42, ГК: 54°23; б) ВК: 178°12, ГК: 233°42
8.3. Изучение устройства и поверки теодолита типа Т30
8.3.1. Изучение устройства теодолита типа Т30
При изучении устройства теодолита следует обратить внимание на работу наводящих винтов: они должны занимать среднее положение, чтобы была воз можность перемещения подвижных частей теодолита вправо и влево, вверх и вниз. Наводящие винты перемещаются при закрепленном положении закрепи тельных винтов.
До начала наблюдений и снятия отсчетов выполняется фокусировка нитей сетки (установка по глазу) и наблюдаемого предмета (установка по предмету). Во время угловых измерений фокусировку менять не рекомендуется.
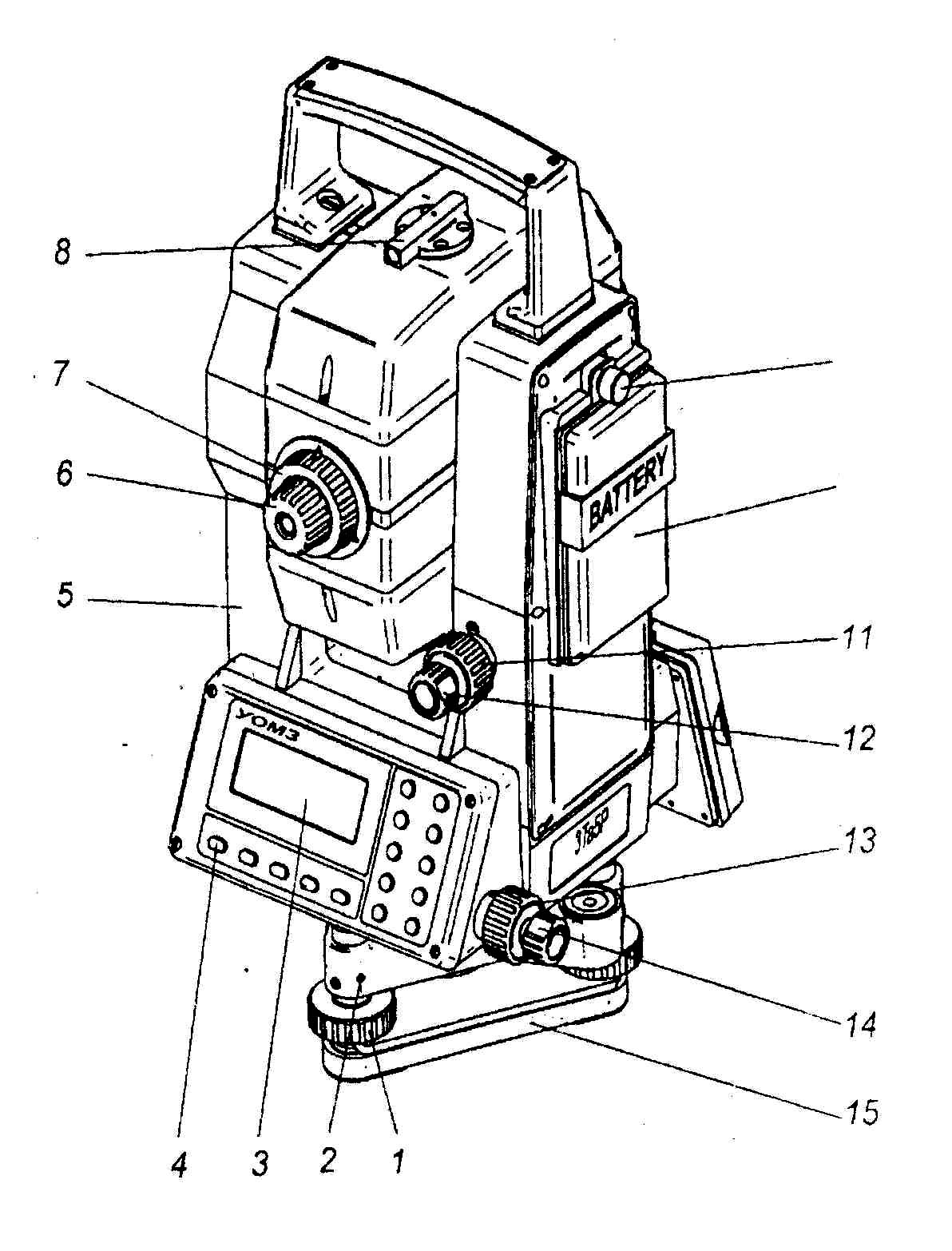
Теодолит типа Т30(рис. 8.9) представляет собой широко применяемый прибор, хорошо зарекомендовавший себя для технических работ на стройке, разбивке и строительстве сооружений и дорог, линий электропередач и связи и т.д.
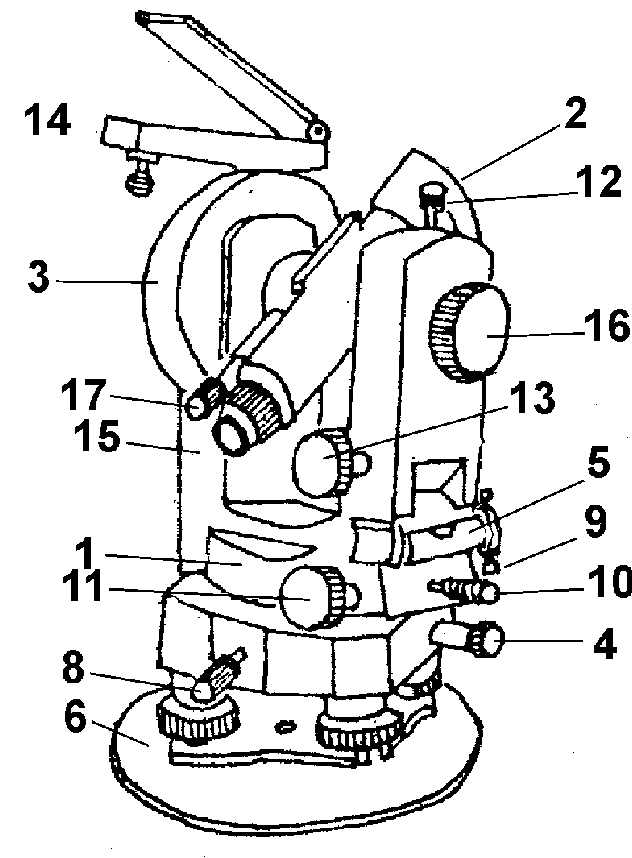
В последнее время появились модификации теодолита Т30 (рис.8.10): прямое изо бражение, отличная система отсчитывания, имеется в наличии винт, переме щающий лимб (см. рис. 8.10, 9), что удобно при ориентировании лимба во время выполнения теодолитной и тахеометрической съемок.
8.3.2. Поверки теодолита
Рис. 8.11. Основные оси и плоскости теодолита:
zz/ основная ось инструмента; uu/ ось цилиндрического
уровня; vv/ ви зирная ось трубы; ww/ ось вращения трубы
Основные геометрические условия, которые должны быть соблюдены в теодолите, вытекают из принципиальной схемы измерения горизонтального угла и заключаются в следующем:
- вертикальная ось инструмента должна быть отвесна;
- плоскость лимба должна быть горизонтальна;
- визирная плоскость должна быть вертикальна.
Проверка правильности работы инструмента и соблюдения его геометриче ских условий называется поверками инструмента.
Для соблюдения этих условий выполняются следующие поверки теодо лита:
1. Ось цилиндрического уровня при алидаде горизонтального круга должна быть перпендикулярна к основной оси инструмента.
Устанавливают ось цилиндрического уровня параллельно двум подъемным винтам инструмента. Вращая винты в противоположные стороны, пузырек уровня устанавливают на середину (рис. 8.12, а). Поворачивают алидаду гори зонтального круга на 180° (см. рис. 8.12, б). При отклонении пузырька уровня от се редины более, чем на 1 деление, положение оси уровня исправляют исправи тельными винтами уровня (см. рис. 8.9, винты 15; рис. 8.10, винты 11) на половину дуги отклонения.
I положение а) II положение б)
Рис. 8.12. К поверке уровня
2. Визирная ось трубы должна быть перпендикулярна к горизонтальной оси вращения трубы.
Угол отклонения визирной оси трубы от перпендикуляра к горизонтальной оси ее вращения называется коллимационной ошибкой трубы С.
Для проверки данного условия выбирают удаленную, находящуюся на го ризонте ясно видимую точку М, визируют на нее при положении КЛ и делают отсчет по лимбу, например, КЛ = 12512.
Затем переводят трубу через зенит, визируют на точку М при положении КП и снова берут отсчет по лимбу, например, КП = 30516 (рис. 8.13, а).
Вычисляют двойную коллимационную ошибку по формуле
2С = КЛ КП 180, (8.1)
2С = 12512 30516 + 180 = 4 2 (допуск), а затем и С коллимационную ошибку С = 2 1 (допуск).
Для исключения влияния коллимационной ошибки устанавливают на лимбе отсчет, вычисляемый по формулам
КЛиспр = КЛ С (8.2)
или КПиспр = КП + С. (8.3)
КЛиспр = 12512 (2) = 12514,
КПиспр = 30516 + (2) = 30514.
Центр сетки нитей при этом сойдет с точки М. Действуя боковыми испра вительными винтами сетки, передвигают ее до совмещения центра сетки нитей с изображением точки М (см. рис. 8.13, б).
а) б)
Рис. 8.13. К поверке коллимационной ошибки
3. Горизонтальная ось вращения трубы должна быть перпендикулярна к вер тикальной оси инструмента.
Установив теодолит в 3040 м от стены какого-либо здания (рис. 8.14) и приведя лимб в горизонтальное положение, центр сетки нитей наводят на неко торую высоко расположенную точку А стены. При закрепленной алидаде (при КЛ) наклоняют трубу до примерно горизонтального положения ее визирной оси и отмечают карандашом на стене точку а1 – проекцию центра сетки нитей. Переводят трубу через зенит, открепляют алидаду и при втором положении трубы (КП) снова наводят центр сетки нитей на точку А. Наклоняют трубу и отмечают карандашом на стене точку а2 – проекцию центра сетки нитей. При совпадении точек а1 и а2 условие выполняется. В противном случае (допуск две проекции не должны выходить за пределы биссектора нитей сетки) ось вращения трубы неперпендикулярна к основной оси инструмента. Эта погреш ность вызывается неравенством подставок, на которых располагается труба. В современных конструкциях инструментов подставки трубы не имеют исправи тельных винтов, поэтому погрешность может быть устранена только в мастер ской.
Рис. 8.14. К поверке равенства подставок
4. Одна из нитей сетки должна быть горизонтальна, другая вертикальна.
Наводят центр нитей сетки на какую-нибудь точку или отвес (рис. 8.15) и медленно поворачивают алидаду вертикального круга вокруг ее оси вращения, наблюдая за положением точки. Если при перемещении трубы изображение точки (отвеса) не будет сходить с вертикальной нити, то условие выполнено. В противном случае поворотом сетки нитей, при ее откреплении, производится исправление положения сетки.
Рис. 8.15. К поверке нитей сетки
5. Поверка места нуля вертикального круга.
Место нуля вертикального круга (МО) – отсчет по вертикальному кругу, когда визирная ось трубы горизонтальна, а пузырек уровня при алидаде нахо дится на середине.
Зрительную трубу при КЛ наводят на некоторую точку М (рис. 8.16) и по сле приведения пузырька уровня при алидаде горизонтального круга на сере дину берут отсчет по вертикальному кругу, например, КЛ = 512. Аналогичные действия выполняют при КП, берут отсчет по вертикальному кругу, например, КП = 17436.
Вычисляют место нуля по формуле
При значении места нуля более допуска, микрометренным винтом трубы (см. рис. 8.9, 13 или рис. 8.10, 16) устанавливают на вертикальном круге отсчеты
КЛиспр = КЛ МО (8.5)
или КПиспр = КП МО. (8.6)
КЛиспр = 512 (6) = 518,
КПиспр = 17436 (6) = 17442.
Наблюдаемая точка М сместится по вертикали. Вертикальными исправительными винтами сетки перемещают изображение точки М до совмещения ее с центром сетки (рис. 8.16).
Рис. 8.16. К поверке места нуля
8.4. Измерение горизонтальных и вертикальных углов
Работа по измерению углов на станции выполняется в следующем порядке:
1) установка теодолита в рабочее положение: центрирование инструмента (рис. 8.17, а), приведение оси инструмента в отвесное положение (нивелирование инстру мента, см. рис. 8.17, б), ориентирование инструмента (см. рис. 8.17, в), установка трубы для визирования;
Рис. 8.17. Установка теодолита в рабочее положение:
а) центрирование; б) нивелирование; в) ориентирование
2) измерение горизонтальных углов (или направлений) (рис. 8.18, 8.19) и углов наклона, обра ботка журнала наблюдений и контроль измерений на станции.
8.4.1. Измерение теодолитом горизонтальных углов
Для измерения горизонтальных углов применяются преимущественно: спо соб приемов для измерения одного угла, способ круговых приемов при измере нии углов на станции между тремя и более направлениями и способ повторе ний.
а) Способ приемов
Для измерения угла АСВ теодолит устанавливают в вершине угла С
Рис. 8.18. Способ приемов
Порядок работы на станции
- При КЛ, при закрепленном лимбе, поворачивают алидаду, пока по ГК
будет отсчет 00;
- при закрепленной алидаде поворачивают лимб, пока стрелка буссоли
укажет на север, закрепляют лимб;
- открепляют алидаду, наводят на заднюю точку А, сни мают отсчет а1
по ГК;
- открепляют алидаду, наводят на переднюю точку В, снимают отсчет а2
по ГК.
Наводящим винтом лимба поворачивают лимб на 1 – 2 (для ослабления
влияния инструментальных ошибок теодолита), трубу переводят через зенит.
- При КП открепляют алидаду, наводят на заднюю точку, снимают отсчет
по ГК;
- открепляют алидаду, наводят на переднюю точку, снимают отсчет
по ГК;
1 и 2 полуприемы составляют один полный прием.
Вычисляют угол 1 = а2 – а1 (левый угол) или = а1 – а2 (правый угол). Вы числяют угол 2 = . Разность углов 2 1 из двух полуприемов допуска ется
1.
Данные угловых измерений заносят в специальный полевой журнал (табл. 8.1):
Таблица 8.1
Журнал измерения горизонтальных углов
|
Точка |
Круг |
Отсчет по гориз. кругу |
Угол |
Среднее из углов |
||||
|
стояния |
на блюд |
|||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
С |
А |
КЛ |
27 |
16 |
||||
|
В |
КЛ |
105 |
36 |
78 |
20 |
|||
|
А |
КП |
210 |
32 |
78 |
20 |
|||
|
В |
КП |
288 |
53 |
78 |
21 |
б) Способ круговых приемов (при n 2)
КЛ: 1, 2, 3, 1
КП: 1, 3, 2, 1
Рис. 8.19. Способ круговых приемов
Порядок работы на станции
- При КЛ, при закрепленном лимбе, поворачивают алидаду, пока
отсчет по ГК будет 0 0;
- при закрепленной алидаде поворачивают лимб, пока центр сетки
будет наведен на 1 точку (со средней удаленностью и наилучшей види-
мостью),
- закрепляют лимб, снимают отсчет по ГК (близкий к 0);
- открепляют алидаду, наводят последовательно на 2, и 3 точки,
(замыкание горизонта), каждый раз снимая отсчет по ГК;
- трубу переводят через зенит, при КП наводят последовательно
на 1, 3, 2 и 1 точки, снимая каждый раз отсчет по ГК.
Лимб переставляют на 90 и все действия повторяют (2 прием).
Данные угловых измерений на пункте С заносят в специальный полевой жур нал (табл. 8.2). Вначале вычисляют значения направлений как среднее из отсчетов при круге лево и круге право (с учетом того, что разность отсчетов 180). Уравненные направления вычисляют как разность значения направлений на каждую точку наведения и значением направления на первую точку: 12416,5 002 = 12414,3. Незамыкание горизонта (разность значений на правлений на первую точку в начале и конце приема): ср = +0,5 распреде ляется пропорционально направлениям: в первое направление одна часть по правки (0,2), во второе – две части (0,4) и т.д.
Таблица 8.2
Журнал измерения горизонтальных направлений
|
№ точек наведения |
Круг |
Отсчет по ГК |
Значение направлений |
Уравненные направления |
|||
|
° |
° |
° |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
Л |
0 |
02 |
0 |
|||
|
П |
180 |
02 |
0 |
02 |
0 |
02 |
|
|
2 |
Л |
124 |
16 |
0,2 |
|||
|
П |
304 |
17 |
124 |
16,5 |
124 |
14,3 |
|
|
3 |
Л |
265 |
39 |
0,4 |
|||
|
П |
85 |
40 |
265 |
39,5 |
265 |
37,1 |
|
|
1 |
Л |
0 |
02 |
0,5 |
|||
|
П |
180 |
03 |
0 |
02,5 |
0 |
|
|
|
л=0 |
п=+1 |
ср=+0,5 |
в) Способ повторений
Способ заключается в последовательном откладывании на лимбе величины измеряемого угла. Способ применяется при измерении теодолитами с отсчет ными приспособлениями малой точности. Т.к. этот способ применяется редко, в пособии он рассмотрен не будет.
8.4.2. Измерение теодолитом вертикальных углов (углов наклона)
Поскольку вертикальные углы измеряются в основном при тригонометри ческом нивелировании, работу начинают с измерения высоты инструмента i. Каждый раз, наводя на наблюдаемую точку, отмечают высоту наведения ви зирной оси v.
Измерение углов наклона выполняется в следующей последовательности:
- при КЛ наводят на наблюдаемую точку, отмечают высоту наведения и сни мают отсчет по вертикальному кругу;
- при КП наводят на ту же точку, снимают отсчет по вертикальному кругу.
Вычисляют место нуля вертикального круга (МО) по формулам
для теодо лита Т30: , (8.7)
для теодолита 2Т30, 4Т30: . (8.8)
Вычисляют угол наклона по формулам
для теодолита Т30:
или = М0 – КП – 180, (8.9)
для теодолита 2Т30, 4Т30:
.
Данные измерений заносят в табл. 8.3.
Таблица 8.3
Журнал измерения углов наклона
|
Точка |
Круг |
Вертикальный круг |
||||||
|
стоя ния |
наблюдения |
отсчет |
место нуля |
угол наклона |
||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
С |
А |
КЛ |
2 |
22 |
1 |
2 |
23 |
|
|
КП |
177 |
36 |
||||||
|
В |
КЛ |
352 |
35 |
1 |
7 |
24 |
||
|
КП |
187 |
23 |
8.5. Теодолитные работы
8.5.1. Полевые работы при прокладке теодолитных ходов
Теодолитные ходы по точности подразделяются на два разряда: первый – с относительной погрешностью не грубее 1:2000 и второй – 1:1000.
Теодолитный ход представляет систему ломаных линий на местности, в которых углы измерены теодолитом, а стороны – 20-метровой стальной лентой или дальномером соответствующей точности.
Теодолитные ходы прокладывают между опорными геодезическими пунктами (рис. 8.20).
а) Схемы построения теодолитных ходов
Одиночный ход Замкнутый ход Висячий ход
Рис. 8.20. Схемы теодолитных ходов
б) Проектирование, рекогносцировка и закрепление точек хода
Проект ходов выполняют на карте (плане), чертеже местности. Длина сторон хода должна быть 20 – 350 м. Длины ходов зависят от масштаба съемки и не должны превышать значений, приведенных в табл. 8.4.
Таблица 8.4
|
Масштаб съемки |
Допустимая длина теодолитного хода между пунктами геодезической основы, км, на территории |
|
|
застроенной |
незастроенной |
|
|
1 |
2 |
3 |
|
1:500 |
0,8 |
1,2 |
|
1:1000 |
1,2 |
1,8 |
|
1:2000 |
2,0 |
3,0 |
|
1:5000 |
4,0 |
6,0 |
Точки хода закрепляют временными знаками: кованными гвоздями, костылями, металлическими трубками, деревянными кольями.
8.5.2. Угловые и линейные измерения
а) Угловые измерения
В теодолитном ходе теодолитом типа Т30 измеряют или правые, или левые по ходу гори зонтальные углы одним полным приемом.
Работа по измерению углов на станции выполняется в следующем порядке:
- установка теодолита в рабочее положение: центрирование инструмента, приведение оси инструмента в отвесное положение (нивелирование инструмента), ориентирование инструмента, установка трубы для визирования;
- измерение горизонтальных углов (направлений) и углов наклона, обработка журнала наблюдений и контроль измерений на станции.
Для измерения горизонтальных углов применяются преимущественно:
- способ приемов для измерения одного угла;
- способ круговых приемов при измерении углов на станции между тремя и более направлениями и способ повторений.
б) Линейные измерения
В теодолитных ходах производят измерение сторон D в прямом и обратном направлениях лентой, рулеткой, дальномером, тахеометром и др. Для средних условий местности разница между измеренным значением линии прямо и обратно должна удовлетворять условию
. (8.11)
В измеренные стороны вводят поправки за компарирование, температуру и угол наклона, получая горизонтальные проложения линий d.
в) Привязка теодолитных ходов к пунктам опорной геодезической сети
Для передачи исходного направления, а также координат на точки теодолитного хода измеряют примычные углы на исходных пунктах (рис. 8.21).
Рис. 8.21. Привязка хода к исходным пунктам
8.5.3. Камеральные работы при обработке результатов измерений
а) Обработка журналов. Составление схемы теодолитных ходов
Камеральные работы начинают с проверки полевых журналов. Затем на бумаге по средним значениям углов и длинам линий составляют схему теодолитных ходов. На схеме показывают твердые пункты.
б) Уравнивание теодолитного хода
Уравнивание углов
Рис. 8.22. Разомкнутый ход
Рис. 8.23. Замкнутый ход
- Подсчет суммы измеренных углов по формуле
изм = 1 + 2 +…. (8.12)
- Вычисление теоретической суммы углов для разомкнутого хода по формулам
теор = (кон н) + 180· n (если измерены левые углы),
теор = (н кон) + 180· n (если измерены правые углы), (8.13)
для замкнутого хода:
теор = 180· (n 2) (для внутренних углов). (8.14)
- Вычисление угловой невязки хода по формуле
f = изм теор. (8.15)
- Вычисление допустимой угловой невязки хода
fдоп = 1n. (8.16)
Если f fдоп, угловые измерения признаны доброкачественными.
- Вычисление поправок в измеренные углы
. (8.17)
- Вычисление уравненных углов ур
ур = изм + v. (8.18)
Контролем правильности вычисления поправок является выполнение условия
v = f, (8.19)
а правильности их введения в углы – условие
ур = теор. (8.20)
- Вычисление дирекционных углов всех линий хода
1 = н + 180 + для левых углов,
1 = н + 180 для правых углов. (8.21)
Контролем правильности вычисления дирекционных углов является получение конечного дирекционного угла кон – для разомкнутого хода и н – для замкнутого хода.
Вычисление координат пунктов
- Вычисление приращений координат по уравненным дирекционным углам и горизонтальным проложениям линий
х = d cos ,
у = d sin . (8.22)
- Вычисление суммы вычисленных приращений координат по осям х и у:
х выч = х1 + х2 +…+хn,
у выч = у1 + у2 +…+уn. (8.23)
- Вычисление теоретической суммы приращений координат для разомкнутого хода:
х теор = хкон хнач,
у теор = укон унач; (8.24)
для замкнутого хода х теор = 0,
у теор = 0. (8.25)
- Вычисление невязок по осям координат для разомкнутого хода
fх = х выч х теор,
fу = у выч у теор; (8.26)
для замкнутого хода fх = х выч,
fу = у выч. (8.27)
- Вычисление абсолютной невязки хода
fS = (8.28)
и относительной невязки хода
(8.29)
характеризующей качество полевых измерений. Должно выполняться условие:
.
- Уравнивание хода состоит в распределении невязок fх и fУ с их обратным знаком на все вычисленные приращения координат пропорционально длинам сторон хода. Поправки vх и vу вычисляют по формулам:
, . (8.30)
- Исправленные приращения координат получают как алгебраическую сумму вычисленных приращений и соответствующих поправок к ним, т.е.:
х испр = х выч + vX,
у испр = у выч + vу. (8.31)
Контролем правильности вычисления поправок является выполнение условий:
vX = fх, vу = fу, (8.32)
а правильности вычисления исправленных приращений координат условий
х испр = х теор,
у испр = у теор. (8.33)
- Вычисление координат точек хода производится по формулам:
хn+1 = хn + х испр,
уn+1 = уn + у испр. (8.34)
Контролем вычислений является получение координат конечного пункта, если ход разомкнутый, и координат начального пункта, если ход замкнутый.
8.6. Топографические съемки
Съемка местности – совокупность угловых и линейных измерений, выполняемых на земной поверхности для создания плана, карты или профиля.
Съемки делятся на:
- наземные (теодолитная, тахеометрическая, мензульная, фототеодолитная, буссольная, глазомерная);
- воздушные (комбинированная, стереотопографическая).
Контурная съемка (горизонтальная) служит для получения плана без рельефа. Топографическая съемка служит для получения плана местности с рельефом. Высотная (вертикальная) съемка выполняется для получения изображения только рельефа.
По виду использованных инструментов съемка бывает:
- теодолитная, инструменты: – теодолит, лента, рейка;
- тахеометрическая – теодолит-тахеометр, рейка;
- мензульная – мензула, кипрегель, рейка;
- фототеодолитная – фототеодолит;
- аэрофотосъемка:
- комбинированная съемка – мензула с планшетом, кипрегель, рейка;
- стереотопографическая съемка – аэрофотоаппарат, стереоприбор;
- буссольная – буссоль;
- глазомерная – планшет, компас, визирная линейка.
Тахеометрическая съемка
Тахеометрическая съемка применяется при изысканиях новых железных и автодорог, проектировании вторых путей, развитии станции, проектировании и строительстве искусственных сооружений. На основании материалов тахеометрической съемки составляют планы трассы в масштабе 1:10 000, на планах более крупных масштабов (1:1000, 1:2000, 1:5000) проектируют строительство зданий, искусственных сооружений, пересечение трассы железнодорожного пути с автодорогами.
Тахеометрическая съемка – съемка, при которой определяют положение точек земной поверхности по 3-м измерениям: направлению, расстоянию и высоте. В результате тахеометрической съемки получают план местности и ее рельеф. Расстояния получают по дальномеру, направления – по горизонтальным углам, превышения – методом тригонометрического нивелирования. Тахеометрическая съемка выполняется на местности с ярко выраженным рельефом для составления планов в масштабах 1:1000, 1:2000, 1:5000.
Полевые работы
- Рекогносцировка местности: уточнение положения станций теодолитного хода на местности, обзор местности.
- Ведение абриса (рис. 8.24):
- ориентирование на север;
- зарисовка контуров, числовые характеристики объектов;
- направление склонов;
- нумерация пикетов.
- Работа на станции:
- устанавливают тахеометр над колышком, центрируют, нивелируют, измеряют высоту теодолита i до 0,01 м;
- определяют на станции место нуля М0;
- ориентируют по одному из исходных пунктов, устанавливают по ГК 000, записывают в журнал № станции ориентирования;
- открепляют алидаду, наводят на рейку на первом пикете, определяют расстояние по дальномеру d;
- опускают зрительную трубу как можно ниже, снимают отсчет по ГК;
- наводят среднюю нить сетки зрительной трубы на высоту v рейки (для удобства v = i), берут отсчет по ВК;
- наводят последовательно на все пикеты, действия повторяют;
- замыкают горизонт, для чего наводят снова на ориентирный пункт, незамыкание допускается 1.
Рис. 8.24. Абрис съемки
Камеральные работы
Обрабатывают полевой журнал:
- вычисляют горизонтальные проложения
d = D·cos2, (8.35)
где D – расстояние, измеренное дальномером,
– угол наклона;
- вычисляют превышения
h = h/ + i v, (8.36)
где h/ = d · tg,
i – высота прибора,
v – высота наведения;
- вычисляют отметки пикетов
Нпк = Нст + h. (8.37)
На бумагу наносят координаты теодолитного хода. Устанавливают транспортир, откладывают все горизонтальные углы, расстояния и подписывают отметки пикетов. С абриса переносят ситуацию по номерам пикетов.
Тема 9. Нивелирные работы
9.1. Нивелирование. Назначение. Методы нивелирования
Нивелирование – процесс геодезических измерений для определения пре вышения точек одной над другой и высот точек над уровнем моря.
Назначение – для определения высот точек при топографической съемке, составлении карт, планов, профилей, для установки строительных конст рукций, для наблюдения за осадкой и деформациями зданий, для строи тельства линейных сооружений, установки ускорителей на АЭС.
Методы нивелирования:
- Геометрическое нивелирование (рис. 9.1) – нивелирование с помощью горизонтального луча (а и b – отсчеты по рейке, i – высота нивелира).
Из середины Вперед
h = a – b h = i – b
Рис. 9.1. Геометрическое нивелирование
Если нивелирование выполняют с одной станции, это простое нивелирование. Чаще приходится выполнять сложное нивелирование (рис.9.2).
Рис. 9.2. Сложное нивелирование: h = а – b
Уравнивание хода: hизм = а – b = hi;
hтеор = Нкон – Ннач (для разомкнутого хода);
hтеор = 0 (для замкнутого хода);
fh = hизм – hтеор;
Допустимые невязки по ходу (полигону)
fh доп = 3 ммLкм для I класса;
fh доп = 6 ммLкм для II класса;
fh доп = 10 ммLкм для III класса;
fh доп = 20 ммLкм для IV класса;
fh доп = 50 ммLкм для технического нивелирования.
- Тригонометрическое нивелирование (рис. 9.3) – нивелирование наклонным лу чом.
h = h + i – v
Рис. 9.3. Тригонометрическое нивелирование:
i – высота нивелира; v – высота наведения;
h – превышение; – угол наклона
h = D sin, где D – расстояние, измеренное лентой;
h = , – расстояние, измеренное нитяным дальномером;
h = d tg, d – горизонтальное проложение (d = D cos или d = cos2).
3) Физическое нивелирование:
а) гидростатическое (рис. 9.4) – для определения превышений по разности уровня жидкости в сообщающихся сосудах;
Рис. 9.4. Гидростатическое нивелирование
б) барометрическое – определение превышений по изменению барометрического давления в зависимости от высоты;
в) радиолокационное – определение высоты АФА над уровнем Земли по времени прохождения радиоволн до Земли и обратно.
4) Автоматическое нивелирование – с помощью специальных приборов, устанавливаемых на велосипеде, автомобиле, ж/д платформе, вычерчивается профиль местности.
9.2. Системы высот
Рис. 9.5. Системы высот:
Н1 – нормальная высота (над квазигеоидом);
Н2 – абсолютная высота (над геоидом);
Н3 – геодезическая высота (над эллипсоидом);
h – относительная высота (превышение между точками L и N).
9.3. Нивелиры, рейки, принадлежности, классификация
Нивелиры, классификация
По ГОСТу – 69, 76 нивелиры бывают:
- высокоточные Н05, Н1, Н2, НС2;
- точные Н3, Н4 НС3, НС4;
- технические Н10, Н10КЛ, НТ, НТС, НЛС.
Принятые обозначения:
- 1, 2 – ср. кв. погрешность определения превышения на 1 км хода (двойного хода);
- С – с самоустанавливающейся линией визирования;
- Л – с лимбом;
- К – с компенсатором;
- Т – технический.
Рейки
Рейки, применяемые в геодезии, бывают 3, 4 и 5-и метровые; складные, цельные; деревянные, металлические, инварные. Для привязки хода нивелирования к стенным знакам применяется специальная подвесная рейка длиной 1,2 м.
Принадлежности
Для исключения ошибок установки реек нивелирование выполняют по башмакам или костылям.
Отсчетные приспособления
На рис. 9.6 показано поле зрения нивелиров, у которых может быть прямое (а) или обратное (б) изображение.
а) б)
1191 мм 1259 мм
Рис. 9.6. Поле зрения нивелира: а) с прямым изображением;
б) с обратным изображением
9.3.1. Устройство, поверки и юстировка нивелира
а) Устройство нивелиров
Линия визирования у нивелира приводится в горизонтальное положение двумя способами:
- с помощью элевационного винта и цилиндрического уровня при трубе, напри мер у нивелира Н3 (рис. 9.7);
- автоматически с помощью компенсатора малых углов наклона визирной оси, например у 3Н3КЛ (рис. 9.8) или С410 (Sokkiл) (рис. 9.9).
Для работы с нивелиром необходимо изучить их устройство по рис. 9.7.9.9.
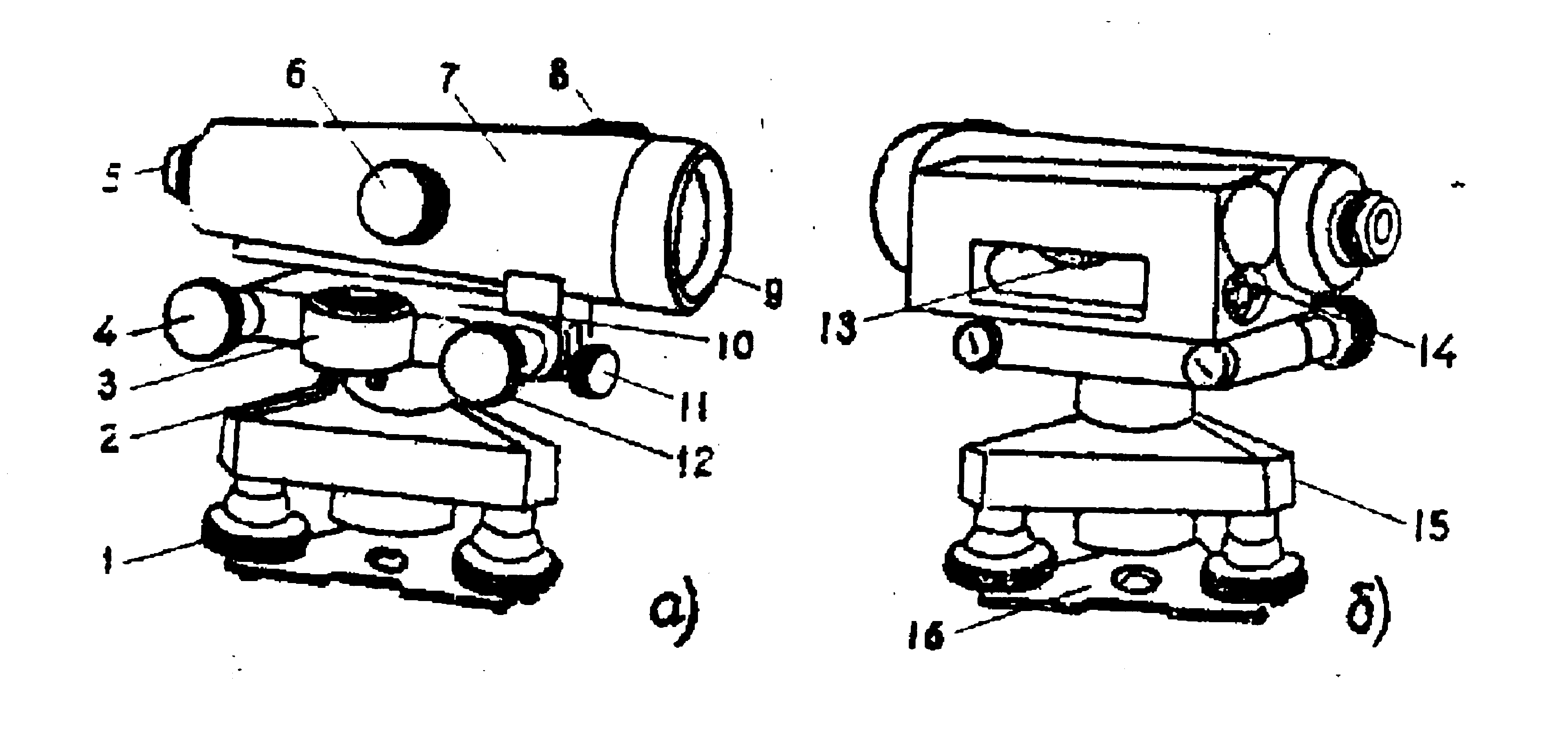
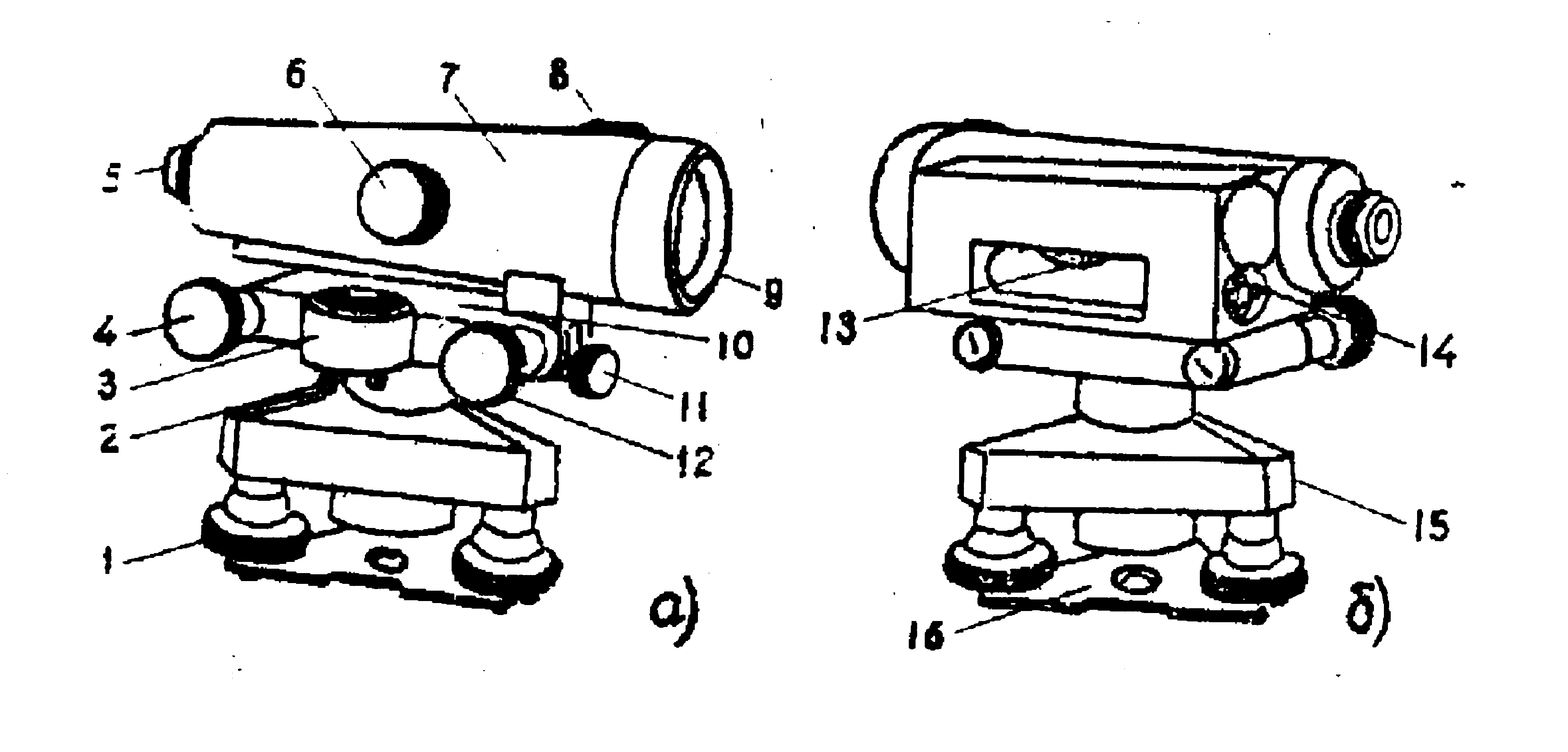
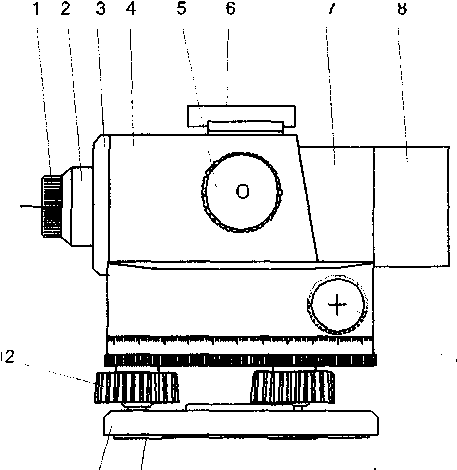
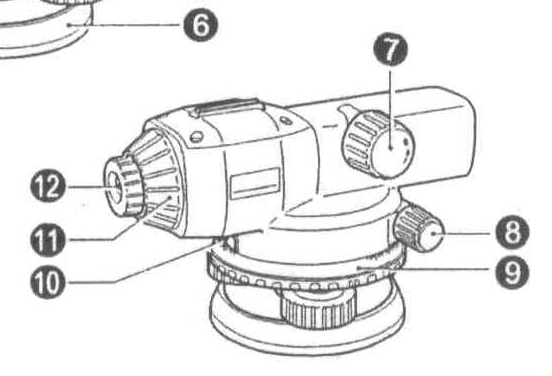
б) Поверки нивелиров
Поверки нивелира связаны с его основными осями, которые для нивелиров с уровнем при трубе показаны на рис. 9.10.
Рис. 9.10. Основные оси нивелира:
ОО ось вращения нивелира; ww ось круглого уровня;
vv визирная ось зри тельной трубы; uu ось цилиндрического
уровня при трубе
Основные геометрические условия, которые должны быть соблюдены в таких нивелирах, заключаются в следующем:
- ось круглого уровня должна быть параллельна оси вращения нивелира;
- вертикальная нить сетки должна быть параллельна оси вращения нивелира;
- ось цилиндрического уровня должна быть параллельна визирной оси зрительной трубы.
Поверки нивелиров с уровнем при трубе
Для соблюдения этих условий выполняются следующие поверки нивелира:
1. Ось круглого уровня должна быть параллельна оси вращения нивелира.
Для поверки этого условия подъемными винтами приводят пузырек круглого уровня в нульпункт и поворачивают трубу нивелира на 180. Если пузырек сме стился с нульпункта более, чем на 0,5 деления, исправительными винтами круг лого уровня (см. рис. 9.7, пункт 2 или рис. 9.8, пункт 10) перемещают пузырек к цен тру на половину дуги отклонения и окончательно совмещают пузырек уровня с центром ампулы с помощью подъемных винтов.
2. Вертикальная нить сетки должна быть параллельна оси вращения ниве лира.
Подвешивают отвес. На расстоянии 20 25 м от отвеса устанавливают ниве лир, при водят его в рабочее положение. Вертикальную нить сетки зрительной трубы совмещают с нитью отвеса. Если нить зрительной трубы не совпала с ни тью отвеса более чем на 0,5 мм, положение нитей сетки исправляют. Для этого от винчивают винты 1 (рис. 9.11), которыми окулярная часть скреплена с корпусом зрительной трубы, снимают окулярную часть, открепляют винты 2 на оборота, а винт 3 на оборота и рукой поворачивают сетку до совмещения вертикальной нити со шнуром отвеса. Винты закрепляют.
Рис. 9.11. К поверке нитей сетки
3. Поверка цилиндрического уровня. Она состоит из 2-х частей:
- отвесная плоскость, проходящая через ось уровня, должна быть парал лельна отвесной плоскости, проходящей через визирную ось трубы;
- ось цилиндрического уровня и визирная ось зрительной трубы должны быть параллельны.
Для первой части поверки на расстоянии 50 м от рейки устанавливают ниве лир так, чтобы один из подъемных винтов располагался в створе визирования на рейку. Два других винта займут симметричное положение относительно линии ви зирования (рис. 9.12).
Рейка
Л П
Рис. 9.12. К поверке цилиндрического уровня (1 часть)
Нивелир приводят в рабочее положение. Зрительную трубу наводят на рейку. Элевационным винтом совмещают концы пузырька уровня, берут отсчет по рейке, например В = 1568 мм.
Вращая в противоположные стороны подъемные винты на 3 полных оборота, наклоняют нивелир влево. Элевационным винтом совмещают концы пузырька уровня, снова берут отсчет по рейке Вл =1566 мм.
Наклоняя нивелир вправо и повторяя еще раз все действия, берут отсчет
Вп= 1570 мм.
Вычисляют средний отсчет Вср и уклонения от него:
(9.1)
В Вср = 1 мм 3 мм; (9.2)
Вп Вл = +4 мм 8 мм. (9.3)
Если Вп Вл больше допуска и со знаком (+), боковыми юстировочными винтами цилиндрического уровня конец уровня перемещают ближе к окуляру. Если со знаком (), конец уровня перемещают от окуляра. После юстировки по верку повторяют.
Рис. 9.13. К поверке цилиндрического уровня (2 часть)
Вторую часть поверки цилиндрического уровня можно выполнять разными способами. Рассмотрим двойное нивелирование способом вперед. Для этого на ровной местности на расстоянии 50 м забивают в землю два колышка. Нивелир устанавливают в пределах 2 3 метров от первой точки. Элевационным винтом совмещают концы пузырька уровня, берут отсчеты на ближнюю (i1) и дальнюю (а2) рейки
(рис. 9.13, а).
Нивелир устанавливают вблизи точки 2, действия повторяют, снимают от счеты на ближнюю (i2) и дальнюю (а1) рейки (рис. 9.13, б).
Пример: i1 =1563 мм, a2 = 1466 мм, i2 =1464 мм, a1 = 1673 мм.
Вычисляют ошибку , указывающую на непараллельность визирной оси и оси цилиндрического уровня:
(9.4)
Если ошибка х превышает 4 мм, вычисляют исправленный отсчет по фор муле
= 1673 56 = 1617 мм. (9.5)
Вычисленный отсчет устанавливают по рейке элевационным винтом. Концы пузырька уровня разойдутся. Вертикальными юстировочными винтами уровня (см. рис. 9.7, пункт 14) совмещают изображение концов пузырька уровня.
Поверки нивелиров с компенсатором
В нивелирах с компенсатором типа 3Н3КЛ (см. рис. 9.8) проводят следующие поверки:
- поверка круглого установочного уровня;
- поверка сетки нитей;
- поверка компенсатора;
- поверка горизонтальности линии визирования.
Первую и вторую поверки проводят аналогично уровенным нивелирам. Перед следующими поверками, а также перед производством измерений необходимо убедиться, что компенсатор в нивелире срабатывает. Для этого нивелир приводят в рабочее положение и берут отсчет по рейке а. Повернув на 1/8 оборота подъем ный винт, задают малый угол наклона вдоль линии визирования. Сетка нитей трубы с работающим компенсатором должна после небольших колебаний вер нуться на тот же отсчет а по рейке. В противном случае нивелиром измерять нельзя, необходим ремонт компенсатора.
3. Поверка компенсатора. Определение диапазона его действия
Диапазон действия компенсатора – это угол наклона вертикальной оси ниве лира, в пределах которого нормально работает маятник компенсатора. Его опреде ляют при помощи отсчетов по рейке (в 50 м от нивелира) как для продольных (), так и для боковых () наклонов нивелира. Перед началом работ поверяется и юстируется круглый уровень.
С помощью подъемных винтов выполняют продольный или боковой наклон нивелир в обе стороны от нульпункта круглого уровня до момента зависания ма ятника компенсатора. Зависание фиксируют в момент резких изменений отсчетов по рейке (сетка нитей начинает перемещаться вместе с наклоном нивелира). Угол наклона при зависании определяют по смещению пузырька уровня или по цене 1 оборота подъемного винта в соответствии с показаниями отсчетов до наклона и по сле наклона в одну, а затем в другую стороны; например: до наклона а = 1570 мм, зависание началось при наклоне 20: +: 1566 мм, : 1569 мм,
+: 1564 мм, : 1565 мм.
4. Поверка горизонтальности линии визирования
После срабатывания компенсатора в нивелире визирная ось должна распола гаться в вертикальной плоскости, проходящей через оптическую ось объектива зрительной трубы, и быть горизонтальной.
Поверка выполняется аналогично поверке 3 нивелира с уровнем. Юстировка для первой части поверки выполняется в сервисных центрах заводаизготовителя.
Вторая часть поверки выполняется двойным нивелированием (см. рис. 9.13). Юстировка проводится поворотом оптического клина, установленного перед объ ективом, или при помощи вертикальных юстировочных винтов сетки, вращением которых устанавливают правильный отсчет , вычисленный по формуле (9.5).
9.4. Геодезические работы при проектировании и строительстве трасс железных и автомобильных дорог, проектировании трасс трубопроводов, ЛЭП и других линейных сооружений
Для составления проекта необходимо знать точное расположение будущей трассы на местности, иметь ее профиль, знать геологические и гидрологические условия по трассе, особенно на неблагоприятных участках (овраги, карсты, оползни, болота). Кроме того, надо выявить и изучить места для добычи строительных материалов – песка, гравия, камня. Все эти сведения и материалы получают в результате инженерных изысканий дороги.
Составление технического проекта начинают с камеральных работ: для проектирования используют топографические карты:
- масштабов 1:10 000 – 1:25 000 – в равнинных районах;
- 1:5000 – 1:10 000 – в холмистой местности;
- 1:2000 – в горной местности.
На карте выбирают наилучшее положение трассы, выполняют подсчет объема земляных работ по насыпям и выемкам. Путем полевого обследования камеральный вариант уточняется и производится окончательная укладка отдельных ее участков на местности.
При перенесении проекта трассы с плана или карты в натуру выполняют следующие геодезические работы:
- детальная рекогносцировка местности;
- определение в натуре положения углов поворота трассы;
- вешение линий;
- измерение углов и сторон хода;
- разбивка пикетажа и поперечников;
- нивелирование, закрепление трассы;
- крупномасштабная съемка переходов, пересечений, примыканий, мест со сложным рельефом.
Одновременно выполняют детальные инженерно-геологические, гидрометрические, почвенные обследования трассы, детальную разведку карьеров строительных материалов.
На основании подробных полевых изысканий составляют проект трассы, состоящий из рабочих чертежей, пояснительной записки с обоснованиями, расчетами, ведомостями объемов работ, документами согласований, геодезическими данными и других смет.
Данные разбивки заносят в пикетажную книжку (трасса шириной 2040 м). В пикетажном журнале фиксируют вершины углов поворота оси трассы, измеренные значения углов и элементы кривых по трассе.
Рис. 9.14. Разбивка трассы, углов поворота, пикетажа
9.4.1. Элементы закруглений. Разбивка главных точек круговой кривой
В местах поворота трассы производят разбивку закруглений.
При предварительных изысканиях на местности закрепляют ВУ, НК, СК, КК. Для этого необходимо знать элементы круговой кривой.
Элементы круговой кривой вычисляются по формулам:
(9.6)
При окончательных изысканиях производится детальная разбивка кривой.
9.4.2. Детальная разбивка кривых
1. Способ прямоугольных координат (в открытой местности при больших радиу сах R).
Рис. 9.16. Способ прямоугольных координат
Кривая разбивается на равные части через k = 1; 5; 10; 20; … м. Для построения точек на местности по значению длины дуги k вычисляется угол , по значению вычисляются координаты точек 1, 2, 3 и т.д. по формулам:
Х1 = Rsin, У1 = ;
Х2 = Rsin2, У2 = . (9.7)
На местности для построения т. 1 отрезок Х1 откладывают от НК по линии тангенсов, по перпендикуляру У1. Для построения т. 2 отрезок Х2 откладывают от НК по линии тангенсов, по перпендикуляру У2.
Более точно положение т. 1 получают откладыванием отрезка k по линии тангенсов и назад отступают на величину k – х1, т. 2 откладыванием отрезка 2k по линии тангенсов и назад отступают на величину 2k – х2 и т.д.
2. Способ продолженных хорд (в стесненных условиях при 200 R 300 м).
Шаг разбивки кривой а. По значению а и радиусу R вычисляют координаты т. 1 по формулам (9.8)
Для построения т. 1 (рис. 9.17) по линии тангенсов на местности откладывают от НК отрезок х1, а по перпендикуляру у1. Для построения т. 2 соединяют НК, т. 1 и далее в створе откладывают отрезок а. Получают вспомогательную т. 2. Из т. 2 отрезком, равным b, а из т. 1 отрезком, равным а, получают т. 2. Для построения т. 3 соединяют т. 1, т. 2 и далее в створе откладывают отрезок а. Получают вспомогательную т.3. Из т. 3 отрезком, равным b, а из т. 2 отрезком, равным а, получают т. 3.
;
у1 = ; . (9.8)
Рис. 9.17. Способ продолженных хорд
3. Способ углов (в любых условиях, при любых R)
Угол вычисляют по формуле sin = . (9.9)
Для построения т. 1 (рис. 9.18) теодолитом от линии тангенсов строят угол , откладывают хорду а. Для построения т. 2 теодолитом от линии тангенсов строят угол 2, из т. 1 делают засечку отрезком, равным а, на построенном луче угла.
Рис. 9.18. Способ углов
9.4.3. Вынос пикета на кривую
Рис. 9.19. Вынос пикета на кривую
От НК до пк 11 (рис. 9.19) вычисляют расстояние = 1100 – 1058,50 = 41,50 м.
С учетом формулы вычисляют (9.10)
= ,
а затем координаты выносимого пикета по формулам:
х = R sin, у = . (9.11)
х = 500 м sin 4°4520 = 41,45 м;
У = 2 500 sin2 2°2240 = 1,72 м.
Для выноса пикета на кривую от пк 11 назад отступают на величину
41,50 – 41,45 = 0,05 м
и по перпендикуляру откладывают у = 1,72 м.
9.4.4. Нивелирование трассы
По пикетным точкам и поперечникам, а также по установленным вдоль трассы постоянным и временным реперам производят техническое нивелирование (рис. 9.20). Постоянные знаки устанавливают через 20 30 км, временные – через 2 3 км. Реперы должны находиться вне зоны земляных работ.
Рис. 9.20. Нивелирование трассы: с – связующие точки; п – промежуточные точки
Пикеты и плюсовые точки закрепляют колышками длиной 15 – 20 см и сторожками (рис. 9.21), на которых надписывают номер пикета или значение плюсовой точки. Вершины угла поворота и главные точки кривых закрепляют кольями или металлическими штырями на глубину 30 – 40 см и опознавательным столбом с надписью организации, даты, номера угла. Ось трассы на длинных прямых участках закрепляют осевыми столбами через 200 – 500 м.
Рис. 9.21. Оформление пикета
Расстояние от нивелира до рейки допускается до 100 м, при благоприятных условиях до 150 м. Связующие точки намечают через 3 – 4 пикета, остальные точки берут как промежуточные. Невязка хода между твердыми пунктами:
fh доп = 50 мм L, км.
Результаты нивелирования записываются в журнал (табл. 9.1), в котором вычисляют отметки всех пикетов и плюсовых точек. Одновременно ведется пикетажная книжка.
Таблица 9.1
Полевой журнал технического нивелирования
|
№ станций |
№ нивелируемых точек |
Отсчеты по рейке |
Превышения |
Средние превышения |
Горизонт инструмента |
Абсолютные отметки |
||
|
задние |
передние |
промежуточные |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Рп19 |
1582 |
501,582 |
500,000 |
|||||
|
1 |
6266 |
102 |
||||||
|
пк0 |
1684 |
104 |
103 |
499,897 |
||||
|
6370 |
||||||||
|
пк0+10 |
1320 |
500,262 |
Связующие точки нивелируются по двум сторонам рейки, остальные пикеты – только по черной стороне рейки. Горизонт инструмента вычисляется по формуле
ГИ = Нст + ачерн.стор.задн.рейки. (9.12)
Отметка промежуточной точки вычисляется по формуле
Нпром = ГИ – bчерн.стор.перед.рейки. (9.13)
После обработки результатов нивелирования вычисляют основные элементы кривой и по ним – значения главных точек кривой. Эти записи ведут в пикетажной книжке.
9.4.5. Камеральные работы при трассировании линейных сооружений
1. Проверка полевого журнала: вычисление превышений, средних превышений.
Вычисляют сумму превышений по ходу между исходными реперами hизм. Теоретическую сумму вычисляют по формуле hтеор = Нкон Ннач. Невязку по ходу определяют по формуле fh = hизм hтеор. Допустимую невязку определяют по формуле fh доп = ± 50 мм L км. Распределяют невязку во все превышения. Вычисляют отметки связующих точек, отметку горизонта инструмента, отметки промежуточных точек.
2. Построение сетки продольного профиля: наносят пикеты, плюсовые точки, расстояния между ними.
3. Строят профиль, для чего из полевого журнала выписывают с точностью до 0,01 м отметки всех пикетов.
4. Выбирают проектную линию с уклонами 0,005 i 0.050. Нпр начальной и конечной точек берут графически с плана. Вычисляют проектные уклоны по формуле
. (9.14)
Вычисляют проектные отметки всех точек, рабочие отметки по формуле
араб = Нпр Нземли. (9.15)
5. Вычисляют расстояния х и у до точек нулевых работ 0 (рис. 9.22) по рабочим отметкам по формулам:
х = , у = , (9.16)
где a и b – рабочие отметки с разными знаками;
d – расстояние между пикетами.
Рис. 9.22. Расстояние до точек нулевых работ
|
Развернутый план дороги |
пашня лес луг Уг2 луг |
|||||||||||
|
пашня Уг1 лес луг луг |
||||||||||||
|
Про ект. данные |
Отметки бровки земляного полотна, м |
|||||||||||
|
Уклоны |
||||||||||||
|
Факт. данные |
Отметки земли, м |
|||||||||||
|
Расстояния, м |
||||||||||||
|
Пикеты Прямые и кривые в плане Указатель километров |
10 11 12 13 14 15 16 17 18 19 20 21
|
Тема 10. Геодезические работы, связанные
со строительством
10.1. Основные элементы разбивочных работ
Разбивочными работами называются геодезические построения, имеющие це лью определение на местности положения сооружения и его частей в плане и по высоте в соответствии с проектом.
Разбивочные работы включают:
- построение на местности линий заданной длины;
- построение на местности заданных углов;
- вынесение на местность точки с заданной отметкой;
- построение на местности линий и плоскостей заданного уклона.
1) Построение на местности линий заданной длины является наиболее распро страненной при разбивочных работах задачей. Подлежащая отложению длина ли нии задается горизонтальным проложением d; в общем случае требуется отложить соответствующее ему расстояние на наклонной топографической поверхности Д:
d = Д + Дк + Дt +Д. (10.1)
Д = d Дк Дt Д. (10.2)
Задача решается при помощи ленты или рулетки двумя способами:
- непосредственное отложение заданной длины на заранее подготовленной гори зонтальной поверхности;
- отложение отрезка заданной длины с последующим перемещением конечной точки отрезка на величину поправки за наклон местности.
При применении обоих способов вводят поправки с обратным знаком за ком парирование мерного прибора , а также за разность температур компариро вания и измерения .
При применении второго способа в непосредственное измерение на местности вводят также с обратным знаком еще и поправку за наклон .
2) Построение на местности заданных углов выполняют в такой последо вательности: теодолит устанавливают в вершине О угла MON, который надо построить от направления на точку М (рис. 10.1). На лимбе откладывают проектный угол (при КП или КЛ) и в полученном направлении закрепляют точку N/.
Аналогично повторяют построение угла при другом положении вертикаль ного круга и отмечают вторую точку N//.
Точка N в середине отрезка N/N// фиксирует направление ON.
Рис. 10.1. Построение проектного горизонтального угла
При построении угла с повышенной точностью (рис. 10.2) строят угол выше описан ным способом. Угол измеряют с установленной точностью. Вычисляют раз ность = пр изм. Вычисляют расстояние NN0, на которое надо переместить по пер пендикуляру точку N в ее проектное положение N0 по формуле
. (10.3)
Рис. 10.2. Построение проектного горизонтального угла повышенной точности
- Вынесение на местность точки с заданной проектной отметкой
При строительстве зданий, дорог бровка земляного полотна, фундаменты мостов, трубы, цоколь здания и др. сооружения должны быть расположены на проектном горизонте.
Проектный горизонт каждой части сооружений в процессе строительства определяют путем выноса проектной отметки на эту часть.
Проектный горизонт Нпр т. В строят на местности с помощью нивелира и рейки (рис. 10.3). Посередине между репером с известной отметкой Нреп и т. В устанавливают нивелир.
По рейке, стоящей на репере, производят отсчет а, вы числяют горизонт инструмента по формуле
Нi = Нреп + а (10.4)
и разность
b = Нi Нпр. (10.5)
После этого в точке В устанавливают рейку так, чтобы по ней был отсчет b, при котором высота пятки рейки и будет равна проектной отметке. Под пяткой рейки, на забитом около нее коле, фиксируют положение искомой точки.
Рис. 10.3. Вынесение в натуру точек с заданной проектной отметкой
4) Построение на местности линий и плоскостей заданного уклона
Построение проектной линии состоит в том, что на местности ставят ряд колышков, их верхний срез должен быть на одной прямой линии с заданным уклоном.
По линии заданного уклона строят земляное полотно, кюветы, укладывают рельсы.
Проектную линию можно построить несколькими способами:
а) построение проектной линии горизонтальным лучом нивелира
На местности разбивают n равных отрезков, длиной d. Первую точку выносят выше изложенным способом (Нпр = Н1). Нивелир устанавливают в се редину участка. Рейку ставят в т. 1, берут отсчет по рейке а. Заданный уклон i. Вычисляют отсчеты b, которые должны быть по рейке, стоящей в точках 2, 3 …n.
b1 = a – di,
b2 = a – 2di,
…………., (10.6)
bn = a – ndi.
Перемещают рейки в точках 2, 3 и т.д. по вертикали, пока отсчет по сред ней нити нивелира будет равен b1, b2 … bn. Под рейкой насыпают или убирают землю. Срезы колышков будут все на проектном уклоне.
Рис. 10.4. Построение проектной линии горизонтальным лучом нивелира
б) построение проектной линии с помощью нивелира и визирок
Рис. 10.5. Построение проектной линии с помощью визирок
На конечных точках забивают колышки на проектные отметки. На промежуточных точках устанавливают визирки так, чтобы верхние срезы их были на одной прямой с крайними. Под основания визирок забивают колья.
в) построение проектной линии с помощью теодолита
Рис. 10.6. Построение проектной линии с помощью теодолита
Теодолит устанавливают над колышком, забитым на проектной отметке в начальной точке. Вычисляют угол наклона по формуле
= arctg i, (10.7)
где i – проектный уклон линии.
Т.к. угол мал, можно принять = / i, где / = 3435/. На вертикальном круге теодолита устанавливают вычисленный угол . На промежуточных точках рейку перемещают, пока отсчет по рейке будет равный высоте теодолита а.
10.2. Геодезические работы при вертикальной планировке
строительной площадки
Для выноса на местность строительной площадки и основных осей здания (рис. 10.7) прокладывают теодолитный ход с расчетом, что с точек хода будут вынесены площадка и оси здания. Точки хода закрепляют на местности временными знаками. Определяют координаты и высоты точек хода.
т. 1
т. 2
т. 3
Рис. 10.7. Разбивка горизонтальной площадки
На плане определяют разбивочные элементы, по которым будут выноситься на местность оси горизонтальной площадки 1 – 11, 11 – 14 (аналогично бу дут выноситься оси здания):
- координаты точек 1, 11, 14 берут с плана с учетом деформации бумаги;
- координаты т. 1, т. 2 и т. 3 берут из ведомости вычисления координат точек теодолитного хода;
- решая обратную геодезическую задачу, вычисляют дирекционные углы направлений с точки на точку :
, (10.8)
где за первую точку берут ту, на которой стоит теодолит, а за вторую – ту, на которую наблюдают.
Например, для направления т.1 – 1: ; (10.9)
- вычисляют разбивочные углы :
1 = т.1, т.2 т.1, 1;
2 = т.2, 11 т.2, т.1;
3 = т.3, 14 т.3, т.2;
- вычисляют горизонтальные проложения di:
. (10.10)
Например, для расстояния . (10.11)
- теодолитом выносят проектные углы , лентой выносят рас стояния D, соответствующие горизонтальным проекциям di, контро лируют проектные расстояния 1 – 11, 11 – 14;
- разбивают площадку размером 1010 м2 или 2020 м2, для чего тео долитом строят прямые углы и лентой откладывают по 10 (или 20) м, закрепляют вершины квадратов колышками;
- вершины квадратов нивелируют нивелиром, снимая отсчеты по черной и красной сторонам рейки, вычисляют высоты всех вер шин квадратов;
- по вычисленным отметкам вершин квадратов вычисляют проект ную отметку балансирующей поверхности по формуле
, (10.12)
где Н1 = Н1 + Н3 + Н10 + Н11 + Н14 (сумма отметок точек, лежащих в одном квадрате),
Н2 = Н2 + Н4 + Н6 + Н7 + Н12 + Н13 (сумма отметок точек, лежащих в двух квадратах),
Н3 = Н9 (сумма отметок точек, лежащих в трех квадратах),
Н4 = Н5 + Н8 (сумма отметок точек, лежащих в четырех квадратах),
k = 7 (число квадратов);
- вычисляют рабочие отметки для каждой вершины квадратов по формуле
аi = Н0 Нi, (10.13)
где Нi – высоты вершин квадратов;
- контроль вычислений выполняют по формуле
= 0; (10.14)
- рабочие отметки выписывают в каждую вершину, при смене знака рабочих отметок вычисляют расстояния до точки нулевых работ по формулам:
(10.15)
где d = 10 м (сторона квадрата).
20,94 19,94
20,10 0,84 20,10 +0,16
Рис. 10.8. Пример вычисления рабочих отметок:
.
- точки нулевых работ соединяют прямыми линиями – линиями нулевых работ, они делят территорию на насыпь (при положительных рабочих отметках) и выемку (при отрицательных):
+
Рис. 10.9. Картограмма земляных работ
- нумеруют полученные фигуры, в них определяют площадь s (по размерам х и у, выписываемым на схему), сумму рабочих отметок, среднюю рабочую отметку аср (как а : n), объем земляных работ v (как аср · s );
- определяют объем земли из котлована здания размером аb:
Рис. 10.10. К расчету объема котлована
Объем котлована определяют по формуле
, (10.16)
где а и b – размеры котлована по низу, а1 и b1 – по верху, h – глубина котлована.
- за счет грунта, вынутого из котлована под здание, и за счет остаточного разрыхления грунта в отметку балансирующей поверхности вводят 2 поправки:
за счет грунта, вынутого из котлована:
(10.17)
за счет разрыхления грунта и учета коэффициента k остаточного разрыхления:
; (10.18)
vост.разр. = (vвыемки + vкотл) k, (10.19)
где k – коэффициент остаточного разрыхления грунта и равен 0,05 (5 %).
Отметка горизонтальной площадки: Нок = Н0 + Н1 + Н2. По уточненной проектной отметке все вычисляется по второму разу. Определяется, сколько земли надо вывезти с участка, чтобы выровнять площадку и выйти на ее проектный уровень.
10.3. Передача отметок на дно котлована и на этаж
а) Передача отметки на этаж
Рис. 10.11. Передача отметки на этаж:
Нрп = 56,789 м; НА = Нрп + а + (d – с) – b. (10.20)
Отметку передают при двух горизонтах нивелира. В формуле а – отсчет по рейке, стоящей на репере, b – отсчет по рейке, стоящей на полу этажа, d и с – отсчеты по ленте, висящей под грузом в свободном состоянии.
б) Передача отметки на дно котлована
Рис. 10.12. Передача отметки на дно котлована:
Нкотл = Нреп + а – (d – с) – b. (10.21)
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
Основной
- Федоров, В.И. Инженерная геодезия / В.И. Федоров, П.И. Шилов.– М.: Недра, 1982.
- Курс инженерной геодезии / Под ред. В.Е. Новака – М.: Недра, 1989.
- Митин, Н.А. Таблицы для разбивки кривых на автомобильных дорогах / Н.А. Митин. – М.: Недра, 1985.
- Условные знаки для топографических планов масштабов 1:5000, 1:2000, 1:1000 и 1:500. – М.: Недра, 1989.
Дополнительный
- Булгаков, Н.П. Прикладная геодезия / Н.П. Булгаков, Е.М. Рывкина,
Г.А. Федотов. – М.: Недра, 1990.
- Кулешов, Д.А. Инженерная геодезия для строителей / Д.А. Кулешов. – М.: Недра, 1990.
- Сироткин, М.П. Справочник по геодезии для строителей / М.П. Сироткин, В.С. Сытник. – М.: Недра, 1987.
- Ворошилов, А.П. Геодезическое обеспечение транспортного строительства / А.П. Ворошилов, Т.Е. Миркина. – Челябинск: Изд. ЮУрГУ, 2004.
- Власов, Д.И. Таблицы для разбивки на железных дорогах / Д.И. Власов, В.Н. Логинов. – М.: Транспорт, 1969.
93
PAGE 1
Инженерная геодезия, Т.Е. Миркина