Системы автоматического управления с ЦВМ

Предисловие

В последние два десятилетия значительно повысилась надёжность и снизилась стоимость цифровых компьютеров. В связи с этим они всё шире стали применяться в системах управления в качестве регуляторов. За время, равное периоду квантования, компьютер способен выполнить большое количество вычислений и сформировать выходной сигнал, который затем используется для управления объектом. Цифровые системы управления в настоящее время используются в самых разных областях, в том числе в химическом производстве, в авиации и космонавтике, в металлургии и станкостроении, в электроэнергетике и промышленной автоматике.

Основным математическим аппаратом теории дискретных систем является

z-преобразование. С его помощью решаются задачи анализа устойчивости и качества, а также синтеза систем управления, в состав которых входят цифровые датчики и микроконтроллеры.

Классификация дискретных систем по виду квантования сигналов

В непрерывных системах автоматического управления рабочая информация представлена в виде сигналов, описываемых непрерывными функциями времени. Наряду с непрерывными способами передачи и преобразования сигналов широко используются дискретные, в которых осуществляется квантование сигналов. Квантование или дискретизация состоит в представлении непрерывного сигнала его дискретными значениями. В зависимости от вида квантования системы автоматического управления подразделяют на дискретные по уровню (релейные),

дискретные по времени (импульсные),

дискретные по уровню и по времени (релейно-импульсные).

Квантование по уровню и по времени осуществляется в цифровых системах управления при преобразовании непрерывных сигналов в цифровую форму или коды.

В многорежимных и многомерных САР, в системах с перестраиваемой структурой, многосвязных, высокоточных и многих других видах САУ получили широкое применение цифровые вычислительные машины.

ЦВМ выполняют функции задатчиков, сравнивающих устройств, устройств коррекции, автоматических регуляторов с быстроперестраиваемыми программами, коммутаторов, управляющих автоматов и других устройств.

Преимущества цифровых регуляторов над аналоговыми:

Цифровой регулятор обладает большей гибкостью, поскольку для изменения какого-либо его параметра достаточно просто изменить число, записанное в ячейке памяти;

Цифровые сигналы менее чувствительны к шумам и дрейфу параметров оборудования;

Цифровая обработка сигналов может производиться с высокой скоростью и точностью;

Сложные алгоритмы обработки сигналов лучше всего реализовать с помощью цифровых устройств, так как при этом точность параметров ограничена лишь длиной слова цифрового процессора. Благодаря большим вычислительным возможностям УВМ в цифровых системах можно реализовать сложные алгоритмы управления и обеспечить такие переходные процессы, которые недостижимы в непрерывных системах.

Функциональная схема САУ с ЦВМ

АЦП обычно проектируют 10–20 разрядными, а ЦАП можно применить с пониженной разрядностью (не менее 7), так как входной сигнал ЦАП имеет малое число двоичных разрядов.

Применение микроЭВМ позволяет:

упростить САУ путём применения простых и надёжных модулей;
расположить цифровую вычислительную часть системы в непосредственной близости от основных элементов канала управления;
сложную обработку поступающей информации;
решение нескольких задач при обслуживании разных каналов управления с разделением во времени поступающей для обработки информации;
реализовать практически любой алгоритм управления;
осуществлять операции оптимизации САУ по статическим и динамическим показателям качества;
проводить операции контроля и поиска неисправностей.

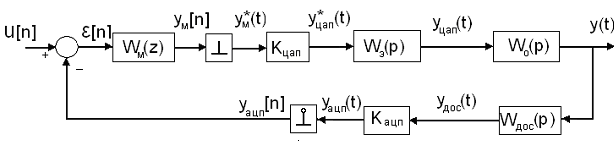
Структурная типовая схема ЦАС

Экстраполятор нулевого порядка

;

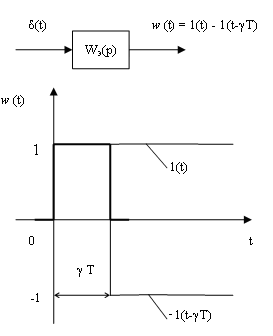
при =1 - передаточная функция экстраполятора 0-го порядка.

Т – такт работы ЦВМ по преобразованию информации (0,0011с).

- передаточная функция ЦВМ, учитывающая временное запаздывание сигнала при прохождении по каналу АЦП–процессор–ЦАП; учитывается в W0(p); <<T (0,11мс);

kАЦП – передаточный коэффициент АЦП;

kЦАП – передаточный коэффициент ЦАП;

- (ИЭ1) идеальный импульсный элемент первого рода, который непрерывную функцию преобразует в решетчатую;

- (ИЭ2) идеальный импульсный элемент второго рода, преобразующий решетчатую функцию yм[n] в последовательность дельта-функций .

Как правило, следует выбирать достаточно малый период квантования, чтобы методы синтеза непрерывных систем были адекватны и на z-плоскости. Однако не следует выбирать и слишком малое значение T из-за ограничений на вычислительные возможности компьютера.

При проектировании цифровых систем автоматического управления стремятся выбрать период Т так, чтобы он был намного меньше основной постоянной времени непрерывной части системы.

Период квантования Т можно определить с помощью приближенных формул:

где n – число двоичных разрядов,

- максимальная скорость изменения непрерывного сигнала,

, где - полоса пропускания непрерывной системы.

Квантование по времени - важнейший признак класса цифровых систем, а квантование по уровню – нелинейных систем.

В приближенных расчетах шумами квантования по уровню и нелинейностями статических характеристик АЦП и ЦАП пренебрегают.

Математическое описание работы

амплитудно–импульсных преобразователей сигналов

во временном пространстве.

Типы преобразователей сигналов:

Ключевой квантователь сигналов;

Математический аппарат исследования дискретных САУ основывается на замене последовательности реальных импульсов последовательностью идеальных импульсов и формирователем сигналов при выполнении условий:

Продолжительность замыкания ключа квантователя значительно меньше такта квантования ();
Период квантования T=const;
Сопротивление ключа квантователя в замкнутом состоянии равно нулю, в разомкнутом ;
Сигнал с выхода квантователя подается на линейную (в ней выполняется принцип суперпозиции) реализуемую непрерывную часть системы;
Если система содержит несколько квантователей, то считаем квантователи одинаковыми по характеристикам и синхронно работающими.

Аналоговая часть системы воспринимает входное воздействие как импульсное, если длительность импульса значительно меньше эквивалентной инерционности аналогового устройства W(p); на выходе системы – реакция на площадь входного реального импульса (аналогично действию импульса силы на твердое тело в механике).

Аналитическое выражение последовательности импульсов , имеющих площадь , имеет вид

при модуляции первого рода, где

- эквивалентная амплитуда импульса в n-ый момент замыкания ключа;

- амплитуда импульса в начальный момент n-го замыкания ключа;

- смещенная дельта-функция, существующая только в моменты времени и равная нулю при всех других значениях t.

Идеальный импульсный элемент можно рассматривать как импульсный модулятор с несущей в виде последовательности мгновенных единичных импульсов

и огибающей в виде входного непрерывного сигнала u(t), т.е.

Функцию называют функцией единичных импульсов и широко используют при исследовании импульсных систем.

C целью упрощения анализа заменим реальный модулятор идеальным импульсным элементом и формирователем импульсов:

- решетчатая функция амплитудно-импульсного модулятора-

уравнение амплитудно-импульсного модулятора во временном

пространстве.

Wэ(p) – экстраполятор нулевого порядка,

Определение: “Решетчатая функция- выходная временная функция элемента САУ, значения которой определены в дискретные моменты времени t=nT (n-числа натурального ряда , T- период квантования) путем повторных равноотстоящих измерений входного воздействия и обозначаемая y[nT] (сокращенно y[n])”.

Дискреты (ординаты входных воздействий) могут определяться также и для смещенных моментов времени , где - константа может быть положительной или отрицательной величиной при условии ,

Решетчатая функция в этом случае называется смещенной и обозначается

В дальнейшем будем считать параметр Непрерывные функции, совпадающие с заданными дискретами, называются огибающими решетчатой функции.

2. Аналого-цифровой модулятор

, где

ИЭ1 – идеальный импульсный элемент первого рода. Вид модуляции: амплитудно-кодовая.

3. Цифро-аналоговый демодулятор

ИЭ2 – идеальный импульсный элемент второго рода. Вид модуляции: амплитудно-импульсная.

, где

Математическое описание работы идеального амплитудно-импульсного элемента в пространстве Фурье

Периодическая последовательность -импульсов может быть представлена в виде комплексного ряда Фурье

где -частота квантования во времени, n-номер гармоники (n=0,1,2,…), -коэффициенты ряда Фурье:

Тогда

преобразование Лапласа этого уравнения дает

преобразование Фурье имеет вид

которое означает, что частотный спектр на выходе идеального импульсного элемента представляет собой сумму частотных спектров непрерывного сигнала на входе элемента, смещенных по оси частот на величину .

Вообще, периодические временные функции имеют дискретные частотные спектры, а дискретные временные функции – периодические частотные спектры.

Частотные спектры входного непрерывного сигнала и выходного сигнала импульсного элемента при и

Расчет цифровых САУ следует вести так, чтобы выполнялись условия импульсной теоремы Котельникова-Шеннона:

“Для того чтобы передаваемая в виде импульсов информация могла быть воспроизведена без существенных искажений, наивысшая частота гармоник со значимыми амплитудами в спектре входного сигнала не должна превышать 1/2 частоты следования импульсов”.

При достаточно большой частоте импульсов образующих выходной сигнал импульсного элемента, непрерывная часть системы реагирует только на низкочастотную составляющую сигнала, несущую информацию о непрерывном сигнале на входе импульсного элемента. Дискретность работы импульсного элемента обусловливает, лишь в качестве побочного явления возникновение на выходе системы высокочастотной составляющей в виде помехи, частотный спектр которой кратен частоте импульсного элемента.

Условие допустимости сведения импульсной системы к непрерывной:

где - частота среза непрерывной части системы,

- частота квантования во времени.

Разностные уравнения

Аналогом первой производной непрерывной функции для решетчатой функции является либо первая обратная разность

f[n] = f[n] - f[n-1],

либо первая прямая разность

f[n] = f[n+1] - f[n].

Прямая разность определяется в момент времени t=nT по будущему значению решетчатой функции при . Это можно сделать в тех случаях, когда будущее значение известно.

Обратная разность определяется для момента времени t=nT по прошлому значению решетчатой функции в момент времени .

Аналогом второй производной служат вторые разности:

oбратная .

Для вычисления k-й разности используют рекуррентную формулу

или формулу общего вида

, (1)

где биномиальные коэффициенты (число сочетаний) .

Обратные разности обладают важной особенностью: если решетчатая функция определена только для положительных значений аргумента, то есть

при n<0, то в точке n=0 k-я разность

для любого целого положительного k.

Аналогами интегралов непрерывных функций в пределах от 0 до t для решетчатых функций являются неполные суммы для обратных разностей

и полные суммы для прямых разностей

В качестве аналогов дифференциальных уравнений рассматриваются уравнения в конечных разностях.

При использовании обратных разностей уравнение в конечных разностях будет иметь вид

С учетом формулы (1) последнее выражение приобретает вид

коэффициенты уравнения определяются выражениями

, .

Общее решение однородного разностного уравнения при некратных корнях характеристического уравнения может быть записано следующим образом: , (2)

где (i=1,2,…,m) – корни характеристического уравнения

а - произвольные постоянные.

Из (2) вытекает условие того, чтобы свободное движение системы, описываемой разностным уравнением, было бы затухающим (условие устойчивости): ||<1 (i=1,2,…,m).

Для исследования решений разностных уравнений используются дискретное преобразование Лапласа, z – преобразование, w – преобразование, а также частотные методы.

Дискретное преобразование Лапласа

Для решетчатых функций введено понятие дискретного преобразования Лапласа в соответствии с формулой

. (3)

Для смещенных решетчатых функций может быть записано аналогичное выражение:

. (4)

В приведенных формулах, как и в случае непрерывного преобразования Лапласа, комплексная величина p=c+j, где с – абсцисса абсолютной сходимости. Если с, то ряд, определяемый формулами (3,4), сходится и решетчатой функции соответствует некоторое изображение.

Z–преобразование

Z–преобразование вытекает из дискретного преобразования Лапласа путем введения новой переменной .

Z–преобразование есть изображение несмещенной или смещенной решетчатых функций, определяемое формулами

, .

Способы перехода от непрерывных моделей к дискретным:

Применение Z – преобразования к решетчатой импульсной переходной функции со следующей цепочкой переходов (точный способ):

Замена производных дифференциального уравнения, описывающего объект, приближенными разностями:

и т. д.;

Данный способ дает приемлемую точность только при малых T.

Приближенный способ, предложенный А.Тастеным и называемый билинейным преобразованием, состоит в замене оператора p в передаточной функции соотношением

т.е.

Если для данной решетчатой функции f[n] существует такое положительное число R, что при |z|>R ряд (5)

сходится, то =1/R называют радиусом сходимости.

Функция внутри круга сходимости (т.е. круга в плоскости z с центром в начале координат и радиусом равным ) будет аналитической функцией, а ряд (5) будет рядом Лорана. Коэффициенты ряда f[nT] выражаются через следующим образом:

Формулы преобразования могут быть записаны и для непрерывной производящей функции в виде

F(z)=Z{f(t)}, t=nT, n=0,1,2,… .

В рассматриваемом пространстве введена единичная импульсная решетчатая функция

Эта функция играет в дискретных системах такую же важную роль, как - функция (функция Дирака) в непрерывных системах.

Основные свойства и теоремы Z-преобразования

Свойство линейности.

Изображение линейной комбинации решетчатых функций равно той же линейной комбинации их изображений.

Теорема запаздывания.

Рассмотрим решетчатую функцию f[n-m], сдвинутую вправо (запаздывающую) на целое число тактов m. Если обозначить n-m=r, то

Z{f[n-m]}===.

Если исходная решетчатая функция f[n] равна нулю при отрицательных значениях аргумента, то Z{f[n-m]}=.

Сдвиг по временной области.

Если имеет z-преобразование , то

где n – положительное целое число.

Доказательство.

По определению ,

что может быть записано как

Предполагая, что равно нулю при t < 0, получим последнее выражение в виде

Для доказательства второго равенства запишем:

Изображение разностей.

Для первой обратной разности

Если для отрицательных аргументов решетчатая функция тождественно равно нулю, то .

Для k-й обратной разности при f[n]0 для n<0

Определение обратной разности и неполной суммы (или прямой разности и полной суммы) решетчатой функции являются обратными операциями. Роль оператора, аналогичного оператору p=c+j в непрерывных системах, в первом случае играет оператор (z-1)z-1, а во втором случае – оператор (z-1). В случае перехода к пределу при T0 обе пары операций над решетчатыми функциями сливаются и превращаются в операции дифференцирования и интегрирования непрерывной функции.

Теорема о конечном значении решетчатой функции.

«Если функция f(t) имеет z – преобразование F(z) и если функция не имеет полюсов на окружности единичного радиуса |z|=1 и вне её на z – плоскости, то при исследовании систем управления, в которых используются обратные разности, справедливо равенство:

».

Доказательство.

Рассмотрим два ряда с конечным числом членов:

полагая, что f(t)=0 при t<0 и, следовательно, f(-T) равно нулю, запишем выражение второго

ряда

Сравнивая эти выражения, видим, что второй ряд может быть записан как

Определим в пределе при разность между выражениями:

В последнем выражении возьмём предел при , тогда

Меняя порядок перехода к пределу в последнем выражении и учитывая, что

получим

что и является доказательством теоремы о конечном значении.

Пример. Конечное значение единичной функции определяется следующим образом:

Теорема о начальном значении решетчатой функции.

«Если функция f(t) имеет z – преобразование F(z) и если существует предел то

».

Доказательство.

По определению F(z) можно представить в виде

Возьмём предел от каждой части последнего выражения и, учитывая, что z стремится к бесконечности, получим

Пример. .

Разложение в ряд Лорана (ряд по убывающим степеням z).

Разложив любым способом изображение F(z) в ряд Лорана:

, и, сравнивая два ряда между собой, можно установить, что

, , ,…, и т.д.

Решение разностных уравнений.

Более удобны для решения разностные уравнения вида

с начальными условиями , .

Изображение решетчатой функции y[n-m], запаздывающей на m тактов, будет .

Подобные зависимости могут быть записаны для запаздывания на (m-1), (m-2),…, 1 тактов.

В случае нулевых начальных условий .

Если предположить, что решетчатая функция y[n] тождественно равна нулю при n < 0 и, кроме того, функция f[n] в правой части прикладывается в момент времени n=0, то переход к изображениям дает

Изображение искомой решетчатой функции можно представить в виде

где W(z) - дискретная передаточная функция.

Пример 1.

Определить z - изображение единичной ступенчатой решетчатой функции ed[n] при T=1c.

ed(t) – производящая функция, преобразование по Лапласу которой Led(t)=.

; ; .

Используем формулу суммирования убывающей геометрической прогрессии

где - знаменатель прогрессии,

тогда .

Для бесконечно убывающей прогрессии n,

тогда . Знаменатель прогрессии .

Тогда для |z|>1 .

Пример 2. Задана решетчатая экспонента , где - постоянная, в общем случае комплексная величина, T=1c.

;

знаменатель прогрессии q=z-1.

Для |z| > e-T

, где d=e-T.

n. n.

w(t)

w(nT)

W(p)

W(z)

Аналого–цифровой преобразователь

Аналоговые входные устройства выдают сигналы, как правило, стандартного диапазона в виде напряжений 0 – 10В или токов 0 – 20мА. Эти сигналы в АЦП квантуются по уровню и переводятся в цифровые коды. На выходе АЦП сигнал представлен в формате с фиксированной точкой.

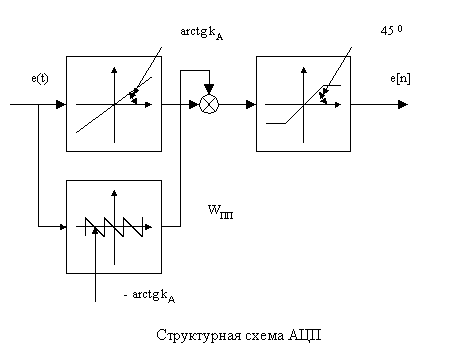
Точность преобразования определяется шагом квантования

где - максимальное количество различных чисел, представимых с помощью двоичного кода разрядности ,

- разрядность преобразователя (длина слова на выходе АЦП за исключением знакового разряда).

- источник шума квантования,

- линеаризованный передаточный коэффициент,

1 - единица младшего разряда АЦП,

- идеальный импульсный элемент первого рода, который непрерывную функцию преобразует в решетчатую,

- цена единицы младшего разряда АЦП (в единицах измерения преобразуемой непрерывной величины).

Число отличных от нуля уровней одной ветви характеристики АЦП определяется по формуле ,

где - число двоичных разрядов (без учета знакового разряда; обычно равно 8-24),

- максимальное значение входного воздействия преобразователя.

Максимальная ошибка не превышает /2. Звено Wnn учитывает шум квантования и ошибку преобразования.

Предполагая, что в каждом такте работы цифрового устройства ошибка округления лежит в пределах /2 и подчиняется равновероятному закону распределения, дисперсия шума округления в АЦП оказывается равной

Задача № 1. Определите передаточный коэффициент цифрового датчика:

[единиц кода/мкм],

где - цена младшего разряда цифрового датчика, мкм;

- допустимая ошибка отработки входного воздействия, мкм.

Требуемое количество разрядов ЦД:

где n - требуемое количество разрядов цифрового датчика без учета знакового разряда;

- максимальная величина перемещения стола ЭЛУ, равная , мкм.

Дискретная передаточная функция ЦВМ

Наличие запоминающих устройств позволяет ЦВМ строить свою работу с учетом не только текущих, но и прошлых значений входных воздействий и выходных функций.

Передаточная функция ЦВМ в общем виде

, .

Для перехода к математической форме алгоритма работы ЦВМ разделим числитель и знаменатель WM (z) на zk:

Разделив на числитель и знаменатель, получим линейный алгоритм работы ЦВМ:

Требование к устойчивости алгоритмов работы ЦВМ

Передаточные функции ЦВМ должны соответствовать устойчивым программам работы. Это означает, что корни знаменателя передаточной функции (полюса передаточной функции) должны лежать внутри круга единичного радиуса, то есть быть по модулю меньше 1 (исключение составляет интегрирующее звено, полюс которого z1=1 лежит на границе апериодической устойчивости – совпадает с кругом единичного радиуса комплексной плоскости корней).

Цифро–аналоговый преобразователь

ИЭ2 – идеальный импульсный элемент второго рода, преобразующий решетчатую функцию в последовательность -функций

;

- передаточный коэффициент ЦАП (линеаризованная часть);

- источник шума квантования (его может не быть);

- передаточная функция экстраполятора.

Введение идеального импульсного элемента второго рода сделано с целью формального изображения экстраполятора в форме динамического звена с передаточной функцией .

При поступлении на вход экстраполятора нулевого порядка единичного импульса изображение выходной функции:

, где .

Если период дискретизации относительно большой, то используют экстраполятор первого порядка, выходная функция которого изменяется по линейному закону при входном воздействии . Передаточная функция экстраполятора первого порядка имеет вид

- цифровое значение входного сигнала в дискретные моменты времени (код);

- непрерывная выходная функция ЦАП;

- цена единицы младшего разряда ЦАП (в единицах измерения выходной функции).

Число отличных от нуля уровней одной ветви статической характеристики , где - число разрядов преобразователя.

Статическая характеристика ЦАП

Линеаризованный передаточный коэффициент преобразователя

В преобразователе образуется дополнительная генерация шума квантования только в том случае, когда цифровое управляющее устройство имеет дополнительные младшие разряды в его арифметическом устройстве. В этом случае полученный результат предварительно округляется, а затем поступает на выход. Эффект округления и вызывает появление шума квантования. Максимальная ошибка округления составляет . При равновероятном законе распределения ошибок округления дисперсия шума квантования, отнесенного к выходу управляющего устройства, составит .

При отсутствии дополнительных разрядов округления не происходит. В случае переполнения разрядной сетки отбрасываются значения не младших, а старших разрядов.

Задача № 2.

Определение параметров цифроаналогового преобразователя. Передаточный коэффициент ЦАП равен цене младшего разряда ЦАП, выраженный в Вольтах на единицу десятичного эквивалента входного кода:

[В/ед.кода],

где - цена младшего разряда кода ЦАП, В;

- амплитуда помехи, приведенной к выходу ЦАП.

Определение требуемого количество разрядов ЦАП:

где n - требуемое количество разрядов цифро–аналогового преобразователя без учета знакового разряда;

- максимальная величина выходного напряжения ЦАП.

Структурные схемы цифровых систем и их дискретные передаточные функции

Последовательное соединение микроЭВМ с непрерывными динамическими звеньями.

В форме преобразований Лапласа:

, обозначим , ,

применим z-преобразование, имея в виду, что

отсюда .

Если система состоит из двух микроЭВМ, соединенных последовательно с непрерывными динамическими звеньями:

то ,

После z-преобразования

отсюда .

Система управления с отрицательной обратной связью.

Базовая структурная схема цифровой САУ

САУ описывается следующей системой уравнений:

тогда

- дискретная передаточная функция системы по сигналу рассогласования;

- в форме z -изображений.

Так как ,

то ,

- дискретная передаточная функция системы по каналу управления;

- в форме -преобразований.

Определим дискретную передаточную функцию системы по каналу возмущения, воздействующего на объект:

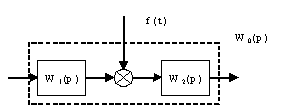
Здесь ;

;

тогда

, отсюда

Параметры входного воздействия входят в полученное выражение неявно, поэтому в явном виде найти дискретную передаточную функцию по каналу возмущения невозможно.

Частотные характеристики цифровых систем

Физический смысл частотных характеристик цифровых и непрерывных систем очень близок. Особенностью этих характеристик для цифровых систем является то, что они устанавливают связь между гармоническими последовательностями (гармоническими решетчатыми функциями) на входе и выходе цифрового звена (системы) с дискретной передаточной функцией W(z). Огибающие решетчатых функций изменяются по гармоническому закону.

по окончании переходного процесса

В отличие от непрерывной гармонической функции гармоническая решетчатая функция в общем случае не является периодической функцией n. Кроме того, амплитуды Аr и Ау не обязательно являются теми максимальными значениями, которых могут достигать те или иные члены соответствующих последовательностей r[n], y[n]. Амплитуды всегда будут определять лишь верхние границы, но не обязательно максимумы членов этих последовательностей.

Для перехода к частотным характеристикам используется замена аргумента

Z=e jT,

в результате которой получаем комплексный передаточный коэффициент цифровой системы

W*(j)=W(e jT).

Пусть дискретная передаточная функция имеет вид

тогда ,

где ,,,- соответственно вещественная, мнимая, амплитудная и фазовая частотные характеристики цифровой системы.

Очевидно,

, .

При фиксированном значении комплексный передаточный коэффициент изображается геометрически вектором на плоскости (P*,jQ*). При изменении конец вектора W*(j) прочерчивает некоторую кривую, которую называют годографом комплексного передаточного коэффициента системы или ее амплитудно-фазовой характеристикой.

Основные особенности частотных характеристик цифровых систем, которые вытекают из свойств дискретной передаточной функции:

1. Частотные характеристики цифровых систем являются периодическими функ-циями относительно частоты с периодом повторения 0=2/T. Это означает, что при построении этих характеристик достаточно ограничиться изменением в диапазоне шириной 2/Т, например от - /Т до /Т. Если же учесть, что участки частотной характеристики в диапазонах от –/Т до 0 и от 0 до /Т симметричны (поскольку W*(j) и W*(-j) – комплексные сопряженные функции), то можно ограничиться построением частотной характеристики в интервале изменения от 0 до /Т;

2. Амплитудно-фазовые частотные характеристики цифровой системы заканчиваются на вещественной оси, так как для =/Т комплексный передаточный коэффициент всегда является действительным числом.

Свойство периодичности частотных характеристик цифровых систем физически объясняется стробоскопическим эффектом, который проявляется в том, что гармоническая решетчатая функция r[n] на входе дискретного звена не изменяется при изменении частоты огибающей на любую величину, кратную 0, т.е. последовательность r[n] будет одной и той же при всех частотах огибающей, равных +k0, k=0,1,2,3,… (рис. 1).

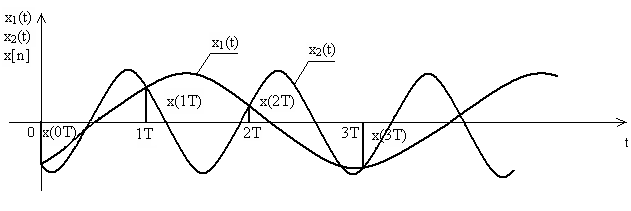
Рис. 1. Гармонические сигналы различных частот, соответствующие одной и той же решетчатой функции

ПРИМЕР:

Дискретная передаточная функция разомкнутой системы имеет вид

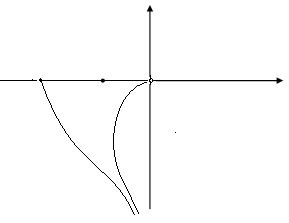
Рис. 2. Годографы W(), (0,/Т)

МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЦИФРОВЫХ СИСТЕМ

В ПРОСТРАНСТВЕ СОСТОЯНИЙ

Классический метод математического описания цифровых систем основан на использовании дискретного преобразования Лапласа, z – преобразования, дискретных передаточных функций, псевдочастотных характеристик, структурных схем и графов. Достоинство этого метода в его наглядности, компактности, глубине и широте проведенных исследований, разработанности методов анализа и синтеза, апробированности при решении множества исследовательских и проектных задач.

В конце 60-х – начале 70-х годов 20-го века был предложен второй метод математического описания цифровых систем – метод пространства состояний. Описание системы в пространстве состояний является естественным и удобным для решения задач на микроЭВМ, позволяет унифицировать математическое описание одномерных и многомерных систем, может применяться к некоторым типам нелинейных и нестационарных систем.

В пространстве состояний непрерывные системы описываются системой дифференциальных уравнений первого порядка, называемых уравнениями состояния. Для цифровых систем уравнения состояния – система разностных уравнений первого порядка. Уравнения состояния можно записать по виду разностного уравнения n-го порядка или дискретной передаточной функции системы. Процедура получения уравнения состояния по дискретной передаточной функции называется декомпозицией. Переход к описанию в пространстве состояний может осуществляться различными способами. Обычно используют векторную форму записи разностного уравнения путём прямой подстановки (метод прямого программирования) новых переменных (переменных состояния) в исходное разностное уравнение.

1. Преобразование разностного уравнения в векторную форму

Пусть уравнение объекта или одномерной линейной цифровой системы в форме прямых разностей имеет вид

(1)

Тогда соответствующая дискретная передаточная функция представима в виде

(2)

Введём следующие переменные состояния:

(3)

(4)

Такой набор переменных состояния не является единственным, но он наиболее удобен для расчётов.

Подставим выражения (3) и (4) в уравнение (1), положив

bn=1, а:

(5)

Система разностных уравнений (4) с учётом уравнения (5) примет вид

Эту систему уравнений можно представить в форме векторного разностного уравнения

(6)

и уравнение выхода

(7)

Обозначим вектор переменных состояния x, матрицу коэффициентов системы A, вектор управления B и вектор наблюдения C:

x(k+1) = A x(k) + Bu(k), (8)

y(k) = C x(k). (9)

Если bn=1, а, то уравнения (2) и (3) можно представить в форме

(10)

Если же , уравнения (2) и (3) приводятся к виду

или

(11)

Кроме того, используя уравнения (4), получим выражение

(12)

Подставив из уравнения (5), получаем окончательный результат

(13)

Это обобщённое уравнение выхода можно также записать в векторной форме:

или

y(k)=Cx(k)+Du(k). (14)

При т.е. для систем без прямой передачи управляющего воздействия, уравнение (14) приобретает вид

(15)

Структурная схема, соответствующая разностному уравнению, полученному исходя из соотношений (4), (5) и (12) и записанному в пространстве состояний, представлена на рис.1 в нормальной форме.

Рис.1. Структурная схема разностного уравнения, записанного в

пространстве состояний (нормальная форма)

Предполагается, что векторное разностное уравнение и уравнение выхода имеют вид

x(k+1) = A x(k) + Bu(k), (16)

y(k) = Cx(k)+Du(k). (17)

Данным уравнениям соответствует структурная схема, показанная на рис.2.

Рис.2. Структурная схема системы, описываемой векторным разностным уравнением

первого порядка

Общий вид уравнений состояния для многомерной линейной дискретной системы с постоянными параметрами (линейная стационарная модель) выглядит следующим образом

x(k+1) = Ax(k) + Bu(k), (18)

y(k) = Cx(k) + Du(k), (19)

где x(k) – вектор состояния размерностью вектор входа u(k) – размерность вектор выхода y(k) – размерность . Матрица D характеризует непосредственную связь между входом и выходом системы.

Если матрицы зависят от k, то система нестационарна. Блок-схема матричного пространства состояний приведена на рис.3.

Рис.3. Блок-схема матричного пространства состояний системы

Пример 1.

Пусть дискретная система описывается разностным уравнением в форме обратных разностей второго порядка:

где u(k) – вход системы, а y(k) – её выход.

Применив к этому уравнению z-преобразование, получим передаточную функцию

Схемы моделирования приведены на рис.4,5.

Рис.4. Алгоритмическая структура системы (каноническая форма

программирования)

Рис.5. Граф системы

Модель в переменных состояния можно получить, приняв выход каждого элемента задержки в схеме моделирования за переменную состояния.

Уравнения состояния запишутся в виде

Эти уравнения можно представить в векторно-матричной форме:

2. Методы решения векторного разностного уравнения

2.1 Итерационный метод

Пусть разностное уравнение задано в векторной форме (16), (17).

Построим рекуррентную процедуру решения разностного уравнения для заданной последовательности входных сигналов u(k) при начальных условиях x(0). Эта процедура описывается соотношениями

x(1) = Ax(0)+Bu(0),

x(2) = Ax(1)+Bu(1)=A2x(0)+ABu(0)+Bu(1),

. . . . . . . . . . . .

x(k) = Akx(0) + Ai-1Bu(k-i). (20)

Первый член в выражении (20) представляет собой решение однородного разностного уравнения, второй – частное решение неоднородного уравнения.

Выходной сигнал y(k) вычисляется из уравнения (17).

Пример 2.

Рассмотрим дискретную систему с передаточной функцией

Чтобы получить модель в переменных состояния, изобразим сначала схему моделирования (рис.6) системы и выход каждого элемента задержки примем за переменную состояния.

Рис.6. Схема моделирования системы

По этой схеме запишем уравнения состояния:

Решим эти уравнения итерационным методом, считая, что x(0)=0 и u(k)=1 для всех k. Так как x(0)=0, то y(0)=0. Последовательно увеличивая k, получим:

Следующий скрипт MATLAB возвращает в окно команд те же значения:

u=1;

A=[0 1;-2 3];

B=[0;1];

C=[0 1];

D=[0];

x=[0;0];

iter=4

for k=0:iter

y(k+1)=C*x+D*u;

[k y(k+1)]

x1=A*x+B*u;

x=x1;

end

2.2 Операторный метод

Если u(k) задаётся неявно, в форме z-преобразования, можно воспользоваться операторным методом решения.

Запишем z-преобразование для вектора состояния:

Z{x(k)} = X(z),

Z{x(k+1)} = z[X(z) – x(0)]

по теореме о сдвиге влево.

Из уравнения (16) следует, что

z[X(z) - x(0)] = AX(z) + BU(z) (21)

или

X(z) = [zI-A]-1zx(0) + [zI-A]-1BU(z). (22)

Применив к (22) обратное z-преобразование, получим тот же результат, что и в (20).

Подставляя это выражение в уравнение (17), получаем

Y(z) = C[zI-A]-1zx(0) + {C[zI-A]-1B+D}U(z). (23)

Сравнивая уравнения (22) и (20), получим матрицу перехода

Ф(k) = Z-1{[zI-A]-1z} = Ak. (24)

Тогда (20) можно записать как

x(k) = Ф(k)x(0) + Ф(i-1)Bu(k-i). (25)

Пример 3.

Решим уравнения состояния из примера 2 с помощью z-преобразования:

[zI-A] = , det(zI-A) = z2-3z+2, adj[zI-A] = .

Следовательно,

[zI-A]-1 =

Согласно (22), учитывая, что x(0)=0, получим:

X(z)=[zI-A]-1BU(z) = .

Поскольку , то

Y(z) = CX(z) =

или

Обратное z-преобразование Y(z) имеет вид

y(k) = - k - 2 + 2*(2)k.

Следовательно, числовая последовательность y(k) равна 0,1,4,11,26,…,

что подтверждает результат, полученный в примере 2.

3. Вычисление дискретной передаточной функции

Из уравнения (23) при нулевых начальных условиях x(0)=0 следует, что

C[zI-A]-1B+D. (26)

Знаменатель полученной передаточной функции составляет левую часть характеристического уравнения

det[zI-A] = 0. (27)

Таким образом, передаточную функцию по уравнениям состояния можно определить двояким образом – либо с помощью матричной процедуры, либо с помощью формулы Мейсона, применив её к графу, соответствующему уравнениям состояния.

Априорное требование к дискретной передаточной функции W(z) состоит в том, что она должна быть физически реализуема. Условие физической реализуемости произвольной линейной системы предполагает, что выходной сигнал системы не может возникнуть прежде, чем будет приложен входной сигнал. Для физической реализуемости цифровой системы при разложении W(z) в степенной ряд в нём не должно содержаться членов с положительным показателем степени. Поэтому, чтобы W(z) представляла собой физически реализуемую передаточную функцию, наивысший показатель степени знаменателя должен быть равным соответствующему показателю степени числителя или превосходить его.

Реализация дискретной передаточной функции на ЭВМ может осуществляться тремя различными способами: непосредственной, последовательной или параллельной декомпозицией.

Пример 4.

Определим передаточную функцию по уравнениям состояния. Рассмотрим систему, которая описывается уравнениями состояния:

Матрица [zI-A]-1 была получена в примере 3:

[zI-A]-1 = где = z2 - 3z + 2.

Тогда на основании (26), учитывая, что D = 0, определим передаточную функцию системы:

C[zI-A]-1B =

Как видим, этот результат совпадает с передаточной функцией из примера 2. Его можно проверить с помощью программы MATLAB:

A=[0 1;-2 3];

B=[0;1];

C=[0 1];

[Wnum,Wden]=ss2tf(A,B,C,0)

4. Вычисление импульсной переходной функции

Объединим уравнения (17) и (20), положив x(0)=0:

y(k) = CAi-1Bu(k-i) + Du(k). (28)

Пусть входной сигнал имеет вид

тогда импульсная переходная функция определяется рекуррентной формулой

g(0)=d,

g(k)=CAk-1B для k>0. (29)

Отсюда можно получить соотношение, связывающее импульсную переходную функцию и z-передаточную функцию

W(z)== D + CAk-1Bz-k. (30)

5. Управляемость дискретных САУ

Линейный динамический объект называют управляемым, если существует реализуемая последовательность управляющих воздействий u(k), позволяющая перевести объект из произвольного начального состояния x(0) в любое конечное состояние x(N) на ограниченном интервале времени, равном N тактов квантования.

Для того чтобы получить указанную последовательность u(k), можно воспользоваться уравнением (20). Для объекта со скалярным входом

x(N) = ANx(0) + [B, AB, …,AN-1B]uN, (31)

где

uNT = [u(n-1) u(n-2) … u(0)]. (32)

При N=m неизвестный вектор входных воздействий определяется однозначно по формулам

um = Qs-1[x(m) – Amx(0)], (33)

Qs = [B AB…Am-1B], (34)

если

detQs 0. (35)

Матрица Qs называется матрицей управляемости. Она не должна иметь линейно зависимых столбцов (строк). Следовательно, объект управляем, если выполняется условие

Rank Qs = m, (36)

где m – порядок матрицы A. Если N<m, решения относительно вектора u не существует, а при N>m оно становится неоднозначным.

6. Наблюдаемость дискретных САУ

Линейный динамический объект с выходной переменной y(k) называют наблюдаемым, если произвольное состояние x(k) можно определить, имея конечный набор выходных переменных y(k), y(k+1),…,y(k+N-1). Условия наблюдаемости выведем следующим образом.

Воспользовавшись уравнением выхода

y(k) = Cx(k)

и векторным разностным уравнением (16), сформируем последовательность уравнений

y(k) = Cx(k),

y(k+1) = CAx(k) + CBu(k),

y(k+2) = CA2x(k) + CABu(k) + CBu(k+1),

…..

y(k+N-1) = CAN-1x(k) + [0, CB, CAB, … ,CAN-2B]uN. (37)

Здесь

uNT = [u(k+N-1)…u(k+1) u(k)]. (38)

Если все составляющие вектора входных воздействий uNT известны, для однозначного определения m неизвестных, образующих вектор состояния x(k), из системы (37) достаточно взять m уравнений. Таким образом, N=m. При этом систему (37) можно записать в виде

ym = QBx(k) + Sum, (39)

где

ymT = [y(k) y(k+1) … y(k+m-1)],

umT = [u(k+m-1) … u(k+1) u(k)],

QB = [C CA … CAm-1]T,

S =

Отсюда найдём искомый вектор состояния

x(k) = QB-1[ym – Sum]. (40)

Решение существует, если detQB 0. Следовательно, динамический объект наблюдаем, если его матрица наблюдаемости QB имеет полный ранг

RankQB =m, (41)

т.е. все m строк (столбцов) матрицы QB должны быть линейно независимы.

Устойчивость работы цифровых САУ

Линейная цифровая система считается устойчивой, если ограниченному внешнему воздействию соответствует ограниченная реакция.

Условие устойчивости для цифровых систем записывается в виде

где - переходная составляющая движения.

Корневой критерий устойчивости.

Из теории линейных непрерывных систем известно: если все полюсы передаточной функции расположены в левой половине p – плоскости, то система устойчива. P – плоскость и z – плоскость связаны преобразованием

отсюда следует, что и

В левой половине p – плоскости <0, поэтому Мнимая ось

p - плоскости отображается в единичную окружность на z - плоскости при , а область внутри этой окружности соответствует всей левой половине p-плоскости.

Таким образом, выполнимость условия (1) обеспечивается, если , где - корни характеристического уравнения системы.

Формулировка критерия:

«Для того чтобы цифровая САУ была устойчива, необходимо и достаточно, чтобы модули корней характеристического уравнения системы были меньше 1».

Система находится на апериодической границе устойчивости, если в её характеристическом уравнении

a0zn + a1zn-1 + …+ an = 0

имеется корень , а остальные корни располагаются внутри круга единичного радиуса. В этом случае переходная составляющая решения разностного уравнения с течением времени стремится к значению .

Если в характеристическом уравнении имеется пара комплексных сопряженных корней, расположенных на окружности единичного радиуса, то имеет место колебательная граница устойчивости. В этом случае с течением времени в системе устанавливаются незатухающие периодические колебания. Вещественная часть корней может быть положительной, отрицательной или нулевой.

Типичной для дискретных систем является граница устойчивости третьего типа, которой соответствует наличие в характеристическом уравнении корня .

Критерий Михайлова.

Пусть известен многочлен знаменателя дискретной передаточной функции цифровой САУ , где , - корни характеристического уравнения системы.

Если корень характеристического уравнения располагается внутри круга единичного радиуса, то при изменении от до . Если вне круга, то , , T – период квантования сигналов.

Будем рассматривать .

Формулировка критерия Михайлова:

«Для того чтобы система была устойчива, необходимо и достаточно, чтобы при изменении от 0 до характеристический вектор имел приращение аргумента , где n – степень характеристического уравнения системы».

Кривая Михайлова должна поворачиваться на угол n.

Если имеются полюсы на окружности единичного радиуса(=1), а все остальные – внутри круга, то цифровая система находится на границе устойчивости. Если это полюс =+1, то цифровая система называется нейтральной.

Цифровые системы первого и второго порядка, в отличие от непрерывных систем такого же порядка, могут быть неустойчивыми даже при положительных коэффициентах характеристического уравнения. Это объясняется тем, что фиксатор, содержащийся обычно в контуре цифровой системы, вносит дополнительное отставание по фазе.

Пример.

Критерий Найквиста.

Комплексный спектр дискретной передаточной функции называют частотной передаточной функцией дискретной системы (звена).

Так как , где - дискретная передаточная функция прямого канала системы с единичной отрицательной обратной связью, то .

В этом случае

где n - общее число корней;

m - число корней характеристического уравнения разомкнутой системы

по модулю больше 1.

Формулировка критерия Найквиста №1

Для того чтобы замкнутая система была устойчивой, необходимо и достаточно, чтобы при изменении от 0 до вектор F(z) равный 1+W(z) имел приращение аргумента m, где m - число корней характеристического уравнения разомкнутой цифровой системы, лежащих вне круга единичного радиуса.

Пример 1 Пример 2

Формулировка критерия Найквиста №2

Для того чтобы замкнутая система была устойчивой, необходимо и достаточно, чтобы при изменении от 0 до амплитудно-фазовая характеристика разомкнутой системы охватывала точку с координатами (-1,j0) m/2 раз против часовой стрелки, где m - число корней характеристического уравнения разомкнутой системы по модулю > 1.

Формулировка критерия Найквиста для ЛПЧХ совпадает с формулировкой для непрерывных систем.

Устойчивость разомкнутого контура цифровой системы определяется устойчивостью её непрерывной части: если последняя устойчива, то и весь разомкнутый контур (включая импульсный элемент) устойчивы.

4. Критерий Гурвица.

Формулировка критерия Гурвица для непрерывных систем справедлива и для дискретных систем, если в характеристическом уравнении системы произвести замену .

Введем комплексную переменную w, связанную с комплексной переменной z билинейным преобразованием:

, где , относительная безразмерная

псевдочастота.

Тогда, произведя замену в характеристическом полиноме |, получим характеристический полином , по которому определим устойчивость системы по критерию Гурвица.

При изменении частоты в пределах относительная псевдочастотапробегает все значения от - до +, а комплексная переменная w движется по оси мнимых чисел от -j до +j. Внутренняя часть круга единичного радиуса отображается при этом на левую полуплоскость.

При помощи w - преобразования осуществляется конформное отображение внутренности окружности единичного радиуса на плоскости z в левую полуплоскость w. При этом контур окружности единичного радиуса переходит в мнимую ось плоскости w.

При исследовании дискретных систем по преобразованным при помощи w - преобразования передаточным функциям могут использоваться обычные приемы и критерии, справедливые для непрерывных систем, в том числе и критерий Гурвица.

Логарифмические псевдочастотные характеристики цифровых систем

Осуществим подстановку в W(z) , ,

где - относительная безразмерная псевдочастота.

Введем понятие абсолютной псевдочастоты :

, с-1; ;

При малых углах , тогда при выполнении условия можно в расчетах заменить псевдочастоту действительной круговой частотой, что может быть использовано, в частности, при расчетах реакции ЦАС на медленно меняющиеся гармонические сигналы на входе.

Получим псевдочастотную передаточную функцию разомкнутой цифровой системы

/=, здесь соответствует р непрерывной системы, поэтому ЛПЧХ строятся по правилам для непрерывных систем. Затем применяется критерий устойчивости Найквиста для ЛЧХ.

Пример 1. Пусть - интегратор; , .

Тогда .

Чтобы перейти к логарифмическим частотным характеристикам произведем подстановку : , если вместо w подставить , получим псевдочастотную функцию : .

- комплексный передаточный коэффициент интегрирующего звена с фиксатором 0-го порядка.

Свойства :

C уменьшением периода дискретизации (T0, =2/T ) характеристика приближается к характеристике непрерывной системы;
Предельный фазовый сдвиг равен -, такая замкнутая система приближается к границе устойчивости при больших k.

Пример 2.

Пусть , тогда

где .

Перейдем к псевдочастотным функциям :

так как . (1)

Исследуем это выражение :

Пусть период дискретности [] и определим :

, это видно из выражения (1), отсюда , при этих соотношениях .

- неминимально - фазовый множитель.

Пусть , тогда , .

Построим частотные характеристики:

1. 2.

Пример 3.

Построить логарифмические псевдочастотные характеристики системы, если передаточная функция непрерывной части имеет вид

Экстраполятор нулевого порядка.

Зададим период дискретности T=0.1с. На графике отложим частоту , выделим НЧ и ВЧ части характеристики;

, .

Теперь запишем выражение для псевдочастотной функции:

На основании этого выражения построим ЛПЧХ, где.

Замечание: фазовые характеристики непрерывных и цифровых систем существенно различаются.

Анализ точности цифровых систем в установившемся режиме

Оценка точности в установившемся режиме цифровых систем производится по величине установившейся ошибки при различных типовых воздействиях, наиболее характерных для исследуемой системы.

В замкнутой ЦАС рассогласование (инверсная ошибка при ) , задающее и возмущающее воздействия связаны следующим уравнением относительно z-изображений:

Полученное выражение содержит две составляющие ошибки, первая из которых обусловлена задающим воздействием, а вторая - возмущающим.

Установившаяся ошибка цифровой системы может быть вычислена по выражению, определяющему конечное значение оригинала, т.е.

Определим установившуюся ошибку системы по задающему воздействию, положив Получим

(1)

В статическом режиме работы системы на вход подается постоянное воздействие , z-изображение которого В соответствии с (1) статическая ошибка по положению

В динамическом режиме:

при входном воздействии линейно изменяющемся во времени, z-изображение

а установившаяся ошибка определяется выражением

и называется ошибкой системы по скорости.

если входной сигнал изменяется с постоянным ускорением, т.е.

то z-изображение имеет вид

Установившаяся ошибка

называется ошибкой системы по ускорению.

В общем случае, если воздействие представлено в виде степенной функции времени

его z-изображение можно записать так

где - полином степени (k-1) относительно z и такой, что

Установившаяся ошибка по этому воздействию определяется выражением

(1)

Допустим, что передаточная функция Wpc(z) разомкнутой системы может быть представлена в виде

(2)

где - порядок астатизма системы, а не имеет нулей и полюсов, равных единице. Подставив (2) в выражение (1), после несложных преобразований получим:

Для того чтобы цифровая система имела нулевую установившуюся ошибку по задающему воздействию, необходимо чтобы порядок ее астатизма превышал степень входного воздействия k.

Рассмотренный способ определения установившейся ошибки системы удобен только при типовых входных воздействиях. Если функция r(t) имеет произвольную форму, достаточно плавную вдали от начальной точки, т.е. имеет там конечное число производных, не равных нулю, то для вычисления ошибки можно воспользоваться понятием коэффициентов ошибок. Разложив передаточную функцию системы по сигналу ошибки для задающего воздействия в степенной ряд по (1-z-1), получим

. (3)

Коэффициенты С0,C1,C2,…,Cm,… называют коэффициентами ошибок.

Из соотношения (3) следует, что для статической системы ()

где k=W1(1)- передаточный коэффициент разомкнутой системы.

Для системы с астатизмом первого порядка () С0=0, поэтому из (3) имеем

где - добротность системы по скорости.

Для системы с астатизмом второго порядка С0 =C1=0, поэтому из (3) следует, что

где - добротность системы по ускорению.

Аналогичным образом могут быть найдены и другие коэффициенты ошибок Cm.

По коэффициентам ошибок можно построить ряд, представляющий решетчатую функцию [nT ], начиная с некоторого момента t=kT после начала переходного процесса. Такой ряд имеет вид

(4)

где -производные функции r(t).

Применимость рассмотренного способа расчета установившейся ошибки зависит от скорости сходимости ряда (4).

Качество динамики цифровых САУ

Качество ЦАС может быть оценено по прямым либо косвенным показателям качества, разработанных для непрерывных систем.

В ЦАС качество удобно оценивать по показателю колебательности, который определяется по амплитудной псевдочастотной характеристике

Под желаемыми понимают такие ЛЧХ, которые удовлетворяют заданному показателю колебательности.

Различают три типа желаемых ЛЧХ цифровых систем:

Характеристика 0-го типа, имеющая наклон 0 дБ в области НЧ (для статических систем регулирования):

2. Характеристика астатической системы 1-го порядка (следящие системы):

Системы с астатизмом 2-го порядка:

Бесекерский В.А. и Федоров С.М. получили аналитические соотношения, связывающие параметры характеристик с показателем колебательности М:

Для области НЧ: ;
Для области ВЧ: .

Методы построения ЛПЧХ цифровых САУ

1. Метод прямого расчёта и построение по ней ЛПЧХ.

Для построения ЛПЧХ разомкнутой ЦАС определяют дискретную передаточную функцию разомкнутой системы, затем путем подстановки

получают дискретную частотную передаточную функцию разомкнутой цифровой системы . Порядок построения ЛЧХ цифровых систем по дискретным частотным передаточным функциям такой же, как и для непрерывных систем.

Такой путь определения ЛПЧХ, как правило, ведет к громоздким и трудоемким построениям и промежуточным вычислениям, что связано с утратой основного достоинства метода – простоты и наглядности использования ЛЧХ.

Поэтому построение ЛПЧХ цифровых систем проводят обычно приближенными способами. Применимость этих способов зависит от вида передаточных функций непрерывной части САУ правее частоты , наличия колебательных, консервативных и неминимально-фазовых звеньев, а также расположения их сопрягающих и резонансных частот относительно частоты , порядка экстраполятора и вида . Обычно используют или метод ограничений, или метод упрощенного расчета дискретной ЛЧХ в области высоких частот.

2. Метод ограничений.

ЛПЧХ целесообразно строить раздельно для области низких частот () и для области высоких частот ().

В методе ограничений в области низких частот (левее частоты ) ЛЧХ дискретной частотной передаточной функции совпадает с ЛЧХ непрерывной части ЦАС, если , а передаточные коэффициенты преобразователей приведены к передаточной функции непрерывной части системы.

Если передаточная функция непрерывной части имеет вид

где постоянные времени делятся на две группы : к первой группе (, , …, ) отнесем те из них, которым соответствуют сопрягающие частоты меньше (большие постоянные времени), они участвуют в формировании низкочастотной части логарифмических характеристик; ко второй группе (, , …, ) отнесем постоянные времени, которым соответствуют сопрягающие частоты больше чем (малые постоянные времени). Постоянным времени , , …, соответствуют сопрягающие частоты, меньшие частоты , то при пересечении ЛАЧХ САУ вертикальной прямой асимптотой с наклоном –20 дБ/дек дискретная частотная передаточная функция имеет вид

где ;

при пересечении вертикальной линии асимптотической ЛАЧХ непрерывной части системы с наклоном –40 дБ/дек

3.Метод упрощенного расчета.

Этот метод используют, например, когда в области частот передаточную функцию непрерывной части исходной системы можно аппроксимировать выражением, для которого либо известна , либо может быть легко определена.

Например, если

, где ,

- частота, определяемая точкой пересечения асимптоты, имеющей наклон –60 дБ/дек с осью частот (эта асимптота проходит через точку сопряжения с низкочастотной частью ЛАЧХ на линии ), то построение псевдочастотной ЛЧХ производится по дискретной частотной передаточной функции :

Учет постоянного временного запаздывания

Исследованиями установлено, что для сохранения одних и тех же динамических свойств системы (точности, запаса устойчивости, качества переходного процесса) период дискретности в ЦАС с запаздыванием должен быть меньше приблизительно в раза периода дискретности в аналогичной системе без запаздывания, т. е.

где Т – максимально допустимый период дискретности в системе с запаздыванием;

- максимально допустимый период дискретности в аналогичной системе без запаздывания;

- суммарное постоянное временное запаздывание в непрерывной и дискретной частях САУ;

k - целое число , равное целой части ;

- постоянное временное запаздывание, меньшее ;

- относительное временное запаздывание.

Стандартные цифровые регуляторы

Цифровой П-регулятор

Уравнение регулятора во временной области .

Дискретная передаточная функция .

Цифровой И-регулятор

Непрерывный аналог 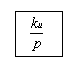, интегральное уравнение дифференциальное уравнение .

Численное интегрирование функции u(t) при нулевых

начальных условиях по методу Эйлера (метод прямоугольников):

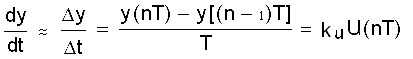отсюда -рекуррентное уравнение при интегрировании входного воздействия.

Применим дискретное преобразование Лапласа:

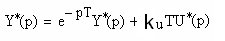, отсюда ,

, ,

- дискретная передаточная функция цифрового интегратора.

Цифровой Д-регулятор

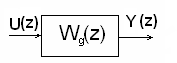
Непрерывный аналог

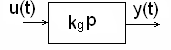
Численное дифференцирование функции u(t) при нулевых начальных условиях методом простой разности:отсюда рекуррентное уравнение при дифференциро-вании входного воздействия.

Определим z-преобразование:

отсюда

Цифровой ПД-регулятор

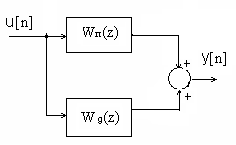
Закон регулирования в форме разностного уравнения имеет вид

Z – преобразование разностного уравнения имеет вид

отсюда

Цифровой ПИ-регулятор

Здесь так как

Тогда разностное уравнение регулятора имеет вид

Найдём z – преобразование этого уравнения:

отсюда определяем дискретную передаточную функцию регулятора

Цифровой ПИД-регулятор

Разностное уравнение регулятора:

Найдём z – преобразование разностного уравнения

отсюда

где Т-такт квантования сигналов.

Системы с конечной длительностью затухания переходных процессов

В общем случае переходный процесс в линейной импульсной системе протекает неограниченно долго. Однако в отличие от непрерывных систем, здесь возможно создание условий, при которых длительность переходных процессов при произвольных воздействиях оказывается конечной. В таких системах, начиная с некоторого момента времени, импульсная характеристика тождественно равна нулю:

w при , (1)

т.е. затухает для дискретных значений за периодов дискретности.

Учитывая связь между решетчатой весовой функцией цифровой системы и её дискретной передаточной функцией в виде

получаем, что ДПФ цифровой системы, для которой справедливо условие (1), должна удовлетворять равенству

. (2)

В общем случае дискретная передаточная функция замкнутой цифровой системы имеет вид отношения двух многочленов:

, . (3)

Сравнивая правые части (2) и (3), замечаем, что они могут быть тождественны лишь тогда, когда дробь в правой части равенства (3) превратится в многочлен. Но это может иметь место лишь тогда, когда

, (4)

т.е. , . (5)

Действительно, при выполнении условий (4) из (5) получаем при учете (2):

откуда следует, что .

Таким образом, при выполнении условий (4) весовая функция цифровой системы (ее дискретные значения) затухает за время, равное , где -порядок полинома в знаменателе передаточной функции .

Пример 1

Для цифровой системы определить условия, при которых переходный поцесс заканчивается за конечное число периодов дискретности .

Случай 1: , .

Дискретная передаточная функция замкнутой системы имеет вид

Для того чтобы переходный процесс заканчивался за время (здесь ), необходимо, чтобы полюс был равен нулю. Это условие выполняется в том случае, если , т.е. при выборе .

Случай 2: , , где .

Дискретная передаточная функция замкнутой системы имеет вид

Аналогично предыдущему случаю получаем, что переходный процесс в такой системе будет заканчиваться за один период дискретности при условии, если

т.е. при выборе .

Рассмотренные в примере простейшие импульсные системы отличает возможность достижения конечной длительности переходных процессов только за счет изменения параметров системы без изменения её структуры. В более общем случае для реализации условий (4) требуется введение в импульсную систему дополнительных корректирующих звеньев.

Рассмотрим включение корректирующего цифрового устройства последовательно в канал рассогласования системы.

Предположим, что мы хотим реализовать желаемую передаточную функцию замкнутой цифровой системы, удовлетворяющую условию (4), т.е. имеющую вид

, (6)

где -некоторый многочлен по степени (условие физической реализуемости передаточной функции).

Передаточная функция замкнутой цифровой системы с последовательным дискретным корректирующим устройством определяется выражением

, (7)

где (8)

- передаточная функция исходной (нескорректированной) системы в разомкнутом состоянии.

Подставив в (7) и разрешив это уравнение относительно , получим с учетом (6) необходимую передаточную функцию фильтра коррекции

, (9)

где , - многочлены по степени и соответственно, причем .

Поскольку в числителе дроби (9) степень многочлена равна , а в знаменателе , то из условия физической реализуемости следует, что желаемое число периодов затухания переходных процессов в системе должно удовлетворять условию

. (10)

Минимальное число периодов затухания переходного процесса при неизменяемой части из (10) равно

, (11)

что соответствует , т.е. выбору в числителе (6) многочлена нулевой степени или

. (12)

Подставив в (9), получим соответствующую передаточную функцию фильтра коррекции

. (13)

Свобода выбора коэффициента в (12) может быть использована для придания системе некоторых добавочных полезных свойств. Например, если потребовать чтобы система помимо конечной длительности переходных процессов имела астатизм по управляющему воздействию , т.е.

необходимо, чтобы коэффициент в (12), (13) был выбран равным единице.

Пример 2

Для цифровой системы определить передаточную функцию , обеспечивающую минимальное конечное время затухания переходного процесса и нулевую установившуюся ошибку при скачкообразном входном воздействии,

Дискретная передаточная функция исходной (нескорректированной) системы в разомкнутом состоянии равна

, (14)

где , , .

Учитывая, что степени многочленов и в (14) соответственно равны , , из (11) определяем , т.е.передаточную функцию замкнутой скорректированной системы принимаем в виде (с учетом (12), положив ) . Тогда, используя (13), находим искомую передаточную функцию корректирующего дискретного фильтра

, (15)

где обозначено: , .

При исследовании поведения цифровой системы с передаточной функцией дискретного фильтра коррекции, определяемой выражениями (9), (13) или (15) в промежутках между моментами замыкания импульсного элемента может оказаться, что в действительности в ней имют место скрытые колебания выходной величины в промежутках между моментами , , при в (1) равном двум. Появление подобных колебаний физически объясняется тем, что дискретный фильтр

а) б)

коррекции даже после того как исчезли импульсы на его входе (на рис. б) это соответствует ) продолжает формировать импульсы на выходе. Удовлетворение требованию отсутствия скрытых колебаний приводит к увеличению числа периодов затухания переходного процесса.

Особенности синтеза систем управления с ЭВМ в качестве управляющего устройства

Величина периода квантования Т существенно влияет на устойчивость и качество работы цифровой САУ.
Цифровые системы 2-го порядка, в отличие от непрерывных САУ, могут быть неустойчивыми, так как квантователь сигналов вносит дополнительное запаздывание.
Программирование корректирующего алгоритма (последовательное, параллельное, последовательно-параллельное, прямое) существенно влияет на качество работы системы.
Следует учитывать преимущества цифровых регуляторов над аналоговыми:
1. Цифровой регулятор обладает большей гибкостью, поскольку для изменения какого-либо его параметра достаточно просто изменить число, записанное в ячейке памяти;
2. Цифровые сигналы менее чувствительны к шумам и дрейфу параметров оборудования;
3. Цифровая обработка сигналов может производиться с высокой точностью и скоростью;
4. Сложные алгоритмы обработки сигналов лучше всего реализовать с помощью цифровых устройств, так как при этом точность параметров ограничена лишь длиной слова цифрового процессора;
5. Благодаря большим вычислительным возможностям ЭВМ в цифровых системах можно реализовать сложные алгоритмы управления и обеспечить такие переходные процессы, которые недостижимы в непрерывных системах.
Аналог дифференциального уравнения записывается в рекуррентной форме по текущим и прошлым значениям входного воздействия и выходной функции.

Методы синтеза цифровых управляющих алгоритмов

1. Формирование цифровых управляющих алгоритмов по аналоговым моделям.

2. Графо – аналитический метод синтеза по ЛПЧХ.

3. Синтез цифровых систем с апериодическим переходным процессом.

4. Синтез цифровых регуляторов на основе имитационного моделирования.

5. Системы с конечной длительностью затухания переходных процессов и др.

Литература

Бесекерский В.А. Цифровые автоматические системы. М.: Наука, 1976.
Куо Б. Теория и проектирование цифровых систем управления. М.: Машиностроение, 1986.
Микропроцессорные системы автоматического управления. Под общ. ред. В.А. Бесекерского. Л.: Машиностроение, 1988.
Проектирование микропроцессорных систем автоматического управления. Ч.1. Синтез системы автоматического управления: Учеб. пособие/ Г.Г.Диркс, В.Г. Коломыцев; ПГТУ. Пермь, 1997.
Фёдоров С.М., Литвинов А.П. Автоматические системы с цифровыми управляющими машинами. М.-Л.: Энергия, 1965.
Теория автоматического управления. Под ред. В.Б.Яковлева. М.: Высшая школа, 2003.
Дорф Р., Бишоп Р. Современные системы управления. М.: Лаборатория Базовых Знаний, 2004.
Филлипс Ч., Харбор Р.Системы управления с обратной связью. М.: Лаборатория Базовых Знаний, 2001.

r,y

t10

t11

t12

r(t)

y(t)

Квантование по уровню

r,y

r(t)

Квантование по времени;T-период квантования

r(t)

r,y

y[n]

ЦАП

АЦП

u(t)

модуляция

первого рода

Реальный импульсный элемент

модуляция

второго рода

W(p)

yc(t)

ИЭ2

u[n]

u*(t)

kЦАП

Wэ(p)

y[n]

y(t)

ЦАП

Преобразование физической формы сигнала

W(p)

W(z)

и обратно

y[n]

1(t)

jQ*()

пл. W(ejT)

P*()

k=0.15

k=68

Z= -1

-1,j0

Z= -1

D()-кривая Михайлова

(система устойчива)

yцап[n]

yцап(t)

ЦАП

,с-1

u(t)

y(t)

Системы автоматического управления с ЦВМ