Принципы управления объектами

PAGE \* MERGEFORMAT 17

Лекция №2

Общая структура проектируемой системы, её основные элементы и принцип управления в значительной мере определяются свойствами объекта регулирования, условиями работы системы и требованиями, предъявляемыми к её точности. САУ должна решать две основные задачи

Обеспечить требуемое изменение регулируемых величин;
Скомпенсировать действие на объект регулирования возмущений.

Преобразуем обобщённую структурную схему САУ к виду

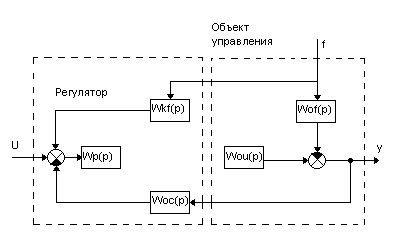
Структурная схема САУ

В общем случае управление регулирующим органом осуществляется в функции , y, x:

Это уравнение преобразуем по Лапласу при нулевых начальных условиях, полагая систему линейной:

(1)

Уравнение объекта регулирования с одной регулируемой функцией при воздействии на него возмущения имеет вид

(2)

Подставив (1) в (2), получим закон функционирования системы:

или

Отсюда

=Wзх(p)X(p)+Wзf(p)F(p) , (3)

где Wзх(p) – передаточная функция системы по каналу управления,

Wзf(p) - передаточная функция системы по каналу возмущения.

Для того чтобы регулируемая функция y изменялась по закону x(t) при любых внешних возмущениях, необходимо, чтобы Wзf(p) 0 , а Wзx(p) 1 (если неединичная обратная связь, то Wзx(p) 1/Kос) при всех условиях работы системы, т.е. необходимо с помощью сил, создаваемых регулирующим органом, скомпенсировать влияние возмущающих воздействий, действующих на объект регулирования, и приложить к объекту такие силы, которые бы обеспечили требуемое изменение регулируемой величины у(t).

Из (3) видно, что эти задачи могут быть решены различными способами, так как при этом необходимо выполнить два условия, а в законе управления (1) имеется три варьируемых оператора Wp(p), Wkf(p), Wос(p). Один из операторов может быть произвольным.

Принцип разомкнутого управления (принцип прямой связи).

Если известны действующие на систему возмущения и известна желаемая реакция на выходе системы, то можно определить передаточную функцию регулятора.

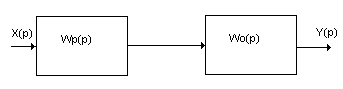
Сущность принципа состоит в том, что алгоритм управления строится только на основе заданного алгоритма функционирования и не контролируется по фактическому значению управляемой координаты объекта.

Достоинства:

Высокая скорость реакции на внешние воздействия;
Система не может быть в принципе неустойчивой.

Недостатки:

Чувствительность к изменению параметров элементов;
Невозможно получить высокую точность при неизвестных возмущениях и низкой точности модели объекта;
Невозможность полной компенсации возмущений для объектов с транспортной задержкой;
Проблема физической реализуемости обратных операторов.

Примеры: пневмо - и гидроэлектроклапаны, которые по получении электрического сигнала открывают или закрывают проход топлива, воздуха или парогаза к агрегатам, автоматические станочные линии, торговые автоматы, информационные табло железнодорожных и аэровокзалов и др.

Принцип обратной связи (принцип управления по отклонению контролируемой функции от входного воздействия, принцип Ползунова-Уатта)

Сущность принципа обратной связи заключается в том, что регулятор вступает в работу только тогда, когда между текущим и заданным значениями регулируемой функции появляется рассогласование, и регулятор воздействует на объект таким образом, чтобы свести это рассогласование к нулю или к малой величине.

Принцип внутренне противоречив, ибо прежде чем ликвидировать ошибку необходимо допустить ее возникновение.

Без обратной связи невозможно учесть влияние неизвестных факторов, неполноту знаний об объекте.

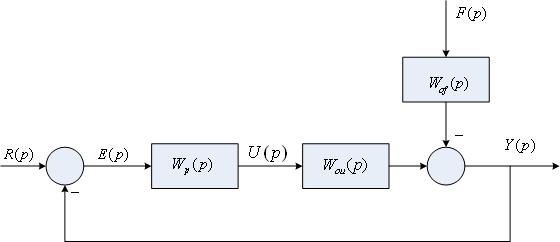
В рассматриваемом случае уравнение системы регулирования будет иметь вид

Если Wp(p) по модулю во всех режимах работы системы сделать достаточно большим [в идеале |Wp(j)|], то уr, так как при этом условии Wзf(p) будет стремиться к нулю, а Wзr(p) - к единице. Следовательно, регулирование по отклонению позволяет одновременно уменьшить влияние на систему возмущающих воздействий f и увеличить точность воспроизведения заданного входного воздействия r.

Регулятор вырабатывает в системе изменение y(t), направленное навстречу начальному отклонению, вызвавшему работу регулятора, то есть стремится компенсировать возникшее отклонение.

Обратные связи в регуляторе или объекте называются местными обратными связями.

Если система линейная и звенья статические, то в установившемся режиме тогда где обозначим k=kpky – общий передаточный коэффициент разомкнутой цепи регулирования.

Уравнение статического равновесия имеет вид

При увеличении k влияние уменьшается, поэтому достоинством этого принципа регулирования является его универсальность по отношению к возмущениям, а недостатком – склонность системы к неустойчивому режиму работы.

Установившаяся ошибка регулирования в статической системе с единичной отрицательной обратной связью (статическая ошибка) если k>>1, то

Достоинства:

Регулирование по отклонению позволяет уменьшить влияние на систему всех возмущающих воздействий;
Увеличивается точность воспроизведения заданного входного воздействия;
На динамические свойства объекта никаких ограничений не накладывается. Следовательно, регулирование по отклонению применимо к любым объектам, в том числе и к неустойчивым;
Отсутствие необходимости замера возмущений, что очень важно с практической точки зрения;
Отсутствие жёстких требований к стабильности характеристик элементов регулятора и объекта.

Недостатки:

Принципиально нельзя получить регулирование без ошибки, так как ошибка

регулирования является сигналом, который управляет регулирующим органом;

Склонность системы к неустойчивому режиму работы;
Замедленная реакция системы на изменения возмущающего воздействия, так как управляющее воздействие на объект формируется по изменению выходной координаты;
Уменьшается коэффициент усиления замкнутой системы относительно коэффициента усиления разомкнутой системы.

Управление – фундаментальная философская категория, решающая задачу формирования управляющих воздействий.

Регулирование – производная философская категория, решающая задачу отработки заданных воздействий.

Системы автоматического регулирования (САР) отличаются от систем автоматического управления (САУ) тем, что в последних происходит как формирование (выработка) желаемого поведения объекта на основании цели управления в виде задающих (управляющих) воздействий, так и их отработка в САР происходит лишь их отработка, а сами управляющие воздействия, поступающие на элемент сравнения, считаются заданными.

Теория автоматического регулирования является основой построения первого уровня, а теория автоматического управления – основой всей иерархической структуры информационных процессов управления, необходимых для комплексной автоматизации сложных объектов.

Принцип действия любой САР состоит в том, чтобы обнаружить отклонения регулируемых величин, характеризующих работу машины, или протекание процесса от требуемого режима, и при этом воздействовать на машину или процесс так, чтобы устранить возникшие отклонения.

В теории автоматического регулирования основными являются проблемы устойчивости, управляемости, наблюдаемости, качества переходных процессов, динамической точности, автоколебаний, оптимизации, синтеза и идентификации.

Пример 3. Определить уравнение статики системы регулирования напряжения генератора постоянного тока.

где k=kгkу, kг=F(Uг) определяется при Iн=0.

Выходная статическая характеристика САР.

Принцип управления по возмущению (принцип компенсации, принцип Понселе).

Сущность принципа Понселе заключается в том, что возмущение измеряется и формируется управляющее воздействие по каналу возмущения на объект так, чтобы скомпенсировать влияние возмущения на регулируемую координату.

Регулирующий орган управляется только в функции внешних воздействий F(р) и R(р). Фактическое изменение регулируемой функции у на работу регулятора влиять не будет, т.е. управление осуществляется по разомкнутому циклу.

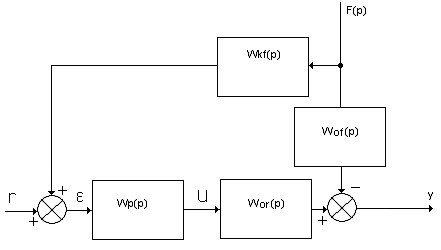
Y(p)=Yr(p)+Yf(p)=Wp(p)Wor(p)R(p)+[Wkf(p)Wp(p)Wor(p)-Wof(p)]F(p);

при выполнении условия Wp(p)Wor(p)=1 и Wkf(p)Wp(p)Wor(p) -Wof(p)=0 ,

Y(p)=R(p).

Структура автоматической системы принципиально позволяет получить управление без ошибок. Однако практическая реализация такой системы наталкивается на затруднения.

Достоинства:

Возможна полная компенсация действия возмущения.
Компенсирующее устройство не влияет на устойчивость.
Простота регулятора.

Недостатки:

Необходимо сравнительно точно измерять возмущающие воздействия, что не всегда может быть выполнено, так как возмущающие силы обычно не поддаются точному измерению.
Реализация регулятора в общем случае невозможна, так как в передаточной функции Wp(p)=1/Wor(p) порядок числителя, как правило, выше порядка знаменателя.
Регулирование по возмущению может быть использовано лишь для объектов устойчивых.
Компенсируется только измеренное возмущение.
Приборы для измерения возмущений сложные и дорогие.

Такие системы применяются в тех случаях, когда не требуется высокая точность выполнения алгоритма функционирования объекта.

Пример. Проведем анализ установившегося режима работы генератора постоянного тока с компенсирующей обмоткой ОВ2.

При условии компенсируется влияние Iн.

4. Комбинированный принцип управления.

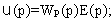
Если , ,то Y(p)=R(p).

Здесь одновременно используются как принцип регулирования по отклонению, так и по возмущению.

Такая структура обеспечивает наибольшие возможности в отношении получения заданной точности регулирования. Так как регулирование производится по отклонению, то возможно регулирование объектов с любыми динамическими свойствами, а наличие дополнительных связей по возмущению и входному воздействию позволяет добиться высокой точности регулирования без существенного усложнения замкнутого контура регулирования.

Если Wkr(p), Wp(p) и Wkf(p) выбрать так, чтобы Wз(p)=0, а Wзr(p)=1, то =0 во всех режимах работы, т.е. комбинированная система в основном будет работать, как система регулирования по возмущению, а на долю связи по отклонению останется лишь компенсация всех неучтённых возмущений, приводящих к изменению регулируемой величины. Так как эти возмущения имеют обычно 2-й порядок малости, то высоких требований к регулятору Wp(p) можно не предъявлять. Однако на практике введение связи по возмущению используется редко, так как возмущение трудно измерить, а в некоторых системах влияние возмущения бывает мало и его не учитывают (например, в большинстве следящих приводов, особенно быстродействующих). В системах стабилизации (r(t)=const) применение дополнительных связей от входного воздействия обычно не используют.

Достоинства:

Наличие ООС делает систему менее чувствительной к изменению параметров регулируемого объекта;
Добавление канала, чувствительного к заданию или к возмущению, не влияет на устойчивость контура с ООС.

Недостатки:

Каналы, чувствительные к заданию или к возмущению, обычно содержат дифференцирующие звенья. Их практическая реализация затруднена.
Не все объекты допускают форсирование.

Статические и астатические САУ.

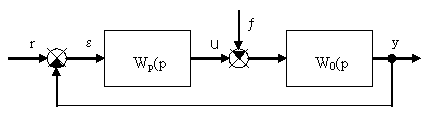
Теорема о предельном (конечном) значении функции.

Пусть непрерывная функция h(t) имеет предел, тогда справедливо равенство:

Если - ошибка системы, а yэm(t) – эталонная (безошибочная) выходная функция, то статическая ошибка системы

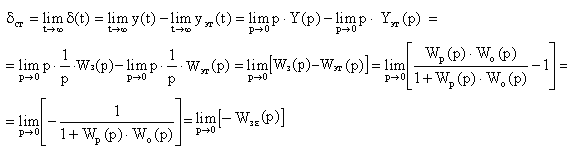Передаточная функция по отклонению

Система регулирования называется статической по отношению к управляющему воздействию, если при воздействии стремящемся к установившемуся постоянному значению, ошибка регулируемой функции также стремится к постоянному значению, зависящему от величины воздействия.

Критерием того, что система статическая, является выражение

, где Wз(p) – передаточная функция замкнутой системы по отклонению.

Автоматическая система называется астатической по отношению к управляющему воздействию, если при воздействии стремящемся к некоторому установившемуся постоянному значению отклонение регулируемой функции стремится к нулю вне зависимости от величины воздействия.

Одна и та же система может быть статической по отношению к возмущающему воздействию и астатической по отношению к управляющему воздействию.

Признаком астатической системы по каналу управления является наличие нулевых полюсов в передаточной функции прямого канала системы; признаком астатической системы по каналу возмущения является наличие нулевых полюсов передаточной функции регулятора.

Астатические системы могут быть I–го и более высокого порядков. На практике находят применение астатические системы 1-3 порядков.

В передаточной функции разомкнутой системы с астатизмом I–го порядка по каналу управления имеется 1 нулевой полюс .

В системе регулирования с астатизмом второго порядка

то есть имеется два нулевых полюса в передаточной функции разомкнутой системы:

Наличие двух нулевых полюсов приводит к тому, что система становится структурно-неустойчивой, и для её стабилизации обязательно применение корректирующих устройств. Вместе с тем ясно, что скоростная ошибка такой системы равна нулю.

Порядок астатизма автоматической системы при введении корректирующих устройств может измениться, например статическая система может приобрести свойства астатической и наоборот.

Поэтому при проектировании автоматических систем выбор статической или астатической системы определяется конструктивными особенностями системы, свойствами объекта регулирования и его регулирующего органа, возможностями проектируемой системы и требованиями, предъявляемыми к ней.

Статизм регулирования - статическая ошибка от действия номинального возмущения, выраженная в % относительно значения выходной функции при отсутствии возмущения либо номинальном возмущении или относительно ном.

Рис. 1.

К статическим регуляторам принято относить такие, у которых от действия ступенчатого сигнала на входе выходной сигнал асимптотически устанавливается на уровне некоторой конечной величины.

У астатических регуляторов от действия ступенчатого сигнала на входе происходит линейное или нелинейное нарастание сигнала на выходе без ограничения по уровню.

Статические характеристики звеньев и объектов САУ

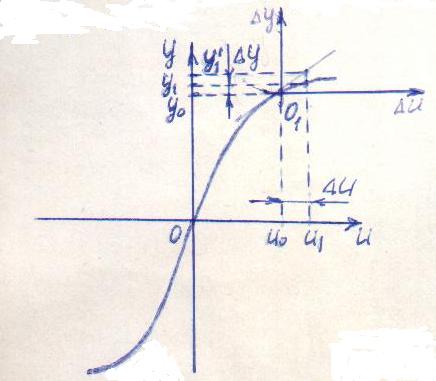
Статическая характеристика объекта

Статической характеристикой по каналу управления (возмущения) объекта называется функциональная зависимость выход-вход при отсутствии или постоянном значении возмущения (управления), все точки которой сняты в установившемся режиме (при t).

Пусть О1 – рабочая точка объекта, тогда статический передаточный коэффициент объекта определяют по выражению:

Для характеристики динамических свойств в окрестности рабочей точки О1 определяется приращение , соответствующее приращению u входного воздействия. Чтобы упростить динамическую модель объекта производят линеаризацию характеристики. Достаточным условием возможности проведения линеаризации математической модели звена или системы является отсутствие разрывности и неоднозначности функций. Линеаризация нелинейной аналитической функции основана на том, что непрерывная и имеющая все производные в окрестности некоторой (рабочей) точки функция (например, статическая характеристика звена) может быть разложена в ряд Тейлора по степеням малых отклонений аргумента относительно рабочей точки:

Если при этом отклонения аргумента достаточно малы, то можно ограничиться первыми линейными членами разложения и рассматривать вместо нелинейной функции линейную, откуда

где - динамический передаточный коэффициент.

Линеаризацию нелинейных статических характеристик производят методами малых отклонений, касательной, секущей, кусочно – линейной аппроксимации.

У объектов регулирования определяют статические характеристики по каналам управления и возмущения:

Возмущение обычно Внешние характеристики объекта

действует со знаком “-”

Пример

Линеаризация алгебраических уравнений

Резервуар с жидкостью

Бак с водой приведен на рис. 1. В нижней части бака просверлено отверстие, через которое вытекает вода. Площадь сечения бака обозначим через S, а площадь сечения отверстия – через .

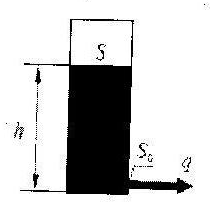
Рис. 1. Резервуар с жидкостью

Построим модель, которая связывает уровень воды в баке (в метрах) и расход вытекающей воды (в м3/c). Эту связь можно найти с помощью закона Бернулли, который в данном случае принимает вид

где - плотность жидкости (в кг/м3), м/с2 – ускорение свободного падения, - скорость вытекания жидкости (в м/с). Отсюда получаем . Учитывая, что расход воды вычисляется как , находим

, (1)

где - постоянная величина. Это статическая нелинейная модель. Статическая модель описывает установившееся состояние (статический режим), когда в баке поддерживается постоянный уровень воды и поток вытекающей воды тоже постоянный.

Линеаризовать модель – значит приближённо заменить нелинейное уравнение линейным:

где - некоторый коэффициент.

Предположим, что уровень воды изменяется в интервале от 0 до 1м. Тогда один из вариантов – вычислить коэффициент как угол наклона отрезка, соединяющего точки кривой на концах этого интервала. Для определённости принимаем , тогда получаем (рис.2). Эта модель очень грубая и даёт большую ошибку, особенно для уровней в диапазоне от 0,1 до 0,6. Чтобы уменьшить ошибку, можно попробовать несколько изменить (например, увеличив его до 1,2), однако точность приближения по-прежнему будет невысока, хотя и несколько лучше, чем в первом случае.

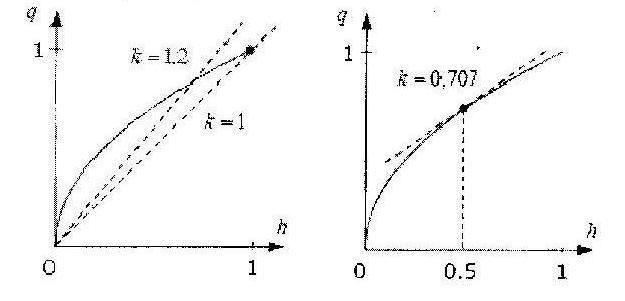
Рис. 2. Статические характеристики объекта

Теперь предположим, что обычно уровень мало изменяется вблизи среднего значения . В этом случае можно применить другой подход. В этой области кривая почти совпадает с касательной в точке (0,5;), угол наклона которой равен производной

Касательная – это прямая с наклоном , проходящая через точку (0,5;), её уравнение имеет вид . Свободный член определим из равенства

так что получаем модель

. (2)

Это линейное уравнение, однако модель (2) – нелинейная, поскольку для неё не выполняется, например, свойство умножения на константу. Это легко проверить, сравнив и :

Принцип суперпозиции также не выполняется.

Для того чтобы получить из (2) линейную модель, нужно записать уравнение в отклонениях от рабочей точки , в которой определили наклон касательной. Тогда

. (3)

Поскольку график зависимости (2) проходит через точку , можно применить равенство

Тогда из (3) находим

. (4)

Полученное таким образом уравнение – это линейная модель объекта, записанная в отклонениях входа и выхода от номинальной (рабочей) точки . Приближённая модель (4) точнее всего соответствует объекту вблизи этой точки, а при больших отклонениях от неё ошибка значительно возрастает.

Динамические характеристики:

Переходная характеристика;
Импульсная переходная характеристика;
Реакция объектов и систем на типовые и требуемые по технологии работы воздействия.

Типовые входные воздействия

Ступенчатое (скачкообразное) воздействие.

если U0=1 [размерность входного воздействия], то u(t)=1(t) – единичное ступенчатое воздействие.

Функция Хевисайда (в Matlab – heaviside(t))

Линейно-возрастающее (с постоянной скоростью) воздействие.

где u(t) – линейная функция времени.

Для систем управления движением в качестве тестового сигнала обычно используют не функцию скачка, а линейно нарастающий сигнал, поскольку электромеханические системы имеют ограниченную скорость нарастания выходной функции.

Параболическое (с постоянным ускорением) воздействие.

где

Синусоидальное воздействие.

Воздействия в виде степенных функций времени.

изображение по Лапласу степенных функций времени имеет вид

При исследовании точности работы станков с программным управлением в установившихся режимах широко используются управляющие воздействия в виде степенных функций времени.

В нормальных режимах работы управляющее воздействие в виде линейной функции времени u(t)=At1(t) имеет место в следящих системах станков с программным управлением при обработке изделия с постоянной скоростью по одной или двум координатам. Управляющее воздействие в виде квадратичной степенной функции может быть, например, при обработке изделия с постоянным ускорением по одной из координат.

В ряде случаев более сложные воздействия на систему можно представить в виде суммы S степенных функций времени

6. Дельта-функция (единичная импульсная функция, функция Дирака (в Matlab – dirac(t))).

Рассмотрим функцию

Если эту функцию трактовать как силу, действующую за промежуток времени от 0 до h, а в остальное время равную нулю, то, очевидно, импульс этой силы будет равен единице. Изображение этой функции будет т.е.

В механике и электротехнике удобно рассматривать силы, действующие очень короткий промежуток времени, как силы действующие мгновенно, но имеющие конечный импульс. Поэтому вводят функцию (t) как предел функции 1(t,h) при

Следует иметь в виду, что (t) не есть функция в обычном понимании. Многие авторы-физики функцию (t) называют функцией Дирака.

Эту функцию называют также единичной импульсной функцией или дельта-функцией. Естественно положить

L – изображение функции (t) определим как предел изображения функции 1(t,h) при (здесь воспользовались правилом Лопиталя для нахождения предела).

Частотные характеристики

Частотными называются характеристики звеньев (систем) в форме графиков или таблиц, отображающие изменение амплитуды и фазы выходной функции (т.е. реакцию) звеньев или систем относительно синусоидального входного воздействия в установившемся режиме при изменении частоты от 0 до .

Частотная область даёт возможность наглядно оценить динамические свойства системы:

Резонансные;

Свойства в установившемся режиме;

Полосу пропускания;

Усилительные свойства в различных областях частот.

Для линейных систем справедлив ПРИНЦИП СУПЕРПОЗИЦИИ, который можно сформулировать следующим образом.

Реакция системы на несколько одновременно действующих входных воздействий равна сумме реакций на каждое воздействие в отдельности.

Это позволяет ограничиться изучением систем только с одним входом.

В качестве входных воздействий были выбраны гармонические воздействия в виду нескольких обстоятельств

реально встречающиеся воздействия, как правило, могут быть представлены в виде суммы гармоник различных частот (разложение Фурье)
в установившихся режимах гармонические сигналы передаются линейными элементами и системами без искажений
обычно не возникает затруднений в экспериментальном исследовании поведения систем .

Функцию называют частотной передаточной функцией (график – амплитудно – фазовой характеристикой – АФХ).

Функцию W( j) можно представить в виде

где амплитудно-частотная функция (график АЧХ); - фазо-частотная функция (график ФЧХ),

U() – вещественная частотная функция (график – ВЧХ),

V() – мнимая частотная функция (график – МЧХ).

Если то

АФХ несёт информацию о реакциях на гармонические входные сигналы.

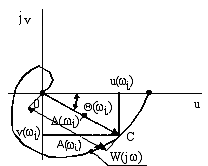
На комплексной плоскости частотную передаточную функцию W(j) определяет вектор , длина которого равна А(), а аргумент (угол, образованный этим вектором с действительной положительной полуосью) - (). Кривую, которую описывает конец этого вектора при изменении частоты от 0 до (иногда от - до ), называют амплитудно-фазовой частотной характеристикой (АФХ).

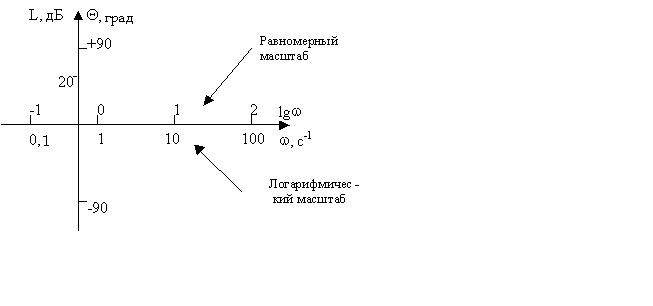
L ()= 20 lg A()= 20 lgW( j)- логарифмическая амплитудная частотная функция (график - ЛАЧХ).

ЛФЧХ называют график зависимости фазового сдвига функции () от логарифма частоты lg.

Единицей измерения L() является децибел, а единицей логарифма частоты в ЛЧХ – декада. Декадой называют интервал, на котором частота изменяется в 10 раз. Ось ординат при построении ЛЧХ проводят через произвольную точку оси абсцисс, а не через точку =0. Частоте =0 соответствует бесконечно удалённая точка lg- при 0.

Белл - логарифмическая единица десятикратного увеличения мощности. Так как А()- отношение напряжений, токов, перемещений, то увеличение этого отношения в 10 раз будет соответствовать увеличению отношения мощностей в 100 раз, что соответствует 2 Белам или 20 дБ.

1мВт – базовая мощность в устройствах связи.

Методика построения логарифмических частотных характеристик САУ

Пусть передаточная функция разомкнутой статической САУ, состоящей из минимально-фазовых звеньев 1-го порядка, имеет вид в реальных системах n(m-n).

Отобразим W(р) в область преобразований Фурье преобразуем математическое описание каждого элементарного звена к форме и расположим в порядке убывания величины Тi:

Тогда

Алгоритм построения ЛАЧХ

На оси нанесите точки i=1/Ti. Проведите через эти точки вертикальные штриховые линии.
Проведите контурную линию с ординатой 20lgk слева до первой вертикальной линии при отсутствии нулевых полюсов и нулей в передаточной функции или линию с наклоном -20дБ/дек через точку при одном нулевом полюсе, или линию с наклоном -40 дБ/дек через точку при двух нулевых полюсах, или линию с наклоном +20 дБ/дек через точку при одном корне числителя, равном нулю, или линию с наклоном +40 дБ/дек через точку при двух нулях, равных нулю, и т.д.
До следующей вертикальной линии проведите контурную линию с наклоном -20* дБ/дек ( – количество элементарных звеньев с одинаковыми Ti), если звенья апериодические, или +20* дБ/дек для дифференцирующих звеньев первого порядка.
Уменьшите (увеличьте) наклон на -20* дБ/дек (+20* дБ/дек) на следующей вертикальной линии до полного построения L().

Высокочастотные асимптоты ЛАЧХ (справа от наибольшей сопрягающей частоты) проводят в требуемом диапазоне частот.

Примечания

Для построения ЛАЧХ звена второго порядка используются приведенные характеристики в технической литературе или строятся по точкам вблизи i=1/Ti, вдали с асимптотами левой 0 дБ/дек , правой -40 дБ/дек для колебательного звена и +40 дБ/дек для звена дифференцирующего второго порядка.
Правило построения ЛЧХ систем с неминимально-фазовыми звеньями остаётся тем же.
ЛФЧХ строятся по точкам, рассчитанным аналитически.

Пример

Пусть задана передаточная функция объекта

Требуется построить асимптотическую ЛАЧХ объекта.

1. Выделение элементарных звеньев.

Вынесем множитель из каждой скобки так, чтобы свободный член в этой скобке был равен 1:

Корни квадратного трёхчлена в знаменателе комплексно-сопряжённые, поэтому можно представить заданную передаточную функцию в виде произведения передаточного коэффициента и четырёх передаточных функций элементарных звеньев:

,
где .

Звенья с передаточными функциями и - идеальные звенья с введением производной, второе из них – неминимально - фазовое. Звено с передаточной функцией - апериодическое звено, а звено с - колебательное, поскольку .

2. Определение сопрягающих частот.

Сопрягающие частоты – это точки излома ЛАЧХ. Они определяются как . Таким образом,

рад/с, рад/с,

рад/с, рад/с.

Поскольку при построении ЛАЧХ на оси абсцисс откладывается lg, вычислим десятичные логарифмы этих частот:

, ,

, .

3. Построение ЛАЧХ.

Отметим найденные точки излома ЛАЧХ на оси абсцисс:

Поскольку интегрирующие и дифференцирующие звенья в системе отсутствуют, на низких частотах (примерно до первой сопрягающей частоты ) система имеет постоянное усиление, равное k=10. Учитывая, что амплитудная характеристика откладывается в логарифмическом масштабе (в децибеллах) получаем

20lgk=20lg10=20

и можно сразу нарисовать начальный участок ЛАЧХ:

На частоте вступает в действие апериодическое звено, которое даёт наклон -20 дБ/дек, в интервале от до график спускается вниз на

дБ, поэтому ордината для частоты равна дБ:

На частоте идеальное звено с введением производной добавляет наклон +20 дБ/дек, таким образом, общий наклон становится равен нулю:

На частоте неминимально – фазовое идеальное звено с введением производной ещё добавляет наклон +20 дБ/дек, таким образом, общий наклон становится равен +20 дБ/дек. В интервале от до график поднимается на дБ, поэтому ордината для частоты равна 9,6+10,420 дБ:

Наконец, на частоте колебательное звено добавляет наклон -40 дБ/дек, таким образом, общий наклон становится равен -20 дБ/дек:

ЛЧХ контура с отрицательной обратной связью

1. Аналитический метод построения ЛЧХ контура с единичной ООС.

отсюда

2. Построение ЛЧХ контура по номограммам замыкания (Никольса).

Пусть амплитудно-фазовая частотная функция замкнутой системы имеет вид

(1) причем ,

Амплитудную и фазовую частотные функции замкнутой системы Аз() и з() можно выразить через А() и разомкнутой цепи.

Согласно формуле (1) имеем

или, взяв обратные величины слева и справа, получим новое равенство

Подставим сюда и приравняем затем отдельно вещественные и мнимые части. Получим два равенства

Сложив сначала квадраты этих выражений, а затем поделив одно из них на другое, получим искомый результат

L(1)

L3(1)

3(1)

Чтобы не иметь дело на практике с этими формулами, составлены НОМОГРАММЫ ЗАМЫКАНИЯ.

Отложив на осях абсцисс и ординат заданные значения (1) и L(1), находим значения 20lgАз(1) и (1) на поле номограммы в точке с этими координатами. Таким образом по точкам строится вся частотная характеристика замкнутой системы.

Если контур с неединичной ООС, то его следует преобразовать к контуру с единичной ООС.

где WА(j)=WПК(j)WОС(j). Тогда ЛЧХ замкнутой системы строится в два приёма

вначале строятся ЛЧХ контура с единичной ООС, затем строятся ЛЧХ функции и, наконец, результирующие ЛЧХ системы и

Алгоритм построения ЛЧХ

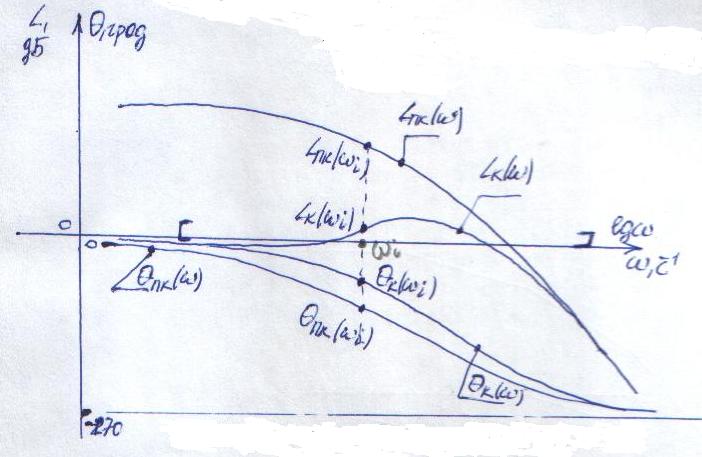
Строится ЛЧХ разомкнутой системы по передаточной функции .
В выделенном диапазоне частот […] задаются рядом контрольных точек , которым соответствуют и .
По номограмме замыкания определяются и соответствующие и .
Соединив плавной кривой полученные точки в логарифмической системе координат, строят и .

3. Построение ЛЧХ по преобразованной передаточной функции контура.

Многочлены числителя и знаменателя передаточной функции замкнутого контура или прямых параллельных звеньев преобразовываются к произведению двух - или трёхчленов, затем по методике 1 строятся ЛЧХ.

4. Построение в Matlab.

Принципы управления объектами