Статистическое исследование и обработка статистических данных
КУРСОВАЯ РАБОТА
на тему Статистическое исследование и обработка статистических данных
АННОТАЦИЯ
Тема курсовой работы: статистическое исследование и обработка статистических данных.
По всей структуре курсовой работы стоит из введения, семи глав, заключения и списка используемых источников.
В курсовой рассматривается следующие темы: статистическое наблюдение, статистическая сводка и группировка, формы выражения статистических показателей, выборочное наблюдение, статистическое изучение взаимосвязи социально-экономических явлений и динамики социально-экономических явлений, экономические индексы.
Курсовая работа содержит 64 страниц, 56 формул, 22 таблицы, 11 график, и семи глав. В работе изложена цель исследования, объект исследования, предмет единицы совокупности. К решению курсовой применены методы статистики, выполнены задачи, разработка программы к наблюдению.
СОДЕРЖАНИЕ
Введение ………………………………………………………………………..6
Статистическое наблюдение ……………………………………………….…7
Статистическая сводка и группировка ……………………………………....12
Формы выражения статистических показателей …………………………...18
Размах вариации. Среднее линейное отклонение.Среднее квадратическое отклонение. Дисперсия…………………………………………………………….19
Гистограмма. Полион распределения. Куммулята ……………………...….21
Средняя величина анализируемого показателя. Мода. Медиана ………….22
Проверка гипотезы о близости к нормальному распределению……..........25
Выборочное наблюдение ……………………………………………………..27
Выборка ………………………………………………………………………..28
Показатели выборочной совокупности ……………………………………...29
Статистическое изучение взаимосвязи социально-экономических явлени…………………………………………………………………………….....32
Изучение связи между зависимой и независимой величинами (парная корреляция) ………………………………………….…………………………..…33
Изучение связи между зависимой и независимой величинами (непарная корреляция)…………………………………………………………………....……40
Статистическое изучение динамики социально-экономических явлений………………………………………………………………………..…….48
Экономические индексы
Заключение……………………………………………………………………63
Список используемых источников…………………………………………..64
ВВЕДЕНИЕ
Статистика — это самостоятельная общественная наука, имеющая свой предмет исследования и специфические методы.
Статистика широко используется в естественных и общественных науках для установления специфических закономерностей. Статистика — это одна из форм практической деятельности людей, цель которой сбор, обработка и анализ массовых данных о тех или иных явлениях. Статистикой называется также различного рода числовые данные, характеризующие различные стороны жизни государства: политические отношения, культуру, население и производство. Основная задача статистики — помочь людям лучше понять современные социально-экономические явления.
Объект статистического исследования называется статистической совокупностью.
Статистическая совокупность — это множество единиц, обладающих массовостью, однородностью, определенной целостностью, взаимосвязью отдельных единиц и наличием вариаций.
Статистические методы наиболее важно применять там, где находятся большие массивы данных, из которых необходимо выделить полезную информацию.
Цель данной курсовой работы – овладеть основами статистики и освоить общие навыки проведения статистического исследования и анализа его результатов.
Задачами работы являются: построение статистических таблиц, организация статистического наблюдения, исчисление показателей статистики (тесноты связи, абсолютных и относительных, динамики, средних, вариации), а также анализ данных и построение выводов.
Объект данной курсовой работы – исследование регионов Российской Федерации. Предметом работы является изучение взаимосвязи между занятыми населениями, средними денежными доходами и социальными выплатами.
Задание №1
Выберите объект статистического наблюдения (например, обследование коммерческих банков, строительных фирм, страховых компаний, предприятий конкретной отрасли промышленности, учебных заведений, регионов и др.).
Для избранного объекта:
1) сформулируйте цель статистического наблюдения;
2) определите избранный объект статистического наблюдения и единицу наблюдения;
3) разработайте программу наблюдения;
4) Спроектируйте инструментарий статистического наблюдения (формуляр (бланк) обследования, инструкцию, организационный план наблюдения);
5) постройте систему макетов статистических таблиц в качестве программы разработки материалов вашего обследования.
- Цель статистического наблюдения: оценить качество обслуживания в банке ВТБ-24 города Тамбова
- Объект статистического наблюдения: клиенты, посещающие ВТБ-24
Единица наблюдения: клиент, посещающий посещающие ВТБ-24 Программа наблюдения:
Форма наблюдения – специально организованное статистическое наблюдение
Вид наблюдения по охвату единиц наблюдения - сплошное наблюдение
Наблюдение предлагается провести социологам при содействии работников средств массовой информации города Тамбова
Срок наблюдения: 10-2011
1. Часто ли вы бываете в этом банке?
2. Всегда ли очереди у кассира-операциониста ?
3. Всегда ли при обращении к продавцу вы получаете исперпывающий ответ на свой?
4. Дружелюбно ли реагируют на наши обращения сотрудники?
5 Долго ли вы прибываете в очереди?
6. Всегда ли при обращении очереди включается дополнительная касса?
7. Всегда ли вас приветствуют кассиры?
8. Всегда ли кассиры называют сумму ?
9. Комфортно ли вам, когда кассир обращается за разменной монетой?
10. Кассиры всегда правильно выдают вам сдачу?
11. Всегда ли говорят на кассе «спасибо »?
12. У вас есть предложения по улучшению качества обслуживания в этом банке?
13. Вам комфортно проводить операции в этом банке?
14. У вас есть предложения по улучшению качества обслуживания в этом банке?
4) Анкета
Таблица 1
|
№ |
да |
нет |
|
|
1 |
Часто ли вы бываете в этом банке? |
||
|
2 |
Всегда ли очереди у кассира-операциониста ? |
||
|
3 |
Всегда ли при обращении к продавцу вы получаете исперпывающий ответ на свойы вопрос? |
||
|
4 |
Дружелюбно ли реагируют на наши обращения сотрудники? |
||
|
5 |
Долго ли вы прибываете в очереди? |
||
|
6 |
Всегда ли при обращении очереди включается дополнительная касса? |
||
|
7 |
Всегда ли вас приветствуют кассиры? |
||
|
8 |
Всегда ли кассиры называют сумму ? |
||
|
9 |
Комфортно ли вам, когда кассир обращается за разменной монетой? |
||
|
10 |
Кассиры всегда правильно выдают вам сдачу? |
||
|
11 |
Всегда ли говорят на кассе «спасибо »? |
||
|
12 |
У вас есть предложения по улучшению качества обслуживания в этом банке |
||
|
13 |
Вам комфортно проводить операции в этом банке? |
||
|
14 |
У вас есть предложения по улучшению качества обслуживания в этом банке? |
5) Для обследования совокупности используются макеты следующих таблиц:
Таблица №1
Расчет среднего линейного отклонения и дисперсии
|
№ п/п |
Показатель |
Вес |
xi |
||||||
|
1 … n |
|||||||||
|
Итого: |
Таблица №2
Вспомогательная таблица для определения моды, медианы, квартилей
|
№ п/п |
Показатель |
Вес |
Накопленная частота |
|
1 … n |
|||
|
Итого |
Таблица №3
Расчет теоретических частот нормального распределения
|
№ п/п |
Показатель |
Вес |
|||||||
|
1 … n |
|||||||||
|
Итого |
Таблица №4
Примерная расчетная таблица для определения выборочной средней и дисперсии
|
№ п/п |
xi |
fi |
xifi |
2 |
2fi |
|
|
1 … n |
||||||
|
Итого |
Таблица №5
Расчетная таблица для определения параметров уравнения регрессии (парная регрессия)
|
№ п/п |
x |
y |
x2 |
xy |
y2 |
|
|
1 … n |
||||||
|
Итого |
Таблица №6
Расчетная таблица для определения параметров уравнения регрессии (множественная регрессия)
|
№ п/п |
Y |
X1 |
X2 |
YX1 |
X12 |
Y2 |
X1X2 |
X22 |
YX2 |
|
|
1 … n |
||||||||||
|
Итого |
Таблица №7
Показатели анализа ряда динамики
|
Период |
Показатели |
Абсолютный прирост (снижение) |
Темпы роста, % |
Темпы прироста, % |
Абсолютное значение 1% прироста |
|||
|
с предыдущим периодом |
с начальным периодом динамического ряда |
с предыдущим периодом |
с начальным периодом динамического ряда |
с предыдущим периодом |
с начальным периодом динамического ряда |
|||
|
1 … n |
||||||||
|
Итого |
Таблица №8
Динамика показателя и расчет скользящих средних
|
№ п/п |
Периоды |
Показатель |
Трехчленные скользящие суммы |
Трехчленные скользящие средние |
|
1 … n |
Таблица №9
Исходные и расчетные данные для определения параметров системы уравнения
|
№ п/п |
Периоды |
Показатель |
t |
t2 |
ty |
()2 |
||
|
1 … n |
||||||||
|
Итого |
Задание №2
По данным любого статистического ежегодника (например, «Россия в цифрах», «Российский статистический ежегодник» Госкомстата России и др.) и периодической печати подберите соответствующий цифровой материал (совокупность объемом 30-50 единиц) для выбранного в задании №1 объекта исследования и выполните следующие задания:
1) постройте интервальный вариационный ряд распределения;
2) к каждой выделенной группе подберите 3-4 наиболее экономически связанных и существенных показателя, а также вычислите показатели в относительном выражении. Результаты группировки изложите в сводных групповых таблицах и проанализируйте;
3) с помощью аналитической группировки проанализируйте зависимость рассматриваемой величины от других экономических показателей. Результаты оформите в таблице. Сделайте выводы;
4) проанализируйте полученную группировку.
Для выполнения заданий данной главы используется совокупность В.
Таблица 2 – Совокупность.
|
№ |
Группы регионов По кредитам |
Физическим лицам- всего. (млрд.рублей) |
В том числе по жилищным кредитам(млрд.рублей) |
Из неё по ипотечным жилищным кредитам(млрд.рублей) |
|
1 |
Брянская обл. |
117,14 |
4,6156 |
3,3518 |
|
2 |
Владимирская обл. |
23,764 |
7,3786 |
4,9886 |
|
3 |
Калужская обл. |
17,646 |
5,2884 |
4,5193 |
|
4 |
Костромская обл. |
10,3442 |
2,1641 |
1,8013 |
|
5 |
Курская обл. |
19,725 |
5,4291 |
3,1857 |
|
6 |
Липецкая обл. |
18,213 |
5,1047 |
4,1314 |
|
7 |
Орловская обл. |
11,02 |
2,7298 |
1,7976 |
|
8 |
Рязанская обл. |
21,469 |
6,1677 |
5,5992 |
|
9 |
Смоленская обл. |
19,402 |
6,7679 |
5,6848 |
|
10 |
Тамбовская обл. |
12,099 |
2,566 |
1,5636 |
|
11 |
Тверская обл. |
22,241 |
7,1909 |
6,9923 |
|
12 |
Ярославская обл. |
22,584 |
6,8038 |
5,9173 |
|
13 |
Рес. Карелия |
17,003 |
5,5319 |
4,6185 |
|
14 |
Рес.Коми |
25,162 |
10,021 |
7,2032 |
|
15 |
Мурманская обл. |
20,283 |
4,5987 |
3,6784 |
|
16 |
Новгородская обл. |
11,488 |
3,2778 |
2,5218 |
|
17 |
Псковская обл. |
8,4539 |
2,0108 |
1,4932 |
|
18 |
Рес. Адыгея |
5,6882 |
1,3241 |
1,0315 |
|
19 |
Кабардино-Балкарская республика |
7,2586 |
2,5625 |
1,2519 |
|
20 |
Рес. Северная Осетия-Алания |
5,3984 |
1,6971 |
0,9404 |
|
21 |
Астраханская обл. |
18,74 |
4,1535 |
3,1263 |
|
22 |
Рес.Марий Эл |
11,053 |
3,933 |
3,3196 |
|
23 |
Рес.Мордовия |
12,748 |
4,3787 |
2,6429 |
|
24 |
Чувашская республика |
23,897 |
11,068 |
9,0845 |
|
25 |
Кировская обл. |
20,883 |
6,1754 |
3,3279 |
|
26 |
Пензенская обл. |
19,812 |
5,4 |
3,6616 |
|
27 |
Саратовская обл |
41,657 |
10,39 |
9,4513 |
|
28 |
Ульяновская обл |
22,035 |
6,1246 |
4,5917 |
|
29 |
Курганская обл. |
16,166 |
5,5151 |
4,4984 |
|
30 |
Рес. Бурятия |
24,742 |
5,2403 |
4,6009 |
|
31 |
Рес.Тыва |
7,07 |
1,8001 |
1,76 |
|
32 |
Рес. Хакасия |
13,145 |
4,4449 |
3,7255 |
|
33 |
Забайкальский край |
25,888 |
6,5035 |
5,486 |
|
34 |
Томская обл |
35,079 |
13,105 |
10,894 |
|
35 |
Камчатский край |
6,4549 |
1,581 |
1,4485 |
|
36 |
Приморский край |
34,203 |
8,0048 |
7,272 |
|
37 |
Хабаровский край |
37,836 |
10,936 |
10,432 |
|
38 |
Амурская обл |
18,092 |
4,9146 |
3,9403 |
|
39 |
Магаданская обл |
4,0263 |
1,2343 |
1,0501 |
|
40 |
Сахалинская обл |
12,118 |
3,281 |
2,9357 |
- найти число групп;
Вычислим количество групп по формуле Стерджесса:
n =1+3,322*lg N,
где n – число групп,
N – число единиц совокупности.
Для исходной совокупности В имеем n = 1+3,322* lg 40 = 6.32
Округлив значение, получаем число групп равное 6. (n = 6)
- найти максимальное и минимальное значения признака по результативным признакам.
= 13,105 (Томская область);
= 1,2343 (Магаданская обл).№39
- найти размах вариации
Найдем размах вариации по формуле :
(2.1)
где – максимальное значение признака,
– минимальное значение признака.
Для совокупности В получили R =13,105- 1,2343=11,8707
- найти шаг:
Для нахождения шага используется формула (3).
h = (2.2)
Шаг h = 11,8707/6 =1,97845 для совокупности В по результативным признакам.
Получили интервалы:
|
1 2 3 4 5 6 |
1,2343 -3,2128 3,2128-5,1912 5,1912–7,1697 7,1697 – 9,1481 9,1481– 11,1266 11,1266–13,10505 |
Построим интервальный вариационный ряд распределения:
Таблица 3 – Интервальный вариационный ряд распределения
|
№ |
Группы регионов числу по жилищных кредитов(млрд.рублей) |
Число регионов |
Удельный вес, % |
|
1 2 3 4 5 6 |
1,2343 -3,2128 3,2128-5,1912 5,1912–7,1697 7,1697 – 9,1481 9,1481– 11,1266 11,1266–13,10505 |
10 9 12 4 3 2 |
25 22,5 30 10 7,5 5 |
|
Итого |
40 |
100 |
Таблица для расчета удельного веса:
У1=11/40*100%=25%
У2= 9/40*100%=22,5%
У3= 12/40*100%=30%
У4=4 /40*100=10%
У5= 3/40*100=7,5%
У6 = 2/40*100% =5 %
По результатам распределения получили наибольшее количество тех регионов, в которых объём в том числе по жилищным кредитам(млрд.рублей приходится на третий интервал [5,1912–7,1697], и составляет 12 регионов , то есть 30% всех данных.
Таблица 4 – Аналитическая группировка
|
№ п/п |
Группы регионов по жилищным кредитам (млрд.рублей) |
№ региона |
Физическим лицам- всего.(млрд.рублей) |
В том числе по жилищным кредитам(млрд.рублей) |
Из неё по ипотечным жилищным кредитам(млрд. рублей) |
|
1 |
1,2343 -3,2128 |
4 7 10 17 18 19 20 31 35 39 |
10,3442 11,02 12,0988 8,4539 5,6882 7,2586 5,3984 7,0700 6,4549 4026,3 |
2,1641 2,7298 2,5660 2,0108 1,3241 2,5625 1,6971 1,8001 1,5810 1,2343 |
1,8013 1,7976 1,5636 1,4932 1,0315 1,2519 0,9404 1,7600 1,4485 1,0501 |
|
Итого |
10 |
77,8132 |
19,6698 |
14,1381 |
|
|
2 |
3,2128-5,1912 |
3 6 15 16 21 22 23 32 40 |
17,646 18,213 20,2832 11,4884 18,7401 11,0534 12,7477 13,1451 12,118 |
5,288 5,1047 4,5987 3,2778 4,1535 3,9330 4,3787 4,4449 3,2810 |
4,519 4,1314 3,6784 2,5218 3,1263 3,3196 2,6429 3,7255 2,9357 |
|
Итого |
9 |
135,4349 |
38,4603 |
30,6006 |
|
|
3 |
5,1912–7,1697 |
3 5 8 9 12 13 25 26 28 29 30 33 |
17,646 19,7245 21,4688 19,402 22,5844 17,0026 20,8827 19,8122 22,0347 16,1659 24,7415 7,070 |
5,2884 5,4291 6,1677 6,7679 6,8038 5,5319 6,1754 5,400 6,1246 5,5151 5,2403 6,5035 |
4,519 3,186 5,599,2 5,6848 5,917,3 4,6185 3,3279 3,6616 4,5917 4,4984 4,6009 5,486 |
|
Итого |
12 |
228,54 |
70,9477 |
55,6913 |
|
|
4 |
7,1697 – 9,1481 |
2 11 36 38 |
23,7644 22,2411 34,202 18,092 |
7,3786 7,191 8,005 4,9146 |
4,9886 6,9923 7,272 3,940, |
|
Итого |
4 |
98,2995 |
27,4892 |
23,1929 |
|
|
5 |
9,1481– 11,1266 |
14 27 37 |
25,1623 41,6565 37,8356 |
10,0209 10,3899 10,9356 |
7,2032 9,4513 10,4313 |
|
Итого |
3 |
104,6544 |
31,3464 |
27,0858 |
|
|
6 |
11,1266-13,10505 |
24 36 |
23,897 35,0786 |
11,068 13,1051 |
9,0845 10,894 |
|
Итого |
2 |
58,9756 |
24,1731 |
19,9785 |
|
|
всего |
40 |
703,71 |
206,555 |
170,687 |
Разбив совокупность на группы, получили шесть групп. Наибольшей частотой обладает третья группа, содержащая 12 регионов (5,1912–7,1697), а наименьшую частоту имеет шестая группа, содержащая 2 региона (интервал 11,1266-13,10505).
Задание №3
По данным ряда распределения рассчитайте:
- размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсию;
- постройте гистограмму и полигон распределения, куммуляту, сформулируйте выводы;
- рассчитайте среднюю величину анализируемого показателя, моду, медиану, квартили и коэффициент вариации;
- с помощью критерия согласия проверить гипотезу о законе распределения.
Необходимые расчеты оформите в табличной форме. Проиллюстрируйте расчеты соответствующими графиками. Результаты проанализируйте.
3.1) Размах вариации. Среднее линейное отклонение. Среднее квадратиче-ское отклонение. Дисперсия.
Произведем расчет среднего линейного отклонения и дисперсии.
Таблица 5 – расчет среднего линейного отклонения и дисперсии
|
№ |
Группы регионов по жилищным кредитам (млрд.руб |
Число регионов, входящих в группу |
Середина интервала |
|
|||||
|
1 |
1,2343-3,2128 |
10 |
2,2236 |
22,2355 |
-3,3139 |
3,31391 |
33,1391 |
10,9820 |
109,8200 |
|
2 |
3,2128-5,1912 |
9 |
4,2020 |
37,8180 |
-1,3355 |
1,3355 |
12,0195 |
1,7835 |
16,0511 |
|
3 |
5,1912–7,1697 |
12 |
6,1805 |
74,1654 |
0,6430 |
0,6430 |
7,716 |
0,4134 |
4,9612 |
|
4 |
7,1697-9,1481 |
4 |
8,1589 |
32,6356 |
2,6214 |
2,6214 |
10,4856 |
109,9512 |
439,8047 |
|
5 |
9,1481– 11,1266 |
3 |
10,1374 |
30,4121 |
4,5999 |
4,5999 |
13,7997 |
21,1590 |
63,4770 |
|
6 |
11,1266-13,1051 |
2 |
12,1158 |
24,2317 |
6,5783 |
6,5783 |
13,1566 |
43,2749 |
86,5498 |
|
221,4982 |
|
|
90,3163 |
|
720,6637 |
Используя данные таблицы 5, найдем следующие показатели:
Средняя величина определяется по форме:
= , где (3.1)
- средняя величина исследуемого явления;
- i-й вариант усредняемого признака (i=1,n);
- вес i-го варианта.
= = = 5,53746
Типичный размер признака у данной однородной совокупности единиц равен 5,53746 .
- Размах вариации:
R =13,105- 1,2343=11,8707
Различие между единицами совокупности, имеющими наибольшее и наименьшее значение, составляет 11,8707
2. Среднее линейное отклонение представляет собой среднюю величину из отклонений вариантов признака от их средней. В нашем случае оно вычисляется как средняя арифметическая взвешенная из абсолютных значений отклонений варианта, формула выглядит следующим образом:
= , (3.2)
= = 2,2579
Среднее линейное отклонение от закономерности равно 2,2579
3. Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины и вычисляется по формулам:
= , (3.3)
= =18,0165
Средний квадрат отклонений индивидуальных значений признака от их средней величины равен 18,0165.
4. Корень квадратный из дисперсии называется средним квадратическим отклонеинием
= , (3.4)
= = 4,2446
Обобщающая характеристика размеров вариации признака в совокупности, т.е. среднеквадратическое отклонение, равна 4,2446
- ) Гистограмма. Полигон распределения. Кумулята.
Построим гистограмму, полигон распределения и кумуляту
.
Рисунок 3 – Кумулята
3.3) Средняя величина анализируемого показателя. Мода. Медиана. Квартили и коэффициент вариации
Таблица 6 – вспомогательная таблица для определения моды, медианы, квартилей.
|
№ |
Группы регионов по жилищным кредитам (млрд.руб |
частоты |
Накопленная частота |
|
1 2 3 4 5 6 |
1,2343 -3,2128 3,2128-5,1912 5,1912–7,1697 7,1697 – 9,1481 9,1481– 11,1266 11,1266–13,10505 |
10 9 12 4 3 2 |
10 19 31 35 38 40 |
|
Итого |
40 |
2) Определяем моду:
Мода (Мо) – это значение признака, наиболее часто встречающееся в исследуемой совокупности.
, (3.5)
где - нижняя граница модального интервала;
- частота модального интервала;
- частота интервала, предшествующего модальному;
- частота интервала, последующего за модальным.
Модальным называется третий интервал, так как он имеет наибольшую частоту, равную 31.
5,7307
Значение признака, повторяющегося с наибольшей частотой, равно 5,7307
3) Определяем медиану:
Медианой (Ме) называется значение признака, приходящееся на середину ранжированной совокупности; для определения медианного значения признака пользуются следующей формулой:
, (3.6)
Где: x0 – нижняя граница медианного интервала;
i – величина медианного интервала;
SMe-1 – накопленная частота интервала, предшествующего медианному;
f Ме - частота медианного интервала;
Медианным называется третьий интервал, так как это первый интервал, накопленная частота которого превышает половину общей суммы частот.
- Нижний и верхний квартиль:
, , (3.7)
где - нижняя граница интервала, содержащего нижний квартиль (интервал определяется по накопленной частоте, первой превышающей 25%);
- нижняя граница интервала, содержащего верхний квартиль (интервал определяется по накопленной частоте, первой превышающей 75%);
i – величина интервала;
- накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль;
- то же для верхнего квартиля;
- частота интервала, содержащего нижний квартиль;
- частота интервала, содержащего верхний квартиль.
- 2-ой интервал содержит нижний квартиль, так как он является первым интервалом, накопленная частота которого превышает 25% от общей суммы частот.
- 4-ый интервал содержит верхний квартиль, так как он является первым интервалом, накопленная частота которого превышает 75% от общей суммы частот.
Выполним подстановку:
.
.
Нижний и верхний квартиль соответственно равны 3,3128 и 7,0048
- Коэффициент вариации:
(3.8);
%.
Коэффициент вариации – v равен 47,29% .
Анализируя проведенные выше расчеты, можно сделать вывод, что наибольшее число регионов имеет задолженность по жилищным кредитам,составляющую5,7307 млрд.рублей, так как Мо =5,7307.
В изучаемой совокупности одна половина физических лиц в регионах имеет задолженность по жилищным кредитам менее 5,3561 млрд.рублей, вторая половина более 5,3561 млрд.рублей, так как Ме = 5,3561
Так как Q1 = 3,2128 и Q3= 7,0048; то 25% рассматриваемых регионов имеет общая численность занятых населений 3,2128 млрд.рублей, а другие 25% более 7,0048 млрд.рублей
Поскольку коэффициент вариации равен 47,29%( а он превышает 33%)можно сделать вывод, что рассматриваемая совокупность является не однородной.
3.4) Проверка гипотезы о близости к нормальному распределению
Для того, чтобы проверить близость полученного распределения к нормальному, необходимо вычислить критерий согласия К. Пирсона.
Используя табличные данные, рассчитаем критерий согласия Пирсона по формуле:
(3.9);
где fэ и fT – эмпирические и теоретические частоты соответственно.
. (3.10);
Где h – шаг интервала;
F(t) = ;
= n -1, где – число степени свободы.
Произведем необходимые расчеты, рассчитаем значение t :
t1 = (2,2236-5,53746) /4,2446 = -0,781
t2 = (4,202 -5,53746) /4,2446 = -0,314
t3 = (6,1805-5,53746) /4,2446 = 0,151
t4 = (8,1589 -5,53746) / 4,2446 = 0,617
t5 = (10,1374- 5,53746) / 4,2446 = 1,083
t6 = (12,1158 -5,53746) /4,2446 = 1,549
перейдем к расчетам теоретических частот, но для расчета рассчитаем значение выражения:
= 1,97845 *40/ 4,2446 = 18,644
ft1 =18,644 *0,29407 =5,4826; ft1 окр =5,483 ;
ft2 = 18,644* 0,3757 =7,0045; ft2 окр = 7,005;
ft3 = 18,644* 0, 39444 =7,3539 ; ft3 окр =7,354;
ft4 = 18,644*0,3298 =6,1487 ft4 окр =6,149 ;
ft5 = 18,644*0,22198 = 4,1385; ft5 окр =4,139;
ft6 = 18,644*0,12019 =2,2408; ft6 окр =2,241;
(fэ - ft)1 = 10-5,483=4,517; ( )1 = (4,517)2 / 5,483=3,721;
(fэ - ft)2 = 9-7,005=-1,995; ( )2 = (-1,995)2 /7,005 =0,568;
(fэ - ft)3 = 12-7,3539=-4,646; ( )3 = (-4,646)2 /7,3539 =2,935
|
№ п.п |
вес |
||||||||
|
1 |
1,2343-3,2128 |
10 |
2,2236 |
-0,781 |
0,29407 |
5,4826 |
5,483 |
4,517 |
3,721 |
|
2 |
3,2128-5,1912 |
9 |
4,2020 |
-0,314 |
0,3757 |
7,0045 |
7,005 |
1,995 |
0,568 |
|
3 |
5,1912–7,1697 |
12 |
6,1805 |
0,151 |
0,39444 |
7,3539 |
7,354 |
4,646 |
2,935 |
|
4 |
7,1697 -9,1481 |
4 |
8,1589 |
0,617 |
0,3298 |
6,1487 |
6,149 |
-2,149 |
0,751 |
|
5 |
9,1481-11,1266 |
3 |
10,1373 |
1,083 |
0,22198 |
4,1385 |
4,139 |
-1,139 |
0,313 |
|
6 |
11,1266-13,1051 |
2 |
12,1158 |
1,549 |
0,12019 |
2,2408 |
2,241 |
-0,241 |
0,026 |
|
Итого |
40 |
8,332 |
(fэ - ft)4 = 4-6,149=-2,149; ( )4 = (-2,149)2 /6,149 =0,751
(fэ - ft)5 = 3-4,139= -1,139; ( )5 =(-1,139)2/4,139 =0,313
(fэ - ft)6 = 2-2,241 =-0,241; ( )6 =(-0,241)2/2,241=0,026;
Таблица 7 – Расчет теоретических частот нормального распределения
По специальным таблицам определяем, что при заданном уровне значимости = и числе степеней свободы =n-1=6-1=5 то = 15,1; то есть > поэтому гипотеза о близости эмпирического распределения к нормальному распределению подтверждается.
Проиллюстрируем расчеты соответствующим графикам
Рисунок 4 – эмпирическое и теоретическое распределения
По графику видно, что расхождение между эмпирическими и теоретическими значениями не ближе, это еще раз доказывает что гипотеза о распределении близком к нормальному не отвергается.
Задание №4
- На базе отобранных данных произведите репрезентативный отбор по принципам выборочного наблюдения. Способ отбора и вид выборки определите самостоятельно.
- Для сформулированной выборочной совокупности вычислите:
- среднюю величину по выборочной совокупности;
- предельную ошибку выборки и пределы, в которых находится генеральная
средняя (уровень вероятности задайте самостоятельно).
Сформулируйте выводы.
4.1) Выборка
На базе имеющих данных путем собственно-случайной бесповторной выборки было отобрано 15 регионов (процент выборки составил 35%). Результаты отбора представим в виде таблицы:
Таблица 8 - Совокупность С
|
№ п/п |
№ региона в генеральной совокупности |
Регион |
Физическим лицам- всего.(млрд.рублей) |
В том числе по жилищным кредитам(млрд.рублей) |
Из неё по ипотечным жилищным кредитам(млрд. рублей) |
|
1 |
4 |
Костромская обл. |
10,3442 |
2,1641 |
1,8013 |
|
2 |
35 |
Камчатский край |
6,4549 |
1,581 |
1,4485 |
|
3 |
3 |
Липецкая обл. |
18,213 |
5,1047 |
4,1314 |
|
4 |
40 |
Сахалинская обл |
12,118 |
3,281 |
2,9357 |
|
5 |
8 |
Рязанская обл. |
21,469 |
6,1677 |
5,5992 |
|
6 |
28 |
Ульяновская обл |
22,035 |
6,1246 |
4,5917 |
|
7 |
33 |
Забайкальский край |
25,888 |
6,5035 |
5,486 |
|
8 |
36 |
Приморский край |
34,203 |
8,0048 |
7,272 |
|
9 |
27 |
Саратовская обл |
41,657 |
10,39 |
9,4513 |
|
10 |
34 |
Томская обл |
35,079 |
13,105 |
10,894 |
4.2) Найдем число групп по формуле Стерджесса:
Для выборочной совокупности с имеем n=1+3,322lg10 =
Округлив значение, получаем число групп, равное 5.
- Найдем максимальное и минимальное значения признака:
Xmax= 13,105 (Томская область)
Xmin= 1,581 (Камчатский край)
- Найдем размах вариации по формуле (2):
R=13,105 -1,581= 11,524
- Найдем шаг по формуле (3):
h = 11,524 /5 = 2,305
Получили интервалы:
|
№ п/п |
Группы регионов по численности занятых населений |
Число регионов |
Удельный вес |
|
1 |
1,581-3,886 |
3 |
30 |
|
2 |
3,886-6,191 |
3 |
30 |
|
3 |
6,191-8,496 |
2 |
20 |
|
4 |
8,496-10,801 |
1 |
10 |
|
5 |
10,801-13,106 |
1 |
10 |
|
Итого |
10 |
100 |
Таблица 9 - Аналитическая группировка в выборочной совокупности:
|
№ п/п |
Группы регионов по численности занятых населений |
№ региона |
Физическим лицам- всего.(млрд.рублей) |
В том числе по жилищным кредитам(млрд.рублей) |
Из неё по ипотечным жилищным кредитам(млрд. рублей) |
|
1 |
1,581-3,886 |
4 35 40 |
10,3442 6,4549 12,118 |
2,1641 1,581 3,281 |
1,8013 1,4485 2,9357 |
|
Итого |
3 |
28,9171 |
10,0261 |
6,1855 |
|
|
2 |
3,886-6,191 |
6 8 28 |
18,213 21,469 22,035 |
5,1047 6,1677 6,1246 |
1,8013 5,5992 4,5917 |
|
Итого |
3 |
61,717 |
17,397 |
14,3223 |
|
|
3 |
6,191-8,496 |
33 36 |
25,888 34,203 |
6,5035 8,0048 |
5,486 7,272 |
|
Итого |
2 |
60,091 |
14,5083 |
12,758 |
|
|
4 |
8,496-10,801 |
27 |
41,657 |
10,39 |
9,4513 |
|
Итого |
1 |
41,647 |
10,39 |
9,4513 |
|
|
5 |
10,801-13,106 |
34 |
35,079 |
13,105 |
10,894 |
|
Итого |
1 |
35,079 |
13,105 |
10,894 |
|
|
Всего |
10 |
227,4611 |
65,4264 |
53,6111 |
Определим среднюю величину по выборочной совокупности, используя
формулу средней арифметической взвешенной, используя таблицу 9.
Таблица 10 – Расчетная таблица для определения выборочной средней и
дисперсии
|
№ п/п |
Группы регионов по численности занятых населений |
xi |
fi |
xifi |
2 |
2fi |
|
|
1 |
1,581-3,886 |
2,7335 |
3 |
8,2009 |
-3,227 |
10,4135 |
31,2406 |
|
2 |
3,886-6,191 |
5,0385 |
3 |
15,1155 |
-0,922 |
0,8501 |
2,5503 |
|
3 |
6,191-8,496 |
7,3435 |
2 |
14,687 |
1,383 |
1,9127 |
3,6584 |
|
4 |
8,496-10,801 |
9,6485 |
1 |
9,6485 |
3,688 |
13,6013 |
13,6013 |
|
5 |
10,801-13,106 |
11,9535 |
1 |
11,9535 |
5,993 |
35,9160 |
35,9160 |
|
Итого |
10 |
59,605 |
86,9666 |
1. Найдем средную величину в выборочной совокупности по следующей формуле:
, (4.1)
Получим:
2. Рассчитаем среднюю ошибку выборки по формуле:
, (4.2)
где - дисперсия выборочной совокупности,
n – число единиц выборочной совокупности; n = 10
N – число единиц генеральной совокупности; N= 40
Для данной совокупности .
Выполним поставку, получим:
, (4.3)
где t – нормированное отклонение (коэффициент доверия), зависящий от вероятности, с которой гарантируется предельная ошибка выборки.
При вероятности F(t)= 0,683 .
Найдем предельные значения характеристик генеральной совокупности и их доверительные интервалы:
При выполнении поставки, получим:
Следовательно с вероятностью 0,683 можно утверждать, что .в том числе по жилищным кредитам в генеральной совокупности находится в границах от 3,4065 до 8,5145 млрд.рублей
Задание №5
Для изучения связи между зависимой и независимой величинами на базе отобранных данных:
- постройте корреляционную таблицу, характеризующую зависимость результативного признака от факторного. Сделайте выводы о характере связи между признаками;
- изобразите связь между изучаемыми признаками графически;
- постройте уравнение регрессии по сгруппированным данным. Параметры уравнения определите методом наименьших квадратов. Рассчитайте теоретические (полученные по уравнению регрессии) значения результативного признака и нанесите их на построенный в п.2 график. Определите форму связи между признаками;
- на основе F- критерия Фишера и t-критерия Стьюдента проверьте значимость: в первом случае – уравнения регрессии; во втором – его параметров. Дайте экономическую интерпретацию параметров уравнения связи;
- по сгруппированным данным вычислите линейный коэффициент корреляции и корреляционное отношение. Сделайте выводы о степени и направлении связи между изучаемыми признаками;
- с экономической точки зрения сформулируйте выводы относительно исследуемой вами связи.
5.1) Изучение связи между зависимым и независимым переменными (парная корреляция)
Построим таблицу, характеризующую зависимость социальных выплат от численности занятых населений (см. таблицу 10).
Таблица 11 – Зависимость результативного признака от факторного
|
№ п/п |
Группы регионов по жилищным кредитам (млрд.рублей) |
В том числе по жилищным кредитам(млрд.руб) (xi) |
Физическим лицам- всего.(млрд.рублей) (y) |
|
1 |
Костромская обл. |
2,1641 |
10,3442 |
|
2 |
Камчатский край |
1,581 |
6,4549 |
|
3 |
Липецкая обл. |
5,1047 |
18,213 |
|
4 |
Сахалинская обл |
3,281 |
12,118 |
|
5 |
Рязанская обл. |
6,1677 |
21,469 |
|
6 |
Ульяновская обл |
6,1246 |
22,035 |
|
7 |
Забайкальский край |
6,5035 |
25,888 |
|
8 |
Приморский край |
8,0048 |
34,203 |
|
9 |
Саратовская обл |
10,39 |
41,657 |
|
10 |
Томская обл |
13,105 |
35,079 |
x – факторный признак
у – результативный признак
Анализируя представленную таблицу можно предположить что между признаками существует прямой характер связи, т.е. с увеличением численности занятых населений будет увеличиваться социальные выплаты.
5.2) На основе корреляционной таблицы 10 изобразим связь между изучаемыми признаками графически.
Рисунок 5 – Графическое выражение зависимости между факторным и результативным признаком
Данный график показывает что между изучаемыми признаками существует линейная зависимость, т. е. с ростом В том числе по жилищным кредитам и растёт Физическим лицам- всего
5.3) При статистическом изучении связи показателей чаше всего применяется прямолинейная форма зависимости между признаками x и y. Эта зависимость выражается следующей формулой:
, (5.1)
где - теоретические значения результативного признака, полученные по уравнению регрессии;
а0, а1 – коэффициенты (параметры) уравнения регрессии.
Параметры уравнения определим с помощью метода наименьших квадратов. В основу этого метода положено требование минимальности сумм квадратов отклонений эмпирических данных (Yi) от выровненных ():
.
Для прямой зависимости:
.
Для нахождения минимума данной функции приравняем к нулю ее частные производные и получим систему двух линейных уравнений, которая называется системой нормальных уравнений:
Для решения данной системы составляется расчетная таблица:
Таблица 12 – Расчетная таблица для определения параметров уравнения регрессии (парная регрессия)
|
№ п/п |
x |
y |
x2 |
x*y |
y2 |
|
|
1 |
2,1641 |
10,3442 |
4,683 |
22,386 |
107,002 |
10,65902 |
|
2 |
1,581 |
6,4549 |
2,500 |
10,205 |
41,666 |
8,92138 |
|
3 |
5,1047 |
18,213 |
26,058 |
92,972 |
331,713 |
19,42201 |
|
4 |
3,281 |
12,118 |
10,765 |
39,759 |
146,846 |
13,98738 |
|
5 |
6,1677 |
21,469 |
38,041 |
132,414 |
460,918 |
22,58975 |
|
6 |
6,1246 |
22,035 |
37,511 |
134,956 |
485,541 |
22,46131 |
|
7 |
6,5035 |
25,888 |
42,296 |
168,363 |
670,189 |
23,59043 |
|
8 |
8,0048 |
34,203 |
64,077 |
273,788 |
11669,845 |
28,0643 |
|
9 |
10,39 |
41,657 |
107,952 |
432,816 |
1735,306 |
35,1722 |
|
10 |
13,105 |
35,079 |
171,741 |
459,710 |
1230,536 |
43,2629 |
|
итого |
62,426 |
227,461 |
505,623 |
1767,369 |
6379,562 |
228,1307 |
Выполним подставку полученных значений в систему уравнений:
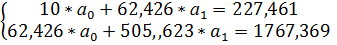
=10 62,426 =1206(главный определитель)
62,426 505,623
1= 227,461 62,426 =5081(Первый определитель)
1767,369 505,623
2=10 227,461 = 3596 (Второй определитель )
62,426 1767,369
Найдем решения данной системы уравнений. Согласно описанному выше методу, данная система уравнений имеет решения:
а0 = 1/ 4,21
а1= 2/ 2,98
Решая систему уравнений, найдем значения параметров а0 4,21; а1 2,98
Поставляя значения вычисленных параметров в уравнение регрессии, получаем: =4,21+2,98 * x
Рассчитаем при соответствующих значениях x:
1 = 4,21+ 2.98 * 2,1641=10,65902; 9 = 4,21+ 2.98 *10,39=35,1722
2 = 4,21+ 2.98 *1,581 =8,92138; 10 =4,21+ 2.98 *13,105=43,2629
3 =4,21+ 2.98 * 5,1047=19,42201;
4 =4,21+ 2.98 * 3,281=13,98738;
5 = 4,21+ 2.98 * 6,1677=22,58975
6 = 4,21+ 2.98 *6,1246 =22,46131;
7 = 4,21+ 2.98 *6,5035 =23,59043;
8 = 4,21+ 2.98 *8,0048=28,0643;
Таким образом, мы рассчитаем теоретические (рассчитанные по уравнению регрессии) значения результативного признака.
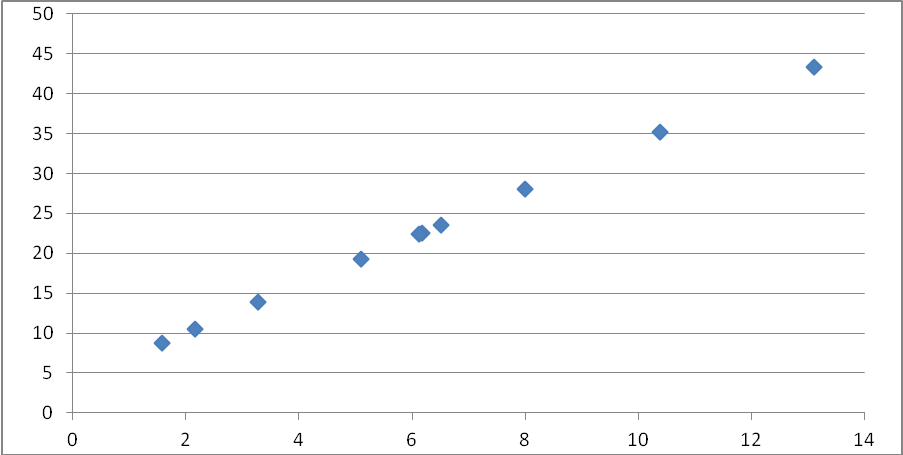
Рисунок 6 – Графическое выражение зависимости между В том числе по жилищным кредитам и Физическим лицам- всего.
5.4) Теперь нам необходимо проверить значимость уравнения регрессии и его параметров. Значимость уравнения регрессии проверяется на основе вычисления F-критерия Фишера
, (5.2)
где m – число параметров в уравнении регрессии.
. (5.3)
Таблица 13 – Расчетная таблица для определения значения критерия Фишера
|
x |
y |
Y- |
(Y-)2 |
(Y-)2 |
|
|
2,1641 |
10,3442 |
10,65902 |
-0,1786 |
0,0319 |
153,8071 |
|
1,581 |
6,4549 |
8,92138 |
-2,3204 |
5,3843 |
265,4032 |
|
5,1047 |
18,213 |
19,42201 |
-1,1228 |
1,2607 |
20,5490 |
|
3,281 |
12,118 |
13,98738 |
-1,7522 |
3,0702 |
112,9565 |
|
6,1677 |
21,469 |
22,58975 |
-1,0526 |
1,1080 |
1,6310 |
|
6,1246 |
22,035 |
22,46131 |
-0,3574 |
0,1277 |
0,5057 |
|
6,5035 |
25,888 |
23,59043 |
2,36 |
5,5696 |
9,8715 |
|
8,0048 |
34,203 |
28,0643 |
6,1756 |
38,1380 |
131,2606 |
|
10,39 |
41,657 |
35,1722 |
6,4812 |
42,0060 |
357,6221 |
|
13,105 |
35,079 |
43,2629 |
-8,2337 |
67,7938 |
152,1004 |
|
62,426 |
227,461 |
228,1307 |
- |
164,5681 |
1205,7071 |
Для данных таблицы 10 значение F-критерия Фишера равно:
бост = = 4,057
= - ()2 = 6379,562 / 10 - (227,461/10)2 = 120,5711
Выполнив поставку, найдем значение F-критерия:
Таким образом, при уровне значимости =0,05 и степени свободы 1=2-1=1 и 2=10-2=8табличное значение Fтабл.=5,32, следовательно при > Fтабл. уравнение регрессии может быть использовано для практических целей. Отсюда следует, что данное уравнение регрессии статистически значимо.
Значимость параметров уравнения регрессии осуществляется с помощью t-критерия Стьюдента. При этом вычисляют расчетные (фактические) значения t- критерии
Для параметра а0: (5.4);
Для параметра а1: , (5.5);
- ()2 = 505,623/10 – (62,426/10)2 = 11,5922
бx = = 3,4047
.
Для заданного уровня значимости =0,05 и числа степеней свободы 1=2-1=1 и 2 =n-2=10-2=8 табличное значение(Таблица распределение Фишера-Снедекора) tтабл.= 5,32 . Таким образом, tтабл.<tрасч. и для а1 и для а0, значит, с вероятностью 0,95 можно утверждать, что найденные параметры уравнения регрессии и являются значимыми.
Для удобства интерпретации параметра а1 используют коэффициент эластичности.
, (5.6);
.
значит при изменении факторного признака (В том числе по жилищным кредитам на 1%, среднее изменение результативного признака (Физическим лицам- всего.) составляет 82,27%.
5.5) Производим оценку практической значимости модели. Для прямолинейной связи это выполняется посредством линейного коэффициента корреляции:
r = (5.7);
Он принимает значение в интервале – 1<= r <= 1
Выполним подставку:
r=1767.369/10- (62.426/10*227.461/10)/(3,4047*10,9805)=0,9293
Положительное значение r указывает на прямую связь (с увеличением факторного признака увеличивается результативный признак) значит сделанное нами ранее предположение верно.
Теперь рассчитаем теоретическое корреляционное отношение. Для этого воспользуется следующей формулой:
, (5.8)
Имея все необходимые для расчета данные получаем:
Значение корреляционного отношения является показатель тесноты связи, в нашем случае r = 0,9293 это значит связь между В том числе по жилищным кредитам и растёт Физическим лицам- всего сильная и прямая.
5.6) С экономической точки зрения, на основе произведенных расчетов можно сделать следующие выводы:
Во-первых, построенное нами уравнение регрессии и входящие в него коэффициенты практически все значимы за исключением одного
Во вторых, исчисление линейный коэффициент корреляции и теоретическое корреляционное отношение (r = 0,9293, = 0,9293) свидетельствует о сильной линейной прямой связи межу изучаемыми признаками.
В-третьих, построенная модель по F-критерию Фишера адеквата, следовательно построенная модель может быть использована для приятия решений и осуществления прогнозов.
Задание №6
Для изучения связи между зависимой и независимой величинами на базе отобранных данных:
- определите результативный и не менее 2-х факторных признаков. Оцените с экономической точки зрения важность факторов и последовательность их включения в уравнение регрессии;
- определите форму корреляционного уравнения и обоснуйте его выбор. По исходным данным постройте графики зависимости результативного признака с каждым из факторных. Проанализируйте характер связей;
- рассчитайте линейные (парные) коэффициенты корреляции, проверьте их значимость. Проанализируйте характер парных зависимостей между признаками. Исключите коллинеарно связанные факторы. Рассчитать множественный коэффициент корреляции и проверить его значимость;
- постройте расчетную таблицу для определения параметров уравнения регрессии. Постройте множественное уравнение регрессии. Параметры уравнения регрессии определите методом наименьших квадратов;
- проверить значимость уравнения регрессии на основе:
- F-критерия Фишера;
- средней ошибки аппроксимации;
6) проверьте значимость коэффициентов регрессии на основе t-критерия Стьюдента.
6.1) Изучение связи между зависимой и двумя независимыми величинами (множественная корреляция)
Построим таблицу, характеризующую зависимость социальных выплат (Y) от занятых населений (X1) и средних денежных доходов (X1), (см. таблицу 13).
Таблица 14 – Зависимость результативного признака от двух факторных
|
№ |
Группы регионов по жилищным кредитам (млрд.рублей) |
В том числе по жилищным кредитам(млрд.руб (X1) |
Из неё по ипотечным жилищным кредитам(млрд.рублей (X2) |
Физическим лицам- всего.(млрд.рублей) (Y) |
|
1 |
Костромская обл. |
2,1641 |
1,8013 |
10,3442 |
|
2 |
Камчатский край |
1,581 |
1,4485 |
6,4549 |
|
3 |
Липецкая обл. |
5,1047 |
4,1314 |
18,213 |
|
4 |
Сахалинская обл |
3,281 |
2,9357 |
12,118 |
|
5 |
Рязанская обл. |
6,1677 |
5,5992 |
21,469 |
|
6 |
Ульяновская обл |
6,1246 |
4,5917 |
22,035 |
|
7 |
Забайкальский край |
6,5035 |
5,486 |
25,888 |
|
8 |
Приморский край |
8,0048 |
7,272 |
34,203 |
|
9 |
Саратовская обл |
10,39 |
9,4513 |
41,657 |
|
10 |
Томская обл |
13,105 |
10,894 |
35,079 |
(X2)
C экономической точки зрения наиболее важным является фактор X1-это есть В том числе по жилищным кредитам, а всё потому что показатель показывает наибольшее влияние на значение результативного признака. Поэтому правильнее в первую очередь включить в уравнение регрессии именно (В том числе по жилищным кредитам(млрд.руб)), а только затем Из неё по ипотечным жилищным кредитам(млрд.рублей
6.2) В качестве формы корреляционного уравнения выбрана линейная модель (так как она наиболее простота)
График зависимости от X1, и от X2
Рисунок 7 –зависимость между физическим лицам всего, а также в том числе по жилищным кредитам
Рисунок 8 – зависимость между физическим лицам всего и из неё по ипотечным жилищным кредитам
Анализируя графики, можно предположить что зависимости являются прямолинейными, поэтому выбор уравнения корреляции падает на линейную форму зависимости
Форма = a0 + a1 *x1 + a2 * x2 (6.1)
Где x1 , x2 - факторные признаки
- теоретическое значение результативного признака, полученное по уравнению регрессии
a0 , a1 , a2 - параметры уравнения регрессии
Параметры уравнения определим методом наименьших квадратов. В основу этого метода положено требование минимальности сумм квадратов отклонений эмпирических данных (Yi) от выравненных ():
.
Для прямолинейной зависимости:
Для нахождения минимума данной функции приравняем к нулю ее частные производные, получим систему линейных уравнений:
Для решения данной системы поставляет расчетная таблица:
Таблица 15 – Расчетная таблица для определения параметров уравнения регрессии (множественная регрессия)
|
№ п/п |
y |
X1 |
X2 |
Yx1 |
|
|
X1x2 |
|
Yx2 |
|
|
1 |
10,3442 |
2,1641 |
1,8013 |
22,3859 |
4,683 |
107,002 |
3,898 |
3,245 |
18,633 |
10,169 |
|
2 |
6,4549 |
1,581 |
1,4485 |
10,2052 |
2,500 |
41,666 |
2,290 |
2,098 |
9,350 |
9,462 |
|
3 |
18,213 |
5,1047 |
4,1314 |
92,9719 |
26,058 |
331,713 |
21,090 |
17,068 |
75,245 |
17,582 |
|
4 |
12,118 |
3,281 |
2,9357 |
39,7592 |
10,765 |
146,846 |
9,632 |
8,618 |
35,575 |
14,725 |
|
5 |
21,469 |
6,1677 |
5,5992 |
132,4144 |
38,041 |
460,918 |
34,534 |
31,351 |
120,209 |
24,628 |
|
6 |
22,035 |
6,1246 |
4,5917 |
134,9556 |
37,511 |
485,541 |
28,122 |
21,084 |
101,178 |
17,725 |
|
7 |
25,888 |
6,5035 |
5,486 |
168,3626 |
42,296 |
670,189 |
35,678 |
30,096 |
142,022 |
22,827 |
|
8 |
34,203 |
8,0048 |
7,272 |
273,7882 |
64,077 |
1169,845 |
58,211 |
52,882 |
248,724 |
30,774 |
|
9 |
41,657 |
10,39 |
9,4513 |
432,8162 |
107,952 |
1735,306 |
98,199 |
89,327 |
393,713 |
38,806 |
|
10 |
35,079 |
13,105 |
10,894 |
459,7103 |
171,741 |
1230,536 |
142,766 |
118,679 |
382,151 |
40,704 |
|
итого |
227,461 |
62,426 |
53,611 |
1767,3694 |
505,623 |
6379,562 |
434,420 |
374,449 |
1526,799 |
227,402 |
Из данной таблицы составляет полученные значения в систему нормальных уравнений, то есть:
Решая систему уравнений, получим следующие значения параметры:
4,11 a1a2 = 6,98
Подставляя значения вычисленных параметров в уравнение регрессии получаем следующую модель: = 4,11+ (-3,01)* x1 +6,98* x2
Рассчитаем при соответствующих значениях x1 и x2 , результаты занесем в таблицу 15
Таким образом, мы рассчитали теоретические полученные по уравнению регрессии значения результативного признака
6.4) Для измерения тесноты связи между двумя из рассматриваемых переменных применяют парные коэффициенты корреляции. Для этого применяют следующие формулы:
= (6.2); = (6.3);
= (6.4)
где:
= (6.5); = (6.6);
= (6.7);
Произведем необходимые расчеты:
= 1767,3694 / 10 = 176.7370
= 1526,799 /10 =152,6799
= 434,420 /10 = 43.4420
= 227,461/ 10 =22,7461
= 62,426/ 10 =6,2426 = 53,611/ 10 =5,3611
= = 3,4047
= =2,95012
= = 10,9808
= 0,929
= = 0,9480
= = 0,993
Полученная величина 0,929 означает что установленная по уравнению регрессии связь между x1 и у сильная, связь между x2 и у является сильной и связь между факторами x1 и x2 также сильна, потому что = 0,993.
Показателем тесноты связи, устанавливаемой между результативными и двумя и более факторными признаками является множественный коэффициент корреляции:
= (6.8);
Рассчитаем множественный коэффициент корреляции:
= 0,9538
Из полученного значения, то можно говорить о сильной связи между признаками.
Теперь проверки значимость коэффициента множественной корреляции. Проверка осуществляется на основе F-критерия Фишера
Fр = (6.9);
Подставляя полученное значение , получаем:
Fр = =17,637
Таким образом, при уровне значимости = 0,05 и степенях 1 = 2, 2 = 10-3=7 то табличное значение Fтаб =4,78 Следовательно при Fр > Fтаб гипотеза о не значимости коэффициента множественной регрессии не подтверждается, то есть коэффициент значим.
6.5) Теперь нам необходимо проверить значимость уравнения регрессии. Проверка адекватности всей модели осуществляется с помощью расчета F-критерия Фишера
F = * (6.10);
Где m - число параметров в уравнение регрессии
= (6.11);
= (10,3442–10,169)2 =0,031;
= (6,4549-9,462)2=9,041 (35,079-40,704)2=31,641
=(18,213-17,582)2=0,398
=(12,118-14,725)2=6,798
=(21,469-24,628)2=9,977
=(22,035-17,725)2=18,576
=(25,888-22,827)2=9,371
= (34,203-30,774)2=11,757
=(41,657-38,806)2 =8,127
= 105,718
Следовательно = = 10,5718
Выполнив подставку, найдем расчетное значение F-критерия Фишера
F = * = 2,43
Таким образом, при уровне значимости = 0,05 и степенях 1 = 2, 2 = 10-3=7,то табличное значение Fтаб= 5,32 . Следовательно в нашем случае Fр > Fтаб . Уравнение регрессии может быть использовано для практических целей.
Проверка адекватности построенной модели проверяется так же с помощью средней ошибки аппроксимации
= **100 (6.12);
Рассчитаем среднюю ошибку аппроксимации
= * *100 = *1,263*100= 12,63
Так как средняя ошибка аппроксимации не превышает 15% , а значит построенная модель может быть использована для практических целей, то есть на ее основе можно осуществлять прогнозы и принимать решения.
6.6) Для оценки значимости коэффициентов регрессии при линейной зависимости используются t-критерия Стьюдента
Для параметра a1
= (6.13);
Для параметра а2
= (6.14);
Выше нами были рассчитаны все значения необходимо для подставки
Найдем значения параметров:
= = 0,896
и == 1,8004
При уровне значимости = 0,05 и числе степеней свободы = 6 и табличное значение tтаб = 2,247. Таким образом tтаб < tрас и значит коэффициент уравнения регрессии а1 является статистическим значимым.
Задание №7
По данным любого статистического ежегодника выполните следующее:
- выберите интервальный ряд динамики, состоящий из уровней, выраженных абсолютными величинами за 5-15 периодов подряд (месяцев, лет, кварталов и т.д.);
- изобразите графически динамику ряда с помощью статистической кривой;
- по данным этого ряда вычислите абсолютные и относительные показатели динамики;
- результаты расчетов изложите в табличной форме и их проанализируйте;
- вычислите средние показатели динамики и проанализируйте;
- произведите сглаживание ряда динамики с помощью скользящей средней и аналитического выравнивания. Расчетные уровни нанесите на график, построенный в п.2. Сделайте выводы о характере тенденции рассмотренного ряда динамики.
7.1) Выберем интервальный ряд динамики, состоящий из 10 показателей.
Данные для интервального ряда динамики показаны в таблице 17.
Выберем интервальный ряд динамики, состоящий из уровней, выраженных абсолютными величинами за 5 лет подряд: объём возвращённых кредитов физическими лицами по Московской области за 2007 – 2011 годы.
Таблица 23
|
годы |
2007 |
2008 |
2009 |
2010 |
2011 |
|
объём возвращённых кредитов физическими лицами(м.руб) |
201944 |
212086 |
243824 |
269738 |
340731 |
Изобразим графически динамику ряда с помощью статистической кривой:
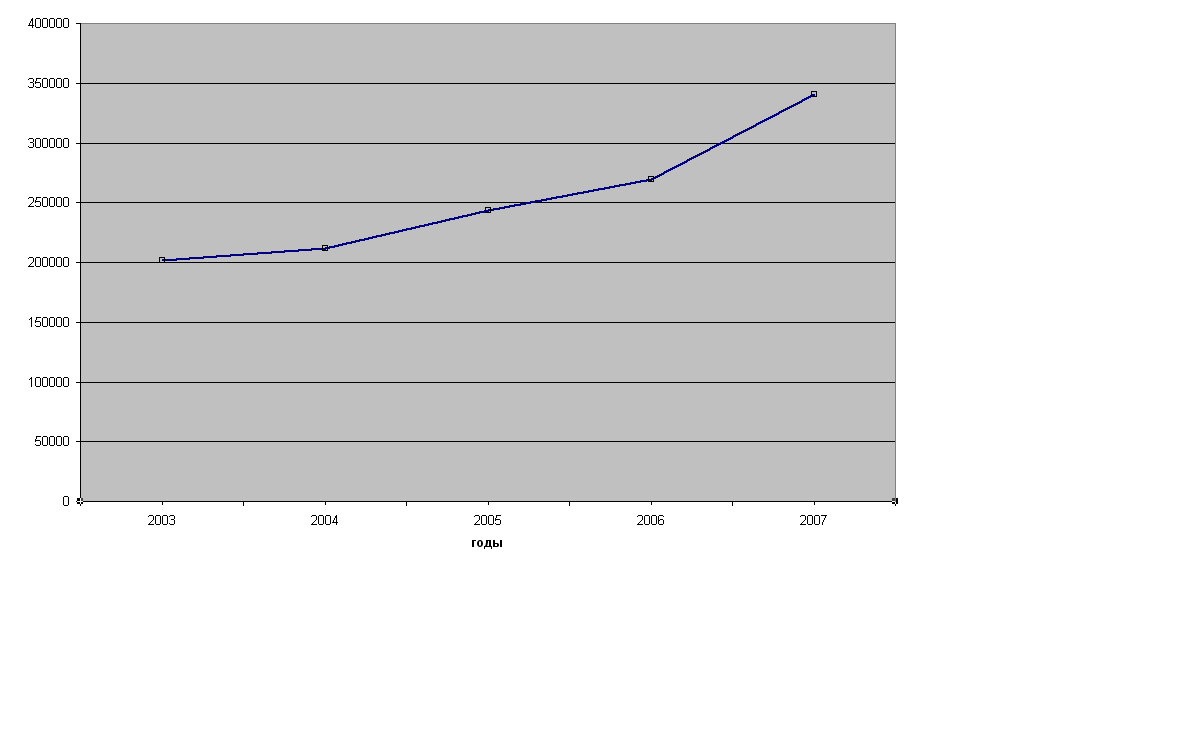
Рис.8. Динамика объёма возвращённых кредитов физическими лицами по Московской области за 2007 – 2011 годы
По данным ряда вычислим абсолютные и относительные показатели динамики.
Абсолютный прирост (цепной):
, (49)
где yi – уровень сравниваемого периода;
yi-1 – уровень предшествующего периода
Абсолютный прирост (базисный):
, (50)
где yo – уровень базисного периода.
Таблица 24
|
Период |
Показатели(млн.рублей ) |
Абсолютный прирост (снижение) |
Темпы роста, % |
Темпы прироста, % |
Абсолютное значение 1% прироста |
|||
|
с преды- дущим годом |
с началь- ным годом динами- ческого ряда |
с предыду- щим годом |
с начальным годом динамичес- кого ряда |
с предыду- щим годом |
с преды- дущим годом |
|||
|
2007 |
201944 |
– |
– |
– |
100 |
– |
0,000 |
– |
|
2008 |
212086 |
10142 |
10142 |
105,022 |
105,022 |
5,022 |
5,022 |
2019,44 |
|
2009 |
243824 |
31738 |
41880 |
114,965 |
120,738 |
14,965 |
20,738 |
2120,86 |
|
2010 |
269738 |
25914 |
67794 |
110,628 |
133,571 |
10,628 |
33,571 |
2438,24 |
|
2011 |
340731 |
70993 |
138787 |
126,319 |
168,725 |
26,319 |
68,725 |
2697,38 |
|
Итого |
1268323 |
Темп роста (цепной):
(51)
Темп роста (базисный):
(52)
Темп прироста (цепной):
или (53)
Темп прироста (базисный):
или (54)
Абсолютное значение 1% прироста:
(55)
Результаты вычислений оформим в таблице:
Таблица 24
Вывод: по данным таблицы можно сказать о том, что объём возвращённых кредитов физическими лицами в период с 2007 года по 2011год имели стабильный характер и наблюдалась тенденция увеличения возвращения кредитов
Вычислим средние показатели динамики:
средняя стоимость всех возвращённых кредитов физическими лицами в динамическом ряду:
(56)
средний абсолютный прирост (цепной):
(57)
=
средний темп роста:
(58)
= 1,14 или 114%
средний темп прироста:
(59)
Вывод: в результате расчётов получили, что в среднем увеличение уровня ряда динамики за 2007 – 2011 годы происходит на 34696,75 миллионов рублей. Среднее относительное увеличение уровня динамики за рассматриваемый период происходит с коэффициентом 1,14 или 114% от уровня, принятого за базу сравнения, т.е. уровень ряда динамики в среднем больше базового уровня на 14%.
Произведём сглаживание ряда динамики с помощью скользящей средней, данные оформим в табличной форме:
Таблица 25
|
№ п/п |
Периоды |
объём возвращённых кредитов физическими лицами |
Трёхчленные скользящие суммы |
Трёхчленные скользящие средние |
|
1 |
2007 |
201944 |
– |
– |
|
2 |
2008 |
212086 |
657854 |
219284,667 |
|
3 |
2009 |
243824 |
725648 |
241882,667 |
|
4 |
2010 |
269738 |
854293 |
284764,333 |
|
5 |
2011 |
340731 |
– |
– |
Произведем сглаживание ряда динамики с помощью аналитического выравнивания.
Для выравнивания ряда динамики по прямой используем уравнение:
(60)
Найдём параметры данного уравнения ao и a1 методом наименьших квадратов, для этого решим систему двух нормальных уравнений:
, (61)
где y – исходный уровень ряда динамики;
n – число членов ряда;
t – показатель времени, который имеет условное обозначение, так как число уровней ряда нечетное (5):
Таблица 26
|
годы |
2007 |
2008 |
2009 |
2010 |
2011 |
|
t |
-2 |
-1 |
0 |
+1 |
+2 |
При этом уравнения системы примут вид:
, (62)
Откуда:
(63)
(64)
-Уравнение Тренда
Все исходные и расчётные данные для определения параметров системы уравнения представим в таблице:
Таблица 27
|
№ п/п |
Годы |
Общий доход |
t |
t2 |
ty |
|||
|
1 |
2007 |
201944 |
-2 |
4 |
-403888 |
186619,4 |
15324,6 |
234843365,16 |
|
2 |
2008 |
212086 |
-1 |
1 |
-212086 |
220142 |
-8056 |
64899136 |
|
3 |
2009 |
243824 |
0 |
0 |
0 |
253664,6 |
-9840,6 |
96837408,36 |
|
4 |
2010 |
269738 |
+1 |
1 |
269738 |
287187,2 |
-17449,2 |
304474580,64 |
|
5 |
2011 |
340731 |
+2 |
4 |
681462 |
320709,8 |
20061,2 |
400848449,44 |
|
Итого |
1766480 |
0 |
10 |
335226 |
1268323 |
1101902939,6 |
Отобразим сглаживание ряда динамики с помощью скользящей средней и аналитического выравнивания на ранее построенном графике рисунка 8:
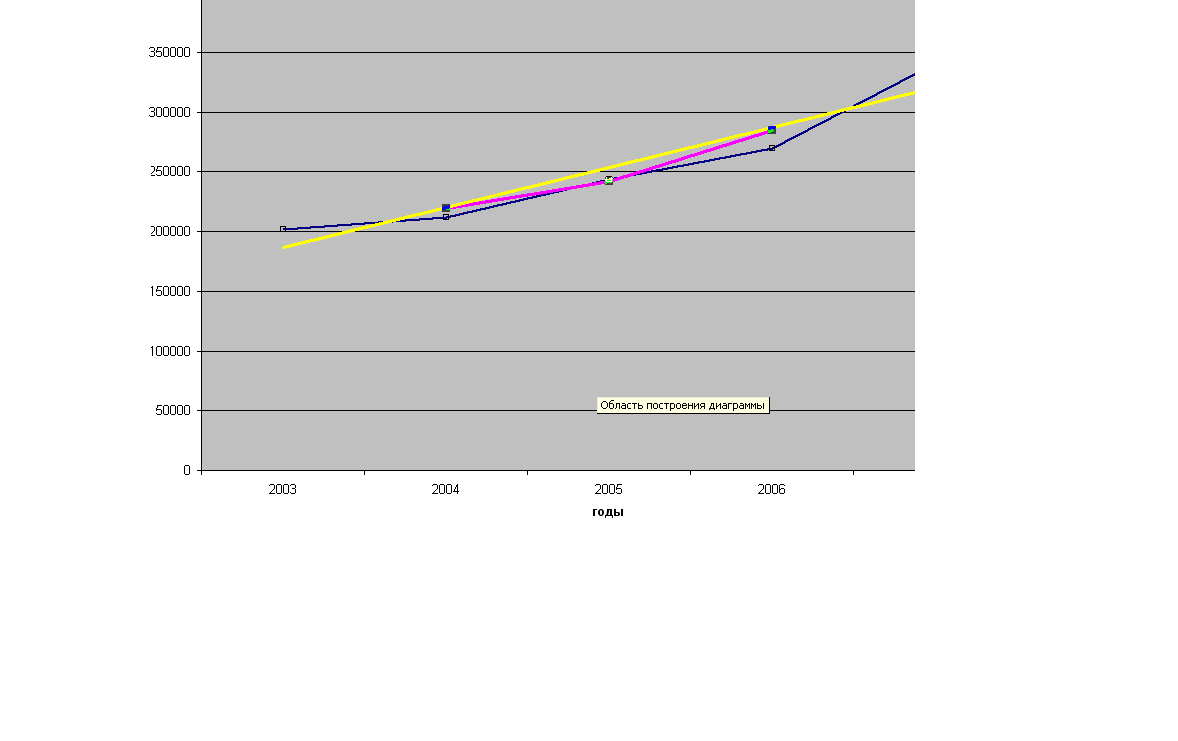
Рис.9. Динамика объёма возвращённых кредитов физическими лицами по Московской области за 2007 – 2011 годы с учётом сглаживания ряда
Основная тенденция (тренд) показывает, как воздействуют систематические факторы на уровень ряда динамики, а колеблемость уровней около тренда служит мерой воздействия остаточных факторов. Ее можно измерить по формуле:
(65)
= 14845,221
Относительной мерой колеблемости является коэффициент вариации:
(66)
= 0,117 или 11,7%
Вывод: проанализировав полученные данные можно говорить о том, что основной тенденцией в динамике является объём возвращённых кредитов физическими лицами за 2007 – 2011 годы является их постепенный рост, а колеблемость стоимости за рассматриваемый период времени составляет 11,7%.
Задание №8
По данным любого статистического ежегодника и периодической печати подберите соответствующий цифровой материал (3-4 показателя за 2-3 периода) (можно взять например, данные об объеме реализованной продукции, об уровне цен, о товарообороте и т.д.):
- исчислите индивидуальные цепные индексы;
- исчислите сводные индексы показателей;
- проверьте правильность расчета сводных индексов, используя их взаимосвязь;
- исчислите сводные индексы в средней гармонической и средней арифметической формах.
Экономический индекс – это относительная величина, которая характеризует изменение исследуемого явления во времени , в пространстве или по сравнению с некоторым эталоном (планируемым, нормативным уровнем и т.д.). Если в качестве базы сравнения используется уровень за какой-либо предшествующий период – получают динамический индекс ,если же базой является уровень того же явления по другой территории – территориальный индекс.
Для вычисления экономических индексов представлены исходные данные в предприятии “тамбовмясо” в таблице 20.
Таблица 20 – Исходные данные для вычисления экономических индексов
|
Товар |
Единица измерения |
Объем проданной продукции (кг) |
Средний уровень цен на продукцию (руб / kг) |
Товарооборот (руб) |
|||
|
2013 |
2014 |
2013 |
2014 |
2013 |
2014 |
||
|
Свинина (лопатка) |
Kг. |
234 570 |
248730 |
168 |
179 |
39407760 |
44522670 |
|
Говяжьи (язык) |
Kг. |
194220 |
140650 |
255 |
297 |
49526100 |
41773050 |
|
Цыпленок |
Кг. |
345600 |
395440 |
142 |
120 |
49075200 |
47452800 |
- Рассчитаем индивидуальные цепные индексы. Расчет ведется по формуле:
Для расчета индивидуальных индексов цен:
ip = (8.1);
где р2013, р2014 - цены проданной продукции соответственно за 2013 и 2014 годы
рассчитаем:
= = 1,065 или 106,5%
= = 1,164 или 116,4%
= = 0,845 или 84,5%
Из полученных данных видно, что объем продаж «свинины» повышался в 2014 году по сравнению с 2013 годом на 6%, и объем «цыпленок» – на 14.4%; а объем «говяжьи» спадался на 27,6%.
Аналогично для расчета индивидуальных индексов физического объема продукций
iq = (8.2);
где q2013, q2014 – физический объем проданной продукции за 2013 и 2014 годы соответственно.
рассчитаем:
= = 1,06 или 106%
= = 0,724 или 72,4%
= = 1,144 или 114,4%
Видно что, средний уровень цен «свинина» увеличился на 6,5%, «говяжьи» – на 16,4%, а уровень цен «цыпленок» снизился на 15,4%.
Для расчета индивидуальных индексов товарооборота
= = 1,13 или 113%
= = 0,843 или 84,3%
= = 0,9669 или 96,69%
Из расчетных результатов по индексам товарооборота, можем заметить что, стоимость продукции в данном предприятии на продукцию «свинина» вырос на 13% в 2014 году при сравнении с 2013 годом, а на продукции « говяжьи» и «цыпленок» спады 15,7% и 3,31% соответственно.
Ведется расчетные результаты индивидуальных индексов среднего уровня цен и физического объема в таблице 21.
Таблица 21 – Индивидуальные цепные индексы
|
Товар |
Индекс физического объема проданной продукции (%) |
Индекс среднего уровня цен на данную продукцию (%) |
Индекс товарооборота % |
|
Свинина (лопатка) |
106 |
106,5 |
113 |
|
Говяжьи (язык) |
72,4 |
116,4 |
84,3 |
|
Цыпленок |
114,4 |
84,5 |
96,69 |
- Рассчитаем сводные индексы.
Агрегатный индекс – сложный относительный показатель который характеризует среднее изменение социально-экономического явления, состоящего из несоизмеримых элементов.
Прием за базису сравнения в нашем случае 2013 год за отчетный период прием 2014 год. Для удобства расчетов построим вспомогательную таблицу
Таблица 22 – вспомогательная таблица для расчета
|
продукции |
2013 |
2014 |
Расчетные графы |
||||
|
Цена (Р2013) |
Объем (q2013) |
Цена (p2014) |
Объем (q2014) |
P2013 q2013 |
P2014 q2014 |
P2013q2014 |
|
|
свинина |
168 |
234570 |
179 |
248730 |
39407760 |
44522670 |
41786640 |
|
говяжьи |
255 |
194220 |
297 |
140650 |
49526100 |
41773050 |
35865750 |
|
цыпленок |
142 |
345600 |
120 |
395440 |
49075200 |
47452800 |
47452800 |
|
итого |
774390 |
784820 |
138009060 |
133748520 |
133804870 |
- Сводный индекс товарооборота:
, (8.3);
. или 96,91%
- Сводный индекс физического объема продукции:
, (8.4);
или 96,95%
- Сводный индекс цен
, (8.5);
или 99,96%
Из полученных результатов можно делать вывод о том, что стоимость продукции в предприятии Тамбовмясо в 2014 году снижалась на 3,09% по сравнению с 2013 годом из-за спада физического объема на 3,05% и среднего уровня цен на 0,04%
- Для проверки правильности расчета сводных индексов, используя их взаимосвязь:
, (8.6);
.
проверим правильность расчета сводных индексов:
0,9691=0,9695*0,9996
0,9691=0,9691 - верно.
Значит выше произведенные расчеты верны
Разность числителя и знаменателя каждого индекса сомножителя выражает размер изменения общей абсолютной величины под влиянием изменения одного фактора. Сумма этих разностей равна разности числителя и знаменателя индекса товарооборота:
(8.7);
(133804870-138009060) + (133748520-133804870) = (133784520-138009060)
- 4224540 = - 4224540
Значит выше произведенные расчеты верны
- Средний индекс – это индекс, вычисленный как средняя величина из индивидуальных индексов.
При исчислении средних индексов используется две формы средних: арифметическая и гармоническая
Средний арифметический индекс физического объема продукции вычисляется по формуле:
, (8.8);
Выполнив подстановку, получим следующие значения индексов:
;
или 96,91%
Средний гармонический индекс цен определяется формулой:
, (8.9);
Выполнив подстановку, получим следующие значения индексов
.
или 99,95%
Среднее индексы тождественны агрегатным – это подтверждается нашими расчетами
ЗАКЛЮЧЕНИЕ
В данной курсовой работе мы получили обобщающие показатели и выявили закономерности социально-экономических явлений и процессов в конкретных условиях места и времени. Также была изучена количественная сторона массовых социально-экономических явлений, отражаемых посредством статистических показателей.
Первым этапом статистического исследования является сбор статистической информации. На этом этапе были своевременно получены достоверные статистические данные, характеризующие социально-экономические явления и процессы общественной жизни.
В данной работе был рассмотрен ряд основных принципов и положений обработки первичных данных в целях получения обобщенных характеристик изучаемого явления по ряду существенных признаков.
Большое внимание при этом было уделено методу группировок, который решает многие задачи. Все результаты представлены в виде статистических таблиц и графиков.
Также были определены относительные, абсолютные и средние величины, показатели вариации, динамики, структуры взаимосвязи и обобщающие показатели (индексы).
Была подвергнута исследованию взаимосвязь между занятыми населениями и социальными выплатами. Исследование выявило наличие сильной связи между данными показателями.
Заключительным этапом курсовой работы является анализ статистических данных с целью получения теоретических выводов и практических заключений о тенденциях и закономерностях изучаемых явлений.
СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ
1. Курс лекций по общей теории статистики /Под ред. А.В. Пархоменко: - Тамбов: ТГТУ, 2010-2011.
2. Российский статистический ежегодник, 2011.
3. Теория статистики: Учебник/ Под ред. Р.А. Шмойловой. – 2-е изд., доп. И перераб. – М.: Финансы и статистика, 1998. – 576 с.
4. Френкель А.А., Адамова Е.В. Вариационные ряды и их статистические характеристики. – М.: МЭСИ, 2010.
5. Четыркин Е.М. Статистические методы прогнозирования. – М.: Статистика, 2013 – 184 с.
6. Методические указания по выполнению курсовой работы для студентов/ под ред. А.В. Пархоменко – Тамбов: ТГТУ, 2011
Статистическое исследование и обработка статистических данных