Застосування програмного забезпечення для рентгеноструктурного аналізу

Міністерство освіти і науки України

Сумський державний університет

3747 Методичні вказівки

до лабораторної роботи

на тему «Застосування програмного забезпечення для рентгеноструктурного аналізу»

з курсу «Основи комп’ютерного матеріалознавства»

для студентів спеціальності 7(8).05040301

«Прикладне матеріалознавство»

денної і заочної форм навчання

Суми

Сумський державний університет

2014

Методичні вказівки до лабораторної роботи на тему «Застосування програмного забезпечення для рентгеноструктурного аналізу» з курсу «Основи комп’ютерного матеріалознавства» укладачі: М. В. Карпець, А. І. Дегула, О. М. Мисливченко. – Суми : Сумський державний університет, 2014. – 30 с.

Кафедра прикладного матеріалознавства і ТКМ

ЗМІСТ

	С.
1. Мета роботи…………………………………………...	4
2. Обладнання та інструмент……………………………	4
3. Загальні положення…………………………………...	4
4. Хід роботи……………………………………………..	11
Висновки………………………………………………….	28
Список літератури……………………………………….	29

МЕТА РОБОТИ

Освоїти методику проведення рентгеноструктурного аналізу та проведення повнопрофільного аналізу дифрактограм за допомогою програми PowderCell 2.4. Провести якісний та кількісний аналіз фазового складу заданої речовини.

ОБЛАДНАННЯ ТА ІНСТРУМЕНТ

Персональний комп’ютер.
Інстальований програмний комплекс PowderCell 2.4.
Набір шліфів з різних марок сталей і сплавів.
Файли дифрактограм у цифровому ASCII форматі.

ЗАГАЛЬНІ ПОЛОЖЕННЯ

Рентгенівські промені були відкриті в 1895 р. німецьким фізиком В. К. Рентгеном і одержали назву Х-променів. Саме така назва (‘X-Ray’) переважно використовується в іноземній науковій літературі. У 1901 р. Рентгену – першому з фізиків – присуджується Нобелівська премія. Необхідно відзначити, що експерименти з катодними трубками на той час проводили й інші дослідники. Серед них і українець – уродженець Тернопільщини (с. Гримайлів) І. П. Пулюй.

Залежно від того, яку властивість рентгенівських променів при взаємодії з речовиною взято за основу, рентгенографію в цілому можна поділити на рентгеноструктурний аналіз, рентгенівську дефектоскопію та рентгеноспектральний аналіз. Рентгеноспектральний аналіз базується на здатності атомів випромінювати характеристичне рентгенівське випромінювання під дією високоенергетичного потоку електронів або квантів жорсткого електромагнітного випромінювання. Аналізуючи зареєстрований характеристичний спектр, одержують інформацію про хімічний склад речовини, енергетичний стан електронних рівнів атомів, особливості хімічного зв’язку. Метод рентгенівської дефектоскопії використовує різну проникаючу здатність рентгенівського випромінювання залежно від густини та товщини досліджуваного об’єкта. Цьому методу притаманна висока чутливість та універсальність. Він широко використовується як в наукових дослідженнях, так і в промисловості та медицині. В основу рентгеноструктурного аналізу покладено явище дифракції рентгенівських променів на кристалічній ґратці, відкрите в 1912 році М. Лауе і його колегами В. Фрідріхом та П. Кніппінгом у вигляді так званого інтерференційного рівняння Лауе, яке у векторній формі має вигляд:

(S - S0) / = H. (1)

Тут S0 – одиничний вектор падаючого променя; S – одиничний вектор променя, розсіяного в напрямку інтерференції; – довжина хвилі; Н – вектор, перпендикулярний до деякого сімейства площин (hkl) в оберненій ґратці кристала, причому довжина його пов'язана з міжплощинною відстанню цього сімейства (d) співвідношенням Н= n/d, де n - ціле число (порядок відбиття), кут між векторами S і S0 називається кутом розсіювання (2).

Виходячи з припущення, що рентгенівські промені можуть відбиватися від кристалографічних площин аналогічно відбиттю видимого світла від дзеркальних поверхонь із виконанням законів геометричної оптики, російський вчений Вульф і, незалежно від нього, англійці батько і син Брегг вивели аналогічне рівняння в 1913 році, але у скалярній формі.

Нехай під кутом до сімейства паралельних площин кристалу падає паралельний пучок рентгенівських променів із довжиною хвилі (рис.1).

Коли різниця ходу променів при розсіюванні від сусідніх паралельних площин (AO + OB) = 2dsin() буде така, що дорівнює цілому числу n довжин хвиль , тоді промені будуть у фазі і в результаті інтерференції підсилюватимуться в напрямку відбиття променя.

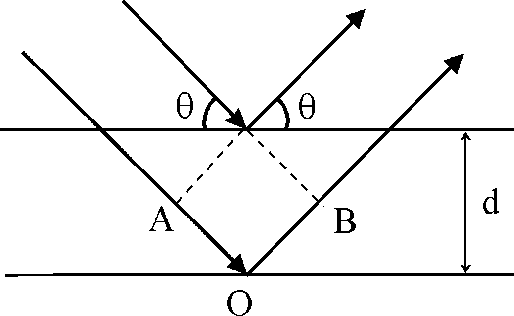
Рисунок 1 – Схема ходу рентгенівських променів при дифракції від сімейства атомних площин: – кут падіння променя; d – міжплощинна відстань

Математично це виражається скалярним рівнянням, яке одержало назву рівняння Вульфа - Брегга:

2dsin() = n . (2)

Дане рівняння пов’язує довжину хвилі та кут 2 відносно падаючого променя, під яким буде спостерігатися дифракційний максимум від сімейства площини з міжплощинною відстанню d (рис.1).

У першому наближенні при одержанні цього рівняння можна знехтувати поглинанням відбитих променів та їх взаємодією з первинним пучком. Такий підхід характерний для кінематичної теорії розсіювання рентгенівських променів. Більш загальною є динамічна теорія розсіювання, в якій враховується ослаблення та обмін енергією всіх пучків у кристалі – як первинного, так і розсіяних. Незважаючи на загальність динамічної теорії, в класичному структурному аналізі вона майже не використовується. Так, оцінка границі застосування кінематичної теорії для розрахунку інтенсивності рентгенівських максимумів знаходиться в межах товщини кристалів 1–10 мкм. Реальний кристал являє собою мозаїку із кристалічних блоків розміром близько 0,1 мкм, які розорієнтовані на кути порядку до 0,01. Тому когерентна взаємодія розсіяних хвиль у такому кристалі проходить у межах одного блока. Це приводить до того, що результати одержані для реальних кристалів у рамках кінематичної і динамічної теорій збігаються.

У рентгеноструктурному аналізі використовують довжини хвиль порядку 0,02 – 0,2 нм. Генерація рентгенівського випромінювання потрібної довжини хвилі здійснюється електронними вакуумними рентгенівськими трубками. Принцип їх роботи аналогічний до роботи телевізійного кінескопа. Джерелом електронів служить розжарений катод у вигляді вольфрамової спіралі, покритий шаром матеріалу, який зменшує роботу виходу електронів. Електрони прискорюються під дією електричного поля (прискорююча напруга U до 60 кВ) та направляються на металічний анод. Енергія електронів при їх різкому гальмуванні перетворюється в фотони рентгенівського випромінювання з різними довжинами хвиль. Мінімальна довжина хвилі min відповідатиме повній зупинці електронів

hc/min = eU, (3)

де h – стала Планка; c – швидкість світла; e – заряд електрона. Так, формується неперервний (білий) спектр, який зі сторони великих довжин хвиль обмежений поглинанням у повітрі та берилієвому вікні трубки. Експерименти показують, що максимум інтенсивності в суцільному спектрі знаходиться приблизно на довжині хвилі 1,5min.

Якщо енергії електрона достатньо для вибивання електронів із внутрішніх електронних оболонок атомів аноду, то на фоні неперервного спектра з’являються лінії характеристичного рентгенівського випромінювання. Їх поява обумовлена випромінюванням фотонів при переході електронів із зовнішніх оболонок на утворені вакантні позиції. Лінії цього спектра поділяються на серії K, L, M,… залежно від того, з якої оболонки був вибитий електрон. Найбільш інтенсивними є лінії K- серії: K1 – 100 %, K2 ~ 50 %, K – 15–25 %, що обумовлює їх використання у рентгеноструктурному аналізі як монохроматичне випромінювання. Довжини хвиль K1- та K2- складових близькі, тому на практиці їх переважно не розділяють. Напруга, при якій з’являються лінії характеристичного спектра певної серії носить назву потенціалу збудження (U0) цієї серії. У випадку ліній K– серії потенціал збудження для Cr становить 6,0 кВ, для Cu – 8,9 кВ, для Mo – 20,0 кВ, для W – 69,3 кВ, а відповідні середні значення довжин хвиль K – випромінювання дорівнюють відповідно: 0,2291002, 0,1541841, 0,071073, 0,021060 нм. Максимум співвідношення між інтенсивністю характеристичного та неперервного спектра при постійному анодному струмі спостерігається при U = 3U0.

Енергія електронного променя рентгенівської трубки витрачається в основному на нагрівання аноду, в рентгенівське випромінювання перетворюється менше 1 %, а в характеристичне – 0,1 % її потужності. Сучасні рентгенівські трубки при охолодженні проточною водою розраховані на максимальну потужність 1 – 3 кВт залежно від матеріалу аноду. Повна потужність трубок може бути підвищена в 10–25 разів при обертанні циліндричного аноду. Останнім часом як потужне джерело рентгенівських променів застосовується магнітне гальмівне випромінювання від кільцевих електронних прискорювачів – синхротронів. У синхротроні електрони рухаються зі круговою орбітою і тому випромінюють квазінеперервний електромагнітний спектр. Таке випромінювання строго поляризоване в площині орбіти електрона і направлено по дотичній до неї. Після монохроматизації одержують пучок випромінювання на три-чотири порядки потужніший від аналогічного пучка рентгенівських трубок.

У багатьох технічно важливих чи природних випадках речовина знаходиться у стані полікристала – великої кількості хаотично орієнтованих у просторі дрібних кристалітів у вигляді порошку або твердого матеріалу щільно зчеплених між собою частинок. Крім того, полікристал може складатися із кристаликів різних фаз і важливо дослідити його структуру та властивості в такому стані. У таких випадках у рентгенографії використовують метод порошків, який також називають методом Дебая – Шерера, а рентгенограму від полікристала іноді називають дебаеграмою. Зйомка в цьому методі ведеться з використанням паралельного або розбіжного монохроматичного пучка (=const). Монохроматизацію рентгенівського випромінювання в методі порошків бажано проводити монохроматором, встановленим між зразком і детектором. Це дозволяє підвищити чутливість експерименту, усунувши флуоресцентну складову в спектрі дифрагованого пучка.

Найвірогідніші дані про інтенсивності піків та значення міжплощинних відстаней одержують за допомогою рентгенівських дифрактометрів для полікристалів. Основним вузлом дифрактометра є гоніометр, який із високою кутовою точністю дозволяє повертати зразок і детектор навколо декількох осей відносно падаючого променя. За детектори використовують сцинтиляційні, напівпровідникові, пропорційні детектори, а також двовимірні ImagingPlate (IP) та CCD-детектори. Сканування дифрактограми здійснюється в горизонтальній або вертикальній площині. Згідно схеми експерименту розрізняють дифрактометричну зйомку на проходження рентгенівського променя через зразок та на відбиття від площини зразка. Перша схема з геометрії еквівалентна зйомці в камері Дебая-Шерера і використовується для дифрактометричної реєстрації дебаеграм від тонких циліндричних зразків та слабопоглинаючих або тонких плоских зразків. При такій схемі є можливість одночасної реєстрації всієї дифракційної картини за допомогою позиційно чутливих детекторів (PSD). Розрізняють плоскі та зігнуті за радіусом дифрактометра детектори. Інтервал кутів у шкалі 2, який охоплює PSD-детектор на основі ImagingPlate, становить більше 200 градусів, а час зйомки можна скоротити до 1 хвилини. Однак роздільна здатність при такій реєстрації дифракційної картини на порядок менше і становить 0,01, ніж при стандартній зйомці за допомогою аналітичної щілини перед детектором.

При дифрактометричній зйомці за схемою відбивання від площини зразка найчастіше використовують симетричну фокусуючу схему за Брегом-Брентано. Ця схема дозволяє повертати зразок у власній площині з метою зменшення впливу на інтенсивність максимумів як текстури, так і великокристалічності в досліджуваному матеріалі. Характерною особливістю фокусування по Брегом-Брентано є необхідність видержувати значення кутів повороту зразка і детектора у співвідношенні 1:2. При цьому проекція фокуса рентгенівської трубки та аналітична щілина детектора розміщуються на колі гоніометра радіуса R, через центр якого проходить поверхня плоского зразка. Для точного фокусування зразок необхідно згинати за радіусом r кола фокусування залежно від кута :

r = R/(2sin). (4)

Практично в більшості випадків це неможливо, тому користуються плоским зразком, зменшуючи ширину первинного пучка. Детальний геометричний аналіз ходу променів при реєстрації дифракційного максимуму hkl свідчить, що у відбиваючому положенні будуть тільки ті кристалики, кристалографічні площини {hkl} яких будуть паралельні площині досліджуваного зразка. Ця особливість дозволяє вивчати текстуру та макронапруги в зразках.

Вирішення більшості завдань на основі даних порошкової дифрактометрії потребує більш точного визначення характеристик дифракційних профілів таких, як інтегральна інтенсивність, кутове положення в шкалі 2 та значення ширини на половині висоти максимуму (FWHM). Одержання цих параметрів ускладнюється при наявності в досліджуваному зразку двох і більше фаз, піки яких накладаються або частково перекриваються. Крім того, дифракційна картина може бути спотворена рядом фізичних факторів, пов’язаних із неточним юстируванням дифрактометра та зміщенням зразка з геометричної осі гоніометра. Наявність у зразку текстури фаз та слабопоглинаючих фазових складових (наприклад BN, C, B4C) також приводить до зміни інтенсивностей піків та їх кутового положення. Дійсно наявність неточної установки нульового значення детектора на кут (2)z відобразиться на зміщенні всіх піків на цю величину. Зміщення зразка з осі гоніометра на величину s, вздовж перпендикуляра до площини зразка виразиться в зміщенні піків пропорційно cos на величину

(2)d = (s/R)cos , (5)

де R – радіус гоніометра. Проникнення променя в зразок на глибину p приведе до зміщення піків пропорціонально sin2 на величину

(2)p = -(p/R)sin2 . (6)

Сучасна реєстрація дифракційної картини в цифровому форматі та застосування для обробки отриманих даних потужних обчислювальних програмних комплексів (PowderCell, GSAS, FullProf, PDXL та ін.) дозволяють в більшості випадків побороти вказані труднощі. Загальноприйнятим у цьому плані є проведення повнопрофільного аналізу дифракційної картини (метод Рітвельда). Вперше цей метод був запропонований в 1969 році для аналізу нейтронографічного експерименту полікристалів [1]. Суть його заключається в порівнянні експериментальної дифрактограми з теоретично розрахованим спектром суміші певної кількості полікристалічних фаз. Критерієм достовірності є найкращий збіг теоретичної та експериментальної картин після уточнення заданих параметрів.

ХІД РОБОТИ

Робота з програмою PowderCell 2.4