Численное интегрирование

Тема 6.4. Численное интегрирование

6.4.1. Постановка задачи

6.4.2. Метод прямоугольников

6.4.3. Формула трапеций

6.4.4. Формула Симпсона

6.4.5. Оценка погрешности численного интегрирования

6.4.6. Технология вычисления интегралов в среде математических пакетов

6.4.1. Постановка задачи

Из курса математического анализа известно, что, если функция f(x) непрерывна на отрезке [a;b] и дифференцируема, то определенный интеграл от этой функции в пределах от a до b существует и может быть вычислен по формуле Ньютона-Лейбница:

Если первообразную функцию F(x) не удается выразить аналитически через элементарные функции или если при проведении практических расчетов подынтегральная функция f(x) задается в виде таблицы, то это приводит к необходимости замены аналитического интегрирования численными методами.

Для функции f(x), заданной в прямоугольной системе координат на интервале [a;b], этот интеграл численно равен площади, ограниченной кривой f(x), осью Ox и двумя ординатами ac и bd.

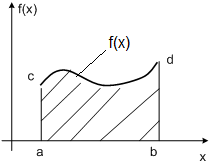
Рис. 6.4.1-1

Задача численного интегрирования заключается в нахождении значения определенного интеграла через ряд значений подынтегральной функции yi=f(xi), заданной в точках xi (i=0,1,…,n). Причем, x0 = a, xn = b. Чаще всего интервал разбивают на подынтервалы длиной h = xi+1 - xi.

Применительно к однократному интегралу, формулы численного интегрирования представляют собой квадратурные формулы вида:

где Ai – числовые коэффициенты, называемые весами квадратурной формулы, а xi – точки из отрезка - узлами квадратурной формулы, n > 0 – целое число.

Искомый определенный интеграл можно представить в виде суммы интегралов:

На каждом i-м отрезке функция аппроксимируется (заменяется) некоторой другой легко интегрируемой функцией gi(x). В результате получаем следующую квадратурную формулу:

Для решения поставленной задачи подынтегральную функцию f(x) необходимо заменить приближенной функцией, которая может быть проинтегрирована в аналитическим виде. В качестве такой функции обычно используют полином Р(х) с узлами интерполяции в точках х0, х1, х2, …,хn. В этих точках значения функции и интерполяционного полинома полностью совпадают f(xi) = Р(xi).

Для получения простых формул интегрирования используют полиномы нулевой, первой и второй степени и соответственно получают формулы численного интегрирования: прямоугольников, трапеций и Симпсона.

Очевидно, что замена функции f(x) интерполирующим полиномом приводит к образованию погрешности вычисления значения интеграла

где I1 – точное значение интеграла, I – значение интеграла, вычисленного численным методом, а – погрешность метода.

Отметим, что увеличение числа подынтервалов n (или уменьшение длины шага интегрирования h) ведет к уменьшению погрешности.

6.4.2. Метод прямоугольников

Заменим подынтегральную функцию f(x) в пределах элементарного отрезка [xi;xi+1] интерполяционным многочленом нулевой степени (рис.6.4.2-1), то есть постоянной величиной, равной либо f(xi), либо f(xi+1).

Рис. 6.4.2-1

Значение элементарного интеграла равно площади прямоугольника, в первом случае
I = hf(xi), а во втором I = hf(xi+1), где h = xi+1 - xi. Для определения значения интеграла на отрезке [a;b] найдем суммы элементарных интегралов, взяв в первом случае в качестве
f(x) – значение подынтегральной функции в левом конце i-го отрезка, а во втором – в правом конце отрезка:

(6.4.2-1)
(6.4.2-2)

Формула (6.4.2-1) называется формулой левых прямоугольников, а формула
(6.4.-2.2) – формулой правых прямоугольников.

Для вычисления определенного интеграла может быть использована и формула средних прямоугольников (6.4.2-3), в которой на элементарном отрезке интегрирования функция f(x) тоже заменяется интерполяционным многочленом нулевой степени, но равным значению функции в середине отрезка:

(6.4.2-3)

6.4.3. Формула трапеций

Разобьем интервал интегрирования [a;b] на n равных отрезков (рис. 6.4.3-1) и восстановим из полученных точек a, х1, x2, …, b перпендикуляры до пересечения с графиком функции. Соединив последовательно точки пересечения, представим площадь полученной криволинейной трапеции как сумму прямолинейных трапеций, площади которых легко подсчитать. Заменив подынтегральную функцию f(x) в пределах элементарного отрезка [xi;xi+1] интерполяционным многочленом первой степени, получим следующие формулы для элементарных площадей:

Рис. 6.4.3-1

Тогда общая площадь равна:

Отсюда получаем формулу трапеций:

(6.4.3-1)

6.4.4. Формула Симпсона

Для получения формулы Симпсона применяется квадратичный интерполирующий полином, следовательно, за элементарный интервал интегрирования принимается отрезок [xi;xi+2]. Поэтому разобьем интервал интегрирования [a;b] на n отрезков, где n=2m – четное число (рис. 6.4.4-1).

Рис. 6.4.4-1

Для получения интерполирующей функции на интервале [xi;xi+2] воспользуемся первой интерполяционной формулой Ньютона, используя в качестве узлов интерполяции точки xi, хi+1 и xi+2.

(6.4.4-1)

В пределах отрезка [xi;xi+2], на котором подынтегральная функция аппроксимирована многочленом (6.4.4-1), получим приближенную формулу Симпсона:

(6.4.4-2)

Для отрезка [x0;x2]

Для отрезка [x2;x4]

Тогда для всего интервала интегрирования [a;b] формула Симпсона выглядит следующим образом:

или

(6.4.4-3)

при

6.4.5. Оценка погрешности численного интегрирования

Замена подынтегральной функции интерполяционным полиномом приводит к погрешности вычисления его значения R=|I1 – I|, где

Очевидно, что вычислить эту погрешность можно только, если известно точное значение интеграла. Поэтому на практике принято проводить оценку погрешности численного интегрирования следующим образом (подынтегральная функция задана таблично (Т) или аналитически (А)):

при использовании формул левых или правых прямоугольников

при использовании формулы средних прямоугольников

при использовании формулы трапеций

при численном интегрировании по формуле Симпсона:

В приведенных выше формулах: a, b – границы интервала интегрирования; h=(b-a)/n – шаг интегрирования; . и – среднее арифметическое, соответственно, первых, вторых и четвертых конечных разностей.

Поскольку в формуле погрешности для метода трапеций присутствует вторая производная, а в формуле Симпсона – четвертая, то формула трапеций точна только для линейных функций, а формула Симпсона для линейных, квадратичных и кубических.

Из приведенных формул видно, что уменьшение шага интегрирования (h) приводит к уменьшению погрешности. При этом, поскольку квадратичная интерполяция представляет функцию с большей точностью, чем линейная, то при использовании формулы Симпсона требуемая точность достигается при меньших значениях n (количестве разбиений), чем, например, при использовании формулы трапеций и формулы прямоугольников.

Формулы для оценки погрешности могут быть также использованы для выбора числа разбиений n или шага интегрирования h, необходимых для обеспечения заданной точности. Однако практическое использование этих формул ограничено в связи с трудоемкостью их вычислений, поэтому при реализации численных методов на ПК используется прием, позволяющий получить оценку погрешности в неявном виде. Этот прием основан на двукратном вычислении значения интеграла вначале с шагом h (где h=(b-a)/n), а затем с шагом h/2. Полученные значения интегралов Ih и Ih/2 могут быть применены для оценки погрешности интегрирования по формуле:

(6.4.5-1)

где: k=1 – для формул левых и правых прямоугольников;

k=2 – для формул трапеции и средних прямоугольников;

k=4 – для формулы Симпсона.

Если полученная погрешность не удовлетворяет требуемой точности, то вычисляется значение интеграла при h=h/4 и снова оценивается погрешность, и т.д. до тех пор, пока не окажется, что погрешность стала меньше заданной точности. Это правило называется правилом Рунге (или правилом двойного просчета).

Пример 6.4.5-1. Вычислить значение определенного интеграла

Предположим, что, подынтегральная функция задана таблично:

x	0.0	0.1	0.2	0.3	0.4	0.5
f(x)	1.0	0.99005	0.960789	0.913913	0.852144	0.778801

0.6	0.7	0.8	0.9	1.0
0.697676	0.612626	0.527292	0.44858	0.367879

Используем формулы правых и левых прямоугольников, считая, что h = 0.2, а n=(b-a)/h=5, имеем:

Используем формулу трапеций:

Используем формулу средних прямоугольников:

Используем формулу Симпсона при m=2n=10(25) и шаге h=0.1:

Произведем оценку погрешности каждого из полученных значений, используя известное аналитическое выражение подынтегральной функции f(x):

Следовательно,

Анализируя значения погрешностей, можно с уверенностью сказать, что самый точный результат получен с использованием формулы Симпсона.

6.4.6. Технология вычисления интегралов в среде математических пакетов

Способ вычисления определенного интеграла с использованием системы Mathcad впрямую зависит от способа задания подынтегральной функции. Если подынтегральная функция задана в аналитическом виде, то интеграл, так же как и производные, может быть вычислен с использованием встроенного в систему оператора, шаблон которого также расположен на палитре Исчисления. При этом выражение для подынтегральной функции может быть или предварительно описано в виде функции, или непосредственно введено в формат интеграла.

Пример 6.4.6-1. Найти определенный интеграл в символьном виде и вычислить его значение.

Однако нередко возникает необходимость вычисления определенного интеграла для таблично заданной функции. Тогда прямое применение встроенного в систему оператора вычисления интеграла оказывается невозможным.

Пример 6.4.6-2. Вычислить определенные интегралы методами трапеций (It) и парабол (Симпсона) (Ic).

Метод трапеций

Метод Симпсона

Пример 6.4.6-3. Вычислить значения определенного интеграла методом средних прямоугольников при условии, что подынтегральная функция задана аналитически.

Метод средних прямоугольников

С помощью средств Mathcad могут быть найдены символьные выражения для производных и интегралов. Символьный знак равенства (стрелка) расположен на палитре Символика панели Математика. Для получения производных и интегралов в символьных выражениях в шаблон производной или интеграла нужно ввести выражение, щелкнуть по изображению символьного знака равенства, а затем щелкнуть по свободному пространству рабочего поля экрана.

Пример 6.4.6-4. Вычислить значения определенного интеграла с шагом и ( и ) по формуле средних прямоугольников и оценить погрешность.

i:=0…n-1