Что такое GeoGebra? Как в GeoGebra можно изображать псевдографы? Степень вершин графа
Что такое GeoGebra? Как в GeoGebra можно изображать псевдографы? Степень вершин графа.
Рассмотрим множество V={v1,v2,...,vn}, n2, и множество E={e1,e2,...,em}, элементами ek которого являются двухэлементные подмножества {vi, vj} множества V. Пара множеств V и E называется неориентированным графом F(V,E) с множеством вершин V и множеством ребер E. При этом говорят, что неориентированное ребро ek соединяет вершины vi, vj или ребро ek и вершины vi, vj инцидентны. Вершины vi и vj называют смежными.
Граф F(V,E) может быть изображен геометрически. Для этого некоторые n точек трехмерного пространства помечаются элементами множества вершин V и вершины vi и vj соединяются линией, если {vi, vj} Е. Геометрическое изображение графа будем называть диаграммой.
Ребро, у которого концевые точки совпадают, называется петлей. Из приведенных определений графов следует, что в них отсутствуют кратные, или параллельные, ребра, соединяющие одни и те же пары вершин. Кроме того, в неориентированном графе не допускаются петли. Однако иногда удобно снять указанные ограничения.
Граф, содержащий кратные ребра называется мультиграфом. Граф, содержащий петли и (или) кратные ребра, называется псевдографом.
Вершина, не инцидентная никакому ребру, называется изолированной. Граф, состоящий только из изолированных вершин, называется нуль-графом (пустым графом) и обозначается через 0. Для нуль-графа множество ребер пустое: Е=.
Другим важным частным случаем является полный граф, в котором каждая вершина множества V соединена ребром со всеми остальными вершинами этого множества. В дельнейшем полный неориентированный граф с n вершинами будем обозначать Kn.
Неориентированный граф называется однородным степени k (регулярным), если степени всех его вершин равны между собой и равны k. Если однородный граф степени k имеет n вершин и m рёбер, то справедливо соотношение
.
Регулярный граф степени 3 называется кубическим. Из леммы 3.1 следует, что каждый кубический граф имеет четное число вершин.
GeoGebra – это программное обеспечение динамической математики в одном легко устанавливаемом пакете. GeoGebra облегчает создание математических построений и моделей обучающимися, которые позволяют проводить интерактивные исследования при перемещении объектов и изменение параметров.
GeoGebra — свободно распространяемая динамическая геометрическая среда. GeoGebra даёт возможность создавать анимированные чертежи.
После запуска программы вы увидите следующее окно:
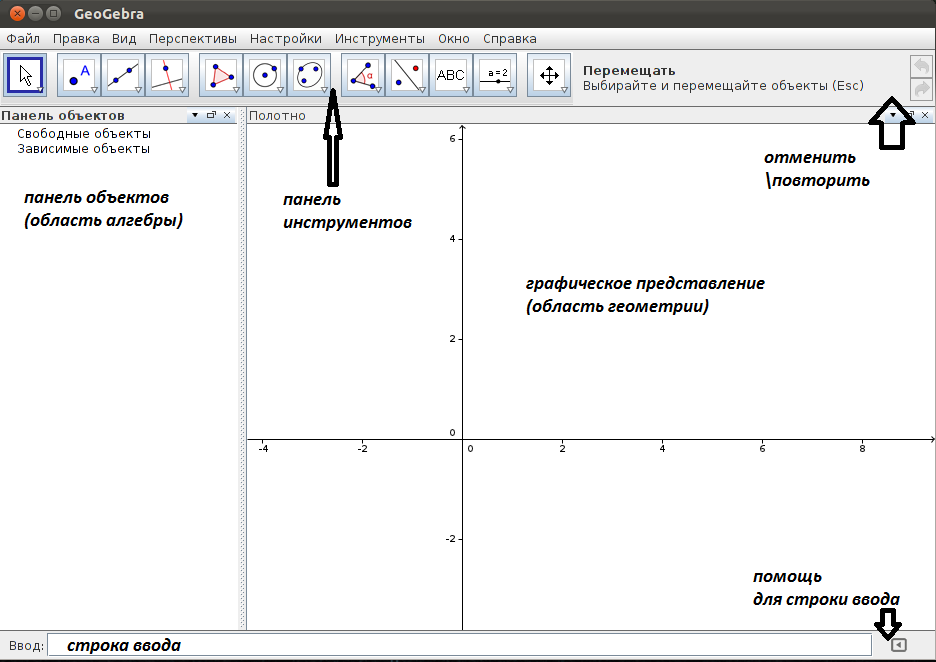
За счёт инструментов в панели инструментов Вы можете выполнять построения в графическом представлении (области геометрии) с помощью мышью. В то же самое время соответствующие координаты и уравнения будут показаны на панели объектов (область алгебры).
Строка ввода используется для ввода координат, уравнений, команд и функций с клавиатуры; все эти объекты будут показаны в графическое представление и на панели объектов сразу после нажатия клавиши ENTER.
1. Уберем сетку и оси координат, если они есть. Для этого найдем в командной строке вкладку Вид, откроем ее и выберем пункт Оси (или Сетка), нажмем на него правой кнопкой мыши. Получаем пустую область геометрии.
2. Задание вершин графа. Нарисуем пустой граф , состоящий из пяти изолированных вершин . Для этого на панели инструментов выбираем рисовать Точку 
. Рисуем произвольным образом пять точек. Например, так:
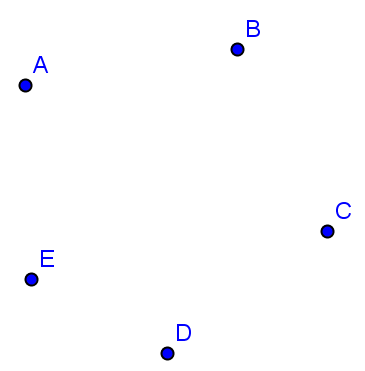
Построили диаграмму графа . Однако вершин имеют не те имена, которые нам нужны. Переименуем их. Для этого выберем вершину с именем А (нажмем на точку левой кнопкой мыши), появится меню, выберем в нем последний пункт Свойства. Появится новое окно Свойства . Во вкладке Основные, поле Имя записываем новое имя точки v1. Затем во вкладке Объекты-Точки, выберем следующую точку В и т.д. В окне Свойства можно так же изменить цвет точек (вкладка Цвет), размер и стиль точки (вкладка Стиль). В результате получим необходимый граф.
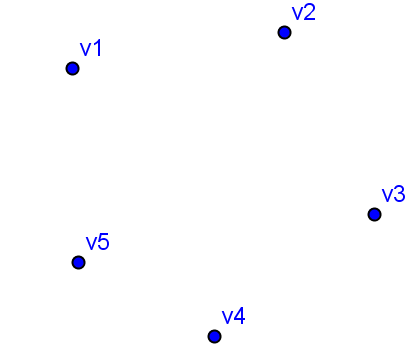
Задание 1. Измените полученный граф в графы и .
3. Изображаем ребра. Нарисуем полный граф , состоящий из пяти вершин , любые две из которых соединены ребром. Воспользуемся уже изображенным графом , изобразим недостающие ребра. Для этого на панели инструментов выбираем рисовать Прямая по двум точкам 
. Наводим мышку на стрелочку внизу, она становится красной, нажимаем на нее правой кнопкой мыши, открывается скрытая вкладка, выбираем в ней Отрезок по двум точкам. В области геометрии выбираем точку v1 (начало ребра), для этого наводим на нее курсор и нажимаем правую кнопку мыши, таким же образом выбираем точку v2 (конец ребра). Таким же образом, изображаем все необходимые ребра.
Получим граф:
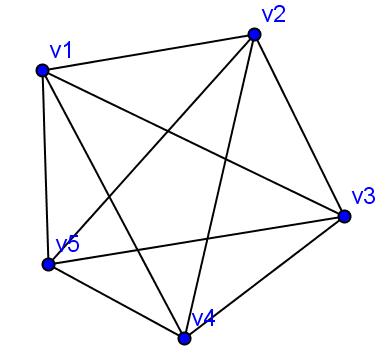
Подпишем ребра графа. Для этого наведем курсор на произвольное ребро, кликнем по нему левой кнопкой, появится меню, выберем в нем последний пункт Свойства . Появится новое окно Свойства. Во вкладке Основные, поле Имя записываем новое имя отрезка e1, так же необходимо включить поле Показать обозначение, для этого наведем курсор на это поле и кликнем правой кнопкой мыши. Затем во вкладке Объекты-Отрезок, выберем следующий отрезок и т.д.
Выберите «Перемещать» 
на панели инструментов и, используя мышь, вы можете изменить положение вершин графа (навести курсор на любую вершину, нажать левую кнопку мыши и, удерживая ее, переместить вершину) так, чтобы обозначения ребер были видны.
Задание 2 . Измените полученный граф в графы и .
4. Нарисуем граф простой цикл , состоящий из пяти вершин . Для этого на панели инструментов выберите «Многоугольник» . Щёлкните левой кнопкой мыши пять раз в разные места на графическое представление, у вас отметятся пять точек A, B, C, D, E. Щёлкните левой кнопкой мыши в точку А и вы получите цикл . Переименуйте вершины, в результате получим:
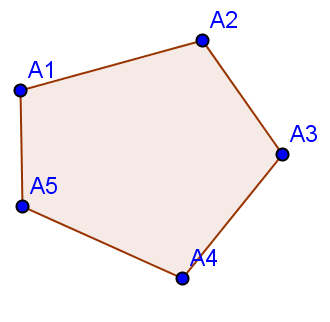
Цвет, толщину, стиль линии, заливку фигуры можно изменить в меню правка свойства.
Задание 3. Постройте диаграммы графов и .
Задание 4. 1. Подбирается экипаж космического корабля из 3-х человек: командира, инженера и врача. Имеются 4 кандидата на должность командира к1, к2, к3, к4, 3 кандидата на должность инженера и1, и2, и3 и 3 кандидата на должность врача в1, в2, в3. Известно, что
к1 психологически совместим с и1, и3, в2, в3;
к2 с и1, и2, в1, в2, в3;
к3 с и1, и2, в1, в3;
к4 с и1, и2, и3, в2.
Кроме того, и1 психологически несовместим с в3, и2 с в1, и3 с в2.
Сколькими способами можно составить экипаж?
Подсказка. Кандидатов можно задать вершинами графа, а психологическую совместимость ребрами. Постройте данный граф, различными цветами изобразите все, полученные треугольники. Посчитайте их количество – это ответ к задаче. Сохраните решение данной задачи. Если весь граф рассмотреть сложно, то рассматривайте каждого капитана отдельно.
2. Лист бумаги Плюшкин разрезает на три части. Некоторые из полученных листов он также разрезает на три части. Несколько новых листочков он вновь разрезает на три более мелких и т.д. сколько Плюшкин получает листочков бумаги, если разрезает к листов?
Подсказка. Рассмотрим граф вершинами, которого будут листья бумаги, ребрами разрезы бумаги. Если Плюшкин разрезает первый листок бумаги, то сколько разрезов он делает и сколько листов получает? Выберете еще одну вершину, сделайте два разреза. Сколько листов получается?
3. Постройте граф понятия «Четырехугольник», если оно содержит следующие понятия: четырехугольник, неправильный четырехугольник, параллелограмм, прямоугольник, ромб, квадрат и трапеция.
Задание 5. Составить множество Еi и нарисовать диаграмму графа i(V, Ei), где V = {1, 2, 5, 6, 8}, а Ei множество двухэлементных подмножеств множества V, удовлетворяющее условию:
а) Е1 = {{a, b} / a = 2k и b = 2n; a, b V; k, n N };
б) Е2 = {{a, b} / a = 2k1 или b = 2n1; a, b V; k, n N };
в) Е3 = {{a, b} / a + b = 2k1; a, b V; k N };
г) Е4 = {{a, b} / a, b V }.
Подсказка. Изобразите все пять вершин, и подпишите их. Для этого наведем курсор на произвольную вершину, кликнем по нему левой кнопкой, появится меню, выберем в нем последний пункт Свойства . Появится новое окно Свойства. Во вкладке Основные, поле Заголовок записываем новое имя вершины 1, так же необходимо включить поле Показать обозначение и в окне Имя, нажать на стрелочку, откроется скрытый список, выбрать Заголовок. Далее, выберем следующую вершину и т.д.
В результате получим:
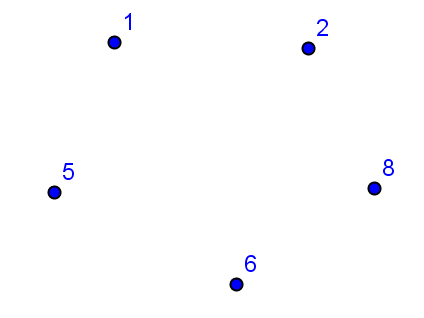
а) Выбираем две вершины, например 2 и 6, они будут соединены ребром, так 2 и 6 – четные числа, вершины 1 и 2, не соединены ребром, так как 1 нечетное число.
Рассуждая, таким образом, построим граф 1(V, E1):
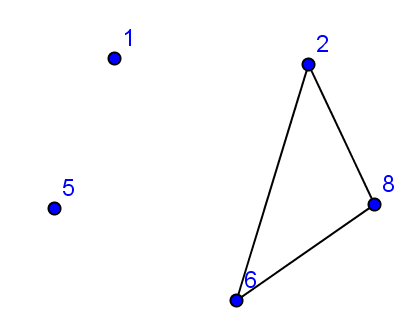
Самостоятельно постройте остальные графы. Перенесите задание и диаграммы графов в тетрадь.
Задание 6. Решение, данных задач должно быть в тетради.
1. Откройте файл с графами , и . Скольким рёбрам инцидентна вершина в графах , и ? Сколько всего рёбер содержит граф , и ? Если граф полный неориентированный и имеет n вершин, то скольким ребрам инцидентна его вершина и сколько всего ребер в данном графе?
Подсказка. Для графов , , и постройте следующую в тетради таблицу.
|
Граф
|
количество ребер инцидентных одной вершине
|
количество вершин
|
количество ребер
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Как подсчитать количество ребер: количество ребер инцидентных одной вершине, умножим на количество вершин и разделим на два, так как каждое ребро учитывалось дважды.
2. На плоскости имеется 87 точек. Сколько существует отрезков с концами в этих точках?
Подсказка. Рассмотреть полный граф с 87 вершинами.
3. 5. Существует ли полный граф, имеющий
а) 107 рёбер? б) 120 ребер?
Подсказка. Общую формулу подсчета вершин через n прировнять к 107 (к 120), решить квадратное уравнение и если существует целое n, то существует такой граф. Если граф существует, то постройте его диаграмму.
4. Откройте файл с графами , и . Сколько рёбер надо добавить к этим графам так, чтобы каждый из них стал полным? Сколько рёбер надо добавить к графу , чтобы он стал полным?
Подсказка. Для графов , , и постройте следующую в тетради таблицу.
|
Граф
|
количество ребер, которое необходимо добавить к одной вершине
|
количество вершин
|
Общее количество ребер, которое необходимо добавить
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Как подсчитать количество ребер: количество ребер, которое необходимо добавить к одной вершине, умножим на количество вершин и разделим на два, так как каждое ребро учитывалось дважды.
5. Сколько диагоналей в выпуклом 92-угольнике?
Подсказка. Сколько ребер необходимо добавить к , чтобы он стал полным.
6. Можно ли устроить такой тренировочный турнир, чтобы в нём участвовало 33 команды, и каждая команда сыграла ровно 3 матча?
Подсказка. Рассмотрим граф вершинами, которого являются команды, ребра данные две команды сыграли матч. Сколько ребер в таком графе?
7. В компании из n человек у каждого ровно трое друзей. Докажите, что n четно.
8. Доказать, что если каждый из 5 человек переписывается ровно с двумя другими, то не найдется трех человек, которые все переписываются между собой.
Подсказка. Изобразите такой граф, содержит ли его диаграмма треугольник?
9. Изобразите регулярный граф степени 2 и 3 с шестью вершинами. Сколько ребер у регулярного графа степени 2 (степени 3) в случае n вершин? Сколько ребер у регулярного графа степени k в случае n вершин?
Подсказка. Для графа количество deg(v) рёбер, инцидентных вершине v, называется локальной степенью или просто степенью этой вершины.
Неориентированный граф называется однородным степени k (регулярным), если степени всех его вершин равны между собой и равны k.
10. Если возможно, изобразите кубический граф с 7 и 8 вершинами. Если данный граф не существует, то объясните почему.
Подсказка. Регулярный граф степени 3 называется кубическим.
11. Существует ли граф с 5 вершинами, степени которых различны между собой?
Подсказка. У такого графа степени должны быть равны 0, 1, 2, 3, 4.
12. Нарисуйте граф с 5 вершинами, у которого ровно 2 вершины имеют одинаковую степень.
Подсказка. Таких графов существует два.
13. Все вершины графа (V, E) (|V| = n, |E| = m) имеют степень k или k+1. Доказать, что если имеет nk вершин степени k и nk+1 вершин степени k+1, то nk = (k+1)n 2m.
Подсказка. Посчитайте сумму степеней всех вершин и приравняйте ее к удвоенному числу ребер графа. Выразите из полученного равенства nk.
14. Существуют ли графы со следующими степенями верши:
а) 2, 3, 4, 7, 7, 8, 6, 3, 0, 5;
б) 2, 1, 10, 7, 9, 8, 5, 4, 0, 7.
Доказать, что в любом графе количество вершин нечётной степени чётно.
Подсказка. Сумма степеней всех вершин графа чётное число, равное удвоенному числу рёбер.
15. Если в графе с 5 вершинами ровно 2 вершины имеют одинаковую степень, то могут ли они обе быть изолированными или обе иметь степень 4?
Подсказка. Попробуйте изобразить оба случая в тетраде.
16. В тренировочном турнире участвовало 12 команд, причём между каждыми двумя командами было сыграно по 3 матча. Сколько всего было проведено матчей?
Подсказка. Сколько ребер у регулярного графа степени 3 в случае 12 вершин?
17. Доказать, что в любой компании, состоящей из 11 человек, найдутся 2 человека, имеющих одинаковое количество знакомых в этой компании.
Подсказка. Компанию рассматриваем как граф, люди – вершины, две вершины соединены ребром, если соответствующие люди знакомы.
Теорема. Во всяком графе с n вершинами, где n 2, всегда найдутся, по меньшей мере, две вершины с одинаковыми степенями.
18. Во всякой ли компании найдутся 3 человека, у которых одинаковое количество знакомых в этой компании?
19. Девять шахматистов проводят турнир в один круг (каждый спортсмен должен сыграть с каждым из остальных по одному разу). Показать, что в любой момент времени найдутся двое, закончившие одинаковое число партий.
Подсказка. Каждому шахматисту поставим в соответствие вершину графа, а каждой сыгранной партии между двумя шахматистами - ребро, соединяющее вершины, соответствующие этим игрокам. В результате мы получим граф с девятью вершинами и некоторым неизвестным числом рёбер.
20. Дети в летнем лагере, познакомившись, обменялись конвертами с адресами. Доказать, что
а) всего было передано четное число конвертов;
б) число детей, обменявшихся конвертами нечетное число раз, четно.
Подсказка. Пусть дети - вершины графа, две вершины соединены ребром, если пара ребят, обменялась конвертами.
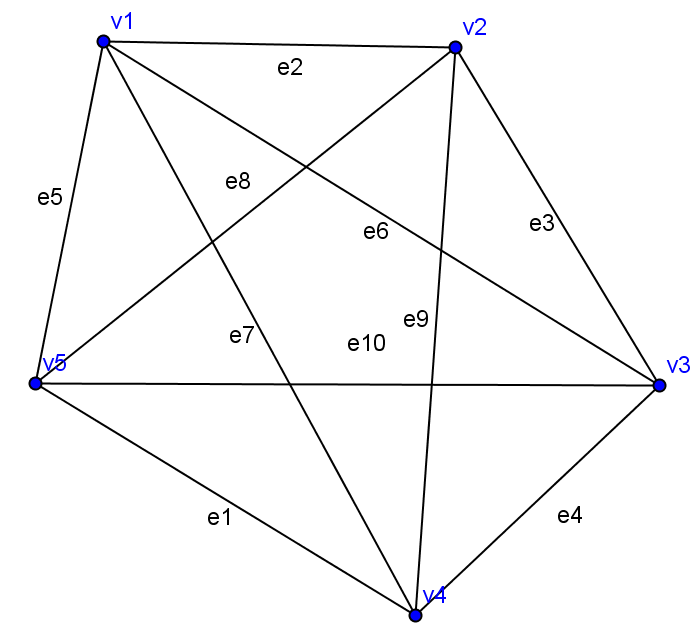
Задание 7. 1. Постройте диаграммы графа с семью вершинами и 10 ребрами.
Например, можно изобразить этот граф так.
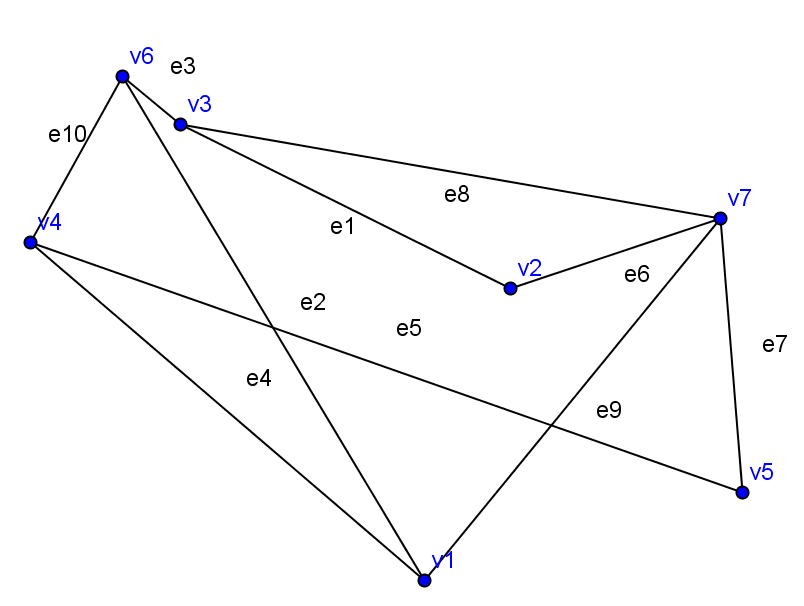
Сохраните файл с этим графом. В меню выбрать Файл-сохранить как… имя файла Граф.
2. Граф с семью вершинами и 10 ребрами преобразуйте в мультиграф, для этого изобразите несколько кратных ребер. Для этого на панели инструментов выбираем рисовать Окружность по центру и точке 
. Наводим мышку на стрелочку внизу, она становится красной, нажимаем на нее правой кнопкой мыши, открывается скрытая вкладка, выбираем в ней Полуокружность по двум точкам. В области геометрии выбираем точку v1 (начало кратного ребра), для этого наводим на нее курсор и нажимаем правую кнопку мыши, таким же образом выбираем точку v4 (конец кратного ребра). Таким же образом, изображаем два кратных ребра. Подписываем ребра.
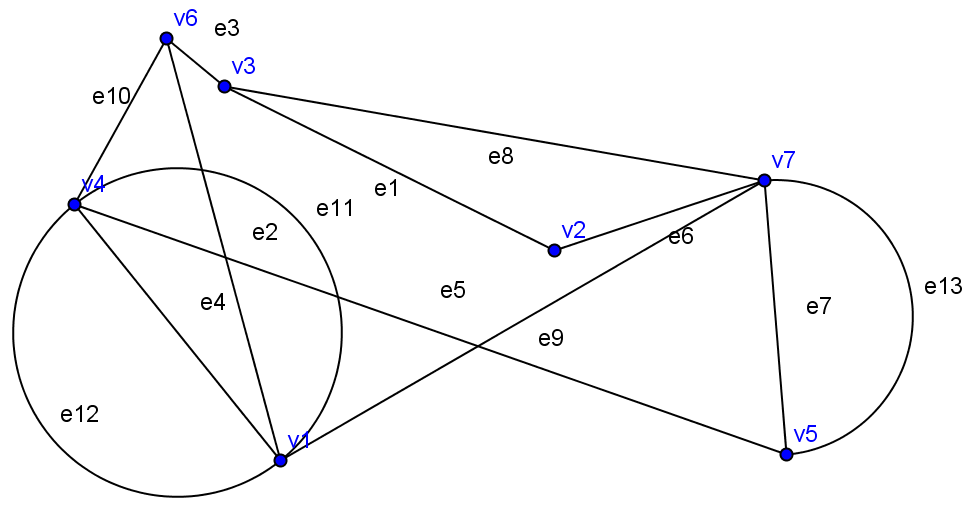
Сохраните файл с этим графом. В меню выбрать Файл-сохранить как… имя файла Мультиграф.
3. Граф с семью вершинами и 10 ребрами преобразуйте в псевдограф, для этого изобразите несколько петель (ребер у которых совпадает начало и конец). Для этого на панели инструментов выбираем рисовать Окружность по центру и точке 
. В области геометрии рядом с выбранной вершиной, поставьте точку и изобразите окружность с центром в этой точке и вершине графа. Получившуюся точку можно скрыть так, в области алгебры Свободные объекты находим данную точку, рядом с ней голубой кружок, щелкните на него правой кнопкой мыши, из области геометрии точка исчезнет.
Сохраните файл с этим графом. В меню выбрать Файл-сохранить как… имя файла Псевдограф1.
4. Мультиграф с семью вершинами и 13 ребрами преобразуйте в псевдограф, для этого изобразите несколько петель.
Сохраните файл с этим графом. В меню выбрать Файл-сохранить как… имя файла Псевдограф2.
5. Для графа, мультиграфа и 2-х псевдографов определите степени всех вершин и их сумму (выпишите в тетрадь диаграммы графа, мультиграфа и 2-х псевдографов, степени каждой вершины и сумму всех степеней вершин для каждого графа).
Подсказка. При изображении на диаграмме петли к этой вершине примыкают два конца петли, т.е. петля вносит в эту степень вклад 2.
Что такое GeoGebra? Как в GeoGebra можно изображать псевдографы? Степень вершин графа