Основные понятия алгебры логики
Тема 1.5. Основные понятия алгебры логики
1.5.1. Основные определения алгебры логики
1.5.2. Cвязь между алгеброй логики и двоичным кодированием
1.5.3. Элементарные логические функции и логические элементы
1.5.4. Произвольные логические функции – ДНФ и КНФ
1.5.5. Контрольные вопросы по теме «Основные понятия алгебры логики»
1.5.6. Тестовые задания по теме «Основные понятия алгебры логики»
1.5.1. Основные определения алгебры логики
Алгебра логики – определенная часть математической логики, называемая исчислением высказываний.
Высказывание – утверждение, которое может быть истинным («да») или ложным («нет»). Одно и то же высказывание не может быть одновременно истинным и ложным. Поэтому в алгебре логики рассматриваются только 2 значения высказываний:
истинное (ему ставится в соответствие значение 1);
ложное (ему ставится в соответствие значение 0).
Алгебра логики, отвлекаясь от смысловой содержательности высказываний, дает возможность определить, истинны или ложны составные высказывания (функции) алгебраическими методами.
Логические переменные величины и функции от них, которые могут принимать только 2 значения – 0 и 1, называются логическими или булевскими переменными и функциями. Значение логической функции зависит от конкретного сочетания значений всех ее n аргументов - набора аргументов.
Логическая функция от n двоичных аргументов полностью определяется таблицей истинности. Таблица истинности - это таблица, в которую записаны значения логической функции для каждого из 2n наборов аргументов на входе. Для того чтобы полностью определить логическую функцию, достаточно перечислить либо все наборы, при которых эта функция принимает значения, равные 1, либо все наборы, при которых эта функция принимает значения, равные 0.
1.5.2. Cвязь между алгеброй логики и двоичным кодированием
Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера, поскольку основной системой счисления, с которой работает компьютер, является двоичная система счисления, в которой используются только цифры 1 и 0.
Из этого следует:
одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных;
на этапе конструирования аппаратных средств алгебра логики позволяет значительно упростить логические функции, описывающие функционирование схем компьютера, и, следовательно, уменьшить число элементарных логических элементов, из десятков тысяч которых состоят основные узлы компьютера.
Данные и команды в компьютере представляются в виде двоичных последовательностей различной структуры и длины. Существуют различные физические способы кодирования двоичной информации. В электронных устройствах компьютера двоичные единицы чаще всего кодируются более высоким уровнем напряжения, чем двоичные нули, например, как показано на рис. 1.5.2-1.
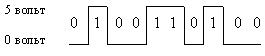
Рис. 1.5.2-1.
Логический элемент компьютера – это часть электронной логической схемы, которая реализует элементарную логическую функцию.
Простейшими логическими элементами компьютеров являются электронные схемы «И», «ИЛИ», «НЕ», «И–НЕ», «ИЛИ–НЕ». Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем.
Работу логических элементов, как и логических функций, описывают с помощью таблиц истинности.
1.5.3. Элементарные логические функции и логические элементы
Логические функции, зависящие от одной или двух переменных, называются элементарными. К основным логическим функциям относятся следующие элементарные функции: отрицание; логическое умножение; отрицание от логического умножения; логическое сложение; отрицание от логического сложения; равнозначность; отрицание равнозначности.
Функция отрицания - это логическая функция от одного аргумента, которая принимает значение 1, если аргумент равен 0, и принимает значение 0, если аргумент равен 1, и называется отрицанием (инверсией) или логической функцией НЕ:
Запись логической функции НЕ – , где черта над переменной – признак инверсии. Логическая функция НЕ от одного аргумента описывается й таблицей истинности:
Логический элемент «НЕ» (инвертор) реализует операцию отрицания. Если на входе этого логического элемента 0, то на выходе 1, а когда на входе 1, на выходе 0.
Условное обозначение инвертора на структурных схемах приведено на рис/ 1.5.3-1.
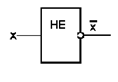
Рис. 1.5.3-1.
Функцией логического умножения n аргументов называется логическая функция, которая принимает значение 1 только в том случае, когда все аргументы равны 1, а 0 – во всех остальных случаях.
Функцию логического умножения называют также конъюнкцией или функцией И.
Элементарная функция логического умножения зависит от двух аргументов и описывается следующей таблицей истинности:
|
X
|
Y
|
F
|
|
0
|
0
|
0
|
|
0
|
1
|
0
|
|
1
|
0
|
0
|
|
1
|
1
|
1
|
Запись логической функции И: F=X Y ; F=X & Y ; F=XY,
где знаки «», «&», «» – знаки, обозначающие операцию логического умножения. Все варианты записи равнозначны.
Логический элемент «И» реализует конъюнкцию двух или более логических значений. Условное обозначение на структурных схемах конъюнкции с двумя входами представлено на рис. 1.5.3-2.
Рис. 1.5.3-2.
Функцией логического сложения n аргументов называется логическая функция, которая принимает значение 0 только в том случае, когда все аргументы равны 0 (т.е. при наборе n нулей), и 1 во всех остальных случаях (т.е. когда хотя бы один аргумент равен 1).
Функцию логического сложения называют также дизъюнкцией или логической функцией ИЛИ.
Элементарная дизъюнкция зависит от двух аргументов и описывается следующей таблицей истинности:
|
X
|
Y
|
F
|
|
0
|
0
|
0
|
|
0
|
1
|
1
|
|
1
|
0
|
1
|
|
1
|
1
|
1
|
Запись логической функции ИЛИ: F=X V Y ; F=X + Y, где знаки «V», «+» – обозначают операцию логического сложения.
Логический элемент «ИЛИ» реализует дизъюнкцию двух или более логических значений. Когда хотя бы на одном входе элемента «ИЛИ» будет единица, на её выходе также будет единица. Условное обозначение на структурных схемах логического элемента «ИЛИ» с двумя входами представлено на рис. 1.5.3-3.
Рис.1.5.3-3.
Функция отрицания от логического умножения принимает значение 0, когда все аргументы равны 1, и 1 – во всех остальных случаях:
|
X
|
Y
|
F
|
|
0
|
0
|
1
|
|
0
|
1
|
1
|
|
1
|
0
|
1
|
|
1
|
1
|
0
|
Запись логической функции:
Логический элемент «И–НЕ» состоит из элемента «И» и инвертора и осуществляет отрицание результата функции И. Условное обозначение на структурных схемах логического элемента «И–НЕ» с двумя входами представлено на рисунке 1.5.3-4.
Рис. 1.5.3-4
Функция отрицания от логического сложения принимает значение 1, когда все аргументы равны 0, и значение 0 – во всех остальных случаях:
|
X
|
Y
|
F
|
|
0
|
0
|
1
|
|
0
|
1
|
0
|
|
1
|
0
|
0
|
|
1
|
1
|
0
|
Запись логической функции:
Логический элемент «ИЛИ–НЕ» состоит из элемента «ИЛИ» и инвертора и
осуществляет отрицание результата логической функции «ИЛИ» .Условное обозначение на структурных схемах логического элемента «ИЛИ–НЕ» с двумя входами представлено на рис. 1.5.3-5.
Рис. 1.5.3-5
В сложных выражениях с использованием логических операций И, ИЛИ, НЕ сначала выполняются операции отрицания НЕ, затем операции конъюнкции И и, в последнюю очередь, операции дизъюнкции ИЛИ.
Для того чтобы изменить указанную последовательность выполнения операций, в выражениях следует использовать скобки.
Например:
1.5.4. Произвольные логические функции – ДНФ и КНФ
Предположим, что произвольная логическая функция n аргументов задана единственным набором аргументов, при котором эта функция принимает значение 1.
Составим конъюнкцию (логическую функцию И) от всех n аргументов: аргументы, которые в указанном наборе равны 0, возьмем со знаком инверсии, а аргументы, равные 1 в указанном наборе, - без знака инверсии, так как согласно определению конъюнкции, чтобы логическая функция И принимала значение 1, необходимо, чтобы все аргументы были равны 1.
Пример 1.5.4-1. Задана логическая функция от 4 аргументов Х1, Х2, Х3, Х4, которая принимает значение 1 при наборе Х1=0, Х2=1, Х3=1, Х4=0 и 0 при всех остальных наборах.
Составим выражение для этой функции:
Предположим, что произвольная логическая функция n аргументов задана единственным набором аргументов, при котором эта функция принимает значение 0.
Составим дизъюнкцию (логическую функцию ИЛИ) от всех n аргументов следующим образом: аргументы, равные 0 в заданном наборе, возьмем без знака инверсии, а аргументы, равные в заданном наборе 1, - со знаком инверсии, так как согласно определению дизъюнкции, чтобы логическая функция ИЛИ принимала значение 0, необходимо, чтобы все аргументы были равны 0.
Пример 1.5.4-2. Задана логическая функция от четырех аргументов Х1, Х2, Х3, Х4, которая принимает значение 0 при следующем наборе Х1=0, Х2=0, Х3=1, Х4=1 и 1 при всех остальных наборах.
Составим выражение для этой функции:
Произвольная логическая функция, заданная перечислением всех наборов аргументов, при которых она принимает значение 1, определяется следующим образом: для каждого из этих наборов составляется конъюнкция, а затем образуется дизъюнкция всех этих конъюнкций.
Пример 1.5.4-3. Предположим, что функция 4 аргументов Х1, Х2, Х3, Х4 принимает значение 1 при наборах:
Х1=1 Х2=0 Х3=1 Х4=0
Х1=0 Х2=0 Х3=1 Х4=1
Х1=1 Х2=1 Х3=0 Х4=1
и 0 на всех остальных наборах.
Тогда функция будет иметь вид:
Для любого из перечисленных наборов функция F(Х1, Х2, Х3, Х4) будет представлять собой дизъюнкцию одной 1 и остальных 0, т.е. будет равна 1, а на остальных наборах будет представлять собой дизъюнкцию одних нулей, т.е. будет равна 0.
Произвольная логическая функция, заданная перечислением всех наборов аргументов, при которых она принимает значение 0, определяется следующим образом: для каждого из этих наборов составляется дизъюнкция, а затем образуется конъюнкция всех этих дизъюнкций.
Пример 1.5.4-4. Предположим, что задана функция от 3 аргументов F(Х1, Х2, Х3), которая принимает значение 0 при наборах
Х1=0 Х2=1 Х3=1
Х1=1 Х2=0 Х3=0
Х1=0 Х2=0 Х3=0
и 1 при всех остальных наборах.
Тогда функция, сформированная таким образом, будет иметь вид:
Для любого из перечисленных наборов функция F(Х1, Х2, Х3) будет представлять собой конъюнкцию одного нуля и остальных единиц, то есть будет равна 0, а на остальных наборах будет представлять конъюнкцию одних единиц, то есть равна 1.
Из вышеизложенного можно сделать следующий вывод: произвольная логическая функция от n аргументов может быть выражена через логические функции И, ИЛИ, НЕ (конъюнкцию, дизъюнкцию, отрицание).
Логические функции, представляющие собой дизъюнкции отдельных членов, каждый из которых есть в свою очередь некоторая функция, содержащая только конъюнкции и инверсии, называются логическими функциями дизъюнктивной формы.
Логические функции дизъюнктивной формы, в которых инверсия применяется лишь непосредственно к аргументам, например, но не к более сложным функциям, как, например, называются нормальными дизъюнктивными функциями.
Если каждый член дизъюнктивной нормальной функции от n аргументов содержит все n аргументов, часть из которых со знаком инверсии, а часть без него, то функция называется совершенной (СДНФ). Например, функция
представляет собой СДНФ.
Каждый член такой формы обращается в 1 лишь при некотором единственном наборе аргументов, а число членов равно числу разных наборов, обращающих функцию в 1.
В несовершенных дизъюнктивных нормальных функциях от n аргументов некоторые члены содержат количество аргументов меньшее, чем n. Такие члены принимают значение 1 при нескольких наборах аргументов. Потому и число членов в несовершенных формах меньше, чем число членов в совершенных формах этих же функций.
Аналогично, функция
представляет собой совершенную конъюнктивную нормальную форму логических функций (СКНФ).
Пример 1.5.4-5. Составить выражение для функции, принимающей значение 1 на наборах 2 и 6.
Запишем числа 2 и 6 в двоичной системе:
2 в двоичной системе – 10 (или 010),
6 в двоичной системе – 110.
Это значит, что искомая функция будет функцией от 3 переменных: Х1, Х2, Х3.
Наборы, на которых функция обращается в 1:
(2) Х1=0 Х2=1 Х3=0
(6) Х1=1 Х2=1 Х3=0.
Составим выражение для функции
Функция F(Х1, Х2, Х3) – СДНФ.
Пример 1.5.4-6. F=0 на наборах 2, 4. Составить выражение для этой функции:
2 в двоичной системе – 010
4 в двоичной системе – 100.
Наборы, на которых функция обращается в 0:
(2) Х1=0 Х2=1 Х3=0
(4) Х1=1 Х2=0 Х3=0.
Логическая функция примет вид:
Функция F(Х1, Х2, Х3) - СКНФ.
В компьютерах и других технических устройствах широко применяются электрические схемы, содержащие сотни и тысячи переключательных элементов: реле, выключателей и т.п. Разработка таких схем - весьма трудоёмкое дело. Оказалось, что здесь с успехом может быть использован аппарат алгебры логики.
Переключательная схема — это схематическое изображение некоторого устройства, состоящего из переключателей и соединяющих их проводников, а также из входов и выходов, на которые подаётся и с которых снимается электрический сигнал.
Каждый переключатель имеет только два состояния: замкнутое и разомкнутое. Переключателю Х поставим в соответствие логическую переменную х, которая принимает значение 1 в том и только в том случае, когда переключатель Х замкнут и схема проводит ток; если же переключатель разомкнут, то х равен нулю.
Будем считать, что два переключателя Х и связаны таким образом, что когда Х замкнут, то разомкнут, и наоборот. Следовательно, если переключателю Х поставлена в соответствие логическая переменная х, то переключателю должна соответствовать переменная .
Всей переключательной схеме также можно поставить в соответствие логическую переменную, равную единице, если схема проводит ток, и равную нулю — если не проводит. Эта переменная является функцией от переменных, соответствующих всем переключателям схемы, и называется функцией проводимости.
Определим функции проводимости F некоторых переключательных схем:
1)
Схема не содержит переключателей и проводит ток всегда, следовательно, F=1 для любых значений x:
2)
Схема содержит один постоянно разомкнутый контакт, следовательно, F=0 для любых значений x:
3)
Схема проводит ток, когда переключатель х замкнут, и не проводит, когда х разомкнут, следовательно, F(x) = x. То есть существует единственный набор (значение аргумента x), на котором функция F=1:
4)
Схема проводит ток, когда переключатель х разомкнут, и не проводит, когда х замкнут, то есть F=0 при x=1. Следовательно, F(x) = :
5)
Схема проводит ток, когда оба переключателя замкнуты, то есть существует единственный набор x=1 и y=1, на котором F=1. Следовательно, F(x, y) = x & y;
|
x
|
y
|
F
|
|
0
|
0
|
0
|
|
0
|
1
|
0
|
|
1
|
0
|
0
|
|
1
|
1
|
1
|
6)
Схема проводит ток, когда хотя бы один из переключателей замкнут, то есть существует единственный набор x=0 и y=0, на котором F=0. Следовательно, F(x, y)=x v y:
|
x
|
y
|
F
|
|
0
|
0
|
0
|
|
0
|
1
|
1
|
|
1
|
0
|
1
|
|
1
|
1
|
1
|
1.5.5. Контрольные вопросы по теме «Основные понятия алгебры логики»
Что такое алгебра логики?
Для чего используется булевская алгебра (алгебра логики)?
Что называется высказыванием?
Какие значения принимают высказывания?
Что изучает алгебра логики?
Какие переменные называются логическими или булевскими?
Какие функции называют логическими?
Чем определяется логическая функция?
Что такое таблица истинности?
Какие логические функции называются элементарными?
Какая функция называется функцией отрицания?
Каким образом описывается функция отрицания?
Какая функция называется функцией логического умножения?
Каким образом описывается функция логического умножения?
Какая функция называется функцией логического сложения?
Каким образом описывается функция логического сложения?
Как описывается функция отрицания от логического умножения?
Как описывается функция отрицания от логического сложения?
Какой порядок выполнения операций отрицания, конъюнкции и дизъюнкции в сложных логических выражениях?
Как выразить произвольную логическую функцию, которая на единственном наборе аргументов принимает значение 1?
Как выразить произвольную логическую функцию, которая на единственном наборе аргументов принимает значение 0?
Как выражается произвольная логическая функция, заданная перечислением наборов аргументов, на которых она принимает значение 1?
Как выражается произвольная логическая функция, заданная перечислением наборов аргументов, на которых она принимает значение 0?
Какие логические функции называются логическими функциями дизъюнктивной формы?
Какие логические функции называются логическими функциями конъюнктивной формы?
Какие логические функции называются нормальными функциями?
Какие логические функции называются совершенными?
Назовите отличие логических функций совершенной и несовершенной форм.
1.5.6. Тестовые задания по теме «Основные понятия алгебры логики»
Логическая функция является
дизъюнктивной нормальной функцией
- совершенной конъюнктивной нормальной функцией (СКНФ)
совершенной дизъюнктивной нормальной функцией (СДНФ)
- функцией другого типа
Алгебра логики – это
- определенная часть математической логики, называемая исчислением высказываний
- часть математики, занимающаяся вычислением выражений
- часть математики, занимающаяся вычислением алгебраических выражений с применением законов логики
Логические переменные и логические функции могут принимать следующие значения …
- 0, 1
- 1
- 0, 1, 2
- 0
Логическая функция полностью определяется
- таблицей истинности
- единичным набором аргументов
- нулевым набором аргументов
- таблицей наборов аргументов
Элементарные логические функции зависят
- от одного или двух аргументов
- от трех аргументов
- от четырех аргументов
- от любого количества аргументов
Порядок выполнения логических операций в сложных логических выражениях следующий
- отрицание, логическое умножение, логическое сложение
- логическое умножение, отрицание, логическое сложение
- логическое умножение, логическое сложение, отрицание
- любой
Логические функции называются нормальными функциями
- если инверсия применяется непосредственно к аргументам
- если инверсия применяется к отдельным логическим функциям
- если инверсия применяется ко всей логической функции
- нет правильного ответа
Логические функции называются совершенными
- если каждый член дизъюнктивной (или конъюнктивной) нормальной функции от n аргументов содержит все n аргументов
- если каждый член дизъюнктивной (или конъюнктивной) нормальной функции от n аргументов содержит n аргументов с отрицаниями
- если каждый член дизъюнктивной (или конъюнктивной) нормальной функции от n аргументов содержит хотя бы один аргумент с отрицанием
- если каждый член дизъюнктивной (или конъюнктивной) нормальной функции от n аргументов содержит все n аргументов без отрицаний
Если логическая функция принимает значение 0 на наборах 0, 2, 3, 5, то она принимает значение 1
- на наборах 1, 4, 6, 7
- на наборах 4, 5, 7
- на наборах 6, 7
- на наборах 1, 2, 3, 4, 5
Совершенной конъюнктивной нормальной функцией (СКНФ является
Логической функции F=0, заданной на наборах 0,1,2, 4, 7 соответствует аналитическое выражение
Логической функции, заданной таблично F= 1 на наборах 1, 3, 4, 5, 7 соответствует аналитическое выражение
Какая из предложенных функций является Совершенной дизъюнктивной формой (СДНФ) логической функцииявляется
Логической функции, заданной таблично F= 0 на наборах 2, 4, 6 соответствует аналитическое выражение
Логических функций является нормальной
Логических функций является совершенной функцией
ема 1.5. Основные понятия алгебры логики Страница 57
Основные понятия алгебры логики