Организация данных в ЭВМ

Тема 1.4. Организация данных в ЭВМ

1.4.1. Представление целых чисел

1.4.2. Представление вещественных чисел

1.4.3. Кодирование текстовой информации

1.4.4. Контрольные вопросы по теме «Организация данных в ЭВМ»

Числа в компьютерах в двоичных кодах представляются как с фиксированной (в естественной форме), так и с плавающей точкой (в экспоненциальной форме).

При представлении в памяти компьютера чисел в естественной форме устанавливается фиксированная длина разрядной сетки. Причем точку можно зафиксировать в начале, середине или в конце разрядной сетки. При этом распределение разрядов между целой и дробной частями остается неизменным для любых чисел. В современных компьютерах эта форма используется для представления целых чисел.

Достоинствами естественной формы являются простота и наглядность представления чисел, простота алгоритмов реализации операций, а, следовательно, простота устройств и высокая скорость выполнения операций. Недостатком – конечный диапазон представления величин, что приводит к переполнению разрядной сетки при выходе за допустимые границы и искажению результата. Неудобство представления чисел в форме с фиксированной точкой проявляется при решении задач, в которых фигурируют как очень малые, так и очень большие числа.

1.4.1. Представление целых чисел

Целые числа могут представляться в компьютере со знаком или без знака.

Целые числа без знака обычно  занимают  в  памяти  компьютера  один  или  два  байта. В  однобайтовом  формате  принимают  значения  от  000000002   до  111111112. В двухбайтовом формате - от  00000000000000002   до  11111111111111112.

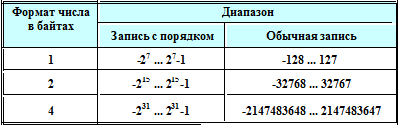
Диапазоны значений целых чисел приведены в табл. 1.4.1.

Пример 1.4.1-1. Представить число 7210 = 10010002 в однобайтовом формате:

Пример 1.4.1-2. Представить это же число в двухбайтовом формате:

Пример 1.4.1-3. Представить число 6553510 в двухбайтовом формате:

   

Целые числа со знаком обычно занимают в памяти компьютера один, два или четыре байта, при этом самый левый (старший) разряд содержит информацию о знаке числа.

Таблица 1.4.1-1.

Диапазоны значений целых чисел со знаком приведены в таблице 1.4.1-2.

Таблица 1.4.1-2

Рассмотрим особенности записи целых чисел со знаком на примере однобайтового формата, при котором для знака отводится один разряд, а для цифр абсолютной величины – семь разрядов.

В компьютерной технике применяются три формы записи (кодирования) целых чисел со знаком:  прямой код,   обратный код,   дополнительный код.

Последние две формы применяются особенно широко, так как позволяют упростить конструкцию арифметико-логического устройства компьютера путем замены разнообразных арифметических операций операцией сложения.

Положительные числа в прямом, обратном и дополнительном кодах изображаются одинаково  -  двоичными кодами с цифрой 0 в знаковом разряде.

Пример 1.4.1-4. Представить положительное число 110=12 в прямом коде:

0

0

0

0

0

0

0

1

+Знак числа

Пример 1.4.1-5. Представить положительное число 12710=11111112 в прямом коде:

0

1

1

1

1

1

1

1

+Знак числа

Отрицательные числа в прямом, обратном и дополнительном кодах имеют разное изображение.

Прямой код. В знаковый разряд помещается цифра 1, а в разряды цифровой части числа – двоичный код его абсолютной величины.

Пример 1.4.1-6. Представить отрицательное число – 110 в прямом коде:

1

0

0

0

0

0

0

1

+Знак числа

Пример 1.4.1-7. Представить отрицательное число – 12710 в прямом коде:

1

1

1

1

1

1

1

1

+Знак числа

Обратный код. Получается инвертированием всех цифр двоичного кода абсолютной величины числа, включая разряд знака: нули заменяются единицами, а единицы – нулями.

Пример 1.4.1-8. Представить отрицательное число – 110 в обратном коде:

Код модуля числа	0	0	0	0	0	0	0	1
Обратный код числа	1	1	1	1	1	1	1	0

Пример 1.4.1-9. Представить отрицательное число – 12710 в обратном коде:

Код модуля числа	0	1	1	1	1	1	1	1
Обратный код числа	1	0	0	0	0	0	0	0

Дополнительный код. Получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду.
 

Пример 1.4.1-10. Представить отрицательное число – 110 в дополнительном коде:

1

1

1

1

1

1

1

1

Пример 1.4.1-11. Представить отрицательное число – 12710 в дополнительном коде:

1

0

0

0

0

0

0

1

Обычно отрицательные десятичные числа при вводе в машину автоматически преобразуются в обратный или дополнительный двоичный код и в таком виде хранятся, перемещаются и участвуют в операциях. При выводе таких чисел из машины происходит обратное преобразование в отрицательные десятичные числа.

 

1.4.2. Представление вещественных чисел

Вещественные числа в математических вычислениях предполагаются непрерывными и бесконечными, то есть не имеющими ограничений на диапазон и точность представления чисел. Однако в компьютерах числа хранятся в регистрах и ячейках памяти с ограниченным количеством разрядов. Вследствие этого, система вещественных чисел, представимых в компьютере, является дискретной (прерывной) и конечной.

При записи вещественных чисел в системах программирования вместо привычной запятой принято ставить точку. Для отображения вещественных чисел, которые могут быть как очень маленькими, так и очень большими, используется форма записи чисел с порядком основания системы счисления (экспоненциальная форма или формат с плавающей точкой). Например, десятичное число 1.25 в этой форме можно представить так:

1.25 . 100 = 0.125 . 101 = 0.0125 . 102 = ...

или так:

12.5 . 10-1 = 125.0 . 10-2 = 1250.0 . 10-3 = ... .

То есть десятичная точка как бы «плавает» по числу.

Любое число N в системе счисления с основанием q можно записать в виде N = M . qp, где M — множитель, содержащий все цифры числа (мантисса), а p — целое число, называемое порядком. Такой способ записи чисел называется представлением числа с плавающей точкой.

Если "плавающая" точка расположена в мантиссе перед первой значащей цифрой, то при фиксированном количестве разрядов, отведённых под мантиссу, обеспечивается запись максимального количества значащих цифр числа, то есть максимальная точность представления числа в машине. Из этого следует:

Мантисса должна быть правильной дробью, у которой первая цифра после точки (запятой в обычной записи) отлична от нуля: 0.1 <=  |M|  <  1. Если это требование выполнено, то число называется нормализованным.

Мантиссу и порядок q-ичного числа принято записывать в системе с основанием q, а само основание — в десятичной системе.

Пример 1.4.2-1. Представить десятичные числа в нормализованном виде.

753.15 = 0.75315 . 103;     
- 0.000034 = - 0.34 . 10-4;  

Пример 1.4.2-2. Представить двоичные числа в нормализованном виде.

-101.012  =-0.10101 . 211 (порядок 112 = 310)

0.0000112 = 0.11 . 2-100 (порядок   —1002  =  —410).

Вещественные числа в компьютерах различных типов записываются по-разному, тем не менее, все компьютеры поддерживают несколько стандартных форматов, различающихся по точности, но имеющих структуру, представленную на рис. 1.4.1.

Рис. 1.4.1.

Здесь порядок n-разрядного нормализованного числа задается в так называемой смещенной форме: если для задания порядка выделено k разрядов, то к истинному значению порядка, представленного в дополнительном коде, прибавляют смещение, равное (2k-1 — 1). Например, порядок, принимающий значения в диапазоне от -128 до +127, представляется смещенным порядком, значения которого меняются от 0 до 255.

Использование смещенной формы позволяет производить операции над порядками, как над незнаковыми числами, что упрощает операции сравнения, сложения и вычитания порядков, а также упрощает операцию сравнения самих нормализованных чисел.

Чем больше разрядов отводится под запись мантиссы, тем выше точность представления числа. Чем больше разрядов занимает порядок, тем шире диапазон от наименьшего отличного от нуля числа до наибольшего числа, представимого в машине при заданном формате.

Стандартные форматы представления вещественных чисел могут быть следующие.

Одинарный  —  32-разрядное нормализованное число со знаком, 8-разрядным смещенным порядком и 24-разрядной мантиссой (старший бит мантиссы, всегда равный 1, не хранится в памяти, и размер поля, выделенного для хранения мантиссы, составляет только 23 разряда).

Двойной  —  64-разрядное нормализованное число со знаком, 11-разрядным смещенным порядком и 53-разрядной мантиссой (старший бит мантиссы не хранится, размер поля, выделенного для хранения мантиссы, составляет 52 разряда).

Расширенный  —  80-разрядное число со знаком, 15-разрядным смещенным порядком и 64-разрядной мантиссой.

Следует отметить, что вещественный формат с m-разрядной мантиссой позволяет абсолютно точно представлять m-разрядные целые числа, т. е. любое двоичное целое число, содержащее не более m разрядов, может быть без искажений преобразовано в вещественный формат.

1.4.3. Кодирование текстовой информации

        В традиционных кодировках для кодирования одного символа используется 8 бит. Легко подсчитать, что такой 8-разрядный код позволяет закодировать 256 различных символов.

        Присвоение символу определенного числового кода – это вопрос соглашения. В качестве международного стандарта принята кодовая таблица ASCII (American Standard Code for Information Interchange), кодирующая первую половину символов с числовыми кодами от 0 до 127 (коды от 0 до 32 отведены не символам, а функциональным клавишам и служебным кодам), которая приведена на рис. 1.4.3-1.

Национальные стандарты кодировочных таблиц включают международную часть кодовой таблицы без изменений, а во второй половине содержат коды национальных алфавитов, символы псевдографики и некоторые математические знаки. К сожалению, в настоящее время существуют пять различных кодировок кириллицы (КОИ8-Р, Windows, MS-DOS, Macintosh и ISO), что вызывает дополнительные трудности при работе с русскоязычными документами.

Рис. 1.4.3-1. Международная кодировка ASCII

       

        Хронологически одним из первых стандартов кодирования русских букв на компьютерах был КОИ8 ("Код обмена информацией, 8-битный"). Эта кодировка применялась еще в 70-ые годы на компьютерах серии ЕС ЭВМ, а с середины 80-х стала использоваться в первых русифицированных версиях операционной системы UNIX.

        Наиболее распространенной в настоящее время является кодировка Microsoft Windows (рис. 1.4.3-2.).

Рис. 1.4.3-2. Кодировка Microsoft Windows

 

        В конце 90-ых годов появился новый международный стандарт Unicode, который отводит под один символ не один байт, а два, и поэтому с его помощью можно закодировать не 256, а 65536 различных символов. Полная спецификация стандарта Unicode включает в себя все существующие, вымершие и искусственно созданные алфавиты мира, а также множество математических, музыкальных, химических и прочих символов.

        Для преобразования русскоязычных текстовых документов из одной кодировки в другую используются специальные программы-конверторы.

1.4.4. Контрольные вопросы по теме «Организация данных в ЭВМ»

Какими способами представляются числа в компьютере?

Что такое естественная форма числа (формат с фиксированной точкой)?

Какие числа представляются в формате с фиксированной точкой?

Каковы недостатки и достоинства формата с фиксированной точкой?

Какие три формы записи целых чисел вы знаете?

Что такое прямой код и для чего он служит?

Что такое обратный код и для чего он служит?

Что такое дополнительный код и для чего он служит?

Как производится выполнение арифметических действий над целыми числами в компьютере?

Как представляются в компьютере вещественные числа?

Как производится выполнение арифметических действий над вещественными числами в компьютере?

Каким образом производится кодирование текстовой информации в компьютере?

1.4.5. Тестовые задания по теме «Организация данных в ЭВМ»

1. За основную единицу измерения количества информации принят
2. 1 бит
3. 1 бод
4. 1 байт
5. 1 Кбайт

1. 1 байт соответствует

8 бит

10 Кбайт

10 бит

1 бод

1. Числа в компьютерах представляются

в двоичном коде

в троичном коде

в логарифмическом коде

в любом из вышеперечисленных

1. Форма представления числа может быть

с фиксированной точкой или с плавающей точкой

естественной или с фиксированной точкой

нормализованной или экспоненциальной

нет верного ответа

1. Для представления целого числа может применяться

прямой, обратный или дополнительный код

нормализованный или ненормализованный код

естественный или экспоненциальный код

1. Положительное число

выглядит одинаково в прямом, обратном и дополнительном кодах

выглядит различно в прямом, обратном и дополнительном кодах

выглядит одинаково только в прямом и обратном кодах

выглядит одинаково только в обратном и дополнительном кодах

1. Прямой код отрицательных и положительных чисел, равных по модулю

имеет различное значение только в знаковом разряде

имеет различное значение

может быть либо одинаковым, либо разным

1. 
   Обратный код отрицательного числа получается

из прямого кода путем замены единиц на нули и нулей на единицы, исключая знаковый разряд

из прямого кода путем замены единиц на нули и нулей на единицы, включая знаковый разряд

из дополнительного кода путем замены единиц на нули и нулей на единицы, исключая знаковый разряд

из дополнительного кода прибавлением единицы к младшему разряду

1. Дополнительный код числа получается

из обратного кода прибавлением единицы к младшему разряду без переноса в знаковый разряд

из обратного кода прибавлением единицы к младшему разряду с переносом в знаковый разряд

из прямого кода прибавлением единицы к младшему разряду без переноса в знаковый разряд

из прямого кода прибавлением единицы к младшему разряду с переносом в знаковый разряд

1. Дополнительный код отрицательного числа

может быть получен из прямого кода заменой всех единиц на нули и всех нулей на единицы, исключая самую младшую единицу и следующие за ней нули

может быть получен из прямого кода заменой всех единиц на нули и всех нулей на единицы

не может быть получен из прямого кода

1. Стандартные форматы представления вещественных чисел – это

с фиксированной или с плавающей точкой

нормализованный или ненормализованный

одинарный, двойной или расширенный

1. Нормализованное и ненормализованное число определяются

значением мантиссы

значением порядка

кодом, в котором записано число

1. Система ASCII служит для кодирования

символов

латинских букв

цифр

букв национальных алфавитов

1. Слово ИНФОРМАТИКА содержит … бит

88

11

44

1

1. В процессе преобразования текстового файла из кодировки MS-DOS в кодировку Windows происходит

перекодировка символов

форматирование документа

нет верного ответа

печать документа

1. Один разряд шестнадцатеричного числа содержит количество информации равное

4 бита

1 бит

1 байт

16 бит

1. Слова ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ содержат ### бит

28

192

24

2

1. Один разряд двоичного числа содержит количество информации равное

1 бит

3 бита

4 бит

1 байт

1. Дополнительный код отрицательного числа
2. может быть получен из прямого кода заменой всех единиц на нули и всех нулей на единицы, исключая самую младшую единицу и следующие за ней нули
3. может быть получен из прямого кода заменой всех единиц на нули и всех нулей на единицы
4. не может быть получен из прямого кода

1. Для кодирования одной буквы необходимо ### бит информации

8

2

1

16

1. Число 3110 в прямом коде будет представлено как

000111112 *

100111112

000011112

1. Число -6310 в прямом коде будет представлено как
2. 101111112
3. 001111112
4. 100111112

1. 
   Число 6510 в прямом коде будет представлено как
2. 010000012
3. 100000012
4. 000000012

1. Число -910 в обратном коде будет представлено как
2. 111101102
3. 011111102
4. 111111112

1. Число -1510 в обратном коде будет представлено как
2. 111100002
3. 011000002
4. 001000002

1. Число -12710 в обратном коде будет представлено как
2. 100000002
3. 000000002
4. 111111112

1. Число -910 в дополнительном коде будет представлено как
2. 111101112
3. 111110112
4. 111011112

1. Число -1510 в дополнительном коде будет представлено как
2. 111100012
3. 111111112
4. 111100102

1. Число -12710 в дополнительном коде будет представлено как
2. 100000012 *
3. 100000002
4. 000000012

1. Десятичное представление записанного в дополнительном коде числа 111110002 будет

-810

-710

-910

1. Десятичное представление записанного в дополнительном коде числа 100110112 будет

-10110

-10010

-11010

1. Десятичное представление записанного в дополнительном коде числа 111010012 будет

-2310

-2210

-15310

PAGE 42

Организация данных в ЭВМ