Курс виртуальных лабораторных работ по дисциплине «Оптические методы и устройства обработки информации»
Министерство образования и науки Российской Федерации
ФГАОУ ВП «Северо-Восточный федеральный университет имени М.К. Аммосова»
Физико-технический институт
Кафедра радиотехники и информационных технологий
ДИПЛОМНАЯ РАБОТА
Курс виртуальных лабораторных работ по дисциплине «Оптические методы и устройства обработки информации»
Допущено к защите
« » 2010г.
Зав. кафедрой
РТиИТ
Мельчинов В.П.
Рецензент
к. т. н.
доцент кафедры РТиИТ
Дипломная работа
студента гр. РТ-06
Пахомов Василий
Николаевич
Руководитель:
Леонтьев Ньургун Анатольевич,
доцент кафедры РТиИТ
Работа защищена
Протокол №
Оценка
Якутск 2011
СОДЕРЖАНИЕ
ВВЕДЕНИЕ……………………………………………………………………………………....3
1. ОПТИЧЕСКИЕ МЕТОДЫ……………..............................………………………..................4
1.1Преобразование Фурье в оптике………………………………………………….....5
1.2 Перспективы развития оптических методов обработки информации……………6
1.3 Управляемый транспарант…………………………………………………………..8
1.4 Голография………………………………………………………………………….11
2. MathCAD И ВИРТУАЛЬНЫЕ ЭЛЕМЕНТЫ……………………………………….……...12
2.1 Элементы MathCAD………………………………………………………………..15
2.2 Документы MathCAD………………………………………………………………18
3. ВЫЧИСЛЕНИЯ НА ПРОГРАММЕ MathCAD ………………………………………........22
3.1 Ввод формул………………………………………………………………………...23
3.2Функции для вычислений…………………………………………………………..25
ЗАКЛЮЧЕНИЕ…………………………………………………………………………………28
ЛИТЕРАТУРА………………………………………...………………………….…………….29
ПРИЛОЖЕНИЕ…………………………………………………………………………………30
ВВЕДЕНИЕ
В основе оптических методов обработки информации лежат явления преобразования пространственно-модулированных оптических сигналов в оптических устройствах и системах на принципах как геометрической, так и волновой оптики. «Обработка информации» здесь означает «преобразование, анализ и синтез многомерных функций, описывающих свойства и состояние объектов материального мира». Оптическая обработка информации осуществляется в оптическом процессоре – аналоговом оптическом либо оптоэлектронном устройстве, определенным образом изменяющем амплитуду и фазу пространственно-модулированного оптического сигнала, содержащего информацию об объекте. Системы оптической обработки информации, как правило, являются составной частью комплексной оптоэлектронной системы обработки информации или высокопроизводительного вычислительного устройства, включающих
как электронные, так и оптические компоненты.
Тема моей дипломной работы - Курс виртуальных лабораторных работ по дисциплине «Оптические методы и устройства обработки информации». Главной целью работы является создание и изучение лабораторных работ на программе MadhCAD для студентов Северо-Восточного федерального университета имени М.К. Аммосова.
- ОПТИЧЕСКИЕ МЕТОДЫ
Значительная часть оптической обработки информации основана на свойстве преобразования Фурье. Уникальность тонкой положительной линзы заключается в выполнении преобразования Фурье: в когерентном свете распределение амплитуды излучения в задней фокальной плоскости линзы может быть представлено как двумерное комплексное преобразование Фурье от функции распределения амплитуды света в передней фокальной плоскости линзы. Основные геометрические соотношения при действии тонкой положительной линзы показаны на Рис. 1. Дифракционный интеграл, описывающий взаимосвязь распределений поля во входной и выходной плоскостях такой системы имеет вид: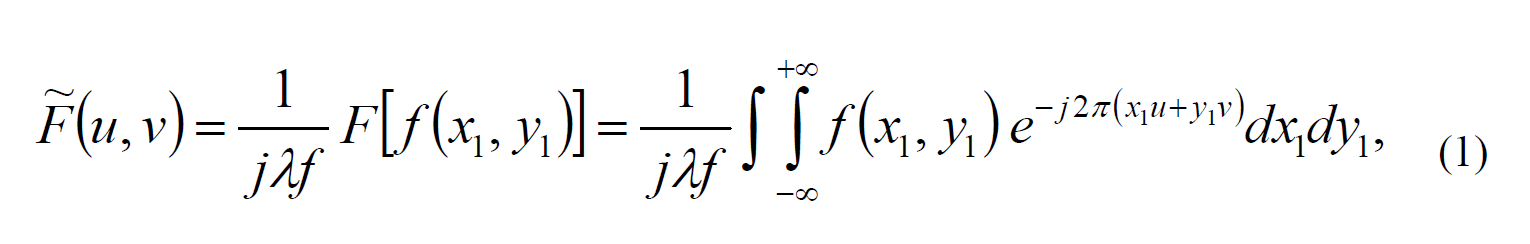
Где u = /f , v = /f ; - длина волны света, f – фокусное расстояние линзы;
f() - комплексная амплитуда световой волны в передней (входной) фокальной плоскости , F(u,v) - комплексная амплитуда световой волны в задней (выходной, спектральной) фокальной плоскости .
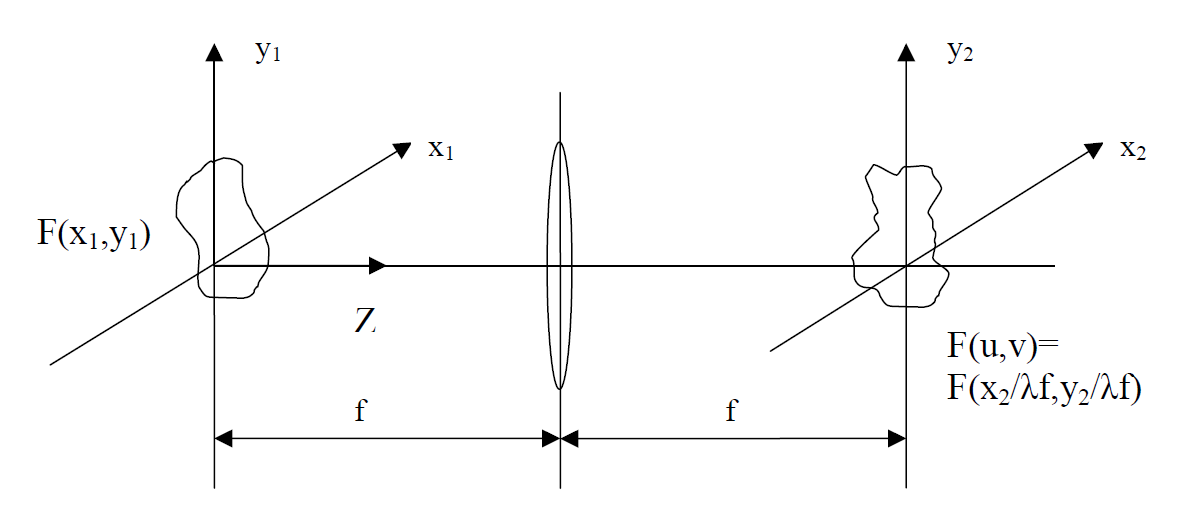
Рис 1. Преобразование оптического сигнала тонкой положительной линзой
- Преобразования Фурье в оптике
Математически преобразование Фурье является частным случаем интегрального преобразования Фредгольма с ядром в виде экспоненты с мнимым, линейным по аргументу, показателем. Преобразование Фурье в оптике «реализуется» с помощью аналогового устройства – положительной линзы, и основные свойства этого преобразования могут быть наглядно демонстрированы при рассмотрении прохождения световых волн через оптическую систему, содержащую линзы, диафрагмы, оптические транспаранты и др.
Различают прямое (2) и обратное (3) преобразования Фурье
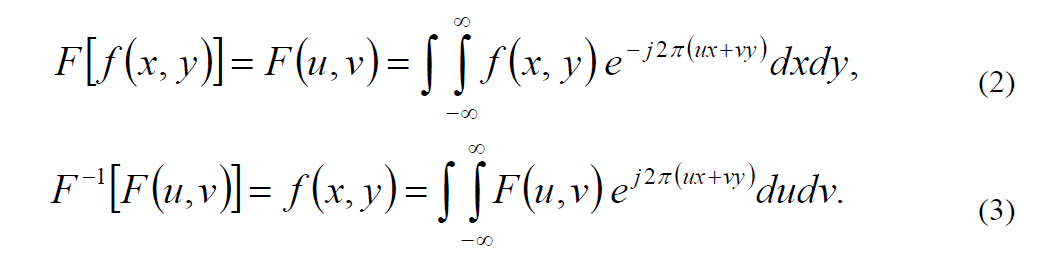
- Линейность - означает, что через одну линзу, осуществляющую преобразование Фу-
рье, одновременно может проходить множество световых сигналов.
- Подобие - изменение масштаба изображения на входе системы приводит к сжатию либо
растяжению области его пространственного спектра.
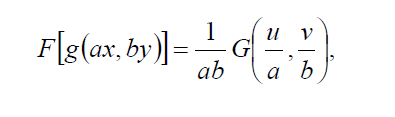
- Смещение - сдвиг изображения вызывает изменение фазы спектральной функции, но сохраняет неизменной ее амплитуду.
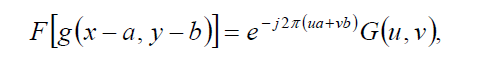
- Производная
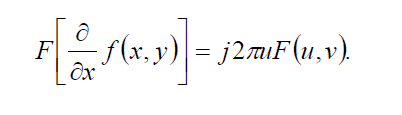
Для функций с ограниченным спектром (финитных функций) выполняется
теорема Парсеваля:
Это свойство означает постоянство полной мощности (квадрата амплитуды) излучения, проходящего через идеально прозрачную линзу. В фурье-анализе часто используется понятие «свертка» двух функций. Свертка определяется как интеграл от произведения двух функций, смещенных друг относительно друга по осям координат, при этом величина смещения есть аргумент (независимая переменная) интеграла свертки.
1.2 Перспективы развития оптических методов обработки информации
Исследования оптических методов и систем обработки информации ведутся уже более 20 лет. Оптические системы обработки характеризуются высоким быстродействием, возможностью параллельного выполнения операций над большими массивами данных, отсутствием взаимных помех при передаче сигналов по оптическим каналам, а также возможностью организации программируемых локальных и глобальных связей между отдельными узлами оптических систем. Эти достоинства открывают интересные перспективы для выполнения многих традиционных видов обработки сигналов, когда цифровая электронная техника становится неадекватной. В качестве примеров областей, где потребности в цифровой обработке превышают возможности современной электронной техники, можно назвать обработку и анализ изображений, обработку радиолокационных сигналов, машинное зрение, искусственный интеллект. Поэтому наряду с разработкой традиционных оптических устройств обработки в последнее время большое внимание уделяется созданию универсальных оптических вычислительных систем, по своим возможностям намного превосходящих ЭВМ. Исследования по созданию средств оптической вычислительной техники проводятся в настоящее время в следующих основных направлениях. Разработка оптических устройств для повышения быстродействия современных и перспективных ЭВМ (например, оптических устройств распределения синхросигналов, оптических соединений на различных уровнях и т.д.);разработка оптических процессоров специального назначения для решения ограниченного круга проблем. К таким устройствам относятся, в частности, матричные и систолические процессоры, в которых в масштабе времени, близком к реальному, выполняются матрично-векторные операции линейной алгебры. Ожидается, что потенциальная производительность этих процессоров достигнет 10 опер./с;.создание универсальных оптических цифровых вычислительных машин (ОЦВМ), по быстродействию на несколько порядков превосходящих существующие ЭВМ; исследование принципиально новых оптических компьютеров, в частности нейронно-сетевых, с необычными архитектурами, по своим возможностям приближающихся к человеческому мозгу.
ОЦВМ, превосходящие по быстродействию современные суперЭВМ на несколько порядков, представляют собой параллельные мультипроцессорные системы, которые позволят не только существенно повысить скорость вычислений, но и будут иметь принципиально отличающиеся от ЭВМ архитектуры, решающие задачи искусственного интеллекта, символьной обработки и ассоциативного распознавания изображений. Специалисты считают, что оптические методы благодаря возможности организации программируемых глобальных и локальных связей открывают большие возможности для создания нейронно-сетевых компьютеров.
В настоящее время еще нет общепринятой архитектуры оптической вычислительной машины (ОВМ). Чтобы выработать архитектурные принципы, нужно прежде всего рассмотреть оптические методы, которые можно использовать при создании новой вычислительной системы.
Одним из наиболее важных и фундаментальных принципов построения ОВМ является применение эффективного оптического метода распараллеливания логических вентилей. Это приводит к новой архитектуре логических систем и делает заманчивым переход на оптическую систему, когда электронный вариант оказывается неудобным. Системы с большим количеством связей зачастую легче создать в сравнительно простом оптическом варианте, тогда как уже сейчас ограничения, вносимые соединениями, начинают серьезным образом сказываться на системах, использующих СБИС.
Описаные современные нетрадиционные методы и схемотехнические варианты построения многоканальных оптических цифровых логических систем, основаны на парафазном представлении информации на всех этапах обработки. Важной и интересной особенностью этих устройств является легкость и оперативность переключения на вычисление любой булевой логической функции как электрическими, так и оптическими сигналами, простота, компактность и возможность выполнения методами интегральной технологии. Рассмотрены оригинальные оптические системы связи, обеспечивающие возможность оперативного изменения топологии соединений многоканальных оптических логических устройств. Показано, что производительность многоканальных оптоэлектронных процессоров, построенных на таких схемах, может достигать 1013опер./с.
К наиболее перспективным следует отнести схемотехнические варианты создания таких логических устройств на основе световодной (волоконной и интегральной) оптики, которая обеспечивает конструктивную совместимость с электронными интегральными схемами. Идеологически они хорошо сопрягаются с перспективными устройствами вычислительных и поисковых систем с целью образования единой аппаратуры. Такая оптоэлектронная аппаратура, использующая одновременно достоинства оптики и электроники при обработке информации, может широко использоваться в радиоэлектронных системах различного назначения как наземного, так и бортового базирования.
1.3 Управляемый транспарант
Управляемы в оптических системах находят широкое применение: ввод-вывод данных, кодирование и распознавание оптических сигналов, реализация логических операций, усиление яркости изображений, перестраиваемые фильтры. По способу управления модуляцией светового пучка различают электрически (ЭУТ) и оптически (ОУТ) управляемые транспаранты. Оба типа транспарантов могут осуществлять дискретную или аналоговую модуляцию светового пучка.
Существуют различные подходы к конструированию УТ, зависящие от используемых материалов и физических эффектов. Хотя было исследовано множество материалов, однако модели УТ с удовлетворительными характеристиками удалось построить лишь на PLZT-керамике и жидких кристаллах. УТ на PLZT-керамике. PLZT-керамика —класс прозрачной сегнетоэлектрической керамики с сильно выраженными электрооптическими свойствами, зависящими от электрической поляризации материала. Изменение поляризации сопровождается изменением двулучепреломления материала. PLZT-керамика обладает и упругооптическими свойствами, подобными электрооптическим. Создание механического напряжения вдоль определенного направления вызывает появление двулучепреломления. Для пространственной модуляции света используют следующие основные эффекты, наблюдающиеся в PLZT-керамике, помещенной в электрическое поле: наведенное двулучепреломление (электрооптический эффект); динамическое рассеяние, краевой эффект и изменение толщины керамической пластинки (обратный пьезоэффект). Используя тот или иной эффект, на основе PLZT-керамики можно построить УТ, способные осуществлять пространственную модуляцию объектного пучка как по амплитуде, так и по фазе или поляризации.
Основным достоинством PLZT-керамики является возможность ее использования в режиме работы с запоминанием, основанным на гистерезисном характере зависимости поляризации Р от напряжения управляющего электрического поля Vz. Обычно состояние с остаточной поляризацией принимается за двоичную единицу («1»), а деполяризованное (Р = 0) — за двоичный нуль («0»). Для переключения из одного состояния в другое требуются импульсы напряжения порядка 50 – 300 В длительностью 1 – 10 мкс.
УТ на жидких кристаллах. Жидкие кристаллы (ЖК) обладают электрооптическими свойствами и являются почти совершенными модуляторами света, легко управляемыми электрическим полем. Особенностью тонких жидкокристаллических слоев является их способность изменять оптические свойства под действием низких рабочих напряжений (1 – 50 В) при малом потреблении мощности (1 мкВт/см2). Благодаря этому ЖК находят широкое применение в оптических системах. Известны три типа ЖК (нематические, холестерические и смектические), из которых для построения УТ наибольший интерес представляют нематические. Для пространственной модуляции света используют два электрически управляемых эффекта, наблюдающихся в ЖК: наведенное двулучепреломление и динамическое рассеяние. Процесс изменения оптических свойств слоя ЖК носит пороговый характер, что также является достоинством ЖК.
УТ на основе ЖК, использующее эффект динамического рассеяния, применяют для амплитудной модуляции как проходящего, так и отраженного светового пучка. Эффект динамического рассеивания заключается в следующем. В невозбужденном состоянии слой ЖК совершенно прозрачен. При создании электрического поля в ЖК происходят два процесса: 1) под действием электрического поля молекулы ориентируются параллельно либо перпендикулярно полю в зависимости от того, имеет ли ЖК положительную или отрицательную «диэлектрическую анизотропию»; 2) поток зарядов через слой ЖК нарушает ориентацию молекул, в результате чего возникает турбулентность, что, в свою очередь, вызывает рассеяние света вследствие пространственного изменения коэффициента преломления. При этом происходит сильное ослабление интенсивности светового пучка в направлении его распространения, а также потеря его когерентности. По окончании действия электрического поля слой ЖК вновь приобретает исходную структуру и становится прозрачным. Длительность этого процесса измеряется миллисекундами. Если требуемое время экспонирования регистрирующей среды составляет доли миллисекунд, то достаточно естественной памяти ЖК-слоя. В противном случае каждый элемент жидкокристаллического УТ должен быть снабжен интегральной управляющей схемой с памятью.
Оптически управляемые транспаранты (ОУТ). Характерной особенностью ОУТ является возможность параллельного преобразования страницы данных. В связи с этим требования к времени хранения оптического состояния значительно снижаются. При работе в отраженном свете между DKDP-фотопроводником помещается диэлектрическое зеркало, позволяющее значительно уменьшить влияние считывающего пучка на возбуждение фотопроводника и благодаря этому увеличить яркость оптических сигналов. Для стирания записанного изображения полярность приложенного напряжения изменяют, в результате чего и фотопроводник освещается ультрафиолетовым или синим светом. Для записи информации транспарант освещается модулированным световым пучком с одновременной подачей постоянного напряжения. Генерируемые в полупроводнике носители заряда дрейфуют к границе кристалла с диэлектриком, где захватываются ловушками. Создаваемый носителями пространственный заряд компенсирует заряд на электродах. Следовательно, электрическое поле внутри проводника, наведенное полем двулучепреломления кристалла, благодаря эффекту Поккельса приводит к фазовой или амплитудной (при наличии поляроидов) модуляции считывающего светового пучка, в качестве которого может быть использовано излучение полупроводникового лазера. Считывание можно выполнять и с помощью видимого света, к которому кристалл в 103 – 104 более чувствителен, чем к излучению полупроводниковых лазеров. Если изменить полярность приложенного при считывании постоянного напряжения, то можно получить негативное изображение. При закороченных электродах наблюдается позитивное изображение, так как изменение двулучепреломления происходит в результате образования пространственных зарядов. Для стирания записанного изображения необходимо снизить до нуля напряжение и осветить кристалл ультрафиолетовым или синим светом.
1.4 Голография
Голография — это научно-техническое направление в оптике и в смежных с нею областях, в том числе и в вычислительной технике, основанное на специальных методах записи и восстановления волновых фронтов. Изображение объекта регистрируется в виде интерференционной картины, которая получается при наложении двух когерентных волн. Одна из волн является опорной, другая — предметной. Предметная волна, полученная в результате фазовой и амплитудной модуляции, содержит информацию о предмете, на котором она дифрагировала (рассеялась). При воспроизведении изображения голограмму (интерферограмму) освещают восстанавливающей волной. Восстанавливающая волна обычно совпадает с опорной волной,, используемой при записи. В результате дифракции опорной волны на голограмме образуется волна, совпадающая с предметной при записи, а следовательно, восстанавливается изображение исходного предмета.
Слово «голография» происходит от греческого слова holos — полный, весь. Голография дает полную информацию о предметной волне как амплитудной, так и фазовой. Голография была предложена в 1947 г. английским физиком Деннисом Габором. В дальнейшем она пережила второе рождение благодаря фундаментальным исследованиям советского физика Ю. Н. Денисюка и американских ученых Э. Лейта и Д. Упатниекса. Голограммы в зависимости от материала, на котором они записаны, могут модулировать не только амплитуду, но и фазу за счет изменения рельефа поверхности или показателя преломления регистрирующей среды. В связи с этим различают амплитудные (поглощающие), рельефно-фазовые и объемные фазовые голограммы.
2.MathCAD И ВИРТУАЛЬНЫЕ ЭЛЕМЕНТЫ
Mathcad — система компьютерной алгебры из класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов с вычислениями и визуальным сопровождением, отличается легкостью использования и применения для коллективной работы. Mathcad был задуман и первоначально написан Алленом Раздовом из Массачусетского технологического института (MIT), соучредителем компании Mathsoft, которая с 2006 года является частью корпорации PTC (Parametric Technology Corporation). Mathcad имеет простой и интуитивный для использования интерфейс пользователя. Для ввода формул и данных можно использовать как клавиатуру, так и специальные панели инструментов. Некоторые из математических возможностей Mathcad (версии до 13.1 включительно) основаны на подмножестве системы компьютерной алгебры Maple (MKM, Maple Kernel Mathsoft). Начиная с 14 версии — использует символьное ядро MuPAD. Работа осуществляется в пределах рабочего листа, на котором уравнения и выражения отображаются графически, в противовес текстовой записи в языках программирования. При создании документов-приложений используется принцип WYSIWYG (What You See Is What You Get — «что видишь, то и получаешь»).
Несмотря на то, что эта программа в основном ориентирована на пользователей-непрограммистов, Mathcad также используется в сложных проектах, чтобы визуализировать результаты математического моделирования, путем использования распределённых вычислений и традиционных языков программирования. Также Mathcad часто используется в крупных инженерных проектах, где большое значение имеет трассируемость и соответствие стандартам. Mathcad достаточно удобно использовать для обучения, вычислений и инженерных расчетов . Открытая архитектура приложения в сочетании с поддержкой технологий .NET и XML позволяют легко интегрировать Mathcad практически в любые ИТ-структуры и инженерные приложения. Есть возможность создания электронных книг (e-Book). Количество пользователей в мире — около 1.8 млн.
Основные возможности: Mathcad содержит сотни операторов и встроенных функций для решения различных технических задач. Программа позволяет выполнять численные и символьные вычисления, производить операции с скалярными величинами, векторами и матрицами, автоматически переводить одни единицы измерения в другие. Среди возможностей Mathcad можно выделить:
- Решение дифференциальных уравнений, в том числе и численными методами
- Построение двумерных и трёхмерных графиков функций (в разных системах координат, контурные, векторные и т. д.)
- Использование греческого алфавита как в уравнениях, так и в тексте
- Выполнение вычислений в символьном режиме
- Выполнение операций с векторами и матрицами
- Символьное решение систем уравнений
- Аппроксимация кривых
- Выполнение подпрограмм
- Поиск корней многочленов и функций
- Проведение статистических расчётов и работа с распределением вероятностей
- Поиск собственных чисел и векторов
- Вычисления с единицами измерения
- Интеграция с САПР системами, использование результатов вычислений в качестве управляющих параметров
С помощью Mathcad инженеры могут документировать все вычисления в процессе их проведения.
Интерфейс: Основное отличие Mathcad от аналогичных программ — это графический, а не текстовый режим ввода выражений. Для набора команд, функций, формул можно использовать как клавиатуру, так и кнопки на многочисленных специальных панелях инструментов. В любом случае — формулы будут иметь привычный, аналогичный книжному, вид. То есть особой подготовки для набора формул не нужно. Вычисления с введенными формулами осуществляются по желанию пользователя или мгновенно, одновременно с набором, либо по команде. Обычные формулы вычисляются слева направо и сверху вниз (подобно чтению текста). Любые переменные, формулы, параметры можно изменять, наблюдая воочию соответствующие изменения результата. Это дает возможность организации действительности интерактивных вычислительных документов. В других программах (Maple, MuPAD, Mathematica) вычисления осуществляются в режиме программного интерпретатора, который трансформирует в формулы введенные в виде текста команды. Maple своим интерфейсом ориентирован на тех пользователей, кто уже имеет навыки программирования в среде традиционных языков с введением сложных формул в текстовом режиме. Для пользования Mathcad можно вообще не быть знакомым с программированием в том или ином виде. Mathcad задумывался как средство программирования без программирования, но, если возникает такая потребность — Mathcad имеет довольно простые для усвоения инструменты программирования, позволяющие, впрочем, строить весьма сложные алгоритмы, к чему прибегают, когда встроенных средств решения задачи не хватает, а также когда необходимо выполнять серийные расчеты. Отдельно следует отметить возможность использования в расчетах Mathcad величин с размерностями, причем можно выбрать систему единиц: СИ, СГС, МКС, английскую или построить собственную. Результаты вычислений, разумеется, также получают соответствующую размерность. Польза от такой возможности трудно переоценить, поскольку значительно упрощается отслеживание ошибок в расчетах, особенно в физических и инженерных.
Графика: В среде Mathcad фактически нет графиков функций в математическом понимании термина, а есть визуализация данных, находящихся в векторах и матрицах (то есть осуществляется построение как линий так и поверхностей по точкам с интерполяцией), хотя пользователь может об этом и не знать, поскольку у него есть возможность использования непосредственно функций одной или двух переменных для построения графиков или поверхностей соответственно. Так или иначе, механизм визуализации Mathcad значительно уступает таковому у Maple, где достаточно иметь только вид функции, чтобы построить график или поверхность любого уровня сложности. По сравнению с Maple, графика Mathcad имеет еще такие недостатки, как: невозможность построения поверхностей в непрямоугольные области существования двух аргументов, создание и форматирование графиков только через меню, что ограничивает возможности программного управления параметрами графики. Однако следует помнить об основной области применения Mathcad — для задач инженерного характера и создание учебных интерактивных документов, возможностей визуализации вполне достаточно. Опытные пользователи Mathcad демонстрируют возможность визуализации сложнейших математических конструкций, но объективно это уже выходит за рамки назначения пакета.
2.1 Элементы MathCAD
К основным элементам м MathCAD относятся операторы, константы, переменные, массивы и функции.
Операторы -- элементы MathCAD, с помощью которых можно создавать математические выражения. К ним, например, относятся символы арифметических операций, знаки вычисления сумм, произведений, производной, интеграла и т.д.
Оператор определяет:
а) действие, которое должно выполняться при наличии тех или иных значений операндов;
б) сколько, где и какие операнды должны быть введены в оператор.
Операнд - число или выражение, на которое действует оператор. Например, в выражении 5!+3 числа 5! и 3 -- операнды оператора «+» (плюс), а число 5 - операнд факториала (!).
Любой оператор в MathCAD можно ввести двумя способами:
· нажав клавишу (сочетание клавиш) на клавиатуре;
· используя математическую панель.
Для присвоения или вывода содержимого ячейки памяти, связанной с переменной, используются следующие операторы:
-- знак присвоения (вводится нажатием клавиши : на клавиатуре (двоеточие в английской раскладке клавиатуры) или нажатием соответствующей кнопки на панели Калькулятор);
Такое присвоение называется локальным. До этого присваивания переменная не определена и ее нельзя использовать.
-- глобальный оператор присвоения. Это присвоение может производиться в любом месте документа. К примеру, если переменной присвоено таким образом значение в самом конце документа, то она будет иметь это же значение и в начале документа.
-- оператор приближенного равенства (x1). Используется при решении систем уравнений.
Вводится нажатием клавиши; на клавиатуре (точка с запятой в английской раскладке клавиатуры) или нажатием соответствующей кнопки на Булевой панели.
= -- оператор (простое равно), отведенный для вывода значения константы или переменной. Простейшие вычисления осуществляется при помощи:
Панели Калькулятора, Панели Исчислений и Панели Оценки.
Внимание. Если необходимо поделить все выражение в числителе, то его нужно первоначально выделить, нажав пробел на клавиатуре или поместив в скобки.
Константы -- поименованные объекты, хранящие некоторые значения, которые не могут быть изменены. Например, = 3.14. Размерные константы -- это общепринятые единицы измерения. Например, метры, секунды и т.д. Чтобы записать размерную константу, необходимо после числа ввести знак * (умножить), выбрать пункт меню Вставка подпункт Юнит. В измерениях наиболее известные вам категории: Length -- длина (м, км, см); Mass -- вес (гр, кг, т); Time -- время (мин, сек, час).
Переменные являются поименованными объектами, имеющими некоторое значение, которое может изменяться по ходу выполнения программы. Переменные могут быть числовыми, строковыми, символьными и т.д. Значения переменным задаются с помощью знака присвоить (: =). Внимание. MathCAD прописные и строчные буквы воспринимает как разные идентификаторы. Системные переменные, в MathCAD содержится небольшая группа особых объектов, которые нельзя отнести ни к классу констант, ни к классу переменных, значения которых определены сразу после запуска программы. Их правильнее считать системными переменными. Это, например, TOL [0.001]- погрешность числовых расчетов, ORIGIN [0] -- нижняя граница значения индекса индексации векторов, матриц и др. Значения этим переменным при необходимости можно задать другие.
Эти переменные имеют ряд фиксированных значений, либо целочисленных, либо изменяющихся с определенным шагом от начального значения до конечного.
Для создания ранжированной переменной используется выражение:
Name =Nbegin,(Nbegin+Step)..Nend, где Name -- имя переменной;
Nbegin -- начальное значение;
Step -- заданный шаг изменения переменной;
Nend -- конечное значение.
Ранжированные переменные широко применяются при построении графиков. Например, для построения графика некоторой функции f(x) прежде всего необходимо создать ряд значений переменной x -- для этого она должна быть ранжированной переменной.
Внимание. Если в диапазоне изменения переменной не указывать шаг, то программа автоматически примет его равным 1.
Пример. Переменная x изменяется в диапазоне от -16 до +16 с шагом 0.1
Чтобы записать ранжированную переменную, нужно ввести:
- имя переменной (x);
- знак присвоения (:=)
- первое значение диапазона (-16);
- запятую;
- второе значение диапазона, которое является суммой первого значения и шага (-16+0.1);
- многоточие (..) -- изменение переменной в заданных пределах (многоточие вводится нажатием точки с запятой в английской раскладке клавиатуры);
- последнее значение диапазона (16).
В результате у вас получится: x := -16,-16+0.1..16.
Любое выражение с ранжированными переменными после знака равенства инициирует таблицу вывода.
В таблицы вывода можно и вставлять числовые значения и корректировать их.
Переменная с индексом
Переменная с индексом -- это переменная, которой присвоен набор не связанных друг с другом чисел, каждое из которых имеет свой номер (индекс).
Ввод индекса осуществляется нажатием левой квадратной скобки на клавиатуре или при помощи кнопки xn на панели Калькулятор.
В качестве индекса можно использовать как константу, так и выражение. Для инициализации переменной с индексом необходимо ввести элементы массива, разделяя их запятыми.
Пример. Ввод индексных переменных.
i:= 0..2 -- индекс изменяется от 0 до 2 (индексная переменная будет содержать 3 элемента).
-- ввод числовых значений в таблицу производится через запятую;
-- вывод значения первого элемента вектора S;
-- вывод значения нулевого элемента вектора S.
Массив -- имеющая уникальное имя совокупность конечного числа числовых или символьных элементов, упорядоченных некоторым образом и имеющих определенные адреса. В пакете MathCAD используются массивы двух наиболее распространенных типов:
одномерные (векторы);
двухмерные (матрицы).
Вывести шаблон матрицы или вектора можно одним из способов:
выбрать пункт меню Вставка - Матрица;
нажать комбинацию клавиш Ctrl + M;
нажать кнопку на Панели векторов и матриц.
В результате появится диалоговое окно, в котором задается необходимое число строк и столбцов:
Rows - число строк
Columns - число столбцов
Если матрице (вектору) нужно присвоить имя, то вначале вводится имя матрицы (вектора), затем -- оператор присвоения и после -- шаблон матрицы.
Например:Матрица -- двухмерный массив с именем Мn,m, состоящий из n строк и m столбцов.С матрицами можно выполнять различные математические операции.
Функция -- выражение, согласно которому производятся некоторые вычисления с аргументами и определяется его числовое значение. Примеры функций: sin(x), tan(x) и др.
Функции в пакете MathCAD могут быть как встроенными, так и определенными пользователем. Способы вставки встроенной функции: Выбрать пункт меню Вставка - Функция. Нажать комбинацию клавиш Ctrl + E. Щелкнуть по кнопке на панели инструментов. Набрать имя функции на клавиатуре. Функции пользователя обычно используются при многократных вычислениях одного и того же выражения. Для того чтобы задать функцию пользователя необходимо:
· ввести имя функции с обязательным указанием в скобках аргумента, например, f(x);
· ввести оператор присвоения (:=);
· ввести вычисляемое выражение.
Пример. f(z) := sin(2z2)
2.2 Документы MathCAD
Документом MathCAD называют описание математического алгоритма решения задачи с текстовыми комментариями и результатами вычислений в форме символов, чисел, таблиц или графиков. В документе MathCAD вместе с программой выводятся результаты расчета. Как программа, так и результаты расчета могут сопровождаться комментариями программиста. Комментарии не являются обязательной частью документа, но отсутствие их усложняет работу с документом, особенно, если в работе с документом был значительный перерыв. Забываются, какими символами описываются переменные, сам алгоритм вычисления функций, те или иные оригинальные приемы в отдельных фрагментах программы. Особенно актуальны комментарии, если пользователь, которым является студент, решает несколько задач по разным предметам.
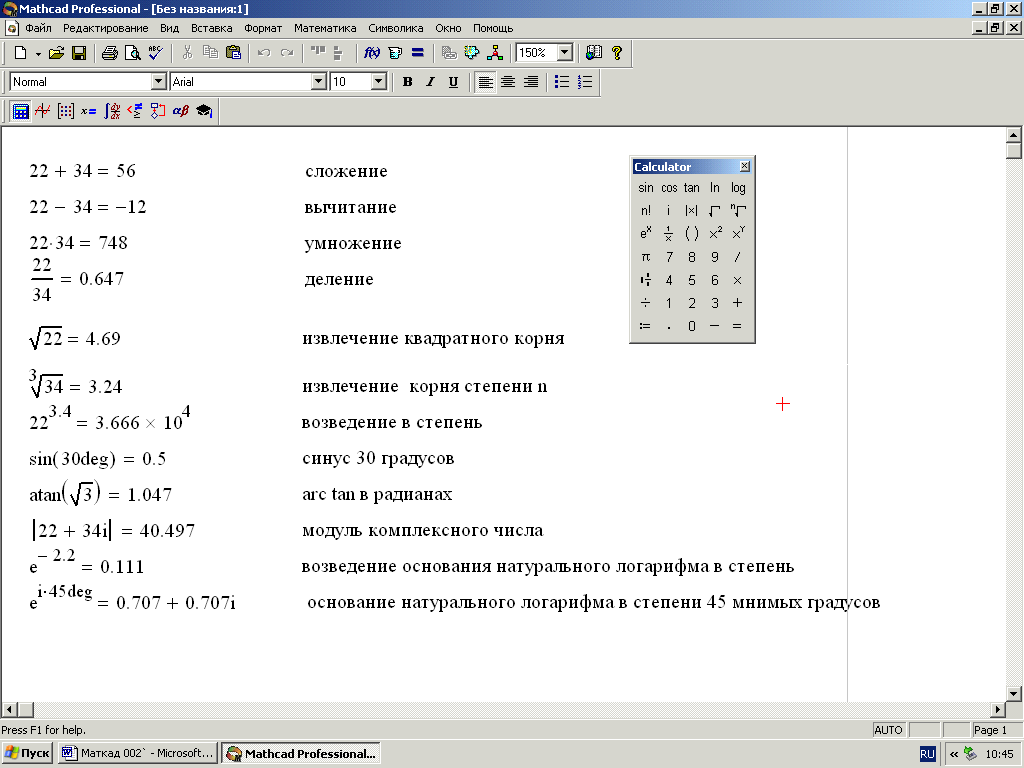
Язык программирования MathCAD практически не отличается от обычного языка математических статей, отчетов и книг. Это делает понятными документы MathCAD даже школьнику старших классов и студенту младших курсов вузов. На рис. 1 приведены примеры задания вычислений и действий с числами. Следует иметь в виду, что вычисления в системе MathCAD выполняются только на английской клавиатуре. Операции с числами можно задавать через меню Calculator или через клавиатуру. Деление через клавиатуру выполняется клавишей / , квадратный корень – клавишей \ , возведение в степень – клавишей 6 с одновременным нажатием клавиши Shift.
Рис. 2. Примеры действий с простыми и комплексными числами
Привычная запись программируемых выражений избавляет студента от изучения языков программирования как высокого, так и низкого уровня. Подавляющее большинство решаемых задач требуют лишь корректной записи используемых формул.
Однако использование системы MathCAD в виде, приведенном на рис. 2 – это, если грубо сравнивать, все равно, что забивать гвозди компьютером. Можно, но не рационально. Система MathCAD предназначена для решения очень сложных задач с применением формул и уравнений, записанных в буквенном виде. Для этого разработан математически ориентированный входной язык общения. Большинство операторов и функций входного языка общепринятые в математике. Будем стараться придерживаться обозначений физических величин и констант, принятых в электротехнике и электроэнергетике. Это позволит не вводить некоторые комментарии к выполняемым вычислениям.
Алфавит входного языка обширен и позволяет использовать латинскую, русскую и греческую азбуки, арабские цифры, общепринятые константы, математические операторы, встроенные функции.
Началом документа MathCAD рекомендуем указать название задачи, ее цель, используемые методы расчета. Далее следует описать переменные, используемые в математических выражениях, применяемых при вычислениях. Переменные имеют имена, принадлежащие только им. Имена переменных, констант, других объектов называются идентификаторами. Например, при вычислении выражения с = a + b идентификаторами являются a, b и с. Что подразумевается под идентификаторами, зависит от программиста. Переменные могут быть числами, результатом предыдущих вычислений, константами, функциями переменных. Например, а = 4, b = sin(x), где х в свою очередь переменная.
Идентификаторы могут иметь любую длину, но без пробелов и обязательно начинаться с буквы любого алфавита. Желательно избегать русской азбуки, потому что в используемых версиях системы MathCAD после повторного вызова документа русские буквы иногда заменяются на нечитаемые символы. Программа работать будет, но трудно воспринимается. А если программа длинная, понять результаты ее работы практически невозможно. Примеры идентификаторов, используемых в энергетике: S, u, control, U_I, Потери_напряжения, U.
Чтобы работать с переменными, необходимо задать их значения. Эта операция называется присваиванием. Основным знаком присваивания является составной :=, который можно получить вызвав меню Calculator или Evaluation или через клавиатуру одновременным нажатием клавиши Shift и двоеточия. Такое присваивание называется локальным. Следует отметить, что знак присваивания в системе MathCAD можно получить только с латинской клавиатурой. Например, вычисление с = a + b осуществляется сначала через присваивание переменных a, и b, а затем через вычисление с.
Вычисления выполняются слева направо и сверху вниз. Если третье присваивание окажется выше второго или первого, вычисления не произойдет. Однако иногда требуется получить зависимость результата от каких-либо параметров, находящихся в самом начале вычислений. Если присваивание переменной и результат вычислений не помещаются в окно монитора, очень неудобно следить за изменением результата при изменении значения переменной. Для этой цели в системе MathCAD имеется оператор глобального присваивания (три горизонтальных черточки). Переменная с этим оператором может описываться в любом месте программы. Например, предыдущее вычисление можно выполнить как
Знак глобального присваивания можно получить, вызвав меню Evaluation.
3.ВЫЧИСЛЕНИЯ НА ПРОГРАММЕ Mathcad
Для начала работы с программой MathCAD необходимо установить ее на свой компьютер, после чего запускаем из меню в пуске.
В открывшемся окне на чистом листе бумаги мы собственно и будем делать все наши лабораторные работы.
3.1 Ввод формул
Формулы — основные объекты рабочего листа. Новый объект по умолчанию является формулой. Чтобы начать ввод формулы, надо установить крестообразный курсор в нужное место и начать ввод букв, цифр, знаков операций. При этом создается область формулы, в которой появляется уголковый курсор, охватывающий текущий элемент формулы, например имя переменной (функции) или число. При вводе бинарного оператора по другую сторону знака операции автоматически появляется заполнитель в виде черного прямоугольника. В это место вводят очередной операнд. Для управления порядком операций используют скобки, которые можно вводить вручную. Уголковый курсор позволяет автоматизировать такие действия. Чтобы выделить элементы формулы, которые в рамках операции должны рассматриваться как единое целое, используют клавишу ПРОБЕЛ. При каждом ее нажатии уголковый курсор «расширяется», охватывая элементы формулы, примыкающие к данному. После ввода знака операции элементы в пределах уголкового курсора автоматически заключаются в скобки. Элементы формул можно вводить с клавиатуры или с помощью специальных панелей управления. Панели управления (рис. 1) открывают с помощью меню View (Вид) или кнопками панели управления Math (Математика).
Для ввода элементов формул предназначены следующие панели:
- панель управления Arithmetic (Счет) для ввода чисел, знаков типичных математических операций и наиболее часто употребляемых стандартных функций;
- панель управления Evaluation (Вычисление) для ввода операторов вычисления и знаков логических операций;
- панель управления Graph (График) для построения графиков;
- панель управления Matrix (Матрица) для ввода векторов и матриц и задания матричных операций;
- панель управления Calculus (Исчисление) для задания операций, относящихся к математическому анализу;
- панель управления Greek (Греческий алфавит) для ввода греческих букв (их можно также вводить с клавиатуры, если сразу после ввода соответствующего латинского символа нажимать сочетание клавиш CTRL+G, например [a][CTRL+G] — , [W][CTRL+G]-);
- панель управления Symbolic (Аналитические вычисления) для управления аналитическими преобразованиями.
Введенное выражение обычно вычисляют или присваивают переменной. Для вывода результата выражения используют знак вычисления, который выглядит как знак равенства и вводится при помощи кнопки Evaluate Expression (Вычислить выражение) на панели инструментов Evaluation (Вычисление).

Рис. 5. Панели инструментов программы Маthcad для ввода формул.
Знак присваивания изображается как «:=», а вводится при помощи кнопки Assign Value (Присвоить значение) на панели инструментов Evaluation (Вычисление). Слева от знака присваивания указывают имя переменной. Оно может содержать латинские и греческие буквы, цифры, символы «»,«_» и «», а также описательный индекс. Описательный индекс вводится с помощью символа «.» и изображается как нижний индекс, но является частью имени переменной, например Vinit. «Настоящие» индексы, определяющие отдельный элемент вектора или матрицы, задаются по-другому. Переменную, которой присвоено значение, можно использовать далее в документе в вычисляемых выражениях. Чтобы узнать значение переменной, следует использовать оператор вычисления.
3.2Функции для вычислений
Произвольные зависимости между входными и выходными параметрами задаются при помощи функций. Функции принимают набор параметров и возвращают значение, скалярное или векторное (матричное). В формулах можно использовать стандартные встроенные функции, а также функции, определенные пользователем.
Пользовательские функции должны быть сначала определены. Определение задается при помощи оператора присваивания. В левой части указывается имя пользовательской функции и, в скобках, формальные параметры — переменные, от которых она зависит. Справа от знака присваивания эти переменные должны использоваться в выражении. При использовании пользовательской функции в последующих формулах ее имя вводят вручную. В диалоговом окне Insert Function (Вставка функции) оно не отображается. Основные обозначения функций:
Тригонометрические и обратные функции:
- sin(z), cos(z), tan(z), asin(z), acos(z), atan(z)
- z - угол в радианах
Гиперболические и обратные функции:
- sinh(z), cosh(z), tanh(z), asinh(z), acosh(z), atanh(z)
Экспоненциальные и логарифмические:
- exp(z) - ez
- ln(z) - натуральный логарифм
- log(z) - десятичный логарифм
- Cтатистические функции:
- mean(x) - среднее значение
- var(x) - дисперсия
- stdev(x) - среднеквадратическое отклонение
- cnorm(x)- функция нормального рапределения
- erf(x) - функция ошибки
- Г(x) - гамма-функция Эйлера
Функции Бесселя:
- J0(x), J1(x), Jn(n,x) - функции Бесселя первого порядка
- Y0(x), Y1(x), Yn(n,x) - функции Бесселя второго порядка
Функции комплексного переменного:
- Re(z) - вещественная часть комплексного числа
- Im(z) - мнимая часть комплексного числа
- arg(z) - аргумент комплексного числа
Преобразование Фурье:
- U:=fft(V) - прямое преобразование (V- вещественное)
- V:=ifft(U) - обратное преобразование (V- вещественное)
- U:=cfft(V) - прямое преобразование (V- комплексное)
- V:=icfft(U) - обратное преобразование (V- комплексное)
Корреляционная функция - позволяет рассчитывать коэффициент корреляции двух векторов vx и vy и определить уравнение линейной регрессии:
- corr(vx,vy) - коэффициент корреляции
- slope(vx,vy) - коэффициент наклона линии регрессии
- intercept(vx,vy) - начальная координата линии регрессии
Линейная интерполяция:
- linterp(vx,vy,x)
- vx,vy- векторы значений аргумента и функций. x- значение аргумента, для которого проводится интерполяция
Функция для определения корней алгебраических и трансцендентных уравнений:
- root(уравнения, переменная) - значение переменной, когда уравнение равно нулю
Датчик случайных чисел:
- rnd(x) - случайное число с равномерным распределением от 0 до x
- Целая часть переменной:
- floor(x)- ближайшее наименьшее целое число
- ceil(x)- ближайшее наибольшее целое число
Выделение остатка:
- mod(x,y)- остаток от деления x на y
Остановка итерации:
Функция условного перехода:
- if(условие,x,y) - если условие выполняется, то функция равняется x, иначе y
Единичная функция (функция Хевисайда):
- Ф(x) - если x>0. То функция равна 1, иначе 0
ЗАКЛЮЧЕНИЕ
В ходе дипломной работы мы с моим руководителем сделали 7 лабораторных работ по дисциплине «Оптические методы и устройства обработки информации». Где студенты будут изучать линзы как элемент выполняющие преобразования фурье, оптические транспаранты (амплитудный и фазовый), оптическую фильтрацию пространственных сигналов, оптическое преобразование Меллина, коррелятор Ван Дер Люгта и повторят опыт Аббе-Портера.
ЛИТЕРАТУРА
1. А. Л. Дмитриев Оптические методы обработки информации –Учебное пособие.
СПб: СПбГУИТМО 2005.
2. В. С. Днепровский Оптическая бистабильность и проблема создания оптического транзистора – МГУ 1999.
3. Kenichi Iga, Yasuo Kokubum Encyclopedic Handbook of Integra Optics 2006.
4. В. В. Богатырева , А. Л. Дмитриев Оптические методы обработки информации –Учебное пособие.СПб: СПбГУИТМО 2009.
5. Королюк Ю.Ф., Клименко Д.В. MATHCAD - Учебное пособие Якутск 2007.
6.А.А.Акаев, С.А.Майоров Оптические методы обработки информации М.:1988
7.Дж.Гудмен Введение в Фурье-оптику - М.:Мир 1970
8.http://www.exponenta.ru/soft/Mathcad/Mathcad.asp – руководство по программе MathCAD.
9. А. Папулис Теория систем и преобразований в оптике - изд. «Мир», М., 1971 г.
10. Н. Евтихеев Информационная оптика - изд. МЭИ, М., 2000 г.
ПРИЛОЖЕНИЕ
Лабораторная работа № 1
Линзы как элемент, выполняющие преобразование Фурье.
Свойства преобразование Фурье.
Цель работы: изучение свойств линзы, изучение свойства преобразования Фурье.
Свойства линзы
Значительная часть оптической обработки информации основана на свойстве преобразования Фурье. Уникальность тонкой положительной линзы заключается в выполнении преобразования Фурье: в когерентном свете распределение амплитуды излучения в задней фокальной плоскости линзы может быть представлено как двумерное комплексное преобразование Фурье от функции распределения амплитуды света в передней фокальной плоскости линзы. Основные геометрические соотношения при действии тонкой положительной линзы показаны на Рис. 1. Дифракционный интеграл, описывающий взаимосвязь распределений поля во входной и выходной плоскостях такой системы имеет вид: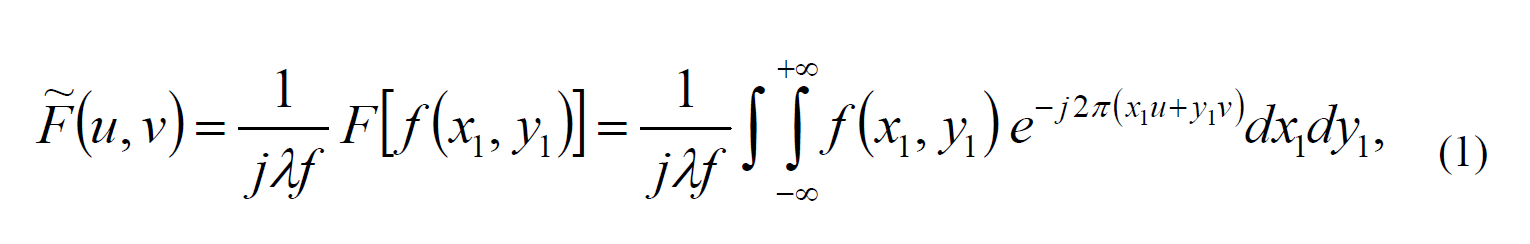
Где u = /f , v = /f ; - длина волны света, f – фокусное расстояние линзы;
f() - комплексная амплитуда световой волны в передней (входной) фокальной плоскости , F(u,v) - комплексная амплитуда световой волны в задней (выходной, спектральной) фокальной плоскости .
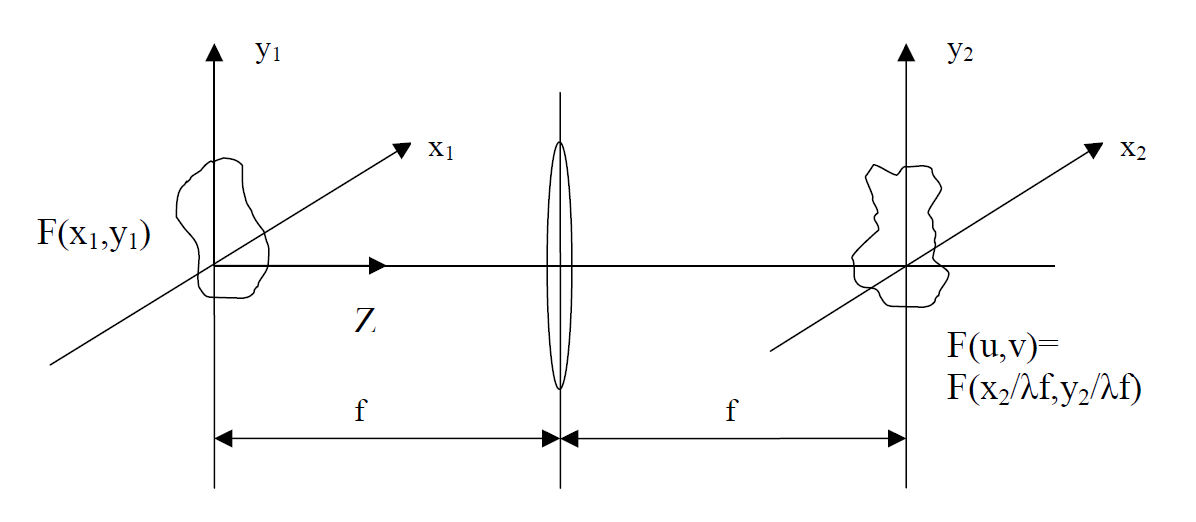
Рис 1. Преобразование оптического сигнала тонкой положительной линзой
Свойства преобразования Фурье
Математически преобразование Фурье является частным случаем интегрального преобразования Фредгольма с ядром в виде экспоненты с мнимым, линейным по аргументу, показателем. Преобразование Фурье в оптике «реализуется» с помощью аналогового устройства – положительной линзы, и основные свойства этого преобразования могут быть наглядно демонстрированы при рассмотрении прохождения световых волн через оптическую систему, содержащую линзы, диафрагмы, оптические транспаранты и др.
Различают прямое (2) и обратное (3) преобразования Фурье
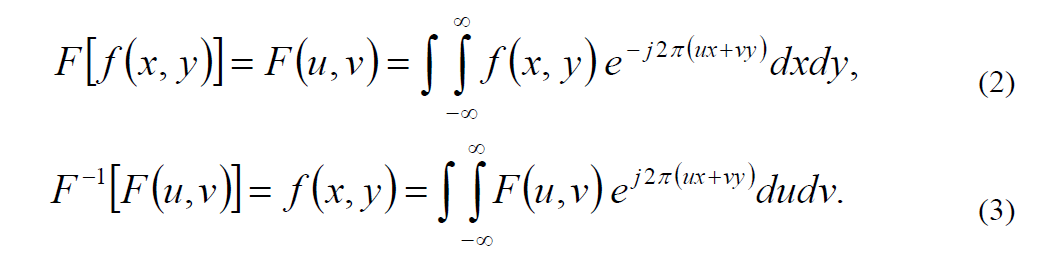
- Линейность - означает, что через одну линзу, осуществляющую преобразование Фу-
рье, одновременно может проходить множество световых сигналов.
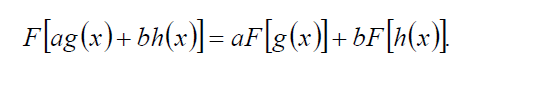
- Подобие - изменение масштаба изображения на входе системы приводит к сжатию либо
растяжению области его пространственного спектра.
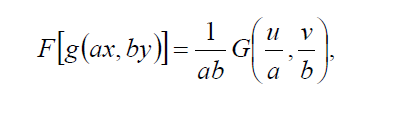
- Смещение - сдвиг изображения вызывает изменение фазы спектральной функции, но сохраняет неизменной ее амплитуду.
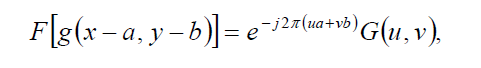
- Производная
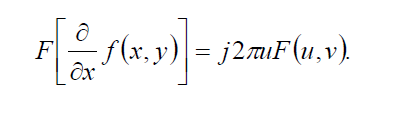
Задание: В программе MathCAD освоить прямое и обратно преобразование Фурье и его свойства. В программе paintbrush создать рисунок размером 80х80 пикселей, фон черный, нарисовать белый круг радиусом примерно 50 пикселей. Сохранить в виде файла с именем krug.bmp – в формате BMP. В программе paintbrush создать рисунок размером 80х80 пикселей, фон черный, нарисовать треугольник высотой примерно 50 пикселей.
- Для изучения свойств линейности
- сосчитать в двумерные массивы A и B рисунки.
- совершить Фурье преобразование над каждым из них.
- просуммировать результирующие массивы в массив D
- совершить преобразование Фурье над массивом C и сохранить в массиве E
- сравнить массивы D и E
- Проверить следующие свойства двумерного преобразования Фурье: подобие, смещение, производную.
Контрольные вопросы:
- Как изменяется спектр сигнала при его уменьшении масштаба сигнала?
- Как в программе MathCAD производить преобразование Фурье?
- Как в программе MathCAD происходить двумерное преобразование Фурье?
Литература:
- Оптические методы обработки информации. А.Л. Дмитриев. Учебное пособие. СПб. СПюГУИТМО 2005. 46 с.
- А.А.Акаев, С.А.Майоров «Оптические методы обработки информации» М.:1988
- Дж.Гудмен «Введение в Фурье-оптику» М.:Мир 1970
Лабораторная работа № 2
Оптический транспарант. Амплитудный транспарант.
Цель работы: изучение оптических транспарантов. Изучение амплитудного транспаранта.
Оптический транспарант
Оптическим транспарантом (ОТ) называется оптическое устройство (например, диапозитив, диафрагма, поляроид, фазовая пластинка и т. п.), устанавливаемое на пути пучка света и выполняющее заданное преобразование амплитуды и фазы световой волны. Действие ОТ характеризуется комплексной функцией пропускания t(x, y) , при этом
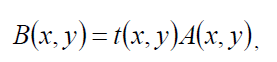
Где A(x,y) распределение амплитуды светового поля перед транспарантом и B(x,y) после транспаранта
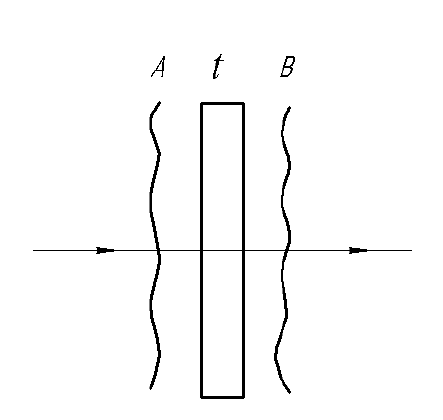
Рис.1 Действие оптического транспаранта; показаны поверхности постоянной фазы падающей и прошедшей световых волн.
Различают амплитудные (например, щели, сетки, диафрагмы), фазовые (призмы, линзы) и амплитудно-фазовые (светофильтры, голограммы, линзы с амплитудной маской) оптические транспаранты. Тонкая положительная линза может рассматриваться как чисто-фазовый транспарант с функцией пропускания t (x, y) вида
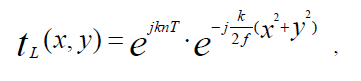
где T - толщина линзы, n - средний показатель преломления материала линзы, f - фокусное расстояние линзы, x, y - координаты в плоскости сечения линзы, k = 2 / - волновое число. Вследствие квадратичного фазового преобразования волнового фронта вида, положительная линза преобразует плоский волновой фронт световой волны в сходящийся сферический (Рис.2)
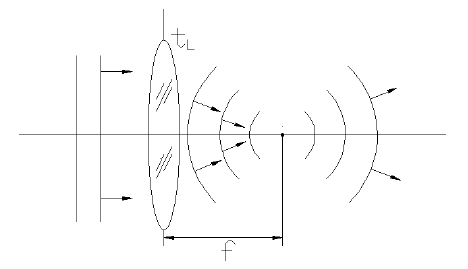
Рис.2 Преобразование плоского волнового фронта собирающей линзой с фокусным расстоянием f .
Различают неуправляемые (с постоянными оптическими характеристиками) и управляемые внешним сигналом (с изменяющимися характеристиками) оптические транспаранты. В зависимости от способа внешнего управления, управляемые транспаранты подразделяются на электрически (ЭУТ) и оптически (ОУТ) управляемые транспаранты. Такие ЭУТ и ОУТ применяются для ввода информации в оптический процессор и в качестве управляемых пространственных фильтров, устанавливаемых в разных (спектральной, входной или выходной) областях оптического процессора.
Задание: изучить свойства щели, сетки и диафрагмы. В программе paintbrush нарисовать амплитудные транспаранты в виде вертикальной щели, сетки и диафрагмы. Фон черный, свет фигур белый, так как черный цвет имеет код 0, а белый код 255 или 1, в зависимости от типа файла. Сохранить в восьмибитовом цвете в формате BMP. Разрешение рисунка 80х80 пикселей. Создать также рисунок для исходного сигнала азрешением 80х80 пикселей

а)щель б)сетка в)диафрагма
Контрольные вопросы:
- Как измениться спектр сигнала при установки вертикальной щели?
- Как измениться спектр сигнала при установки диафрагмы?
- Как зависит окончательный сигнал при изменении размера диафрагмы?
Литература:
- Оптические методы обработки информации. А.Л. Дмитриев. Учебное пособие. СПб. СПюГУИТМО 2005. 46 с.
- А.А.Акаев, С.А.Майоров «Оптические методы обработки информации» М.:1988
- Дж.Гудмен «Введение в Фурье-оптику» М.:Мир 1970
Лабораторная работа № 3
Фазовый транспарант.
Цель работы: изучение оптических транспарантов. Изучение фазового транспаранта и фазового контраста.
Фазовый контраст
Наибольшее практическое применение в микроскопии биологических объектов имеет фазовый контраст, идея которого была предложена Цернике. Сущность фазового контраста состоит в использовании фазового пространственного фильтра, установленного в спектральной области оптической системы объектива микроскопа. Такой фильтр характеризуется амплитудным пропусканием вида

и может быть выполнен, например, в виде диэлектрической пластинки с оптической длиной пути («толщиной»), кратной нечетному числу / 4 , установленной строго в центре (в области нулевых пространственных частот) фокальной плоскости объектива микроскопа. На практике конструкция пространственного фильтра нередко содержит кольцевую фазовую пластинку, расположенную вне оптической оси. В обоих случаях назначение пространственного фильтра – ввести искусственный сдвиг фазы величиной / 2 между волнами, соответствующими пространственным частотам нулевого и остальных порядков дифракции. В результате мощность излучения в выходной плоскости изобразительной системы микроскопа зависит от фазы предметной волны, определяемой структурой прозрачного объекта – неоднородным распределением плотности его материала. Представляя предметную волну функцией вида
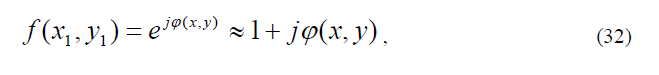
в обычном микроскопе изображение на его выходе характеризуется распределением мощности
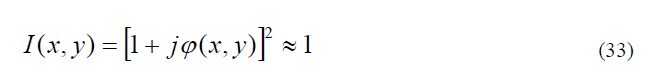
то есть информация о фазе (x, y) 1 такой волны утрачивается. При использовании в микроскопе пространственного фильтра с функцией пропускания (31) мощность излучения в области регистрируемого изображения, как можно показать, представляется в виде
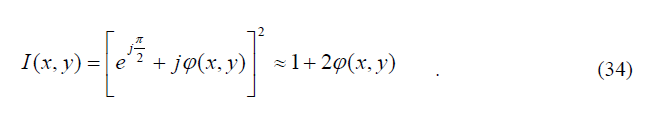
Следовательно, структура прозрачных фазовых объектов (какими и являются большинство биологических объектов – клетки, хромосомы и др.) отображается в виде неоднородного распределения мощности света в области изображения, то есть становится наблюдаемой.
Пространственный фильтр с комплексным пропусканием вида

позволяет выполнить вычисление частной производной (дифференцирование функции) распределения на входе системы фильтрации, в соответствии со свойствами преобразования Фурье - см. 7. Выполняя обратное преобразование Фурье, с учетом (27), следует
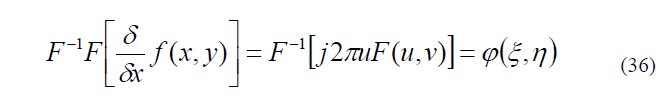
то есть амплитудный фильтр с пропусканием (35) действительно обеспечивает на выходе системы пространственной фильтрации распределение поля, соответствующее частной производной от двумерного распределения входного сигнала.
Задание: изучить принципы фазового контраста. Создать фильтрующую функцию. Ввести изображение в виде тонкого круга. Произвести фильтрацию сигнала.
Контрольные вопросы:
1.В чем отличие фазовой фильтрации от амплитудной фильтрации?
2.Какие виды оптических транспарантов используют для фазовой фильтрации?
Литература:
- Оптические методы обработки информации. А.Л. Дмитриев. Учебное пособие. СПб. СПюГУИТМО 2005. 46 с.
- А.А.Акаев, С.А.Майоров «Оптические методы обработки информации» М.:1988
- Дж.Гудмен «Введение в Фурье-оптику» М.:Мир 1970
Лабораторная работа № 4
Оптическая фильтрация пространственных сигналов.
Цель работы: изучить оптическую фильтрацию пространственных сигналов, научиться оконтурировать изображения.
Пространственная фильтрация оптических сигналов
Основная идея оптической пространственной фильтрации в состоит в использовании различных амплитудных, фазовых или амплитудно-фазовых оптических фильтров (светофильтров, фазовых пластинок, диафрагм, голограмм и др.), размещаемых в области локализации фурье-спектра передаваемого через оптическую систему изображения. В результате двумерный фурье-спектр передаваемых сигналов заданным образом изменяется, что и обусловливает требуемое изменение формы сигналов на выходе такой оптической системы. Простейший пространственный фильтр для обработки изображений содержит две линзы с совмещенными задней (для первой линзы) и передней (для второй линзы) фокальными плоскостями, и фильтр-транспарант, расположенный в
плоскости совмещения (Рис.5)
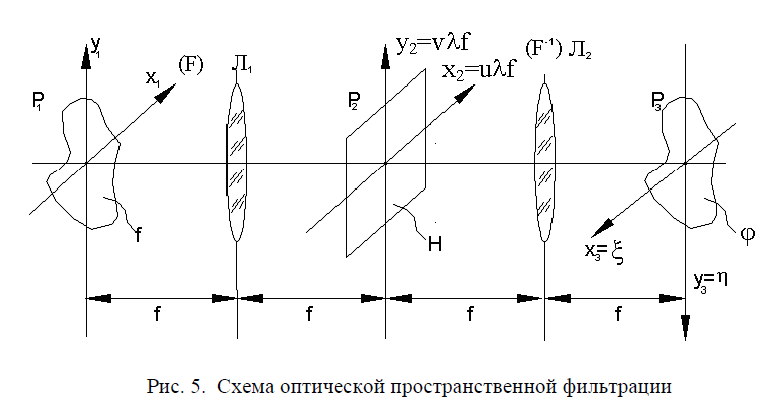
В передней фокальной плоскости первой линзы посредством транспаранта, освещаемого пространственно-когерентной волной, создается исходное распределение светового поля . Первая линза f осуществляет первое (прямое) преобразование Фурье исходной функции, при этом в ее задней фокальной плоскости формируется распределение амплитуды излучения F(u,v) соответствующее пространственному спектру подводимого сигнала,
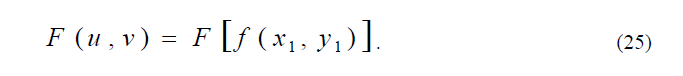
В спектральной плоскости установлен пространственный фильтр с комплексной амплитудной функцией пропускания H(u,v). Действие такого фильтра сводится к умножению функции пропускания фильтра на распределение спектра вводимой функции,
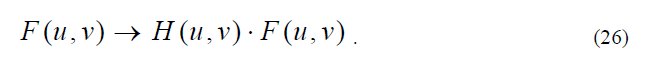
Вторая линза выполняет второе (условно обратное) преобразование Фурье, в результате чего распределение ( ,) амплитуды светового поля в ее задней фокальной плоскости имеет вид
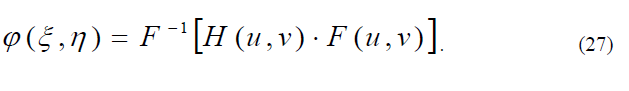
На основании теоремы свертки выполняется
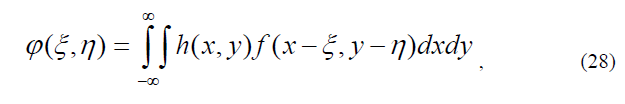
откуда видно, что распределение комплексной амплитуды излучения в выходной плоскости оптической системы на Рис. 5 представляет собой двумерную свертку исходной функции f (x, y) и функции h(x, y), равной обратному преобразованию Фурье от функции H(u,v)
пропускания пространственного фильтра,

Функцию h(x, y) (29) называют импульсным откликом пространственного фильтра.
Задавая различные значения функции пропускания H(u,v) транспаранта, устанавливаемого в плоскости системы на Рис.5, можно практически мгновенно осуществлять вычисление двойного интеграла свертки вида (28). Если пространственный фильтр отсутствует, то есть его пропускание тождественно равно единице, импульсный отклик (29) равен дельта-функции и,
согласно (17) и (28), функции ( ,) и f (x, y) идентичны. При этом в плоскости будет сформировано перевернутое изображение распределения поля в плоскости . Установив в плоскости фильтр низких частот с функцией пропускания вида
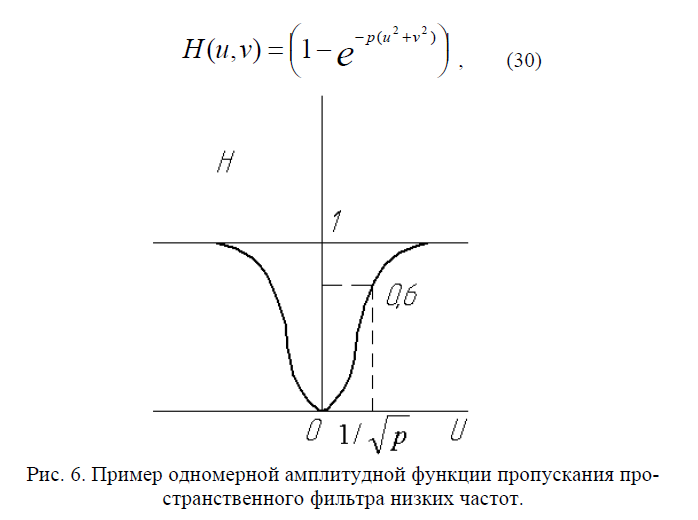
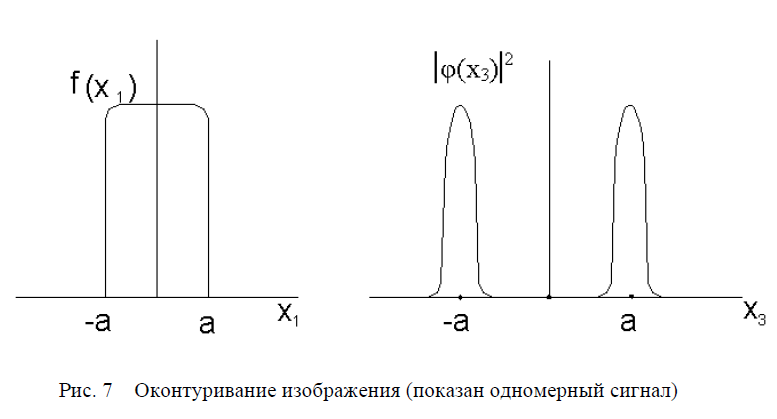
(см. Рис. 6), в процессоре выполняется операция оконтуривания изображений. При этом распределение мощности излучения в плоскости будет отображать области наибольшего изменения амплитуды входного изображения, см. Рис. 7.
Задание: в программе paintbrush нарисовать исходный сигнал. Фон черный цвет фигур белый, так как черный цвет имеет код 0, а белый код 255 или 1, в зависимости от типа файла. Сохранить в восьмибитовом цвете в формате BMP. Разрешение рисунка 80х80 пикселей. Произвести оптическую пространственную фильтрацию сигнала. Получить и обьяснить окончательный результат.
Контрольные вопросы:
- Основная идея оптической пространственной фильтрации?
- Что означает оконтуривание изображения?
Литература:
- Оптические методы обработки информации. А.Л. Дмитриев. Учебное пособие. СПб. СПюГУИТМО 2005. 46 с.
- А.А.Акаев, С.А.Майоров «Оптические методы обработки информации» М.:1988
- Дж.Гудмен «Введение в Фурье-оптику» М.:Мир 1970
Лабораторная работа № 5
Эксперимент Аббе-Портера.
Цель работы: повторить эксперимент Аббе-Портера.
Опыт Аббе-Портера
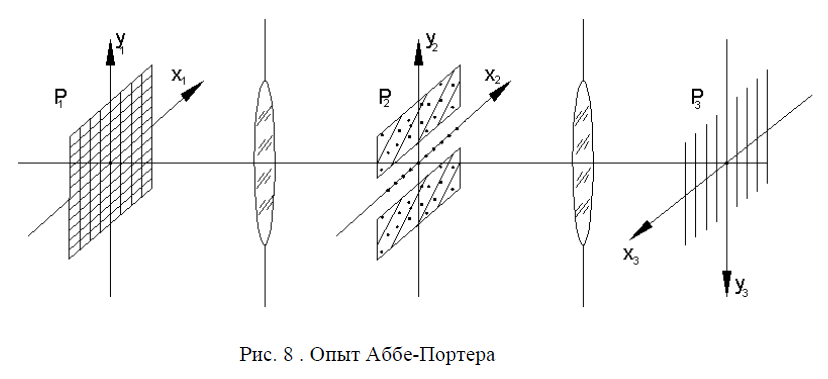
Амплитудный пространственный фильтр, расположенный в спектральной области на Рис. 5, может существенно изменить структуру изображения, вводимого в систему пространственной фильтрации. Это иллюстрирует эксперимент Аббе-Портера (Рис. 8).
Здесь входным изображением является двумерная дифракционная решетка, пространственный спектр которой представляет собой также двумерный массив ярких «точек» (кружков Эйри) в фокальной плоскости первой линзы. Пространственный фильтр в виде щелевой диафрагмы пропускает лишь спектральные составляющие, расположенные вдоль одной из осей . В результате в выходной плоскости изображения формируется одномерная решетка, периодическая вдоль оси . Наибольшее практическое применение в микроскопии биологических объектов имеет фазовый контраст, идея которого была предложена Цернике. Сущность фазового контраста состоит в использовании фазового пространственного фильтра, установленного в спектральной области оптической системы объектива микроскопа. Такой фильтр характеризуется амплитудным пропусканием вида

и может быть выполнен, например, в виде диэлектрической пластинки с оптической длиной пути («толщиной»), кратной нечетному числу / 4 , установленной строго в центре (в области нулевых пространственных частот) фокальной плоскости объектива микроскопа. На практике конструкция пространственного фильтра нередко содержит кольцевую фазовую пластинку, расположенную вне оптической оси. В обоих случаях назначение пространственного фильтра – ввести искусственный сдвиг фазы величиной / 2 между волнами, соответствующими пространственным частотам нулевого и остальных порядков дифракции. В результате мощность излучения в выходной плоскости изобразительной системы микроскопа зависит от фазы предметной волны, определяемой структурой прозрачного объекта – неоднородным распределением плотности его материала. Представляя предметную волну функцией вида
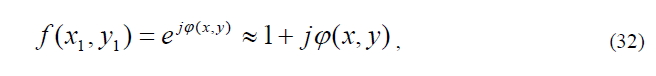
в обычном микроскопе изображение на его выходе характеризуется распределением мощности
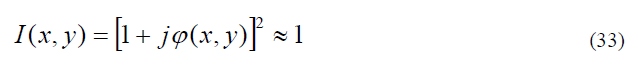
то есть информация о фазе (x, y) 1 такой волны утрачивается. При использовании в микроскопе пространственного фильтра с функцией пропускания (31) мощность излучения в области регистрируемого изображения, как можно показать, представляется в виде
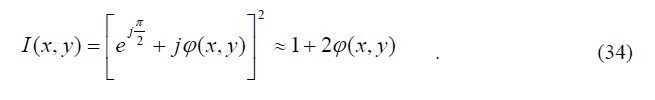
Следовательно, структура прозрачных фазовых объектов (какими и являются большинство биологических объектов – клетки, хромосомы и др.) отображается в виде неоднородного распределения мощности света в области изображения, то есть становится наблюдаемой.
Пространственный фильтр с комплексным пропусканием вида

позволяет выполнить вычисление частной производной (дифференцирование функции) распределения на входе системы фильтрации, в соответствии со свойствами преобразования Фурье - см. 7. Выполняя обратное преобразование Фурье, с учетом (27), следует
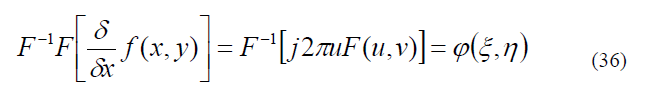
то есть амплитудный фильтр с пропусканием (35) действительно обеспечивает на выходе системы пространственной фильтрации распределение поля, соответствующее частной производной от двумерного распределения входного сигнала.
Задание: сформировать входной массив данных в виде двумерной сетки. После линзы поставить горизонтальную щель, на выходе после второй линзы получать вертикальные линии.
Контрольные вопросы:
- Обьяснить опыт Аббе-Портера?
- Что получили в выходной плоскости ?
Литература:
- Оптические методы обработки информации. А.Л. Дмитриев. Учебное пособие. СПб. СПюГУИТМО 2005. 46 с.
- А.А.Акаев, С.А.Майоров «Оптические методы обработки информации» М.:1988
- Дж.Гудмен «Введение в Фурье-оптику» М.:Мир 1970
Лабораторная работа № 6
Пространственный фильтр (коррелятор) Вандер Люгта.
Цель работы: изучить фильтр Вандер Люгта
Пространственный фильтр (коррелятор) Вандер Люгта.
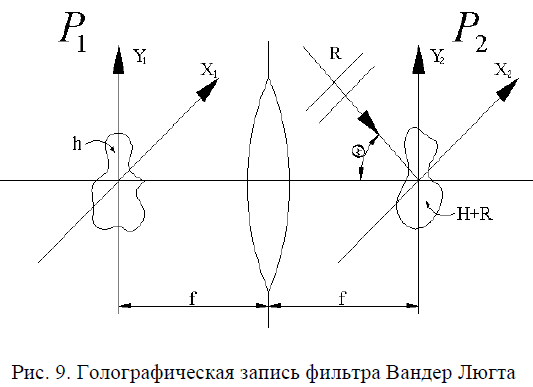
Если в качестве частотного пространственного фильтра в системе, показанной на Рис. 5, используется тонкая амплитудная голограмма, такая система приобретает свойства комплексного согласованного фильтра и может использоваться для распознавания оптических изображений. Изготовление пространственного фильтра Вандер Люгта (ФВЛ) производится
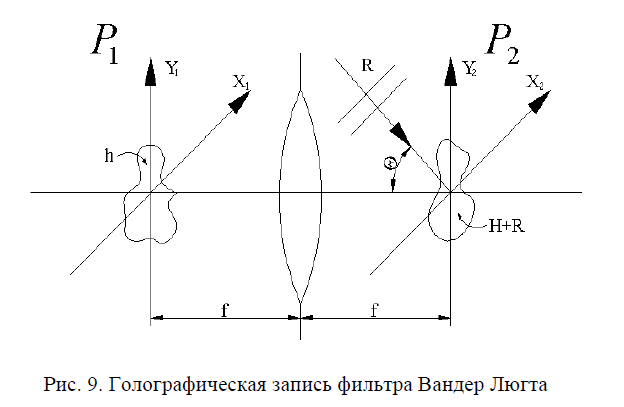
по схеме записи пропускающей голограммы эталонного изображения, показанной на Рис. 9. Здесь в плоскости формируется распределение амплитуды H(u,v) световой волны, пропорциональное преобразованию Фурье от распределения h( эталонного изображения,

и эта волна интерферирует с плоской опорной волной R , падающей под углом к оптической оси. В плоскости амплитуда поля опорной волны равна
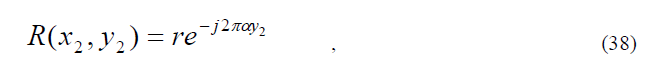
Где 
При записи голограммы картина интерференции этих волн регистрируется в фотоэмульсии и после обработки фотоматериала амплитудное пропускание t( полученной голограммы прямо пропорционально распределению мощности света,

Подставив (37) и (38) в (40), получим выражение для коэффициента пропускания ФВЛ
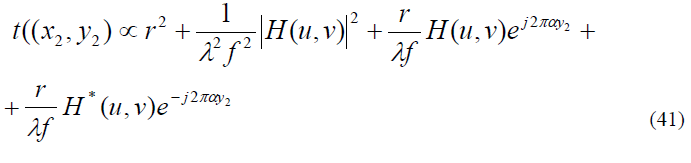
Если на вход системы пространственной фильтрации (Рис. 5) подается сигнал с распределением амплитуды поля g(, в плоскости системы перед фильтром ВДЛ формируется спектральное распределение вида

и за фильтром ВДЛ – распределение (u,v)
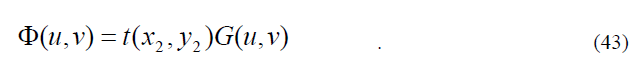
В выходной плоскости системы распределение амплитуды волнового поля описывается выражением
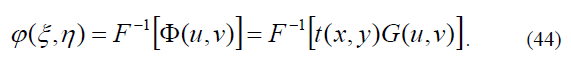
После соответствующих подстановок в (44), с учетом (27, 28) распределение амплитуды поля на выходе коррелятора Вандер Люгта представляется суммой
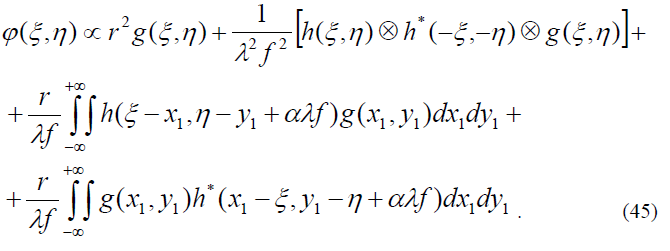
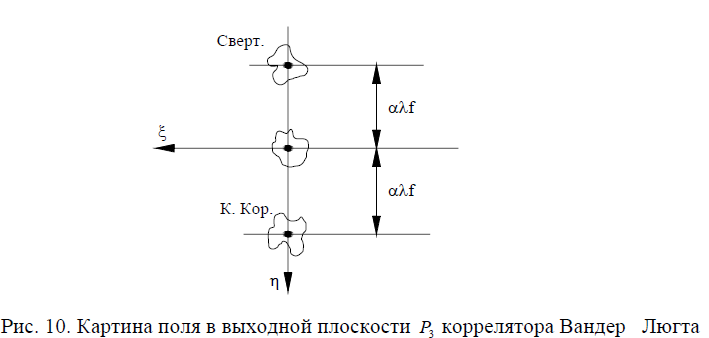
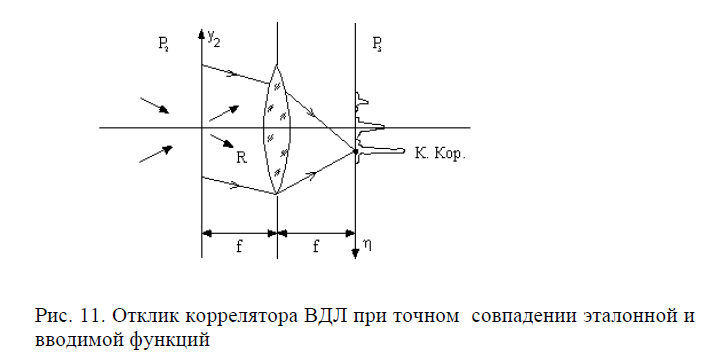
В выражении (45) третий член представляет собой свертку вводимого и эталонного сигналов, распределение которой формируется в плоскости на расстоянии f от оптической оси. Четвертый член в (45) описывает кросс-корреляцию распределений g( и g(, также смещенную относительно оптической оси (Рис. 10). Величина кросс-кореляции достигает максимума при точном совпадении вводимого g и эталонного изображений, а его промежуточные значения (между нулевым и максимальным) характеризуют степень соответствия (сходства) распределений h и q. При равенстве эталонной h и вводимой g функций, в сущности, при дифракции света на голограмме-фильтре ВДЛ происходит восстановление поля опорной волны R , что показано на Рис. 11.
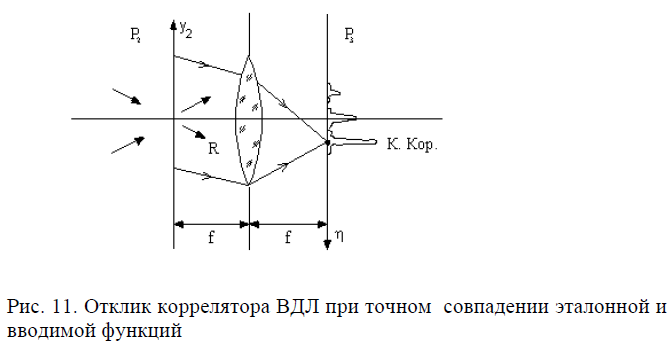
Пространственный фильтр (коррелятор) Вандер Люгта используется в оптических системах распознавания и обработки изображений, например, для идентификации отпечатков пальцев в дактилоскопии, выявлении артефактов (строения, самолеты, корабли и т. п.) на аэрофотоснимках и др. Конструкция фильтра обычно включает несколько параллельно действующих каналов,
при этом отдельным эталонным сигналам соответствуют определенные признаки таких изображений – углы, окружности, прямые линии и т. п. Отклик коррелятора ВДЛ инвариантен к параллельным смещениям вводимого в плоскости (Рис. 5) сигнала, что можно истолковать как следствие сдвиговой инвариантности (6) преобразования Фурье. При этом имеет место взаимно однозначное соответствие координаты отклика в выходной плоскости фильтра ВДЛ и координаты центра вводимого изображения. Недостатками коррелятора ВДЛ являются высокая чувствительность отклика к изменению масштаба и поворотам вводимого изображения. Эта чувствительность возрастает при увеличении частоты пространственного спектра, то есть тонкой
структуры вводимого изображения. Кроме этого, весьма высокие требования предъявляются к качеству оптико-механической конструкции всей системы пространственной фильтрации, например, точность установки пространственного фильтра составляет доли микрометра.
Задание: создать эталонное изображение: треугольник. Вычислить кэффициент пропускания.
Контрольные вопросы:
- Как создается голографическое эталонное изображение?
- Выяснить чувствительность к масштабу исходного сигнала?
Литература:
- Оптические методы обработки информации. А.Л. Дмитриев. Учебное пособие. СПб. СПюГУИТМО 2005. 46 с.
- А.А.Акаев, С.А.Майоров «Оптические методы обработки информации» М.:1988
- Дж.Гудмен «Введение в Фурье-оптику» М.:Мир 1970
Лабораторная работа № 7
Оптическое преобразование Меллина.
Цель работы: изучить оптическое преобразование Меллина.
Оптическое преобразование Меллина
Устранить один из серьезных недостатков коррелятора Вандер Люгта – повышенная чувствительность сигнала отклика к изменениям масштаба изображения – можно, реализовав в оптике преобразование функции, обладающее свойством инвариантности к преобразованиям масштаба функции. Примером такого преобразования является преобразование Меллина, представляемое (например, для одномерных функций) интегралом
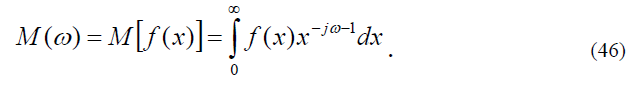
Преобразование Меллина обладает свойством инвариантности к изменению масштаба исходной функции,
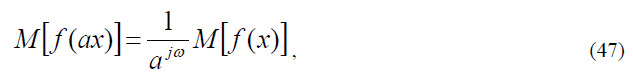
и тесно связано с преобразованиями Лапласа и Фурье,

Свойство (48) показывает, что преобразование Меллина можно представить как преобразование Фурье от исходной функции при экспоненциальном преобразовании ее аргумента,

При этом, очевидно, новые координаты исходной функции логарифмически связаны с начальными, = ln x .Следует отметить, что, в отличие от преобразования Фурье, преобразование Меллина не обладает свойством сдвиговой инвариантности. В корреляторе Меллина запись пространственного фильтра осуществляется по обычной голографической схеме (Рис. 9) при том условии, что вводимое эталонное изображение предварительно преобразуется согласно логарифмическому изменению его масштабов. При этом, например, одномерная периодическая амплитудная решетка отображается в апериодическую решетку с логарифмически изменяющимся периодом. Такое преобразование может быть выполнено при отображении исходного изображения на экране монитора, временная развертка которого управляется логарифмическими усилителями сигналов. Возможен ввод изображения в систему пространственной фильтрации и с помощью электрически управляемого транспаранта с нелинейным (также логарифмическим) преобразованием масштаба функции пропускания транспаранта. Действие коррелятора Меллина аналогично выше описанному действию пространственного фильтра ВДЛ (Рис. 11), при этом вводимое в коррелятор изображение предварительно нелинейно «растягивается» по осям координат с логарифмическим изменением его масштабов. Мощность корреляционного пика на выходе пространственного фильтра Меллина не зависит от масштаба вводимого изображения (определяется исключительно его структурой), а положение этого пика в выходной плоскости коррелятора прямо связано с масштабом вводимого изображения. Импульсный отклик оптического коррелятора Меллина инвариантен к изменениям масштаба вводимого изображения. Экспериментально был реализован коррелятор Меллина, отклик которого нечувствителен даже к двукратному изменению масштаба изображения по сравнению с эталонным. Недостатками оптического коррелятора Меллина является необходимость предварительной оптоэлектронной обработки вводимого изображения (нелинейное изменение его масштабов) и техническая сложность такой системы фильтрации изображений.
Задание: создать эталонное изображение: треугольник. Создать проходящее изображение: треугольник 1.5 масштабе. Вычислить коэффициент пропускания. Для вычислений использовать программу MathCAD.
Контрольные вопросы:
- Как создаеться голографическое эталонное изображение?
- Какова чувствительность к масштабу исходного сигнала?
- Для чего используеться данное преобразование?
Литература:
- Оптические методы обработки информации. А.Л. Дмитриев. Учебное пособие. СПб. СПюГУИТМО 2005. 46 с.
- А.А.Акаев, С.А.Майоров «Оптические методы обработки информации» М.:1988
- Дж.Гудмен «Введение в Фурье-оптику» М.:Мир 1970
PAGE \* MERGEFORMAT 54
Курс виртуальных лабораторных работ по дисциплине «Оптические методы и устройства обработки информации»