Визначення потреби в робочій силі
Курсова робота
з дисципліни:
«Математичні методи дослідження операцій»
на тему:
«Визначення потреби в робочій силі»
Завдання
на курсову роботу
З дисципліни «Методи дослідження операцій»
Студентка гр. ПНК-41
Козій А.М.
Варіант 7.3.1
7.3 . Визначення потреби в робочої силі
Підприємство складає шестимісячний план прийому робітників. Кожний новий робітник повинний пройти попереднє підготування тривалістю q міс., що містить у собі -годинну практику на майбутньому робочому місці, аналізовану як год. робочого часу. Навчений робітник може працювати до 1 год. на місяць, а за необхідності – менше. На початку січня підприємство мало X0 досвідчених робітників. Встановлено, що приблизно p % навчених робітників звільняється за власним бажанням. Досвідчений робітник обходиться підприємству в C грн., а той, якого навчають, - у S грн. на місяць. Потреба підприємства в кількості робочих часів задана.
Визначити число робітників Xi, навчання яких має початися в місяці і.
|
Показник |
№ |
|
1 |
|
|
Q |
0.6 |
|
60 |
|
|
1 |
150 |
|
X0 |
70 |
|
Р |
10 |
|
C1 |
850 |
|
C2 |
450 |
|
Потреба підприємства в робочу часі: |
|
|
січень |
10000 |
|
лютий |
8000 |
|
березень |
10000 |
|
квітень |
12000 |
|
травень |
9000 |
|
червень |
12000 |
Методи вирішення:
Гоморі-2, метод розгалужень та обмежень.
Математична модель:
Математична модель складається з:
- Цільової функції
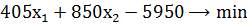
де - к січні, лютому, березні, квітні, травні та червні відповідно.
- Обчислення:
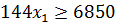
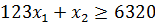
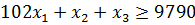
81
60
39
- Умова цільової системи:
- результат повинен бути цілими.
Перевірив:
Бабіч В. І.
Зміст
|
[0.1] Алгоритм програми [0.2] Висновнок [1] 5.Дослідження на чутливість
[2]
[3] |
-
Вступ
Необхідно визначити число робітників Xi, навчання яких має початися в місяці і. Підприємство складає шестимісячний план прийому робітників. Кожний новий робітник повинний пройти попереднє підготування тривалістю q міс., що містить у собі -годинну практику на майбутньому робочому місці, аналізовану як год. робочого часу. Навчений робітник може працювати до 1 год. на місяць, а за необхідності – менше. На початку січня підприємство мало X0 досвідчених робітників. Встановлено, що приблизно p % навчених робітників звільняється за власним бажанням. Досвідчений робітник обходиться підприємству в C грн., а той, якого навчають, - у S грн. на місяць. Потреба підприємства в кількості робочих часів задана. Необхідно визначити число робітників Xi, навчання яких має початися в місяці і.
|
Показник |
№ |
|
1 |
|
|
Q |
0.6 |
|
60 |
|
|
1 |
150 |
|
X0 |
70 |
|
Р |
10 |
|
C1 |
850 |
|
C2 |
450 |
|
Потреба підприємства в робочу часі: |
|
|
січень |
10000 |
|
лютий |
8000 |
|
березень |
10000 |
|
квітень |
12000 |
|
травень |
9000 |
|
червень |
12000 |
- Розробка математичної моделі та аналіз методів
Математична модель:
Математична модель складається з:
- Цільової функції
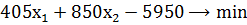
де - к січні, лютому, березні, квітні, травні та червні відповідно.
- Обчислення:
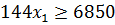

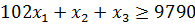
81
60
39
Методи вирішення:
Гоморі-2, метод розгалужень та обмежень.
Даний курсовий проект запропоновано розв'язати двома методами цілочисленого ділення: метод Гоморі 2, який реалізується програмно та метод розгалуджень та обмежень, розрахунок яким відбувається вручну.
Методи цілочислового ділення основані на введені в задачу додаткових обмежень, що дозволяють врахувати вимоги цілочисленності. Основна ідея методів відсікання полягає в тому, що на отримане оптимальне не цілочислового рішення накладається додаткове обмеження, котре робить це рішення недопустимим, але і не відсікає ні одного цілочислового рішення от області допустимих рішень.
Суть методу Гоморі полягає у наступному:
- отримання першого опорного рішення з використанням звичайної симплекс таблиці або двоїстого симплекс методу;
- на основі максимальної дробної змінної формується нове обмеження, щоб відсікати дробну частину;
- Рішення нової системи розмірністю m+1, n+1 відбувається за допомогою двоїстого симплекс метода;
- Повтор другого та третього пункту відбувається до тих пір всі значення не будуть цілими або рішення не буде відсутнє.
Формування обмеження: -{yi}=
Перерахунок нової модель відбувається за такими формулами:
{bi}, якщо j=0
, якщо Xj – ціле та {aij} >={b0}
{aij}, якщо {aij} <{b0}
aij , якщо Xj – не ціле та {aij} >{b0}
, якщо {aij} <{b0}
Гоморі 2, на відміну від Гоморі, майже завжди дає відповідь та відрізняється тим, що не на всі змінні накладаються обмеження.
Метод розгалужень та обмежень - один із комбінаторних методів. Його зміст полягає у впорядкованому переборі варіантів та перегляді лише тих які виявляються по певним ознакам перспективними, і відкиданні безперспективних варіантів.
Цей метод полягає в наступному : множина допустимих рішень (планів) деяким способом розбивається на підмножини, кожна з яких тим же способом розбивається на підмножини. Процес продовжується доти доки не буде отримане оптимальне цілочисельне рішення
Зміст методу полягає в наступному:
1.Знаходимо рішення задачі лінійного програмування без обліку цілочисельних змінних.
2. Складаємо додаткові обмеження на дробову компоненту плану.
3. Знаходимо рішення двох задач з обмеженнями на компоненту.
4. Будуємо в разі потреби додаткові обмеження, відповідно до
можливих чотирьох випадків одержуємо цілочисельний план, або
встановлюємо нерозв’язаність системи.
Метод оснований на припущенні, що наш оптимальний нецілочисельний план дає значення функції, більше ніж усякий наступний план переходу.
задачі.
3.Розв’язок задачі за допомогою методу Гоморі 2
- Алгоритм програми
Для початку розрахунку задачі за допомогою методу Гоморі 2, користувач має вручну розрахувати псевдо-план. В свою чергу псевдоплан – це нова модель, яка вміщує одиничний спряжений (знайдений одиничний) базис та недопустиме опорне рішення.
Для цього потрібно привести цільову функцію до max (Якщо вона спрямована на мінімізацію, то знак цільової функції змінюється на „-”), а обмеження до рівнянь. В цілюву функцію ніякі змінні не додаються. Всі знаки замінюються на знак „ = ”, враховуючи відповідні правила переведення моделей від звичайної моделі до її канонічного вигляду (вони відмінні від правил переводу до канонічного моделі при симплекс методі). Правила переводу є наступними: якщо обмеження має знак „<” то при переведенні до канонічного вигляду, то додається одну змінна; якщо - „>” то віднімається одна змінна; якщо знак „=” то ніякі змінні не додаються.
Наступним етапом буде записана двоїста задача, на основі якої будуть сформовані незалежні вектори за допомогою введення А0...Аn. Після чого вибираємо спряжений базис розмірності m:
- Вибираємо m-рівнянь
- Вирішуємо систему
- Підставляємо рішення в інші обмеження (якщо рішення інших обмежень задовольняє рівняння, то базис знайдено, в іншому випадку шукаємо далі).
Після формування та розрахунку симплекс таблиці переписуємо з таблиці нову модель, данні якої передаються далі на розрахунок за допомогою двоїстого симплекс метода. Якщо рішення після розрахунку за допомогою двоїстого симплекс-метода не буде цілочислене формуємо певні обмеження:
- Від max А0 відсікається дробна частина та створюється нова змінна (таким чином розмірність задачі збільшується).
- Розрахунок всіх останніх елементів рядка відбувається за допомогою вище перечислених правил.
Процес буде повторюватись до того часу поки не буде знайдене цілочислене рішення, або рішення не буде відсутнє.
Розв’язок за допомогою Гоморі 2
(c) Koziy Alena ...PNK-41
Rozmirnist zadachi: 6x12
-405x1-850x2->max
-144x1+1x7=-6850
-123x1-1x2+1x8=-6320
-102x1-1x2-1x3+1x9=-9790
-81x1-1x2-1x3-1x4+1x10=-13260
-60x1-1x2-1x3-1x4-1x5+1x11=-11730
-39x1-1x2-1x3-1x4-1x5-1x6+1x12=-16200
Ymova cilochusesnosti:
0 0 0 0 0 0 0 0 0 0 0 0
Z=-214245
X=( 47.57 14344.79 0 0 0 0 0 13875.83 9406.88 4937.92 5468.96 0 )
4.Розрахунок задачі методом „Розгалуджень та обмежень”.
4.1 Алгоритм методу