Розробка керуючого автомата і синтез комбінаційних схем

КУРСОВА РОБОТА

«Комп’ютерна логіка»

Розробка керуючого автомата і синтез комбінаційних схем

Зміст

Вступ

1. Синтез автомата
   1. Побудова графічної схеми алгоритму та розмітка станів автомата __2
   2. Побудова графа та кодування станів автомата ______________________3
   3. Побудова таблиці переходів тригера __________________________________3
   4. Побудова структурної таблиці автомата _____________________________4
   5. Синтез комбінаційних схем для функцій збудження тригерів і

вихідних сигналів ______________________________________________________4

1. Синтез комбінаційних схем
   1. Представлення функції f4 в канонічних формах алгебр Буля,

Жегалкіна, ПІрса і Шеффера____________________________________________6

1. Визначення належності f4 до п’яти передповних класів______________8
   1. Мінімізація функції f4__________________________________________________8
   2. Спільна мінімізація системи функцій f1, f2, f3_________________________11

1. Одержання операторних форм для реалізації на ПЛМ_________________15

Висновок_____________________________________________________________________17

Список літератури___________________________________________________________18

Додаток___________________________________________________________18

Вступ

Керуючий автомат – це електрична схема, призначена для зберігання й перетворення двійкових змінних по заданому алгоритму.

Комбінаційні схеми здійснюють відображення визначеної множини вхідних логічних змінних у вихідні.

Практичнее застосування данного автомата можливе в області обчислювальної техніки.

У даній роботі розробка керуючого автомата і синтез комбінаційних схем виконується на підставі «Технічного завдання ІАЛЦ.463626.002 ТЗ».

1. Синтез автомата
   1. Побудова графічної схеми алгоритму та розмітка станів автомата

Відповідно до технічного завдання складаємо графічну схему алгоритму (рис 1.1) з урахуванням тривалості сигналів і виконуємо розмітку станів автомата.

1. Побудова графа та кодування станів автомата
   Згідно з блок-схемою алгоритму будуємо граф автомата Мура та виконуємо кодування станів (рис 1.2).
   
   

Рисунок 1.2 Граф автомата зі закодованими вершинами.

1. Побудова таблиці переходів тригера.
   Для синтезу логічної схеми автомата необхідно виконати синтез функцій збудження тригерів та вихідних функції автомата. Автомата має 9 станів, тому кількість тригерів за формулою дорівнює K >= ]log2N[ = ]log29[ = 4.

Запишемо таблицю переходів RS-тригерів, на яких необхідно використати у побудові автомата (рис.1.3):

Рисунок 1.3 Таблиця переходів тригера

1. Побудова структурної таблиці автомата
   Використовуючи дані графа автомата з рис.1.2 заповнюємо структурну таблицю (табл. 1.1).

Перехід	Старий стан	Новий стан	Вхідні сигнали	Вихідні сигнали	Функції збудження тригерів
	Q4	Q3	Q2	Q1	Q4	Q3	Q2	Q1	X2	X1	Y1	Y2	Y3	Y4	Y5	R4	S4	R3	S3	R2	S2	R1	S1
Z1->Z2	0	0	0	0	0	1	0	0	1	-	0	0	0	0	0	-	0	0	1	-	0	-	0
Z2->Z3	0	1	0	0	0	1	0	1	-	-	1	1	0	0	0	-	0	0	-	-	0	0	1
Z3->Z2	0	1	0	1	0	1	0	0	1	-	1	0	0	0	0	-	0	0	-	-	0	1	0
Z3->Z4	0	1	0	1	0	0	0	1	0	-	1	0	0	0	0	-	0	1	0	-	0	0	-
Z1->Z4	0	0	0	0	0	0	0	1	0	-	0	0	0	0	0	-	0	-	0	-	0	0	1
Z4->Z5	0	0	0	1	0	0	1	1	-	-	0	0	0	1	1	-	0	-	0	0	1	0	-
Z5->Z5	0	0	1	1	0	0	1	1	0	-	0	1	0	0	0	-	0	0	-	0	-	0	-
Z5->Z6	0	0	1	1	0	1	1	1	1	-	0	1	0	0	0	-	0	0	1	0	-	0	-
Z6->Z7	0	1	1	1	1	1	1	1	-	-	0	0	1	0	0	0	1	0	-	0	-	0	-
Z7->Z8	1	1	1	1	1	1	1	0	-	-	1	0	1	0	0	0	-	0	-	0	-	1	0
Z8->Z9	1	1	1	0	0	1	1	0	-	1	1	0	0	0	0	1	0	0	-	0	-	-	0
Z8->Z1	1	1	1	0	0	0	0	0	-	0	1	0	0	0	0	1	0	1	0	1	0	-	0
Z9->Z1	0	1	1	0	0	0	0	0	-	-	0	0	1	0	0	-	0	1	0	1	0	-	0

Таблиця 1.1 Структурна таблиця автомата.

1.5 На основі структурної таблиці автомата (табл.1.1) виконаємо синтез комбінаційних схем для вихідних сигналів та функцій збудження тригерів. Аргументами функцій збудження тригерів у автоматі Мура є коди станів та вхідні сигнали, для вихідних сигналів - лише коди станів. Виконаємо мінімізацію вищевказаних функцій за допомогою діаграм Вейча (рис. 1.4, 1.5). Зауважимо, що операторні представлення функцій сформовані враховуючи елементний базис: 3І-НЕ, 2І.

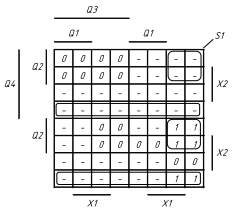
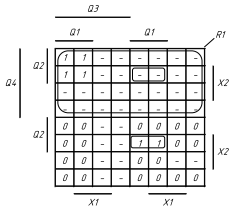
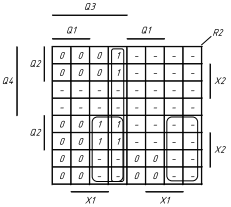
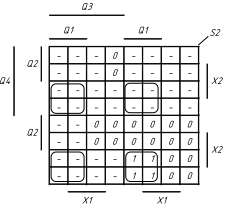
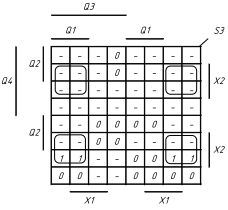
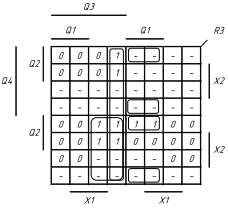
Рисунок 1.4 Мінімізація функцій збудження тригерів

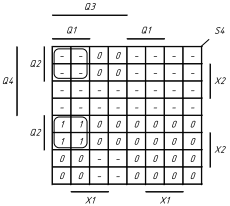
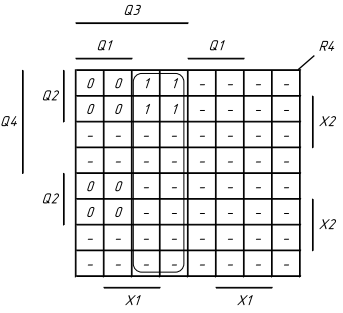
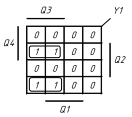
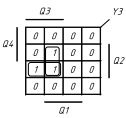
Рисунок 1.5 Мінімізація функцій збудження тригерів та вихідних сигналів

R4 = S4 =

R3 = S3 =

R2 = S2 =

R1 = S1 =
Y1 =

Y2 =

Y3 =

Y4 = Y5 =

Даних достатньо для побудови функцій збудження тригерів та вихідних сигналів, з яких складається автомат. Автомат будуємо на RS-тригерах, роботу яких синхронізує генератор.

Схема даного пристрою виконана згідно з єдиною системою конструкторської документації (ЕСКД) і наведена у документі «Автомат керуючий. Схема електрична функціональна ІАЛЦ.463626.003 Э2».

1. Синтез комбінаційних схем

X4	X3	X2	X1	F4
0	0	0	0	0
0	0	0	1	1
0	0	1	0	0
0	0	1	1	1
0	1	0	0	0
0	1	0	1	0
0	1	1	0	0
0	1	1	1	0
1	0	0	0	1
1	0	0	1	1
1	0	1	0	1
1	0	1	1	0
1	1	0	0	1
1	1	0	1	0
1	1	1	0	0
1	1	1	1	1

Функцію задано таблицею істинності:

Таблиця 2.1 Таблиця істинності функції.

2.1 Представимо функцію f4 в канонічних формах алгебри Буля, Желагкіна, Пірса та Шеффера.

Алгебра Буля (І, АБО, НЕ)

Запишемо функцію в диз’юнктивній та кон’юнктивній нормальних формах:

FДДНФ =

.

FДКНФ = .

Алгебра Жегалкіна (викл. АБО, І, const 1)

Одержуємо з ДДНФ шляхом наступних замін:

АБО замінити на викл. АБО

= X 1

FДДНФ =

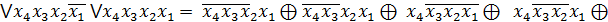
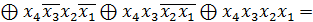
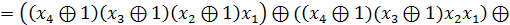
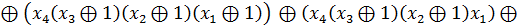
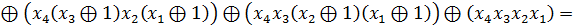
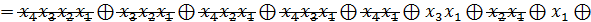
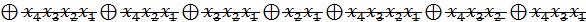
Алгебра Пірса(АБО-НЕ)

Одержуємо з ДКНФ шляхом застосування правила де-Моргана:

FДКНФ =

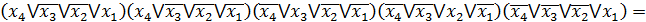
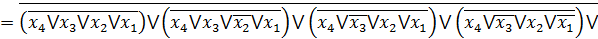
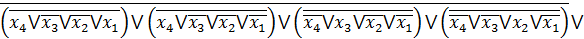
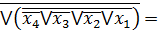
Алгебра Шеффера (І-НЕ)

Отримуємо з ДДНФ шляхом застосування правила де-Моргана

FДДНФ =

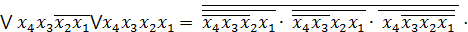
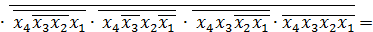
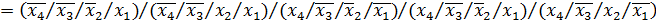
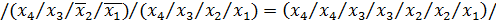
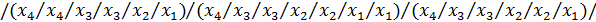
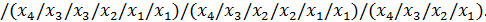
2.2 Визначимо належність функції f4 до 5 передповних класів.

К0 - включає всі функції, які зберігають 0;

К1 - включає всі функції, які зберігають 1;

КС - включає всі самодвоїсті функції;

КЛ - включає всі лінійні функції;

КМ - включає всі функції, які монотонні.

Класи	К0	К1	КС	КЛ	КМ
f4	+	+	-	-	-

K0 – зберігає нуль f(0000)=0;

K1 – зберігає одиницю f(1111)=1;

КС – не самодвоїста f(0001)=1 f(1110)=1;

КЛ – поліном Жегалкіна не є лінійним;

КМ – не монотонна f(0011)=1 f(0111)=0.

2.3 Мінімізація функції f4

Мінімізація функції методом невизначених коефіцієнтів

Суть методу полягає в знаходженні ненульових коефіцієнтів при кожній імпліканті. Запишемо рівняння для знаходження коефіцієнтів у вигляді таблиці (таб.2.1). Викреслимо рядки, де функція приймає нульові значення. Викреслимо вже знайдені нульові коефіцієнти в тих рядках таблиці, що залишилися. Не викреслені імпліканти поглинають імпліканти розташовані справа від них.

f4	X4	X3	X2	X1	X4X3	X4X2	X4X1	X3X2	X3X1	X2X1	X4X3X2	X4X3X1	X4X2X1	X3X2X1	X4X3X2X1
0	0	0	0	0	00	00	00	00	00	00	000	000	000	000	0000
1	0	0	0	1	00	00	01	00	01	01	000	001+	001	001-	0001*
0	0	0	1	0	00	01	00	01	00	10	001	000	010	010	0010
1	0	0	1	1	00	01	01	01	01	11	001	001+	011	011	0011*
0	0	1	0	0	01	00	00	10	10	00	010	010	000	100	0100
0	0	1	0	1	01	00	01	10	11	01	010	011	001	101	0101
0	0	1	1	0	01	01	00	11	10	10	011	010	010	110	0110
0	0	1	1	1	01	01	01	11	11	11	011	011	011	111	0111
1	1	0	0	0	10	10	10	00	00	00	100-	100+	100+	000	1000*
1	1	0	0	1	10	10	11	00	01	01	100-	101	101	001-	1001*
1	1	0	1	0	10	11	10	01	00	10	101	100+	110	010	1010*
0	1	0	1	1	10	11	11	01	01	11	101	101	111	011	1011
1	1	1	0	0	11	10	10	10	10	00	110	110	100+	100	1100*
0	1	1	0	1	11	10	11	10	11	01	110	111	101	101	1101
0	1	1	1	0	11	11	10	11	10	10	111	110	110	110	1110
1	1	1	1	1	11	11	11	11	11	11	111	111	111	111	1111+

Таб.2.2 Мінімізація методом невизначених коефіцієнтів

Ядро

FТДНФ1 =

FТДНФ2 =

FМДНФ = .

Мінімізація методом Квайна-Мак-Класкі

Виходячи з таблиці істинності запишемо стовпчик ДДНФ, розподіливши терми за кількістю одиниць. Проведемо попарне склеювання між сусідніми групами.

К0:

К1:

0001

1000

0011

1001

1010

1100

1111
00X1
X001
100X
10X0
1X00

Подальше склеювання не можливе. Виконаємо поглинання термів:

К0: К1:

0001

1000

0011

1001

1010

1100
1111+
00X1+
X001+
100X+
10X0+
1X00+

Побудуємо таблицю покриття (таб.2.3):

	0001	1000	0011	1001	1010	1100	1111
00X1	V		V
X001	V			V
100X		V		V
10X0		V			V
1X00		V				V
1111							V

Таблиця 2.3 Таблиця покриття

Ядро

FТДНФ1 =

FТДНФ2 =

FМДНФ = .

Мінімізація методом діаграм Вейча

Виконаємо мінімізацію методом діаграм Вейча. Цей метод зручний, коли кількість аргументів функції не перевищує п’яти. Кожна клітинка відповідає одній костітуенті, а об’єднання з декількох клітинок – імпліканті (рис. 2.1):

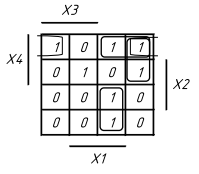
Рисунок 2.1 Діаграма Вейча

FМДНФ =

2.4 Спільна мінімізація системи функцій f1 , f2 , f3

Система перемикальних функцій задана таблицею істинності (таб.2.4):

X4	X3	X2	X1	F1	F2	F3	F4
0	0	0	0	1	1	1	0
0	0	0	1	1	1	0	1
0	0	1	0	1	1	1	0
0	0	1	1	0	0	0	1
0	1	0	0		0	1	0
0	1	0	1	0	0	0	0
0	1	1	0	1			0
0	1	1	1			1	0
1	0	0	0	1	1	1	1
1	0	0	1	0	0	1	1
1	0	1	0	0	0	0	1
1	0	1	1	0	0	0	0
1	1	0	0	1		1	1
1	1	0	1	0	0	0	0
1	1	1	0	0	0	0	0
1	1	1	1	1	1	1	1

Таблиця 2.4 Таблиця істинності системи функцій

Щоб одержати схему з мінімальними параметрами, необхідно виконати сумісну мінімізацію системи функцій.

Виконаємо мінімізацію системи функцій f1 , f2 , f3 методом Квайна-Мак-Класкі. Цей метод базується на співвідношеннях неповного склеювання та поглинання. Особливістю методу є використання цифрової форми запису термів перемикальних функцій. У цьому випадку зменшується кількість символів для подання термів і кількість операцій у процесі мінімізації, що робить метод зручним для програмної реалізації.

К0:

0000 (1,2,3)+

0001 (1,2) +
0010 (1,2,3) +
0100 (1*,3)
1000 (1,2,3) +

0110 (1,2*,3*)+
1001 (3) +
1100 (1,2*,3)+

0111 (1*,2*,3) +

1111 (1,2,3) +К1:

000X (1,2) +
00X0 (1,2,3) +
0X00 (1*,3)
X000 (1,2,3) +

0X10 (1,2,3) +
01X0 (1,3)
X100 (1,3)
100X (3) +
1X00 (1,2,3) +

011X (1,2,3) +

X111 (1,2,3) +К2:

OXXO (1,3)
0XX0 (1,3) +
XX00 (1,3)
XX00 (1,3) +

Побудуємо таблицю покриття (таб.2.5):

y1

y2

y3

0000

0001

0010

1000

0110

1100

1111

0000

0001

0010

1000

1111

0000

0010

0100

1000

1001

1100

0111

1111

0000

1,2,3

v

v

v

0001

1,2

v

v

1000

1,2,3

v

v

v

0110

1

v

1001

3

v

1100

1,3

v

v

0111

3

v

1111

1,2,3

v

v

v

000x

1,2

v

v

v

v

00x0

1,2,3

v

v

v

v

v

x000

1,2,3

v

v

v

v

v

v

0x10

1,2,3

v

v

v

v

100x

3

v

v

1x00

1,2,3

v

v

v

v

v

011x

1,2,3

v

v

x111

1,2,3

v

v

v

v

0xx0

1,3

v

v

v

v

v

v

xx00

1,3

v

v

v

v

v

v

v

Таблиця 2.5 Таблиця покриття

Визначимо кожну з функцій (базис І, АБО):

f1 =

f2 =

f3 =

Представимо функції у базисі І-НЕ/І-НЕ:

f1 =

f2 =

f3 =

Представимо функції у базисі АБО/І-НЕ:

f1 =

f2 =

f3 =

Представимо функції у базисі АБО-НЕ/АБО:

f1 =

f2 =

f3 =

Виконаємо мінімізацію системи перемикальних функцій заданих таблицею істинності методом Квайна-Мак-Класкі по нулям.

К0 :

0001 (3)
0100 (1*,2)

0011 (1,2,3)
0101 (1,2,3)
0110 (2*,3*)
1001 (1,2)
1010 (1,2,3)
1100 (2*)

0111(1*,2*)
1011 (1,2,3)
1101 (1,2,3)
1110 (1,2,3) K1 :

00X1 (3) +
0X01 (3) +
010X (1,2) +
01X0 (2)
X100 (2) +

0X11 (1,2) +
X011 (1,2,3) +
01X1 (1,2) +
X101 (1,2,3) +
011X (2*)
X110 (2,3) +
10X1 (1,2) +
1X01 (1,2) +
101X (1,2,3) +
1X10 (1,2,3) +
110X (2)
11X0 (2) K2 :

01XX (2)
X10X (2)
01XX (2) +
X1X0 (2)
X10X (2) +
X1X0 (2) +

Будуємо таблицю покриття (табл. 2.6):

y1

y2

y3

0011

0101

1001

1010

1011

1101

1110

0011

0100

0101

1001

1010

1011

1101

1110

0001

0011

0101

1010

1011

1101

1110

00x1

3

v

v

0x01

3

v

v

010x

1,2

v

v

v

0x11

1,2

v

v

x011

1,2,3

v

v

v

v

v

v

01x1

1,2

v

v

x101

1,2,3

v

v

v

v

v

v

x110

2,3

v

v

10x1

1,2

v

v

v

v

1x01

1,2

v

v

v

v

101x

1,2,3

v

v

v

v

v

v

1x10

1,2,3

v

v

v

v

v

v

01xx

2

v

v

x10x

2

v

v

v

x1x0

2

v

v

Таблиця 2.6 Таблиця покриття

Визначимо кожну з функцій (базис І/АБО-НЕ):

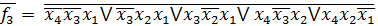
Представимо функції у базисі І-НЕ/І:

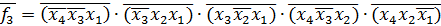
Представимо функції у базисі АБО/І:

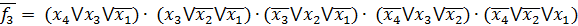
Представимо функції у базисі АБО-НЕ/АБО-НЕ:

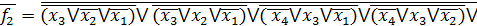
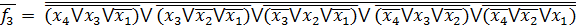
2.5 Одержання операторного представлення функцій на ПЛМ

Для програмування ПЛМ використовують нормальні форми І/АБО
та І/АБО-НЕ. Розглянемо програмування ПЛМ для реалізації системи перемикальних функцій, що подані в нормальній формі І/АБО:

f1 =

f2 =

f3 =

Зробимо заміну позначень термів системи:

Р1 Р2 Р3 Р4 Р5

Р6 Р7

Тоді функції виходів описуються системою:

f1 = Р1 Р2 Р3 Р4

f2 = Р3 Р4 Р5 Р6

f3 = Р1 Р2 Р3 Р7

Визначимо мінімальні параметри ПЛМ:

N = 4 – кількість інформаційних входів, що дорівнює кількості аргументів системи перемикальних функцій.

Р = 7 – число проміжних внутрішніх шин, яке дорівнює кількості різних термів системи.

М = 3 – число інформаційних виходів, що дорівнює кількості функцій виходів.

Побудуємо спрощену мнемонічну схему ПЛМ (4,7,3) (рис. 2.2):

Рисунок 2.2 Мнемонічна схема ПЛМ

Складемо карту програмування ПЛМ (4,7,3) (табл.2.7):

№ шини	Входи	Виходи
	Х1	Х2	Х3	Х4	Y1	Y2	Y3
1	0	-	-	0	1	-	1
2	0	0	-	-	1	-	1
3	1	1	1	-	1	1	1
4	-	0	0	0	1	1	-
5	0	0	0	-	-	1	-
6	0	-	0	0	-	1	-
7	-	0	0	1	-	-	1

Таблиця 2.7 Карта програмування ПЛМ

Висновок

Згідно з завданням даної курсової роботи необхідно було за номером залікової книжки, переведеним в двійкову систему числення, побудувати
блок-схему автомата, визначити тип автомата, типи використовуваних тригерів, набір логічних елементів, сигнал з подвійною тривалістю, визначити систему з чотирьох перемикальних функцій. Використовуючи ці дані, треба було провести абстрактний та структурний синтез автомата і побудувати його. Систему з перших трьох перемикальних функцій із заданої таблиці необхідно було мінімізувати і отримати операторні представлення для реалізації системи на програмованих логічних матрицях.

Для виконання завдання були розкодовані вихідні таблиці завдання варіанта. При побудові автомата була проведена побудова графа з урахуванням сигналів подвійної тривалості, зашифровані стани автомата, побудована структурна схема автомата, мінімізована система з функцій виходів і функцій збудження тригерів, був побудований і відлагоджений автомат. При виконанні другої частини роботи: мінімізована функція f4 різними методами, f4 представлена в канонічних формах алгебр Буля, Жегалкіна, Пірса і Шеффера, а також проведена сумісна мінімізація системи функцій з наступною реалізацією на програмованих логічних матрицях.

Список літератури

Жабин В.И., Жуков И.А., Клименко И.А., Ткаченко В.В.. Прикладная теория цифровых автоматов. - К.: Книжное издательство НАУ, 2011. - 364 с.

ДОДАТОК

Вхідні дані

Варіант завдання визначається дев’ятьма молодшими розрядами залікової книжки представлений у двійковій системі числення.

Запишемо дані у таблиці:

Таблиця 2.1

h9	h8	h7	h6	h5	h4	h3	h2	h1
0	1	1	0	0	1	0	0	0

Таблиця 2.2

h8	h4	h2	Порядок з’єднання фрагментів
1	1	0	4, 1, 2

Таблиця 2.3

h8	h7	h3	Логічні умови
1	1	0	not X2, X2, X1

Таблиця 2.4

h9	h4	h1	Послідовність сигналів
0	1	0	(Y1 Y2), (Y4 Y5), Y2, Y3, (Y1 Y3), Y3

Таблиця 2.5

h6	h2	Сигнал тривалістю 2t
0	1	Y1

Таблиця 2.6

h6	h5	Тип триггера
0	0	RS

Таблиця 2.7

h3	h2	h1	Логічні елементи
0	0	0	3 І-НЕ, 2 I
h4	Тип автомата
1	Мура

Таблиця 2.8

X4	X3	X2	X1	F1	F2	F3	F4
0	0	0	0	1	1	1	0
0	0	0	1	1	1	0	1
0	0	1	0	1	1	1	0
0	0	1	1	0	0	0	1
0	1	0	0		0	1	0
0	1	0	1	0	0	0	0
0	1	1	0	1			0
0	1	1	1			1	0
1	0	0	0	1	1	1	1
1	0	0	1	0	0	1	1
1	0	1	0	0	0	0	1
1	0	1	1	0	0	0	0
1	1	0	0	1		1	1
1	1	0	1	0	0	0	0
1	1	1	0	0	0	0	0
1	1	1	1	1	1	1	1

Таблиця істинності функцій:

Таблиця 2.9

Необхідно виконати сумісну мінімізацію функцій f1, f2 ,f3. Отримати операторні представлення для реалізації системи функцій на програмувальних логічних матрицях.

Функцію f4 необхідно представити в канонічних формах алгебри Буля, Жегалкіна, Пірса та Шеффера. Визначити приналежність даної функції до п’яти перед повних класів. Виконати мінімізацію функції методами:

• Невизначених коефіцієнтів;
• Квайна (Квайна-Мак-Класкі);
• Діаграм Вейча.

Склад пристроїв

Керуючий автомат.

Керуючий автомат складається з комбінаційної схеми і пам’яті на тригерах. Тип тригерів і елементний базис задані в технічному завданні.

Програмувальна логічна матриця.

ПЛМ складається із двох (кон’юктивної і диз’юнктивної ) матриць, де виходи першої приєднуються на входи другої і дозволяють реалізувати комбінаційні схеми в базисі {І/АБО, І/АБО-НЕ}.

Зм.ю.

Арк.

№ докум.

Пiдп.

Дата

Розроб.

Перевiр.

Н. контр.

Затв.

Селіверстов Д.О.

Лiт.

Аркуш

Аркушiв

ІАЛЦ.463626.004 П3

Пристрій управляючий

Пояснювальна записка

НТУУ “КПІ” ФІОТ

Гр. ІО-12

112

1

4

Зм.

рк.

№ докум.

Підп.

Дата

Арк.

2

ІАЛЦ.463626.004 ПЗ

Зм.

Арк.

№ докум.

Підп.

Дата

Арк.

2

ІАЛЦ.463626.002 ТЗ

Зм.

Арк.

№ докум.

Підп.

Дата

Арк.

3

ІАЛЦ.463626.004 ПЗ

Зм.

Арк.

№ докум.

Підп.

Дата

Арк.

4

ІАЛЦ.463626.004 ПЗ

Зм.

Арк.

№ докум.

Підп.

Дата

Арк.

5

ІАЛЦ.463626.004 ПЗ

Зм.

Арк.

№ докум.

Підп.

Дата

Арк.

6

ІАЛЦ.463626.004 ПЗ

Зм.

Арк.

№ докум.

Підп.

Дата

Арк.

7

ІАЛЦ.463626.004 ПЗ

Зм.

Арк.

№ докум.

Підп.

Дата

Арк.

8

ІАЛЦ.463626.004 ПЗ

Зм.

Арк.

№ докум.

Підп.

Дата

Арк.

9

ІАЛЦ.463626.004 ПЗ

Зм.

Арк.

№ докум.

Підп.

Дата

Арк.

10

ІАЛЦ.463626.004 ПЗ

Зм.

Арк.

№ докум.

Підп.

Дата

Арк.

11

ІАЛЦ.463626.004 ПЗ

Зм.

Арк.

№ докум.

Підп.

Дата

Арк.

12

ІАЛЦ.463626.004 ПЗ

Зм.

Арк.

№ докум.

Підп.

Дата

Арк.

13

ІАЛЦ.463626.004 ПЗ

Зм.

Арк.

№ докум.

Підп.

Дата

Арк.

14

ІАЛЦ.463626.004 ПЗ

Зм.

Арк.

№ докум.

Підп.

Дата

Арк.

15

ІАЛЦ.463626.004 ПЗ

Зм.

Арк.

№ докум.

Підп.

Дата

Арк.

16

ІАЛЦ.463626.004 ПЗ

Зм.

Арк.

№ докум.

Підп.

Дата

Арк.

17

ІАЛЦ.463626.004 ПЗ

Зм.

Арк.

№ докум.

Підп.

Дата

Арк.

18

ІАЛЦ.463626.04 ПЗ

Зм.

Арк.

№ докум.

Підп.

Дата

Арк.

3

ІАЛЦ.463626.002 ТЗ

Розробка керуючого автомата і синтез комбінаційних схем