Исследование последовательного колебательного контура (резонанс напряжений)
Лабораторная работа № 6
Исследование последовательного колебательного контура (резонанс напряжений)
Краткое содержание работы.
В процессе выполнения работы исследуются и изучаются следующие вопросы:
- Явление резонанса, возникающее в неразветвленной цепи, содержащей катушку индуктивности и конденсатор (последовательный колебательный контур);
- Условие возникновения резонанса в цепи и его проверка в лабораторных условиях;
- Методика измерения резонансных кривых;
- Аналитические соотношения при резонансе и их экспериментальная проверка.
Подготовка к работе.
1. Ознакомиться с рабочим заданием и методическими указаниями. Ответить на вопросы:
а) что понимают под явлением резонанса и при условиях он возникает?
б) изменением каких параметров можно достичь резонанса в последовательном контуре?
в) почему явление резонанса в последовательном контуре называют резонансом напряжений?
г) какие энергетические процессы происходят в контуре при резонансе?
д) чему равно сопротивление последовательного коле бательного контура при резонансе?
е) что называют волновым сопротивлением, доброт ностью, затуханием резонансного контура и обобщенной расстройкой?
ж) как изменяется полная , активная и реактивная мощность, которую потребляет последовательный колебательный контур при изменении частоты в диапазоне, включающем резонансную частоту?
з) дайте определение, характеризуйте вид и назначение обобщенной резонансной характеристики последовательного резонансного контура.
2. Составить протокол отчета лабораторной работы в соответствии с вариантом задания.
Рассчитать теоретически резонансные кривые для напряжений на элементах цепи которые будут получены практически в п.3 рабочего задания. Постройте также графические зависимости этих резонансных кривых ( для каждого из случаев а), б), в) – свой совмещенный график).
При теоретических расчетах сначала нужно вычислить резонансную частоту контура, его добротность Q и определить значение полосы пропускания контура 2f для приведенных схем измерений. Тогда диапазон изменения частоты f при расчете резонансной кривой будет:
f0-5f f f0+5f т. е. частота f будет изменяться в районе f0 с отклонением ( 5f/ f0)*100%. Аналогично рассчитывается, при расчете резонансных кривых, диапазон изменения параметра контура L или C. Так эти параметры будут изменяться в районе значений, приведенных в варианте задания с отклонением:
для L - ; для С - .
Вычисленные в этом пункте изменения параметров должны быть использованы при выполнении рабочего задания.
Рабочее задание
1. Собрать схему цепи последо вательного контура согласно рис.6.1 и соответствии с вариантом задания, приведенным в табл.6.2.
I R C
RВН
U L
e
Рис.6.1
2. Установить значение частоты синусоидального генератора (e) равное резонансной частоте цепи f0. Выходное напряжение генератора задать 1 В.
3. Моделируя цепь во временной области произвести измерения величин, указанных в таблице 6.1 , для следующих трех случаев:
а) при неизменной емкости С, в соответствии с вариантом задания, частоте генератора fо, варьи руя в возможных пределах индуктивность катушки L;
б) при неизменной индуктивности L, в соответствии с вариантом задания,, частоте генератора fо, варьи руя в возможных пределах емкость конденсатора С;
в) при неизменной емкости С, индуктивности L, в соответствии с вариантом задания, изменяя частоту генератора f.
4.. По данным п3 построить построить резонансные кривые на одном графике I, UL,UC, для каждого из случаев а),б),в), вычислить добротность контура и его полосу пропускания, сравнить их значения с полученным в п.2 рабочего задания. По данным п.3-в) построить векторные диаграммы напряжения на элементах цепи для случаев: C<C0; C=C0;C>C0 (C0-резонансное значение)
5.Установить внутреннее сопротивление генератора RВН:
- RВН=R; 2) RВН=0,1*R.
и провести измерения величин, указанных в табл. 6.1 для каждого из случаев 1),2) только в зависимости от частоты f, при значениях L,C соответствующих варианту задания.
Табл. 6.1 Парам.1____=_______( L/C/f), Парам.2____=______( L/C/f), Вар. параметр_____
|
Знач. Вар.
Парам.
L/C/f
(____)
|
U
(напр.
на конт.)
|
UL
|
UC
|
I
|
между
U--I
|
P
активн.
|
Q
реакт.
|
S
полная
|
|
1_____
|
|
|
|
|
|
|
|
|
|
……
|
|
|
|
|
|
|
|
|
|
10____
|
|
|
|
|
|
|
|
|
6. По данным п.5 построить резонансные кривые, наложив их на имеющиеся графики, построенные по п.4. Определить условие согласования на переменном токе и объяснить полученный результат теоретически.
7. Сделать выводы и обобщения по проделанной работе.
Методические указания
Резонансными или колебательными цепями называются электрические цепи, в которых могут возникать явления резонанса напряжений или токов.
При воздействии гармонического тока или напряжения на пассивную электрическую цепь, которая содержит резисторы катушки индуктивности и конденсаторы, наблюдается режим, при котором ее входное реактивное сопротивление равно нулю. Такой режим называется резонансом. Для этого режима характерно то, что реактивная мощность на входных зажимах цепи оказывается равной нулю и вся электрическая энергия, поступающая в цепь от источника, преобразуется в теплоту.
Резонанс напряжений наблюдается в электрической цепи с последовательным соединением участков, содержащих индуктивности и емкости. Неразветвленная цепь, состоящая из последовательно соединенных элементов R, С и L (рис.6.2), представляет собой один из простейших случаев такой цепи. Ее называют последовательным колебательным контуром.
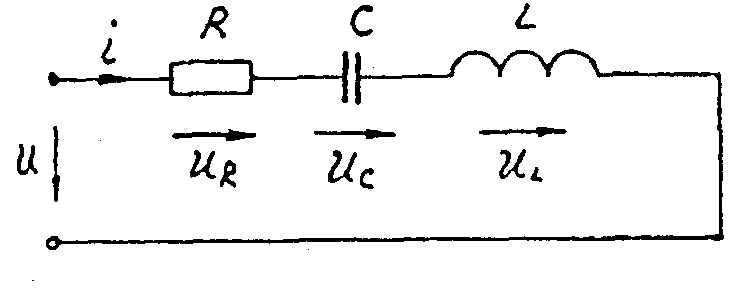Рис.6.2
Если в цепи течет синусоидальный ток i=Imsint, то мгновенные напряжения на элементах цепи можно определить: UR=RImsint; UL=Ldi/dt=LImsin(t+/2)=XL Imsin(t+/2);
UC=1/C=Imsin(t-/2)=XCImsin(t-/2).
Значение мгновенного напряжения на элементах цепи:
U=UR+UL+UC= RImsint+(XL-XC) RImcost= Imsin(t+);
где: =arctg() – угол сдвига фазы между током и напряжением в цепи.
Активная P , Реактивная S , полная Q , мощности, которые потребляются цепью, могут быть
определены: P=UIcos=I2R; Q= UIsin=I2(XL-XC); S=UI==I2
Где U=Um /; I=Im / – действующие амплитуды токов и напряжений на внешних выводах цепи.
Условие резонанса для такой цепи: XВХ=L-1/C=0.
Резонанс может быть получен путем изменения одной из трех переменных , L, C, при неизменных двух остальных, значения которых для цепи при резонансе должны удовлетворять соотношению: 0=1/. Где 0=2f0 – круговая резонансная частота, L0, C0 – номинальные значения элементов цепи при резонансе.
Полное сопротивление цепи при резонансе напряжений: Z= =R – минимально и равно активному сопротивлению. При этом ток и потребляемая активная мощность достигают наибольших значений.
Если реактивные сопротивления XL=L и XC=1/C при резонансе превышают по величине сопротивление R, то напряжение на зажимах катушки и конденсатора также больше входного напряжения генератора. Поэтому резонанс в последовательном контуре называется резонансом напряжений. Превышение напряжений имеет место, если R<0L=1/0C==.
Здесь имеет размерность сопротивления, численно равняется сопротивлению реактивного элемента при резонансе и носит название волнового сопротивления контура.
Отношение Q=UC0/U=UL0/U=I00L0/I0R=0L0/R=/R – определяет кратность превышения напряжения на катушке индуктивности и конденсаторе над напряжением входного генератора и называется добротностью контура.
Величина, обратная добротности, называется затуханием: =1/Q.
Зависимости величин (R ,Xi.,Xc, Zвх) от частоты, характеризующих поведение цепи при изменении частоты входного сигнала - называют частотными харак теристиками, а зависимости действующих значений тока и напряжений (или их отношений) на элементах от частоты - резонансными кривыми. На рис.6.З изображены частотные характеристики последовательного контура, построенные в соответствии с выражениями:
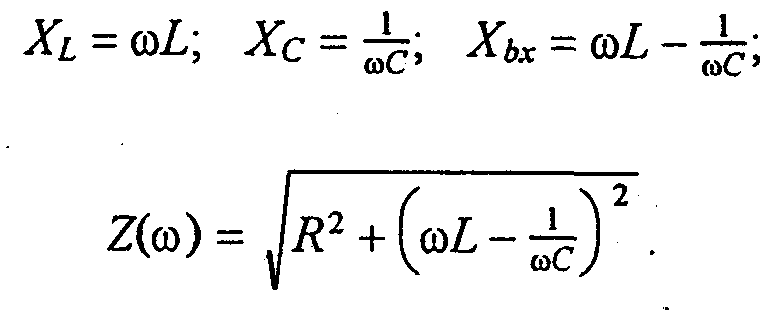
Рис.6.3
В теории контуров вводится понятие другой частотной переменной . При резонансе , поэтому эту частотную переменную называют обобщенной частотной расстройкой контура. При использовании обобщенной частотной расстройки контура строятся нормированные резонансные кривые (нормированные значения тока или напряжения на элементе цепи по отношению к его значению при резонансе). Например:
- выражение для комплексного входного сопротивления последовательного контура:
-выражение для нормированной резонансной кривой напряжения на реактивном элементе контура:
где: Um0 –амплитудное значение напряжение на реактивном элементе при резонансе..
Представляет технический интерес условие согласования на переменном токе, когда от генератора передается активная максимальная мощность в электрическую цепь (в данном случае резонансный контур). В соответствии с рис.6.4 для комплексных амплитуд тока и напряжения на нагрузке:
; .
е
Рис.6.4
Полная мощность: =
Активная мощность: P=.
Для нашей цепи : RГ+RН= RВН+R, XГ+XН=(L-1/C).
Тогда условие передачи максимальной мощности в резонансную цепь: (L-1/C)=0, RВН=R, при этом условии полного согласования получим мощность в цепи: .
Таблица 6.2 Варианты заданий.
|
Вариант
|
R Ом
|
C нФ
|
L мкГн
|
RВН Ом
|
|
1
|
0.3
|
1000
|
1000
|
0.1
|
|
2
|
1.0
|
100
|
500
|
0.3
|
|
3
|
0.7
|
500
|
1000
|
0.2
|
|
4
|
0.3
|
25
|
50
|
0.2
|
|
5
|
0.5
|
100
|
250
|
0.2
|
|
6
|
0.8
|
250
|
1000
|
0.3
|
|
7
|
0.5
|
100
|
200
|
0.2
|
|
8
|
0.3
|
300
|
500
|
0.1
|
|
9
|
1.3
|
30
|
300
|
0.9
|
|
10
|
0.5
|
150
|
400
|
0.2
|
Исследование последовательного колебательного контура (резонанс напряжений)