Исследование параллельного колебательного контура (резонанс токов)
Лабораторная работа №7
Исследование параллельного колебательного контура (резонанс токов)
Краткое содержание работы
В процессе выполнения работы исследуются и изучаются следующие вопросы:
1) Явление резонанса, возникающее в параллельном контуре, содержащем катушку индуктивности и кон�денсатор;
2) Условие возникновения резонанса в парал�лельном контуре и его проверка в лабораторных условиях;
3) Резонансные характеристики цепи и их особенности;
4) Проверка аналитических соотношений при резонансе .
Подготовка к работе
1. Ознакомиться с рабочим заданием и методическими указаниями. Ответить на следующие вопросы:
а) что понимают под явлением резонанса?
б) изменением каких параметров можно достичь резо�нанса в параллельном контуре?
в) почему явление резонанса в параллельном контуре называют резонансом токов?
г) какие энергетические процессы происходят в контуре при резонансе?
д) как определить резонансную частоту идеального и реального параллельных контуров?
е) что называют волновой проводимостью, добротностью, обобщенной расстройкой и затуханием параллельного контура?
ж) как определить резонансное состояние цепи значению токов и напряжений на элементах цепи?
з) приведите примеры и дайте характеристику параметров частичного включения параллельного контура;
е) как определяется нагруженная добротность параллельного контура, в том числе с учетом частичного включения контура.
2. Составить протокол отчета лабораторной работы в соответствии с вариантом задания. Рассчитать резонансные кривые для переменных токов, которые будут получены практически в п.3 рабочего задания, а также построить графические зависимости этих резонансных кривых ( для каждого из случаев а), б), в) – свой совмещенный график). При этом рассчитать ( см. п.2 к ЛР №6 раздел «Подготовка к работе») резонансную частоту контура f0, его нагруженную добротность Q, и диапазоны изменения величин f, L, C для построения резонансных кривых и исследований контура в разделе рабочего задания.
Рабочее задание
- Собрать схему цепи параллельного контура согласно рис.7.1.
RВН I
C L
IC IL U
E RC RL
Рис.7.1
2. Установить значение частоты синусоидального генератора Е равным резонансной частоте цепи f0. Выходное напряжение генератора установить 100 В.
3. В параллельном контуре (см. рис. 7.1 и вариант задания табл. 7.2 ), произвести измерение и записать в протокол величины, указанные в таблице 7.1, для следующих трех случаев:
а) при неизменной емкости С, в соответствии с вариантом задания, частоте генератора fо, варьи�руя в возможных пределах индуктивность катушки L;
б) при неизменной индуктивности L, в соответствии с вариантом задания,, частоте генератора fо, варьи�руя в возможных пределах емкость конденсатора С;
в) при неизменной емкости С, индуктивности L, в соответствии с вариантом задания, изменяя частоту генератора f.
4.. По данным п.3 построить резонансные кривые на одном графике I, IL, IC, для каждого из случаев а),б),в), вычислить добротность контура и его полосу пропускания, сравнить их значения с полученным в п.2 раздела «Подготовка к работе» по графическим зависимостям. По данным п.3-в) построить векторные диаграммы тока через элементы цепи RВН,L,C для случаев: C<C0;C=C0;C>C0 (C0-резонансное значение)
5.Установить внутреннее сопротивление генератора RВН:
- RВН= *; 2) RВН=0,1 *;
и провести измерения величин, указанных в табл. 7.1 для каждого из случаев 1),2) - при значениях L,C соответствующих варианту задания только в зависимости от частоты f.
Табл. 7.1 Парам.1___=_____( L/C/f), Парам.2___=_____( L/C/f), Вар. параметр __________
|
Знач. Вар.
Парам.
L/C/f
(____)
|
U
(напр.
на конт.)
|
IL
|
IC
|
I
|
C
между
U—IC
|
L
между
U—IL
|
между
U--I
|
P
активн.
|
Q
реакт.
|
S
полная
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. По данным п.5 построить резонансные кривые, наложив их на имеющиеся графики, построенные по п.4. Определить условие согласования и схему включения параллельного контура с генератором, который используется в этой ЛР, объяснить полученный результат теоретически (см. методические указания к ЛР №6).
7. Сделать выводы и обобщения по проделанной работе.
Методические указания
Для выявления характерных особенностей резонансных режимов в электрических цепях синусоидального тока следует первоначально ознакомиться с методическими указаниями к лабораторной работе № 6.
Резонанс токов наблюдается в электрической цепи с параллельным соединением катушки индуктивности и конденсатора рис.7.2. В случае, если R1=0 и R2=0, то цепь рассматривается как идеальный резонансный контур.
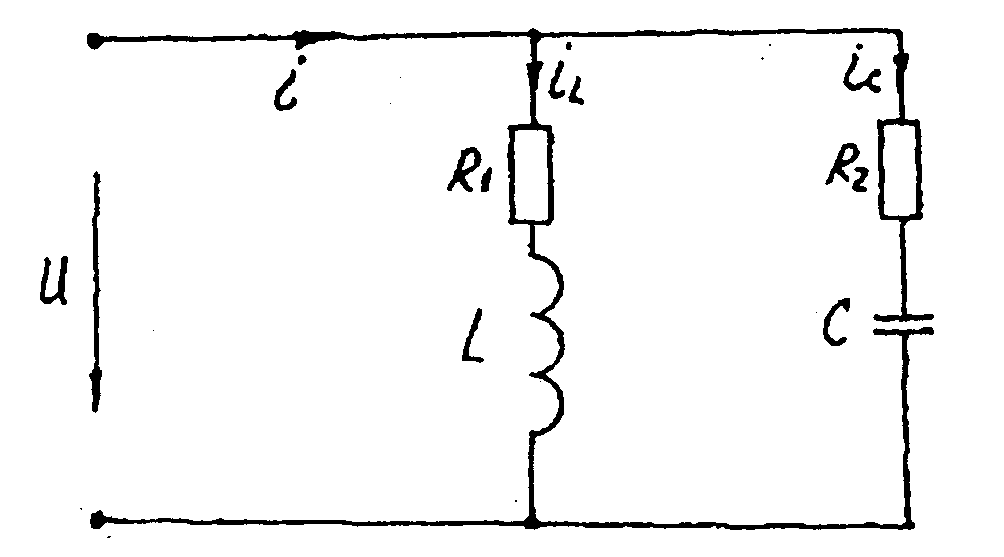
Рис.7.2
Резонанс в цепи (рис.7.2) наступает, когда входная реактивная проводимость равна нулю: BВХ=BC-BL=0
Постановка реактивных проводимостей BC и BL, выраженных через параметры цепи на переменном токе приводит к уравнению:
;
Таким образом, резонанс в рассматриваемой цепи, может быть достигнут изменением одного из параметров (, L, C, R1, R2) при остальных четырех постоянных. Решение последнего уравнения относительно дает следующее значение для резонансной частоты:
0= =;
При резонансе равны и противоположны по фазе реактивные составляющие токов в ветвях. При чем эти значения могут быть значительно больше тока на входе цепи. Поэтому такой резонанс получил название резонанса токов.
Для схемы рис.7.2, в которой R2=0, при изменении индуктивности L или частоты минимум полной проводимости цепи, а также минимум общего тока наступает на другой частоте, отличной от резонансной частоты 0. Если же переменным параметром является емкость С, то проводимость и общий ток достигают минимума при резонансе токов.
В радиотехнике широко применяются резонансные контура с малыми потерями, для которых R1 и
R2 пренебрежимо малы по сравнению с . Поэтому далее рассматриваются особенности контура с параллельным соединением R, L, C (рис.7.3). Проводимость G=1/R, может быть найдена при малых R1, R2, из соотношения: G=(R1+R2)/2
i
iG iC iL
u G C L
Рис 7.3
Мгновенные значения токов в ветвях цепи при значении входного напряжения u=Umsint:
iG=GUmsin(t); iL=(1/L)=(1/L)Umsin(t-/2); iC=Cdu/dt=CUmsin(t+/2);
Суммарный ток в цепи: i= iG+ iL+ iC= GUmsin(t)-(1/L-C)Umsin(t-/2)=Y Umsin(t-)
Где: Y=- модуль входнойпроводимости цепи;
=arctg (BL-BC)/G= arctg BВХ/G – сдвиг фаз между током и напряжением на входе цепи;
BL=1/L, BC=C; - проводимости реактивных элементов;
BВХ= BL-BC – входная проводимость цепи.
Если рассматривать комплексную амплитуду суммарного тока, то ее можно представить как векторную сумму комплексных амплитуд токов: .
Суммарная амплитуда тока цепи:
Выражение для активной P, реактивной Q, полной мощности S, которую потребляет цепь:
P=0.5UmImcos=0.5U2mG; Q=0.5UmIm sin =0.5U2mBBX; S =0.5UmIm=0.5U2m Y=.
Условие передачи максимальной активной мощности в цепи определяется аналогично тому, как это описано в ЛР-№6. Сопротивление нагрузки ZН (см. рис. 6.4) при резонансе цепи: ZН=LG/C.
Резонансная частота параллельного колебательного контура (см. рис. 7.3):
Волновая проводимость численно равна проводимости реактивного элемента при резонансе:
=0С=1/0L=.
Превышение токов в реактивных элементах над входным током цепи имеет место при условии:
G<0С=1/0L=.
Величина, обратная добротности, называется затуханием контура: =1/Q=ImG/ImL= ImG/IC=G0L.
Где ImG, ImL, ImC – амплитудные значения токов на элементах цепи при резонансе.
Зависимость величин ( BL, BC, BBX, Y ), характеризующих цепь от частоты, называют частотными характеристиками цепи, а зависимости значений токов в ветвях и входного тока или отношений токов от частоты – резонансными характеристиками (кривыми).
На рис. 7.4 построены частотные характеристики идеального параллельного контура, а на рис.7.5 представлены его резонансные характеристики, питаемого от источника синусоидального напряжения. На рис.7.5 приведены также векторные диаграммы токов в цепи, где:
IR=U/R, IL=U/L, IC=UC, I=UY (все для действующих амплитуд).
При введении обобщенной расстройки ( см. к методические указания к ЛР №6 ), входное сопротивление параллельного контура может быть представлено:
; где - активное сопротивление параллельного контура при резонансе.
Выражение для нормированной резонансной кривой тока в реактивных элементах контура:
; где Im0 – амплитудное значение резонансного тока через реактивный элемент.
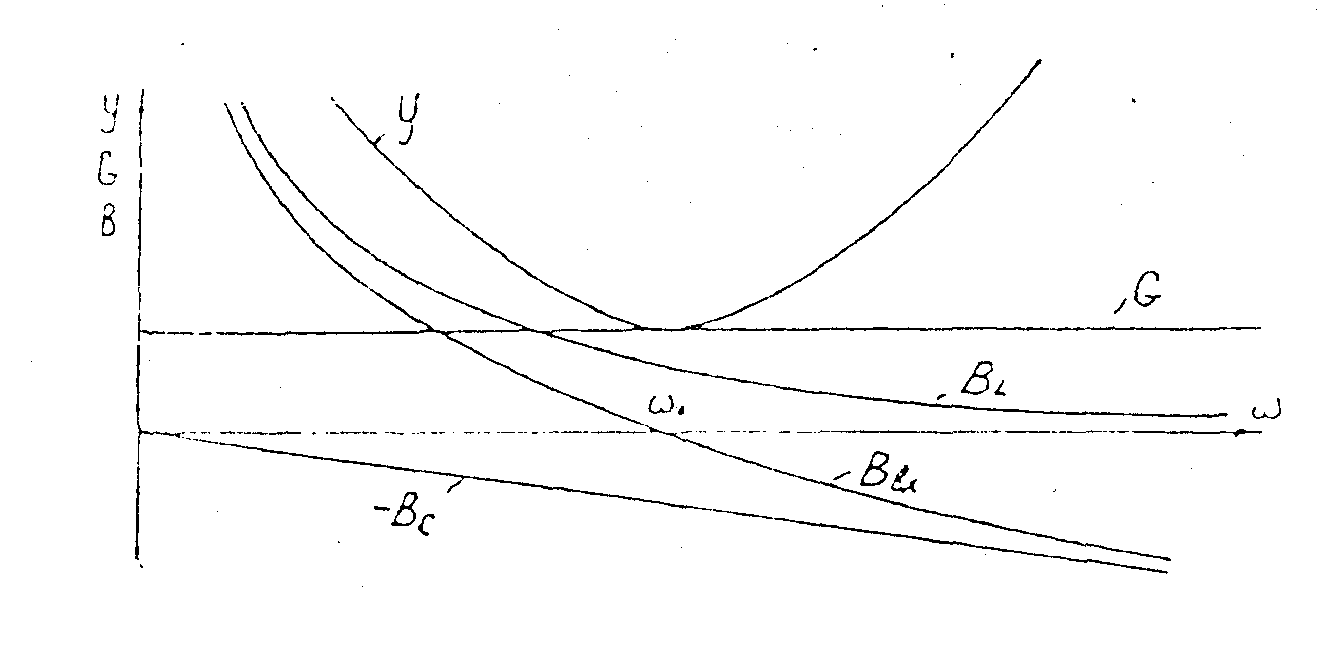
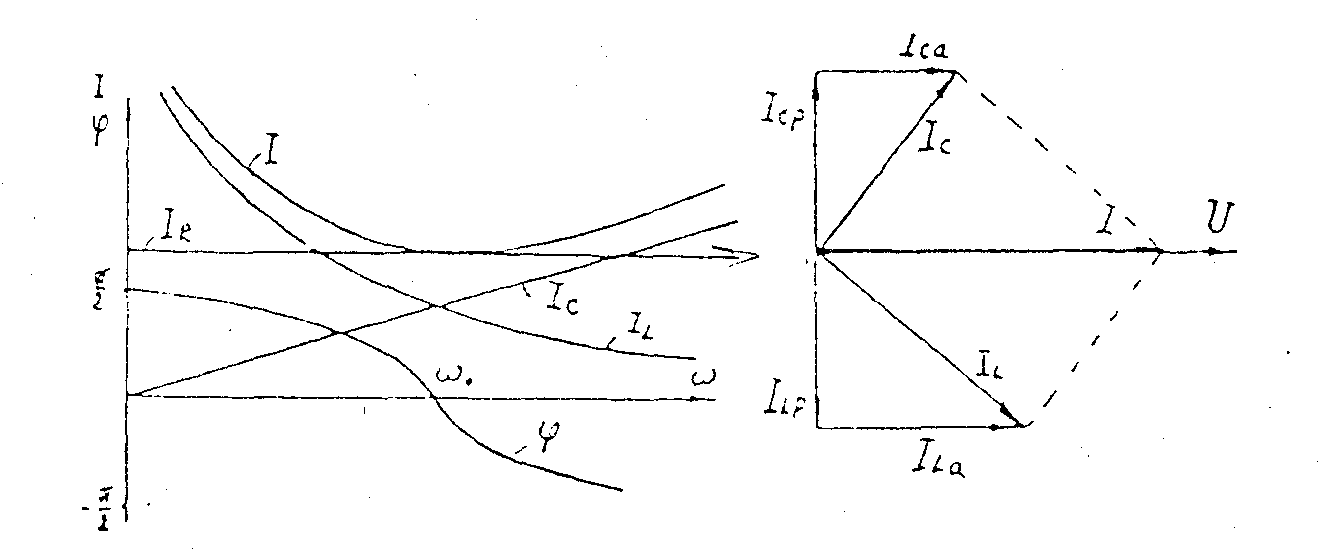
Рис. 7.4. Рис.7.5
Таблица 7.2 Варианты заданий.
|
Вариант
|
R L Ом
|
RC
Ом
|
C нФ
|
L мкГн
|
RВН к Ом
|
|
1
|
0.2
|
0.1
|
1000
|
1000
|
1.5
|
|
2
|
0.8
|
0.2
|
100
|
500
|
3
|
|
3
|
0.6
|
0.2
|
500
|
1000
|
1
|
|
4
|
0.3
|
0.1
|
25
|
50
|
2
|
|
5
|
0.4
|
0.1
|
100
|
250
|
3
|
|
6
|
0.6
|
0.5
|
250
|
1000
|
2
|
|
7
|
0.4
|
0.1
|
100
|
200
|
2
|
|
8
|
0.2
|
0.1
|
300
|
500
|
4
|
|
9
|
1.7
|
0.
|
30
|
300
|
3
|
|
10
|
0.4
|
0.1
|
150
|
400
|
3
|
Исследование параллельного колебательного контура (резонанс токов)