Исследование магнитной связи и связанных колебательных контуров
Лабораторная робота № 8
Исследование магнитной связи и связанных колебательных контуров.
Краткое содержание работы
В процессе выполнения работы исследуются и изучаются следующие вопросы:
1) Магнитная связь между катушками, входящими в разные колебательные контура;
2 Явление резонанса в двух одинаковых связанных колебательных контурах:
-полная настройка в резонанс связанных колебательных контуров;
-вид резонансных кривых и проверка аналитических соотношений.
Подготовка к работе
1. Ознакомиться с рабочим заданием и методическими указаниями. Ответить на следующие вопросы:
а) как учитывается влияние магнитной связи между двумя катушками при составлении уравнений цепи по второму закону Кирхгофа ?
б) характеризуйте встречное и взаимосогласованное включение двух последовательных катушек и определите теоретически их суммарное сопротивление в каждом из случаев;
в)как экспериментально определить одноименные выводы двух магнитосвязанных катушек и величину их взаимной индуктивности?
г) что собой представляет система двух связанных колебательных контуров (характеризуйте коэффициент связи и возможные типы и виды связи) ?
д) характеризуйте возможные виды резонансных кривых коэффициента передачи по напряжению системы двух связанных одинаковых контуров в зависимости от параметра связи;
ж) перечислите виды настройки системы двух связанных контуров и дайте их характеристику.
2. Составить протокол отчета по лабораторной работе.
Рассчитать цепи в соответствии с вариантом задания:
а) Для таблиц п.2 и п.4 рабочего задания;
б) Для таблиц п.8 рабочего задания в случае частного резонанса. Теоретически доказать этот случай – частный резонанс 2-х связанных контуров и построить графические зависимости КU(j), U();
в) Для таблиц п.9 рабочего задания в случае полного резонанса. Теоретически доказать этот случай – полный резонанс 2-х связанных контуров и построить графические зависимости КU(j), U(). Рассчитать критический коэффициент связи между связанными контурами КсКР по которому определить значение критической магнитной связи М КР;
Рабочее задание
1. Собрать схему для исследования связанных катушек индуктивности в соотв. с рис.8.1 и вариантом задания (см. табл. 8.3). Значение номиналов сопротивлений R1, R2 умножить на значение коэффициента К в соответствии с вариантом задания.
I M
R1
L1 L2 R2
EГ
Рис.8.1
2.Установить частоту генератора ЕГ в соответствии с вариантом задания (см. табл. 8.3). Выходное напряжение генератора установить 10 В. В режиме временного моделирования цепи измерять ток в цепи, напряжения на элементах и сдвиг фаз между током в цепи и напряжением на ее входе . Данные занести в табл. 8.1
табл. 8.1 ЕГ = fГ=
|
I |
UR1 |
UL1 |
UR2 |
UL2 |
|||
|
Эксперим. |
|||||||
|
Расчет |
3. Собрать схему для исследования связанных катушек индуктивности в соотв. с рис.8.2 и вариантом задания (см. табл. 8.3). Значение номиналов сопротивлений R1, R2 умножить на значение коэффициента К в соответствии с вариантом задания.
4. Установить частоту генератора ЕГ в соответствии с вариантом задания (см. табл. 8.3). Выходное напряжение генератора установить 10 В. В режиме временного моделирования цепи измерять токи в цепи, напряжения на элементах. Измерять также сдвиг фаз 1- между током в цепи I1 и напряжением на ее входе (на генераторе), сдвиг фаз U -- между напряжением на выходе цепи U2 и напряжением на ее входе U1 (на генераторе), коэффициент передачи по напряжению- КU(j)=U2/EГ. Данные занести в табл. 8.2
I1 M I2
R1
L1 L2 R2 U2
EГ
Рис.8.2
табл.8.2 ЕГ = fГ=
|
I1 |
UL1 |
UR1 |
1 |
I2 |
UR2 |
U |
КU(j) |
||
|
Экспер. |
|||||||||
|
Расчет |
5. Записать исходные уравнения для схем на рис 8.1 и 8.2. Произвести расчет величин, приведенных в табл. 8.1 и 8.2. Сделать выводы о действии магнитной связи.
6. Собрать схему для исследования связанных резонансных контуров в соотв. с рис.8.3 и вариантом задания (см. табл. 8.3). Дополнительные параметры схемы ( значение М, С2 ) рассчитать в соотв. с п.7
I1 M I2
R1 C1 R2
L1 L2 C2 U2
EГ
Рис.8.3
7.Считая, что первый контур (L1, C1) настроен на частоту настройки 2-х связанных контуров –f0, вычислить необходимое значение емкости конденсатора C2 из формулы собственного резонанса второго контура (L2, C2) на частоте f0.Вычислить также по известным соотношениям (см. ЛР.7) добротности контуров- Q1, Q2.
По вычисленным добротностям, ориентировочно рассчитать коэффициент связи между контурами, когда должна наблюдаться «двугорбая» резонансная кривая коэффициента передачи контуров по напряжению с полосой между максимумами, равной полосе пропускания единичного контура:
kсв= откуда: М = kсв
8. Изменяя емкость конденсатора С2 в небольших пределах ( примерно +-10%) от расчетного значения, снимать в режиме АС семейство резонансных кривых коэффициента передачи по напряжению для системы связанных контуров (К(j)=U2/EГ). По семейству полученных характеристик найти ту, которая соответствует частному резонансу системы связанных контуров (максимальная амплитуда напряжения на выходе и симметричный вид резонансной кривой по отношению к резонансной частоте f0). Данные о характере зависимости резонансной кривых вблизи и при частном резонансе 3…4 кривые для КU(j)=КU(j)ехр(jU()) занести в несколько табл.8.4 и построить графики КU(j), U(), совместив их с теоретическими, полученными в п 2 раздела «Подготовка к работе».
9. В состоянии частного резонанса системы связанных контуров ( см. п. 8), Изменять дискретно величину связи М в пределах примерно +-100% наблюдать изменение характера резонансных кривых коэффициента передачи по напряжению для системы связанных контуров (КU(j)=U2/EГ и U()). Добиться величины связи М, при которой резонансная кривая КU(j) будет превращаться из «двугорбой» в «одногорбую» при этом форма кривой должна быть симметрична по отношению к вертикальной линии, проходящей через частоту f0 и иметь максимально-возможную амплитуду напряжения на выходе. Это состояние системы связанных контуров будет соответствовать полному резонансу, а величина связи между контурами считается критической. Данные (для 3…4 кривых) о характере резонансных кривых вблизи и при полном резонансе занести в таблицы, аналогичные табл.8.4 и построить графики КU(j), U(),совместив их с теоретическими, полученными в п 2 раздела «Подготовка к работе»..
10. Сделать выводы и обобщения по проделанной работе.
Табл. 8.3 ЕГ – выбрать синусоидальным со значением частоты f.
|
№ вар. |
R1 Oм |
С1 нФ |
L1 мкГн |
L2 мкГн |
R1 Oм |
f кГц |
K |
|
1 |
0.3 |
1000 |
1000 |
500 |
0.1 |
5.0 |
80 |
|
2 |
1.0 |
100 |
500 |
200 |
0.3 |
20.0 |
50 |
|
3 |
0.7 |
500 |
1000 |
300 |
0.2 |
7.0 |
50 |
|
4 |
0.3 |
25 |
50 |
30 |
0.2 |
70.0 |
30 |
|
5 |
0.5 |
100 |
250 |
100 |
0.2 |
30.0 |
70 |
|
6 |
0.8 |
250 |
1000 |
200 |
0.3 |
10.0 |
60 |
|
7 |
0.5 |
100 |
200 |
100 |
0.2 |
15.0 |
70 |
|
8 |
0.3 |
300 |
500 |
150 |
0.1 |
13.0 |
100 |
|
9 |
1.3 |
30 |
300 |
200 |
0.9 |
50 |
40 |
|
10 |
0.5 |
150 |
400 |
200 |
0.2 |
25 |
70 |
Табл.8.4 f0=_______; C2=________; Q1=________; Q2=_________; KCB=________; M=________.
|
f |
||||||||||||
|
КU(j) |
расчет |
|||||||||||
|
экспер |
||||||||||||
|
U() |
расчет |
|||||||||||
|
экспер |
Примечание: графы «расчет» необходимо обязательно заполнить только для двух случаев- полного и частного резонанса.
Методические указания
Все теоретические соотношения, которые характеризуют работу исследуемых в ЛР цепей, могут быть получены путем анализа цепей на переменном токе с составлением и решением соответствующих уравнений.
Так для цепи на рис.8.1: EГ=R1I+jL1I+jMI+R2I+ jL2I+ jMI
Для цепи на рис.8.2: I1(R1+ jL1)-I2 jMI2= EГ; I2(R2+ jL2)-I1 jMI1=0.----- Решение этой системы уравнений, например, в отношении коэффициента передачи по напряжению:
К(j)=К(j)ехр(j())= U2/EГ= jMR2/((( R1+ jL1) (R2+ jL2))+ 2M2).
Для теоретического анализа цепи представленной на рис.8.3 может бить составлена и решена система уравнений, аналогичная той, которая была составлена для цепи на рис.8.2. Решение этой системы уравнений в отношении коэффициента передачи по напряжению КU(j)= U2/EГ для двух одинаковых резонансных контуров: R=R1=R2; L=L1=L2; C=C1=C2: КU(j)=M/C, где:
=(R+(L-1/C))2+2M2=R2(1+j)2+2M2 ---определитель системы уравнений;
=(L-1/C)/R---обобщенная расстройка - новая частотная переменная. ___
Если предположить, что в окрестности резонансной частоты для обоих контуров 0=1/LC
можно приближенно считать: 2M2 = 02M2 = М2/ LC, а также если ввести два понятия:
kC=M/L---коэффициент связи; и А= kCQ--- параметр связи, где Q-добротность контура, то выражение для КU(j) может представлено с учетом замены частотной переменной на :
_____________
КU(j:) = AQ/((1+j)2+A2) или КU(j:) = AQ/(1+2+A2) 2+44; U()= - arctg (2/(1+2+A2)).
Анализ выражения КU(j:) показывает, что при А1 характеристика «одногорбая», при А1 – «двугорбая» ( см рис. 8.4). При А=1 наблюдается критический режим резонанса в связанных контурах и ему соответствует критический коэффициент связи kCКР.
При А1, резонансная кривая «двугорбая» с координатами максимумов по оси абсцисс мах и значением обобщенных *, которые соответствуют полосе пропускания цепи, состоящей из двух связанных контуров по уровню неравномерности кривой при =0:
____ __ ____
мах=А2-1 ; *=2*А2-1 (см. рис. 8.4).
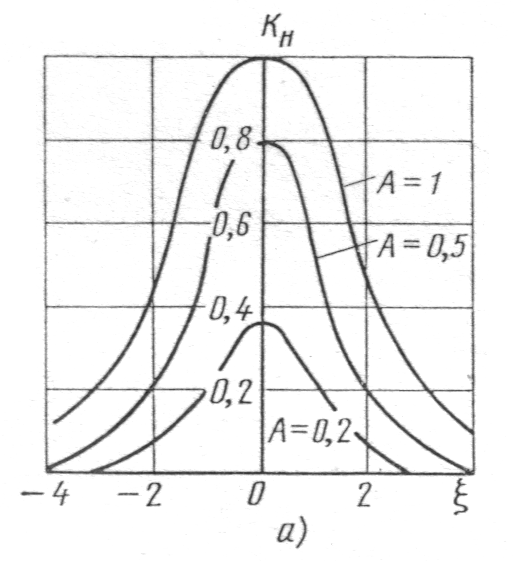
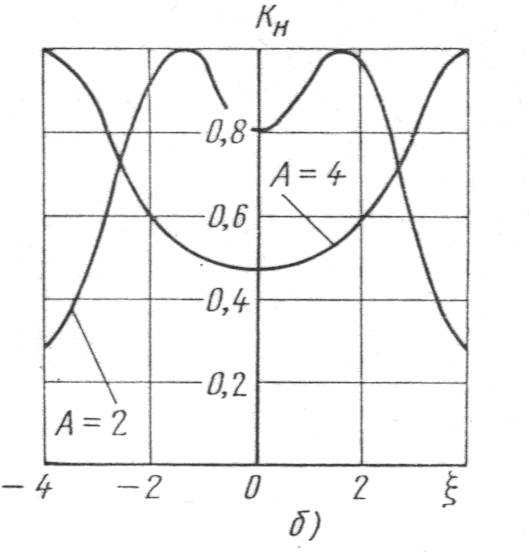
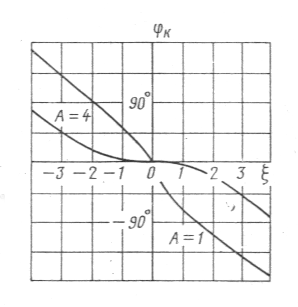
Рис. 8.4
Исследование магнитной связи и связанных колебательных контуров