D-алгоритм

D-алгоритм построения тестов для обнаружения неисправносетй (метод D-кубов, алг. Рота)

Алгоритм Рота сформулирован на языке кубических комплексов, координатой кубического комплекса является одно из значений алгоритма {0, x, 1, d, не d}. Алгоритм начинается с места проверяемой неисправности и дялее двигается от места неисправности к выходам схемы, при этом на каждом цикле вычислений отбрасываются несущественные пути. Эта процедура называется прямой фазой продвижения алгоритма.

Далее алгоритм двигается в обратную сторону – от выходов ко входу, при этом учитываются решения полученные на прямой фазе продвижения алгоритма.

Основные понятия алгоритмов

1. Вырожденное покрытие

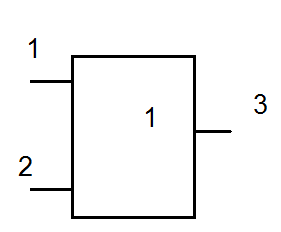
В данном алгоритме принято входы и выходы схемы называть вершинами и обозначать их цифрами, причем для упорядочения алгоритма номер выхода должен быть больше номеров его входа. Вырожденное покрытие представляет собой сокращенную запись таблицы истинности работы элементов. Вырожденное покрытие для схемы состоти из вырожденных покрытий ее элементов.

1	2	3
1	х	1
х	1	1
0	0	0

1	2	3	4	5	6
0	х	х	0	х	Х
Х	0	х	0	х	х
1	1	х	1	х	Х
	1	х	1
	х	1	1
	0	0	0
		1	х	0
		х	1	0
		0	0	1

Х==’ ‘

Каждая строка вырожденного покрытия элементов называется кубом.

2. d

1	2	3
d	0	d
0	d	d

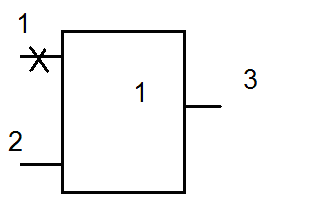
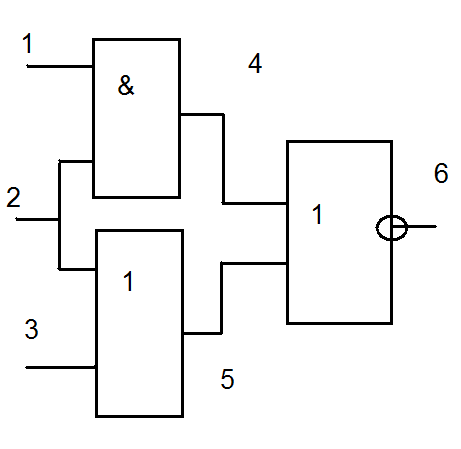
Первый куб означает, что если на первой вершине какая-либо неисправность (d), то для того, чтобы эта неисправность проявилась на выходе на второй вершине должен быть 0, аналогично и для второго куба, т.е. d - элемент транспортирования неисправности от входа элемента к его выходу. В отличии от символа Х в каждом кубе символ d может принимать только 1 значение – 0 или 1.

Существует формальное правило построения d элементов. Для этого надо по определенным правилам пересекать пары кубов вырожденного покрытия элементов, причем пересекают такие пары кубов. Которые имеют различные значения на выходе.

00=х0=0х=0

11=х1=1х=1

Хх=х, 10=d, 01=d

3. Простой d неисправностей – текст неисправного элемента с которого начинается работа алгоритма.

Символ d на 3й вершине поставлен потому, что без неисправности на этой вершине 0, а с неисправностью – 1.

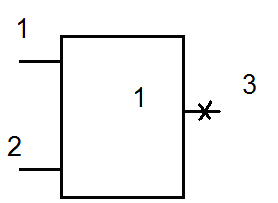
Существует формально правило построения простых d-кубов: для этого надо пересекать пары кубов вырожденных покрытий исправного или неисправного элементов, причем пересекают такие пары, которые имеют различные значения сигналов на выходе.

Без неиспр. С неиспр.

1	2	3
1	х	1
х	1	1
0	0	0
1	2	3
1	х	1
х	1	1
0	0	1

4. d-пересечение.

Выполняя операцию d-пересечения находят существенные пути от места неисправности, до выхода схемы, т.е. эта операция связывает между собой существенные пути между элементами.

Операция d-пересечения выполняется по следующему равилу:

	0	1	x	d	d
0	0	ф	0	ф	Ф
1	Ф	1	1	ф	ф
Х	0	1	х	d	d
d	Ф	Ф	d	µ
d	ф	ф	d		µ

Ф – данное пересечение пусто или не определенно, в этом случае решение отбрасывается.

Рассмотрим ход алгоритма на примере:

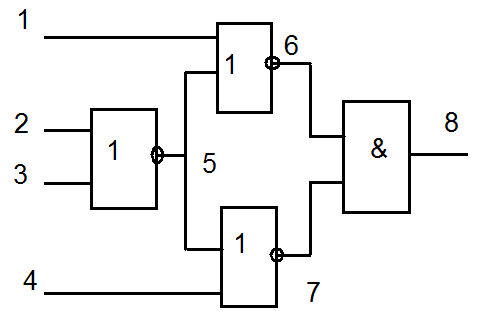
1	2	3	4	5	6	7	8
	Х	1		0
	1	Х		0
	0	0		1
Х				1	0
1				Х	0
0				0	1
				х	1	0
				1	Х	0
				0	0	1
					1	1	1
					х	0	0
					0	х	0

1	2	3	4	5	6	7	8
	0	D		d
	d	0		d
0				D	d
d				0	d
			0	D		d
			d	0		d
					1	d	d
					d	1	d

Первый цикл вычислений:

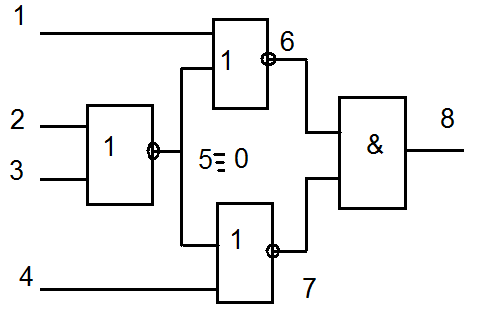
Испр 5 эл. Неиспр 5эл.

2	3	5
х	1	0
1	х	0
0	0	0

2	3	5
х	1	0
1	х	0
0	0	1

Tс = 235

00d

В каждом цикле вычислений для определения дальнейшего хода алгоритма после каждого полученного решения записываются 2 параметра:

A(tс)

Координатой вектора активности векторного куба может быть любая вершина данного куба, удовлетворяющая следующим трем условиям:

Вершина должна принадлежать данному кубу
Значение вершины в данном кубе должно быть d или d
Вершина должна быть связана с другими вершинами последующих элементов, не входящих в данный тестовый куб

d-ветвление – просто список номеров элементов, с которыми связаны вершины, входящие в данный тестовый куб.

Результат первого цикла вычислений:

A(tс) = {5}

d-ветвление = {6,7}

D-алгоритм