Построение тестов для обнаружения кратных неисправностей в 2х ступенчатых схемах «И-ИЛИ»
Построение тестов для обнаружения кратных неисправностей в 2х ступенчатых схемах «И-ИЛИ»
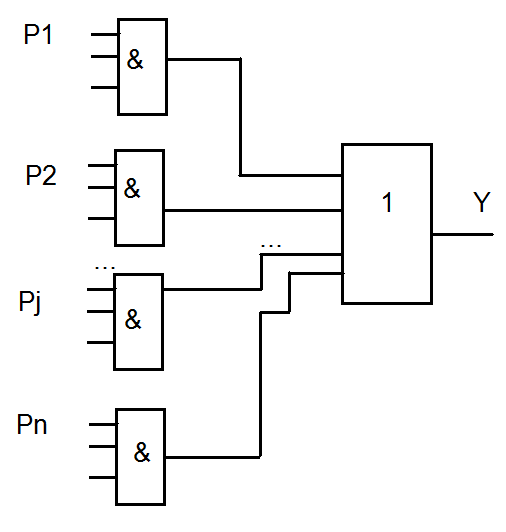
n
Y= Pj
j=1
Как для одиночных неисправностей для обнаружения кратных неисправностей различают тест для проверки нулевых неисправностей (тест A) и тест для проверки единичных неисправностей (тест B).
В тесте A кол-во наборов соответствует кол-ву элементов «И», т.к. одновременно проверить сразу несколько элементов «И» невозможно (смотри ЭНФ).
Кол-во наборов в тесте B максимально равно кол-ву переменных, но может быть и меньше, т.к. одним тестовым набором может проверяться несколько неисправностей в различных элементах «И».
Графический метод построения тестов с помощью карт Карно
Рассмотрим построение на следующем примере:
Y=A D + B C + A B + A B C
|
|
|
|
A |
|
|
|
|
0 |
4 |
12 |
8 |
|
|
D |
1 |
5 |
13 |
9 |
|
|
2 |
7 |
15 |
11 |
C |
|
|
|
3 |
6 |
14 |
10 |
|
|
|
|
B |
|
|
|
№ Набора |
A |
B |
C |
D |
Y |
|
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
0 |
|
2 |
0 |
0 |
1 |
0 |
0 |
|
3 |
0 |
0 |
1 |
1 |
0 |
|
4 |
0 |
1 |
0 |
0 |
1 |
|
5 |
0 |
1 |
0 |
1 |
1 |
|
6 |
0 |
1 |
1 |
0 |
1 |
|
7 |
0 |
1 |
1 |
1 |
1 |
|
8 |
1 |
0 |
0 |
0 |
1 |
|
9 |
1 |
0 |
0 |
1 |
0 |
|
10 |
1 |
0 |
1 |
0 |
1 |
|
11 |
1 |
0 |
1 |
1 |
1 |
|
12 |
1 |
1 |
0 |
0 |
1 |
|
13 |
1 |
1 |
0 |
1 |
1 |
|
14 |
1 |
1 |
1 |
0 |
1 |
|
15 |
1 |
1 |
1 |
1 |
0 |
На карте буквой A отмечены наборы, на которых эта переменная имеет значение 1.
Соответственно тоже самое и для B, C, D.
Построение теста А
На карте Карно в виде прямоугольников изображаются произведения.
В данной задаче таких произведений 4.
Как видно из карты, на тех наборах, которые пересекают прямоугольники, функция Y всегда равна 1.
При построении теста А надо для каждого произведения выбрать по одному набору, причем следует выбирать наборы без пересечений (наборы с пересечениями пытаются одновременно проверить несколько произведений, что невозможно).
T(А) = {7 14
6 13 8 11}
[см. схему с линиями у Миши]
|
№ Набора |
A |
B |
C |
D |
Y |
|
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
0 |
|
2 |
0 |
0 |
1 |
0 |
0 |
|
3 |
0 |
0 |
1 |
1 |
0 |
|
4 |
0 |
1 |
0 |
0 |
1 |
|
5 |
0 |
1 |
0 |
1 |
1 |
|
6 |
0 |
1 |
1 |
0 |
1 |
|
7 |
0 |
1 |
1 |
1 |
1 |
|
8 |
1 |
0 |
0 |
0 |
1 |
|
9 |
1 |
0 |
0 |
1 |
0 |
|
10 |
1 |
0 |
1 |
0 |
1 |
|
11 |
1 |
0 |
1 |
1 |
1 |
|
12 |
1 |
1 |
0 |
0 |
1 |
|
13 |
1 |
1 |
0 |
1 |
1 |
|
14 |
1 |
1 |
1 |
0 |
1 |
|
15 |
1 |
1 |
1 |
1 |
0 |
Построение теста B
Рассмотрим одно из произведений функции, например A B C и предположим, что неисправность типа 1 находится на входе А, тогда:
A B C = 1 * B C = (A + A) * BC = A B C + A B C.
Как видно, наличие единичной неисправности по переменной А приводит к тому, что реализуется правильное произведение A B C и кроме того дополнительное произведение A B C, которое отличается от правильного только одной инверсной буквой. Такие произведения называются смежными.
Смежное – такое произведение, которое состоит из тех же самых букв, но отличается только одной инверсной буквой. Можно показать появление смежных произведений и для других переменных, таким образом тест B должен проверять наличие смежных произведений.
Построим все смежные произведения функции Y и нанесем их на карту Карно.
[Карту см. у Глеба]
|
Основное произведение |
Смежное произведение |
|
|
1 |
AD |
AD |
|
|
|
AD |
|
2 |
BC |
BC |
|
|
|
BC |
|
3 |
AB |
AB |
|
|
|
AB |
|
4 |
ABC |
ABC |
|
|
|
ABC |
|
|
|
ABC |
Для построения теста необходимо выбрать такие наборы, для проверки всех смежных произведений на которых функция Y равна 0. При том следует выбирать такие наборы, которые проверяют несколько произведений одновременно, т.е. графически, это наборы с максимальным пересечением (4,5,7,6,12,13,14,8,10,11).
T(B) = {2, 15, 9}
Tобщий = {7,14
6,8,11,12,2,9,13}
Данный графический метод используется при кол-ве переменных не более 5.
Построение тестов для обнаружения кратных неисправностей в 2х ступенчатых схемах «И-ИЛИ»