Троичное моделирование
В РП2 получилась временная диаграмма работы схемы, только в ней время откладывается по оси ординат – сверху вниз. Нарисуем по этой таблице временную диаграмму, отражающуюся на экране монитора.
Троичное моделирование
Троичное моделирование широко используется для выявления состязаний сигналов, которые могут иметь место в схеме. Состязания сигналов недопустимы, как на временной диаграмме работы схемы, так и на тестовых последовательностях, которые разрабатываются для контроля и диагностики ЭВА. При моделировании используется троичный алфавит {0, x, 1}. В соответствии с определением X составляются троичные таблицы истинности работы эл-в на основании следующих логических выражений:
1 x = x x=x 0=x x=1+x=x+x=0+x=x
X 0 = 0
X 1=1
x=¬x – это равенство определяется следующим образом: нам не известно что такое х – 0 или 1 и нам неизвестно что такое ¬х – 0 или 1.
|
|
0
|
x
|
1
|
|
0
|
0
|
0
|
0
|
|
x
|
0
|
x
|
x
|
|
1
|
0
|
x
|
1
|
|
|
0
|
x
|
1
|
|
0
|
0
|
x
|
1
|
|
x
|
x
|
x
|
1
|
|
1
|
1
|
1
|
1
|
|
+
|
0
|
х
|
1
|
|
0
|
0
|
x
|
1
|
|
x
|
x
|
x
|
1
|
|
1
|
1
|
x
|
0
|
Метод Эйхельбергера
Этот метод основан на том, что соотношение задержек в эл-х и линиях связи является произвольным, т.е. соотношение может быть каким угодно, но в реальности это не совсем так.
Моделирование входного набора происходит в 2 этапа.
На первом этапе моделируются промежуточный набор Vn’.
Символ х в этом наборе ставится на тех входах схемы, на которых произошло изменение значения сигналов по сравнению с предыдущим набором Vn-1
|
|
1
|
2
|
3
|
4
|
|
Vn-1
|
0
|
1
|
1
|
0
|
|
Vn
|
1
|
1
|
0
|
0
|
|
Vn'
|
x
|
1
|
x
|
1
|
Гипотетический процесс имеющий место в схеме.
На втором жтапе моделируется основной набор Vn. Если в результате моделирования этого набора на каких либо узлах схемы остается значение х, то это означает что на этом узле имеет место состязание сигналов.
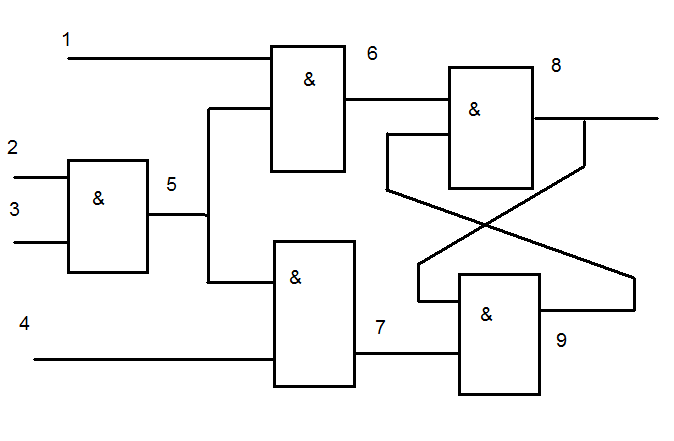
Пример: провести троичное логическое моделирование методом Э. на след. Схеме:
1234
V1 1100
V2 0101
V3 1101
V4 1111
|
|
|
Входы
|
|
|
ВХ. Вых
|
|
|
|
|
Набор
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
/-
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
|
V1
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
|
V2'
|
x
|
1
|
0
|
x
|
1
|
x
|
x
|
x
|
x
|
|
V2
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
|
V3'
|
x
|
1
|
0
|
1
|
1
|
x
|
0
|
x
|
1
|
|
V3
|
1
|
1
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
|
V4'
|
1
|
1
|
x
|
1
|
x
|
x
|
x
|
x
|
x
|
|
V4
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
x
|
x
|
Как видно из таблицы состязания сигналов имеют место только на наборе V4 т.к. на 8м и 9м выходе остались Х.
К достоинствам данного алгоритма относятся гарантированная сходимость, простота реализации и высокое быстродействие.
Недостаток . Основной недостаток заключается в том, что выявляются лишние, реально не существующие, состязания сигналов. Это происходит из-за взятого предположении о произвольном соотношении задержек в эл-х и линиях связи. Как правило для любого элемента можно указать минимальную и максимальную задержку. Для устраннения необходимо вводить разброс задержек элементов.
Троичное моделирование с нарастающей неопределенностью
В данном алгоритме для каждого л-та указывается максимальное и минимальное значение задержки, т.е. модельная задержка ri каждого эл-та лежит в пределах 0<rmin<=ri<=rrmax
Моделирование рассмотрим только с точки зрения поведения элемента задержки.
Поведение эл-та задержки определим следующим образом:
Значение сигнала на выходе равно 1 или 0 в момент времени m в том и только в том случае, когда значение сигнала на входе равно 1 или 0 в интервале времени от r- rrmax до r- rmin , в остальных случаях значение сигнала равно х.
Рассмотрим пример:
[Перерисовать у Себя]
Область неопределенности на выходе эл-та задержки сдвинута относительно области неопределенности на его входе на rmin и расширина на rrmax – rmin.
[Перерисовать у Себя]
Троичное моделирование