Диференціальні рівняння теплообміну та основи теорії подібності
PAGE 9
Лекція 2.2. Диференціальні рівняння теплообміну та основи теорії подібності.
Диференціальні рівняння теплообміну: енергії, руху, тепловіддачі та суцільності. Крайові умови.
Теоретичний і експериментальний методи досліджень. Поняття класу явищ, групи і одиночного явища. Основні положення теорії подібності. Критерії (числа) подібності для конвективного теплообміну та їх фізичний смисл. Теорема подібності. Рівняння подібності (критеріальні рівняння). Умови подібності процесів конвективного теплообміну. Узагальнення дослідних даних на основі теорії подібності. Отримання рівнянь подібності. Визначальні температура і розмір.
Джерела інформації: [1], с.352-369; [2], с.151-162; [8], с.38-68.
Диференціальні рівняння теплообміну: енергії, руху, тепловіддачі та суцільності. Конвективний теплообмін визначається не тільки тепловими, але й гідродинамічними явищами. Тому математичний опис задач конвективнго теплообміну включає диференціальні рівняння енергії, тепловіддачі, руху і суцільності, а також крайові умови (умови однозначності), що конкретизують задачу.
Рівняння енергії. Виведемо диференціальне рівняння енергії, що описує температурне поле у рухомій рідині. В основі рівняння лежить закон збереження енергії. Уважаємо, що рідина однорідна і ізотропна, її фізичні параметри постійні, внутрішні джерела теплоти рівномірно розподілені по всьому об’єму рідини. Під внутрішніми джерелами теплоти розуміють тепловиділення усередині тіла, наприклад, внаслідок хімічних реакцій, проходження електричного струму і т. д, які характеризуються об’ємною густиною тепловиділення – тепловим потоком, який віднесений до одиниці об’єму, Вт/м3.
Виділимо у потоку рідини нерухомий відносно координатної системи елементарний паралелепіпед з ребрами dx, dy, dz (рис. 2.1) і позначимо кількість теплоти, що входить до нього за час , , , , а виходить – , , , проекції швидкості руху середовища , , .
Рис. 2.1. До виведення диференціального рівняння енергії
Вважаючи, що процес відбувається при постійному тиску (що характерно для більшості процесів тепловіддачі), на основі закону збереження енергії маємо
, (2.1)
де – теплота, що вноситься до елементарного паралелепіпеда ззовні; – внутрішнє тепловиділення; – зміна ентальпії в елементарному паралелепіпеді.
Теплота, що входить до паралелепіпеда в напрямку осі ,
, (2.2)
де – густина теплового потоку на вході до паралелепіпеда.
Примітка. Ізотропність – однаковість фізичних властивостей тіла (середовища) за усіма напрямками; характерна для газів, рідин і аморфних тіл.
Теплота, що виходить з паралелепіпеда в напрямку осі ,
. (2.3)
Різниця між кількістю теплоти, що входить до паралелепіпеда і виходить з нього уздовж осі , становить
, (2.4)
де – об’єм паралелепіпеда.
Аналогічно визначаються різниці між кількістю теплоти, що входить до паралелепіпеда і виходить з нього уздовж осей і :
; . (2.5)
Загальна кількість теплоти, що акумульована паралелепіпедом,
. (2.6)
Внутрішнє тепловиділення у паралелепіпеді за час
. (2.7)
Зміну ентальпії в елементарному паралелепіпеді визначимо через його масу , теплоємність і приріст температури :
. (2.8)
Якщо підставити вирази (2.6), (2.7) і (2.8) в рівняння (1.1), отримаємо
. (2.9)
Величина є сума густин теплового потоку, що входить до паралелепіпеда шляхом теплопровідності і конвекції уздовж вісі ,
. (2.10)
На основі закону Фур’є , а густина конвективного теплового потоку . Отже,
. (2.11)
При маємо
. (2.12)
Аналогічний вигляд мають частинні похідні від густини теплового потоку в напрямках вісей і паралелепіпеда:
; (2.13)
. (2.14)
Якщо підставити (2.12), (2.13), (2.14) в рівняння (2.9) і урахувати, що для нестисливої рідини , отримаємо
. (2.15)
У цьому рівнянні – коефіцієнт температуропровідності, м2/с. Ліва частина рівняння (2.15) є повна похідна функції за часом, яка називається субстанціональною похідною:
. (2.16)
Частинна похідна характеризує зміну температури у часі у будь-якій точці рідини (локальна зміна температури); сума – зміна температури при переході від однієї точки простору до іншої (конвективна зміна температури).
Вираз у круглих дужках правої частини рівняння (2.15) є оператор Лапласа у декартовій системі координат
. (2.17)
Отже диференціальне рівняння енергії можна записати у виді
. (2.18)
Рівняння тепловіддачі. При обтіканні в’язкою рідиною поверхні швидкість рідини на ній дорівнює нулю. Ця умова «прилипання» в’язкої рідини є наслідком того, що між поверхнею твердого тіла і рідиною діють сили молекулярного зчеплення, у результаті чого безпосередньо прилеглий до твердої стінки шар рідини стає нерухомим. Теплота крізь цей шар передається тільки теплопровідністю, і густину теплового потоку можна виразити за законом Фур’є через температурний градієнт у шарі рідини і її коефіцієнт теплопровідності :
. (2.19)
З іншого боку цей тепловий потік визначається рівнянням Ньютона-Ріхмана
. (2.20)
Якщо прирівняти праві частини рівностей (2.19) і (2.20) отримаємо диференціальне рівняння тепловіддачі
. (2.21)
З рівняння (2.21) витікає, що для визначення необхідно знайти температурний градієнт середовища поблизу від поверхні. Температурний градієнт може бути знайдений з диференціального рівняння енергії (2.18). Оскільки в це рівняння входять складові швидкості, для визначення температурного поля необхідно скласти ще диференціальне рівняння, яке дозволяє знайти поле швидкостей.
Рівняння руху. У класичній гідродинаміці рівняння руху в’язкої нестисливої рідини записується у формі диференціального рівняння Нав’є-Стокса, яке виводиться з другого закону Ньютона. В проекції на вісь це рівняння має вид:
. (2.22)
Тут – складова прискорення вільного падіння; – тиск середовища; – динамічний коефіцієнт в’язкості. Ліва частина рівняння (2.22) характеризує інерційні сили потоку, перший член правої частини – дію сил тяжіння, другий – сил тиску, третій – сил в’язкого тертя.
В рівнянні (2.22) не урахована залежність густини рідини від температури, яка визначається виразом
. (2.23)
де – густина рідини при температурі ; – теж при температурі ; – коефіцієнт об’ємного розширення, К-1; .
Після підстановки (2.23) в (2.22), остаточно отримаємо
Перший член правої частини цього рівняння визначає підйомну силу, що виникає внаслідок різниці густин холодних і нагрітих об’ємів рідини.
Рішення диференціального рівняння руху дозволяє визначити поле швидкостей .
Аналіз показує, що для розв’язання задачі конвективного теплообміну до рівнянь енергії і руху необхідно додати ще одне рівняння – рівняння суцільності.
Рівняння суцільності. В рівнянні руху з’явилася нова невідома величина – тиск . Отже кількість невідомих більше за кількість рівнянь і система є незамкнутою. Щоб замкнути систему, необхідно додати ще одне рівняння – рівняння суцільності. Це рівняння виводиться на основі закону збереження маси і записується таким:
. (2.24)
Для нестисливої рідини це рівняння прийме вигляд
. (2.25)
Крайові умови. Отримані диференціальні рівняння теплообміну охоплюють нескінченну кількість процесів тепловіддачі, тобто описують цілий клас фізичних явищ переносу теплоти. Під класом розуміють сукупність явищ однієї фізичної природи, що описуються тотожними диференціальними рівняннями. Для виділення з класу конкретної задачі до системи диференціальних рівнянь необхідно приєднати математичний опис усіх часткових особливостей процесу, що розглядається. Ці додаткові дані, які характеризують конкретне одиночне явище (конкретний процес теплообміну), називаються крайовими умовами (або умовами однозначності). Умови однозначності складаються з:
геометричних умов, які характеризують форму і розміри тіла або поверхонь, що беруть участь у теплообміні;
фізичних умов, які характеризують властивості тіл, що беруть участь у теплообміні;
граничних умов, які характеризують умови протікання процесу на границях тіла;
часових умов, які характеризують початковий стан системи при нестаціонарних процесах.
Система диференціальних рівнянь разом з умовами однозначності представляє собою математичний опис задачі теплообміну. Після розв’язання системи рівнянь можна отримати повний опис процесу в усіх деталях: поле температур, швидкостей, тисків, значення коефіцієнтів тепловіддачі.
Теоретичний і експериментальний методи досліджень. Поняття класу явищ, групи і одиночного явища. Для конвективного теплообміну ми записали чотири диференціальні рівняння: енергії, руху, тепловіддачі і суцільності (див. тему 2). Ця система рівнянь описує цілий клас явищ конвективного теплообміну.
Під класом явищ розуміють сукупність явищ однієї фізичної природи, які описуються тотожними диференціальними рівняннями, однаковими як за формою запису, так і за фізичним змістом величин, що входять до цих рівнянь. Щоб з класу явищ виділити конкретне одиничне явище, необхідно до диференціальних рівнянь додати умови однозначності. Сукупність фізичних процесів, які описуються однаковими за формою і змістом диференціальними рівняннями і однаковими за формою і змістом розмірними умовами однозначності, утворює групу явищ. Відмінність між окремими явищами, що віднесені до групи, полягає лише в відмінності числових значень величин, що входять до умов однозначності. Група явищ об’єднує всі процеси, на які можна поширити результати одиничного досліду.
При вивченні різних фізичних явищ використовують два методи досліджень, які дають змогу отримати кількісні закономірності для досліджуваних явищ: експериментальний і теоретичний. Отримані при експериментальному методі досліджень результати відрізняються достовірністю, що є превагою цього методу. Але ці результати дійсні лише для одиничного явища, яке відповідає конкретним умовам однозначності. Застосування теоретичних методів до явищ теплообміну дозволяє отримати систему диференціальних рівнянь, які описують увесь клас явищ, встановити найбільш загальні зв’язки між параметрами явища. Але перехід від класу явищ до конкретного явища утруднений внаслідок складності аналітичного розв’язання системи рівнянь. Лише об’єднання теоретичних методів з експериментальними з використанням теорії подібності дає змогу розповсюдити результати одиничного досліду на цілу групу явищ.
Основні положення теорії подібності. Теорія подібності – вчення про подібні явища. Поняття подібності можна розповсюджувати на будь-які фізичні явища, у тому числі і на теплові. Можна говорити про подібність картин руху двох потоків рідини – кінематичну подібність; про подібність сил, що спричинюють подібні між собою рухи – динамічну подібність; про подібність картин розподілу температур і теплових потоків – теплову подібність і так далі. Поняття подібності фізичних явищ зводиться до наступних положень:
поняття подібності можна застосовувати тільки до явищ одного і того ж класу, які якісно однакові і аналітично описуються рівняннями, однаковими як за формою, так і за змістом. Якщо ж математичний опис двох явищ однаковий за формою, але відмінний за фізичним змістом, такі явища називаються аналогічними. Така аналогія існує між процесами теплопровідності, електропровідності та дифузії;
обов’язковою передумовою подібності фізичних явищ має бути геометрична подібність, тобто подібні явища завжди протікають у геометрично подібних системах;
при аналізі подібних явищ співставляти між собою можна тільки однорідні величини і лише у схожих точках простору і у схожі моменти часу. Однорідними називають такі величини, котрі мають однаковий фізичний смисл і однакову розмірність. Схожими точками геометрично подібних систем називають такі, координати яких задовольняють умові: ; ; . Два проміжки часу і називаються схожими, якщо вони мають загальний початок відліку і пов’язані перетворюванням подібності ;
подібність двох фізичних явищ означає подібність усіх величин, що характеризують явище, яке розглядається. Це означає, що в схожих точках простору і в схожі моменти часу будь-яка величина першого явища пропорційна однорідній з нею величині другого явища, тобто .
Коефіцієнт пропорційності називають константою подібності; ні від координати, ні від часу не залежить. Кожна фізична величина має свою константу подібності (наприклад ). Таким чином подібність двох явищ означає подібність полів однойменних фізичних величин, що визначають ці явища.
Критерії (числа) подібності для конвективного теплообміну та їх фізичний смисл. Між константами подібності у подібних явищах завжди існують точно визначені співвідношення. Ці співвідношення виводяться з аналізу математичного опису процесів. Вони мають центральне значення в теорії подібності, бо установлюють існування особливих величин, які називають числами (критеріями) подібності.
Числа подібності – це безрозмірні комплекси, складені з величин, що характеризують явище, і які для подібних явищ у схожих точках зберігають одне і теж числове значення. Числа подібності називають іменами вчених і позначають двома початковими буквами їх прізвищ: наприклад, число Рейнольдса – Re, Нусельта – Nu. Аналіз рівнянь конвективного теплообміну дозволяє отримати такі числа подібності:
– число Нусельта, яке характеризує інтенсивність конвективного теплообміну між рідиною і поверхнею твердого тіла (l – характерний розмір системи);
– число Прандтля, яке характеризує теплофізичні властивості теплоносія;
– число Грасгофа, яке характеризує співвідношення між піднімальною силою, що виникає внаслідок різниці густин холодної і нагрітої рідини, та силами в’язкості;
– число Рейнольда, яке характеризує співвідношення між силами інерції та силами в’язкості;
– число Ейлера, яке характеризує співвідношення між силами тиску і силами інерції (визначає гідромеханічну подібність течій теплоносіїв).
Числа подібності можуть бути отримані безпосередньо з диференціальних рівнянь без їх інтегрування. Для прикладу розглянемо отримання числа Nu. Запишемо диференціальне рівняння теплообміну (див. тему 2), що виражає умови теплообміну на межі твердого тіла і рідини, для схожих точок двох подібних між собою систем:
для першої системи
; (3.1)
для другої системи
. (3.2)
Позначимо константи подібності:
; ; ; . (3.3)
Зі співвідношення (3.3) маємо
; ; ; ; .
Якщо підставити ці вирази в рівняння (3.2), отримаємо
. (3.4)
Для величин з індексом ‘ маємо два рівняння (3.1) і (3.4), які пов’язують ті ж самі змінні, тому ці рівняння тотожні. З умови тотожності рівнянь (3.1) і (3.4) витікає
. (3.5)
Рівняння (3.5) виражає зв'язок між константами подібності, який отримано з диференціального рівняння теплообміну. Величину С називають індикатором подібності. Як витікає з рівняння (3.5), для подібних явищ індикатори подібності дорівнюють одиниці. Якщо замінити константи подібності в (3.5) співвідношеннями (3.3), отримаємо
. (3.6)
З останньої рівності можна зробити висновок: існують такі безрозмірні співвідношення між параметрами, що характеризують процес, які для подібних явищ у схожих точках мають чисельно однакові значення. Ці безрозмірні співвідношення називають числами подібності. Отримане безрозмірне співвідношення (3.6) називають числом Нусельта. Таким чином можна отримати і інші числа подібності , , , якщо використати диференціальні рівняння енергії, руху, суцільності.
Теореми подібності. Основні положення теорії подібності можна сформулювати у вигляді трьох теорем.
Перша теорема подібності: подібні між собою процеси мають чисельно однакові числа подібності.
Друга теорема подібності: залежність між параметрами, що характеризують будь-який процес, може бути представлена у вигляді залежності між числами подібності. Ці залежності між числами подібності називають рівняннями подібності. Для явищ тепловіддачі рівняння подібності у загальному випадку має вид: .
Для подібних між собою процесів рівняння подібності однакові. Отже, представляючи результати будь-якого досліду в числах подібності, ми отримуємо узагальнену залежність, яка справедлива для всіх подібних між собою процесів.
Третя теорема подібності відповідає на запитання: які умови необхідні і достатні, щоб процеси були подібними. Третя теорема подібності формулюється так: подібні ті процеси, умови однозначності яких подібні, а числа подібності, які складені з величин, що входять до умов однозначності, мають однакове числове значення.
Числа подібності, які складені з величин, що входять до умов однозначності, називаються визначальними або критеріями подібності. Числа подібності, які визначаються з рівнянь подібності і містять і інші величини, що не входять до умов однозначності, називаються визначуваними (наприклад є визначальні числа, а – визначуване число).
Таким чином, теорія подібності дозволяє без інтегрування диференціальних рівнянь отримати з них числа подібності і, використовуючи дослідні дані, установити рівняння подібності, які дійсні для всіх подібних між собою процесів.
Умови подібності процесів конвективного теплообміну. При вимушеному русі теплоносія ці умови формулюються наступним чином:
подібними можуть бути лише процеси теплообміну, які протікають у геометрично подібних системах;
необхідною передумовою подібності є подібність полів швидкостей, температур і тисків у вхідному перерізі таких систем.
При виконанні цих умов стаціонарні процеси конвективного теплообміну при вимушеному русі будуть подібні, якщо
; .
Число Re визначає гідромеханічну подібність течій теплоносіїв. При рівності чисел Re умова однаковості чисел Pr забезпечує теплову подібність, тобто подібність полів температурних напорів і теплових потоків у всьому об’ємі системи, що розглядається. Відповідно до теорії подібності для подібних процесів мають бути однаковими також і визначувані числа подібності, тобто числа Nu.
Рівняння подібності для процесів конвективного теплообміну при вимушеному русі має вигляд
.
При вільній конвекції умови подібності процесів теплообміну формулюються таким чином:
подібними можуть бути процеси, що протікають у геометрично подібних системах;
необхідно забезпечити подібність температурних полів на поверхнях нагріву або охолодження.
При виконанні цих вимог стаціонарні процеси вільної конвенції будуть подібними, якщо виконується умови
; .
Рівність чисел і забезпечує подібність процесів вільної конвекції, тобто подібність полів температурних напорів, теплових потоків і швидкостей у геометрично подібних системах. Визначуване число подібності, число Nu, також стає однаковим в таких системах.
Рівняння подібності для процесів теплообміну при вільній конвекції має вид
.
Узагальнення дослідних даних на основі теорії подібності. При постановці будь-якого експерименту завжди необхідно попередньо знати:
які величини необхідно вимірювати у досліді;
як обробляти результати досліду;
які явища подібні досліджуваному.
Відповіді на ці запитання містяться у трьох теоремах подібності. На перше запитання відповідає перша теорема: у дослідах необхідно вимірювати ті величини, що входять до чисел подібності процесу, який вивчається. На друге запитання відповідає друга теорема: результати досліду необхідно обробляти у числах подібності, а залежність між ними представляти у вигляді рівнянь подібності; це дозволяє знайти загальну закономірність, яка справедлива для всіх процесів, що подібні. На третє запитання дає відповідь третя теорема: подібні ті явища, для яких подібні умови однозначності і рівні чисельно визначальні числа подібності (критерії подібності). Завдяки цим відповідям теорія подібності за сутністю є теорією експерименту.
Отримання рівнянь подібності. Визначальні температура і розмір. Покажемо на прикладі вільної конвекції, як отримують рівняння подібності. Дослід показує, що залежність між числами подібності може бути представлена у вигляді степеневої функції. Для вільної конвекції , де коефіцієнт і показник визначаються експериментально. Для розрахунку чисел подібності, що входять до цього рівняння, необхідно установити визначальну температуру і визначальний геометричний розмір.
В процесі теплообміну температура рідини змінюється, а отже змінюється значення її фізичних властивостей, що має ураховуватися при узагальненні дослідних даних. Один з шляхів урахування полягає в осередненні фізичних властивостей за допомогою введення так званої визначальної температури. По цій температурі визначаються з довідкових таблиць фізичні властивості, що входять до чисел подібності. Наприклад, при русі рідини у каналах в якості визначальної вибирають середню температуру рідини , де – температури рідини на вході до каналу, а – на виході з нього. При вільній конвекції за визначальну температуру приймають температури рідини на віддалі від поверхні. Визначальна температура указується нижнім індексом біля числа подібності: «р», «ст», «п. ш» – відповідно середня температура рідини, стінки, примежового шару.
При узагальнені дослідних даних важливим також є питання про вибір визначального розміру, в якості якого доцільно вибирати той розмір, яким визначається розвиток процесу. Наприклад, при конвективному теплообміні у круглих трубах в якості визначального розміру береться внутрішній діаметр. Для каналів неправильного і складного перерізу беруть еквівалентний діаметр
, (3.7)
де – площа поперечного перерізу каналу; – повний змочений периметр перерізу. При поперечному обтіканні труби і пучків труб в якості визначального розміру береться діаметр труби, а при обтіканні плити – її довжина у напрямку руху. При вільній конвекції на вертикальній поверхні – висота поверхні. Визначальний розмір також може бути вказаний нижнім індексом біля числа подібності: l і h – довжина і висота поверхні, d – діаметр труби.
У відповідності до першої теореми подібності у дослідах необхідно вимірювати ті величини, що входять до чисел подібності. Для задачі, що розглядається, це , , . Фізичні властивості рідини , , , вибираються з таблиць за визначальною температурою. Отже при проведенні експерименту необхідно вимірювати температуру стінки і оточуючого середовища , а для визначення з рівняння Ньютона-Ріхмана коефіцієнта тепловіддачі також і тепловий потік, що відводиться від поверхні теплообміну. Якщо необхідно отримати рівняння подібності для середніх коефіцієнтів тепловіддачі, в якості визначального розміру приймаємо висоту поверхні , а температура стінки осереднюється. Якщо шуканим є рівняння подібності для локальних коефіцієнтів тепловіддачі, в якості визначального розміру береться координата точки по висоті , а в розрахунках використовується місцева температура стінки.
Якщо злогарифмувати залежність і позначити , і , отримаємо . Останнє співвідношення є рівнянням прямої, де , – кут нахилу прямої до осі абсцис (рис. 3.1 ).
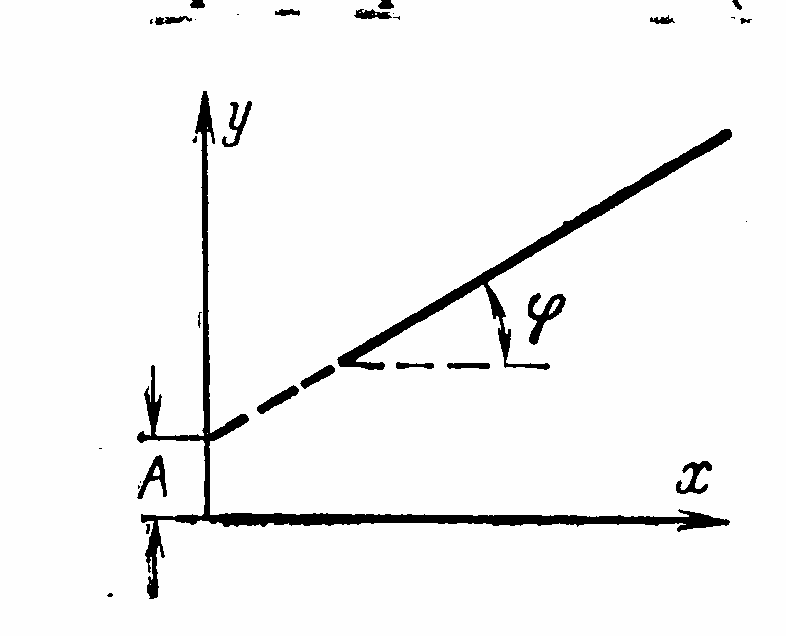
Рис. 3.1. Графічний спосіб установлення степеневої залежності між змінними
Після проведення серіії дослідів і визначення чисел подібності , , будується графік залежності , за допомогою якого визначається значення як відношення катетів. Після визначення , розраховують і значення постійної зі співвідношенням , якому задовольняє будь-яка точка прямої. Перевіркою застосування степеневої залежності є той факт, що у логарифмічних координатах усі дослідні точки ускладнюються на пряму. Якщо токи розміщуються уздовж кривої, таку криву замінюють ламаною. Для окремих ділянок такої кривої значення і різні.
Узагальнена формула дозволяє установити, який вплив на коефіцієнт тепловіддачі чинять такі величини, як геометричний розмір системи l, кінематичний коефіцієнт в’язкості середовища і т.д., які в дослідах не змінювались. Тим самим відпадає необхідність у проведені додаткових вимірювань.
Диференціальні рівняння теплообміну та основи теорії подібності