Конвективний теплообмін

PAGE 7

Л е к ц і я 2.5. Конвективний теплообмін.

Тепловіддача при вимушеному русі теплоносія. Повздовжнє обтікання пластини. Обтікання кулі. Поперечне обтікання одиночної труби і пучка труб. Течія теплоносія у трубах. Тепловіддача при вільному русі теплоносія. Характер руху рідини. Розрахунок тепловіддачі. Теплообмін у прошарках.

Джерела інформації: [1], с.370-394; [2], с.199-215; [8], с.69-110

Тепловіддача при вимушеному русі теплоносія. Повздовжнє обтікання пластини. Гідродинамічні умови розвитку процесу при поздовжньому обтіканні пластини розглянуті в лекції 1.1, рис. 1.3. Локальний коефіцієнт тепловіддачі (на відстані від початку пластини довжиною ) при ламінарній течії теплоносія (рідини) в примежовому шарі можна розраховувати за формулою

(6.1)

Межі зміни безрозмірних чисел Рейнольда і Прандтля: . У (6.1) число Нусельта (див тему 3). Індекс «р» означає, що всі теплофізичні параметри, що входять до даного безрозмірного числа (критерію), слід брати при температурі потоку , що набігає на пластину, при температурі пластини

Відношення , яке зустрічатиметься і в інших формулах, враховує зміну властивостей теплоносія за товщиною примежового шару зі зміною температури. Для газів з достатньою точністю можна вважати, що = 1.

При режим течії рідини в примежовому шарі турбулентний і розрахункова залежність для локального коефіцієнта тепловіддачі має вид

(6.2)

Від’ємні степені при X в (6.1) і (6.2) вказують на зменшення коефіцієнта тепловіддачі уздовж пластини (див. рис. 1.3). Якщо замінити всі безрозмірні числа відношеннями відповідних розмірних величин, можна виявити ступінь впливу параметрів процесу на коефіцієнт тепловіддачі: наприклад, на ділянці ламінарного примежового шару ~, а на ділянці турбулентного ~, показник степеня для коефіцієнта теплопровідності відповідно дорівнює 0,67 і 0,57.

Формули для розрахунку середніх за довжиною пластини значень чисел можна одержати інтегруванням за х рівнянь (6.1) і (6.2). Так, якщо на всій пластині режим течії в примежовому шарі ламінарний , то

(6.3)

Якщо , тобто майже на всій довжині пластини режим течії рідини в примежовому шарі турбулентний,

(6.4)

Обтікання кулі. Середній по поверхні кулі коефіцієнт тепловіддачі при вимушеному омиванні її потоком теплоносія можна розрахувати за формулою

(6.5)

За визначальний розмір тут прийнятий діаметр кулі. Межі застосування рівняння (6.5): ,

Тепловіддача при течії газу () через щільний шар куль або частинок довільної форми може бути розрахована за формулами В. І. Тімофєєва:

(6.6)

За визначальний розмір у формулах (6.6) прийнятий діаметр кулі (якщо частинки не сферичні, то , де V – об’єм частинки). Визначальна температура середня між температурами газу на вході до шару куль і виході з нього. Швидкість газу розраховується за повним перерізом, без урахування заповнення його частинками.

Поперечне обтікання одиночної труби і пучка труб. При малих числах (швидкість віднесена до найбільш вузького перерізу каналу) характер обтікання труби плавний, безвідривний (рис.6.1, а). При більших значення числа Рейнольда обтікання труби завжди супроводжується утворенням у кормовій частині вихрової зони (рис. 6.1, б).

а) б)

Рис. 6.1. Обтікання одиночного циліндра: а) безвідривне; б) відрив примежового шару

Примежовий шар, що утворюється на поверхні труби, має найменшу товщину у лобовій точці і далі поступово збільшується до тих пір, поки не відбудеться відривання потоку і утворення вихрової зони. Коефіцієнт тепловіддачі приймає найбільше значення у лобовій точці труби, де товщина примежового шару мінімальна. Зі збільшенням товщини примежового шару по периметру труби коефіцієнт тепловіддачі зменшується, приймаючи найменшого значення у точці відриву потоку. У області вихрової зони відбувається збільшення коефіцієнта тепловіддачі за рахунок руйнування примежового шару.

Експериментальні дані по тепловіддачі при поперечному обтіканні одиночної круглої труби спокійним, нетурбулізованим потоком узагальнюються формулою

. (6.7)

Параметри теплоносія у формулі (6.7) відповідають умовам потоку, що набігає; визначальним розміром є зовнішній діаметр труби. Значення коефіцієнта С і показника степеня п залежно від критерія наведені нижче:

	1 … 4103	4103 … 4104	4104 … 4105
С	0,55	0,2	0,027
п	0,5	0,62	0,8

Коефіцієнт враховує кут між напрямком течії потоку і віссю труби. Найбільші значення коефіцієнта тепловіддачі спостерігаються при розташуванні труб перпендикулярно потоку (кут = 90о і =1). При менших кутах значення можна знайти з графіка (рис. 6.2).

Турбулізация набігаючого потоку покращує теплообмін. Значення поправок, що враховують турбулізацию, для ряду практично важливих випадків можна знайти у довідниках.

У багатьох теплообмінниках труби розташовуються у вигляді шахових (рис. 6.3, а) або коридорних (рис. 6.3, б) пучків.

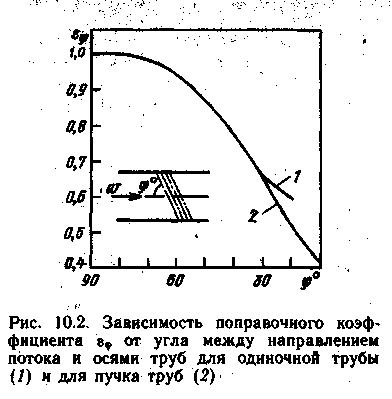
Рис. 6.2. Залежність поправкового коефіцієнта від кута між напрямком потоку і віссю труби для одиночної труби (1) і пучка труб (2)

Параметрами пучка є: поперечний крок , поздовжній крок , зовнішній діаметр труб , кількість рядів труб у напрямку руху рідини . На основі експериментальних досліджень виявлено, що тепловіддача труб другого і третього рядів вище, ніж першого. Причиною цього є збільшення турбулентності потоку при проходженні крізь пучок. Починаючи з третього ряду і далі, структура потоку залишається незмінною, тому коефіцієнт тепловіддачі приймає постійне значення.

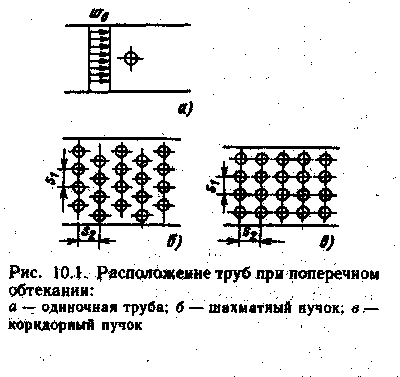
а) б)

Рис. 6.3. Шахове а) і коридорне б) розміщення труб у пучках

Середній коефіцієнт тепловіддачі при поперечному обтіканні пучків в інтервалі = 103 … 105 можна розраховувати за формулою

. (6.8)

Для шахових пучків С=0,41, п= 0,6; для коридорних – С = 0,26, п = 0,65. Визначальним розміром в (6.8) є зовнішній діаметр труб, визначальною температурою – середнє значення між температурами рідини до пучка і після нього. Швидкість розраховується як відношення об'ємної витрати теплоносія при до найвужчого перерізу в пучку, ширина якого менше ширини каналу на значення добутку зовнішнього діаметра труб на їх кількість в одному ряду. Поправковий коефіцієнт враховує вплив відносних поперечного і повздовжнього кроків. Для шахових пучків при і при . Для коридорних пучків . Поправковий коефіцієнт визначається з рис. 6.2.

Поправковий коефіцієнт ураховує номер ряду труб у пучку. Для першого ряду труб шахового і коридорного пучка = 0,6; для другого ряду труб шахового пучка = 0,7, коридорного – = 0,9; для третього і наступних рядів коридорних і шахових пучків = 1.

Середнє значення коефіцієнта тепловіддачі для усього пучка труб можна розрахувати за формулою

, (6.9)

де – середній коефіцієнт тепловіддачі і-го ряду труб за формулою (6.8); – поверхня теплообміну і-го ряду труб; – кількість рядів труб у пучку.

За інших однакових умов коефіцієнт тепловіддачі від труб шахового пучка вищий, ніж від труб коридорного, внаслідок більшої турбулізації потоку в шаховому пучку.

Течія теплоносія у трубах. При течії рідини в трубі товщина гідродинамічного примежового шару спочатку збільшується симетрично по всьому периметру до тих пір, поки шари не зіллються на осі труби (рис. 6.4). Далі рух стабілізується і гідродинамічний примежовий шар заповнює весь переріз труби. Початкова ділянка труби або каналу , на якій установлюється стабілізований розподіл швидкостей рідини, називається ділянкою гідродинамічної стабілізації.

Залежно від конкретних умов примежовий шар на початковій ділянці може встигнути перейти в турбулентний, а може і не встигнути. Відповідно стабілізований режим течії в трубі буде або турбулентним з ламінарним підшаром біля стінки, або ламінарним по всьому перерізу. При режим течії ламінарний, при установлюється сталий турбулентний режим. Режим течії у області називається перехідним.

Рис. 6.4. Гідродинамічна стабілізація течії рідини у трубі:

а) ламінарний режим течії; б) турбулентний режим течії

При ламінарному режимі у будь-якому перерізі стабілізованого потоку рідини розподіл швидкостей має вид квадратичної параболи (див. рис. 6.4, а). При турбулентному режимі основна зміна швидкості відбувається у в’язкому підшарі, а у ядрі потоку швидкість рідини по всьому перерізу практично однакова (див. рис. 6.4, б).

Поряд з ділянкою гідродинамічної стабілізації є ділянка теплової стабілізації (рис. 6.5, а), на довжині якої теплообмін між рідиною і стінкою труби (каналу) здійснюється тільки у межах теплового примежового шару, а у центральній області потоку зберігається постійна температура, що дорівнює температурі рідини на вході до труби. При змиканні теплового примежового шару у теплообміні починає приймати участь весь потік.

Локальний коефіцієнт тепловіддачі на ділянці теплової стабілізації зменшується (див. рис. 6.5, б), що пов’язано зі збільшенням товщини теплового примежового шару (див. формулу (1.9)). На ділянці стабілізованої течії , оскільки товщина теплового примежового шару постійна і дорівнює радіусу труби. Із збільшенням швидкості течії теплоносія в трубі зростає через зменшення товщини ламінарного підшару, а із збільшенням діаметру труби зменшується, оскільки росте товщина всього примежового шару. Довжина ділянки теплової стабілізації при турбулентному режимі .

Рис. 6.5. До розгляду ділянки теплової стабілізації

У зв'язку з особливостями течії рідини в трубі змінюється і саме поняття коефіцієнта тепловіддачі. Для пластини коефіцієнт розраховувався як відношення густини теплового потоку до різниці температур зовнішнього спокійного потоку і поверхні (або навпаки при ). У трубі примежовий шар займає весь переріз і спокійного потоку немає, тому під локальним коефіцієнтом тепловіддачі розуміють відношення густини теплового потоку до різниці температури стінки і середньомасової температури рідини, що протікає через даний переріз труби. Експериментально середньомасова температура рідини визначається вимірюванням її температури після перемішування.

Механізм перенесення теплоти від стінки труби до рідини визначається характером руху теплоносія. У випадку ламінарної течії теплота переноситься теплопровідністю. При значній зміні температури по перерізу та уздовж труби внаслідок різниці густин окремих шарів рідини на вимушений рух накладається вільній рух. Внаслідок цього змінюється картина руху рідини і інтенсивність тепловіддачі. Відповідний режим течії рідини у трубі називається в’язкісно-гравітаційним. Для орієнтовного розрахунку середнього коефіцієнта тепловіддачі у цьому режимі (, ) можна рекомендувати формулу

, (6.10)

де як визначальна температура прийнята середня температура рідини в трубі, а як визначальний розмір – діаметр труби або еквівалентний діаметр каналу (див. формулу (3.9)).

Коефіцієнт у (6.10) ураховує вплив ділянки теплової стабілізації. При , для коротких труб () дорівнює:

1 2 5 10 15 20 30 40

1,90 1,70 1,44 1,28 1,18 1,13 1,05 1,02

При і режим течії у трубі (каналі) називається в’язкісним. Розрахункові формули для цього режиму можна знайти у [1, 2].

При настає стабілізований турбулентний рух, коли в потоці переважають сили інерції. Для розрахунку середнього за довжиною труби (каналу) коефіцієнта тепловіддачі у цьому випадку рекомендується формула:

, (6.11)

якою можна користуватися при , . За визначальний розмір тут прийнятий внутрішній діаметр труби або еквівалентний діаметр каналу:

, (6.12)

де – площа поперечного перерізу каналу; – повний змочений периметр перерізу. Визначальною температурою є середня між температурами теплоносія на вході і виході з труби. За густиною теплоносія , яка відповідає цій температурі, і його масовою витратою розраховується середня за перерізом каналу швидкість потоку , де – площа його поперечного перерізу. Поправковий коефіцієнт , що враховує вплив ділянки теплової стабілізації (див. рис. 6.5), у випадку коротких труб () вибирається з табл. 6.1 в залежності від значення і . При .

При течії рідини у зігнутих трубах (змійовиках) коефіцієнт тепловіддачі збільшується внаслідок виникнення вторинної циркуляції рідини під дією відцентрових сил. Розрахунок коефіцієнта тепловіддачі в таких трубах виконується за формулами, що отримані для прямих труб, але знайдене значення коефіцієнта тепловіддачі помножується на поправковий коефіцієнт , де – діаметр труби; – радіус змійовика.

Таблиця 6.1. Залежність коефіцієнта від для різних

	Відношення
	5	10	20	40
1104	1,34	1,23	1,13	1,03
5104	1,18	1,13	1,08	1,02
1105	1,15	1,1	1,06	1,02
1106	1,08	1,05	1,03	1,01

Тепловіддача при вільному русі теплоносія. Характер руху рідини. Фізична природа виникнення вільного руху рідини розглянута у темі 1 (див. рис. 1.2 і рівняння (1.8)). Характерна картина вільного руху рідини уздовж гарячої вертикальної поверхні зображена на рис. 6.6, а.

Рис. 6.6. Вільний рух рідини уздовж вертикальної гарячої поверхні (а)

і вільна конвекція рідини у обмеженому об’ємі (б)

Спочатку товщина прогрітого шару рідини, що рухається уздовж поверхні, мала і її течія має ламінарний характер. Поступово до руху утягується все більша кількість рідини, товщина ламінарного шару зростає, а потім він руйнується і виникає турбулентний режим течії рідини. При ламінарному режимі коефіцієнт тепловіддачі зі збільшенням товщини шару рідини, що рухається, зменшується, а при турбулентному – різко зростає і потім по висоті поверхні залишається постійним. Межа ламінарного і турбулентного режимів течії рідини залежить головним чином від температурного напору . Форма поверхні у розвитку вільного руху має другорядне значення, тут важлива її довжина.

Розрахунок тепловіддачі. Розглянута картина руху рідини відноситься до випадків, коли поверхні, які замикають середовище, на розвиток вільного руху не впливають. Такий рух називається вільним рухом у великому об’ємі. Коефіцієнт тепловіддачі при цьому розраховується за формулою

, (6.13)

яка узагальнює обширні експериментальні дані. Значення коефіцієнта В і показника степеня п у (6.13) для вертикальної і горизонтальної поверхонь залежно від добутку наведені в табл. 6.2.

Таблиця 6.2. Значення коефіцієнта В і показника степеня п

	Вертикальна поверхня	Горизонтальна поверхня
	B	n	B	n
103 … 109	0,76	0,25	–	–
> 109	0,15	0,33	–	–
103 … 108	–	–	0,5	0,25

У (6.13) визначальною температурою є температура оточуючого середовища. Визначальним розміром для горизонтальних труб є діаметр, а вертикальних труб і пластин – висота. Формулою (6.13) можна користуватися і для горизонтальних плит. Але у цьому випадку розрахований коефіцієнт тепловіддачі слід збільшити на 30 %, якщо поверхня плити звернена уверх, і зменшити на 30 %, якщо поверхня плити звернена униз. У обох випадках визначальним є найменший розмір плити в плані.

Теплообмін у прошарках. Досить часто доводиться розраховувати теплообмін вільною конвекцією у вузьких каналах і щілинах (див. рис. 6.6, б). Типовий приклад – перенесення теплоти між шибками. У цьому випадку середню густину теплового потоку між поверхнями, розділеними прошарком газу або рідини товщиною , можна розраховувати, як у випадку перенесення теплоти теплопровідністю крізь плоску стінку:

, (6.13)

де і – більша і менша температури обмежуючих поверхонь; – еквівалентний коефіцієнт теплопровідності, який враховує перенесення теплоти як теплопровідністю, так і конвекцією.

При значення розраховується за формулою , де поправка на конвекцію – коефіцієнт конвекції визначається залежністю

. (6.14)

Визначальний розмір при розрахунку числа товщина прошарку , а визначальна температура – середня між поверхнями: .

При вільну конвекцію можна не враховувати, вважаючи = 1, а .

Конвективний теплообмін