Перший закон термодинаміки. Теплоємність

PAGE 6

EMBED Equation.3

Л е к ц і я 1.3. Перший закон термодинаміки. Теплоємність.

Перший закон термодинаміки. Принцип еквівалентності теплоти і роботи. Вічний двигун першого роду. Форми запису першого закону термодинаміки.

Теплоємність газів та її класифікація. Рівняння Майера. Коефіцієнт Пуасона. Молекулярно-кінетична теорієя теплоємності. Залежність теплоємності від температури. Теплоємність газових сумішей.

Джерела інформації: [1], с.45-59, 63-74, 180-182; [2], с.24-33, 84-86; [8], с.29-41, 86--91, 95-96.

Перший закон термодинаміки. У термодинамічних процесах зміни стану робочих тіл останні можуть отримувати від зовнішнього середовища або, навпаки, віддавати йому енергію у формі роботи і теплоти . Внаслідок цього енергія робочого тіла буде змінюватись чисельно на . Згідно закону збереження енергії з урахуванням знаків теплоти і роботи (при однакових напрямках потоків теплоти і роботи знаки їх протилежні) рівняння енергетичного балансу прийме вигляд

,

або

. (3.1)

Рівняння (3.1) є математичним виразом першого закону термодинаміки: у термодинамічному процесі підведена теплота у загальному випадку витрачається на зміну енергії робочого тіла і здійснення зовнішньої роботи. У загальному випадку зміна повної енергії робочого тіла:

. (3.2)

Тоді перший закон термодинамки можна записати так:

,

та для 1 кг робочого тіла

. (3.3)

Якщо робоче тіло не рухається (його центр ваги нерухомий), а потенціальною енергією зовнішнього поля можна знехтувати, повна енергія робочого тіла буде складатися тільки з його внутрішньої енергії . Отже,

. (3.4)

Для 1 кг робочого тіла перший закон термодинаміки у інтегральній формі прийме вигляд

(3.5)

або у диференціальній формі

, (3.6)

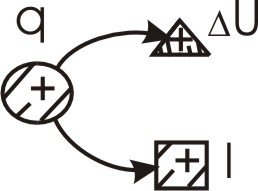
де – повний диференціал внутрішньої енергії, яка є функцією стану робочого тіла; і – нескінченно малі величини, які залежать від шляху протікання процесу (функції процесу). Рівняння першого закону термодинаміки можна представити у вигляді схеми енергетичного балансу у термодинамічному процесі (рис. 3.1).

Рис. 3.1. Схема енергетичного балансу

Принцип еквівалентності теплоти і роботи. Вічний двигун першого роду. Для кругового процесу вираз першого закону термодинаміки має вигляд

,

або з урахуванням

. (3.7)

З останньої рівності витікає, що робота кругового процесу здійснюється лише за рахунок витраченої ззовні певної кількості теплоти. Якщо б виявилось, що , можна б було створити вічний двигун першого роду, який здійснював би роботу без витрат енергії. У зв'язку з цим перший закон термодинаміки формується ще так: вічний двигун першого роду неможливий.

Рівність (3.7) виражає принцип еквівалентності теплоти і роботи: у кругових процесах телота і робота взаємоперетворюються у еквівалентних кількостях.

Форми запису першого закону термодинаміки. Математичний вираз першого закону термодинаміки має дві форми запису. Перша форма витікає з рівняння (3.6) з урахуванням виразу

, (3.8)

друга форма – виходячи з поняття питомої ентальпії :

.

З урахуванням рівняння (3.8)

,

звідки друга форма аналітичного запису першого закону термодинаміки прийме вигляд

. (3.9)

Якщо об'єднати рівняння (3.8) і (3.9) з виразом для ентропії , отримаємо основне рівняння термодинаміки, або термодинамічну тотожність:

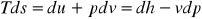
(3.10)

У необоротних процесах, пов'язаних, наприклад, з тертям або завихренням (внутрішньонеоборотні процеси), ефективна питома робота завжди зменшується: . При цьому питома робота на подолання опору перетворюється у еквівалентну питому кількість теплоти . Тоді рівняння першого закону термодинаміки для необоротних процесів прийме вигляд

,

або

.

З рівнянь (3.8) і (3.10) та рівняння стану можна отримати диференціальні рівняння термодинаміки.

Рівняння першого закону термодинаміки для потоку речовини. Розглянемо відкриту (проточну) систему зі стаціонарним потоком речовини (рис. 9.1), до якої підводиться питома теплота q, а також підводиться (у компресорі) або відводиться (у турбіні) питома технічна робота на валу lтехн. Технічна робота – це робота робочого тіла у проточній системі, яка не пов’язана з дефомацією границь системи, тобто зміною її об’єму Ця робота, наприклад, здійснюється газом при обертанні ротора турбіни. На відміну від закритих у відкритих системах потік робочого тіла несе з собою крім внутрішньої енергії також і кінетичну енергію свого руху відносно границь системи. У деяких випадках необхідно ураховувати зміну потенціальної енергії робочого тіла у полі зовнішніх сил. При введенні робочого тіла необхідно долати дію внутрішнього тиску у системі. Отже, над робочим тілом, що надходить до системи, має бути здійснена деяка робота зовнішньої сили – робота введення (-), яка збільшує повну енергію системи. При виведенні робочого тіла з системи має витрачатися робота на подолання тиску зовнішнього середовища – робота виведення робочого тіла (). Роботу введення – виведення робочого тіла називають роботою проштовхування

.

Математичний вираз першого закону термодинаміки для потоку у інтегральній формі:

або з урахуванням того, що ,

(9.3)

У диференціальній формі

(9.4)

Отже, теплота, що підводиться до потоку речовини, витрачається на зміну ентальпії, кінетичної і потенціальної енергії речовини, а також на виконання технічної роботи.

У багатьох випадках зміною потенціальної енергії можна знехтувати, а отже рівняння (9.3) набуде вигляду

(9.5)

Якщо зіставити рівняння (9.5) з рівнянням першого закону термодинаміки для закритої системи, отримаємо

(9.6)

Інтеграл у (9.6) зображається у p – v координатах (рис. 9.2) площею 12p2 p1 і являє собою частину питомої роботи зміни об’єму робочого тіла, яка може бути корисно використана на зміну його питомої кінетичної енергії і виконання питомої технічної роботи. У зв’язку з цим інтеграл (9.6) називають питомою наявною роботою:

(9.7)

Питома наявна робота політропного процесу визначається за формулою (4.32).

Рис. 9.1. Схема відкритої термодина- Рис. 9.2. Графічне зображення мічної системи наявної роботи

Якщо зіставити рівняння (9.6) і (9.7), вираз першого закону термодинаміки для потоку можна записати у такому виді:

(9.8)

Теплоємність газів та її класифікація. Теплоємністю робочого тіла називається відношення кількості теплоти у будь-якому процесі до відповідної зміни температури. Теплоємність робочого тіла, яка відповідає нескінченно малій зміні його температури, називається істинною теплоємністю:

. (3.11)

Теплоємність робочого тіла, що відповідає кінцевій зміні його температури (від до ), називається середньою теплоємністю (з індексом ):

. (3.12)

В залежності від обраної одиниці кількості речовини розрізняють теплоємності:

питому, віднесену до 1 кг робочого тіла: , кДж/(кг·К);

об'ємну, віднесену до 1 м3 речовини при нормальних умовах (температура 273,15 К і тиск 101325 Па): , кДж/(м3·К);

молярну, віднесену до 1кмоль речовини: , кДж/(кмоль·К).

Ці теплоємності пов'язані між собою співвідношеннями:

; . (3.13)

Одна й таж речовина може мати безліч теплоємностей в залежності від виду процесу, тому що кількість теплоти є функцією процесу. У загальному випадку теплоємність газу може змінюватися від нуля для адіабатного процесу () до для ізотермічного процесу (). Крім того, теплоємність може мати від’ємне значення, коли знаки теплоти і зміни температури різні. В термодинамічному аналізі і теплових розрахунках найважливіше значення мають ізохорна та ізобарна теплоємності газів.

Ізохорною теплоємністю називається теплоємність, що визначається при умові незмінності об'єму робочого тіла

. (3.14)

Ізобарною теплоємністю називається теплоємність робочого тіла, яка визначається при умові незмінності тиску

. (3.15)

Таким чином теплоємності розрізняються в залежності від одиниці кількості речовини (питома, об'ємна, молярна) і в залежності від процесу (ізохорна та ізобарна).

Теплоємність, як і теплота, є функцією процесу і не слугує параметром стану. Між тим, перший закон термодинаміки дозволяє виявити зв'язок між теплоємністю і термодинамічними параметрами. З урахуванням рівняння перший закон термодинаміки прийме вид

. (3.16)

Оскільки , отримаємо вираз для теплоємності у будь-якому процесі:

. (3.17)

Для ізохорного процесу (, ) вираз (3.17) прийме вид

. (3.18)

Для ізобарного процесу на основі (3.17) і (3.18) отримаємо вираз для ізобарної теплоємності будь-якої речовини

. (3.19)

Рівняння (3.17) ... (3.19) дозволяють розрахувати всі теплофізичні характеристики речовини за експериментальними даними деяких його параметрів.

Рівняння Майєра. У випадку ідеального газу його внутрішня енергія не залежить від об'єму, тому і, користуючись рівнянням стану , знаходимо

. (3.20)

При цьому вираз (3.19) прийме вид , або

. (3.21)

Це співвідношення має важливе значення у теорії теплоємності і носить назву рівняння Майєра.

Якщо помножити ліву і праву частини рівняння (3.21) на , отримаємо

кДж/(кмоль·К). (3.22)

З рівняння (3.21) виходить, що ізобарна теплоємність більше за ізохорну на значення газової сталої . Це пояснюється тим, що в ізохорному процесі зовнішня робота не виконується, і теплота витрачається лише на зміну внутрішньої енергії. Тоді як у ізобарному процесі теплота витрачається не тільки на зміну внутрішньої енергії, а ще й на здійснення роботи. Для реальних газів , тому що при їх розширенні і здійснюється робота не тільки проти зовнішніх сил, а й внутрішня робота проти сил взаємодії між молекулами газу.У теплотехніці широко використовується відношення теплоємностей

, (3.23)

яке носиь назву коефіцієнт Пуасона (показника адіабати).

Молекулярно-кінетична теорієя теплоємності. Теплоємність визначають за допомогою експерименту, але для багатьох речовин її можна розрахувати методами статистичної фізики. Молекулярно-кінетична теорія теплоємності установлює значення теплоємності ідеального газу в залежності від його атомності (степенів вільності). В основі цієї теорії лежить закон про рівномірний розподіл внутрішньої енергії за степенями вільності поступального та обертального руху молекул. Відповідно до цього закону внутрішня енергія ідеального газу прямо пропорційна числу степенів вільності молекул і енергії , яка припадає на одну степінь вільності. Для 1 кмоль газу

, (3.24)

де – число Авогардо; – число степенів вільності (число незалежних координат, які треба задати для того, щоб повністю визначити положення молекули у просторі): для одноатомних атомів (три складові поступального руху); для двоатомних газів (три складові поступального руху і дві обертального); для три- і багатоатомних газів (три складові поступального руху і стільки ж обертального).

Оскільки для ідеального газу , з урахуванням (3.24) отримаємо вираз для молярної ізохорної теплоємності

, (3.25)

а з урахуванням рівняня Майєра (3.22) отримаємо вираз для молярної ізобарної теплоємності

. (3.26)

Вирази (3.25) і (3.26) показують, що молярні теплоємності залежать лише від числа степенів вільності і для даного газу мають постійні значення. Результати молекулярно-кінетичної теорії теплоємності достатньо добре погоджуються з експериментальними даними лише для одноатомних та частково двоатомних газів. Однак основний висновок теорії про незалежність теплоємності від температури експеримент не підтверджує. Розходження, особливо суттєві у області низьких і достатньо великих температур, пов'язані з квантовою поведінкою молекул і знаходять пояснення у рамках квантової теорії теплоємності. У багатоатомних газах при високих температурах виникають коливальні рухи атомів у молекулі (додаткові степені вільності), на які також витрачається енергія і теплоємність підвищується. Квантова теорія теплоємності ураховує енергію коливального руху атомів у молекулі і встановлює залежність теплоємності багатоатомних газів від температури. У загальному випадку ця залежність описується степеневим поліномом

Залежність теплоємності від температури. У технічних розрахунках приймають лінійну залежність теплоємності від температури

. (3.27)

Графічно ця залежність показана на рис. 3.2. Оскільки кожній температурі відповідає своя теплоємність, для розрахунку кількості теплоти, яка зображена на рис. заштрихованою площею, використовують поняття середньої теплоємноті для визначеного інтервалу температур від до . Тоді можна розглядати як висоту прямокутнику з основою і площею, яка дорівнює площі . Таким чином середня теплоємність дорівнює

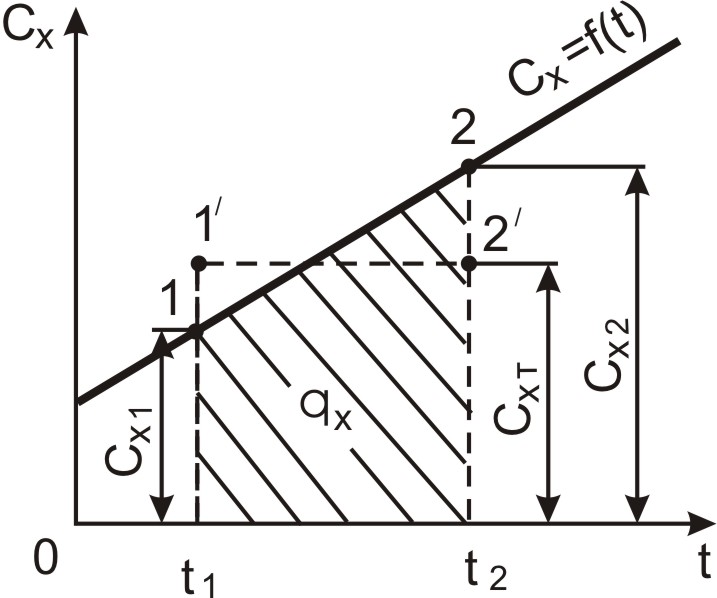
. (3.28)

При нескінченно малій зміні температури відношення (3.29)

визначає теплоємність при даній температурі і називається істинною теплоємністю.

Чисельні значення теплоємності широко використовуються при визначенні кількості теплоти у термодинамічних процесах та розрахунку калоричних параметрів стану.

Рис. 3.2. Залежність теплоємності від температури

Виходячи з поняття істинної теплоємності можна отримати вираз для визначення питомої кількості теплоти у термодинамічному процесі

, (3.30)

або

. (3.31)

Цю ж кількість теплоти можна визначити, знаючи середню теплоємність у інтервалі температур від до :

. (3.32)

Із виразів (3.31) і (3.32) витікає, що для визначення питомої кількості теплоти необхідно знати залежність істинної теплоємності від температури або середню теплоємність у заданому інтервалі від до . У першому випадку під знак інтеграла підставляється одна з інтерполяційних залежностей теплоємності від температури виду (3.27), які наводяться у довідковій літературі. У другому випадку питома кількість теплоти дорівнює

, (3.33)

де і – середні значення теплоємностей відповідно в інтервалі температур 0...t1 і 0... t2, які вибираються з таблиць для даного газу.

Якщо у термодинамічному процесі використовується (кг) або (м3 при нормальних умовах) газу, то кількість теплоти

, (3.34)

або

. (3.35)

На основі табличних даних можна знайти середню теплоємність у інтервалі температур :

. (3.36)

Теплоємність газових сумішей. Визначення теплоємності газових сумішей базується на рівнянні теплового балансу, згідно з яким теплота, підведена до суміші, дорівнює сумі теплот, підведених до її компонентів.

Для масового складу суміші , звідки .

Для об'ємного складу суміші , звідки .

Для молярного складу аналогічно .

Перший закон термодинаміки. Теплоємність