Термодинамічні властивості реальних газів та процеси з ними
PAGE 10
Л е к ц і я 1. 6. Термодинамічні властивості реальних газів та процеси з ними.
Загальні властивості реальних газів. Коефіцієнт стисливості. Рівняння Ван-дер-Ваальса та його аналіз. Критичний стан речовини. Діаграма Ендрюса (p-v діаграма реальної речовини). Фазові переходи та фазові діаграми. Рівняння Клапейрона –Клаузіуса. Приведене рівняння стану реального газу. Закон відповідних станів. Термодинамічна подібність.
Водяна пара та її характеристики. Аналіз трьох стадій отримання перегрітої пари та їх зображення у p-v, T-s і h-s діаграмах. Аналіз основних термодинамічних процесів з водяною парою.
Вологе повітря та його характеристики. Діаграма H-d вологого повітря. Основні процеси з вологим повітрям ( нагрівання, охолодження, адіабатне зволоження) та їх зображення на H-d діаграмі. Конвективне сушіння.
Джерела інформації: [1], с.37-42, 172-197; 236-245; [2], с.57-83.
Загальні властивості реальних газів. При достатньо високих тисках, а також при порівняно низьких температурах, гази не підлягають законам ідеальних газів. Гази при цьому називають реальними. Основні відмінності реальних газів від ідеальних пов’язані з проявом впливу сил взаємодії між молекулами, які мають електромагнітну і квантову природу, і розмірів молекул, а також з іншими особливостями механізму молекулярної взаємодії (наприклад, асоціацією молекул газу). Внаслідок сил взаємодії між молекулами і скінченності їх об’єму закони ідеальних газів ні при яких умовах не можуть бути точно застосовані до реальних газів, зокрема для реального газу непридатне рівняння стану ідеального газу: для реальних газів pv RT. Відмінність властивостей реального газу від ідеального характеризує коефіцієнт стисливості z, який дорівнює
(6.1)
Для ідеального газу z = 1, а для реальних газів z залежить від тиску і температури газу, і може бути як більше, так і менше за одиницю і тільки при дуже малому тиску та великих температурах z практично дорівнює одиниці. На практиці досить часто доводиться мати діло з процесами, коли робочі тіла є реальні гази, але умови їх протікання такі, що дозволяють застосовувати для розрахунків параметрів системи рівняння стану ідеального газу. Рівняння стану ідеальних газів достатньо добре описує поведінку реальних газів при високих температурах і низьких тисках. При цьому, чим вище температура, тим для більшого діапазону тисків справедливе рівняння pv = RT. Часто це рівняння уживають при розрахунках параметрів робочих тіл теплових двигуніув (ГТД, ДВЗ, ракетних двигунів). Робочі тіла у цих двигунах мають тиск 2·105 ... 2·107 Па і температуру 1500 ... 4000 К.
Рівняння Ван-дер-Ваальса. Відмінність властивостей реальних газів від ідеального примусило вчених розробляти нові рівняння стану, які б зв’язували параметри p, v і Т і давали б змогу розраховувати властивості газів, не вживаючи дорогих вимірювань.
Найбільш простим рівнянням стану реального газу з урахуванням поправок на сили взаємодії між його молекулами і на об’єм самих молекул є рівняння Ван-дер-Ваальса (1873 р.). Він увів дві поправки до рівняння стану pv = RТ. Перша поправка ураховує об’єм молекул. Для реального газу, у якого молекули мають кінцевий об’єм, рівняння Клапейрона прийме інший вигляд
v - b = RT/p,
де b – той найменший об’єм, до якого можна стискати газ. Різниця v - b представляє так званий вільний об’єм – об’єм простору, у якому можуть переміщатися молекули. Для кожного газу b має конкретне значення.
Друга поправка ураховує вплив сил взаємодії між молекулами. У реальному газі тиск на стінку буде менше у порівнянні з ідеальним на величину p внаслідок того, що молекули біля стінки притягуються сусідніми молекулами усередину посудини. Ця поправка p прямо пропорційна як кількості молекул, що притягуються, так і кількості молекул, які притягуюють, або прямо пропорційна квадрату густини газу. Отже
де а – коефіцієнт пропорційності, який для кожного газу має конкретне значення і не залежить від параметрів стану. Уводячи другу поправку, отримаємо:
p = RT/( v- b) - p або p = RT/(v - b) - a/v2.
Остаточно рівняння Ван-дер-Ваальса прийме такий вид:
|
(6.2) |
Величину а/v2 називають внутрішнім тиском. Для рідин внутрішній тиск приймає дуже велике значення (для води при Т = 293 К а/v2 1080 МПа). Для газів а/v2 порівняно невелике і залежить від тиску і температури газу. Рівняння Ван-дер-Вальса якісно вірно відображає поведінку реальних речовин у рідкій та газоподібній фазах. Для двофазних станів його застосовувати неможливо.
Аналіз рівняння Ван-дер-Ваальса. Критичний стан речовини. Якщо у рівнянні Ван-дер-Ваальса розкрити дужки, отримаємо рівняння третього степеня відносно питомого об’єму газу:
|
pv3 - (bp + RT) v2 + av - ab = 0. |
(6.3) |
Таке рівняння має три корені. При цьому можливі три випадки: 1) усі три корені різні й дійсні; 2) усі три корені дійсні й рівні між собою; 3) один корінь дійсний і два уявних. Уявні корені не мають фізичного смислу, реальне значення має тільки дійсний корінь. Ізотерми, побудовані за рівнянням Ван-дер-Ваальса, показані на рис. 6.1, а. При порівняно низьких температурах вони мають у середній частині хвилеподібний характер з максимумом та мінімумом. Чим вище температура, тим коротше хвиляста частина ізотерми. Пряма еа, яка перетинає такого типу ізотерму, дає три дійсних значення питомого об’єму у точках е, с та а. Отже ці ізотерми відповідають першому випадку рівняння (6.3): три різних дійсних кореня. Найбільший корінь (точка а) відноситься до пароподібного стану, а найменший (точка е) – до стану рідини. Оскільки рівняння (6.3) не може описувати двофазні стани, воно указує (у вигляді хвилястої кривої) на безперервний перехід із рідкого стану у пароподібний при даній температурі.
|
Рис. 6.1 Теоретичні (а) і дійсні (б) ізотерми реального газу |
В дійсності, як показують досліди, цей перехід завжди відбувається через двофазні стани речовини, які представляють суміш рідини і пари. При цьому при даній температурі процес переходу відбувається також і при незмінному тиску, оскільки об’єм зменшується за рахунок часткової конденсації пароподібної фази. Практично для особливо чистих речовин можуть існувати ділянки хвилястої кривої еd і ba. У першому випадку має місце нестійкий стан перегрітої рідини, а у другому - переохолодженої пари. Ділянка dcb взагалі існувати не може, тому що це суперечить умові термодинамічної стійкості, відповідно до якої для однорідної речовини частинна похідна не може бути більше за нуль.
Дійсна лінія процесу переходу з рідини у пару зображується на рис. 6.1, б прямою еа. При цьому точка е відповідає стану киплячої рідини, а точка а – стану сухої насиченої пари, коли закінчився процес переходу. Гілка ізотерми, яка проходить правіше точки а, відповідає стану перегрітої пари.
При певній температурі Ткр, яка називається критичною, ізотерма рівняння (6.3) не буде мати хвилястої ділянки. На цій ізотермі є точка перегину (критична точка К), дотична до якої горизонтальна. Це відповідає другому випадку розв’язання рівняння (6.3), коли усі три корені дійсні і рівні між собою. Параметри Ткр, pкр і vкр, які відповідають точці К, називають критичними, а стан речовини – критичним. Критичним станом речовини називається такий її стан, який характеризується відсутністю відмінності між двома фазами: рідиною і парою. Для чистих речовин критична температура Ткр – найбільша температура, при якій можливо існування рідини у стані рівноваги з парою. При Т > Ткр речовина може перебувати тільки у газоподібному стані. Критичний тиск pкр – найбільший тиск насиченої пари речовини. Насиченою парою називають пару, яка перебуває в рівновазі з рідиною, з якої вона утворюється, і має найбільший можливий при даній температурі тиск. Критичний питомий об’єм vкр – найбільший питомий об’єм рідкої фази речовини у стані насичення. При критичній температурі перехід газоподібного стану у рідкий або навпаки відбувається без зміни яких-небудь фізичних властивостей (у даному випадку густини рідини і газу), тому у критичній точці зникає відмінність між рідким і газоподібним станами. Критичний стан речовини вперше був відкритий Менделєєвим у 1861 р. Критичні параметри ркр, Ткр і vкр, які відповідають критичній точці, характерні для кожної речовини і визначаються експериментально.
При температурах більших за критичну (Т > Ткр) ізотерми мають монотонно спадаючий характер, наближуючись, при збільшенні температури, до гіперболи (ізотерми реального газу наближаються до ізотерм ідеального газу). При цих температурах має місце третій випадок розв’язання рівняння (6.3), коли один корень дійсний, а два уявних.
Якщо з’єднати усі точки е, е', е" і так далі (див. рис. 6.1, б), отримаємо криву, на якій рідина знаходиться у стані кипіння (насичення). Криву е-К називають пограничною кривою рідини (або нижньою пограничною кривою). Крива К-а називається пограничною кривою пари (або верхньою пограничною кривою) і являє собою сукупність станів сухої насиченої пари (без домішок рідини) .
Таким чином, для реальної речовини р-v діаграму можна розділити на три характерні області (див. рис. 6.1, б): I – область однофазної рідини – ліворуч від пограничної кривої рідини; II – область двофазних станів (вологої насиченої пари, тобто пари з домішками рідини) – в проміжку між пограничними кривими рідини та пари; III – область однофазної перегрітої пари (або газу) – праворуч від пограничної кривої пари. Перегрітою парою називається пара, яка має вищу температуру, ніж температура насиченої пари з тим самим тиском. Умовно область рідини обмежують зверху лінією К-ркр, яка представляє собою критичну ізобару. Часто р-v діаграму реальної речовини називають діаграмою Ендрюса, який у 1869 р. вперше побудував її для вуглекислоти.
Будь-яка речовина в залежності від зовнішніх умов (тиску і температури) може перебувати у твердому, рідкому і газоподібному агрегатних станах, або фазах, а також одночасно бути у двох або трьох станах. Фазою називається частина термодинамічної системи з однаковим фізичними властивостями у всіх її точках, яка обмежена поверхнею розділу. Стан, в якому знаходяться у рівновазі тверда, рідка і парова фази речовини, називається потрійною точкою. Перехід речовини з одног агрегатного стану у іншій називається фазовим переходом, або фазовим перетворенням. Тому термодинамічні діаграми (p-v, T-s і інші) для реального газу на відміну від діаграм для ідеального газу є фазовими діаграмами. Крім пароутворення (перехід речовини з рідкого стану в пароподібний), відомі ще процеси плавлення (перехід із твердого стану в рідкоий) і возгонки або сублімації (перехід із твердого стану в газоподібний). Можна відзначити ще й протилежно спрямовані процеси фазових переходів: конденсацію, затвердіння і десублімацію.
Залежність тиску фазового переходу від температури описується рівнянням Клапейрона – Клаузіуса. Стосовно до випадку рівноваги фаз при пароутворенні воно має вид:
, (6.4)
де – температура насичення, що відповідає тиску ; , – відповідно питомий об’єм
сухої насиченої пари і рідини у стані насичення; – питома теплота пароутворення (фазового переходу) – кількість теплоти, яка витрачається на перетворення 1 кг рідини у суху насичену пару. Із збільшенням тиску зменшується і у критичній точці дорівнює нулю.
Співвідношення (6.4) справедливе для будь-якого фазового переходу (пароутворення, плавлення, возгонки ) і дає можливість визначити теплоту фазового переходу.
Правило фаз Гібса визначає залежність між кількістю незалежних параметрів системи N у стані рівноваги, кількістю компонентів n і кількістю фаз системи :
Величину N називають також кількістю термодинамічних степенів вільності системи. Вона показує, яку кількість параметрів системи, що знаходиться у стані рівноваги, можна змінювати довільно, не змінюючи при цьому кількості фаз у системі. Наприклад, для однокомпонентної системи, яка складається з однієї фази (ідеальний газ, однорідна рідина) N = 2. Це означає, що стан простих однорідних систем визначається двома незалежними параметрами. У потрійній точці N = 0.
Приведене рівняння стану реального газу. Закон відповідних станів. Термодинамічна подібність. З аналізу рівняння Ван-дер-Ваальса стосовно до критичного стану можна виразити критичні параметри через константи рівняння а і b або визначити константи а і b, якщо відомі критичні параметри. Вихідним положенням для отримання залежності між критичними параметрами і константами а і b є той факт, що у критичній точці ізотерма має перегин і дотична у точці перегину горизонтальна. Якщо здиференціювати рівняння (6.3) два рази і прирівняти до нуля похідні, отримаємо:
звідки
.
Після підстановки цих виразів у (6.1) отримаємо так зване приведене рівняння стану
де – безрозмірні змінні ( відповідно приведені тиск, об’єм і температура).
В це рівняння входять тільки приведені параметри , і і числові коефіцієнти, але не входять величини, що характеризують дане робоче тіло і його індивідуальні властивості. Тому приведене рівняння стану має узагальнений універсальний характер і однаково придатне для всіх речовин, які підлягають рівнянню Ван-дер-Ваальса.
Стани речовин, у яких приведені параметри однакові, називають відповідними. У критичних точках усі приведені параметри дорівнюють одиниці, тому критичні стани усіх речовин є відповідними. Якщо речовини, які задовольняють одному й тому ж приведеному рівнянню стану, мають які-небудь два однакові приведені параметри, то й третій приведений параметр у них буде однаковий. Це твердження відоме як закон відповідних станів. Речовини, які підкоряються закону відповідних станів і задовольняють одному й тому ж приведеному рівнянню стану, називають термодинамічно подібними. Термодинамічна подібність дозволяє оцінювати властивості однієї речовини, якщо відомі властивості іншої.
Водяна пара та її характеристики. Пара речовин широко використовуються у багатьох галузях техніки у якості робочих тіл, наприклад, у теплосилових та холодильних установках. У першу чергу це відноситься до пари найбільш поширеної у природі речовини – води, яка не чинить шкідливого впливу на живі організми і має відносно добрі термодинамічні властивості (зокрема, має відносно велику теплоємність і теплоту пароутворення). Усі закономірності для водяної пари дійсні для пари інших речовин. Пара становить окремий випадок реальних газів, а саме: парою називається реальний газ, близький до стану зрідження.
Процес отримання пари з рідини може здійснюватися випаровуванням і кипінням. Випаровуванням називають пароутворення, яке відбувається тільки з вільної поверхні рідини та при будь-якій температурі, а кипінням – інтенсивне пароутворення по всій масі рідини, яке відбувається при підведенні до рідини через стінку посудини теплоти.
Процес кипіння починається при досягненні рідиною певної температури, яка називається температурою кипіння (насичення) ts і під час всього процесу залишається незмінною, оскільки уся підведена теплота витрачається тільки на пароутоворення. Значення ts залежить від природи речовини і тиску, при чому з підвищенням тиску ts збільшується. Тиск, який відповідає температурі ts, називають тиском насичення ps. Зворотний процес переходу пари у рідкий стан, який супроводжується відведенням теплоти, називається конденсацією.
Розрізняють пару насичену і перегріту. Насиченою парою називають пару, яка перебуває у термічній і динамічній рівновазі з рідиною, з якої вона утворюється в процесі кипіння, і має найбільший, можливий при даній температурі тиск. Динамічна рівновага полягає у тому, що кількість молекул, які вилітають з води у паровий простір, дорівнює кількості молекул, які конденсуються на її поверхні. У паровому просторі при цьому рівноважному стані знаходиться максимально можлива при даній температурі кількість молекул. При збільшенні температури кількість молекул, які володіють енергією, достатньою для вильоту, збільшується. Рівновага поновлюється за рахунок зростання тиску пари, яке призводить до збільшення його густини і, отже, кількості молекул, які конденсуються на поверхні води. З цього витікає, що тиск насиченої пари є монотонно зростаючою функцією його температури. При збільшенні об’єму над поверхнею рідини, яка має незмінну температуру насичення, деяка кількість рідини переходить у пару. При зменшенні об’єму “надлишкова” пара знову переходить у рідину, але в обох випадках тиск пари залишається незмінним.
Насичена пара поділяється на суху й вологу. Сухою насиченою парою називається пара, яка не вміщує рідини і має температуру насичення при даному тиску. Термодинамічний стан сухої насиченої пари визначається одним параметром, наприклад, тиском або температурою. Двофазна система, яка складається з сухої насиченої пари і рідини, називається вологою насиченою парою. Термодинамічний стан вологої насиченої пари, як двофазної системи, крім тиску або температури насичення, визначається ще величиною ступеня сухості (паровмісту). Ступенем сухості вологої насиченої пари називається масова частка сухої пари у вологій парі (позначається буквою х):
де – маса сухої насиченої пари; – маса вологої насиченої пари; – маса рідини.
Ступенем вологості пари називається масова частка рідини у вологій насиченій парі. Вона дорівнює 1 - х. Для киплячої рідини ( = 0) х = 0, для сухої насиченої пари ( = 0) х = 1, для вологої пари 0 < х < 1.
Перегрітою парою називається пара, яка має вищу температуру, ніж температура насиченої пари з тим самим тиском, тобто для перегрітої пари t > ts. Різниця температур (t – ts) називається ступенем перегріву. За своїми властивостями перегріта пара наближається до ідеальних газів: чим вищий степінь перегріву, тим більше властивості перегрітої пари наближаються до властивостей ідеальних газів.
Для технічних потреб водяну пару отримують у парових котлах (котлоагрегатах). Слід підкреслити, що пароутворення у котлоагрегатах практично відбувається при сталому тиску (ізобарне пароутворення). Процес отримання перегрітої пари складається з трьох послідовно здійснюваних стадій: підігрівання води до температури насичення, пароутворення і перегрівання пари. Усі ці стадії протікають при постійному тиску і на термодинамічних діаграмах зображаються ізобарою. На фазовій p – v діаграмі (рис. 6.2, а), де область двофазного стану обмежена кривими х = 0 і х = 1, ізобарний процес отримання перегрітої пари зображається горизонтальною прямою аd. Тут ці три стадії пароутворення характеризуються відрізками: аb – підігрівання рідини до температури кипіння; bc – пароутворення; сd – перегрівання пари. Ізобара АВ проходить трішки вище від вісі абсцис, бо у потрійній точці pА = 611 Па.
|
а б Рис.6.2. Фазові діаграми процесу пароутворення у p – v координатах (а) і T – s координатах (б) |
Аналіз трьох стадій отримання перегрітої пари та їх зображення у p-v, T-s і h-s діаграмах. Задачею аналізу трьох стадій отримання перегрітої пари є установлення для кожної стадії особливостей початкового і кінцевого стану речовини, зміни питомих калоричних параметрів u , h, s і визначення питомої кількості теплоти. При цьому слід взяти до уваги, що для реального газу , оскільки питома внутрішня енергія реального газу залежить не тільки від температури, але й від об’єму. Відповідно до першого закону термодинаміки кількість теплоти в ізобарних процесах чисельно визначається зміною ентальпії робочого тіла
|
qp = h = h2 – h1, |
(6.5) |
а зміна внутрішньої енергії його становить
|
u = qp – pv. |
(6.6) |
За другим законом термодинаміки можна оцінити зміну ентропії робочого тіла:
|
(6.7) |
Підігрівання води до температури насичення. За початкову температуру води, яка надходить до котлоагрегату при будь-якому тиску, приймають температуру ta = 0 оС. Отже линія АА1 на p-v діаграмі (див. рис. 6.2, а) буде відповідати станам так званої холодної рідини при різних тисках, яка має температуру 0 оС (ізотерма холодної рідини).
Термодинамічні характеристики стану, що відповідають початковому стану холодної рідини, позначаються з індексом 0, наприклад, , і т. ін. Внаслідок незначної стисливості води лінія АА1, яка характеризує залежність між тиском і питомим об’ємом холодної рідини , розміщується майже вертикально (з невеликим нахилом до вісі тисків). Можна зазначити, що в широкому інтервалі тисків від 0,04 до 220 бар величина для води змінюється лише від 0,0010002 до 0,0009896 м3/кг, тобто зменшується всього на 1,1 %. Лівіше від лінії АА1 знаходиться область рівноважного співіснування води і льоду.
Умовним початком відліку u = 0, h = 0, s = 0 для води прийнято вважати потрійну точку, у якій речовина може одночасно перебувати у твердому, рідкому і газоподібному станах (точка А на рис. 6.2). Кожній речовині у потрійній точці відповідають певні параметри (для води pА = 0,000611 МПа, ТА = 273,16 К і vA = 0,001 м3/кг). Процес пароутворення при тиску pА = 0,00061 МПа зображається ізобарою АВ. При більш низьких тисках пара може існувати лише у рівновазі з льодом. Нехтуючи впливом тиску на зміну об’єму води, вважають для всіх станів її на лінії АА1 = 0,001 м3/кг, = 0, = 0 і = 0. Кінцевий стан води в стадії підігрівання (точка b) визначається досягненням нею температури насичення при заданому тиску , причому = f(). Ця залежність установлюється експериментально і приводиться у таблицях.
Cтани киплячої води при різних тисках будуть відповідати пограничній кривій рідини АК, яка зображає залежність питомого об’єму киплячої води від тиску. Іноді цю криву називають нижньою пограничною кривою, бо ця лінія відокремлює область однофазної рідини від області насиченої пари (області співіснування рідкої і пароподібної фаз). Зміна величини уздовж кривої рідини порівняно невелика. Так, наприклад, для води при зміні тиску від 0,04 до 220 бар величина збільшується від 0,001004 до 0,00238 м3/кг, тобто в 2,37 рази. На кривій рідини ступінь сухості пари х = 0.
Параметри киплячої рідини позначаються відповідними буквами з штрихом (, , , і т. ін.) і приводяться у таблицях в залежності від або . Питома кількість теплоти, яка необхідна для здійснення цієї стадії отримання перегрітої пари, називається питомим теплом рідини і визначається співвідношенням
|
(6.8) |
або при = 0 і середній теплоємності рідини
|
6.9) |
Зміна питомої внутрішньої енергії при підігріванні води
|
(6.10) |
Термодинамічна робота процесу при малих тисках внаслідок малості питомих об’ємів невелика, отже теплота витрачається переважно на зміну внутрішньої енергії. Зміна питомої ентропії води в процесі ab
|
(6.11) |
отже на Т – s діаграмі (див. рис. 6.2, б) ізобарний процес підігрівання води відповідно до рівняня (6.11) забражається логарифмічною кривою ab, яка практично збігається з пограничною кривою рідини. Оскільки питома ентропія води при 0 оС умовно дорівнює нулю, точка а на вісі ординат буде знаходитись на 273,16 К вище точки абсолютного нуля.
В дійсності ізобари підігрівання води на Т – s діаграмі мають більш складний характер і розміщуються лівіше пограничної кривої рідини х = 0. Однак для спрощення вважається, що вони збігаються з кривою х = 0. У цьому випадку критична ізобара води ркр проходить по лінії АК, а потім переходить у ізобару перегрітої пари.
Процес пароутворення. Подальше підведення теплоти до киплячої рідини, яке відбувається у випапрному контурі котлоагрегату, супроводжується інтенсивним пароутворенням усередині рідини і переходом частини води у пару. Ділянці bс на рис. 6.2 відповідає рівноважний стан суміші рідини і пари (волога насичена пара), який характеризується у кожній точці процесу масовою часткою сухої насиченої пари у суміші (ступенем сухості пари х). Кінцевий стан у цій стадії характеризується повним перетворенням рідини у пару, яка буде мати температуру насичення при заданому тиску. Така пара носить назву сухої насиченої пари. Таким чином, процес пароутворення є ізобарно-ізотермічним, що характерно для процесів фазових переходів (теплота витрачається не на підвищення температури, а тільки на подолання сил притягання між молекулами і на роботу розширення пари). Стан сухої насиченої пари визначається тільки одним параметром – тиском або температурою.
Станам сухої насиченої пари при різних тисках буде відповідати лінії ВК на рис. 6.2, яку називають пограничною кривою пари. У кожній точці цієї кривої х = 1. Параметри сухої насиченої пари позначаються відповідними буквами з двома штрихами ( і т. д) і наводяться у таблицях в залежності від тиску або температури.
Слід зазначити, що в процесі пароутворення питомий об’єм речовини різко збільшується. Наприклад, для води при тиску 0,1 МПа питомий об’єм нагрітої рідини = 0,001043 м3/кг, а питомий об’єм сухої насиченої водяної пари становить = 1,696 м3/кг, тобто в процесі пароутворення її об’єм збільшується більше ніж у 1600 разів. При інших тисках це співвідношення значно змінюється: при p = 10,0 МПа / = 12,8, а при p = 0,005 МПа / 28700. У критичній точці К = 0,0032 м3/кг.
Питома кількість теплоти, яка витрачається на пароутворення в процесі bс, називається питомою теплотою пароутворення r, або питомою теплотою фазового перетворення, яка за формулою (6.5) дорівнює
|
(6.12) |
звідки питома ентальпія сухої насиченої пари
|
(6.13) |
З рівняння першого закону термодинаміки
|
(6.14) |
витікає, що питома теплота пароутворення витрачається, по-перше, на зміну питомої внутрішньої енергії робочого тіла при постійній температури (тобто на подолання сил зчеплення між молекулами, або на роботу дисгрегації), по-друге, на питому роботу розширення , отже
|
(6.15) |
Величину називають питомою внутрішньою теплотою пароутворення (вона складає більше 80 %), а величину – питомою зовнішньою теплотою пароутворення. Чисельні означення r в залежності від тиску насичення ps (або температури ts) наводяться в таблицях. З Т – s діаграми витікає, що з підвищенням тиску ps питома теплота пароутворення r зменшується і при критичних параметрах (точка К) дорівнює нулю.
Стан вологої насиченої пари (точка e на діаграмах) може бути визначений, якщо, крім ps або ts, відомий ще склад суміші, тобто ступінь сухості х. Тому що 1 кг вологої пари складається з х кг сухої насиченої пари питомим об’ємом та (1-х) кг киплячої води питомим об’ємом , питомий об’єм вологої пари
|
(6.16) |
Для звичайних умов , тому другим доданком у (6.16) можна знехтувати. Отже
|
(6.17) |
звідки ступінь сухості вологої пари
|
(6.18) |
тобто будь-яка точка поділяє відрізок bс на частки, які пропорційні ступеню сухості (відрізок be) і степеню вологості (відрізок ес) пари, що використовується для побудови ліній сталого степеня сухості (х = const) пари.
Ентальпія вологої пари визначається за правилом адитивності
|
(6.19) |
Внутрішня енергія вологої пари:
|
. |
(6.20) |
Ентропія вологої пари визначається за правилом адитивності
|
(6.21) |
звідки, враховуючи і рівняння (6.11),
|
(6.22) |
З виразів (6.16), (6.19) і (6.21) отримаємо співвідношення
|
(6.23) |
які можна використовувати для побудови ліній сталої сухості х пари у будь-якій діаграмі.
Процес перегріву пари. Цей процес характеризується підвищенням температури від температури насичення ts до потрібної температури перегрітої пари tп.п при сталому тиску за рахунок додаткового підведення теплоти до сухої насиченої пари у пароперегрівнику котлоагрегату (процес сd на діаграмах). Питомий об’єм пари при перегріванні збільшується: . Отже, пара, яка має при даному тиску температуру і питомий об’єм більші, ніж відповідні параметри сухої насиченої пари, буде перегрітою. Різниця температур називається ступенем перегріву пари. Стан перегрітої пари на відміну від насиченої у відповідності до правила фаз Гібса визначається не одним, а двома незалежними параметрами – тиском і температурою , отже .
Ддя перегрітої пари отримано безліч рівнянь стану (наприклад, рівняння Вукаловича- Новікова), але внаслідок їх складності у практичних розрахунках використовують таблиці питомих параметрів перегрітої водяної пари , і в залежності від тиску і температури .
Кількість теплоти, яка необхідної для перегріву 1 кг сухої пари до потрібної температури при сталому тиску, називається питомою теплотою перегріву
|
(6.24) |
звідки
|
(6.25) |
де – питома середня ізобарна теплоємність перегрітої пари в температурному інтервалі від до , яка залежить як від температури, так і від тиску.
Оскільки відповідно до першого закону термодинаміки
|
(6.26) |
зміна питомої внутрішньої енергії при перегріванні пари
|
(6.27) |
Зміна питомої ентропії в процесі ізобарного перегрівання пари
|
(6.28) |
Отже процес перегріву пари на Т – s діаграмі (див. рис. 6.2, б) зображається логарифмічною кривою сd, а питома теплота перегріву qпер – площею під цією кривою.
Оскільки питома кількість теплоти в ізобарному процесі дорівнює різниці питомих ентальпій ( ; ), площа під ізобарою на Т – s діаграмі визначає питому ентальпію в даній точці ізобари. Наприклад, питома ентальпія перегрітої пари = пл.abcdsп.п0a. Зображення питомих теплоти процесу і ентальпії у вигляді площ вельми наочне, що є перевагою Т – s діаграми у порівнянні з іншими діаграмами. Крім того, питома робота будь-якого оборотного циклу дорівнює l = q1 – q2 і зображається на Т – s диаграмі площею циклу. За допомогою Т – s діаграми легко визначити термічний ККД оборотного циклу.
h – s діаграма водяної пари (діаграма Мольє, 1904 р.). Для практичних розрахунків процесів з водяною парою широке використання знайшла h – s діаграма, на якій питома теплота і ентальпія вимірюються не площами, а лінійними відрізками. У системі координат h – s (рис. 6.3) будують пограничні криві АК і КВ за табличними даними і . Погранична крива рідини АК проходить через початок координат, бо у потрійній точці питома ентропія і ентальпія рідини вважаються рівними нулю. Потім наносять ізобари, які в області насиченої пари є одночасно і ізотермами, і мають вигляд прямих ліній, оскільки на h – s діаграмі кутовий коефіцієнт ізобари = сonst , тобто в області вологої пари є постійною величиною.
|
|
|
Рис. 6.3 h – s діаграма водяної пари |
Таким чином для процесу p = const в області вологої насиченої пари h = sTs + const, тобто рівняння ізобари (ізотерми) є рівнянням прямої лінії з кутовим коефіцієнтом, який дорівнює температурі Ts. Оскільки при підвищенні тиску температура насичення пари збільшується, кут нахилу ізобар в області насиченої пари також збільшується, отже ізобари між пограничними кривими стають розбіжними прямими. Чим більше тиск, тим вище лежить ізобара. Усі ізобари починаються на пограничній кривій рідини (точки b, b', ... .) і перехрещуються з пограничною кривою пари в точках с, с', .... Криві сталого степеня сухості вологої пари (x = const) будують за допомогою рівняння
Для побудови кривих р = const, Т = const, v = const в області перегрітої пари використовують відповідні значення h і s, які беруть з таблиць перегрітої пари. В області перегрітої пари ізобари і ізотерми розходяться. Ізохори v = const, як і в Т – s діаграмі, проходять дещо крутіше ізобар, розміщених поруч (на рис. 6.3 штрихові лінії). Ізобари і ізохори у цій області мають вигляд слабо увігнутих логарифмічних кривих. Ізотерми є випуклими кривими, які піднімаються зліва уверх направо. Чим більше температура, тим вище розміщується ізотерма. Віддаляючись від пограничної кривої пари х = 1 ізотерма асимптотично наближається до горизонталі h = const. Останнє пояснюється тим, що зі зниженням тиску перегріта пара за своїми властивостями наближається до ідеального газу, ентальпія якого залежить тільки від температури, тобто лінія t = const одночасно є і лінією h = const. Для практичного використання у великому масштабі будують лише робочу частину діаграми (на рис. 6.3 ця частина обмежена штрихпунктирною лінією).
Діаграма h – s у порівнянні з Т – s діаграмою має ряд суттєвих переваг: для будь-якої точки на h – s діаграмі можна знайти значення параметрів пари р, v, t, h, s, x, а технічна робота і кількість теплоти зображаються відрізками ординат. Це спричинило широке використання h – s діаграми при розв’язанні різних технічних задач (витікання та дроселювання пари, розрахунку парових турбін і т. д.).
Аналіз основних термодинамічних процесів з водяною парою. До задач аналізу термодинамічних процесів з водяною парою входять ті ж самі питання, що і з ідеальним газом: установлення закономірностей зміни термічних (p, v і T) і калоричних (u, h і s) параметрів стану, визначення роботи і теплоти процесу.
Пара, як реальний газ, не підлягає простим закономірностям ідеального газу, тому розрахунки процесів з водяною парою виконують з застосуванням таблиць (більш точно) або графічно за допомогою діаграм. У першому випадку усі необхідні вихідні дані і кінцеві параметри беруть з таблиць насиченої і перегрітої пари. У другому випадку використовується h – s діаграма. При цьому за заданими параметрами установлюється початковий стан пари, потім проводиться лінія процесу і визначаються параметри його кінцевого стану. Після цього обчислюють зміну питомої внутрішньої енергії u, питомі роботу l і теплоту q процесу. Графічний метод відрізняється простотою і наочністю.
Розглянемо деякі особливості основних термодинамічних процесів з водяною парою. Для графічного зображення на діаграмах виберемо початковий стан в області вологої насиченої пари і кінцевий стан в області перегрітої пари.
Ізохорний процес (v = const). З p – v діаграми (див. рис. 6.4, а) витікає, якщо початоковий питомий об’єм вологої пари v1 > vкр, то при v = const вологу пару можна перевести у суху насичену і перегріту (пряма 1-2). Якщо v1 < vкр, то підведення теплоти до вологої пари (пряма 1'-2') супроводжується не підсушенням, а зволоженням (ступінь сухості вологої пари зменшується). У цьому процесі питома робота розширення l = 0, тому у відповідності до першого закону термодинаміки питома теплота
.
Оскільки значення питомої внутрішньої енергії у довідкових таблицях не наводяться і їх неможливо отримати безпосередньо з h – s діаграми (рис. 6.4, в), використавши формулу h = u + pv, запишемо
або
|
а б в Рис. 6.4. Ізохорна зміна стану пари |
Ізохорний процес на Т – s діаграмі (див. рис. 6.4, б) зображається кривою лінією, яка в області вологої пари спрямована випуклістю уверх, а в області перегрітої пари – випуклістю униз. На h – s діаграмі ізохора в області вологої пари має вигляд кривої, близької до похилої прямої, а в області перегрітої пари – кривої з випуклістю униз. При чому на цих діаграмах ізохори йдуть крутіше ізобар. На Т – s діаграмі ізохори, які перехрещують пограничну криву пари, не можуть перехрещувати пограничну криву рідини, оскільки завжди питомий об’єм рідини (х = 0) менший за питомий об’єм сухої насиченої пари (х = 1). На Т – s діаграмі дорівнює площі 12s2s1.
Ізобарний процес (р = const). На р – v діаграмі (рис. 6.5, а) ізобара зображається горизонтальною прямою 1 – 2. В області вологої пари ізобара одночасно є і ізотермою. При підведенні теплоти волога пара переходить у суху насичену, а потім у перегріту. На Т – s діаграмі (рис. 6.5, б) в області вологої насиченої пари ізобара також є прямою горизонтальною лінією, а в області перегрітої – кривою з випуклістю униз , яка спрямована уверх. На h – s діаграмі (рис. 6.5, в) ізобара в області вологої пари має вигляд похилої прямої, а в області перегрітої – кривої з випуклістю униз.
|
а б в Рис. 6.5. Ізобарна зміна стану пари |
Питома теплота процесу з першого закону термодинаміки
На Т – s діаграмі дорівнює площі 12s2s1, а на h – s діаграмі – різниці ординат точок 2 і 1.
Питома робота процесу
.
В р – v діаграмі робота розширення дорівнює площі прямокутника 12v2v1 під ізобарою.
Зміна питомої внутрішньої енергії пари
Для ізобарного процесу, який протікає в області вологої пари, маємо
і .
Звідки находимо
Нехтуючи питомим об’ємом (v1 >> і v2 >> ), дістаємо ступінь сухості у точці 2:
Ізотермічний процес (Т = const). На р – v діаграмі (рис.6.6, а) ізотерма в області вологої пари зображається відрізком горизонтальної прямої, яка одночасно є ізобарою. В області перегрітої пари вона переходить у гіперболу, більш пологу, ніж рівнобічна гіпербола (ізотерма ідеального газу). При цьому тиск пари зменшується. На Т – s діаграмі (рис. 6.6, б) ізотермічний процес зображається відрізком горизонтальної прямої. На h – s діаграмі (рис. 6.6, в) ізотерма в області вологої пари має виглад похилої прямої, в області перегрітої пари – кривої, яка спрямована випуклістю уверх. По мірі віддалення від пограничної кривої пари ця крива асимптотично наближається до горизонталі.
Питома теплота у ізотермічному процесі визначається за формулою
і на Т – s діаграмі зображається площею 12s2s1.
На відміну від ідеального газу у водяній пари в ізотермічному процесі відбувається зміна питомої внутрішньої енергії
.
Питома робота розширення в ізотермічному процесі визначається на основі першого закону термодинаміки
|
а б в Рис. 6.6. Ізотермічна зміна стану пари |
Адіабатний процес (s = const). Рівноважний адіабатний процес протікає при сталій ентропії, тому на Т – s і h – s діаграмах (рис. 6.7, б і в) адіабати зображаються відрізком вертикальної прямої. При адіабатному розширенні волога пара або зволожується, або підсушується в залежності від того, ближче до якої пограничної кривої (рідини або пари) розміщена початкова точка. На р – v діаграмі (рис. 6.7, а) адіабатний процес має вигляд кривої, яка нагадує гіперболу. Ця крива може бути приблизно описана емпіричним рівнянням, подібним до рівняння адіабати ідеального газу
|
|
|
а б в Рис. 6.7. Адіабатна зміна стану пари |
В цьому рівнянні показник степеня k не дорівнює відношенню cp/cv , як для ідеального газу, а є емпіричною величиною. В області вологої насиченої пари показник степеня k визначається за формулою k = 1,035 + 0,1х, де значення ступеня сухості х при розширенні пари беруть у початковому, а при стисненні – у кінцевому стані процесу.
Для адіабати, яка починається або закінчується на пограничній кривій пари (х = 1), k = 1,135. Для адіабати, яка повністю розміщена в області перегрітої пари, k = 1,3. Тому на р – v діаграмі на пограничній кривій пари адіабата має перегин (точка 1"). Але при точних розрахунках цими значеннями k користуватися не можна. Точний розрахунок адіабатних процесів пари здійснюється за допомогою таблиць. У адіабатному процесі qs = 0, тому питома робота розширення здійснюється за рахунок зміни питомої внутрішньої енергії пари
Ця робота для перегрітої пари може бути обчислена за формулою питомої термодинамічної роботи ідеального газу у адіабатному процесі, яка при k = 1,3 прийме вид,
.
Вологе повітря та його характеристики. В техніці часто використовуються суміші газів з парами, які при певних умовах легко конденсуються. Найбільш характерним прикладом парогазових сумішей є атмосферне повітря, в якому завжди знаходяться водяні пари. Суміш сухого повітря з водяною парою називається вологим повітрям. Знання властивостей вологого повітря має особливо велике значення для проектування і експлуатації сушильних та вентиляційно-зволожуючих установок. В атмосферному повітрі, як правило, пар знаходиться під невеликим парціальним тиском і в перегрітому стані. Тому вологе повітря можна розглядати як суміш ідеальних газів, за виключенням того, що при певних умовах в ній відбувається конденсація водяної пари (фазове перетворення).
Згідно до закону Дальтона тиск вологого повітря, яке дорівнює барометричному рбар, являє собою суму парціальних тисків сухого повітря рс.п і водяної пари рп, тобто
рбар = рс.п + рп. (6.29)
Стан перегрітої пари в суміші характеризується на p-v-діаграмі точкою А (рис. 6.8).
Суміш сухого повітря і перегрітої пари називається ненасиченим вологим повітрям. При заданих температурі і тиску вологого повітря завжди існує такий стан, коли в ньому міститься максимально можлива у цих умовах кількість водяної пари. Цьому стану на р-v діаграмі буде відповідати точка В, де водяна пара є сухою насиченою. При цьому густина водяної пари буде максимальною і дорівнювати густині сухої насиченої пари н при заданій температурі вологого повітря t,тобто . Суміш сухого повітря і сухої насиченої водяної пари називається насиченим вологим повітрям. Таким чином, точка В на рис. 6.8 відповідає максимально можливій кількості водяної пари у вологому повітрі при даній температурі і є границею насичення.
Процес насичення може відбуватися і при незмінній кількості водяної пари, якщо охолоджувати насичене вологе повітря при постійному парціальному тиску пари рп (процес А-С). В точці С пара стає насиченою, і при подальшому незначному зниженні її температури утворюється туман (відбувається випадіння роси). Температура, до якої необхідно охолоджувати вологе повітря при постійному тиску, щоб воно стало насиченим, називається температурою точки роси . Отже, температура точки роси в будь-якому стані вологого повітря дорівнює температурі насичення, що відповідає даному парціальному тиску пари, і визначається за таблицями для насиченої пари.
Щоб охарактеризувати пароповітряну суміш, потрібно знати її склад. Про склад вологого повітря судять за його вологістю і вологовмістом. Розрізняють абсолютну і відносну вологість. Абсолютною вологістю повітря, або масовою концентрацією водяної пари у повітрі, називається кількість водяної пари, що приходиться на 1м3 вологого повітря, тобто
(6.30)
Оскільки об’єм вологого повітря дорівнює об’єму пари , абсолютна вологість повітря чисельно дорівнює густині водяної пари , що вміщується в ньому.
Відношення абсолютної вологості до максимально можливої абсолютної вологості = , що відповідає температурі насичення , характеризує ступінь насичення і називається відносною вологістю повітря,тобто
. (6.31)
Відносна вологість може змінюватися від = 0 (сухе повітря) до = 100 % (вологе насичене повітря), тобто 0 1, і характеризує ступінь насичення повітря водяною парою по відношенню до стану повного насичення при тій же температурі. З урахуванням того, що пара, яка знаходиться у повітрі, розглядається як ідеальний газ, відношення густин на ізотермі АВ можна замінити відношенням тисків:
(6.32)
Парціальний тиск в стані насичення знаходять з таблиць для насиченої пари за температурою. Парціальний тиск рп також визначають за цими таблицями, знаючи температуру точки роси . Оскільки в процесах з вологим повітрям (підігрів, охолодження) кількість сухого повітря не змінюється, доцільно всі питомі величини відносити до 1 кг сухого повітря. Маса водяної пари, що приходиться на 1 кг сухого повітря, називається вологовмістом:
. (6.33)
При введеному припущені про ідеальність водяної пари та сухого повітря можна записати:
рпVп = mпRпTп; рс.пVс..п = mс.пRс.пTс.п.
Вважаючи, що Vп= Vс..п і Tп = Tс.п, одержимо
d = mп/mс.п= Rс.прп./(Rпрс.п) = 287рп/(462рс.п) = 0,622 рп/рс.п. (6.34)
Якщо врахувати, що рбар = рс.п+ рп і рп = , то
. (6.35)
Значення d, виражені в кілограмах пари на 1 кг сухого повітря, малі; тому в практичних розрахунках воловміст d виражають в грамах вологи на кілограм сухого повітря, тобто
(6.36)
Густину вологого повітря можна визначити як суму густин пари і сухого повітря при їх парціальних тисках:
.
Враховуючи, що , отримаємо
=(1+) (6.37)
Ентальпію вологого повітря відносять до 1 кг сухого повітря або до (1+d) кг вологого повітря і визначають як суму ентальпій 1 кг сухого повітря і d кг водяної пари:
. (6.38)
При температурах і тисках, що застосовуються в сушильних установках, приблизно можна вважати питому теплоємність сухого повітря = 1 кДж/(кг К), а питому ентальпію водяної перегрітої пари кДж/кг. При малих тисках питома теплота пароутворення r = 2500 кДж/кг, питома теплоємність перегрітої пари = 1,9 кДж/кг і вираз (6.38) приймає вигляд
H = t+ (2500+1,9t) d. (6.39)
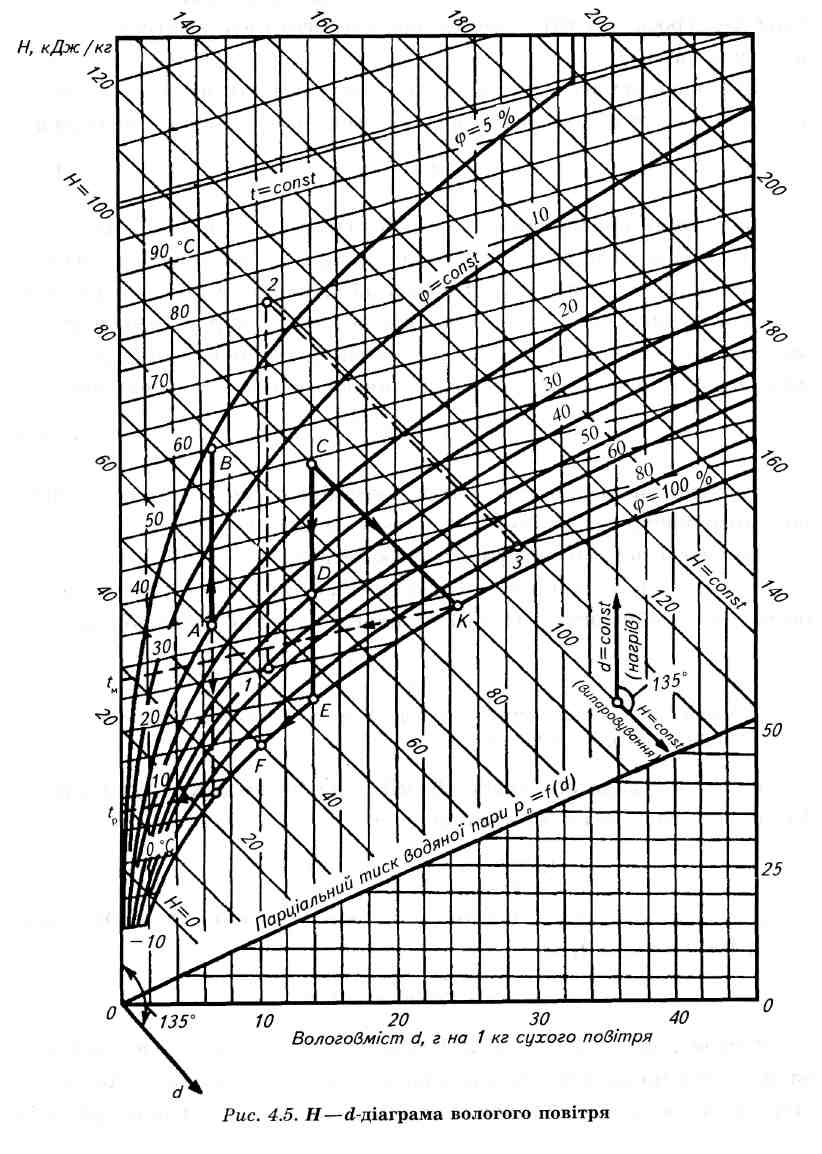
Діаграма H – d вологого повітря. Визначення параметрів вологого повітря, дослідження процесів з ним значно спрощується і стають наочними, якщо використовувати Н – d-діаграму вологого повітря, запропоновану в 1918 р. проф. Л. К. Рамзіним (рис. 6.9).
Рис. 6.9. H – d діаграма вологого повітря
Для зручності (збільшення площі діаграми) вісь абсцис спрямована під кутом 135 до осі ординат. Тому лінії Н =const виявляються нахиленими під кутом 45 до горизонту. Щоб скоротити розміри діаграми, значення вологовмісту d з вісі абсцис знесені на горизонтальну умовну вісь О - О. На діаграму наносять сітку ізотерм, побудовану за формулою (6.39). Ці ізотерми являють собою прямі лінії, кутовий коефіцієнт яких визначається рівнянням = 2500+1,9t. На кожній ізотермі знаходять точки з однаковими значеннями відносної вологості повітря . З’єднавши їх, отримують сітку кривих = const. Крива = 100 % зображує стан волого насиченого повітря і є граничною. Вона поділяє область ненасиченого вологого повітря (зверху) і область перенасиченого повітря (знизу), в якому волога частково знаходиться в крапельному (або твердому – сніг, лід) стані.
Н – d діаграму будують звичайно для тиску волого повітря рбар 99 кПа, що відповідає середньому річному барометричному тиску. Лінії = const піднімаються до ізотерми 99,4С (температура насичення при р = 99 кПа), після чого стають майже вертикальними, бо при > відносна вологість повітря залежить тільки від вологовмісту d. Дійсно, при > парціальний тиск пари рп = рбар.Тоді
d = 0, 622 рбар/ ( рбар+ рбар) = 0,662/ (1-),
або
= d/ (d+0,662).
Отже, при d = const і = const. В нижній частині діаграми по формулі (6.34) побудована лінія парціального тиску рп = (d).
Стан вологого повітря (точка А) можна визначити за будь-якими двома параметрам ( і t або рп і t), після чого легко знайти Н і d. Для цього ж стану можна встановити і температуру точки роси, для чого слід з точки А провести вертикаль (d = const) до перетину з лінією = 100 % . Тоді ізотерма, яка проходить через точку перетину, буде відповідати температурі точки роси tр. Початковими для визначення параметрів стану вологого повітря по Н – d діаграмі служать показники сухого і мокрого термометрів, які в комплекті утворюють прилад, який називається психрометром.
Ртутна кулька мокрого термометра обернена тканиною, змоченою водою. При обдуванні цього термометра повітрям відбувається випаровувуння води з поверхні вологої тканини, внаслідок чого її температура буде знижуватися до тих пір, доки не встановиться рівновага за рахунок припливу теплоти з навколишніх шарів повітря. Встановлена температура буде більше температури точки роси, але менша температури навколишнього повітря (сухого термометра). Цю встановлену температуру води називають температурою мокрого термометра (tм). Різниця між температурами сухого (tс) і мокрого (tм) термометрів є мірою кількості водяної пари в суміші. Якщо повітря насичене водяною парою, то tс = tм. Залежність вологовмісту повітря d від температур tс і tм встановлюється експерементально і складаються спеціальні психрометричні таблиці або діаграми.
Якщо припустити, що температура вологої поверхні (випаровуваної вологи) дорівнює 0 С, то випаровування буде відбууватися тільки за рахунок теплоти вологого повітря, температура якого знижується, а вологовміст збільшується. Проте ентальпія вологого повітря залишиться незмінною (Н = const), так як частина її, затрачена на випаровування вологи, повертається назад до вологого повітря, з випареною вологою, тобто даний процес протікає без зовнішнього теплообміну. В цьому сенсі процес насичення повітря можна вважати адіабатним. Тому температура, яку набуває повітря в кінці процесу насичення ( = 100 %), називається температурою адіабатного насичення tа. При вказаних припущеннях ця температура дуже близька до температури мокрого термометра.
Отже, на Н – d діаграмі процес адіабатного зволоження буде протікати по лінії Н = const ( процес С-К на рис. 6.9). Межою адіабатного зволоження повітря буде температура, яка співпадає з його повним насиченням ( = 100 %).
Якщо випаровування проходить з поверхні рідини, температура якої tр > 0 С, то цей процес пробігає не по лінії Н = const, а по лінії tм = const, яка являється геометричним місцем точок з однаковою температурою мокрого термометра. Лінії tм = const проходять більш полого за лінії Н = const, методика їх побудови викладається в спеціальних посібниках.
Показання психрометра дають змогу по Н – d діаграмі встановити відносну вологість та інші характеристики вологого повітря. Для цього необхідно за показаннями мокрого термометра знайти ізотерму tм, яка на перехрещенні з кривою = 100 % дасть точку К. Провівши з цієї точки пряму Н = const до перетину з ізотермою tс, отримаємо шукану точку, яка відповідає стану вологого повітря, яка і визначає всі параметри вологого повітря (, d, Н, рп) в приміщені.
Основні процеси з вологим повітрям ( нагрівання, охолодження, адіабатне зволоження ) та їх зображення на H-d діаграмі. Н – d діаграма широко застосовується при розрахунках процесів, що забезпечують сушку різних матеріалів і виробів, кондиціювання повітря, вентиляцію і опалення.
Процес підігріву повітря на Н – d діаграмі зображується вертикальною лінією d = const, оскільки кількість водяної пари в повітрі при його підігріві не змінюється (лінія АВ на рис. 6.9). Стан вологого повітря після підігріву (точка В) можна встановити по температурі повітря за підігрівачем. Процес охолодження повітря протікає також без змін його вологовмісту, якщо при охолодженні повітря не стає насиченим (лінія СD на рис.6.9). Якщо охолодження повітря відбувається до стану повного насичення з = 100 % (лінія СЕ), то перетин лінії d = const з лінією = 100 % (точка Е) встановлює температуру точки роси. Подальше охолодження повітря нижче точки роси (лінія ЕF) приводить до конденсації частини водяної пари, тобто до осушення вологого повітря. Кількість вологи, що конденсується, визначається різницею вологовмісту в точках Е і F.
Конвективне сушіння. Процес видалення вологи з матеріалу шляхом підведення до нього теплоти називається сушкою. Здійснюється він в сушильних установках, з яких найбільше розповсюдження отримали конвективні сушарки, де теплота до матеріалу від газоподібного теплоносія передається конвекцією. В якості теплоносія використовуються звичайно попередньо нагріте повітря. Основними елементами конвективної сушарки (рис. 6.10, а) є вентилятор 1 для подавання повітря, калорифер 2 – пристрій для нагрівання повітря і сушильна камера 3, в якій відбувається процес випаровування вологи з матеріалу або виробу.
Розглянемо процеси, що протікають в так званій теоретичній сушарці, що не має втрат теплоти до зовнішнього середовища і на нагрівання матеріалу. З попереднього відомо, що процес підігріву повітря у калорифері протікає при d = const і зображається вертикальною прямою 1-2 (6.10, б). Різниця ентальпій кінцевої та початкової точок Н2 - Н1 відповідає витратам теплоти на підігрів (1+d) кг вологого повітря. Після калорифера вологе повітря поступає до сушильної камери, де воно використовується для випаровування вологи з матеріалу і при цьому зволожується. Процес адіабатного зволоження повітря в сушильній камері теоретично протікає по лінії Н = const (лінія 2-3). При цьому різниця вологовмісту кінцевої та початкової точок d3 - d2 визначає кількість вологи, випареної 1 кг сухого повітря. Маса сухого повітря (в кілограмах) для випаровування 1 кг вологи становить
mc.п = 1000/(d3 - d2), (6.40)
а витрата теплоти (в кілоджоулях на кілограм випареної вологи) визначається виразом
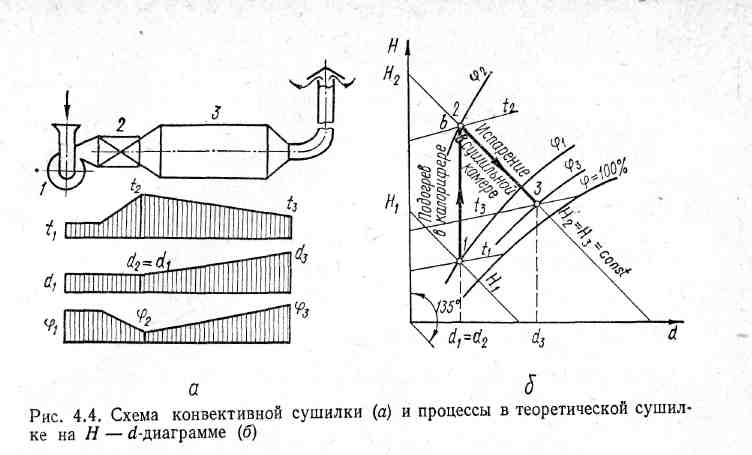
q = mс.п (Н2 - Н1). (6.41)
Рис. 6.10. Схема конвективної сушарки (а) і процеси в теоретичній сушарці на Н – d діаграмі (б)
Термодинамічні властивості реальних газів та процеси з ними